Abstract
Advances in high-throughput technologies allow for measurements of many types of omics data, yet the meaningful integration of several different data types remains a significant challenge. Another important and difficult problem is the discovery of molecular disease subtypes characterized by relevant clinical differences, such as survival. Here we present a novel approach, called perturbation clustering for data integration and disease subtyping (PINS), which is able to address both challenges. The framework has been validated on thousands of cancer samples, using gene expression, DNA methylation, noncoding microRNA, and copy number variation data available from the Gene Expression Omnibus, the Broad Institute, The Cancer Genome Atlas (TCGA), and the European Genome-Phenome Archive. This simultaneous subtyping approach accurately identifies known cancer subtypes and novel subgroups of patients with significantly different survival profiles. The results were obtained from genome-scale molecular data without any other type of prior knowledge. The approach is sufficiently general to replace existing unsupervised clustering approaches outside the scope of bio-medical research, with the additional ability to integrate multiple types of data.
Once heralded as the holy grail, the capability of obtaining a comprehensive list of genes, proteins, or metabolites that are different between disease and normal phenotypes is routine today. And yet, the holy grail of high-throughput has not delivered so far. Even though such high-throughput comparisons have become relatively easy to perform at a single level, integrating data of various types in a meaningful way has become the new challenge of our time (Verhaak et al. 2010; The Cancer Genome Atlas Research Network 2011, 2012a,b,c, 2013, 2014, 2015; Yang et al. 2013; Davis et al. 2014; Hoadley et al. 2014; Robinson et al. 2015).
Concurrently, we understand that many diseases, such as cancer, evolve through the interplay between the disease itself and the host immune system (Coussens and Werb 2002; Yu et al. 2007). The treatment options, as well as the ultimate treatment success, are highly dependent on the specific tumor subtype for any given stage (Choi et al. 2014; Lehmann and Pietenpol 2014; Linnekamp et al. 2015). The challenge is to discover the molecular subtypes of disease and subgroups of patients.
Cluster analysis has been a basic tool for subtype discovery using gene expression data. Agglomerative hierarchical clustering (HC) is a frequently used approach for clustering genes or samples that show similar expression patterns (Eisen et al. 1998; Alizadeh et al. 2000; Perou et al. 2000). Other approaches, such as neural network–based methods (Kohonen 1990; Golub et al. 1999; Tamayo et al. 1999; Herrero et al. 2001; Luo et al. 2004), model-based approaches (Ghosh and Chinnaiyan 2002; McLachlan et al. 2002; Jiang et al. 2004), matrix factorization (Brunet et al. 2004; Gao and Church 2005), large-margin methods (Li et al. 2009; Xu et al. 2004; Zhang et al. 2009), and graph-theoretical approaches (Ben-Dor et al. 1999; Hartuv and Shamir 2000; Sharan and Shamir 2000), have also been used. Arguably the state-of-the-art approach in this area is consensus clustering (CC) (Monti et al. 2003; Wilkerson and Hayes 2010). CC develops a general, model-independent resampling-based methodology of class discovery and cluster validation (Ben-Hur et al. 2001; Dudoit and Fridlyand 2002; Tseng and Wong 2005). Unfortunately, many approaches mentioned above are not able to combine multiple data types, and many attempts for subtype discovery based solely on gene expression have been undertaken but yielded only modest success so far (very few gene expression tests are FDA approved).
The goal of an integrative analysis is to identify subgroups of samples that are similar not only at one level (e.g., mRNA) but from a holistic perspective that can take into consideration phenomena at various other levels (DNA methylation, miRNA, etc.). One strategy is to analyze each data type independently before combining them with the help of experts in the field (Verhaak et al. 2010; The Cancer Genome Atlas Research Network 2012a,b,c). However, this might lead to discordant results that are hard to interpret. Another approach, integrative phenotyping framework (iPF) (Kim et al. 2015), integrates multiple data types by concatenating all measurements to a single matrix and then clusters the patients using correlation distance and partitioning around medoids (PAM) (Kaufman and Rousseeuw 1987). This concatenation-based integration, however, further aggravates the “curse of dimensionality” (Bellman 1957). In turn, this leads to the use of gene filtering, which can introduce bias. Another challenge of this approach is identifying the best way to concatenate multiple data types that come from different platforms (microarray, sequencing, etc.) and different scales (Ritchie et al. 2015).
Machine learning approaches, such as Bayesian CC (Lock and Dunson 2013), MDI (Kirk et al. 2012), iCluster+ (Mo et al. 2013), and iCluster (Shen et al. 2012, 2009), address the challenge of integration by using joint statistical modeling. They model the distribution of each data type and then maximize the likelihood of the observed data. The recent iCluster+ makes an extra effort to reduce the parameter space by imposing sparse models, such as lasso (Tibshirani 1996). Though powerful, these approaches are limited by their strong assumptions about the data and by the gene selection step used to reduce the computational complexity. Similarity network fusion (SNF) (Wang et al. 2014) was the first approach that allows for discovery of disease subtypes through integration of several types of high-throughput data on a genomic scale. SNF creates a fused network of patients using a metric fusion technique (Wang et al. 2012) and then partitions the data using spectral clustering (Von Luxburg 2007). SNF appears to be the state of the art in this area and has proven to be very powerful (Wang et al. 2014). However, the unstable nature of kernel-based clustering makes the algorithm sensitive to small changes in molecular measurements or in its parameter settings.
Here we propose a radically different integrative approach, perturbation clustering for data integration and disease subtyping (PINS), that addresses both challenges above: subtype discovery, as well as integration of multiple data types. The algorithm is built upon the resilience of patient connectivity and cluster ensembles (Strehl and Ghosh 2003) to ensure robustness against noise and bias. In an extensive analysis, we compare PINS with three subtyping algorithms that are selected to represent each of the main existing subtyping strategies: CC (Monti et al. 2003), SNF (Wang et al. 2014), and iCluster+ (Mo et al. 2013). CC is a resampling-based approach that has been widely used for subtype discovery (Verhaak et al. 2010; The Cancer Genome Atlas Research Network 2011, 2012a,b,c, 2013, 2014, 2015; Yang et al. 2013; Davis et al. 2014; Hoadley et al. 2014). SNF is a graph-theoretical approach purported to allow discovery of disease subtypes based on either a single data type or through integration of several data types. The third method, iCluster+, is a model-based approach and is the enhanced version iCluster (Shen et al. 2009, 2012) and iCluster2 (Shen et al. 2013).
Results
Here, we first present the workflow to construct the optimal connectivity and the results obtained on a single data type. We then describe the two-stage procedure to address the challenge of integrating multiple types of data and the results obtained on cancer diseases by integrating mRNA, miRNA, methylation, and copy number variation (CNV) data. We compare the proposed approach with these state-of-the-art methods on eight gene expression data sets involving a total of 12 tissues types and over 1000 samples. In each of these data sets, we show that PINS is better able to retrieve known subtypes. In order to compare the data integration abilities of these four approaches, we also applied them to eight cancer data sets, involving mRNA, methylation, miRNA, and CNV data. These results also show that PINS is better able to discover subtypes that have significant survival differences compared with existing approaches.
Discovering subtypes based on a single data type
The approach is based on the observation that differences are naturally present between individuals, even in the most homogeneous population. Therefore, we hypothesize that if true subtypes of a disease do exist, they should be stable with respect to small changes in the features that we measure.
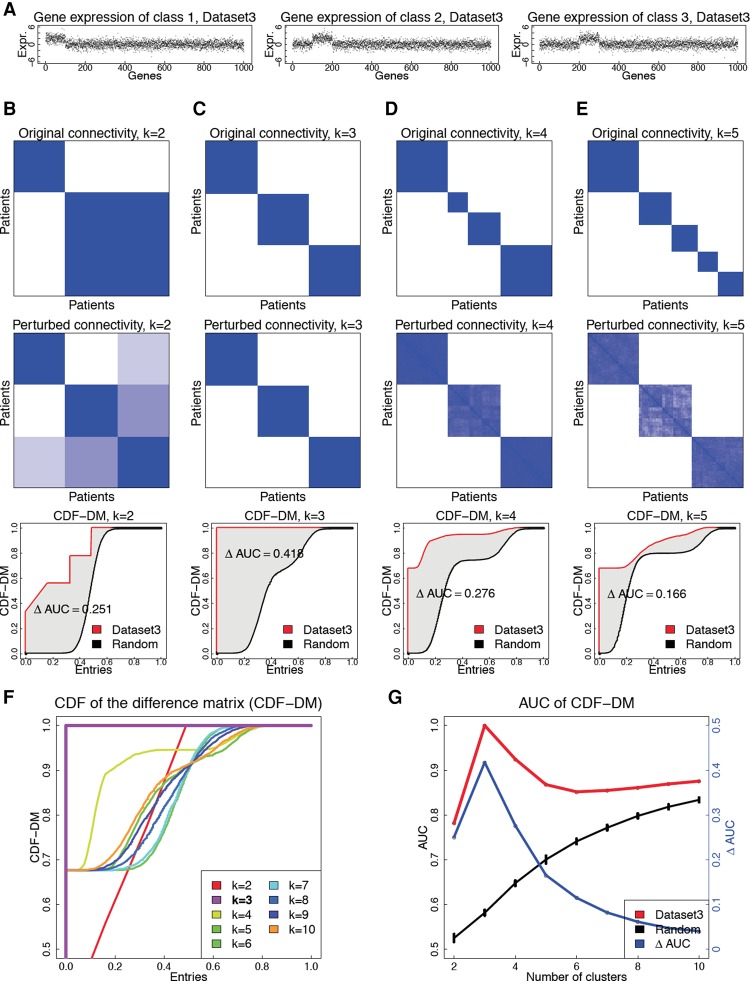
We will describe this approach using an illustrative example shown in Figure 1A. In this simulated data set, we have three distinct classes of patients in which each class has a different set of differentially expressed genes (DEGs). Without any loss of generality, the genes are ordered such that the DEGs in the first class are plotted first (1–100), the DEGs in the second class are plotted second (101–200), etc. In order to find subtypes, we repeatedly perturb the data (by adding Gaussian noise) and partition the samples/patients using any classical clustering algorithm (by default k-means, repeated 200 times). We test a range of potential cluster numbers k (by default k ∈ [2..10]) and identify the partitioning that is least affected by such perturbations. We then assess the cluster stability by comparing the partitionings obtained from the original data to those found with perturbed data for any given k. To quantify these differences, we first construct a binary connectivity matrix, in which the element (i, j) represents the connectivity between patients i and j, and is equal to 1 (blue) if they belong to the same cluster, and 0 (white) otherwise. The upper parts in Figure 1, B through E, show the original connectivity. The middle parts of the same panels show the average connectivity for k ∈ [2..5] over the 200 trials. Next, we calculate the absolute difference between the original and the perturbed connectivity matrices and compute the empirical cumulative distribution functions (CDFs) of the entries of the difference matrix (CDF-DM) (Fig. 1F). The area under this CDF-DM curve (AUC) is used to assess the stability of the clustering. Figure 1G shows the behavior of the AUC (red curve), as the number of clusters varies from two to 10. In the ideal case of perfectly stable clusters, the original and perturbed connectivity matrices are identical, yielding a difference matrix of zeros, a CDF-DM that jumps from zero to one at the origin, and an AUC of one. Based on this criterion, we chose the partitioning with the highest AUC. As shown in Figure 1G, the correct number of subtypes is three, as this corresponds to the largest AUC. The connectivity corresponding to this partitioning is considered the optimal connectivity, which will serve as input for data integration.
Figure 1.
The PINS algorithm applied on a single data type, using the simulated data named Dataset3. (A) The data set consists of 100 patients and three subtypes, each having a different set of 100 differentially expressed genes. The numbers of patients in each subtype are 33, 33, and 34, respectively. (B–E) Original connectivity matrix (top), perturbed connectivity matrix (middle), and CDF of the difference matrix (bottom) for k = 2, 3, 4, and 5, respectively. (F) CDF of the difference matrix (CDF-DM) for k ∈ [2..10]. (G) AUC values for Dataset3 (red curve), random data (black curve), and the difference (blue) between the two curves.
Interestingly, the perturbed connectivity matrices (middle parts of Fig. 1B–E) clearly suggest that there are three distinct classes of patients. This demonstrates that for truly distinct subtypes the true connectivity between patients within each class is recovered when the data are perturbed, no matter how we set the value of k. This resilience of patient connectivity occurs consistently regardless of the clustering algorithm being used (e.g., k-means, HC, or PAM) or the distribution of the data. When there are no truly distinct subtypes, the connectivity is randomly distributed (Supplemental Fig. S2). When the number of true classes changes, the perturbed connectivity always reflects the true structure of the data (Supplemental Figs. S2–S7).
One of the disadvantages of existing clustering approaches, such as k-means, is that they will produce k clusters even for completely random data. The question is whether this artificially forced partitioning will also translate to the proposed approach. In order to demonstrate that this is not the case, we show the CDF-DM curves for completely random data as the black curves in the lower panels of Figure 1, B through E. For each case of k ∈ {2, 4, 5}, the red curve (Dataset3) and the black curve (random data) are close to each other, reflecting that the perturbed connectivity for Dataset3 is almost as unstable as that of data without any structure. In contrast, for the correct number of clusters (k = 3) the red curve is far from the black curve, indicating that the clustering obtained for this number of clusters is very different from random. Figure 1G contrasts the behavior of the AUC for Dataset3 against that of random data for all values of k from two to 10. The red and black curves show the AUC values for Dataset3 and random data, whereas the blue curve displays the difference (ΔAUC) between the two sets of AUC for k ∈ [2..10].
In summary, the number of subtypes present in the data can be identified based on any of the following three equivalent criteria: (1) the best (closest to upper left corner) CDF-DM (see Fig. 1F), (2) the highest AUC value (the peak of the red curve in Fig. 1G), or (3) the maximum difference between the AUC constructed from the data and the AUCs of random data (the peak of the blue curve in Fig. 1G).
Results on gene expression data (single data type)
In order to validate this approach, we tested it first using real data with known subtypes. Also, we first start by using a single data type. In order to do this, we used eight gene expression data sets, selected to include many samples (more than 1000), a large variety of conditions and tissues, and a varied number of known subtypes. To address the particular challenge posed by situations in which a subtype is poorly represented in the data, we include both balanced data sets with a ratio of almost 1:1 between the number of samples in the smallest and the largest subtype, as well as unbalanced sets with ratios between 1:3 and 1:33. We also note that some of these data sets were used in the publication of classical subtyping procedures, such as CC (Monti et al. 2003) and nonnegative matrix factorization (Brunet et al. 2004).
Five of the data sets, GSE10245 (Kuner et al. 2009), GSE19188 (Hou et al. 2010), GSE43580 (Tarca et al. 2013), GSE14924 (Le Dieu et al. 2009), and GSE15061 (Mills et al. 2009), were downloaded from Gene Expression Omnibus, while the other three data sets were downloaded from the Broad Institute: AML2004 (Golub et al. 1999; Brunet et al. 2004), Lung2001 (Bhattacharjee et al. 2001), and Brain2002 (Pomeroy et al. 2002). See the Methods section and Supplemental Table S1 for more details of these eight data sets.
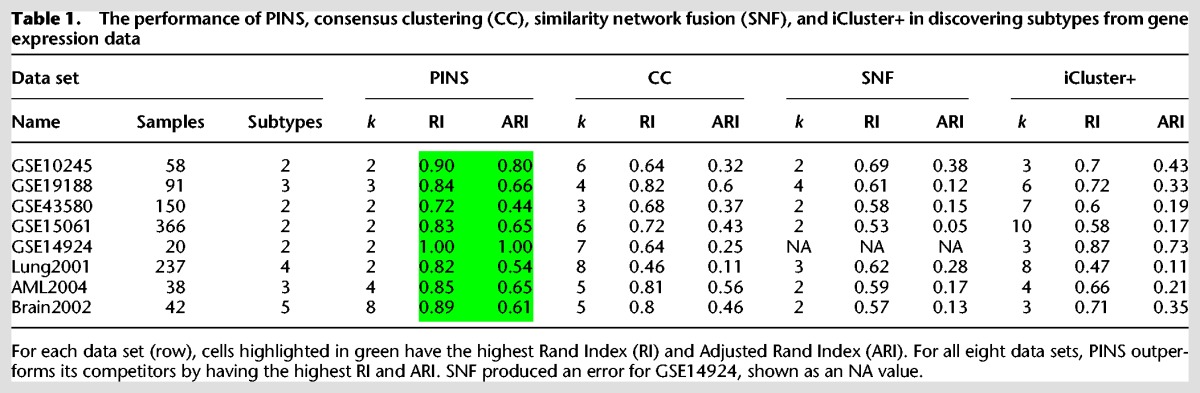
Since the true disease subtypes are known in these data sets, we use the Rand Index (RI) (Rand 1971) and Adjusted Rand Index (ARI) (Hubert and Arabie 1985) to assess the performance of the resulted subtypes. RI measures the agreement between a given clustering and the ground truth. In short, , where a is the number of pairs that belong to the same true subtype and are clustered together, b is the number of pairs that belong to different true subtypes and are not clustered together, and is the number of possible pairs that can be formed from the N samples. Intuitively, RI is the fraction of pairs that are grouped in the same way (either together or not) in the two partitions compared (e.g., 0.9 means 90% of pairs are grouped in the same way). The ARI is the corrected-for-chance version of the RI. The ARI takes values from −1 to 1, with the ARI expected to be zero for a random subtyping.
Table 1 shows the clustering results of PINS, CC, SNF, and iCluster+ for the eight gene expression data sets. Cells highlighted in green have the highest RI and ARI in their respective rows. For all eight data sets, PINS considerably outperforms existing approaches in identifying the known subtypes of each disease. More specifically, PINS yields the highest RI and ARI values for every single data set tested.
Table 1.
The performance of PINS, consensus clustering (CC), similarity network fusion (SNF), and iCluster+ in discovering subtypes from gene expression data
To assess the stability of the clustering algorithms, we also analyzed the gene expression data sets using different parameters for PINS, SNF, and iCluster+. We demonstrate that PINS is robust to the perturbation magnitude, while SNF and iCluster+ are very sensitive to their parameters (Supplemental Tables S3–S5). In addition, PINS is also the most reliable when the signal to noise ratio diminishes (Supplemental Fig. S8; Supplemental Table S2). Time complexity for each of the subtyping methods is reported in Supplemental Table S14 and Supplemental Figure S17.
Integrating multiple types of data
The challenge of integrating multiple types of data is addressed in two stages. In the first stage, we identify subgroups of patients that are strongly connected across heterogeneous data types. In the second stage, we analyze each subgroup to decide whether or not it may warrant further splitting.
Let us consider T data types from N patients. In the first stage, PINS works with each data type to build T connectivity matrices, one for each data type. A connectivity matrix can be represented as a graph, with patients as nodes and with connectivity between patients as edges. Our goal is to identify subgraphs that are strongly connected across all data types. We merge the T connectivity matrices into a combined similarity matrix that represents the overall connectivity between patients. This matrix is used as input for similarity-based clustering algorithms, such as HC, PAM (Kaufman and Rousseeuw 1987), and Dynamic Tree Cut (Langfelder et al. 2008). By default, we use all three algorithms to partition the patients and then choose the partitioning that agrees the most with the partitionings of individual data types (Strehl and Ghosh 2003). This completes stage I. Since a very strong signal may dominate the clustering in stage I, we next consider each group one at a time and decide whether to split it further. A group may be split again if the data types are separable according to gap statistics (Tibshirani et al. 2001), and the stage I clustering is extremely unbalanced with low normalized entropy (for details, see Methods) (Cover and Thomas 2012)
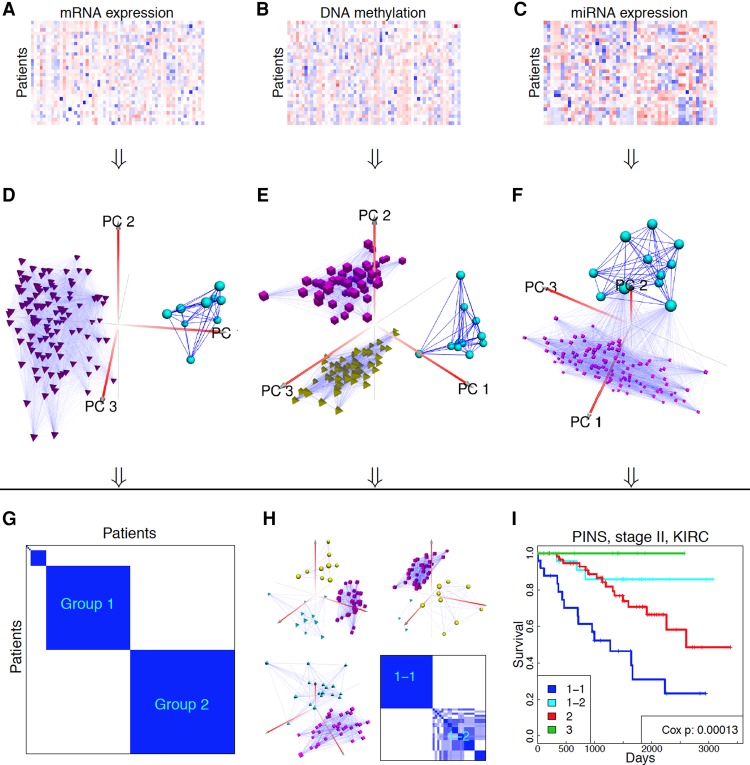
We illustrate the two stages of the procedure on the kidney renal clear cell carcinoma (KIRC) data set from TCGA (Fig. 2). The input consists of sample-matched mRNA, methylation, and miRNA measurements (Fig. 2A–C). We first build the optimal connectivity between patients for each data type (Fig. 2D–F). We then construct the similarity between patients that is consistent across all data types (Fig. 2G). Partitioning this similarity matrix results in three groups of patients. Group 1 corresponds to the second largest blue square, while group 2 corresponds to the largest blue square. Group 3 includes all other patients.
Figure 2.
Data integration and disease subtyping illustrated on the kidney renal clear cell carcinoma (KIRC) data set. (A–C) The input consists of three matrices that have the same set of patients but different sets of measurements. (D–F) The optimal connectivity between the samples for each data type. (G) The similarity between patients that are consistent across all data types. Partitioning this matrix results in three groups of patients. (H) Group 1 is further split into two subgroups in stage II. (I) Kaplan-Meier survival curves of four subtypes after stage II splitting of group 1. The survival analysis indicates that the four groups discovered after stage II have significantly different survival profiles (Cox P-value 0.00013).
In stage II, we check each discovered group independently to decide if it can be further divided. As a result, only group 1 is further split into two subgroups (Fig. 2H). The first PCA plot shows the connectivity between patients in group 1 using mRNA data, while the second and third PCA plots show that for methylation and miRNA data, respectively. The connectivity reflects that this group 1 consists of two subgroups of patients: subgroup “1-1” in which patients are strongly connected to each other's across all the three data types, and subgroup “1-2” in which patients are loosely connected to each other's. Figure 2I displays the four groups discovered by PINS. These groups have very different survival profiles.
Subtyping by integrating mRNA, miRNA, and methylation data
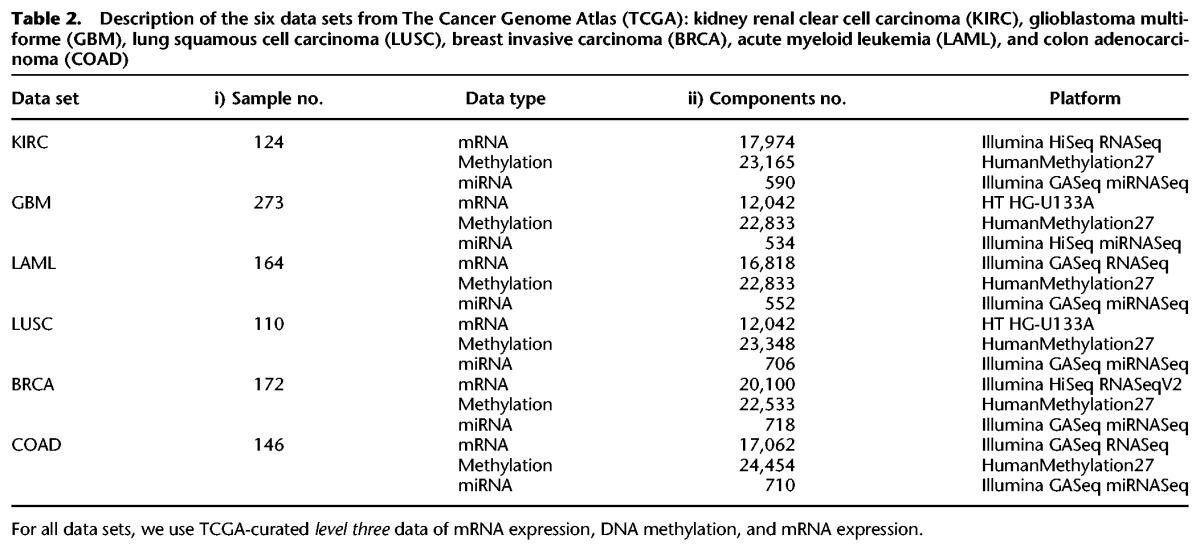
We analyzed six different cancers which have curated level-three data, available at the TCGA website (https://cancergenome.nih.gov): KIRC, glioblastoma multiforme (GBM), acute myeloid leukemia (LAML), lung squamous cell carcinoma (LUSC), breast invasive carcinoma (BRCA), and colon adenocarcinoma (COAD). We used mRNA expression, DNA methylation, and miRNA expression data for each of the six cancers. TCGA contains multiple platform for each data type. We chose the platforms giving the largest set of common tumor samples across the three data types while still using a single platform for each data type. Table 2 shows more details of the six TCGA cancer data sets.
Table 2.
Description of the six data sets from The Cancer Genome Atlas (TCGA): kidney renal clear cell carcinoma (KIRC), glioblastoma multiforme (GBM), lung squamous cell carcinoma (LUSC), breast invasive carcinoma (BRCA), acute myeloid leukemia (LAML), and colon adenocarcinoma (COAD)
For each cancer, we first analyze each data type independently and report the resulting subtypes. We then analyze the three data types together. PINS and SNF take the three matrices as input without any further processing. Since CC and maxSilhouette (Rousseeuw 1987) are not designed to integrate multiple data types, we concatenate the three data types for the integrative analysis. For iCluster+, we used the 2000 features with largest median absolute deviation for each data type. For some cancers, iCluster+ is unable to analyze the microRNA data.
We note that our approach focuses on maximizing the stability of the subtypes, based on cluster ensemble and connectivity similarity, instead of maximizing the Euclidean distance between discovered subtypes. In order to compare the proposed approach with the classical approach, we also include a clustering method that maximizes the silhouette index (Rousseeuw 1987). For this maxSilhouette method, we use k-means as the clustering algorithm and the silhouette index as the objective function to identify the optimal number of clusters.
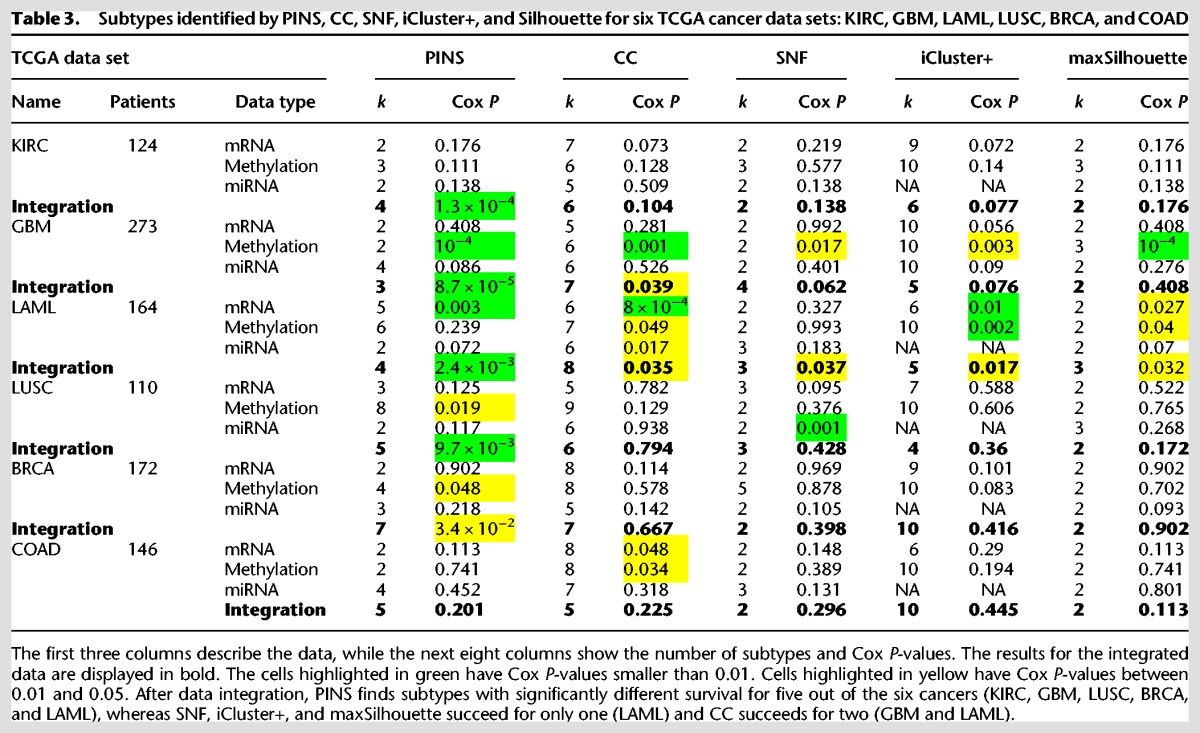
The subtypes identified by the four approaches are analyzed using the Kaplan-Meier survival analysis (Supplemental Fig. S9–S14; Kaplan and Meier 1958), and their statistical significance is assessed using Cox regression (Table 3; Therneau and Grambsch 2000). After data integration, CC finds groups with significant survival differences in two out of the six cancers: GBM (P = 0.039) and LAML (P = 0.035). SNF, iCluster+, and maxSilhouette find subgroups with significantly different survival only for LAML (P = 0.037, P = 0.017, and P = 0.032, respectively). In contrast, PINS identifies groups that have statistically significant survival differences in five out of the six cancers—KIRC (P = 10−4), GBM (P = 8.7 × 10−5), LAML (P = 0.0024), LUSC (P = 0.0097), and BRCA (P = 0.034), showing a clear advantage of PINS over this state-of-the-art method.
Table 3.
Subtypes identified by PINS, CC, SNF, iCluster+, and Silhouette for six TCGA cancer data sets: KIRC, GBM, LAML, LUSC, BRCA, and COAD
We also analyzed the subtypes discovered by the five methods using the concordance index (CI) and silhouette index (Supplemental Tables S6, S7). In terms of silhouette, maxSilhouette outperforms all existing methods in all but one case (23/24). This is expected because maxSilhouette aims to maximize the silhouette values. However, higher silhouette values do not necessarily translate into better clinical correlation, especially for data integration. As shown in Table 3, PINS finds subtypes with significantly different survival for five out of the six cancers, while the maxSilhouette method does so for only one. Similarly, in terms of CI, PINS outperforms maxSilhouette in all of the six cancers (for more discussion about Silhouette index, see Supplemental Figs. S15, S16; Supplemental Section 3.6).
We also analyzed different combinations of the three data types, e.g., mRNA plus methylation, mRNA plus miRNA, and methylation plus miRNA. Overall, PINS outperforms the other four methods across the three different combinations (Supplemental Table S8). To investigate how stable PINS is with respect to the agreement cutoff, we reran our analysis using five different cutoffs: 0.4, 0.45, 0.5, 0.6, and 0.7 (Supplemental Table S9). In four out of the six data sets (GBM, LAML, LUCS, COAD), there is no change whatsoever, when this threshold varies from 0.4 to 0.7. In the remaining two data sets (KIRC and BRCA), the results remain the same in seven out of 10 cases. For KIRC, when the cutoff changes from 0.5 to 0.6, (i.e., increases our requirement for agreement), PINS does not split the female group in stage II anymore. The second case is BRCA, when the cutoff changes from 0.45 to 0.4. With the low agreement cutoff, PINS clusters the patients using the strong similarity matrix when this matrix is not supported by the majority of patient pairs. Overall, the results are stable with respect to the choice of this parameter. Furthermore, for all choices of this parameter, the results obtained continue to be better than those obtained with CC, SNF, and iCluster+.
Notably, the six data sets illustrated here include several interesting cases. In the KIRC data, no single data type appears to carry sufficient information for any of the four methods to be able to identify groups with significant survival differences. However, when the three data types are integrated and analyzed together, PINS is able to extract four groups with very significant survival differences (P = 10−4). Note that none of the other algorithms are able to identify groups with significantly different survival profiles for this disease.
Another interesting situation is that in which a single data type is sufficient for the discovery of significantly different subtypes. For instance, methylation appears to be a key phenomenon in GBM since all four methods are able to identify subgroups with significant survival differences based on this data type alone (P = 10−4 for PINS, 10−3 for CC, P = 0.017 for SNF, and 3 × 10−3 for iCluster+). However, when the methylation data are integrated with mRNA and miRNA data, SNF and iCluster+ lose their ability to accurately separate the patients into different survival groups (P = 0.062 for SNF and P = 0.076 for iCluster+). In contrast, PINS is able to combine the complementary signals available in the three data types to obtain subtypes with even more significant survival differences (P = 8.7 × 10−5).
We studied the clinical information available for BRCA, and we realized that most patients are estrogen receptor positive. Out of 172 patients, there are 34 ER-negative (ER−), 134 ER-positive (ER+), and four not evaluated. Supplemental Tables S10 through S13 show the comparisons between ER subtypes and subtypes discovered by PINS, CC, SNF, and iCluster+. These approaches perform poorly on this breast cancer data set (Cox P-value = 0.034, 0.667, 0.398, 0.416 for PINS, CC, SNF, iCluster+, respectively) partially because most patients belong to the ER+ subtype.
For LAML, LUSC, and BRCA, PINS is able to find subtypes with significantly different survivals based on a single data type alone, but the integrative analysis of all three data types greatly enhances the significance of the survival differences. Finally, we include the COAD as a negative control, i.e., an example of a condition in which no subtypes are known and for which none of the approaches identify subgroups with significant survival differences after data integration.
In summary, for every single integrative analysis, PINS outperforms the three other approaches in identifying subtypes with significantly different survival profiles. Furthermore, the results show a clear advantage of data integration over analysis of individual data types.
Subtyping by integrating mRNA and CNV data
We analyzed two breast cancer cohorts obtain from the Molecular Taxonomy of Breast Cancer International Consortium (METABRIC) (Curtis et al. 2012). This data set consists of a discovery cohort (997 patients) and a validation cohort (995 patients). For each of these patients, matched DNA and RNA were subjected to copy number analysis and transcriptional profiling on the Affymetrix SNP 6.0 and Illumina HT 12 v3 platforms, respectively. We downloaded the mRNA and CNV data from the European Genome-Phenome Archive (https://www.ebi.ac.uk/ega/) and high-quality follow up clinical data from cBioPortal (http://www.cbioportal.org). There are patients that were followed up to ∼30 yr. The clinical data include PAM50 subtypes, overall survival, and disease-free survival (DFS) information. For the discovery set, the clinical data of all of the 997 patients are available. For the validation set, there are high-quality clinical data for 983 patients.
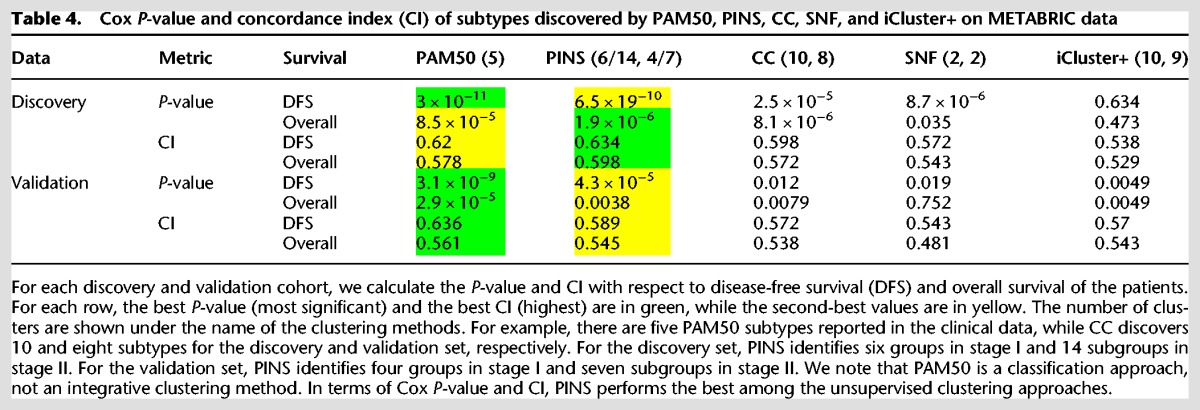
Table 4 shows the Cox P-value and CI of the subtypes discovered by the four unsupervised clustering approaches. For each row, the best P-value (most significant) and the best CI (highest) are in green. PINS continues to perform better than CC, SNF, and iCluster+.
Table 4.
Cox P-value and concordance index (CI) of subtypes discovered by PAM50, PINS, CC, SNF, and iCluster+ on METABRIC data
Functional analysis of discovered subtypes
We examined the detailed mechanisms captured by our subtypes, for the three TCGA data sets with the best Cox P-values, in terms of clinical variables, pathways, gene ontology, and functional analysis. The discovered subtypes corroborate the results of formerly reported subtypes and identify new and potentially important associations. Interestingly, both KIRC and LAML include a mitochondrial subgroup which has not previously been described.
The significant Cox P-values for KIRC subgroups implies the existence of disease subtypes related to gender, which are not defined by a purely gender-based signal. The most aggressive KIRC subtype (group “1-1”) (Fig. 2I, blue) appears to affect only females (100% of samples in this subgroup are female). This poor survival female group includes 86% of stage IV cases among females. There are 3137 genes differentially expressed between long-term and short-term survivors (Supplemental Table S15). Ninety-two percent (2880) of these were down-regulated in the poor survivors.
Functional analysis using WebGestalt (Wang et al. 2013; see Supplemental Table S17) shows that the poorest surviving female group had damage to the brush border membrane of the kidney proximal tubules, acute phase reaction, decreased transmembrane ion transport, and elevated response to erythropoietin compared with the females with better survival. The significant cellular component terms are related to plasma membrane, in particular “brush border membrane.” The biological process and pathway terms concern known proximal tubule functions: metabolic processes and transmembrane and ionic transport. The molecular function term “glycosides activity” is also related, since alpha-glucosidase precursor has been localized to the proximal tubule brush border, where it is secreted into the urine (Klumperman et al. 1989). Another process that is highly significant among the genes down-regulated in poor survivors is protein folding and the ability to dispose of incorrectly folded proteins. Functional analysis using iPathwayGuide (Advaita) also points to damaged proximal tubules in the nephrons of women with poor outcome. The most significant signaling pathway is mineral absorption at FDR = 0.002. Several differentially expressed solute carriers on the Mineral absorption pathway are located in “brush border membrane” (Supplemental Fig. S19a). In the kidney, brush border membranes are found in the proximal tubules, which carry filtrate away from the glomerulus in the nephron, and support the secretion and absorption of charged molecules into and out of the filtrate. Other significantly impacted pathways were all metabolic, except the PPAR signaling pathway (Supplemental Fig. S19b). PPAR signaling is down-regulated in poor surviving women and may reflect the advanced age of this group (Sung et al. 2004).
The less aggressive KIRC subtype (group 2) (Fig. 2I, red) is 98% male. This group shows up-regulation of pathways associated with metastasis, including cell migration and vascularization. It also shows down-regulation of mitochondrial ATP production, potentially due to an X-linked disorder. This is particularly interesting because all but one patient in this group are males (and the subgroup was identified without using the sex information). Group “1-2” (cyan), which has a better survival rate than the male group, is 100% female and consists of mostly stage I cases. The fourth subtype (group 3) (Fig. 2, green) consists of patients who all survived until the end of the study. Variant analysis shows that the gene VHL is mutated in subgroups “1-1,” “1-2,” and “2” but not in “3,” in which all patients survive at the end of the study. See Supplemental Section 4.1, Supplemental Tables S15 through S18, and Supplemental Figures S18 through S20 for more analysis.
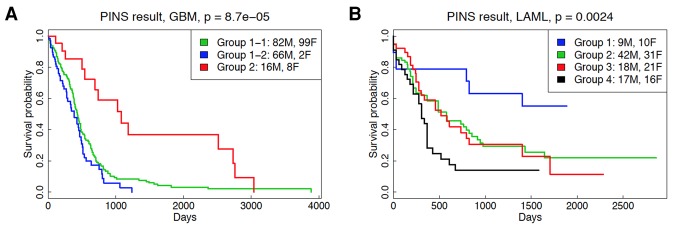
GBM subtypes found by PINS can be correlated to subtypes described by other investigators. Our data show that GBM subtypes are highly influenced by methylation profiles (Table 3). Of the three GBM groups (Fig. 3A), the one with the best survival (group 2, red) is significantly rich in IDH1 mutations (P = 2 × 10−8). Among the 45 patients that have IDH1 mutation information, all seven mutated samples belong to this group and all 38 wild-type samples belong to other groups. This group consists of younger patients with a tendency for recurrent tumor events. Therefore, it is similar to the proneural subtype (Verhaak et al. 2010) and may respond to temozolomide (Phillips et al. 2006; Wang et al. 2014), a drug that interferes with DNA replication.
Figure 3.
Kaplan-Meier survival analysis for glioblastoma multiforme (A) and acute myeloid leukemia (B). The horizontal axes represent the time passed after entry into the study, while the vertical axes represent estimated survival percentage.
Enrichment analysis of both clusters “1-1” and “1-2” compared with the good survivors (“2”) shows high invasiveness and vascularization, as should be expected. Like the proliferative and mesenchymal subgroups identified by Phillips et al. (2006), these clusters have close, parallel survival curves. Pathway analysis contrasting these two reveals that subtype “1-1” is more collagenous than “1-2,” with more extracellular matrix and calcium ion binding and thus may be more mesenchymal than proliferative. Collagen and extracellular matrix terms are associated with invasiveness in GBM (Mammoto et al. 2013; Payne and Huang 2013). GO analysis suggests that “1-2” is a subtype with strong regulation of glial and astrocyte differentiation and thus may be more proliferative than mesenchymal. In addition, “1-2” is significantly enriched in glycine and serine metabolism compared with “1-1,” a phenomenon reported in aggressive glioma (Chinnaiyan et al. 2012). Serine and glycine metabolism are implicated in oncogenesis and, notably, provide methyl groups for DNA and histone methylation (Chinnaiyan et al. 2012; Amelio et al. 2014), a possible explanation for the dominant influence of methylation profile on our subtyping results.
Over 90% of the genes that are differentially expressed between the short-term surviving males (group “1-2”) and the medium-term surviving males (group “1-1”) are up-regulated in the poor survivors. The only significant KEGG pathway is glycine, serine, and threonine metabolism, which is up-regulated in the poor survival group “1-2” (Supplemental Fig. S22). An abundance of serine and glycine in glioblastoma, a sign of the metabolic reprogramming, is a hallmark in many cancers (Chinnaiyan et al. 2012). This “glycolytic shunt” is characterized by overproduction of the gene PHGDH (De Berardinis 2011), and indeed, PHGDH overexpression is observed in group “1-2” compared with “1-1.” Many microRNAs are more highly expressed in “1-2.” The most significant up-regulated microRNAs are in the family including miR-200B and miR-200C (FDR-corrected = 10−10). MiR-200C is known to associate with high-grade gliomas, and the miR-200 family is implicated in GBM for the epithelial–mesenchymal transition (Lavon et al. 2010). See Supplemental Section 4.2, Supplemental Tables S19 through S22, and Supplemental Figure S21 through S23 for more analysis.
Genes from the cytogenetic bands 14q and 19q are also enriched in “1-2,” or lacking in group “1-1” as the case may be, since the differential expression is relative. Loss of heterozygosity (LOH) in the cytogenetic region 14q, at several sites, has been observed to correlate with glioblastoma development. The subregion 14q23-31 is suspected to be rich in tumor-suppressor genes (Hu et al. 2002; Misra et al. 2005) and is represented in our results by the enriched cytoband 14q24 (FDR-corrected P-value = e−5). Thus, we may assume that it is down-regulated in group “1-1” as opposed to “1-2” as well as normal tissue. The cytoband subregion 19q13 (FDR-corrected P-value = e−6) has been observed to be amplified in some glioblastomas at 19q13.2 (Vranova et al. 2007), but deletions within the region 19q13.33-q13.41 are also reported in astrocytic tumors (Vogazianou et al. 2010).
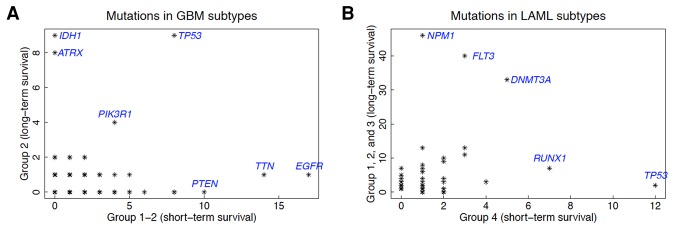
We look for mutations that are highly abundant in the short-term survival group “1-2” but not in the long-term survival group “2” as shown in Figure 4A. In this figure, each point represents a gene, and its coordinates are the number of patients having at least a variant in that gene in each group. In principle, we would look for groups of mutated genes in the top left and the bottom right corner. There are two sets of mutated genes that can be associated with one of the groups. Mutated genes, which are abundant in group “2” (high survival), are IDH1 and ATRX, while the set of mutated genes enriched in group “1-2” (low survival) comprises EGFR, TTN, and PTEN. When we look at the specific variants present in these genes, we note that all patients with variants in IDH1 have exactly the same variant, rs121913500 (in dbSNP). Interestingly, all the eight patients with ATRX mutations also have the same IDH1 mutation. Previous work has shown that patients with this IDH1 mutation usually have a significantly improved prognosis with longer survival compared with patients with wild-type IDH1 (Parsons et al. 2008). This mutation is known to be a target for therapy and drug development (Wick et al. 2009).
Figure 4.
Number of patients in each group for each mutated gene for GBM (A) and LAML (B). The horizontal axes represent the count in short-term survival group, while the vertical axes show the count for long-term survival group(s). Interesting genes/variants will appear in the lower right or upper left corners. (A) There are nine patients in group “1-1” that have a mutation in IDH1, while there is no patient in group 2 reported to have any mutation in this gene. Furthermore, all patients in group 1 share exactly the same mutation, rs121913500 (in dbSNP), which is a T replacing a C on Chromosome 2. (B) Mutations in TP53 are associated with short-term survival in LAML.
Each of the four AML subtypes found by PINS consists of a mixture of males and females (Fig. 3B). The subgroup 1 (blue) with the best survival matches the acute promyelocytic leukemia (APL) subtype. This group is characterized by younger patients, lower percentage bone marrow blasts, and higher percentage bone marrow lymphocytes. All FAB M3 cases and 83% M3 cases belong to this group 1. FAB M3 is the APL subtype, caused by the fusion of part of the RAR-alpha gene from Chromosome 17 to the PML region on Chromosome 15. Patients in group 1 are seen to be in better CALB risk groups. This group is also associated with negative CD34 and negative HLA-DR (human leukocyte antigen); negativity of both together is highly indicative of the APL subtype.
The subtype with the poorest survival (group 4) (Fig. 3B, black) includes older patients, with multiple and various mutations and lymphocytic signals, identifying it as “mixed lineage,” patients with both AML and ALL. Of the two intermediate survival subtypes, group 3 (red) is dominated by myelocyte (neutrophil) and monocyte (macrophage) lineages, inflammation, and phagocytosis terms. The other intermediate subtype (group 2, green) shows abnormality of mitochondrial translation and may be a specific subtype treatable with the antibiotic tigecycline (Skrtic et al. 2011). See Supplemental Section 4.3, Supplemental Tables S23 through S32, and Supplemental Fig. S24 through S29 for more analysis.
Group 4 has the worst survival and includes the patients with the greatest variety of mutations. All representatives of FAB M6 (erythroleukemia) and FAB M7 (acute megakaryoblastic leukemia) are in this group, although there are also members of other FAB subtypes (except M3 and M5). Up-regulation of genes on the KEGG pathway Hematopoietic Lineage (Supplemental Fig. S25) shows that it has higher lymphoid markers than the other groups and therefore may be “mixed phenotype acute leukemia” (MPAL) (The American Cancer Society 2014). Patients with MPAL present with a large number of cytogenetic abnormalities are difficult to treat and have high mortality rates (Wolach and Stone 2015). MPAL accounts for between 2% and 5% of AML cases (Matutes et al. 2011; Wolach and Stone 2015), although there are other AML classes with MPAL phenotype. Group 4 comprises 20% of the AML cases in this study and therefore is probably not purely MPAL. However, 64% of group 4 have FISH abnormalities, which is consistent with the study of Yan et al. (2012), who tested 92 patients with MPAL and showed that 64% had cytogenic abnormalities. HLA-DR and CD34 tend to be positive in MPAL, but MPAL is heterogeneous and may not be a distinct entity. Associated with these highly significant cytogenetic abnormalities in Supplemental Table S26, including the highest number of 5q and 7q deletions (Supplemental Table S24), we observe poor risk (Supplemental Table S23), interaction with the CALGB risk group, and confounding of several cytogenetic abnormalities with other clinical variables (Supplemental Table S27). WebGestalt results (Supplemental Table S32) support the strong presence of T-cell leukemia (ALL) along with B-cell leukemia (AML). In addition, we note that there is a highly significant overabundance of genes on Chromosomes 22, 11, and 19 but significant loss of genes on Chromosomes 5 and 7. Variant analysis shows that TP53 mutation is enriched in group 4 (short-term survival), while NPM1 is abundant in groups 1, 2, and 3 with higher survival rate (see Fig. 4B).
Discussion
Regarding time complexity, PINS needs a significantly longer time than CC and SNF to perform an analysis on large data sets. This is due to two reasons. The first reason is that we rely on data perturbation and repeated clustering to discover patterns of patients that are stable against small changes of molecular data. Second, we run k-means multiple times to make sure that the results are stable and reproducible. This problem can be addressed in a number of ways, e.g., by performing the computation in parallel. We plan to fully develop our current software to exploit multiple cores whenever possible.
Another limitation of PINS is that we treat all data types equally in determining subtypes. This may not always be appropriate. For instance, for GBM, the results show that methylation plays a major role in determining distinct subtypes. If only this information were available before hand, each of the four methods compared (PINS, CC, SNF, iCluster+) could discover subtypes with significantly different survival using methylation alone. The good news is that PINS is able to extract subtypes with significant survival differences even after data integration, unlike all other existing approaches. However, in theory, there could be situations in which data types that are irrelevant to the correct subtyping may drown the signal coming from a single relevant data type. One way to preempt this is to combine the connectivity matrices in a weighted manner. This improvement would require an evaluation of the quality of the clusters obtained on individual data types, quality assessment that can subsequently be used to determine the weights.
Nevertheless, the novel approach described here is able to address two very important challenges: data integration and disease subtype discovery. We show that PINS is able to (1) effectively integrate mRNA, microRNA and methylation data and, (2) in an unbiased and unsupervised manner, discover disease subtypes characterized by significant survival differences. PINS outperforms current state-of-the-art approaches as a method not only for subtype discovery based on a single data type but also for identifying novel subtypes with significantly different survival profiles by integrating multiple types of data. In addition, the visualization of pair-wise connectivity between patients can provide additional insight into the discovered subtypes.
In conclusion, PINS can be used to integrate many other high-throughput data types for the purpose of disease characterization, understanding of disease mechanisms, or biomarker detection. It can also be used to integrate pharmacokinetic data and drug response data for drug development and repurposing. Finally, this method provides a powerful alternative to CC, a prominent technique in machine learning, with the additional ability to integrate multiple types of data. Unlike many existing machine learning approaches, PINS can effectively analyze data sets with tens of thousands of variables and hundreds of samples, without requiring a preliminary step involving data filtering or feature selection. These capabilities make PINS highly relevant for immediate practical applications rather than just a theoretical advance. Since PINS is completely independent of the data types being used, it can be applied in many areas to tackle unsupervised machine learning problems involving either single or multiple types of high-dimensional data.
Methods
Data processing and normalization
For single data type analysis, we used eight gene expression data sets with known subtypes. Five data sets, GSE10245, GSE19188, GSE43580, GSE14924, and GSE15061, were downloaded from Gene Expression Omnibus (https://www.ncbi.nlm.nih.gov/geo/), while the other three were downloaded from the Broad Institute: AML2004 (https://archive.broadinstitute.org/cancer/pub/nmf/), Lung2001 (https://www.broadinstitute.org/mpr/lung/), and Brain2002 (https://archive.broadinstitute.org/mpr/CNS/). The data set AML2004 was already processed and normalized (Brunet et al. 2004). For the other seven, Affymetrix CEL files containing raw expression data were downloaded and processed using the three-step function from the package affyPLM (Bolstad 2004).
For integrative analysis of mRNA, methylation, and miRNA, we downloaded level-three data of six different cancers from TCGA (https://cancergenome.nih.gov): KIRC, GBM, LAML, LUSC, BRCA, and COAD. The only processing step we did is to perform log transformation (base 2) to rescale sequencing data (GASeq and HiSeq platforms). Clinical data were also obtained from the same website.
For integrative analysis of mRNA and CNV, we downloaded the normalized data for METABRIC data sets from the European Genome-Phenome Archive (https://www.ebi.ac.uk/ega/) with accession IDs: EGAD00010000210 (expression data, discovery), EGAD00010000214 (CNV, discovery), EGAD00010000211 (expression data, validation), and EGAD00010000216 (CNV, validation). The only preprocessing step we did is to map CNVs to genes using the CNTools package (https://bioconductor.org/packages/release/bioc/html/CNTools.html). We also downloaded high-quality follow-up clinical data from cBioPortal (http://www.cbioportal.org).
Perturbation clustering
The pipeline of the algorithm is shown in Supplemental Figure S1. The input is a data set (matrix) E ∈ RN×M, where N is the number of patients and M is the number of measurements for each patient.
Construction of original connectivity (steps 1–2)
In step 1, we partition the patients using all possible number of clusters k ∈ [2..K]. Formally, the input E can be presented as a set of N patients E = {e1, e2, …, eN}, where each element vector ei ∈ RM represents the molecular profile of the ith patient (i ∈ [1..N]). A partitioning Pk (k clusters) of E can be written in the form , where is a set of patients such that and , , i ≠ j. After step 1, we have (K − 1) partitionings: {P2, …, PK}, one for each value of k ∈ [2..K].
In step 2, we build the pair-wise connectivity for each partitioning obtained from step 1. For a partitioning Pk, two patients are connected if they are clustered together. We build the connectivity matrix Ck ∈ {0,1}N×N from the partitioning as follows:
| (1) |
In other words, the connectivity between two patients is 1 if and only if they belong to the same cluster. For example, we cluster a set of five elements into two clusters with the resulted partitioning , where and . In this case, e1 is connected to e2 and is not connected to other elements (e3, e4, e5). Similarly, elements {e3, e4, e5} are all connected to each other but not to elements {e1, e2}. The constructed connectivity matrix for P2 is as follows:
Intuitively, a partitioning can be presented as a graph in which each patient is a node and the connectivity between two patients is an edge, such that the edge exists if and only if the two patients have similar molecular profile and thus are clustered together. Any two patients of a cluster are connected by an edge, and any two patients of different clusters are not connected. The connectivity matrix of the clustering is exactly the adjacency matrix of the graph.
We construct one connectivity matrix for each value of k ∈ [2..K]. After step 2, we have (K − 1) connectivity matrices C2, …, CK. We refer to these matrices as original connectivity matrices because they were constructed from the original data without data perturbation.
Generating perturbed data sets (step 3)
In order to assess the stability of the partitionings obtained in steps 1 and 2, we generate H new data sets by perturbing the data. One way to do so is to add Gaussian noise to the original data E. However, if the variance of the noise we add is much lower than the intrinsic variance of the data, the added noise will not perturb data sufficiently. On the other hand, if the variance of the noise we add is much higher than the intrinsic variance of the data, differences between true subtypes may be drowned by the added noise. For this reason, we will perturb the data with a noise that has the variance equal to the variance of the data. By setting the variance of the perturbation noise equal to the median variance of the data, we aim to automatically set the magnitude of the perturbation we apply to be comparable to the noise of the system. By default, the noise variance is calculated as follows:
| (2) |
where
We then generate H new data sets J(h) ∈ RN×M, h ∈ [1..H] by adding Gaussian noise to the original data:
| (3) |
where σ2 is calculated as in equation 2. After this step, we have H perturbed data sets J(1), J(2), …, J(H) that will be used to compute the perturbed connectivity matrices.
Construction of perturbed connectivity (steps 4–6)
To construct the connectivity between patients for the perturbed data (step 4), we cluster each of the H perturbed data sets using k-means with varying values of k ∈ [2..K]. For example, for k = 2, we partition the data set J(1) into two clusters and get the partitioning. We perform k-means with k = 2 for each of the H perturbed data sets and get H different partitionings for k = 2. Note that all of these perturbed data sets were generated by adding a small amount of noise to the same input E. In the ideal case, adding noise to the data would not influence the clustering results; i.e., all of the partitionings would be identical to P2. The more differences there are between the perturbed partitionings, the less reliable the original P2 partitioning is.
Now we have H different partitionings , , …, for each value of k ∈ [2..K]. In step 5, we construct a connectivity matrix for each partitioning created in step 4. Specifically, for the partitioning (h ∈ [1..H], k ∈ [2..K]), we construct the connectivity matrix as follows:
| (4) |
After this step, we have H connectivity matrices , , …, for each value of k. In step 6, we calculate the perturbed connectivity matrix by averaging the connectivity from , , …, as follows:
| (5) |
where Ak ∈ [0, 1]N×N and k ∈ [2..K]. We refer to these matrices as perturbed connectivity matrices. For each value of k ∈ [2..K], we have one original connectivity matrix and one perturbed connectivity matrix.
Stability assessment (steps 7–9)
Given the number of clusters k, we would like to quantify the discrepancy between Ck and Ak. In step 7, we calculate the difference matrix Dk ∈ [0, 1]N×N as follows:
| (6) |
Dk (i, j) represents the absolute change in connectivity between ei and ej when the data are perturbed. The smaller Dk (i, j), the more robust the connectivity between ei and ej. Ideally, when the clustering is the most stable, there would be no differences between Ck and Ak; i.e., all entries of Dk are equal to zero. The distribution of the entries of Dk reflect the stability of the clustering. The more this distribution shifts toward 1, the less robust the clustering. In step 8, we compute the empirical CDF Fk of the elements of Dk. For a value c on the interval [0, 1], we calculate Fk (c) as follows:
| (7) |
where the card{ · } operator in the numerator represents the cardinality of a set. In essence, the numerator is the number of elements in Dk that are smaller than or equal to c, while the denominator represents the total number of elements in the matrix Dk.
In step 9, we calculate AUCk, for each of the Fk CDF. If Ck and Ak are identical, then the data perturbations do not change the clustering results, the difference matrix Dk will consist of only 0’s, Fk (0) = 1, and AUCk = 1. However, if Ck and Ak differ, then the entries of Dk shift toward 1, and AUCk < 1. In step 10, we choose the optimal for which the AUC is maximized as follows:
| (8) |
This is the optimal number of clusters found by the algorithm. This is the number of clusters that produces the clustering exhibiting the least disruption when the original data are perturbed by the added noise. Upon finishing, the algorithm returns the optimal value of , the partitioning , the original connectivity matrix , and the perturbed connectivity matrix .
Subtyping multiomic data
Here we describe the workflow of PINS for integrating multiomics data. The input of PINS is now a set of T matrices , where T is the number of data types, represents the measurements of the ith data type, N is the number of patients, and Mi is the number of measurements per patient for the ith data type. The T matrices have the same number of rows (patients) but might have different number of columns. For example, for KIRC, we have three data types: mRNA, DNA methylation, and microRNA. The three data types have the same number of patients, N = 124, but different numbers of measurements. The numbers of measurements for mRNA, methylation, and microRNA are M1 = 17,974, M2 = 23,165, and M3 = 590, respectively.
The workflow consists of two stages. In stage I, we construct the combined similarity matrix between patients using the connectivity information from individual data types. We then partition the patients using the integrated similarity matrix. In stage II, we further split each discovered group of patients into subgroups if possible.
Stage I: data integration and subtyping
The algorithm starts by clustering each data type using the perturbation clustering described above. Consider the ith data type with the data matrix Ei. The perturbation clustering estimates as the number of subtypes for this data type and then partitions the data into clusters. The algorithm then constructs the original connectivity matrix Ci for this data type, in which the connectivity between elements of the same cluster is 1 and the connectivity between elements of different clusters is 0. Note that the index i here denotes the index of the data type. For T data types, we have T original connectivity matrices C1, C2, …, CT. If we consider each patient as a node and the connectivity between two patients as an edge, then each connectivity matrix for each data type represents a graph. Each graph represents the connection between patients from the perspective of one specific data type. Our goal is to identify groups of patients that are strongly connected across all data types.
In the ideal case, different data types give consistent connectivity between patients, and thus, we can easily identify the subtypes. Otherwise, we need to rely on the average connectivity between data types to partition the samples. To start with, we measure the agreement between the T data types using a concept similar to the pair-wise agreement of the RI. Given two partitionings of the same set of items, the RI is calculated as the number of pairs that “agree” divided by the total number of possible pairs. A pair “agrees” if the two samples are either grouped together in both partitionings or they are separated in both partitionings. We extend this concept to T partitionings of T data types. First, we define that the connectivity between two patients is consistent if it does not change across data types; i.e., the two patients are either connected in all the data types or are not connected at all in any data type. We then define the agreement of T data types as the number of pairs having consistent connectivity, divided by the total number of possible pairs.
We first calculate the average pair-wise connectivity between patients as follows:
| (9) |
We refer to SC as the original similarity matrix because it is constructed from the original connectivity matrices. An entry SC (i, j) will be zero if the elements i and j are never clustered together; it will be one if the elements i and j are always clustered together, and it will be between zero and one if the two elements are clustered together only in some data types. We then calculate the agreement between the data types as follows:
| (10) |
In this equation, the numerator counts only the situations in which the connectivity of the pair is consistent across all data types (either the two samples are always together or always separated). If the majority of pairs are consistent (agree(SC) > 50%), we say that the T data types have a strong agreement. In this case, we also define a strong similarity matrix as follows:
| (11) |
where if and only if i and j are clustered together in all data types. A HC is then applied directly on this matrix, and the resulting tree is cut at the height that provides maximum cluster separation.
Each data type represents a different but important perspective, supported by its own type of evidence. In the ideal case, we would like to have a partitioning that is confirmed by all patient pairs across all types of evidence. In this case, the strong similarity matrix would clearly define groups of patients that are strongly connected across all data types. However, this is not always the case in practice, where different data types provide different and often contradictory signals. In this case, we are forced to use the average similarity matrix to determine the groups. Intuitively, the 50% threshold corresponds to a situation in which the partitioning is supported by more than half of all patient pairs (for the stability of PINS with respect to this cutoff, see Supplemental Table S9).
When the data types do not have a strong agreement, we need to partition the patients using the average connectivity between them. The matrix SC represents the overall similarity between patients and therefore {1 − SC} represents the distance between patients. The matrix of pair-wise distance can be directly used by similarity-based clustering algorithms (methods that can use pair-wise distances and do not require coordinates in the original space), such as HC, PAM (Kaufman and Rousseeuw 1987), or dynamic tree cut (Langfelder et al. 2008). Here we use all the three algorithms to partition the patients and then choose the partition that agrees the most with the partitionings of individual data types.
The dynamic tree cut algorithm can automatically determine the number of clusters, but the other two algorithms, HC and PAM, require that the number of clusters is provided. To determine the number of clusters for HC and PAM, we introduce the perturbed similarity matrix, which is the average of the perturbed connectivity between patients across T data types:
| (12) |
where Ai is the perturbed connectivity matrix of the ith data type. Note that SC is constructed by averaging the original connectivity of T data types, while SA is constructed by averaging the perturbed connectivity of T data types. Analogous to the case of using a single data type, we use both matrices to determine the number of subtypes for HC and PAM.
For HC, we first build the H1 tree using the original similarity matrix SC, and then we build the H2 tree using the perturbed similarity matrix SA. For each value of k ∈ [2..10], we cut H1 to get k clusters and then build the connectivity matrix. We cut the tree H2 for the same value of k and then construct another connectivity matrix. We then calculate the instability dk as the sum of absolute difference between the two connectivity matrices. We choose for which the dk is the smallest, i.e., .
For PAM, we partition the patients using both original and perturbed similarity matrices. For each value of k, we have one partitioning using the original similarity matrix SC and one partitioning using the perturbed similarity matrix bfSA. We build the connectivity matrices for the two partitionings and then calculate the instability dk as the absolute difference between the two connectivity matrices. We choose for which the dk is the smallest, i.e., .
After finding the three partitionings using the three similarity-based clustering algorithms, we calculate the agreement between each partitioning and the T data types. Again, we use the agreement concept introduced in equation 10. For each algorithm, we calculate the agreement between its partitioning and the T partitionings for the T data types. We then choose the result of the algorithm that has the highest agreement with the T data types.
Stage II: further splitting discovered groups
In stage II, the goal is to discover true partitions whose presence may have been obscured by the dominant signal in the first stage. Since our approach is an unsupervised approach, we do not have prior information to take into account important covariates, such as gender, race, or demographic. If these signals are predominant, we are likely to miss the real subtypes. Another motivation is that there are often heterogeneous subgroups of patients that share clinically relevant characteristics even within a subtype. One example is that Luminal A and Luminal B are both estrogen receptor positive. If the data follow a hierarchical structure, the distances between subgroups at the second level are smaller than the distances between groups at the first level. Therefore, one-round clustering would likely overlook the subgroups within the groups identified in stage I.
We attempt to subsplit each discovered group individually based on several reasonable conditions set to avoid oversplitting. First, we check if the connectivity of the data types found in stage I strongly agrees. In the first case, when the connectivity between patients are consistent in stage I (i.e., agree(SC) > 50%), we continue to check the consistency between patients within each group. We use the same procedure as described in stage I to further split each group. For a group, we partition the patients for each data type, build the connectivity, and then check if the connectivity of patients is consistent across all data types. If each data type of a group can be further partitioned and the optimal partitionings of all data types strongly agree, we further split the group using the strong similarity matrix generated for the patients only in that group.
In the second case, when the data types do not have strong agreement in stage I, the connectivity is likely to have even weaker agreement in stage II. To avoid extremely unbalanced subtyping, which might be caused by extreme outliers, we also proceed to stage II but only with the support of entropy (Cover and Thomas 2012) and the gap statistic (Tibshirani et al. 2001). Briefly, the entropy of a partitioning can be calculated as follows. Consider a set of N samples that are divided into k bins. Each bin consists of ni samples, i ∈ [1..k]. The multiplicity W, which is the total number of ways of arranging the samples into the bins, can be calculated as . The entropy is then defined as the logarithm of the multiplicity scaled by a constant: . For large values of N, and using Stirling's approximation, ln (N!) ≃ N ln N − N, the entropy can be calculated as
| (13) |
In equation 13, is the fraction of elements that belongs to the ith bin. The entropy value is maximized when the elements are equally distributed in k bins, i.e., . In this case, . To scale the metric, we use the normalized entropy which is the ratio between H and Hmax:
| (14) |
where .
We note that represents an ideally balanced clustering, and represents an unrealistically unbalanced clustering, e.g. all the N elements fall into one bin. We proceed to stage II only when the entropy is <50% of the maximum entropy, i.e., normalized entropy . In addition to entropy, we also use the gap statistic to check if the data can be further clustered before we proceed to stage II. Briefly, the gap statistic compares the total within cluster variation Wk (residual sum of square for k-means) for different values of k, with their expected values under the null reference distribution, i.e., the distribution with no obvious clustering:
| (15) |
where denotes the expectation under a sample of size N from the reference distribution. is calculated via bootstrapping by generating B copies of the reference data sets and by computing the average . The gap statistic measures the deviation of the observed Wk value from its expected value under the null hypothesis. The algorithm returns the first k such that gapN (k) ≥ gapN (k + 1) − sk+1, where sk+1 is the standard deviation of . The null hypothesis is that the data are from the reference distribution (no obvious clustering). If the algorithm returns 1, we say that we do not find enough evidence to reject the null hypothesis (Tibshirani et al. 2001). We only proceed to stage II if the majority of data types can be clearly separated using the gap statistic.
In summary, when the data types are not consistent, we avoid unbalanced clustering by attempting to further split each group based on two conditions. First, the normalized entropy of the clustering in stage I must be very low (<0.5). Second, the gap statistic must clearly support a separation of the patients.
Software availability
The PINS package and R scripts are included as Supplemental Data S5 and are also available at http://www.cs.wayne.edu/tinnguyen/PINS/PINS.html.
Data access
The eight gene expression data sets from this study are available as Supplemental Data S1. The six cancer data sets and clinical information from TCGA are available as Supplemental Data S2. The METABRIC discovery and validation data sets are available as Supplemental Data S3 and S4, respectively.
Supplementary Material
Acknowledgments
This work has been partially supported by the following grants: National Institutes of Health (R01 DK089167, R42 GM087013) and National Science Foundation (DBI-0965741) to S.D. This work has also been supported by the Robert J. Sokol, MD, Endowed Chair in Systems Biology (Wayne State University). We thank Michele Donato, Sahar Ansari, and Aliccia Bollig-Fischer for useful discussions.
Author contributions: T.N. and S.D. conceived of and designed the approach. T.N. implemented the method in R and performed the data analysis and all computational experiments. D.D. performed data preparation from TCGA and helped with some data analysis. R.T. performed the biological interpretation of the case studies. T.N., R.T., and S.D. wrote the manuscript. All authors reviewed the manuscript.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.215129.116.
References
- Alizadeh AA, Eisen MB, Davis RE, Ma C, Lossos IS, Rosenwald A, Boldrick JC, Sabet H, Tran T, Yu X, et al. 2000. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature 403: 503–511. [DOI] [PubMed] [Google Scholar]
- Amelio I, Cutruzzola F, Antonov A, Agostini M, Melino G. 2014. Serine and glycine metabolism in cancer. Trends Biochem Sci 39: 191–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The American Cancer Society. 2014. How is acute myeloid leukemia classified? http://www.cancer.org/cancer/leukemia-acutemyeloidaml/detailedguide/leukemia-acute-myeloid-myelogenous-classified.
- Bellman R. 1957. Dynamic programming. Princeton University Press, Princeton, NJ. [Google Scholar]
- Ben-Dor A, Shamir R, Yakhini Z. 1999. Clustering gene expression patterns. J Comput Biol 6: 281–297. [DOI] [PubMed] [Google Scholar]
- Ben-Hur A, Elisseeff A, Guyon I. 2001. A stability based method for discovering structure in clustered data. Pac Symp Biocomput 7: 6–17. [PubMed] [Google Scholar]
- Bhattacharjee A, Richards W, Staunton J, Li C, Monti S, Vasa P, Ladd C, Beheshti J, Bueno R, Gillette M, et al. 2001. Classification of human lung carcinomas by mRNA expression profiling reveals distinct adenocarcinoma subclasses. Proc Natl Acad Sci 98: 13790–13795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolstad BM. 2004. “Low-level analysis of high-density oligonucleotide array data: background, normalization and summarization.” PhD thesis, University of California. [Google Scholar]
- Brunet J-P, Tamayo P, Golub TR, Mesirov JP. 2004. Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci 101: 4164–4169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2011. Integrated genomic analyses of ovarian carcinoma. Nature 474: 609–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2012a. Comprehensive genomic characterization of squamous cell lung cancers. Nature 489: 519–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2012b. Comprehensive molecular characterization of human colon and rectal cancer. Nature 487: 330–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2012c. Comprehensive molecular portraits of human breast tumours. Nature 490: 61–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2013. Integrated genomic characterization of endometrial carcinoma. Nature 497: 67–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2014. Integrated genomic characterization of papillary thyroid carcinoma. Cell 159: 676–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Cancer Genome Atlas Research Network. 2015. Comprehensive genomic characterization of head and neck squamous cell carcinomas. Nature 517: 576–582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chinnaiyan P, Kensicki E, Bloom G, Prabhu A, Sarcar B, Kahali S, Eschrich S, Qu X, Forsyth P, Gillies R, et al. 2012. The metabolomic signature of malignant glioma reflects accelerated anabolic metabolism. Cancer Res 72: 5878–5888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi W, Porten S, Kim S, Willis D, Plimack ER, Hoffman-Censits J, Roth B, Cheng T, Tran M, Lee I-L, et al. 2014. Identification of distinct basal and luminal subtypes of muscle-invasive bladder cancer with different sensitivities to frontline chemotherapy. Cancer Cell 25: 152–165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coussens LM, Werb Z. 2002. Inflammation and cancer. Nature 420: 860–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cover TM, Thomas JA. 2012. Elements of information theory, 2nd ed John Wiley & Sons, Hoboken, NJ. [Google Scholar]
- Curtis C, Shah SP, Chin S-F, Turashvili G, Rueda OM, Dunning MJ, Speed D, Lynch AG, Samarajiwa S, Yuan Y, et al. 2012. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature 486: 346–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis CF, Ricketts CJ, Wang M, Yang L, Cherniack AD, Shen H, Buhay C, Kang H, Kim SC, Fahey CC, et al. 2014. The somatic genomic landscape of chromophobe renal cell carcinoma. Cancer Cell 26: 319–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeBerardinis RJ. 2011. Serine metabolism: Some tumors take the road less traveled. Cell Metab 14: 285–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudoit S, Fridlyand J. 2002. A prediction-based resampling method for estimating the number of clusters in a dataset. Genome Biol 3: 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisen MB, Spellman PT, Brown PO, Botstein D. 1998. Cluster analysis and display of genome-wide expression patterns. Proc Natl Acad Sci 95: 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y, Church G. 2005. Improving molecular cancer class discovery through sparse non-negative matrix factorization. Bioinformatics 21: 3970–3975. [DOI] [PubMed] [Google Scholar]
- Ghosh D, Chinnaiyan AM. 2002. Mixture modelling of gene expression data from microarray experiments. Bioinformatics 18: 275–286. [DOI] [PubMed] [Google Scholar]
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, et al. 1999. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science 286: 531–537. [DOI] [PubMed] [Google Scholar]
- Hartuv E, Shamir R. 2000. A clustering algorithm based on graph connectivity. Inform Process Lett 76: 175–181. [Google Scholar]
- Herrero J, Valencia A, Dopazo J. 2001. A hierarchical unsupervised growing neural network for clustering gene expression patterns. Bioinformatics 17: 126–136. [DOI] [PubMed] [Google Scholar]
- Hoadley KA, Yau C, Wolf DM, Cherniack AD, Tamborero D, Ng S, Leiserson MD, Niu B, McLellan MD, Uzunangelov V, et al. 2014. Multiplatform analysis of 12 cancer types reveals molecular classification within and across tissues of origin. Cell 158: 929–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou J, Aerts J, Den Hamer B, Van Ijcken W, Den Bakker M, Riegman P, van der Leest C, van der Spek P, Foekens JA, Hoogsteden HC, et al. 2010. Gene expression-based classification of non-small cell lung carcinomas and survival prediction. PLoS One 5: e10312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J, Jiang C, Ng H, Pang J, Tong C. 2002. Chromosome 14q may harbor multiple tumor suppressor genes in primary glioblastoma multiforme. Chin Med J 115: 1201–1204. [PubMed] [Google Scholar]
- Hubert L, Arabie P. 1985. Comparing partitions. J Classif 2: 193–218. [Google Scholar]
- Jiang D, Tang C, Zhang A. 2004. Cluster analysis for gene expression data: a survey. IEEE Trans Knowl Data Eng 16: 1370–1386. [Google Scholar]
- Kaplan EL, Meier P. 1958. Nonparametric estimation from incomplete observations. J Am Stat Assoc 53: 457–481. [Google Scholar]
- Kaufman L, Rousseeuw P. 1987. Clustering by means of medoids. In Statistical data analysis based on the L1-norm and related methods (ed. Dodge Y), pp. 405–416. North-Holland, Amsterdam. [Google Scholar]
- Kim S, Herazo-Maya JD, Kang DD, Juan-Guardela BM, Tedrow J, Martinez FJ, Sciurba FC, Tseng GC, Kaminski N. 2015. Integrative phenotyping framework (iPF): integrative clustering of multiple omics data identifies novel lung disease subphenotypes. BMC Genomics 16: 924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirk P, Griffin JE, Savage RS, Ghahramani Z, Wild DL. 2012. Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 28: 3290–3297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klumperman J, Oude Elferink R, Fransen J, Ginsel L, Tager JM. 1989. Secretion of a precursor form of lysosomal alpha-glucosidase from the brush border of human kidney proximal tubule cells. Eur J Cell Biol 50: 299–303. [PubMed] [Google Scholar]
- Kohonen T. 1990. The self-organizing map. Proc IEEE 78: 1464–1480. [Google Scholar]
- Kuner R, Muley T, Meister M, Ruschhaupt M, Buness A, Xu EC, Schnabel P, Warth A, Poustka A, Sültmann H, et al. 2009. Global gene expression analysis reveals specific patterns of cell junctions in non-small cell lung cancer subtypes. Lung Cancer 63: 32–38. [DOI] [PubMed] [Google Scholar]
- Langfelder P, Zhang B, Horvath S. 2008. Defining clusters from a hierarchical cluster tree: the Dynamic Tree Cut package for R. Bioinformatics 24: 719–720. [DOI] [PubMed] [Google Scholar]
- Lavon I, Zrihan D, Granit A, Einstein O, Fainstein N, Cohen MA, Cohen MA, Zelikovitch B, Shoshan Y, Spektor S, et al. 2010. Gliomas display a microRNA expression profile reminiscent of neural precursor cells. Neuro Oncol 12: 422–433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Dieu R, Taussig DC, Ramsay AG, Mitter R, Miraki-Moud F, Fatah R, Lee AM, Lister TA, Gribben JG. 2009. Peripheral blood T cells in acute myeloid leukemia (AML) patients at diagnosis have abnormal phenotype and genotype and form defective immune synapses with AML blasts. Blood 114: 3909–3916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehmann BD, Pietenpol JA. 2014. Identification and use of biomarkers in treatment strategies for triple-negative breast cancer subtypes. J Pathol 232: 142–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y-F, Tsang IW, Kwok JT, Zhou ZH. 2009. Tighter and convex maximum margin clustering. In Proceedings of the 12th international conference on artificial intelligence and statistics (AISTATS), pp. 344–351. International conference on artificial intelligence and statistics, Clearwater Beach, FL. [Google Scholar]
- Linnekamp JF, Wang X, Medema JP, Vermeulen L. 2015. Colorectal cancer heterogeneity and targeted therapy: a case for molecular disease subtypes. Cancer Res 75: 245–249. [DOI] [PubMed] [Google Scholar]
- Lock EF, Dunson DB. 2013. Bayesian consensus clustering. Bioinformatics 29: 2610–2616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo F, Khan L, Bastani F, Yen IL, Zhou J. 2004. A dynamically growing self-organizing tree (DGSOT) for hierarchical clustering gene expression profiles. Bioinformatics 20: 2605–2617. [DOI] [PubMed] [Google Scholar]
- Mammoto T, Jiang A, Jiang E, Panigrahy D, Kieran MW, Mammoto A. 2013. Role of collagen matrix in tumor angiogenesis and glioblastoma multiforme progression. Am J Pathol 183: 1293–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matutes E, Pickl WF, van't Veer M, Morilla R, Swansbury J, Strobl H, Attarbaschi A, Hopfinger G, Ashley S, Bene MC, et al. 2011. Mixed-phenotype acute leukemia: clinical and laboratory features and outcome in 100 patients defined according to the WHO 2008 classification. Blood 117: 3163–3171. [DOI] [PubMed] [Google Scholar]
- McLachlan GJ, Bean R, Peel D. 2002. A mixture model-based approach to the clustering of microarray expression data. Bioinformatics 18: 413–422. [DOI] [PubMed] [Google Scholar]
- Mills KI, Kohlmann A, Williams PM, Wieczorek L, Liu W-m, Li R, Wei W, Bowen DT, Loeffler H, Hernandez JM, et al. 2009. Microarray-based classifiers and prognosis models identify subgroups with distinct clinical outcomes and high risk of AML transformation of myelodysplastic syndrome. Blood 114: 1063–1072. [DOI] [PubMed] [Google Scholar]
- Misra A, Pellarin M, Nigro J, Smirnov I, Moore D, Lamborn KR, Pinkel D, Albertson DG, Feuerstein BG. 2005. Array comparative genomic hybridization identifies genetic subgroups in grade 4 human astrocytoma. Clin Cancer Res 11: 2907–2918. [DOI] [PubMed] [Google Scholar]
- Mo Q, Wang S, Seshan VE, Olshen AB, Schultz N, Sander C, Powers RS, Ladanyi M, Shen R. 2013. Pattern discovery and cancer gene identification in integrated cancer genomic data. Proc Natl Acad Sci 110: 4245–4250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Monti S, Tamayo P, Mesirov J, Golub T. 2003. Consensus clustering: a resampling-based method for class discovery and visualization of gene expression microarray data. Mach Learn 52: 91–118. [Google Scholar]
- Parsons DW, Jones S, Zhang X, Lin JCH, Leary RJ, Angenendt P, Mankoo P, Carter H, Siu IM, Gallia GL, et al. 2008. An integrated genomic analysis of human glioblastoma multiforme. Science 321: 1807–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Payne LS, Huang PH. 2013. The pathobiology of collagens in glioma. Mol Cancer Res 11: 1129–1140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perou CM, Sørlie T, Eisen MB, van de Rijn M, Jeffrey SS, Rees CA, Pollack JR, Ross DT, Johnsen H, Akslen LA, et al. 2000. Molecular portraits of human breast tumours. Nature 406: 747–752. [DOI] [PubMed] [Google Scholar]
- Phillips HS, Kharbanda S, Chen R, Forrest WF, Soriano RH, Wu TD, Misra A, Nigro JM, Colman H, Soroceanu L, et al. 2006. Molecular subclasses of high-grade glioma predict prognosis, delineate a pattern of disease progression, and resemble stages in neurogenesis. Cancer Cell 9: 157–173. [DOI] [PubMed] [Google Scholar]
- Pomeroy S, Tamayo P, Gaasenbeek M, Sturla L, Angelo M, McLaughlin M, Kim J, Goumnerova L, Black P, Lau C, et al. 2002. Prediction of central nervous system embryonal tumour outcome based on gene expression. Nature 415: 436–442. [DOI] [PubMed] [Google Scholar]
- Rand WM. 1971. Objective criteria for the evaluation of clustering methods. J Am Stat Assoc 66: 846–850. [Google Scholar]
- Ritchie MD, Holzinger ER, Li R, Pendergrass SA, Kim D. 2015. Methods of integrating data to uncover genotype-phenotype interactions. Nat Rev Genet 16: 85–97. [DOI] [PubMed] [Google Scholar]
- Robinson D, Van Allen EM, Wu YM, Schultz N, Lonigro RJ, Mosquera JM, Montgomery B, Taplin ME, Pritchard CC, Attard G, et al. 2015. Integrative clinical genomics of advanced prostate cancer. Cell 161: 1215–1228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseeuw PJ. 1987. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. J Comput Appl Math 20: 53–65. [Google Scholar]
- Sharan R, Shamir R. 2000. CLICK: a clustering algorithm with applications to gene expression analysis. In Proc Int Conf Intell Syst Mol Biol 8: 16. [PubMed] [Google Scholar]
- Shen R, Olshen AB, Ladanyi M. 2009. Integrative clustering of multiple genomic data types using a joint latent variable model with application to breast and lung cancer subtype analysis. Bioinformatics 25: 2906–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R, Mo Q, Schultz N, Seshan VE, Olshen AB, Huse J, Ladanyi M, Sander C. 2012. Integrative subtype discovery in glioblastoma using iCluster. PLoS One 7: e35236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen R, Wang S, Mo Q. 2013. Sparse integrative clustering of multiple omics data sets. Ann Appl Stat 7: 269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skrtic M, Sriskanthadevan S, Jhas B, Gebbia M, Wang X, Wang Z, Hurren R, Jitkova Y, Gronda M, Maclean N, et al. 2011. Inhibition of mitochondrial translation as a therapeutic strategy for human acute myeloid leukemia. Cancer Cell 20: 674–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strehl A, Ghosh J. 2003. Cluster ensembles: a knowledge reuse framework for combining multiple partitions. J Mach Learn Res 3: 583–617. [Google Scholar]
- Sung B, Park S, Yu BP, Chung HY. 2004. Modulation of PPAR in aging, inflammation, and calorie restriction. J Gerontol A Biol Sci Med Sci 59: B997–B1006. [DOI] [PubMed] [Google Scholar]
- Tamayo P, Slonim D, Mesirov J, Zhu Q, Kitareewan S, Dmitrovsky E, Lander ES, Golub TR. 1999. Interpreting patterns of gene expression with self-organizing maps: methods and application to hematopoietic differentiation. Proc Natl Acad Sci 96: 2907–2912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tarca AL, Lauria M, Unger M, Bilal E, Boue S, Dey KK, Hoeng J, Koeppl H, Martin F, Meyer P, et al. 2013. Strengths and limitations of microarray-based phenotype prediction: lessons learned from the IMPROVER diagnostic signature challenge. Bioinformatics 29: 2892–2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Therneau TM, Grambsch PM. 2000. Modeling survival data: extending the Cox model. Springer, New York. [Google Scholar]
- Tibshirani R. 1996. Regression shrinkage and selection via the lasso. J R Stat Soc B (Methodol) 58: 267–288. [Google Scholar]
- Tibshirani R, Walther G, Hastie T. 2001. Estimating the number of clusters in a data set via the gap statistic. J R Stat Soc B (Methodol) 63: 411–423. [Google Scholar]
- Tseng GC, Wong WH. 2005. Tight clustering: a resampling-based approach for identifying stable and tight patterns in data. Biometrics 61: 10–16. [DOI] [PubMed] [Google Scholar]
- Verhaak RG, Hoadley KA, Purdom E, Wang V, Qi Y, Wilkerson MD, Miller CR, Ding L, Golub T, Mesirov JP, et al. 2010. Integrated genomic analysis identifies clinically relevant subtypes of glioblastoma characterized by abnormalities in PDGFRA, IDH1, EGFR, and NF1. Cancer Cell 17: 98–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogazianou AP, Chan R, Backlund LM, Pearson DM, Liu L, Langford CF, Gregory SG, Collins VP, Ichimura K. 2010. Distinct patterns of 1p and 19q alterations identify subtypes of human gliomas that have different prognoses. Neuro Oncol 12: 664–678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Von Luxburg U. 2007. A tutorial on spectral clustering. Stat Comput 17: 395–416. [Google Scholar]
- Vranova V, NeCesalova E, Kuglik P, Cejpek P, PeSakova M, Budinska E, Relichova J, Veselska R. 2007. Screening of genomic imbalances in glioblastoma multiforme using high-resolution comparative genomic hybridization. Oncol Rep 17: 457–464. [PubMed] [Google Scholar]
- Wang B, Jiang J, Wang W, Zhou ZH, Tu Z. 2012. Unsupervised metric fusion by cross diffusion. In Proceedings of the 2012 IEEE conference on computer vision and pattern recognition (CVPR), pp. 2997–3004. IEEE conference on computer vision and pattern recognition, Providence, RI. [Google Scholar]
- Wang J, Duncan D, Shi Z, Zhang B. 2013. WEB-based GEne SeT AnaLysis Toolkit (WebGestalt): update 2013. Nucleic Acids Res 41(Web Server Issue): W77–W83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang B, Mezlini AM, Demir F, Fiume M, Tu Z, Brudno M, Haibe-Kains B, Goldenberg A. 2014. Similarity network fusion for aggregating data types on a genomic scale. Nat Methods 11: 333–337. [DOI] [PubMed] [Google Scholar]
- Wick W, Hartmann C, Engel C, Stoffels M, Felsberg J, Stockhammer F, Sabel MC, Koeppen S, Ketter R, Meyermann R, et al. 2009. NOA-04 randomized phase III trial of sequential radiochemotherapy of anaplastic glioma with procarbazine, lomustine, and vincristine or temozolomide. J Clin Oncol 27: 5874–5880. [DOI] [PubMed] [Google Scholar]
- Wilkerson MD, Hayes DN. 2010. ConsensusClusterPlus: a class discovery tool with confidence assessments and item tracking. Bioinformatics 26: 1572–1573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolach O, Stone RM. 2015. How I treat mixed-phenotype acute leukemia. Blood 125: 2477–2485. [DOI] [PubMed] [Google Scholar]
- Xu L, Neufeld J, Larson B, Schuurmans D. 2004. Maximum margin clustering. In Advances in neural information processing systems 17 (ed. Saul LK, et al.), pp. 1537–1544. The MIT Press, Cambridge. [Google Scholar]
- Yan L, Ping N, Zhu M, Sun A, Xue Y, Ruan C, Drexler HG, MacLeod RA, Wu D, Chen S, et al. 2012. Clinical, immunophenotypic, cytogenetic, and molecular genetic features in 117 adult patients with mixed-phenotype acute leukemia defined by WHO-2008 classification. Haematologica 97: 1708–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang D, Sun Y, Hu L, Zheng H, Ji P, Pecot CV, Zhao Y, Reynolds S, Cheng H, Rupaimoole R, et al. 2013. Integrated analyses identify a master microRNA regulatory network for the mesenchymal subtype in serous ovarian cancer. Cancer Cell 23: 186–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, Kortylewski M, Pardoll D. 2007. Crosstalk between cancer and immune cells: role of STAT3 in the tumour microenvironment. Nat Rev Immunol 7: 41–51. [DOI] [PubMed] [Google Scholar]
- Zhang K, Tsang IW, Kwok JT. 2009. Maximum margin clustering made practical. IEEE Trans Neural Netw 20: 583–596. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.