Identify bilayer modules via pseudo-3D clustering: applications to miRNA-gene bilayer networks

Abstract

Module identification is a frequently used approach for mining local structures with more significance in global networks. Recently, a wide variety of bilayer networks are emerging to characterize the more complex biological processes. In the light of special topological properties of bilayer networks and the accompanying challenges, there is yet no effective method aiming at bilayer module identification to probe the modular organizations from the more inspiring bilayer networks. To this end, we proposed the pseudo-3D clustering algorithm, which starts from extracting initial non-hierarchically organized modules and then iteratively deciphers the hierarchical organization of modules according to a bottom-up strategy. Specifically, a modularity function for bilayer modules was proposed to facilitate the algorithm reporting the optimal partition that gives the most accurate characterization of the bilayer network. Simulation studies demonstrated its robustness and outperformance against alternative competing methods. Specific applications to both the soybean and human miRNA-gene bilayer networks demonstrated that the pseudo-3D clustering algorithm successfully identified the overlapping, hierarchically organized and highly cohesive bilayer modules. The analyses on topology, functional and human disease enrichment and the bilayer subnetwork involved in soybean fat biosynthesis provided both the theoretical and biological evidence supporting the effectiveness and robustness of pseudo-3D clustering algorithm.

INTRODUCTION

A biological network exhibits a modular organization. Module identification and analysis is one of the most frequently used approaches to exploring knowledge from complex biological networks. In parallel with the small world, scale-free property and other basic local and/or global characteristics, the modular structure dependent on functional module is of great significance in understanding the organization and dynamics of network functions. Modularization is a ubiquitous phenomenon in various network systems (1). A functional module, composed of many types of interacting molecules, is a discrete local structure whose members have more internal links among themselves than external links with members of other modules (2). Normally, a module's function is separable from those of other modules (3), and many cellular functions are carried out by modules (2). Modular organization has been observed in metabolic (4), transcriptional regulation (5) and protein–protein interaction (PPI) (6) networks. Moreover, the exploration of modular structure has been proposed as a key factor in understanding the complexity of biological systems (7). In the past decade, researchers have proposed a wide variety of module identification or network decomposition methods, which can be broadly classified into six major categories: traditional clustering algorithms (8–19), network topological approaches (20–28), modularity optimization (29–32), seed expansion (33–36), matrix decomposition/factorization (37–41) and comparative network analysis (42–45). A detailed review of the above categories is beyond the scope of this paper and has already been presented by Chen et al. (46).

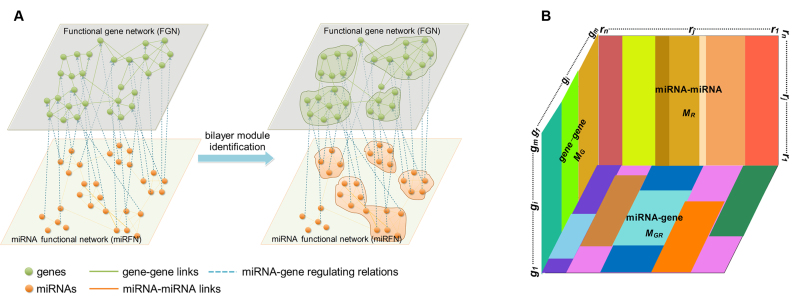
Nevertheless, there is yet no effective method for bilayer module identification from the increasingly booming bilayer networks, such as gene-disease bilayer network (47,48), gene-phenotype bilayer network (49), drug-target bilayer network (50), miRNA-disease bilayer network (51) and the miRNA-gene bilayer networks that we presented in this paper. A bilayer network often consists of three types of linkages between two kinds of nodes. Specifically, a miRNA-gene bilayer network contains two types of biomolecules (miRNAs and genes) and three types of interacting associations (miRNA–miRNA and gene–gene functional interactions, as well as miRNA–gene regulating relations) (Figure 1A). Existing module identification methods seem to have reported good results for traditional monolayer networks, but in the light of the special topological properties of bilayer networks, there are still many challenges that need to be overcome for bilayer module identification. Consequently, this work aims to present a method (or algorithm) to identify bilayer modules from a bilayer network, with specific applications to the miRNA–gene bilayer networks from both plant and human.

Figure 1.

Bilayer module identification and pseudo-3D clustering. (A) The topological view of a toy miRNA–gene bilayer network; (B) The pseudo-3D view of bilayer module identification using clustering approach.

We constructed one bilayer network each of plant and human, respectively, by combining network topological information based on previously presented gene–gene interactions and miRNA–miRNA interactions, as well as targeting information introduced by miRNAs binding their targets (52–55). Clustering is commonly accepted as a powerful approach to partition the data items into a list of disjoint groups, such that the similarities within each group are maximized and those between different groups are minimized. For such a bilayer network, module identification means simultaneously clustering two kinds of objects and three types of links (Figure 1A). Without loss of generality, the miRNA–gene bilayer network can be mathematically expressed as three adjacency matrices: 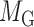for gene–gene links, 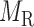for miRNA–miRNA links and 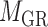for miRNA–gene regulating relations. From the traditional clustering viewpoint, the bilayer module identification consists of two traditional one-way clustering processes ( 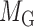and 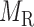) and one two-way clustering (biclustering) process (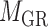), which can be organized as the pseudo 3-dimensional (pseudo-3D) view as shown in Figure 1B. Based on this concept, we proposed a method (or algorithm) called pseudo-3D clustering to achieve bilayer module identification, because it is neither a simple combination of traditional one- and two-way clustering methods, nor a real 3D clustering (or triclustering) method used in gene expression data (56).

In addition, the research reported in this paper has its roots in works which study the identification of miRNA–gene (or miRNA–mRNA) regulatory modules. Various methods were proposed to discover miRNA–gene regulatory modules (also named co-modules). However, the miRNA–gene regulatory module identification is different from the miRNA–gene bilayer module detection referred to herein; the former is either based only on the predicted miRNA–gene regulatory relations (57,58), or based only on the (anti-) expression correlations between miRNAs and genes (59–61), or at best incorporates the gene–gene relationships inferred from protein–protein interactions (62). However, the latter aims to respectively clustering the miRNAs and genes in two connecting layers based on three types of relations (Figure 1A). Zhang et al. (62) and Pio et al. (58) have given the detailed reviews of existing methods. Furthermore, specifically for a biological application, the bilayer module identification method has to consider a number of other important issues, of which the most critical is that the resulting bilayer modules should meet the following conditions:

1. Module overlap, since genes and miRNAs can be involved in multiple biological processes for the pleiotropy. Generally speaking, module overlaps show that nodes or links may belong to two or more modules. Several common clustering algorithms, including CFinder (12), MCL (63), MCODE (15), DetMod (11), ClusterONE (64) and MINE (65) permit overlaps between the modules. The pseudo-3D clustering algorithm will identify the overlaps either on gene layer or miRNA layer.

2. Hierarchical organization, a fundamental characteristic of many complex networks, implies that small groups of nodes organize in a hierarchical manner into increasingly large groups (66,67). A module at a higher level should contain multiple modules of lower levels. Some algorithms, like hierarchical clustering, can destruct this kind of organization by tuning a cutoff. Hierarchical modules allow studying the intermolecular interactions of different granularity. Bilayer modules should also be hierarchically organized.

3. High cohesiveness, which means the dense connections within the module, but only sparse connections between different modules. Specific to miRNA–gene bilayer modules, high cohesiveness means that the genes and miRNAs in the same bilayer module should be closely linked in respective layer and show strong regulation from miRNA layer to gene layer.

Taking into account all above considerations, we propose a method, named pseudo-3D clustering algorithm that provides a solution to the issues raised up by the specific module identification task for the mushrooming bilayer biological networks. The pseudo-3D clustering algorithm is demonstrated to be able to identify the overlapping, hierarchically organized and highly cohesive bilayer modules from, but not limited to, the miRNA–gene bilayer networks and further reveal their implications to specific biological process, such as soybean fatty acid synthesis.

MATERIALS AND METHODS

The mathematical representation of bilayer network and necessary definitions

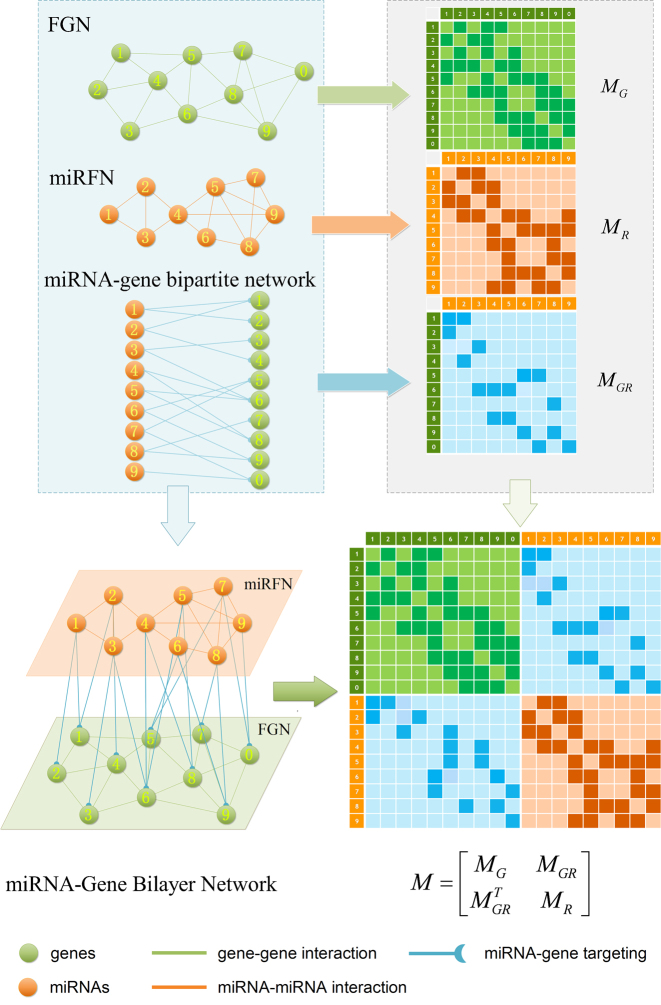
To be algorithm-friendly, some useful definitions are necessary. Figure 2 provides the workflow for construction and mathematical representation of a bilayer network, taking the soybean miRNA–gene bilayer network for instance. In previous studies, we have reconstructed four functional gene networks (FGN) and four miRNA functional networks (miRFN) of soybean (Glycine max), respectively (52,53). Integrating the predicted regulating relations between miRNAs and their target genes, we can easily consolidate a FGN and a miRFN to form a bilayer network such as shown in Figure 1A. For simplicity, we only integrate the most inclusive FGN and miRFN (i.e. FGN–INT and miRFN–INT) without considering all other possible combinations between four FGNs and four miRFNs. The brief statistics of the final bilayer network and the component networks are shown in Supplementary Table S1.

Figure 2.

The construction and mathematical representation of the miRNA–gene bilayer network.

Let 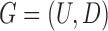and 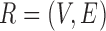be the FGN and miRFN, where 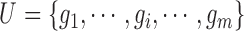and 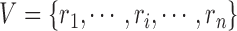are node sets representing 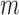genes and 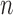miRNAs, respectively; 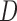and 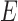denote edges corresponding to respective gene–gene and miRNA–miRNA interactions. The topology structures can be mathematically captured by their corresponding adjacency matrices 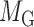and :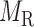

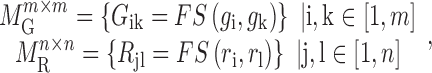(1)

where 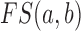is the functional similarity of the genes (or miRNAs) 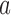and .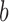

Let 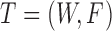be the miRNA–gene bipartite network, where 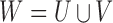is the union of genes in FGN and miRNAs in miRFN; denotes the edge set that with each edge having exact one end vertex in 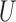and the other end vertex in 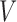, corresponding to the regulating relations between miRNAs and their target genes. Homoplastically, the topology structure can be mathematically captured by its corresponding adjacency matrix:

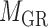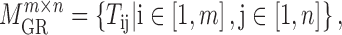(2)

where 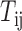is the regulatory strength value for a given miRNA–gene targeting relation (), which was defined in our previous work (52).

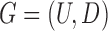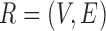Therefore, we define the bilayer miRNA–gene network by integrating the three networks, and 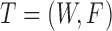, which share the same set of nodes 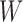. The bilayer network 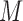has three types of interactions, where 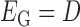represents the gene-gene interactions within the FGN, 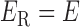represents the miRNA–miRNA interactions within miRFN and 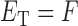the miRNA-gene targeting information. The topology structure of this bilayer network can be mathematically captured by the block adjacency matrix :

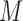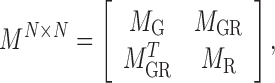(3)

where 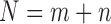. As an example shown in Supplementary Table S1, 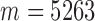and 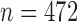for soybean bilayer network. In the later actual use, the matrix is also considered to consist of row vectors for genes and 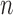row vectors for miRNAs, namely

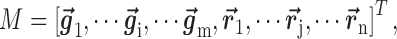(4)

where each gene (or miRNA) in the bilayer network is represented as a row vector in a (m+n)-dimension space, i.e.

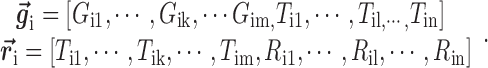(5)

Let 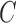denotes a bilayer module, which is defined in this research as a bilayer sub-network that consists of two objects (genes and miRNAs) and three inter-object relations. Subsequently, a bilayer module containing p (≤ m) genes and q (≤ n) miRNAs can also be represented by a sub-matrix with p + q row vectors in the (m+n)-dimension space. To be noted that, in order to facilitate the description of the psedo-3D algorithm, hereafter a bilayer module 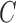refers specifically to a collection of genes and miRNAs (also known as a bicluster), and does not include the relations between them. Nevertheless, it will not hamper the identification of bilayer modules defined hereinbefore, since each one of these biclusters will be easily reverted to a previously defined module with bilayer topology by decoding the relations from the matrix M. Based on this specific definition of a bilayer module 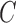, we use C_g = U ∩ C to denote the gene set of the module, and C_r = V ∩ C to denote the miRNA set.

The problem description of bilayer module identification in miRNA–gene bilayer network

As aforementioned, our aim in this work is to identify the bilayer network modules with the characteristics of overlap, hierarchy and high cohesiveness. Based on the mathematical representations and definitions, the bilayer module identification problem raised in this research can be described as follows:

Given:

• the set of genes 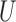and the set of miRNAs ;

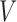• the block adjacency matrix ;

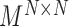• a cohesiveness function 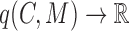, 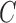is a bilayer module;

• a cohesiveness threshold 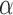for ;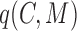

• a modularity function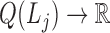, 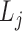is the j-th level bilayer modules.

Find: a list of bilayer modules 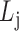, for each level 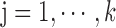such that:

• for each list 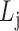, , 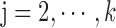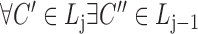satisfies 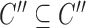(hierarchy);

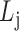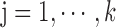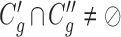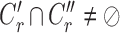• for each list , , satisfies or (overlapping);

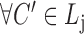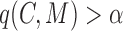• , (cohesiveness);

• the optimal level of bilayer modules 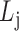according to .

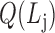Pseudo-3D clustering algorithm

The pseudo-3D clustering starts from extracting initial non-hierarchically organized modules and then iteratively decipher the hierarchical organization of modules according to a bottom-up strategy. Based on the above descriptions, we here describe the pseudo-3D clustering algorithm in high-level as Supplementary Figure S1 and following subsections. Supplementary Method M1 provides the full idea and detailed descriptions of the algorithm.

Initial module identification

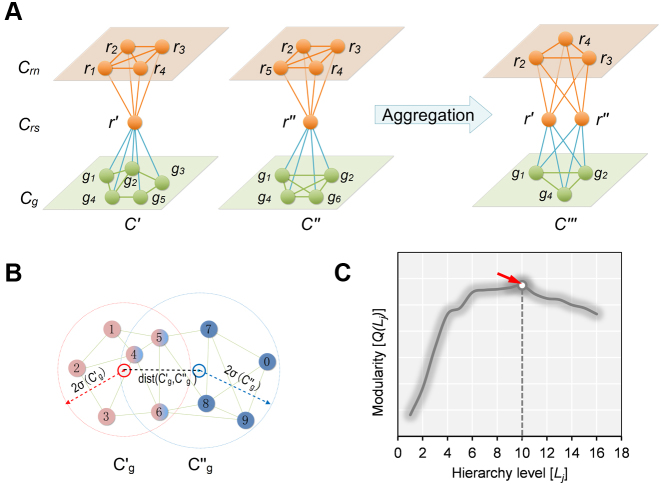
The pseudo-3D clustering algorithm starts from extraction of a set of initial non-hierarchically organized bilayer modules, namely the lowest-level module partition (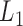). Each initial module is a primary bicluster aggregated from bicliques (Figure 3A, left), which are subgraphs extracted from the miRNA-gene bipartite network in two directions, i.e. miRNA-to-gene and gene-to-miRNA. The algorithm starts the identification by extracting a set of initial bicliques and then iteratively aggregates two bicliques into a new one (Figure 3A). The iteration will stop when there are no candidates for aggregation. The resulting initial modules derived from both in miRNA-to-gene and gene-to-miRNA direction are combined to form 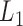level modules, by simply removing modules that appear more than once and those that are a subset of others. The bidirectional biclique extraction and aggregation process not only cluster the miRNA–gene regulating relations, but also the interactions of miRNA–miRNA and gene–gene, so that it realize the simultaneous clustering of two kinds of objects (genes and miRNA) and their three types of interrelationships, namely the original idea of a pseudo-3D clustering algorithm.

Figure 3.

The schematic view of the biclique aggregation and module merging. (A)The initial bicliques and the process of biclique aggregation (miRNA-to-gene direction); (B) An example of the object distribution of two candidate gene clusters for merging. (C) A toy example of the modularity curve and the corresponding optimal hierarchy level (red arrow).

Iteration of overlap detection and module merging

Overlap detection means to determine whether some objects (miRNAs or genes) belonging to a module appear in another module of the same level. However, not all pairs of overlapping bilayer modules will be merged subsequently. Module merging processes merge the overlapping modules when the spheres in gene (or miRNA) space of two merging candidates are close enough with their distance less than a heuristic threshold (Figure 3B). At each iteration, several pairs of modules can be merged, and an additional level of the hierarchy may or may not be added depending on whether merging is performed. Obviously, a module could be the merging candidate with more than one other module. In order to obtain a result independent of the order in which pairs of modules are considered, merging is actually performed after finding out all merging candidates and guarantees to maximize the cohesiveness of the resulting modules. The iteration will stop when neither overlaps nor merges are performed in the last iteration.

Determination of the optimal module partition

The iteration of overlap detection and merging will produce the partitions of a bilayer network in different levels. We need to further determine the optimal level at which the partition gives a more accurate characterization of the modular organization of the bilayer network. We here, based on the modularity function proposed by Newman (30) specifically for evaluation of a monolayer network partition, give a modularity function for the bilayer network partition. According to the modularity value, the optimal partition is specified as the level that produces the maximum modularity value across all hierarchy levels (Figure 3C).

Time complexity

The time complexity of the pseudo-3D algorithm depends on the time complexity of each single step. The initial module identification occupies a complexity of 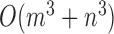in two directions. One iteration of overlap detection, merging and computing the 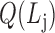value occupies 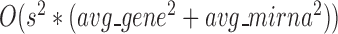, where 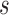denotes the number of modules. So, for 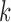levels of partitions with maximum 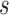modules at each level, the pseudo-3D algorithm will occupy a total complexity of 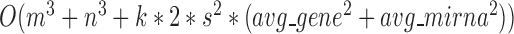; it will be reduced to 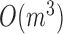in the most cases that 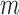(the number of genes in the bilayer network) is significantly larger than the other parameters. A detailed analysis of time complexity is provided in Supplementary Methods M1.

RESULTS AND DISCUSSION

Simulation and performance evaluation

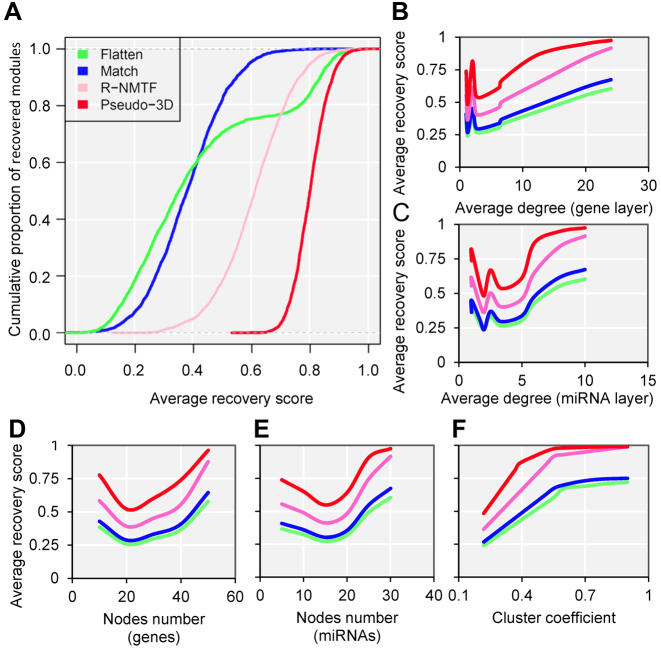
To explore the advantages of pseudo-3D clustering algorithm in terms of graph theory before the specific biological applications, we performed the comparison with other network clustering strategies using a stimulated bilayer network (Supplementary Methods, M2). One well-defined bilayer miRNA–gene network with extremely modular structure was simulated (Supplementary Figure S4A, B and Table S1) and three clustering strategies were used for comparison: (i) clustering the gene network and miRNA network separately and match them together via miRNA–gene links (‘Match’); (ii) Combining the three networks as one network and doing clustering (‘Flatten’); (iii) clustering the bilayer network using R-NMTF (68), a method was developed to co-cluster phenotypes and genes, which are also organized as a bilayer network. The performance was evaluated by the extent, to what a clustering method can recover the maintained bilayer modules from a randomly perturbed bilayer network. Based on 1000 perturbations, the pseudo-3D clustering outperforms all three other strategies significantly (P-value < 2.2e-16, Kolmogorov–Smirnov test), followed by R-NMTF (Figure 4A and Supplementary Figure S4C), and the Flatten gets the worst performance. This indicates that, for a bilayer network, the connections between two layers are important to get better module detection and that simultaneously clustering on three types of edges between two types of nodes will reinforce the clustering performance. The superior performance than another bilayer-like module detection method, R-NMTF, indicates the outstanding role of pseudo-3D clustering algorithm specifically for module identification of bilayer networks.

Figure 4.

Pseudo-3D clustering algorithm outperforms other methods based on simulation. (A) The cumulative proportion of recovered modules for each methods based on a simulated bilayer network. (B–F) The performance of each method regarding different node numbers, cluster densities and degree distributions. The (B and C) average degrees and (F) cluster coefficients are of the whole bilayer networks, while the (D and E) node numbers are of the individual bilayer modules.

To investigate how the network density and other relevant topological properties affect the clustering performances and further verify the robustness of pseudo-3D clustering algorithm with respect to the node numbers, cluster densities and degree distributions, we generated 10 simulated miRNA–gene bilayer networks; each bilayer network is composed of 100 well-defined bilayer modules and possess the combination of different node numbers, cluster coefficients and degree distributions (Supplementary Method M2, Supplementary Table S2). Simulation results were provided as boxplots in Supplementary Table S2, shown as the average recovery scores of all four clustering strategies varying coordinately with the nodes number, degree distribution and cluster coefficient, with the same trend that pseudo-3D outperforms other three methods (Figure 4B–F). Specifically, the average degree of the network will facilitate the clustering when the average degree is more than 5 for gene layer and more than 3 for miRNA layer, which indicates that a higher density will produce better performance for all methods (Figure 4B and C). Nevertheless, the absolute node number (either genes or miRNAs) does not contribute consistently to the performance of clustering (Figure 4D and E). Additionally, we found a significantly consistent correlation between the cluster coefficients and recovery scores, indicating that cluster coefficient is the most important determining factor for clustering. This is in line with the expectation that a well modularized network has a larger cluster coefficient and is easier to be partitioned into clusters (modules). Moreover, extremely high cluster coefficient reduces the difference in performance between pseudo-3D and R-NMTF rather than between these two bilayer clustering methods and the other two conventional monolayer clustering methods (Flatten and Match), indicating that considering bilayer structure will improve the clustering performance. Taken together, the simulation studies based on either one benchmark or a series of bilayer networks of the combination of different cluster densities and degree distributions, demonstrated outperformance and robustness of the pseudo-3D clustering method.

The bilayer module identification of the soybean miRNA–gene network

We then applied pseudo-3D clustering to the soybean miRNA–gene network. In the phase of initial module identification, we obtained 472 initial bicliques for ‘miRNA-to-gene’ direction and 5263 for ‘gene-to-miRNA’ direction. After aggregation, all bicliques were consolidated into 300 and 2823 initial modules, respectively. A pruning process was performed to incorporate these two sets of initial modules and generate the first level partition of the miRNA–gene bilayer network, i.e.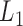, which contains 1497 modules. The modules at 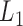have 83 genes and 6 miRNAs in average, with the average clustering coefficient (0.7363, see Supplementary Table S3) is much higher than the global bilayer network (0.696, see Supplementary Table S1).

Taking 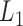as the input of the iteration for overlap detection and merging, we got another 8 upper levels of module partitions, i.e. 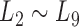. In other words, the soybean miRNA–gene bilayer network was partitioned into modules that hierarchically organized at 9 different levels. The compositions and main topological properties of the 9 levels of bilayer modules are given in Supplementary Table S3. It shows that, with the increasing of module level from 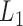to 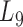, the average module size increases, the number of modules decreases and the average cohesiveness diminishes, which are consistent with the theoretical characterizations of merging modules into larger ones. However, the average clustering coefficient of the modules at different levels have no significant increasing or decreasing trend (with the variance of 0.000346), indicating that all modules identified by pseudo-3D clustering algorithm are valid. In addition, the average clustering coefficients of modules at all levels (0.7507) are larger than that of the global miRNA–gene bilayer network (0.696, Supplementary Table S1), further illustrating the effectiveness of module partition at each level.

Based on the aforementioned definition, the maximum modularity corresponds to the best module partition. Therefore, 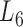(in bold font, Supplementary Table S3) is the optimal level of module partitions. In the subsequent sections, 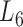are used to perform deep analyses and discussions on the module topologies, functional enrichments and biological experimental evidences, aiming at getting the insight into the regulatory characteristics between the soybean miRNAs and their target genes at module level and the further evaluation of the effectiveness of the pseudo-3D clustering algorithm.

The topological analysis of the soybean bilayer modules

At the 6th level (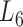), the soybean miRNA–gene bilayer network is partitioned into 100 overlapping bilayer modules. 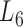has an average of 333 genes and 72 miRNAs per module, with the average cohesiveness of 0.457 and the average clustering coefficient of 0.7464. Supplementary file 2 (sheet 1) provides the summary statistics of the 100 modules at 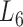. In average, each miRNA targets 9.3 intra-module genes (i.e. 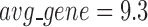), and each gene is targeted by 1.5 intra-module miRNAs (i.e. ).

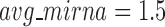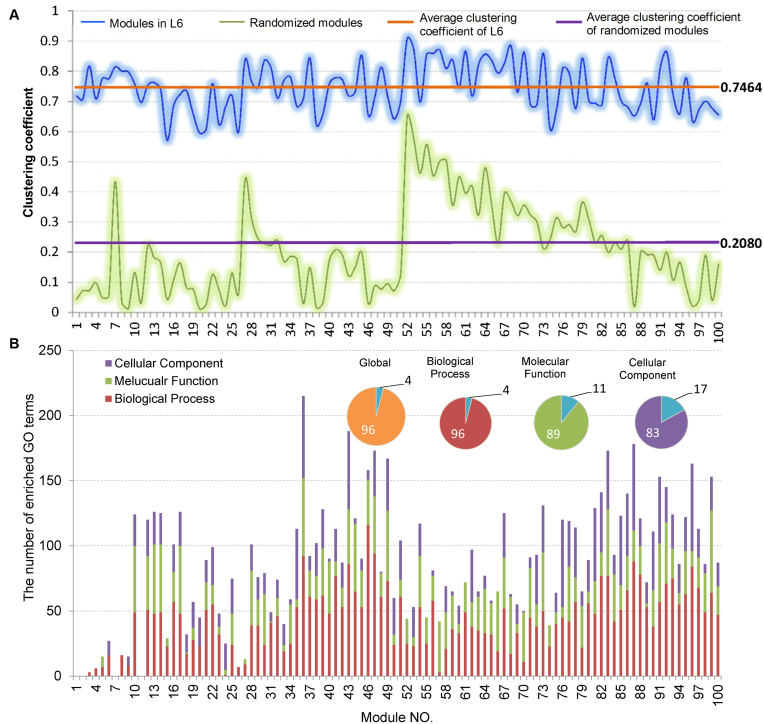
Firstly, we analyzed the variation of the clustering coefficients of 100 modules at 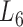. Shown in Figure 5A and Supplementary File 2 (sheet 1), the most of clustering coefficients vary insignificantly from 0.7 to 0.8 with the average of 0.7464 and the variance of 0.006. To compare, we built a set of 100 randomized modules maintaining as same node numbers and degree distributions for each module as those at L₆ by edge perturbations. In contrast, the clustering coefficients of the 100 randomized modules vary significantly from 0.01 to 0.65 with a lower average of 0.2080 and a larger variance of 0.022. There was additional significant difference between the two sets of modules regarding the clustering coefficients (P-value = 1.2e-81 by ANOVA). The above results show that the nodes (genes or miRNAs) of the modules at L₆ are connected more closely than those of the randomized ones, which implies the modular characterization of the genes and/or miRNAs in functionality.

Figure 5.

Topological and functional analysis on the optimally partitioned bilayer modules. (A) The clustering coefficient distribution of the 100 modules at L6. Horizontal lines indicate the average cluster coefficients. (B) The statistics for GO functional enrichment of the 100 modules at L6. Inset pies show the percentage of enriched (color filled) and unenriched (blue filled) modules.

Secondly, based on the conclusion of our previous research (52) that the miRNAs in the same family or in the same cluster share a larger functional similarities than randomly selected miRNAs, we investigated whether the miRNAs in the same family or in the same cluster tend to be clustered in the same module. For the 81 miRNA families, 76 families (94%) have more than half of their member miRNAs been clustered in same modules, of which 50 families (62%) are completely clustered in same modules. For the 50 families, half of them are completely clustered in more than one module, with the maximum of 15 modules. These suggest that the miRNAs in the same family tend to participate in forming the same functional module and have pleiotropy.

For the 59 miRNA clusters, 50 clusters (85%) have more than half of their members been clustered in same modules, of which 39 clusters (66%) are completely clustered in same modules. This suggests a similar conclusion to miRNA family that the miRNAs located in the same cluster tend to be a same functional module. However, we also found a significant difference between them. That is only three of 59 miRNA clusters are completely clustered in more than one module, wherein only one cluster is completely in maximum 3 modules, another two are completely in 2 modules. It suggests that the miRNAs in the same cluster do not exhibit characterization of pleiotropy as the miRNA in the same family. We speculated on the reason for the difference is that miRNA regulates its target genes by base-pared binding the UTR (untranslated region) of the mRNA, so that the pleiotropy of a set of miRNAs depends more on whether they share the same seed sequences rather than the locations in the genome, because a miRNA family always shares a same seed sequence.

Functional enrichment analysis and a case study in soybean fatty acid synthesis

Enrichment analysis is a computational method that widely used to determine whether an a priori defined set of genes shows statistically significant, concordant differences between two biological states (e.g. Gene Ontology) (69). To estimate whether the genes are significantly enriched in a module extracted by pseudo-3D clustering algorithm, we performed functional enrichment analysis on 100 bilayer modules at 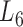based on Gene ontology (GO) annotation. Except four modules (i.e. #1, #2, #7 and #11), the rest 96 modules are significantly enriched in three aspects of GO, i.e. biological process (BP), molecular function (MF) and cellular component (CC) (see Figure 5B). In details, 96 modules are enriched in BP, 89 modules in MF and 83 modules in CC, covering an average of 91% genes of each module (#34 module has the maximum coverage of 99.435%). The online database SoyFN (70) allows the retrieval of detailed enrichment results for all modules (http://nclab.hit.edu.cn/SoyFN/SoyModule.php).

Soybean is the largest oilseed crop produced and consumed worldwide, accounting for 56% of the world oilseed production (SoyStats 2014, http://soystats.com). In this subsection, therefore, we take soybean oil (fat) synthesis as an example to investigate whether and/or how the bilayer modules produced by pseudo-3D clustering algorithm can characterize a real biological process. In order to get the genes and miRNAs involved in fat synthesis, we searched in four public databases and consulted seven literatures (Supplementary Methods, M3). As a result, we got 177 genes that encode 24 key enzymes and 102 miRNA types (see Supplementary Methods M3 for ‘miRNA type’ definition), which are also represented as Supplementary Figure S5 according to the three stages of fat synthesis.

We firstly analyzed the distribution of 177 genes encoding 23 key enzymes (except MCMT, EC:2.3.1.39) in the 100 bilayer modules at L₆. The results are provided as a matching matrix shown in Supplementary Figure S6 and show that the enzyme encoding genes of glycolysis and fatty acid synthesis are significantly concentrated in the different functional modules, indicating that the genes in the modules partitioned by pseudo-3D clustering algorithm have a higher correlation in function. Exceptionally, the genes that encode the enzymes involved in fatty acid modification and TAG assembly (the third stage of the fat synthesis) are not matched to any modules. We think the possible reasons are: (i) compared with such basic metabolic processes as glycolysis, the research of this process was not thorough enough, accumulating less functional annotation data of the related genes; (ii) there are relatively less enzyme encoding genes involved in this process. We also found that different modules can gather the same enzyme encoding gene (set), which is the evidence that the functional modules identified by pseudo-3D clustering algorithm are overlapping.

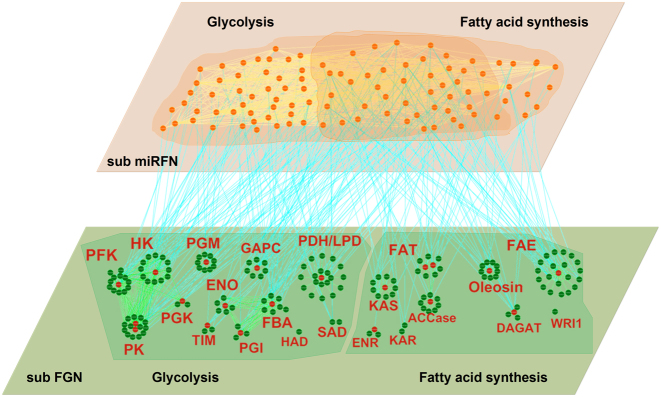
Secondly, using the 177 genes and 102 miRNA types, we extracted a subnetwork regarding fat synthesis from the global soybean miRNA–gene bilayer network. As shown in Figure 6, the subnetwork contains 380 edges among 175 genes (gene–gene), 553 edges among 102 miRNA types (miRNA–miRNA) and 242 edges between 102 miRNAs and 68 their target genes (miRNA–gene). Supplementary file 3 provides the detailed information of the sub network, which can be recreated by imported into Cytoscape 3.3.0 (71). Supplementary Table S4 provides the detailed statistics of the global topological properties of this subnetwork.

Figure 6.

A graphic view of the miRNA–gene bilayer subnetwork for soybean fat synthesis. All abbreviations of the enzyme names are given in Supplementary Figure S5.

As apparent from Supplementary Table S4, in the miRNA–gene bilayer subnetwork for soybean fat synthesis, there are relatively sparse connections among genes with smaller clustering coefficient (0.333) and network density (0.025), but dense connections among miRNAs with larger clustering coefficient (0.528) and density (0.107). This indicates that the genes, as the enzyme encoding units, are relatively more homogeneous in function, while the miRNAs, as the post-transcriptional regulators, exhibit multifunctional and synergistic characteristics. Figure 6 shows that genes encoding the same enzyme (in red font) themselves constitute a spokewise module with one or two genes as the hub (red nodes). The hub genes play more critical roles in encoding corresponding enzymes and should be the preferential candidates for biological verification. Also the spokewise topology results in the small clustering coefficient and density. The spokewise modules are not completely independent. The modules encoding the same type of enzymes, such as the modules PFK, HK, PGK and PK, are connected to form a complete module network (the left of lower layer, Figure 6).

Application to human miRNA–gene bilayer network reveals the consistent robustness of pseudo-3D clustering

We further employed a more informative human bilayer network to better illustrate the usefulness and biological implications of pseudo-3D clustering algorithm. The human bilayer network was constructed based on the public available data sources in the context of disease (54,55,72) (Supplementary Methods M4) that contains much more biological information than that from an unpopular plant, soybean. Pseudo-3D clustering algorithm clustered this human bilayer network at 14 different hierarchies, with the 14th level (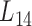) being the optimal partition based on the modularity measure (Supplementary Table S5). At 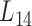, the human miRNA–gene bilayer network is partitioned into 37 overlapping bilayer modules. L₁₄ has an average of 696 genes and 158 miRNAs per module, with the average cohesiveness of 0.4404 and the average clustering coefficient of 0.4343. Supplementary File 2 (sheet 2) provides the summary statistics of the 37 modules at L₁₄. In average, each miRNA targets 8.9 intra-module genes (i.e. 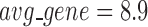), and each gene is targeted by 2.0 intra-module miRNAs (i.e. ).

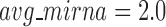To further illustrate how the pseudo-3D clustering algorithm groups the human bilayer network consistently with the functional categories, we first performed GO enrichment analysis (biological process) on the gene set of each module, separately, to investigate the enriched functions. The top ten enriched GO terms were merged to compare the functional similarity of pair-wise modules (Supplementary Methods M4 and Supplementary File 4). Then the hierarchical clustering was performed based on functional enrichment and pseudo-3D partitions to compare their consistency. We found that all modules were completely clustered into the same three clusters based on these two types of independent information (Supplementary Figure S7). A quantitative score, named consensus score, was defined to indicate this consistency (Supplementary Methods M4). The results shows that pseudo-3D clustering algorithm can produce a bilayer network partition with a significantly high consistency with the functional enrichment (consensus score = 1.0, P-value < 2.2e-16).

Additionally, enrichment analysis of human diseases on all 37 modules shows additional evidence indicating the robustness of pseudo-3D algorithm (Supplementary Methods M4). We found that only a small part of 37 modules significantly enriched in a sub group of diseases, therein most of these disease-related modules are extremely enriched in one or a limited diseases, such as module 31 (m31) is significantly related to breast cancer (Supplementary Figure S8A). Hierarchical clustering based on disease enrichment also shows a significantly high consistency with the pseudo-3D partitioned hierarchies (consensus score = 1.0, P-value < 2.2e-16) (Supplementary Figure S8B).

To sum up, the pseudo-3D clustering algorithm is demonstrated to successfully cluster the bilayer networks from both the plant and human into hierarchically organized and overlapping bilayer modules with high topological cohesiveness. Furthermore, functional enrichment analyses, as well as the biological evidence derived from database retrieval and literature collection, proved its excellent performance in identifying bilayer modules with functional consistency from a bilayer network. Additionally, the pseudo-3D clustering algorithm has been implemented as a runnable JAR file for public download and application to other types of bilayer networks. The manual and JAR file can be accessed at http://nclab.hit.edu.cn/SoyFN/SoyModule.php.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Natural Science Foundation of China [61571163, 61532014, 61402132, 91335112 and 61271346]. Funding for open access charge: National Natural Science Foundation of China [61571163].

Conflict of interest statement. None declared.