Origin of the blueshift of water molecules at interfaces of hydrophilic cyclic compounds

Molecular mechanism of the blueshift of water molecules.

Abstract

Water molecules at interfaces of materials exhibit enigmatic properties. A variety of spectroscopic studies have observed a high-frequency motion in these water molecules, represented by a blueshift, at both hydrophobic and hydrophilic interfaces. However, the molecular mechanism behind this blueshift has remained unclear. Using Raman spectroscopy and ab initio molecular dynamics simulations, we reveal the molecular mechanism of the blueshift of water molecules around six monosaccharide isomers. In the first hydration shell, we found weak hydrogen-bonded water molecules that cannot have a stable tetrahedral water network. In the water molecules, the vibrational state of the OH bond oriented toward the bulk solvent strongly contributes to the observed blueshift. Our work suggests that the blueshift in various solutions originates from the vibrational motions of these observed water molecules.

INTRODUCTION

The molecular behavior of water molecules at interfaces of materials plays an important role in all chemical, thermodynamic, and biological processes (1–3). Materials are classified as either being hydrophobic or hydrophilic, according to their affinity to water. At hydrophobic interfaces, the hydrogen-bond (H-bond) network between water molecules is perturbed by the material, and consequently, the H-bonds of some water molecules are broken, forming a “dangling water molecule” (4). Using either Raman spectroscopy or infrared-visible sum frequency generation (SFG) spectroscopy, these weak H-bonded water molecules have been observed to exhibit a blueshift at many interfaces, such as alcohol (5, 6), tetraalkylammonium (7), fullerene derivatives (8), polyethylene glycol (9), and neopentane (10).

On the other hand, hydrophilic materials form stable H-bonds with water molecules. This interaction causes the spectral peak around 3200 cm⁻¹ to become red-shifted, as a response to changes in the strength of the H-bond (11, 12). Nevertheless, some experimental studies have reported that a blueshift was also observed in the aqueous solutions of hydrophilic materials, for example, alkali halide ions (13) and acetonitrile (14). These controversial phenomena demonstrated by hydrophilic materials have been attributed to a combination of both inter- and intramolecular interactions. Although the observed blueshift has been linked to the presence of weak H-bonded water molecules at the interfaces, the exact molecular mechanism governing the blueshift has remained unclear for both hydrophobic and hydrophilic interfaces to date.

Saccharides are the most abundant biological materials and play various important roles in living organisms. Monosaccharide is the basic unit of all the saccharides and is a main target of various applications. Here, we combine ab initio and classical molecular dynamics (MD) simulations with Raman spectroscopy to investigate the molecular mechanism of the blueshift around six isomers of a monosaccharide. Our results show that the blueshift arises from the weak H-bonded water molecules located in the first hydration shell. The vibrational state of the OH bond, which is oriented toward the bulk solvent, contributes significantly to the observed blueshift. These observations provide an enhanced depiction of the current experimental blueshift at aqueous interfaces.

RESULTS AND DISCUSSION

Hydration-shell spectra of monosaccharides

We applied multivariate curve resolution (MCR) (15) to Raman spectra of d-glucose solutions at concentrations between 0 and 0.5 M (fig. S1). Our Raman-MCR results were obtained using the self-modeling curve resolution (SMCR) algorithm (16) (see Materials and Methods for more details). The SMCR algorithm is used to decompose spectra into bulk water–correlated and solute-correlated (SC) components. Figure 1A shows the SC and bulk water spectra. The peak at 2900 cm⁻¹ denotes the monosaccharide CH groups, and the two overlapping peaks at 3200 and 3400 cm⁻¹ correspond to H-bonded OH groups (6). The OH peaks in the SC spectra arise from the monosaccharide itself and water molecules in the hydration shell. However, a previous study showed that the SC spectra mostly contain information arising from water molecules in the hydration shell by using various aqueous alcohols (6). Moreover, the OH peaks of the SC spectrum were as broad as those of the bulk water spectrum, which provides evidence that the peaks were correlated to water molecules in the hydration shell of the monosaccharide. Compared with the bulk water spectrum, blueshift of the OH peaks was observed in the SC spectrum.

Fig. 1. Spectra of water molecules in the d-glucose solution.

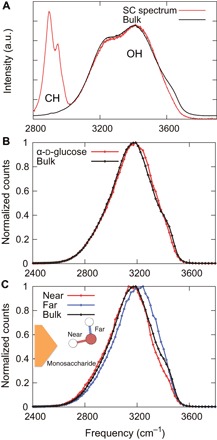
(A) Experimental Raman spectrum of the bulk (black line) and SC spectrum (red line). The SC spectrum was obtained using the spectra of d-glucose solutions in 0, 0.05, 0.1, 0.3, and 0.5 M. (B and C) The OH vibrational spectra of water molecules obtained by the Car-Parrinello MD (CPMD) simulations using the wavelet analysis within 3.5 Å of α-d-glucose (red line) (B) and near (red line) and far (blue line) OH bonds (C). The “near” and “far” represent the OH bonds from the monosaccharide oxygen atoms. a.u., arbitrary unit.

To reveal molecular mechanism of the blueshift, we also calculated OH vibrational spectra around the monosaccharide using the ab initio MD simulations (fig. S2). Most hydration shells in aqueous monosaccharide solutions are known to be distributed around monosaccharide oxygen atoms (17, 18). Therefore, in this study, we focused on the hydration shells around all oxygen atoms present in the monosaccharide. Figure 1B shows the OH vibrational spectra obtained by the wavelet analysis (see Materials and Methods for more details) of the water molecules that are within 3.5 Å of the monosaccharide oxygen atoms. Notably, we also observed blueshift of OH peak in hydration shell of the monosaccharide, which is in agreement with the result of SC-Raman spectrum. In a water molecule, the OH bond that is H-bonded with the monosaccharide is classified as the “near” OH bond, and the opposing OH bond is classified as the “far” OH bond. We observed a large blueshift in the far OH vibrational spectra; however, no blueshift was observed in the spectra of the near OH vibrational spectra (Fig. 1C). The presence of this blueshift around all six isomers of the monosaccharide suggests that blueshift is a fundamental phenomenon found at the interfaces of many cyclic compounds (fig. S3).

The relationship between water arrangement and the observed blueshift

In liquid water, the water molecules are tetrahedrally arranged, and each water molecule has four H-bonds (two donors and two acceptors) (19). To understand the correlation between the observed blueshift and the water molecule network, we first calculated the tetrahedral order parameter (TOP) (20), which represents the degree of the tetrahedral arrangement of water molecules. Two forms of the TOP were calculated: (i) the TOP between water and sugar oxygen atoms and (ii) the TOP between only water oxygen atoms (see Materials and Methods for more details). Figure 2A shows the TOPs of water molecules as a function of the distance between the oxygen atoms of monosaccharide and water molecules. In the first hydration shell, the TOP between only water oxygen atoms is lower than that of the bulk solution because the tetrahedral arrangement of these water molecules is perturbed by the monosaccharide. On the other hand, the TOP between water and sugar oxygen atoms is equal to or greater than that of the bulk solution, which means that the sugar oxygen atoms are involved in the tetrahedral arrangement of water molecules. At a distance of 4 Å, both the TOPs converge to 0.8, corresponding to the value for the bulk solvent.

Fig. 2. Relationship between water arrangement and vibration in the α-d-glucose solution.

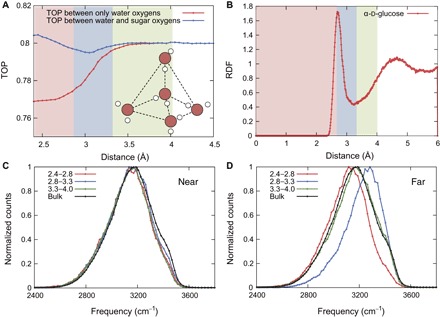
(A) Average TOPs as a function of the distance between the oxygen atoms of monosaccharide and water molecules. Red and blue lines show the calculation without and with monosaccharide oxygen atoms, respectively. (B) RDF as a function of the distance between the oxygen atoms of monosaccharide and water molecules. (C and D) Near and far OH vibrational spectra of water molecules separated by the characteristic regions in the TOP between water and sugar oxygen atoms. Colored lines are the spectra using water molecules located between 2.4 and 2.8 Å (red), 2.8 and 3.3 Å (blue), and 3.3 and 4.0 Å (green).

Next, we separated the hydration shell into three regions according to the TOP values between water and sugar oxygen atoms: (i) The TOP is equal to or greater than that in the bulk (near_TOP region; the water molecule oxygen is located between 2.4 and 2.8 Å), (ii) the TOP is lower than that in the bulk (middle_TOP region; the water molecule oxygen is located between 2.8 and 3.3 Å), and (iii) the TOP is equal to that in the bulk (far_TOP region; the water molecule oxygen is located between 3.3 and 4.0 Å). To clarify the relationship between these regions and the hydration shell depth, we calculated the radial distribution function (RDF) between the water molecules and monosaccharide oxygen atoms (Fig. 2B). The boundary between the near_TOP and middle_TOP regions is represented by the first peak of the RDF at a distance of 2.8 Å. The boundary between the middle_TOP and far_TOP regions is depicted by the first minimum of the RDF at the distance of 3.3 Å. We demonstrated that the first hydration shell is the most perturbed by the monosaccharide at a distance of 2.8 to 3.3 Å (that is, in the middle region).

Figure 2 (C and D) shows the near and far OH vibrational spectra of water molecules in each of the above three regions. In the near_TOP region, water molecules form a cooperative H-bond network with other water molecules and monosaccharide oxygen atoms. Because of this stable network, the far OH vibrational spectra are shifted to lower frequencies (redshift). Notably, in the middle_TOP region, the far OH vibrational spectra are shifted to higher frequencies (blueshift). As we showed above, the weak H-bonded water molecules in the middle_TOP region contribute to this blueshift, which is similar to the observation at hydrophobic interfaces (7).

Distribution of the weak H-bonded water molecules

We performed simulations for six isomers of a monosaccharide, which differ only in the orientation of their hydroxyl groups. Using the spatial distribution function, we visualize the probability density of the water molecules around the monosaccharides (Fig. 3). Because of the different orientation of the hydroxyl groups, the distribution of the hydration shell is unique to each isomer. The weak H-bonded water molecules are distributed throughout this hydration shell, with all the hydroxyl groups encompassing the water molecules. Thus, the blueshift was observed in all the monosaccharide solutions. Furthermore, these results suggest that weak H-bonded water molecules can be found at the interfaces of many other cyclic compounds.

Fig. 3. Density of water molecule oxygen atoms around all the monosaccharides.

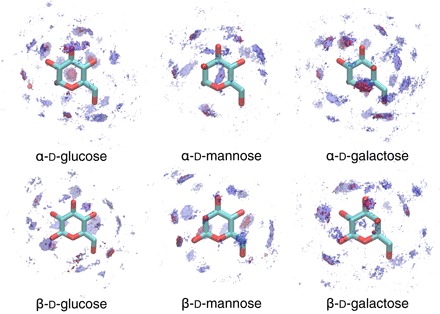
Blue-colored regions represent the first hydration shells, and red-colored regions represent the location of weak H-bonded water molecules, which are defined as water molecules located in the middle_TOP region with low values for TOP between water and sugar oxygen atoms.

To further investigate the mechanism of the blueshift, we analyzed the H-bond status (donor or acceptor) in the different regions of the first hydration shells. To achieve a large ensemble for this analysis, we additionally performed classical MD simulations. Figure 4A shows the average number of H-bonds between water molecules, and the formation process of the observed weak H-bonded water molecules around the monosaccharides is schematically illustrated in Fig. 4B. The regions defined by the TOP using the CPMD are in good agreement with results from the classical MD simulations. In the near_TOP region (2.4 to 2.8 Å), donor H-bonds between water molecules are more abundant than acceptor H-bonds, meaning that the two hydrogen atoms are largely oriented toward the bulk solvent (observed as the red region in Fig. 4B). The H-bonds of these water molecules are very stable, and essentially, the water molecules are compatible with the structure of both the monosaccharide and the bulk solvent. Conversely, in the middle_TOP region (2.8 to 3.3 Å), acceptor H-bonds between water molecules are more abundant than donor H-bonds, meaning that the water molecules predominantly act as a donor to the monosaccharide (observed as the blue region in Fig. 4B). These results are in agreement with the CPMD result that the far OH exhibits a blueshift, whereas the near OH exhibits a redshift (Fig. 2, C and D). We confirmed that these results had no dependence on the water model of classical MD simulation and H-bond definitions (fig. S4).

Fig. 4. Formation process of the observed weak H-bonded water molecules around the monosaccharide.

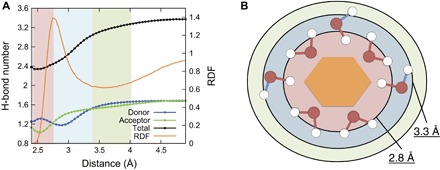
(A) Average number of H-bonds between water molecules and RDF as a function of the distance between the oxygen atoms of monosaccharide and water molecules. These results were obtained by the classical MD simulations of the α-d-glucose solution at 298 K and 0.1 M using the Transferable Intermolecular Potential with 3 Points (TIP3P) water model. Blue, red, and black represent the number of donor, acceptor, and total H-bonds, respectively. (B) Schematic view of the formation process of the weak H-bonded water molecules. Red region shows 2.4 to 2.8 Å, where water molecules mainly form acceptor H-bonds with the monosaccharide. These water molecules are compatible with the structure of both the monosaccharide and the bulk. Blue region shows 2.8 to 3.3 Å, where water molecules mainly act as a donor with the monosaccharide. In these regions, H-bonds with outer water molecules are unstable.

From these results, we propose a mechanism of the formation process of the first hydration shell around the monosaccharide. First, the closest water molecules (in the region of 2.4 to 2.8 Å) primarily form acceptor H-bonds with the monosaccharide, and these water molecules are as stable as the bulk solvent. Second, empty spaces in the first hydration shell are filled with other water molecules (in the region of 2.8 to 3.3 Å). In this region, water molecules mainly form donor H-bonds with the monosaccharide. These inner H-bonds of the water molecules are strongly attracted and perturbed by the monosaccharide; thus, the outer H-bonds between other water molecules become relatively unstable. The unstable H-bond causes the dangling motions, and these water molecules exhibit the observed blueshift.

CONCLUSIONS

In summary, we have used Raman spectroscopy and ab initio MD simulations to investigate the molecular mechanism of the blueshift of water molecules around six isomers of a monosaccharide. We observed the blueshift of water molecules in hydration shells of monosaccharides in both experiments and simulations. Using the simulations, it was demonstrated that in the first hydration shell, the closest water molecules (2.4 to 2.8 Å) mainly form acceptor H-bonds with the monosaccharide, and the water molecules are stable. Conversely, in the region of 2.8 to 3.3 Å, water molecules mainly form donor H-bonds with the monosaccharide, and these water molecules exhibit a blueshift. The vibrational state of the OH bond, which is oriented toward the bulk solvent, highly contributes to the observed blueshift. These results indicate that the weak H-bonded water molecules are arranged to be compatible not with the bulk water molecule but with the monosaccharide.

This molecular mechanism of the blueshift may be general for many other solutions. A previous study also observed the blueshift in an aqueous NaBr solution by using SC-Raman spectroscopy (13). To validate the molecular mechanism, we performed a CPMD simulation of a NaBr solution. We applied the same analysis that we used for the monosaccharide solutions to the hydration shell around Na⁺ and Br⁻. By the near and far analysis, we found the blueshift arising only from far OH bond of water molecules around Br⁻ (fig. S5). This result supports the validity and generality of this molecular mechanism of the blueshift.

Furthermore, we demonstrated the relationship between the blueshift and the perturbation of the tetrahedral structure in water molecules at the hydrophilic interface. This perturbation of water molecules in the first hydration shell has previously been observed for many biological materials, for example, DNA (21), small peptides (22–24), and various proteins (20). Therefore, it can be extrapolated that the observed blueshift occurs not only at monosaccharide interfaces but also at the other materials and that these properties are essential to understanding the complex nature of many water-material interfaces.

MATERIALS AND METHODS

Raman data collection and MCR methods

Here, Raman spectra of d-glucose solutions at 0, 0.05, 0.1, 0.3, and 0.5 M were collected. These experiments were conducted using an I-shaped channel (the detail is shown in fig. S6). The top and bottom walls of the channel were made of borosilicate glass, and the side wall was made of polydimethylsiloxane. The depth and width of the channel was set to 1 and 5 mm, respectively. The measurement point was the midpoint of the channel.

All the Raman spectra were collected using a Raman spectrometer inVia Raman microscope (Renishaw) equipped with a Nd:YAG laser (532 nm) and a DM2500 (Leica) model microscope. The experiments were coupled with a charge-coupled device camera (operating at 1024 × 256 pixel) mounted to a 250-mm focal length imaging spectrograph with a grating of 1800 l/mm. The laser beam was focused on the samples with a 50× objective lens and a numerical aperture of 0.75 to the spot of 0.9 μm. The average laser excitation power was 150 mW, and the exposure time of the camera was set to 5 s. Ten images were accumulated as one spectrum, and this procedure was repeated three times at each concentration.

The SMCR algorithm (16) was performed as an MCR method. In the preprocessing phase, almost zero signals in the spectral regions (~2800 and ~3900 cm⁻¹) were subtracted, and the input Raman spectra were normalized by their area. Then, we concatenated all the spectra into a data matrix (n × m) containing n spectra of the length m, and the SMCR algorithm was applied to the data matrix.

Ab initio MD simulations

Ab initio MD simulations were performed by the CPMD code (25) using the Car-Parrinello method (26). Before the CPMD simulations, we performed classical MD simulations to obtain the initial structure of the systems. The MD simulations and energy minimizations were conducted using the NAnoscale Molecular Dynamics (NAMD) 2.9 software (27) with the GLYCAM06 (28) and TIP3P water model (29). Periodic boundary conditions were applied in all three directions of the cubic box. The last length of the NPT MD simulation was used to determine the side length of the cubic box in the CPMD simulation. Furthermore, the initial structures in the CPMD simulation were taken from the last structures of 10-ns MD simulations.

In the CPMD simulations, our systems were treated according to the density function theory using the Perdew-Burke-Ernzerhof functional for the approximation of the exchange-correlation terms (30). The core electrons were treated using norm-conserving pseudopotentials with the Kleinman-Bylander separation scheme for carbon, hydrogen, and oxygen (31). We described the valence-core interaction using the Troullier-Martins pseudopotentials (32). Plane wave functions were used for the basis of the calculations and set with an energy cutoff of 80 rydberg. The systems were composed of a monosaccharide and a set number of water molecules. Specifically, the monosaccharides α- and β-d-glucose/d-mannose/d-galactose were paired with 108, 108, 101, 107, 103, and 103 water molecules, respectively. The simulation time step was 0.097 fs in the NVT ensemble using the Nosé-Hoover thermostat, and the fictitious electron mass was set to 0.22 atomic mass units. Each simulation was performed for 60 ps, and the analyses were conducted over the last 52-ps trajectories. We also performed the CPMD simulation of NaBr solution with the same parameters and conditions as the monosaccharide solutions. The system contains Na⁺ and Br⁻ and 100 water molecules. The simulation was performed for 96.6 ps, and the analyses were conducted over the last 92.6-ps trajectories.

Classical MD simulations of the α-d-glucose solution with TIP3P (29) and Transferable Intermolecular Potential with 5 Points (TIP5P) (33) were performed using the NAMD 2.9 (27) and GROningen MAchine for Chemical Simulations (GROMACS) 5.1.2 (34) software, respectively. We performed the MD simulations using the modified GLYCAM06 force field (35) for α-d-glucose. The modified GLYCAM06 force field improves the modeling of monosaccharide aggregation compared with that of the original GLYCAM06 force field (28). For the simulation, we chose a 0.1 M α-d-glucose system composed of 20 α-d-glucose and 11,070 water molecules. NPT constant simulations at 298 K and 1 bar were carried out for 200 ns, with the data from the first 10 ns being discarded because of the relaxation. Periodic boundary conditions were applied to all systems. In the simulation using the NAMD software, the temperature was maintained using the Langevin thermostat with a Langevin damping coefficient of 1.0 ps⁻¹ and the Langevin piston barostat. Long-range electrostatic interactions were calculated using the particle mesh Ewald method with a real-space cutoff of 10 Å. Van der Waals interactions were cut off at 10 Å. A time step of 2 fs was used for the SHAKE algorithm that was applied to constrain all H-bonds. In the simulation using the GROMACS software, the pressure and temperature of the system were controlled using the Parrinello-Rahman barostat (36) and velocity-rescaling method (37), respectively. Long-range electrostatic interactions were calculated using the particle mesh Ewald method with a real-space cutoff of 12 Å. Van der Waals interactions were cut off at 12 Å. A time step of 2 fs was used for the LINCS (linear constraint solver) algorithm applied to constrain all H-bonds (38).

Frequency calculations: Fourier and wavelet transforms

Vibrational spectra were obtained from the vibrational density of states (39)

$$\mathit{P}(\mathrm{\omega })={\displaystyle \sum _{\mathit{k}=1}^{\mathit{N}}}{\displaystyle {\int }_{-\infty }^{\infty }}\langle {\stackrel{.}{\mathbf{r}}}_{\mathit{k}}(0){\stackrel{.}{\mathbf{r}}}_{\mathit{k}}(\mathit{t})\rangle {\mathit{e}}^{\mathit{i}\mathrm{\omega }\mathit{t}}\mathit{d}\mathit{t}$$ (1)

where ${\stackrel{.}{\mathbf{r}}}_{\mathit{k}}(0){\stackrel{.}{\mathbf{r}}}_{\mathit{k}}(\mathit{t})$ is the time series velocity autocorrelation function. The velocity autocorrelation function was calculated for 2.8 ps and averaged over all sugar-hydroxyl groups and simulation times. The Hann window function was used for filtering before the Fourier transform (40), and the Loess method was used for smoothing in the MATLAB package with a span of 0.015%.

The time-dependent vibrational spectra were calculated by the wavelet analysis (41)

$${\mathit{L}}_{\mathrm{\psi }}\mathit{f}(\mathit{a},\mathit{b})={\mathit{a}}^{-\frac{1}{2}}{\displaystyle {\int }_{-\infty }^{\infty }}\mathit{f}(\mathit{t})\mathrm{\psi }\left(\frac{\mathit{t}-\mathit{b}}{\mathit{a}}\right)\mathit{d}\mathit{t}$$ (2)

where a and b are the parameters, and the time series of OH relative velocities were used as f(t). The parameter b shifts a window at t = b, and the parameter a determines the window scale and is directly related to frequency. The wavelet function provides a frequency at time t = b. In previous studies, the wavelet analysis was successfully applied for spectral dynamics of water molecules in ion solutions (42–44). Here, the Morlet-Grossmann function (45) was chosen as the mother wavelet ψ(t)

$$\mathrm{\psi }(\mathit{t})=\frac{1}{\mathrm{\sigma }\sqrt{2\mathrm{\pi }}}{\mathit{e}}^{2\mathrm{\pi }\mathrm{\lambda }\mathit{i}\mathit{t}}{\mathit{e}}^{-\frac{{\mathit{t}}^2}{2{\mathrm{\sigma }}^2}}$$ (3)

where λ and σ are the parameters. Following a previous study (41), the values 1 and 2 were set for λ and σ, respectively.

TOP and H-bond definition

The TOP represents the degree of the tetrahedral arrangement of water molecules. The TOP for a water molecule i is calculated by

$$\mathit{q}=1-\frac{3}{8}{\displaystyle \sum _{\mathit{j}=1}^3}{\displaystyle \sum _{\mathit{k}=\mathit{j}+1}^4}{(cos({\mathrm{\theta }}_{\mathit{j},\mathit{k}})+\frac{1}{3})}^2$$ (4)

where θ_j,k is the angle between the vectors r_i,j and r_i,k. The terms j and k represent the four nearest-neighbor water molecule oxygen atoms of the original water molecule i.

Hydrogen bonds were defined geometrically as R_OO ≤ 3.5 Å and θ ≤ 30°, where R_OO is the distance between the two oxygen atoms and θ is the angle of the H-bond (46, 47).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/12/e1701400/DC1

fig. S1. Raman spectra of d-glucose solutions at concentrations between 0 and 0.5 M.

fig. S2. OH vibrational spectra for all water molecules in the system obtained by CPMD simulations.

fig. S3. OH vibrational spectra of water molecules within 3.5 Å of all isomers.

fig. S4. Average number of H-bonds between water molecules and RDF as a function of the distance between the oxygen atoms of monosaccharide and water molecules.

fig. S5. Spectra and water arrangement of water molecules in the NaBr solution.

fig. S6. I-shaped channel used for Raman experiments.