Aggregation-induced emission in lamellar solids of colloidal perovskite quantum wells

The first low-dimensional semiconductor nanocrystal system that increases the photoluminescence quantum yield in aggregates.

Abstract

The outstanding excitonic properties, including photoluminescence quantum yield (η_PL), of individual, quantum-confined semiconductor nanoparticles are often significantly quenched upon aggregation, representing the main obstacle toward scalable photonic devices. We report aggregation-induced emission phenomena in lamellar solids containing layer-controlled colloidal quantum wells (QWs) of hybrid organic-inorganic lead bromide perovskites, resulting in anomalously high solid-state η_PL of up to 94%. Upon forming the QW solids, we observe an inverse correlation between exciton lifetime and η_PL, distinct from that in typical quantum dot solid systems. Our multiscale theoretical analysis reveals that, in a lamellar solid, the collective motion of the surface organic cations is more restricted to orient along the [100] direction, thereby inducing a more direct bandgap that facilitates radiative recombination. Using the QW solids, we demonstrate ultrapure green emission by completely downconverting a blue gallium nitride light-emitting diode at room temperature, with a luminous efficacy higher than 90 lumen W⁻¹ at 5000 cd m⁻², which has never been reached in any nanomaterial assemblies by far.

INTRODUCTION

A long-standing challenge facing quantum-confined semiconductors such as colloidal quantum dots (CQDs) is the scalable manipulation, placement, and assembly of the nanoscale components, without compromising the outstanding excitonic properties observed in their isolated forms (1). Specifically, because of an effective reduction of the dielectric constant in low-dimensional semiconductors (2), a near-unity photoluminescence (PL) quantum yield (η_PL), namely, that nearly 100% of the photoexcited electron-hole pairs (or excitons) recombine radiatively, has been observed in the individual core/shell CQDs in solution (3). However, upon aggregation and forming crystalline QD solids, the η_PL values typically drop to ~10 to 20% or lower (4–7), with only a few studies reporting up to ~60% (8, 9), which is undesirable for high-intensity photonic applications, such as light-emitting diodes (LEDs) (4), downconversion (DC) phosphors (10), and lasers (11). For example, in the state-of-the-art QD LEDs, it has been proven that the thin-film η_PL represents the upper limit of the internal quantum efficiency in devices (12–14).

The origin of the observed quantum yield quenching in QD solids is attributed to an efficient exciton diffusion through the Förster resonance energy transfer (FRET) within the size inhomogeneity of QDs (5, 15), followed by reaching the quenching sites before recombining radiatively. The quenching pathways can be categorized into two types: (i) the defect-mediated midgap states resulting from the dangling bonds on QD surface and (ii) the Auger process involving energy transfer to a neighbor charged particle during diffusion (1). The latter is often a substantial contributor, relative to that in the bulk semiconductor, due to strong many-body Coulombic interactions under spatial confinement (16, 17). To impede energy transfer upon assembly, recent attempts have been focused on incorporating a very thick shell during colloidal synthesis (18). Nevertheless, because FRET is analogous to near-field communication, with an effective range of 1 to 10 nm (19), the degree of η_PL drop in the thick-shell QD assemblies remains significant (9).

New developments in understanding photophysics of the solution-processed hybrid organic-inorganic metal halide perovskites (OIHPs) (20) may shed light on the challenge of aggregation-induced PL quenching in QD solids. In the OIHP systems, the collective motion of organic cations (21), coupled with the transient deformation of lead halide octahedral units (22), has been suggested to (i) create local ferroelectric domains (23); (ii) introduce a direct-indirect character of the bandgap, that is, the Rashba effect (24–26); and (iii) form large polarons that screen the Coulombic interactions from the charged defects (27). Consequently, even with a high defect density, OIHPs still have an extremely long exciton lifetime and diffusion length (28), comparable to those in the single-crystalline compound semiconductors (29). We therefore hypothesized that, in OIHPs, if the exciton binding energy can be greatly enhanced by reduced dimensionality, the accelerated kinetics of radiative recombination might arrest other quenching pathways during exciton diffusion, thereby retaining a high η_PL in solid, as has been observed in epitaxial GaAs quantum wells (QWs) (30).

RESULTS AND DISCUSSION

Here, we report, to our knowledge, the first low-dimensional semiconductor system that exhibits the aggregation-induced emission (AIE) behavior (31) in lamellar solids containing layer-controlled colloidal QWs (CQWs) of OIHPs. The layer-controlled, monodispersed CQWs, with the formula (C₈H₁₇NH₃)₂[APbBr₃]_nPbBr₄, where A is an organic cation and n is the stacking number of perovskite unit cells (32–34), were synthesized and dispersed in toluene by optimizing the protocols developed in our previous work (33). Note that although the CQWs share the same chemical form with the two-dimensional (2D) Ruddlesden-Popper perovskites (RPPs) (35), because of the nature of colloidal synthesis, long-chain ligands are attached to the QW surface, allowing stabilization of individual QW nanocrystals in solution, analogous to the CQD systems. Through extensive experimentation, six high-purity CQW dispersions were prepared, using methylammonium (MA) (A = CH₃NH₃⁺ and n = 1, 3, 5, 7 to 10) and formamidinium (FA) [A = CH(NH₂)₂⁺ and n = 1, 7 to 10] as the organic cations; the n values were determined by comparing the solution emission peak positions with those reported in solid-state RPPs (fig. S1) (36).

The lamellar solids were then prepared by spin-coating the QW colloidal solution onto a glass substrate. After solvent evaporation, the CQWs self-assemble into a superlattice structure with periodic perovskite QW layers separated by long alkyl ligands (in this system, C₈H₁₇NH₃) (Fig. 1A). The surface normal vector of the QW is found to be perpendicular to the substrate plane and is defined as the c axis of the superlattice structure. As revealed by atomic force microscopy (AFM) height and phase images (Fig. 1, B and C), the crystallization process during solvent evaporation seems to follow the Stranski-Krastanov mechanism (37), in which the CQWs assemble in a layer-by-layer fashion, followed by continuously growing on certain places, forming a rough surface. The CQWs of similar lateral size tend to grow further to form topographically higher islands, leaving occasionally large QWs in between. As a result, crystallographic analysis of the films basically reflects QW packing and ordering in the islands. Note that because we focus on the properties of stacked CQWs, the Miller index (abc) used in this report refers to a plane in superlattice, rather than in perovskite structure.

Fig. 1. Crystal structure and surface characterization of lamellar solids containing layer-controlled CQWs.

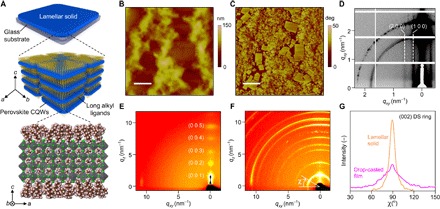
(A) Schematics of the superlattice structure in lamellar solids showing layer-controlled perovskite CQWs (n = 3 here) sandwiched between long alkyl ligands. AFM height (B) and phase (C) images of n = 3 MA lamellar solid deposited on glass substrate. Scale bars, 1 μm. deg, degree. Synchrotron GISAXS (D) and GIWAXS (E) patterns for the same sample, with the superlattice signals labeled. (F) GIWAXS pattern of n = 3 MA drop-casted film showing the extended DS rings along the angular coordinate χ. (G) Comparison of orientation distribution function using the normalized scattering intensity of the (002) DS ring with respect to χ in lamellar and drop-casted solids.

Taking n = 3 MA lamellar solid as an example (for the structure, see Fig. 1A, bottom), the synchrotron grazing-incidence small-angle x-ray scattering (GISAXS) pattern (Fig. 1D) shows two stripes on the q_xy axis, denoted as (100) and (200), which correspond to the first- and second-order Bragg diffraction signals of lateral packing, respectively. Accordingly, the lateral spacing between stacked QWs is determined to be 14.0 nm, consistent with the lateral size quantified with transmission electron microscopy (TEM) (fig. S6). We further look into its grazing-incidence wide-angle x-ray scattering (GIWAXS) pattern (Fig. 1E) and observe clear superlattice diffraction signals along the q_z axis up to fifth order, denoted as (00l), where l is an integer, yielding a layering d-spacing of 3.3 nm, with strong crystallinity and long-range ordering. Considering the unit cell thickness (~0.6 nm), the thickness of the ligand layer separating neighboring wells is estimated to be ~0.9 nm, approximately equivalent to the length of the ligand alkyl chain, that is, –C₈H₁₇. We therefore deduce that the surface coverage of ligands is less than 50%, with remaining sites occupied by MA cations that allow interpenetration of ligands between neighboring wells. For comparison purposes, we also prepared the CQW solids with drop-casting technique and found that the lamellar symmetry with respect to substrate is greatly damaged, extending the (00l) Laue spots to the Debye-Scherrer (DS) rings (Fig. 1F). The pole figure was then obtained by plotting the (002) DS ring intensity as a function of the polar angle χ for both drop-casted and lamellar solid samples, normalized by the exposure time and the thin-film thickness (Fig. 1G). The relative orientation of the CQW assemblies with respect to substrate can therefore be quantified. For example, χ = 90° represents the “face-on” orientation, with the superlattice c axis perpendicular to the substrate plane. Accordingly, although a preferred orientation at χ = 90° is observed in both samples, we estimate that the relative degree of crystallinity is ~205 times higher in the lamellar solid than in the drop-casted film.

Next, we discuss the photophysical properties of QW solids. Under a low-power ultraviolet (UV) lamp, the lamellar solid–coated substrates already exhibit bright PL. Narrow-bandwidth emission, with a full width at half maximum (FWHM) of 15 to 25 nm, remains upon forming solid, with the peak position consistent with that in solution. (Fig. 2A and fig. S1); the change of absorption spectrum is also small (fig. S2). Because a high degree of layering monodispersity is achieved during colloidal synthesis, the spectral components corresponding to the small-bandgap QW traces that could downconvert emission from the thin QWs are not noticed. The interwell coupling appears to be weak; thus, the optical bandgap width in individual QWs remains unchanged. The above features basically share similar properties with typical QD solid systems (5).

Fig. 2. Comparison of photophysical properties between CQW solution and solids.

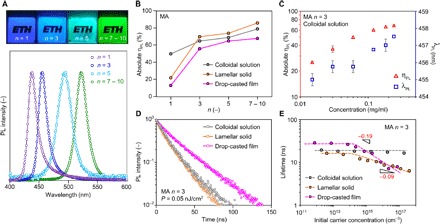
(A) Photographs under UV excitation (top) and emission spectra under 370-nm excitation (bottom) for MA lamellar solids with different n values. (B) Absolute η_PL as a function of n in solution, lamellar solid, and drop-casted film of MA samples. (C) Absolute η_PL and emission wavelength (λ_PL) as a function of CQW concentration. (D) TRPL of n = 3 MA samples under a low pumping energy P, highlighting an inverse correlation between τ_e and η_PL. (E) Extracted monoexponential lifetime as a function of initial carrier density in n = 3 MA samples, showing weak dependence on initial carrier concentration n₀.

For each CQW species synthesized, the absolute η_PL (38) values were independently determined in its as-prepared colloidal solution, lamellar solid, and drop-casted film in an integrating sphere under 370-nm excitation (Fig. 2B, fig. S2, and table S2). Each sample was measured multiple times and most of them exhibit an SD below 1% (table S2). Without any surface passivation, we notice that the solution η_PL values for the six compounds are all higher than 50%, even for the two n = 1 counterparts. After forming lamellar solids, three important observations are highlighted as follows: (i) for the four species with n ≥ 3, a consistent η_PL increase of 5 to 10% is observed as compared to their solution values, exhibiting the AIE behavior; (ii) the solid-state η_PL values all exceed 70%, with a record-high value of 94% reached in the n = 7 to 10 FA lamellar solid (fig. S3); and (iii) on the other hand, a significant quantum yield quenching was observed in the n = 1 solid samples (Fig. 2B and fig. S3). To our knowledge, the AIE phenomena, as well as the extremely high η_PL values in solid, have never been reported in any CQD/CQW systems at room temperature. Note that even for the drop-casted samples, although a degree of η_PL drop is observed for n ≥ 3, the values remain comparably high.

To further corroborate the AIE phenomena, which was only observed in certain organic fluorophores (31), we determine η_PL in colloidal solution as a function of concentration, taking the n = 3 CQWs case as an example (Fig. 2C). Upon dilution of the as-prepared colloidal solution, we observe a considerable degree of η_PL drop by up to 40%, exhibiting an inverse trend compared to typical CQD systems (9). Nevertheless, it is consistent with the trend observed in organic AIE molecules (31). At a low concentration, the distance between individual CQWs is large, such that the probability to form aggregates in solution is low. In other words, the observed solution η_PL approaches the value for a single, isolated nanocrystal. Considering the fact that the dielectric constants for toluene (the solvent) and octane (the alkyl ligand group) are essentially close (ε_r ~ 2.0), we exclude the scenario of the change of dielectric environment. The AIE effect appears to be strong.

Following the hypothesis addressed earlier, we believe that the organic cation–mediated screening from nonradiative quenching sites plays an important role in mitigating nonradiative losses during interwell exciton diffusion, so that a high η_PL can be reached for n ≥ 3 in solid. This is also indirectly endorsed by the relatively low η_PL values obtained in n = 1 solids, in which the organic cation–mediated screening may be less effective. Nevertheless, this mechanism alone does not explain the AIE behavior, which seems to imply that quenching pathways are partially eliminated upon assembly. To this end, the exciton recombination dynamics for the n = 3 MA samples were characterized by time-resolved PL (TRPL) spectroscopy (Fig. 2D). Under a low pumping energy of 0.05 nJ cm⁻², the PL dynamics exhibits a nearly monoexponential decay profile, with lifetimes τ_e of 19.4, 16.3, and 28.7 ns observed in solution, lamellar solid, and drop-casted film, respectively. The values are typically one order of magnitude lower than that in the bulk OIHPs (28), as a consequence of the quantum confinement effect (2). Most notably, a slight degree of τ_e decrease is observed upon forming lamellar solids, together with an increase of η_PL (Fig. 2B). On the other hand, in drop-casted films, τ_e increases and η_PL decreases relative to their solutions. In other words, depending on how the QWs are interacting with each other, there exists an inverse correlation between τ_e and η_PL, which is generally the other way around in typical CQD systems (5).

We further tested PL decay dynamics under higher pumping energy densities (Fig. 2E and fig. S4E). The initial carrier density, n₀, is estimated using the film absorption coefficient, normalized by the optical density for each sample, referring to the number of photons absorbed in single excitation pulse. When CQWs are dispersed in solution, we observe that the monoexponential behavior remains unchanged within the n₀ range considered (10¹² to 10¹⁸ cm⁻³), having a nearly identical τ_e of ~20 ns (fig. S4). A lack of multiexciton components suggests that the decay dynamics is dominated by radiative recombination of single excitons in individual QWs, independent of n₀. On the other hand, in solid samples, the multiexciton component starts to emerge after n₀ ~ 10¹⁵ cm⁻³ but remains subtle. We notice that it is a relatively low threshold to observe the intensity-dependent decay dynamics, possibly owing to the aggregation phenomenon. In aggregates, a large degree of exciton coupling may lead to a high probability for multiple excitons meeting each other, such that the number of excitons per aggregate exceeds unity, higher than that in individual CQWs. This observation is in line with previous reports dealing with hybrid perovskite nanostructures (39, 40). After the crossover point, we fitted the τ_e − n₀ profiles (Fig. 2E) with a power law, yielding exponents of −0.19 and −0.09 for drop-casted films and lamellar solids, respectively. The weak dependence on n₀ in solid is certainly not typical and very different from that in core/shell QD solid systems. In the latter case, a thick shell layer often reduces the exciton coupling between QDs in solid, which results in a higher excitation energy required to exhibit the intensity-dependent PL lifetime (41). Under the strongest pumping power considered here (n₀ ~ 10¹⁸ cm⁻³), the lifetimes reduce by a factor of 2 to 4, which may be a signature of transition to biexciton recombination (42). It remains preliminary to draw a decisive conclusion based on the intensity-dependent dynamics in solution and solid samples, and further experiments will be required to elucidate the details of exciton diffusion. Nevertheless, the spectroscopic findings reported here highlight the uniqueness of the system and indicate a new mechanism underlying the accelerated radiative recombination that results in AIE in the CQW lamellar solids.

To solve the puzzle of AIE in CQW lamellar solids, inspired by the recent findings in indirect-direct bandgap transition in bulk OIHPs due to different organic cation orientations (24), we investigate the role of organic cations by carrying out multiscale analysis that bridges molecular dynamics (MD) and atomistic information (Fig. 3). Classical MD simulations were first carried out to investigate the orientational distribution of surface MA cations in the n = 3 MA samples (Fig. 3A). The directional map (φ and θ, denoting azimuthal and polar angles, respectively; Fig. 3B) of surface MA cations demonstrates that the surface MA cations of CQWs dispersed in toluene orient mostly within the surface plane, with two preferable orientations along the [100] and [011] crystallographic directions (Fig. 3C). These preferable orientations for surface MA cations reflect their dipolar nature when they are positioned on an anisotropic, negatively charged surface with Br anions. However, in a lamellar solid, the collective motion of surface MA cations is even more restricted within the surface plane and only along the [100] direction (Fig. 3D). The difference in the MA orientational distributions is attributed to the distinct molecularly induced geometrical constraint. Specifically, upon complete aggregation of CQWs into a lamellar solid, the neighboring surface ligands interpenetrate each other (see Fig. 3A, bottom), where the penetrated ligands interact with the surface MA cations, thereby greatly restricting MA’s orientational degrees of freedom and making the polar angle θ closer to 90°. While in solution, the surrounding toluene solvent molecules are not able to effectively suppress the rotation of surface MA cations, and therefore, the MA cations can orient more freely along the two preferable directions. On the other hand, because of the more isotropic ionic structure, the orientations of MA cations residing in the perovskite lattice distribute more uniformly than the surface ones, along the [100] direction irrespective of the surroundings (fig. S8). Note that the preferable direction in the 2D structure is distinct from that in the 3D bulk perovskites, that is, [111] (24), due to a stronger Coulombic interaction along the xy plane. Moreover, our MD simulations indicate that the surface coverage of ligands has a minor impact on the orientational distribution of surface MA cations (see fig. S9); nevertheless, we expect that a lower surface coverage of ligands (<50%) should lead to less rotational constraint on the surface MA cations.

Fig. 3. Multiscale analysis of n = 3 MA CQWs in solution and lamellar solid.

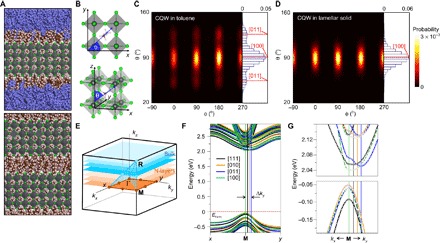
(A) Computer-generated molecular models (brown, carbon; light pink, hydrogen; green, bromine; light blue, nitrogen; gray, lead; violet, carbon in toluene) of individual CQW in toluene (top) and in aggregated CQWs (lamellar solid; bottom) with n = 3 MA compound. (B) Three-dimensional schematics of the orientation of each organic cation (blue arrow corresponding to the N-C axis) defined by a spherical coordinate system with polar axis along the z direction, as well as in-plane azimuthal (φ) and polar (θ) angles. Orientational distribution contour maps (φ, θ) of surface MA cations in (C) toluene solution and (D) lamellar solid. (E) Brillouin zone of bulk (faint blue) and N-layer (faint orange) perovskite QW lattice in an orthorhombic cell. Symmetry points at boundaries of the zone where the bandgap is direct change from R (in bulk) to M (in N-layers). k_z is oriented perpendicular to the QW surface. (F) Calculated band structures of n = 3 MA QWs with different orientations of surface MA cations, along [111], [010], [011], and [100] directions. The most indirect bandgap is observed for the [011] with a wave vector difference Δk_y relative to the M point. The most direct bandgap is observed for the [100] with no relative displacement along k_y. (G) Magnification of the bands around the M point for small k_x and k_y, highlighting the change in the band edges for the different MA configurations. Top and bottom panels show the conduction and valence bands, respectively, highlighted with filled points. Labels follow those in (F).

Such different orientations of the surface MA cations induce variations on the band edges, as revealed by density functional theory (DFT) calculations (Fig. 3, E to G). We consider the orientation of MA cations residing in a perovskite lattice along the [100] direction and vary the orientation of surface cations. The conduction band minimum (CBM) for all geometries is sensitive to the orientation of the surface MA cations, exhibiting a more direct or indirect bandgap accordingly. Among the four orientations of surface cations considered, the [100] orientation is the only one having a direct bandgap at the M point (Fig. 3, F and G). All the other configurations relaxed to an indirect bandgap at the Brillouin zone, with a finite Δk_y relative to the M point. The most indirect bandgap is along [011], where a clear variation in the CBM results in a weakly indirect bandgap of 22 meV away from the M point. This is comparable to the thermal energy at room temperature (~26 meV) and in the same order of magnitude as that observed in the 3D CH₃NH₃PbI₃ system (26). We also notice that there is a slight increase of bandgap width (~12 meV) by changing from the [100] orientation to the [011] orientation. Similar to the 3D CH₃NH₃PbI₃ system, most of this effect is specific to the CBM, whereas the valence band maximum displays a more uniform parabolic shape regardless of the configurations (Fig. 3G, bottom). The momentum-dependent splitting of CBM is a result of the asymmetry of the potential in the direction perpendicular to the 2D plane based on the electrostatic interactions between the surface MA cations with the PbBr₆ octahedra (fig. S10). Because both charged parts tend to compensate for the net charge into the system, the molecules are more free to suffer distortions that propagate throughout the entire material (figs. S11 and S12). Ab initio MD simulations performed at different layer numbers also showed the same trend (movies S1 to S3).

In combination with the MD-simulated orientational distributions of surface MA cations in solution and lamellar solid, the physical picture presented here establishes that, depending on how a perovskite QW interacts with its surroundings, the bandgap can be more direct or indirect, enabled by the orientational degree of freedom of the surface organic cations. It qualitatively explains the experimentally observed correlation between τ_e and η_PL. When the collective motion of surface organic cations is more restricted to orient along the [100] direction, as has been observed in the close packed lamellar solid (Fig. 3D), most recombination events are momentum-conserved and radiative through a direct bandgap, thereby decreasing τ_e and increasing η_PL, and vice versa. These behaviors follow the general trend of direct and indirect bandgap semiconductors. The theory of band structure change upon aggregation is strengthened by the experimental evidence of the emission wavelength (λ_PL) as a function of solution concentration (Fig. 2C). Accordingly, we observed a degree of λ_PL blue shift (~2 nm or ~10 meV) upon dilution (or reduction of the degree of aggregation) in the same order of magnitude as the bandgap change from [100] (preferable in lamellar solids) to [011] (emerging in colloidal solution), as shown in Fig. 3G.We exclude the scenario of CQW exfoliation or thinning because the emission and absorption characteristics remain unchanged, and a one-layer reduction would result in a much larger degree of blue shift (>10 nm). As for the drop-casted films, although we do not have a clear molecular picture in mind due to the nature of random orientation (Fig. 1F), we speculate that the voids formed between small crystalline domains may result in a higher orientational degree of freedom for the surface MA cations.

The high quantum yields in perovskite CQW solids suggest new technological opportunities in the photonic devices that require ultrahigh color purity, for example, the monochromatic green light source, which is the major determinant of color gamut offered by a display (43, 44). The state-of-the-art solid-state lighting technology realizes pure green emission by increasing indium content in an indium gallium nitride (InGaN) LED (45) but generally suffers from a significant drop in its external quantum efficiency, which is known as the “green gap” (45, 46). Here, we propose to tackle this challenge by completely downconverting a high-efficiency blue GaN LED with the CQW solids. A thick n = 7 to 10 MA CQW solid film, without using any polymer additives, is deposited and sandwiched between two quartz-coated glass substrates and then placed on top of a commercial blue GaN LED (for schematic architecture, see Fig. 4A, left). Within the voltage range considered, ultrapure green emission is attained without notable blue light leakage (Fig. 4A, right). The emission spectra of the GaN LED (456 nm) before and after pumping the CQW solid are shown in Fig. 4B, together with those from a commercial green InGaN LED (528 nm) for comparison. Accordingly, the downconverted emission exhibits an even narrower bandwidth (FWHM = 23 ± 0.2 nm) compared to that from the InGaN LED. The color coordinates in the Commission Internationale de l’Éclairage (CIE) chromaticity diagram reach (0.176, 0.738) (fig. S13), representing among the purest green emission ever reported in LEDs (47).

Fig. 4. Demonstration of the ultrapure green emission through DC using n = 7 MA CQW solid.

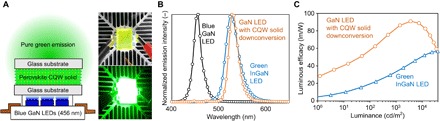
(A) Schematic setup (left) and photographs (right) for the LED device that yields pure green emission pumped by blue GaN LED chips (456 nm). (B) Electroluminescence (EL) spectra before (black) and after CQW solid DC (orange). Emission spectra for a commercial green InGaN LED (blue) are also attached for comparison. (C) Calculated luminous efficacy as a function of luminance for the two green LEDs considered.

We then characterize the current (I) and luminance (L) profiles as a function of voltage (V) for the two green devices (fig. S14) and determine their luminous efficacies (η_LE) (48) (Fig. 4C). The CQW solid-downconverted device exhibits the maximum luminous efficacy (η_LE,max) of 91 lumens (lm) W⁻¹ at I = 4.81 mA and L = 3571 cd m⁻², and η_LE remains higher than 90 lm W⁻¹ at L = 5000 cd m⁻², which is approximately 100% higher than that in the commercial green InGaN LED (η_LE = 45 lm W⁻¹ at L = 5000 cd m⁻²). Note that after DC, the η_LE increases by 34% relative to the blue pumping source (fig. S15) due to a high luminous eye response in the green spectral region (48, 49). We also tested the stability of the CQW solids by continuously pumping them with the GaN LEDs in ambient atmosphere. After 20 hours, we only observe a slight decrease in luminance and η_LE by 18.8 and 22.5%, respectively (fig. S17, A and B). The emission peak position does not show a notable change (fig. S17C). To our knowledge, the high η_LE values, as well as the ultrapure green color coordinates, have never been achieved on the basis of any nanomaterial assemblies by far, through a downconvesion process. With the preliminary success in the proof-of-concept device, we believe that further optimization in the packaging design of the CQW solids will enhance light outcoupling and extraction (48, 49), which should lead to a higher η_LE. We also demonstrate excellent amplified spontaneous emission (ASE) properties using the same film (figs. S18 and S19).

CONCLUSIONS

We report a colloidal low-dimensional semiconductor system that exhibits AIE behavior, resulting in anomalously high η_PL in solid at room temperature. Our results uncover the role of surface organic cations in the 2D systems and shed light on the development of bright quantum dot solids. The existence of quantum-confined semiconductor nanocrystals that do not self-quench upon aggregation is expected to enable high-performance LEDs, lasers, and biomarkers.

MATERIALS AND METHODS

Synthesis of MA bromide and FA bromide

In this work, we used a synthetic protocol previously reported by Pathak et al. (50). MA bromide (MABr) was synthesized by mixing 10 ml of methylamine [33 weight % in absolute ethanol (EtOH), Acros Organics] with 7.5 ml of HBr (48% in H₂O, Sigma-Aldrich) in 100 ml of EtOH (absolute EtOH for analysis, Merck). After stirring the reaction mixture for 1 hour under ambient conditions, the solvent was removed at 60°C by means of a rotary evaporator. The obtained solid was washed several times with diethyl ether (>99.8%, Thommen-Furler AG) and recrystallized with EtOH. Finally, the purified powder was dried overnight in a vacuum oven at 60°C. The FABr salt was prepared according to the procedure developed by Eperon et al. (51). Formamidine acetate (99%, Acros Organics) was dissolved in two molar equivalents of HBr (48% in H₂O) and stirred for 10 min at 50°C, followed by the removal of the solvent at 100°C by means of a rotary evaporator. The resulting solid was washed several times with diethyl ether, recrystallized two times with EtOH, and subsequently dried in a vacuum oven at 60°C.

Synthesis of MAPbBr₃ and FAPbBr₃ CQWs

The synthesis procedure reported previously in our work was adapted from Kumar et al. (33). A round-bottom flask equipped with a magnetic stirrer was loaded with 12.5 ml of toluene (99.8%, Fisher Chemical). To control the layer number n, variable amounts of oleic acid (90% technical grade, Sigma-Aldrich) and octylamine (99%, Sigma-Aldrich) (table S1) were added subsequently. The addition of 375 μl of MABr or FABr [0.533 M, in N,N-dimethylformamide (DMF; >99.8%, Sigma-Aldrich) or EtOH] and 625 μl of lead bromide (PbBr₂; 98+%, Acros Organics) (0.4 M in DMF) was followed by a spontaneous formation of precipitate. In some cases, 10 ml of tert-butanol (for analysis, Fisher Chemical) was added to ensure full precipitation. The solid was separated by means of centrifugation at 8000 rpm for 8 min and redissolved in 2.5 to 3 ml of fresh toluene, resulting in green- or blue-emitting colloidal solutions. All procedures were carried out under ambient conditions.

Morphological characterization

The surface structure of nanoplatelet (NPL) films was obtained with a Nanoscope 3D controller atomic force micrograph (Digital Instruments) operated in the tapping mode at room temperature. Grazing-incidence x-ray diffraction (GIXD) patterns were measured on beamline BL13A at the National Synchrotron Radiation Research Center, Taiwan. A monochromatic beam of λ = 1.0205 Å was used, and the incident angle was 0.12°.

Scanning transmission electron microscopy (STEM) images were captured using FEI NovaNanoSEM 450 operated at 30 kV. Scanning electron microscopy (SEM) images were obtained using Zeiss ULTRA 55 operated at 2 kV.

Preparation of thin films

Colloidal dispersions of perovskite NPLs were prepared on glass microscopy slides previously cut to reach a size of approximately 1 cm × 1 cm and subsequently washed in acetone and isopropanol. To prepare lamellar solids, a spin-coating method was applied. After depositing ~ 25 to 50 μl of perovskite NPL colloidal solution, substrates were rotated at 2500 rpm for 40 s. Drop-casted films were fabricated by depositing a similar amount of the solution, followed by drying in vacuum for several minutes.

Optical characterization

Absorption of colloidal solutions and thin films in the UV-visible region was determined using a Jasco V670 spectrophotometer. Steady-state PL spectra and η_PL of solutions and films were acquired using an absolute η_PL spectrometer (C11347-11; Hamamatsu) equipped with an integrating sphere. The measurement device was calibrated and certified by the manufacturer on 5 January, 2017, and its precision was regularly monitored by measuring standard samples. Excitation source emission wavelength was set to 370 nm if not specified differently. Each sample was examined multiple times at different dilution ratios (liquids) or at different spots (films).

TRPL measurements

TRPL measurements were carried out using a time-correlated single photon counting (TCSPC) setup, equipped with an SPC-130-EM counting module (Becker & Hickl GmbH) and an IDQ-ID-100-20-ULN avalanche photodiode (Quantique), which was used to record the decay traces. To trigger emission from solid and liquid samples, they were excited by 355-nm (frequency-tripled emission of Nd:YAG laser Duetto Time-Bandwidth Products), 10-ps laser pulses with a repetition of 824 kHz and an intensity between approximately 0.05 and 5000 nJ cm⁻² triggering the TCSPC module through an electronic delay generator (DG535 from Stanford Research Systems). The beam power was measured by Si photodiode sensor S120VC from Thorlabs. The beam profiles were recorded by a DP-M17 USB Digital Microscope from Conrad.

Estimation of initial photocarrier density n₀

First, the number of photons absorbed by the sample per unit area, denoted as N_A, was calculated following

$${\mathit{N}}_{\mathit{A}}=\frac{\mathit{J}\mathrm{\lambda }}{\mathit{h}\mathit{c}}(1-{10}^{-\mathrm{\alpha }})$$

where J is the laser beam energy per area, λ is the wavelength of emitted photons, h is the Planck constant, c is the speed of light, and α is the absorbance of the sample. Therefore, the initial photocarrier density for the drop-casted film n_0,drop is given by the following formula

$${\mathit{n}}_{0,\text{drop}}=\frac{{\mathit{N}}_{\mathit{A}}}{{\mathit{d}}_{\text{drop}}}$$

where d_drop is the film thickness of the drop-casted film measured by the profilometer.

For the lamellar solid and solution samples, the thickness was difficult to estimate; thus, we calculated the n₀ values as follows. Because the absorbance is proportional to the number of absorbing nanoparticles, according to the Lambert-Beer law, we estimated n₀ in the remaining samples based on their absorbance. Considering a constant sample area (due to the same laser beam being used here), under the assumptions that (i) every QW has identical volume, (ii) the QW absorbance is independent of surroundings, and (iii) each QW has the same orientation, which is independent on film preparation method, it follows that

$${\mathit{n}}_{0,\text{sample}}={\mathit{n}}_{0,\text{drop}}\frac{{\mathrm{\alpha }}_{\text{drop}}(1-{10}^{-{\mathrm{\alpha }}_{\text{sample}}})}{{\mathrm{\alpha }}_{\text{sample}}(1-{10}^{-{\mathrm{\alpha }}_{\text{drop}}})}$$

For liquid samples, it was assumed that the nanocrystals dispersed in the solvent would form a film with the same absorbing characteristics as in the case of thin-film samples.

MD simulation methods

We conducted MD simulations to simulate the layer-controlled CQWs of hybrid organic-inorganic PbBr₂ perovskites with the formula [CH₃(CH₂)₇NH₃]₂[CH₃NH₃PbBr₃]_nPbBr₄, where n is the layer number of perovskite unit cells. Because the layer-controlled CQWs were constructed by 2D CH₃NH₃PbBr₃ perovskite with capping ligand octylammonium [CH₃(CH₂)₇NH₃⁺] layers, a recently developed classical interatomic potential (force field) (52) for bulk CH₃NH₃PbBr₃ perovskite was used to describe the interatomic interactions in the layer structures. This potential has been demonstrated to reasonably reproduce the dynamic [that is, relaxation time of organic cation CH₃NH₃⁺ (MA)] and structural (that is, lattice constants and phase transition) properties of bulk CH₃NH₃PbBr₃ perovskite. Following the assisted model building with energy refinement (AMBER) force field (53) used to describe interactions within MA cations, we used AMBER to model the intermolecular and intramolecular interactions within the CH₃(CH₂)₇NH₃⁺ ligands in these 2D CH₃NH₃PbBr₃ perovskites, as well as to model the organic solvent toluene. The atomic partial charges within these ligands and toluene molecules were determined from quantum chemistry calculations and Mulliken population analysis with the B3LYP/6-31G* basis set using the Gaussian 09 software package (54).

Using the above force field, all the MD simulations of these CH₃NH₃PbBr₃-based CQWs were carried out using the massively parallelized LAMMPS (Large-Scale Atomic/Molecular Massively Parallel Simulator) package (55) at 300 K. The molecular models of individual CQW dispersed in toluene (colloidal solutions) and aggregated CQWs (lamellar solids) were built with n = 3. Periodic boundary conditions were applied along all the directions. Two different surface coverages (50 and 75%) of ligands for CQWs were taken into account as well to explore their impacts on the orientational distribution of surface organic MA cations. A simulation time step of 1 fs was chosen for all the MD simulations here. The particle-particle particle-mesh (PPPM) method (56) was used here to treat long-range Coulombic interactions via the reciprocal space because the PPPM method is significantly faster than the regular particle Ewald summation method (57). To obtain the initial equilibrium state, these molecular models were first relaxed for 500 ps under the NVT ensemble after energy minimization. Only aggregated CQWs were equilibrated for another 400 ps under the NPT ensemble (58) with a high pressure of 2000 bar along the stacking direction, to obtain the fully packed aggregated CQW structures. All the molecular models were then equilibrated further for 2000 ps under the NPT ensemble with a pressure of 1 bar along all the directions to reach full equilibrium states.

After structural equilibration, the atomistic trajectories of surface MA cations were extracted every 20 fs during a period of 100 ps to explore their collective motions. The molecular orientation of MA cation, $\widehat{\mathbf{n}}$, is defined by the vector connecting the N-C backbone. A spherical coordinate system is used, with the polar axis along the z direction, as well as in-plane azimuthal (φ) and polar (θ) angles (see Fig. 3B). The instantaneous molecular orientation $\widehat{\mathbf{n}}$ can be determined from the above two angles via $\widehat{\mathbf{n}}=(\text{sin}\mathrm{\theta }\text{cos}\mathrm{\phi },\text{sin}\mathrm{\theta }\text{sin}\mathrm{\phi },\text{cos}\mathrm{\theta })$ (59), which corresponds to a single point in the (φ, z = cosθ) plane. Therefore, the molecular orientations of MA cations can be represented by the orientational distribution contour map (φ, θ) of MA cations from the collected trajectories. Note that we corrected the solid-angle biasing effect on the orientational distribution with respect to the polar angle θ by dividing the probability distribution by sin θ. Because only pseudocubic-phase CH₃NH₃PbBr₃ perovskites are stable at 300 K, the following crystallographic directions are identical to each other: [100] ≡ [010] ≡ [001] and [110] ≡ [101] ≡ [011].

First-principles ab initio calculations

The calculations reported here are based on ab initio DFT using the VASP (Vienna Ab initio Simulation Package) code (60, 61). The generalized gradient approximation (62) was used along with a well-converged plane-wave cutoff of 800 eV. The projector augmented-wave method (63, 64) was used in the description of the bonding environment for Pb, Br, N, C, and H. Atomic coordinates were allowed to relax until the forces on the ions were less than 1 × 10⁻⁴ eV Å⁻¹ under the conjugate gradient algorithm. Electronic convergence was set to 1 × 10⁻⁶ eV. Dipole corrections and a 25 Å vacuum space along the out-of-plane direction were included to avoid any further spurious interactions between the CH₃NH₃⁺ cations. The lattice constant for n = 3 thickness on MAPbBr₃ was initially optimized for each configuration of the CH₃NH₃⁺ cations in the cell. We then relaxed the internal coordinates of each geometry, keeping the CH₃NH₃⁺ cations fixed in the z direction. This was carried out to stop a reorientation of the cations during relaxation, which occurs spontaneously. After the relaxation, the in-plane lattice constants were varied systematically to obtain the more energetically stable position, and the internal coordinates were allowed to relax again. This procedure was repeated until the pressure on the cell in the xx and yy directions was less than 0.05 GPa. This led to a pseudocubic cell being used in the calculations. To ensure that the CH₃NH₃⁺ cations remained in their initial orientation, the internal coordinates were fixed. The Brillouin zone was sampled with a 4 × 4 × 1 Gamma-centered grid to perform relaxations. A finer k sampling was used to plot the band structures shown in Fig. 3 (F and G). In addition to this, we used a Fermi-Dirac distribution with an electronic temperature of k_BT = 10 meV to resolve the electronic structure. Ab initio MD simulations were also carried out using a 2 × 2 × 1 supercell. The calculation ran for a total of 1.8 ps using a 0.5-fs time step. The temperature was set to 300 K using the Nosé-Hoover thermostat, and the Pullay stress was set to zero.

Fabrication of DC-LEDs

The DC pure green and blue LEDs were fabricated by using the CQW solids of MAPbBr₃, as phosphors. First, highly pure colloidal solutions of QWs were casted on the 1.1-mm quartz-coated glass substrates. Defect-free, uniform films were obtained using vacuum-assisted solvent evaporation. The perovskite CQW–coated substrates were mounted on commercial GaN-based near-UV (371 nm) and/or blue (456 nm) LED chips. The CQW solid films were pumped by the underlying LEDs to harvest efficient green and blue emission through a DC process. The LED chips were purchased from CH-Town Electronics. Finally, the characteristics of DC-LEDs were measured by using a Photo Research PR 655 spectroradiometer and a Keithley 2400 source meter. The η_LE was calculated through a LabVIEW program that controls the PR655 spectroradiometer and Keithley 2400 source meter. CIE coordinates and EL/PL spectra of blue (456 nm) and UV (371 nm) pumping LEDs and DC LEDs were recorded using a calibrated ASEQ LR1-Tv.2 (CCD) spectrometer. All devices were characterized at 280 ± 10 K. We observed a negligible blue emission at 456 nm, especially at high brightness (fig. S17). The η_LE of DC-LEDs was calculated using the following equation (48)

$${\mathrm{\eta }}_{\text{LE}}=\frac{{\mathrm{\phi }}_{\text{lum}}}{{\mathit{P}}_{\mathrm{e}}}=\frac{683\left(\frac{\text{lm}}{\mathrm{W}}\right){\int }_{380}^{780}\mathit{V}(\mathrm{\lambda })\mathit{P}(\mathrm{\lambda })\mathit{d}\mathrm{\lambda }}{\mathit{I}\times \mathit{V}}$$

where φ_lum is the luminous flux of DC-LED; P_e is the total electrical power applied to the pumping source, blue LED; V(λ) is the CIE eye sensitivity function; P(λ) is the power spectral density; 683 lm W⁻¹ is a normalizing factor; I is the driving current; and V is the applied voltage. The drop-casted thick CQW films demonstrated a red-shifted emission from 8 to 12 nm as compared with the colloidal solutions or spin-coated films and facilitated to approach the Rec. 2020 green spot in the CIE chromaticity diagram.

ASE experiments

Measurements were performed with excitation from a femtosecond laser system consisting of an oscillator (Vitesse 800) and an amplifier (Legend Elite), both from Coherent Inc., with a frequency-doubling external beta-barium borate crystal; it yielded 100-fs pulses at 400 nm, with a repetition rate of 1 kHz and a pulse energy of up to 4 μJ. The laser beam profile had a TEM₀₀ mode with a 1.5-mm FWHM diameter. Laser power was measured by a LabMax TOP laser energy meter (Coherent Inc.) with a nanojoule measuring head. The optical emission was recorded by an ASEQ Instruments LR1-T CCD spectrometer (1-nm spectral resolution). The laser beam intensity profiles were analyzed by a LabMax TOP camera from Coherent Inc.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/12/eaaq0208/DC1

text S1. Blue DC LEDs.

text S2. ASE experiments.

fig. S1. Photoluminescence properties of perovskite CQWs in solution.

fig. S2. Optical absorption of perovskite CQW samples.

fig. S3. Photoluminescence properties of FAPbBr₃ CQWs.

fig. S4. TRPL analysis of MAPbBr₃ perovskite CQWs.

fig. S5. Synchrotron GIWAXS pattern of lamellar solid composed of n = 1 MAPbBr₃ CQWs.

fig. S6. Morphology analysis of perovskite CQWs by means of STEM.

fig. S7. SEM analysis of the film morphology.

fig. S8. The orientation distribution map of bulk MA cations in n = 3 CQW.

fig. S9. Surface MA cation orientation with 75% ligand coverage.

fig. S10. Electronic band structures projected on states of Pb atoms (left column), Br atoms (middle column), and CH₃NH₃ molecules (right column).

fig. S11. Charge density difference plots with different configurations.

fig. S12. Final geometries after relaxation.

fig. S13. CIE chromaticity coordinates of green (n = 7 to 10) and blue (n = 3) CQW solid phosphor-based DC-LEDs.

fig. S14. Driving current (I) and luminance (L) as a function of voltage (V).

fig. S15. Luminous efficacy as a function of luminance for commercial blue GaN LED as pumping source.

fig. S16. Demonstration of blue DC emission using n = 3 MA CQW solid.

fig. S17. Operational stability of n = 7 to 10 MA CQW downconverting film.

fig. S18. Observation of ASE.

fig. S19. The threshold behavior for the intensity of the ASE band.

table S1. Ligand volumes.

table S2. Absolute η_PL summary.

movie S1. Ab initio MD of the n = 1 geometry viewed along the 001 axis.

movie S2. Ab initio MD of the n = 1 geometry viewed along the 100 axis.

movie S3. Ab initio MD of the n = 1 geometry viewed along the 010 axis.

References (65–68)