Augmenting intracortical brain-machine interface with neurally driven error detectors

Abstract

Objective

Making mistakes is inevitable, but identifying them allows us to correct or adapt our behavior to improve future performance. Current brain-machine interfaces (BMIs) make errors that need to be explicitly corrected by the user, thereby consuming time and thus hindering performance. We hypothesized that neural correlates of the user perceiving the mistake could be used by the BMI to automatically correct errors. However, it was unknown whether intracortical outcome error signals were present in the premotor and primary motor cortices, brain regions successfully used for intracortical BMIs.

Approach

We report here for the first time a putative outcome error signal in spiking activity within these cortices when rhesus macaques performed an intracortical BMI computer cursor task.

Main results

We decoded BMI trial outcomes shortly after and even before a trial ended with 96% and 84% accuracy, respectively. This led us to develop and implement in real-time a first-of-its-kind intracortical BMI error “detect-and-act” system that attempts to automatically “undo” or “prevent” mistakes. The detect-and-act system works independently and in parallel to a kinematic BMI decoder. In a challenging task that resulted in substantial errors, this approach improved the performance of a BMI employing two variants of the ubiquitous Kalman velocity filter, including a state-of-the-art decoder (ReFIT-KF).

Significance

Detecting errors in real-time from the same brain regions that are commonly used to control BMIs should improve the clinical viability of BMIs aimed at restoring motor function to people with paralysis.

The nervous system makes widespread use of feedback to correct errors shortly after they occur and to adapt in order to minimize future errors [1–4]. During the control of movement, error signals are used to correct perturbations and update the brain’s internal model [5–8]. The same principle is also of clear utility to engineered systems and underlies control systems [9,10]. In this work, we tested whether an engineered system that directly interfaces with the neural system – a brain-machine interface – can exploit the fact that it shares common error detection goals with the biological system that it is connected to. A variety of neural error signals, which provide feedback on our actions and the environment, have been investigated in the last few decades [11–22] and potentially can be used to improve BMI performance [19,23–26], or even able-bodied performance [27]. Here, we focused on the task-outcome error signal, which arises when the goal of the movement was not achieved [19,21,28–30]. It was previously unknown whether this signal is present in primary motor (M1) and dorsal premotor (PMd) cortices typically targeted for intracortical BMIs. Therefore, in this paper, we asked two primary questions: (1) does an outcome error signal exist in the PMd and M1 cortices?, and (2) can decoding this signal benefit BMI performance?

Current intracortical BMIs decode only neural correlates of movement intention from the cortex, either in pre-clinical animal model experiments [31–43] or clinical trial evaluations in people with paralysis [44–52]. The performance of BMI systems has markedly improved in the last two decades; however, they have not reached natural arm reaching performance, and errors, such as selecting the wrong key during typing, still occur. At the heart of the limitations in BMI movement intention decoding is a tradeoff between speed and accuracy: increasing the complexity or precision required by the task leads to slower performance and/or more mistakes. Since errors usually require the BMI user to make a timely corrective action, such as selecting a delete key on a keyboard, BMI applications are designed to strike a balance between higher task efficiency (e.g., keyboard density) and minimizing error rate [53]. However, we envision BMI users using standard interfaces that will accelerate their independence, e.g., using a cursor to control a tablet [54]. Thus, in real-world use, optimal interfaces (and optimal target sizes) will not always be present, and errors occur more often than when working with an optimally-designed lab system. To date, most efforts at increasing the performance of intracortical BMIs have focused on improving movement intention decoding [31–39,41–43,52,55]. Here we provide a proof-of-principle of a complementary approach: a parallel error detector that executes corrective interventions, thereby prevent or undoing mistakes. We note that the error detection approach is largely independent of the implemented kinematic decoder; thus, our work aims to present a widely-applicable proof-of-concept rather than improve specific state-of-the-art decoders. This approach potentially enables the BMI system to be used for harder and more accurate tasks (e.g., denser grid, smaller key sizes or higher-dimensional prosthetic control) even with the same quality of movement intention decoding. This approach can also be used to rescue BMI performance when sensors degrade, in a fundamentally different and complementary way to existing approaches of rescuing kinematics decoding [56–59].

While there has been substantial work in developing adaptive BMI decoders that update their kinematic decoding parameters in response to externally specified errors [31,50,60–63] or inferred errors from the statistics of the system’s output [64,65], intracortical BMI designs have not explored the utility of a biological task outcome error signal. A BMI user is typically provided constant visual feedback of the BMI-controlled effector (e.g., computer cursor) and the BMI behavioral goal (such as the target on the screen), and is therefore aware of their BMI performance. It is therefore reasonable to postulate that neural correlates of BMI-based behavioral errors exist somewhere in the brain and might be utilized by BMIs as feedback to correct errors. Indeed, error-related potentials have been employed successfully in EEG-based BMIs with discrete decoding for trial-based typing [66–68], trial-based movements [20], and prosthetic device manipulation [69,70]. Encouragingly, outcome errors during a hand control task, recorded through electrocorticographic (ECoG) from motor cortex, were decoded during a post-hoc analysis [71]. However, a similar approach has not been implemented in real-time continuous control BMIs recording neural activity from motor areas (premotor and motor cortex), nor from intracortical recordings of spiking activity. It is important to determine if and how error decoding can increase the performance of such intracortical BMIs, which are to date the highest-performing BMI systems [46,49,51,52].

If such task-outcome error signals exist in PMd and M1, then BMIs could incorporate error detection without the need for implanting sensors in additional brain areas. Importantly, the existence of error signals in other brain areas and their influence on motor behavior do not guarantee that they can be identified in motor cortical areas, let alone decoded accurately for BMI purposes. Much of the research on error signals relies on EEG and fMRI measurement techniques; these studies have not reported clear evidence of error signals, and especially outcome error signal, in motor cortex. Encouraging evidence comes from a recent ECoG study, which found that responses that appear to come from motor cortex are modulated by execution error and task-outcome error [19,71]. Additional motivating evidence comes from an intracerebral study which found that supplementary motor area (SMA) is modulated by a response task outcome [21] making it a prime candidate for electrode targeting in the future. Other intracortical recording studies found evidence for execution error modulation in M1 and premotor cortex [72,73]. Nonetheless, it is not yet clear whether outcome error signals are present in M1 and PMd, which motivates an intracortical investigation. Intracortical recording can also enable a more extended analysis of the related neural modulation, such as accurate latency measurement, high spatial resolution, and single unit and population-level analyses. Accurate mapping of error signals across the brain will shed light on the brain’s motor control mechanisms. Evaluating whether task-outcome error signals can be detected in the M1 and PMd is therefore of scientific value in addition to its translational utility for BMI.

In this study, we used intracortical recordings from two monkeys to search for the existence of an outcome error in neuronal spike activity in PMd and M1. Specifically, we assessed the ability to detect wrong selections during a BMI ‘typing task’. We report three key findings: first, we found, for the first time, that putative task-outcome error signals are present in PMd and M1. Second, we present methods to design a BMI error decoder and predict its effect on performance. Third, we demonstrate for the first time a performance improvement of a closed-loop intracortical BMI augmented with a real-time error decoder.

Methods

Behavioral tasks

All procedures and experiments were approved by the Stanford University Institutional Animal Care and Use Committee. Two male rhesus macaques (monkeys J and L) were trained to perform point-to-point movements of a 6 mm radius virtual cursor in a 2D plane using either hand movements or BMI control. They were free to move their arm even during BMI control [40,74,75]. A keyboard-like task was modeled after the task described in [75,76]. The goal of the task and the experiment timeline is depicted in the Behavioral Task section of the Results and figure 1. The workspace was 40×32 cm and had in its center a 24×24 cm grid uniformly divided into n×n (n=6 to 8, depending on the dataset) contiguous, non-overlapping square target acquisition regions (whose height and width was 24/n cm). Each square target acquisition area contained, at its center, a circular visual representation of a target (8 mm radius, yellow discs in figure 1a). For BMI data collected for offline error decoding analysis (figure 2), we calibrated the task difficulty each day by changing grid size and required target hold time to keep the monkey’s success rate at approximately 80% (actual experimental session success rates ranged from 76% to 82%). This difficulty was chosen to balance having a sufficient number of failed trials with which to study neural activity following a failure versus frustrating the monkey or having failure be the expectation rather than the exception. For online comparison of the ReFIT-KF decoder, we used the optimal hold time of 450 ms as found in [53] with a 6×6 and 7×7 grids. The task had a 5 second time limit; only 3% (J) and 9% (L) of the trials were exceeding the time limit; these were omitted from the offline analyses.

Figure 1. Experiment layout and task timeline.

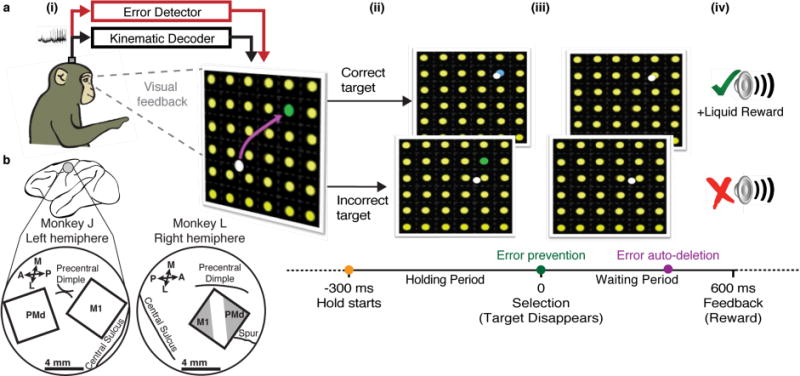
(a) A monkey performs a BMI grid task by controlling the cursor using a kinematic decoder (black pathway). We built an error detector (red path) that was integrated into the BMI to perform closed-loop error prevention before (‘Error prevention’, green timeline dot) or auto-deletion during (‘Error auto-deletion’, purple timeline dot) the waiting period. (i) His goal was to move the cursor (white disk) to the cued green target amongst the potential yellow targets. The target selection areas were non-overlapping and collectively spanned a 24×24 cm² workspace. Therefore, the cursor was always in the acquisition window of a possible target when it was in the grid workspace. The monkey can nominally identify task errors through continuous visual feedback. (ii) When the correct target (green) was being held, the target’s color changed to blue. It reverted to green if the cursor left the target before selection. Holding the cursor over any target (start time indicated by the orange timeline dot) for 300 – 400 ms selected that target. (iii) After selection (green timeline dot), the cued target disappeared (iv) and the monkey waited 600 ms for an auditory feedback tone that matched the outcome and, in successful trials, a liquid reward. A new trial started after an additional 400 ms. (b) Microelectrode array location(s) in motor cortex, as estimated visually during surgery from local anatomical landmarks (A = anterior, P = posterior, L = lateral, M = medial).

Figure 2. Decoding trial outcome-dependent neural differences.

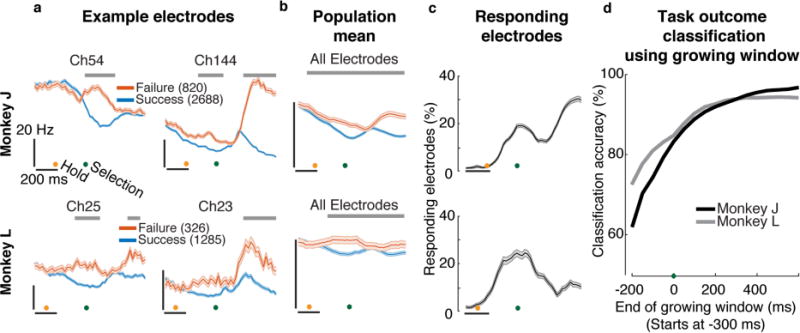
Green dot corresponds to t=0 target selection time, as in figure 1. Orange dot shows target hold start. (a) Trial-averaged firing rates (mean±s.e.) of example electrodes during failed (red) and successful (blue) trials. Gray bars indicate times with significance differences (t-test with Bonferroni correction, p<0.05, Methods). (b) Population trial-averaged firing rates. (c) Percentage of electrodes that show significant differences as a function of time (mean±s.e.). (d) Offline single-trial outcome decoding accuracy as a function of the end of a growing decoded time window, which starts at 300 ms before selection and ended between 200 ms before until 600 ms after target selection. The dataset in panels c and d combine six (J: 12,648 trials) and four (L: 5,528 trials) days of closed-loop BMI experiments.

Neural recording and signal processing

Monkeys were implanted with two (monkey J) or one (monkey L) 96-electrode Utah arrays (Blackrock Microsystems, Inc.), using standard neurosurgical techniques [77] 63–90 (J) and 83–91 (L) months prior to this study. J’s arrays were implanted into the left cortical hemisphere; one array went into the primary motor cortex (M1) and the other into the dorsal premotor cortex (PMd), as estimated visually from local anatomical landmarks (figure 1b). L’s array was implanted into the right hemisphere boundary between motor cortex and premotor cortex, as estimated visually from local anatomical landmarks (figure 1b). Since L had only one array, anterior electrodes were labeled as ‘PMd’ and posterior electrode labeled as ‘M1’ in our analysis (gray areas in figure 1b).

Voltage signals from each of the electrodes were bandpass filtered from 250 to 7500 Hz. A spike was then detected whenever the voltage crossed below a threshold set at the beginning of each day (at −4.5 × rms voltage). Contralateral hand position (for decoder training and hand kinematics analyses) was measured with an infrared reflective bead tracking system (Polaris, Northern Digital) polling at 60 Hz.

Most of the analyses presented accepted all voltage threshold crossing spike events on a given electrode, which may include more than one individual neuron’s activities. These “threshold crossings” have become the standard for BMI applications [46,50,52,55,77]. However, for supplementary analyses we sorted spikes to identify single unit activity using Blackrock Offline Spike Sorter (BOSS, Blackrock Microsystems, Inc.). This sorting was done manually, assisted by BOSS’ k-means algorithm.

BMI cursor control

At the start of each experiment, we collected a training dataset of approximately 500 arm-controlled trials of a planar Random Target Task according to the protocol described by Fan and colleagues [77]. These data were used to train a Feedback Intention-Trained Kalman filter (FIT-KF) decoder [77], which operates on the observed firing rate vector at time t, y_t, ε R(N=192 electrodes for J and 96 for L). For the ReFIT-KF decoder variant, we retrained the decoder from closed-loop BMI control data according to the protocol described in Gilja and colleagues [40]. Both FIT-KF and ReFIT-KF output a velocity command every 25 ms from input consisting of binned spike counts from the preceding 25 ms, and have comparable performance [77]. Briefly, FIT-KF is a streamlined version of the ReFIT-KF decoder [40] because it omits closed-loop recalibration, and it improves upon a standard KF by adjusting kinematics of the training data to better match the subject’s presumed movement intention. Note that for several of the days of the FIT-KF experiment days, we deliberately increased the difficulty of the task by not zeroing out training set velocities during the hold epoch (this calibration step is described by Fan and colleagues [77].

The velocity Kalman filter (VKF) converges quickly to a steady state:

$$v_t=M_1{v}_{t-1}+M_2{y}_t$$

, where v_t ∈ R is the velocity of the cursor at time t [78]. We call the first term (M₁v_t−1) the momentum (a state dynamics matrix that smooths the velocity) and the second term (M₂v_t) the ‘neural push’ (a mapping from neural activity to velocity). The linear mapping M₂ defines a decoder-potent space: neural activity in this subspace will affect the kinematics. However, neural activity outside this subspace, i.e. in the decoder-null space, will have no direct effect on kinematics [73]. The steady state equation can also be written as:

$$v_t={\displaystyle \sum _{\tau =0}^t{M}_1^{t-\tau }\cdot M_2{y}_t}$$

, which shows that the current velocity is a causal smoothing of the neural push. M₂ defines two complementary and orthogonal neural subspaces: one where neural activity affects cursor movement (decoder-potent space) and another where the neural activity does not affect cursor movement (decoder-null space). These subspaces are similar to the task-relevant and task-irrelevant spaces in the study by Flint and colleagues [79], and are closely related to output-potent and output-null subspaces in the study by Kaufman and colleagues [80].

Offline analysis

For all offline analyses, multiunit threshold crossing spike counts recorded on each of the N electrodes were binned every 25 ms (v_t ∈ R^N) and each trial (Y_i ∈ R^N×K, where K is the number of time bins in the trial) was aligned to target selection time (t=0, figure 1A).

We did not use formal effect size calculations to make data sample size decisions, but from the central limit theorem and the high trial number (see Results) we were able to assume normal distributions. All fully completed experimental blocks were included in the analysis, unless stated otherwise. For statistical significance, we assumed unequal variances (Behrens-Fisher problem) and used a two-sided two-sampled t-test with a confidence level of p=0.05 with Bonferroni correction (to account for the family-wise error rate), unless stated otherwise.

PSTHs

Peristimulus time histograms presented in figure 2a,b and Supplementary figure 1 were computed using data from example days: J: 2015-04-22 (3508 trials, 76% success rate) and L: 2015-08-04 (1611 trials, 80% success rate). From the central limit theorem and the high trial number we were able to assume normal distribution of the PSTHs and use a two-sided two-sample t-test as a statistical test to compare the two conditions. We assumed unequal variances (Behrens-Fisher problem) and used a Bonferroni correction (for the number of channels and time bins) to account for the family-wise error rate. When testing whether population firing rates during failed trials are higher than during successful trials (figure 2b), we used a one-sided two-sample t-test.

Percentage of significant electrodes

We evaluated the extent to which task outcome differences were observed across the entire recorded population by computing the percentage of electrodes that showed significant firing rate differences between successful and failed trials. As was the case for comparing PSTHs, we used a two-sided two-sample t-test as a statistical test to compare the two conditions, and performed Bonferroni correction to account for both number of electrodes and number of samples. This test was used to determine if an electrode’s activity during a certain time window is significantly different between the two conditions. To smooth the results, an electrode was considered as significant for the population analysis if it crossed the confidence level on two consecutive time samples. Lastly, we averaged across days the percentage of significant channels at every time bin ( ${\widehat{\theta }}_k$, where k is the bin number). To estimate this measurement’s standard error, s.e. $\left({\widehat{\theta }}_k\right)$, and conduct statistical tests, we used a bootstrap procedure with B=500 repetitions. In the bootstrap, we drew trials with repetitions and repeated the procedure to find the percentage of significant channels for the sampled trials ( ${\widehat{\theta }}_k^{\ast b}$, where b is the repetition number). From the set of bootstrap repetitions of ${\widehat{\theta }}_k^{\ast b}$, we estimated the measurement’s s.e., conducted statistical tests, and computed response latencies. When comparing PMd and M1 (e.g., figure 1B), we used the same technique while restricting the analysis to only the PMd or M1 electrodes.

Dimensionality reduction via principal component analysis (PCA)

In many of the analyses we were interested in isolating the neural signal component specific to the difference between failed and successful trials, i.e., the putative task outcome error signal. Firing rate time series during any two conditions (e.g., success and failure) can be represented with their average Y_cm=(Y_suc+Y_fail)/2 and difference Y_cm=Y_suc−Y_fail i.e., common and differential modes. Here, the common mode contains activity presumably related to performing the task but unrelated to the specific outcome. To focus on the difference between outcomes and filter out common processes, we performed principal component analysis (PCA) on the differential mode; i.e., the difference in the neural activity between the outcome-averaged successful and failed trials at bin k:

$$\Delta y_k=\frac{1}{N_s}{\displaystyle \sum _{i\in \mathit{Suc}}{y}_k^i-\frac{1}{N_f}}{\displaystyle \sum _{i\in \mathit{Suc}}{y}_k^i,\Delta y_k\in R^N}$$

This ‘outcome-targeting’ PCA is filtering out these ‘irrelevant’ (for our purposes) signals and reducing the data’s dimensionality (and thus the number of classifier parameters) increased decoding accuracy (see next section).

Based on similar reasoning, we used an analogous technique (‘direction-targeting’ PCA) to find the subspace that captures neural variance likely to relate to a directional error signal (figure 4). Specifically, we conducted PCA on the trial-averaged differences between success trials and fail trials grouped by which of the four targets directly adjacent to the cued target was selected. PCA was run on a data matrix in which these four subtracted conditions’ data series were concatenated in time (4K × N).

Figure 4. Information related to error direction is present in and can be decoded from motor cortical activity.

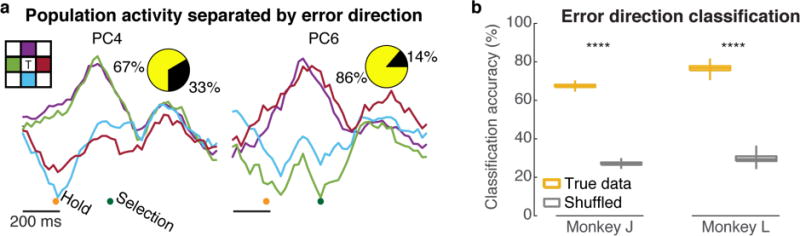
(a) Neural responses exhibited distinct patterns depending on which of the four targets adjacent to the cued target (shown in the colored insert) was incorrectly selected. Here we show monkey J’s neural activity (see Supplementary figure 9 for monkey L) projected onto two neural dimensions (using ‘direction-targeting’ PCA) and were chosen because their variance is mostly explained by the differences between direction conditions. Pie charts show relative variance contribution of the averaged-across-directions error signal (black) and the separated-by-direction error signal (yellow). (b) Classification accuracy when predicting which of the four targets adjacent to the cued target the monkey erroneously selected using neural data from 300 ms before until 600 ms after selection time. To determine chance classification, we decoded data with randomly shuffled error direction labels.

Classification via support vector machine

For all binary classifications in this study, we used a linear support vector machine (SVM) to predict whether each trial was a success or failure. The data were composed of labeled (success or fail) trials (indexed by i), each with an associated data matrix Z_i ∈ R^L×K, where L is the number of number of electrodes or principal components or kinematic components (depending on the specific analysis), and K is the number of time bins in the chosen time window. Given a set of training trials, the SVM fitting algorithm builds a model that can be then used to assign new examples into one of these two categories. In pilot studies, we found that the decoding performance was maximized when using five leading principal components (PCs). We note that different target selection-aligned time windows (figure 2d and Fig 3) had different numbers of time bins, and so we needed to build a separate classifier for each window. Since the online error detector had knowledge of when a target selection occurred (but not whether the correct target was selected, of course), this approach is fully compatible with online BMI use.

Figure 3. BMI error detector design and online improvement demonstration.

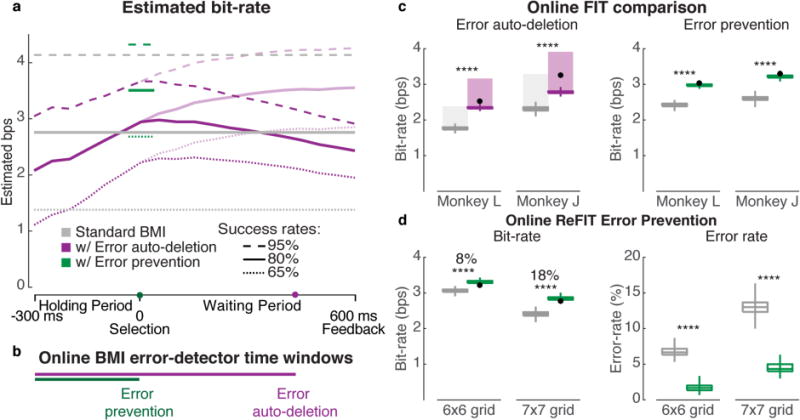
(a) Estimated bit-rate when augmenting the BMI with an error detector as a function of when detection happened and task difficulty (success rate) using Eq. 1–3. The parameters for bit-rate estimation were based on the empirical monkey J data (T=1.3s, N=64) (Supplementary figure 3 and figure 2). The three line types (dashed, solid and dotted) correspond to different base success rates with a standard BMI (gray, i.e. without parallel error decoding). Lower dark and upper light purple lines are worst- and best-case scenarios, respectively, based on whether the next movement is delayed or not as a result of the error classifier latency. (b) Time windows used for online error prevention and error auto-deletion, relative to (a) timeline. (c) Bit-rate comparisons (median, 1st and 3rd quartile, and extreme values of a bootstrap with 500 repetitions) between a standard BMI (FIT-KF, gray) and a BMI augmented with online error detection. Two modes of operation were evaluated online: error auto-deletion (purple) and error prevention (green). The top of the semi-transparent auto-deletion bars show post-hoc re-calculated bit-rate after removing the added delay (400 ms) following each selection. The vertical span of this bar represents a range of scenarios between the best and the worst case of whether the user naturally pauses between key selections (see main text for more details). Auto-deletion helps substantially in the best-case scenario, but does not out-perform a standard BMI in the worse-case scenario. Black dots are the bit-rate estimates (Eq. 2 and 3) of detect-and-act performance, based solely on the empirical data of the corresponding standard BMI (gray bars); note that these predictions fall within the measured closed-loop augmented performance ranges. The error auto-deletion dataset combines five (J: 9611 trials) and five (L: 6676 trials) days of closed-loop BMI experiments. The online error prevention dataset combines five (J: 7555 trials) and four (L: 6002 trials) days of closed-loop BMI experiments. (d) Bit-rate and error-rate comparison when using a state-of-the-art decoder (ReFIT) with and without error prevention. This dataset aggregates monkey J performing a closed-loop BMI experiment using three days each of two grid sizes (6×6: 4926 trials, and 7×7: 2480 trails).

For offline classification, we used 10-fold cross-validation to estimate the classification accuracy and its standard error. To compute naive classifier performance (as a control), we repeated the 10-fold cross validation after the labels of the trials (success or fail) were randomly shuffled across the trials. Moreover, to assess whether the classifier was biased towards one category (e.g., decoding ‘successful trial’ all the time), we computed the detection rate of successful and failed trials separately (i.e., true positive and true negative). When the input features to the classifier were PC activations rather than high-dimensional electrode firing rates, we were careful to not have the test dataset affect identification of the PC subspace: we first conducted PCA on each training set of the cross-validation to find a PC basis set, and then used this basis for subsequently classifying test data. When comparing two methods of classification statistically, we used a two-sided two-sampled t-test on the 10-fold classification accuracy of each classifier.

Online error detector

When comparing BMI error detection online using the FIT-KF decoder, we modified the monkeys’ typing task in two ways to make it more analogous to human typing [43,81]. First, to simulate how users must press the ‘delete’ key after an incorrect selection and then correctly select the missed key, we cued a predefined delete key after every incorrect selection. Once this delete key was selected, we then re-cued the target that was initially missed. Second, we removed the unusually long post-selection feedback delays that we had previously added as a scientific control. Specifically, we shortened the time between selection and the next trial initiation to 20 ms for error prevention experiments and 420 ms for error deletion experiments. When comparing BMI error detection online using the ReFIT decoder, the ‘delete’ key’ was not in use. Rather, the next target came up regardless of whether the previous selection was correct, but erroneous selections still penalized bit-rate and could be avoided by the error detect-and-prevent system. To compute the standard error and conduct statistical tests on measured bitrates, we used a Bootstrap procedure of swapping success and fail trial labels as explained in Methods: Percentage of significant electrodes.

The online error detector used the same two phase signal processing used for the offline classification: first, dimensionality reduction (projection of electrodes’ firing rates to a smaller number of PCs’ subspace), and then classification using SVM. In pilot studies, we found that decoding performance converged after a large quantity of approximately 2000 training trials, and that these decoders worked well across days. Therefore, to improve performance and maximize the amount of time available for performance testing during a given experiment session, we pre-trained the error detector on multiday datasets from previous days. We could take this approach because we expected recordings to be quite stable from day to day [82,83].

ReFIT experiments were performed only with monkey J since monkey L died before those experiments could be performed. We note that the average ReFIT decoder bit-rate of monkey J performing the 6×6 grid typing task presented in this study is lower than his performance on a comparable task previously reported in [42]. This is due to neural signal degradation and monkey behavior changes occurring in the two years between the experiments.

Control for kinematic differences

To regress out neural correlates of kinematics, we first found the least squares linear regression between cursor velocity and the neural activity (y_k=Ax_k+b). Next, we computed the neural activity residual without the contribution to kinematics $({\mathrm{y}}_{\mathrm{k}}{}^{\text{res}}={\mathrm{y}}_{\mathrm{k}}-{\text{Ax}}_{\mathrm{k}}-\mathrm{b})$. We compared the classification accuracy of the task outcome based on the neural activity (y_k) and the residual $({\mathrm{y}}_{\mathrm{k}}{}^{\text{res}})$ in Supplementary figure 5 to assess the effect of kinematics on the classification performance. The data used for these analyses were the six (J: 12,648 trials) and four (L: 5,528 trials) days reported in the Behavioral task section of the Results. When detecting errors using either neural activity (y_k) or its residual $({\mathrm{y}}_{\mathrm{k}}{}^{\text{res}})$, we used dimensionality reduction as explained in the Dimensionality reduction via principal component analysis (PCA) Methods section. We performed two-sided two-sample t-tests on the 10-fold cross validated results.

Control for external cue differences

For the external cue controls, we conducted a guaranteed liquid reward experiment (8,400 trials over three experiment sessions), a no cued target color change experiment (3,104 trials over two days), and a no auditory feedback experiment (3,912 trials over two days), all with monkey J. We measured offline error detection accuracy as explained in the Classification via support vector machine section under these different task modifications. The details of these modifications are described in Supplementary Text 1.

Directional error detection

To estimate the classification accuracy when decoding error direction (figure 4), we used 10-fold cross-validation nearest neighbor classifier (assigning a predicted point the identity of the K=1 nearest neighbor point) operating on the 5-dimensional neural data obtained by projecting firing rates onto the five leading direction-targeting PCs (see Results and Dimensionality reduction via PCs section). We tested the classifier on data from the six (J: 12,648 trials) and four (L: 5,528 trials) days reported in the Behavioral task results section. We computed two-sample two-sided t-test statistics between the 10-fold cross-validated results using true or shuffled data.

Results

Behavioral task

Two rhesus macaques (J and L) were trained to control a BMI cursor using intracortical spikes recorded from multi-electrode arrays in M1 and PMd (figure 1b, Methods). Neural signals were processed in real-time with a mathematical decoding algorithm based on a modified Feedback Intention Trained Kalman Filter [57,59,77] (FIT-KF, which has comparable performance to ReFIT, a state-of-the-art decoder [77], see Method). The decoder output a two-dimensional BMI cursor velocity control signal. Our experiment was designed to resemble a ‘typing task’: the monkeys had to acquire a specific target cued in green amongst a keyboard-like grid of selectable yellow targets using the BMI-controlled cursor [43,75,76] (figure 1a, Methods). We delayed reward and auditory feedback for 600 ms following target selection (figure 1a–iv) to temporally separate neural activity reflecting the monkey’s (presumed) recognition of the task’s outcome from neural activity related to explicitly receiving the liquid reward on successful trials. Since our initial goal was to compare neural responses during successful and failed trials, we calibrated the task difficulty daily (Methods) to make it hard enough that there was a sufficient number of failed trials (76%–82% success rate) for statistical power.

Task outcome-related neural differences

To investigate whether motor cortical activity reflects task outcome, we first compared the trial-averaged activity from successful and failed trials; selected electrodes’ PSTHs are presented in figure 2a, aligned to target selection time. In both monkeys, we found that there were periods before and after target selection when neural activity was significantly different depending on trial outcome (see Methods) in both threshold crossing spikes activity (figure 2a) and spike-sorted single unit activity (Supplementary figure 1). In all subsequent analyses we used ‘threshold crossings’ containing both single- and multi-unit activity to improve statistical power (Methods). We found that the neural activity, on average across all electrodes, tends to have higher firing rates during failed trials when compared to successful trials (figure 2b gray bars, t-test with Bonferroni correction, p<0.05).

To evaluate the extent to which this task outcome difference was observed across the entire recorded population, we computed the percentage of units that showed significant firing rate differences between successful and failed trials as a function of time (figure 2c; bootstrap test, p<0.05 with Bonferroni correction, Methods). We found that the activity of 18±1% (monkey J) and 25±1% (monkey L) of units was modulated by task outcome around target selection time. A substantial fraction of the ensemble was modulated even earlier: we found that at least 10% of units’ activity differed based on upcoming task outcome 155 ± 10 ms (J) and 161 ± 13 ms (L) (mean ± s.e.) after the target hold period started. Units in PMd tended to reflect task outcome earlier than those in M1 (Supplementary figure 2). Specifically, the threshold of least 10% of the population was modulated by task outcome 117 ± 10 ms (J) and 80 ± 20 ms (L) earlier in PMd than in M1 (t-test, p<0.01). From these results, we can infer that the activities of many neurons in M1 and PMd are correlated with task outcome. In subsequent sections we will describe various controls showing that this putative outcome error signal is not merely a result of indirect outcome correlates such as kinematics and reward. First, however, we answer whether this putative outcome error signal can be beneficially incorporated into an intracortical BMI.

Outcome decoding on a single-trial basis

To evaluate the potential for online error detection, we first analyzed trial-outcome decoding accuracy as a function of time relative to selection time. We decoded trial outcome based solely on neural activity in growing time windows using principal components analysis (PCA) for dimensionality reduction and a linear support vector machine (SVM) for classification (Methods). Trial outcome decoding accuracy increased as the trial progressed and converged to 97±0.5% (J) and 94±1% (L) around 400 ms after target selection (figure 2D). In addition, we found that decoding accuracy at selection time was already substantially above chance: 83±1% (J) and 85±2% (L). To verify that our decoder is not biased towards one outcome (e.g., always guessing success), we separately computed the accuracy of detecting successful trials (TP, true positive rate) and failed trials (TN, true negative rate) as a function of time (Supplementary figure 3), and found the decoder performed well in both cases. These high decoding accuracy results encouraged us to implement a real-time error detector; however, the offline decoding time course raises important decoder design questions that are critical to address.

Design for real-time error detection

Two main design properties are central to the error detector: 1) decoder latency, i.e., when the classification occurs relatively to the BMI action (e.g., before selection or some time later?), and 2) the corrective intervention performed upon error detection (e.g., does the system prevent an action before it occurs or undoes it afterward?). The choice of corrective intervention depends on the application and when accurate classification can be made. If the error can only be detected once already made, then the BMI system could only intervene with a corrective “undo” action to minimize the error’s consequences. However, if the error can be detected before the presumed erroneous action is made, then the BMI system can attempt to prevent the error. While it would in principle be better to prevent an erroneous action, or, failing that, to undo it as early as possible, figure 2d reveals that there is a clear tradeoff between the error detector’s latency and its classification accuracy. On the one hand, increasing the detector latency increases its accuracy. But on the other hand, this prolongs the trial, which decreases overall utility.

An error detect-and-act system can be incorporated in parallel to BMI kinematic decoders in many applications. Here, to provide a numerical treatment of this tradeoff, we applied it to the BMI communication application (using a virtual keyboard for ‘typing’) as a proof of concept to investigate the potential benefit of error detection. In a typing task, users typically correct mistakes by selecting the ‘delete’ key. This manual corrective action is highly time-consuming since the user needs to perform two additional selections for each mistake (first delete the wrong character, and then select the correct key). Thus, a helpful corrective intervention is to automatically “detect-and-undo” the previous target selection by deleting the previous character when an error signal is detected. To estimate the effect error auto-deletion would have on a BMI, we considered the bit-rate metric [41,52,53,84,85], which quantifies BMI communication performance. Bit-rate is defined as the rate of correct key selections (weighted by how many bits of information each selection conveys) minus a penalty for incorrect key selections based on the conservative assumption that each incorrect selection must be compensated for with a correct selection (e.g., selecting ‘delete’):

$$\mathit{bps}={\mathit{\text{log}}}_2\left(N-1\right)\frac{s-f}{T}$$ (1)

where T is the total length of the trials, N is the number of potential targets, and s and f are the numbers of success and fail trials, respectively. When error auto-deletion is incorporated into a BMI, the overall system’s bit-rate will depend on the effective success (s′=s·TP) and fail (f′=f·(1-TN)) trial count as well as the task delay imposed by having the error detector decide after target selection (dt). The bit-rate can therefore be estimated as:

$$\mathit{bps}={\mathit{\text{log}}}_2\left(N-1\right)\frac{s^{\prime }-f^{\prime }}{T+dt\cdot \left(s+f\right)}$$ (2)

This conservative estimate assumes that every trial will be delayed (dt) by the detector latency (by a few hundred millisecond). However, in real world applications this penalty might be substantially reduced when considering user strategy (e.g., if the user trusts the error auto-delete, they could continue towards the next key without waiting for the intervention) or if the detector latency overlaps with a cognitive load-imposed natural delay between movements (e.g., thinking about what the next letter should be). We do not suggest that continuous BMI decoders inherently require a post-selection delay to operate, but rather that the user may introduce such a delay when using the BMI for a cognitive task, such as typing.

We estimated the bit-rate as a function of when the error detection was attempted. For the key parameter of the error detector’s success rate as a function of time, we used the empirically observed accuracies from monkey J’s offline error detection data. In figure 3a, the estimated bit-rate (calculated using equation 2) increases until selection time because the classification accuracy increases without any added task delay. We considered two possible scenarios for what would happen if the error detection occurs after selection time: (1) a worst-case scenario in which the detector latency delays the next movement (dark purple lower lines), and (2) a best case scenario (light purple upper lines) in which error detection does not cause any added delay (e.g., if the user is pausing to prepare the next cursor movement anyway). The resulting detect-and-undo performance should therefore be somewhere between these two extrema lines, depending on the user and the task. Our analysis suggests that the performance change due to adding error detection, compared to standard BMI (Eq. 1, gray lines), can range from a more than two-fold communication rate improvement under low task success rate conditions (e.g., 65%), to decreasing performance when success rates are already high (e.g., 95%). Encouragingly, we also found that in a challenging enough task (with relatively low success rate), error auto-deletion can improve performance over a non-augmented decoder that does not have a delay, even when considering the worst-case scenario when a delay is needed for the auto-deleting system. This makes sense intuitively: automatically undoing most errors at a slight cost of time on every trial will be worth it if errors are frequent, but less so (or not at all) if errors are rare.

Since we observed high error detection accuracy even before target selection, we propose an additional mode for a detect-and-act system: “detect-and-prevent” action when an error is predicted right before when the selection would normally occur. In a dwell-typing application, a key is selected by holding the cursor over it (e.g., for 500 ms). We therefore propose to prolong the required hold time (e.g., waiting an additional d=50 ms) when an error is predicted. This intervention will give the user the opportunity to move the cursor out of the presumably incorrect target if it was indeed incorrect, or to keep the cursor over the target if it was in fact their intended key (i.e., after a false positive error detection). One of the benefits of this approach is that the cost of false positive detection will be small compared to erroneous detect-and-undo: rather than forcing the BMI user to re-acquire the target key, the trial length will only be slightly extended. Similar to before, we estimated the effect of error detect-and-prevent on overall performance by:

$$\mathit{bps}={\text{log}}_2\left(N-1\right)\frac{s-f^{\prime }}{T+dt\cdot (s-s^{\prime })}$$ (3)

Since there is no benefit from predicting the outcome earlier than the selection time, we only considered detection immediately preceding selection time (figure 3a).

Closed-loop, real-time error detect-and-act

Our goal is to demonstrate a proof-of-concept of a complementary approach that can presumably improve any decoder (be it the ReFIT-KF, FIT-KF, OLE, etc.) when BMI control becomes more challenging and errors occur. In real-world use, errors may result from a range of causes such as user mistakes (e.g., typos), a suboptimal interface that increases task difficulty (e.g., selectable keys that are very close together), a sub-optimal decoder, or a challenging task that is at the limits of the BMI’s performance (e.g., threading a needle). Thus, to test our hypothesis that a BMI can benefit from error detection in the face of errors, we chose to elicit errors by using a sub-optimal decoder (FIT-KF).

To demonstrate the utility of this system in a closed-loop BMI system, we implemented and tested these two proposed corrective interventions online as a proof-of-concept of a BMI with error detect-and-act capabilities. Across 10 (J) and 9 (L) experiment sessions (days), we used a real-time error detector in parallel to a kinematic decoder (FIT-KF, Methods and figure 1ai), and tested both the error auto-deletion (with dt=400 ms decoder latency) and error prevention (with d=50 ms delay) operation modes in a typing task where the difficulty was adjusted to yield an uncorrected success rate of around 80%. The error decoder used PCA-based feature reduction (keeping five leading principal components) and a linear SVM classifier (Methods). Both error prevention and error auto-deletion modes were compared separately to a standard kinematic decoder without error detection in an A-B-A block format, where A was a standard kinematic decoder (FIT-KF) and B was the same kinematic decoder with a detect-and-act system.

We found that both error detect-and-prevent and detect-and-undo modes improved the monkeys’ bit-rates each day (bootstrap-test, p<0.001). Error prevention increased the average bit-rate by 24% (J) and 23% (L). When evaluating error auto-deletion, we delayed the next trial by 400 ms for both the standard and error detection-augmented BMI (Methods), which mimics the aforementioned scenario where there is a cognitive need for the BMI user to briefly pause before starting to move the cursor towards the next key (figure 3c). Error auto-deletion increased the average bit-rate by 20% (J) and 32% (L) (see Supplementary Movie 1). Additionally, we also estimated what the bit-rates would have been if the system were being used in a scenario without a pause between trials. To do so, we re-calculated the bit-rates after removing the added delay (400 ms) from the trial length (figure 3c, top purple and gray semi-transparent bars). This offline re-analysis corresponds to the best-case scenarios both for the standard BMI system (the user doesn’t need to briefly pause between selections) and for the error detect-and-undo system (the user starts towards the next key without waiting to see whether the error detect-and-undo system executes or not). Detect-and-undo performance should be between the two scenarios (in the range of the transparent bars) depending on the task and the user strategy. We found that some overlap between the two performance ranges (with and without a delay) exist, in particular for monkey J. An overlap means that error auto-deletion is beneficial in some scenarios and not in other. Thus, the benefit of this detect-and-undo system depends on the task and the user strategy.

Based on the figure 3a bit-rate estimates and the figure 3c closed-loop results, we conclude that for these monkeys performing this particular task, error-prevention outperformed error auto-deletion. Thus, we also tested error prevention when using ReFIT-KF, a state-of-the-art decoder [52,53,86]. We evaluated the system in two task difficulties (6×6 and 7×7 grids, figure 3d). The detect-and-prevent system improved the standard ReFIT-KF performance during each day and for each task by 8% and 18% on the 6×6 and 7×7 grid tasks, respectively (figure 3d, bootstrap-test, p<0.001). This performance improvement was due to a reduction in the number of selection errors. As expected, the improvement was greater when performing the harder task (7×7, which is closer to the actual number of keys on a standard English keyboard) with a BMI augmented with detect-and-prevent capability. These online results corroborate our estimated predictions that error detection can provide even greater performance improvement during even more challenging tasks (e.g., when high accuracy is required). Our results show that error detection can improve BMI performance when the targets are optimally placed for bit-rate (6×6 [53]), but the technique becomes even more impactful during a more challenging task (7×7) when high accuracy is required. More demanding task requirements are germane to real-world applications (e.g., when more than 36 keys are needed, or when the key size is smaller than 4 cm, or when browsing a website with dense and non-optimally placed clickable hyperlinks).

Controls for indirect task-outcome correlates

Neural activity in the motor cortex is related to many processes including, but not limited to, kinematics, kinetics, sensory feedback, trial outcome (as reported here), and noise. We therefore wondered whether the neural activity differences we observed between successful and failed trials resulted from other variables that indirectly correlate with trial outcome but are not directly related to the monkey’s internal recognition/prediction of the trial’s outcome. Specifically, we tested whether kinematic differences (in both BMI cursor movement and residual arm movements), reward, and other experimental elements (auditory and color feedback) were major contributors to our outcome decoding. We briefly describe the results here, and report more details and further discussion in Supplementary Text 1.

We conducted two controls related to kinematics. First, we found that regressing out the BMI’s velocity-related component from the neural activity did not affect outcome classification accuracy. Second, we found that outcome detection using BMI cursor and hand kinematics were significantly worse (<80% accuracy, Supplementary figure 5) than decoding using neural activity. Thus, although small kinematic differences did exist between successful and failed trials, this information alone does not account for our ability to decode trial outcome accurately. This is consistent with our finding that less than 1% of the outcome error signal variance could be explained by movement-related neural activity. However, we note that this control should be interpreted while considering its limitations: although the causal mapping between neural activity and kinematics in a BMI framework is completely known, there might be additional kinematic-intention neural activity that is not linearly mapped to kinematics. Thus, these controls do not completely rule out whether differences in movement intentions could affect task-outcome decoding.

In two additional control experiments, we 1) provided rewards on all trials and 2) withheld auditory feedback (Supplementary figure 6). These experiments showed that reward and auditory feedback did not affect error detection performance (t-test, p>0.3), and suggest that the signal being decoded does not contain reward expectation components. This contrasts with recent work [87] that found a reward signal in the motor cortex but did not find outcome-related neural modulation. However, in that work, the monkeys performed reaches guided by uncertain visual cues, without seeing the target itself. Thus, the monkeys could not know the outcome until the reward was provided. As such, the [87] task design precludes dissociating the neural activity resulting from external cues (i.e., a reward signal) versus the monkey’s internal understanding of whether he performed the trail correctly (i.e., an outcome signal). Supplementary Text 1 further discusses these differences. In our task, the color change from green to blue when the correct target was being held was the only external cue about the trial’s upcoming outcome. A further control experiment in which this cue was removed (Supplementary figure 6) showed it had a minor effect (5% detection accuracy difference, t-test p<0.01). This is consistent with the monkey being more uncertain of the trial outcome without the color information. Nevertheless, we observed that outcome error classification accuracy was still high (92%) when target color remained unchanged, indicating that most of the signal we decoded was not due to color change.

Together, these controls are consistent with the hypothesis that the neural modulation we have described and decoded primarily reflects a putative task outcome error signal that cannot be attributed to differing kinematics, reward expectation or experimental cues.

Dissecting the putative outcome error signal

Thus far we have presented evidence that neural activity differs between successful and failed trials. However, it is difficult to understand the latent population-level patterns underlying these differences from examining single unit PSTHs. Dimensionality reduction techniques are often used to summarize properties of high-dimensional data (e.g., neural population activity) for visualization and interpretation [88,89]. Here, we used principal components analysis (PCA, Methods). This enabled us to summarize the population-level activity of the outcome-related neural signal and explore whether this signal differs depending on the relative direction of the correct and (mis)selected target.

First, to determine the putative outcome error signal’s dimensionality and to visualize its dynamics, we examined the outcome-targeting PCs (i.e., PCA on the difference between success and fail trials), which are shown in Supplementary figure 7. The three leading outcome-targeting PCs (which we will call the ‘outcome-error subspace’) capture 88±1% (J) and 82±1% (L) of the variance of the trial-averaged, outcome-related neural activity difference. Encouragingly, both monkeys’ neural activities showed similar dynamics in this subspace. This suggests that a major contributor to the putative outcome error signal is not related to monkey-specific stereotypical movements or monkey-specific neural response patterns following successful versus failed trials. Rather, these dynamics may instead reflect a general pattern of outcome error-related neural dynamics in these cortical areas.

Next, we explored whether the putative outcome error signal reflected the relative direction between the incorrectly selected target and the cued target. We would expect an outcome error signal to be direction-invariant, in contrast to an execution error signal, which should provide directional information about the error. To verify that the proposed signal is largely direction independent, we projected the direction-averaged neural activity into the outcome-error subspace and verified that most (90% (J) and 91% (L)) of the putative outcome error signal variance is common across errors in the different directions (Supplementary figure 8). The high degree of direction invariance in the outcome-targeting neural subspace suggests that this proposed outcome signal component mostly reflects neural activity related to outcome error.

Directional error detection

Despite finding that most of the putative outcome error signal was directionally invariant, we investigated whether we could additionally decode a different motor cortical signal that correlates with the direction of the error. The existence of such a directionally tuned post-execution error signal was recently reported [90]. To construct a different neural subspace that tries to capture variance related to the direction between the cued and incorrectly selected target, we performed a different analysis where we calculated the PCs of the neural differences between the average of successful trials and the activities averaged over erroneous trials to each of the four targets adjacent to the cued target (Methods). This ‘direction-targeting’ PCA technique is similar to our method described earlier to find the putative outcome error subspace (‘outcome-targeting’ PCA), except here we focus on observing the variance specific to which direction points towards the correct target. We found that there did indeed exist a different set of neural projections such that the resulting variance is mostly explained by the differences between direction conditions, rather than by the condition-average signal (figure 4a). Note that this result does not disagree with our previous statement (Sup. figure 8) that more than 90% of the putative outcome error signal variance is common across directions, since here we projected the data into a different neural subspace that was specifically targeted to identify direction-related variance, rather than outcome-related variance. Here, we focused on the potential of detecting the direction of the error for BMI. However, we believe that the relationship between the two signals (e.g., temporal, spatial, and causal relationship, and identifying a common source that might exist in other brain areas, etc.) should be further investigated in future work. Also, we note that in our task, error direction may be highly correlated with the monkey’s movement intention at the end of the trial [35], and thus further work is needed to disassociate these two factors. Despite this scientific caveat, here we were interested in the practical utility of this component of the neural activity (see next section), and for this BMI purpose we are agnostic to whether it reflects the monkey’s perception of error direction versus his intention to make a correction.

Finding these activity differences across error directions motivated us to do an offline analysis to evaluate if we could decode relative error direction (i.e. predict the location of the correct target with respect to the incorrectly selected target) on single trials. As a proof-of-concept for future BMIs, we evaluated the error direction classification accuracy by predicting one of four potential directions after incorrect target selection using a nearest-neighbor classifier (Methods). We were able to decode where the correct target was substantially better than chance in both monkeys (figure 4b; J: 68±1%, L: 76±2%; t-test, p<0.0001). This capability presents an opportunity to further improve BMI performance.

Discussion

This work makes both neural engineering and scientific advances. Its neural engineering contribution is to introduce and validate a new strategy for improving high-performance motor BMIs by simultaneously decoding non-motor cognitive signals. Its scientific advance consists of describing an outcome error signal in motor cortical spiking activity. Here we will discuss each in turn.

Error detect-and-act improves BMI performance

The key neural engineering contribution of this work is the design and closed-loop demonstration of a first-of-its-kind method for augmenting an intracortical BMI with error detection. This system utilized the brain’s error signals – which we show can be accurately detected from the same sensors and cortical area homologues already being used for clinical motor BMIs – to improve the performance of state-of-the-art BMI decoders. This opens a new avenue for improving intracortical motor BMIs, which until now have decoded only neural correlates of movement intentions [31–39,41–43,52,55], by simultaneously detecting additional cognitive signals related to the task being performed. Error detect-and-act can be used in parallel to any kinematic BMI and is more helpful in more error-prone scenarios, meaning that the utility of this strategy will increase as the complexity of tasks being performed with BMIs increases.

These error detection techniques can be applied to a broad range of BMI tasks to intervene with corrective actions. If the task outcome error signal generalizes across tasks, then no task-specific training data would be required; otherwise, calibration data would need to be collected within the context of the specific task. This question of generalization warrants future study. In a computer cursor control task, error detection can be used to prevent or undo incorrect clicks during typing [42,43,49,50]. During control of a robotic arm [45,46], task outcome error detection could be used to cancel the last command (e.g., grasping) and instead return to a previous state (e.g., the state of the robotic arm a second ago). Estimating the direction of the error – rather than just its occurrence – in a real-time BMI could be used to even further improve performance. For instance, the BMI system could automatically select the decoder’s estimate of what the intended key was during typing, or move the effector towards the intended object during robotic arms use. When designing a detect-and-act BMI for a particular application, the optimal corrective action and its corresponding decoder latency would depend on four parameters: the user’s success rate (i.e., task difficulty), the average trial length, the cost of making an error (e.g., additional reaches for deletion), and the error detection accuracy as function of the time. The latency can then be adapted online based on the prevalent error rates given the task difficulty and BMI neural control quality. In addition, error signals can also be used to update decoder parameters and adjust the learning rate of an adaptive algorithm, especially when the ground truth is unknown. For example, outcome error signal can be used to increase the learning rate after errors, while knowledge about the error direction could be utilized to update decoder parameter [31,50,60–63,68,91], thus reducing future errors.

Existing communication BMI workspaces are designed for minimum errors at the expense of complexity and efficiency [50,53] (e.g., keyboard density). Error detect-and-act can improve BMI performance by increasing the tolerable task difficulty. For example, increasing the number of available keys on a keyboard will increase the transmitted information rate from each selection; however, this decreases the target size and as a result reduces the success rate. By using a detect-and-act system, one could increase the number of keys while still keeping the success rate high. To find the optimal keyboard density, a mapping of the success rate as a function of layout needs to be found [53]. When using a BMI with an error detect-and-undo capability, hard tasks will become easier in the sense that the effective success rate will become higher. This may also benefit other types of difficult tasks, such as high-dimensional BMI-driven prosthesis [48] or when very high cursor control accuracy is needed, such as when navigating a link-dense website, game, or computer desktop.

Another application of error detection is in the context of rescuing performance following signal degradation. Chronic intracortical electrode signals degrade with time, which decreases BMI performance and success rates [92–95]. To date, efforts to rescue performance have focused on designing new kinematic decoders [56–59,63,65,96,97]. The error detection methods introduced here provide an alternative approach to increase effective success rates, thus rescuing BMI performance and improving the user experience.

Implementing a similar error detect-and-act system in a clinical human BMI should be straightforward as long as this task outcome error signal also appears in the human brain areas implanted with the electrode arrays, such as the motor cortex, an area typically targeted for BMIs. This open question is an important area for future investigation; recent encouraging ECoG results indeed showed evidence for such activity in motor cortex [71]. We predict that one source of differences that may be encountered during translation stems from human BMI movements being self-initiated by the user, in contrast to experimenter-paced monkey tasks. A benefit of this is that it is more likely that there will be a naturally-occurring delay between selecting a key and the initiation of movement towards the next key. Thus, it may be possible to extend the latency of error detection – which would improve outcome decoding – without increasing the average trial length. Another factor that could result in improved performance is that a human user would be informed of the error detect-and-act system and could change their strategy to better exploit it, perhaps by learning to modulate their neural activity to better emphasize the outcome error signal.

A putative outcome error signal in the premotor and primary motor cortices

The detect-and-act applications demonstrated in these experiments would not have been possible without the discovery of a suitable outcome error signal in relevant cortical areas. Thus, the key scientific contribution of this study is that, to our knowledge, this is the first report of task outcome-related spiking neural activity in M1 and PMd. These results using intracortical recordings significantly expand a recent ECoG study [19,71] which suggested the presence of error signals in motor cortex. First, we showed that error signals are present in both PMd and M1, and that they appear earlier in PMd compared to M1. Second, we also investigated the structure of this error signal and its directional independence at the level of the neural population and ruled out kinematic confounds, strengthening the claim that this is indeed an outcome error signal in the motor cortex. Finally, we have shown that this outcome error signal also exists during BMI use.

Finding a putative task-outcome error signal in the PMd and M1 is perhaps more surprising than finding an execution error signal for the following reason: execution error, which arises from a discrepancy between the intended and the actual movement [71,98], and target error, which arises from unpredictable changes in target location [98], are considered ‘lower-level’ in the error signal hierarchy compared to outcome error [99]. These low-level errors signal a mismatch of desired and estimated effector state that should be corrected immediately by motor cortex. In contrast, outcome error is a higher-level feedback about the end result of the movement [19,71,99,100]. It can indicate the need for changing the motor output on subsequent movements or updating the internal model of the effector [6,101,102], but has no immediate relevance to ongoing movement generation. Hence, one might have a higher expectation of finding execution and target errors in motor cortex, which itself is concerned with low-level details of muscle movements [103–106], and finding the more abstract outcome error signal to be restricted to motor areas believed to be associated with higher levels of movement control, such as supplementary motor area (SMA) [21,107], anterior cingulate cortex (ACC), basal ganglia [100,108–110] and cerebellum [6]. The existence of an outcome error signal in the motor cortex supports the theoretical proposal that motor controllers such as motor cortex use reinforcement learning signals to identify an appropriate response strategy to achieve their movement goal [12]. It is also consistent with recent reports that motor cortex is critical for motor learning [111].

We were able to decode the outcome error signal even before the end of the trial (figure 2d). At first glance, it might appear surprising that a task outcome error signal should be present before the trial is finished. However, we know from previous studies that high-level error signals can be detected even before the end of the trial and even before the response onset [110]. The source of this task outcome error prediction can be a forward model that estimates the probability of future error and plans a proper response. For example, when a person is about to lose his balance, he knows with increasing confidence as time progresses that a fall is unavoidable, and he prepares for the consequences. More specifically, in our case the monkeys were familiar with the task and could presumably recognize that the cursor had remained inside the acquisition area of an incorrect target for close to the selection duration; they therefore could anticipate that an incorrect selection was imminent.

Conclusion

In summary, the identification of a putative task outcome error signal in M1 and PMd raises important questions about how motor cortex adapts and learns as well as about what role this signal serves throughout the nervous system. It also raises key questions regarding the origin of this signal, which may well be outside of motor cortex and the result of cooperating cortical and subcortical networks. Finally, we demonstrated that is possible to leverage this putative outcome error signal to increase BMI performance by corrective interventions. As such, this signal may enable an entirely new way to substantially increase the performance and robustness, user experience, and ultimately the clinical viability of BMI systems.