Determination of Hydrophobic Lengths of Membrane Proteins with the HDGB Implicit Membrane Model

Abstract

A protocol for predicting the hydrophobic length of membrane proteins using the heterogeneous dielectric generalized Born (HDGB) implicit membrane model is presented. The method involves optimal positioning in the membrane, identification of lipid-facing and inward-facing residues, followed by energy optimization of the implicit membrane model to obtain the hydrophobic length from the optimal membrane width. The latest HDGB version 3 (HDGBv3) and HDGB van der Waals (HDGBvdW) models were applied to a test set containing 15 proteins (seven β-barrel and eight α-helical proteins), for which matching membrane widths are available from experiment, and an additional set contains ten α-helical and ten β-barrel proteins without any experimental data. The results with the HDGB model compare favorably with predictions from methods used in the Orientations of Proteins in Membranes (OPM) and Protein Data Bank of Transmembrane Proteins (PDB-TM) databases.

Graphical Abstract

INTRODUCTION

Membrane proteins are a very important and large class of proteins but much still remains to be understood. Structural coverage is rapidly increasing as there are now around 3,000 structures of integral membrane proteins deposited in the protein data bank (PDB).^{1, 2} However, one challenge is their location and orientation in physiological lipid bilayers and the exact length of the hydrophobic, lipid-facing segments since most membrane protein structures are solved in artificial lipid-mimicking or detergent environments. The length of the hydrophobic regions is expected to match the hydrophobic width of the membrane bilayer and therefore can provide clues about lipid-protein interactions in the native physiological environment. The local membrane width is also an important parameter when studying membrane proteins via computer modeling and simulation. Experimental studies have shown that the membrane width is of crucial importance for the function of membrane proteins.^{3, 4} Therefore, matching the membrane width correctly for a given protein is also essential when setting up membrane protein systems to study their structure, dynamics, and function via simulation. Additional experiments such as fluorescence spectroscopy, electron paramagnetic resonance spectroscopy (EPR), X-ray diffraction or nuclear magnetic resonance (NMR) spectroscopy can provide such information.^5–9 Alternatively, computational methods can be applied to predict membrane protein positioning and the extent of the hydrophobic region.

Initial efforts to predict the transmembrane segments for a given membrane protein via computers were based only on sequence information in combination with a suitable hydropathy scale.^10–14 As the number of membrane protein structures has increased, more recent methods determine the length of the hydrophobic region from the 3D structure.^15–19 The prediction of lipid accessibility of membrane proteins is also crucial for determining the transmembrane regions accurately. The residues of proteins which are looking inside may be polar or even charged like in case of ion channel alpha helical proteins or β-barrels. Therefore, this will affect the energetics and the orientation predictions. There are different computational approaches to distinguish inward and outward residues in the literature including the usage of solvent accessible surface area,²⁰ protein sequence^21–23 and algorithms based on 3D geometrical information of the atoms, including concave-convex algorithms and grid-based approaches.^{17, 19, 24, 25} The TMDET algorithm¹⁷ uses 3D structures as input and finds outward residues at every 1 Å slices along a predefined axis. At each slice, the algorithm predicts the membrane-exposed residues from the closest distance to the test points on a rectangle covering all the atoms, although details for this algorithm are not described well in the literature. In another study, Leman et al.²⁴ used a concave/convex algorithm to detect membrane exposed residues and compare their results with their manually curated database. A recent study also utilizes a grid-based approach for the detection of membrane exposed residues using the information gathered from the explicit MD simulations data.²⁵ There are also experimental methods to detect the inward residues,^{7, 26} but, again, the experimental characterization of membrane proteins is challenging, and consequently, there are experimental data only for a few proteins.

The two most widely used methods for the prediction of hydrophobic segments are associated with membrane protein structure databases: the Protein Data Bank of Transmembrane Proteins (PDBTM)^{17, 27, 28} and the Orientations of Proteins in Membranes (OPM)^{16, 29} database. In the method used in PDBTM, an empirical approach is followed to detect membrane spanning regions using an objective function, which is based on hydrophobicity and structural features of the proteins. The program carries out an extensive search of orientation with a predefined width by calculating the objective function at each orientation. After the optimum orientation is reached, the membrane width is extended until the number of membrane spanning segments does not change. OPM rather uses an implicit model of the membrane with a variable hydrophobic width and determines the position, orientation, and length of the hydrophobic region from optimizing the transfer free energy from water to the membrane environment. Other approaches have also generally relied on implicit membrane representation to determine the hydrophobic length of membrane proteins.^{15, 19} However, all of these methods generally use fairly simple membrane representations, and even the latest OPM method,^{30, 31} which involves optimized profiles along the membrane normal for model parameters, is still highly empirical. This raises the question of whether the computational prediction of membrane positioning and the hydrophobic length could be improved with more physics-based implicit membrane models such as those based on the Poisson-Boltzmann (PB) equation³² or generalized Born (GB) formalisms³³.

A number of GB-based implicit membrane models have been proposed,^34–37 but, so far, GB models have not been applied for the prediction of hydrophobic lengths of membrane proteins. Generally, GB-based implicit membrane models describe the membrane hydrophobic region as a low-dielectric continuum with additional terms capturing the varying non-polar component of the solvation free energy in lipid bilayers. The heterogeneous dielectric GB (HDGB) model developed by our group³⁸ involves continuous profiles of the dielectric constant and non-polar parameters along the membrane normal that were optimized against PB solutions, insertion free energies from explicit lipid bilayer simulations, and water-cyclohexane transfer free energies.³⁸ HDGBv3 is the latest version of the standard HDGB model that was further optimized against amino acid sidechain analog interaction free energies within the membrane bilayer.³⁹ Furthermore, the HDGBvdW model adds an implicit van der Waals term to improve the energetics in the membrane interior, where hydrophobic interactions are dominating.⁴⁰ In this study, we applied these recent HDGB models (HDGBv3 and HDGBvdW) to improve the prediction of the length of the hydrophobic region for membrane proteins. Membrane exposed and inward residues were predicted by a grid-based algorithm and HDGB models were modified to treat the surface residues with implicit membrane and inside residues with bulk implicit water. Based on proteins for which the width of membranes near membrane proteins has been determined from experimental methods^41–56 we found a good match with the experiments using our new HDGB-based protocol and better agreement than with the established OPM and PDBTM protocols. In the following, the protocol for predicting hydrophobic lengths is described before test results are presented and discussed.

METHODS

In this study, we examined seven β-barrel and eight α-helical proteins, for which experimental hydrophobic widths of the surrounding physiological membrane bilayer are available: outer membrane protein OMPF (PDB ID: 1hxx), ferric enterobactin receptor (1fep), outer membrane cobalamin transporter (1nqe), outer membrane protein OMPX (1qj8), ferric hydroxamate receptor (1qfg), outer membrane phospholipase A (1qd6), outer membrane protein OMPA (1qjp), bacteriorhodopsin (1m0l), bovine rhodopsin (1gzm), photosynthetic reaction center (1rzh), cytochrome c oxidase (1v55), potassium channel (1r3j), mechanosensitive channel (2oar), F-type Na⁺-ATPase (1yce), and lactose permease (2cfp). All of these protein structures were first minimized using the empirical implicit membrane model IMM1.⁵⁷ Then, the optimal position and orientation inside the membrane was determined using IMM1 and HDGB models. Finally, the length of the hydrophobic region in these proteins was determined by optimizing the membrane width in the HDGB models to minimize the energy. The IMM1 implicit membrane model was used in the initial steps to reduce the computational costs of the entire protocol. Orientation optimization and hydrophobic length prediction by HDGB models were repeated in a second iteration using the hydrophobic lengths predicted at the first iteration to minimize the effects of a possible hydrophobic mismatch. The method was further tested on an additional protein set consisting of the following systems: Neisserial surface protein A (PDB ID: 1p4t), EspP autotransporter β-domain (2qom), outer membrane protein OPMG (2x9k), autotransporter Hbp (3aeh), outer membrane protein from Thermus thermophilus (3dzm), Pseudomonas aeruginosa OccD3 (3syb), alginate transporter (4afk), CymA from Klebsiella (4d5b), KdgM (4fqe), COG4313 outer membrane channel (4rl8), mitochondrial ADP/ATP carrier (1okc), MATE (3wbn), nitric oxide reductase (3wfd), human adiponectin receptor 1 (3wxv), Exiguobacterium sibiricum rhodopsin (4hyj), dopamine transporter (4m48), delta opioid receptor (4n6h), translocator protein (4uc2), SemiSWEET transporter (4x5n), and mPGES-1 inhibitor (4yl3). In the following, the different proteins are referred to just with their PDB codes to simplify the presentation. The details of the protocol are explained in the following.

Initial energy minimization

Proteins were initially oriented along the membrane normal with the center of mass moved to the origin and the first principle axis aligned to the z-axis. Then, the potential energy of the proteins was minimized using steepest descent (SD) and adopted-basis Newton-Raphson (ABNR) algorithms. Using the IMM1 implicit membrane model,⁵⁷ 50 steps of SD minimization was performed followed by 1000 steps of ABNR minimization. Cα and Cβ atoms were restrained by a force constant of 0.10 kcal/mol/Ų during the minimization.

Initial membrane orientation using IMM1 model

To find the optimal orientation, each protein structure was translated first along the z-axis with 1 Å intervals. The maximum translation was determined according to the radius of gyration of each protein based on Eq. 1:

$$z=\frac{R_{\mathit{gyr}}-28.5}{2}$$ (1)

where R_gyr is the radius of gyration and 28.5 is the initial membrane width in Å that is assumed here in the initial optimization of the membrane orientation. For oligomer structures, the monomer chain was used for the calculation of the radius of gyration. The translation was then performed between +z and –z. In this way, protein structures are guaranteed to stay within the membrane during the translation scan. For proteins with small radii of gyration that result in z less than 5 Å, the translation was done between −5 and 5 Å to obtain enough sampling around the membrane center. At each z position, the protein was then rotated around the x and y axes in 5˚ intervals between −90˚ and 90˚. The orientation resulting in the minimum energy during the translation and rotation scan was taken as the optimal orientation. The IMM1 implicit model with a membrane width of 28.5 Å was used as the energy function in this step.

Membrane-exposed and inward-facing residues

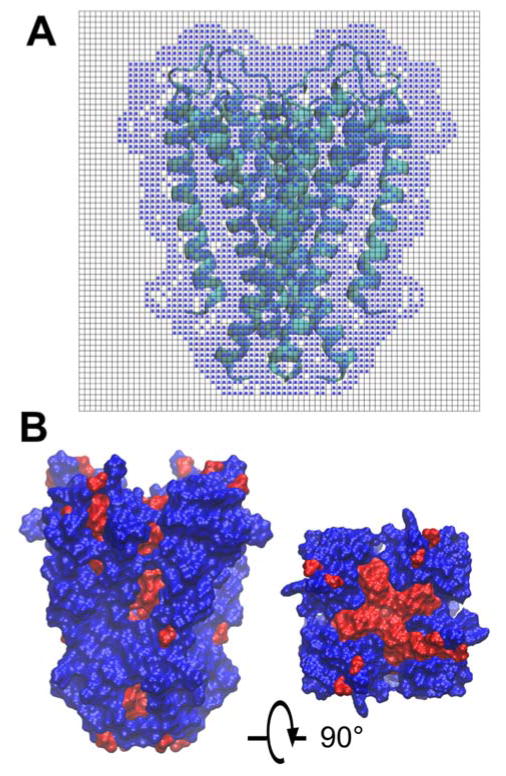
In the next step, membrane-exposed and buried residues were determined using a grid-based algorithm. First, the orientation-optimized structure was placed on a 3D Cartesian grid with a resolution of 1.0 Å. Grid cells were assigned to the protein structure if any protein heavy atom was found within the distance of its respective van der Waals radius (set uniformly to 2.0 Å). Then, solvent molecules were assigned to unassigned grid cells as long as they were further away from protein-occupied cells than the radius of a solvent molecule (set to 1.5 Å). Protein grid cells were then updated based on a cluster analysis of the solvent-occupied grid cells. Clusters with less than five adjacent solvent cells were re-assigned to the closest protein atom as such cavities were presumed to be too small to be occupied by a solvent molecule. Finally, the grid was scanned in slices along the z direction. For each slice, the cells were scanned from all edges of the grid in x and y directions towards the center of the grid. If a cell containing protein atoms was hit, the corresponding residue was considered to be outward-facing and membrane-exposed. On the other hand, residues in contact with solvent-occupied grid cells but not detected by the grid scanning procedure were considered inward facing and in contact with water such as residues lining a channel. To apply this algorithm, an initial orientation is needed. Thus, we used IMM1 to initially orient proteins along the membrane normal. Then, we applied our grid-based algorithm to the oriented structures. Figure 1 shows the 3D grid cells that are detecting the membrane exposed residues (Figure 1.A), and the final inward and outward residues in top and side views (Figure 1.B).

Figure 1.

Illustration of grid-based algorithm to detect inward and outward residues: (A) Grid around the protein 1r3j with blue dots showing the protein surface detected as grid cells by taking account of the van der Waals radius. (B) Side and top views of membrane inward (red) and outward (blue) residues.

Membrane orientation using HDGB models

The initial orientations that were determined by the IMM1 model were further optimized using the HDGB models (HDGBv3 and HDGBvdW). The z-positions of the proteins after the IMM1 optimization were kept constant, but proteins were rotated along the x- and y-axes by angles of −10˚ to 10˚ in 1˚ intervals. Membrane-exposed residues and buried residues, determined as described above, were treated differently. The HDGB dielectric and non-polar profiles were only applied for the outward residues, whereas the parameters for water (equivalent to the profile values at large values of z) were used for the inward-facing residues irrespective of their z-position along the membrane normal. In the case of HDGBvdW, the densities of bulk water were also applied for the inward residues instead of the lipid bilayer density profiles. This treatment allowed the consideration of membrane proteins with internal, water-filled cavities and channels. The optimal orientation was then determined based on the minimum HDGB energy.

Prediction of the hydrophobic length

The final oriented structures were used for predicting the length of the hydrophobic regions based on the minimum HDGBv3 and HDGBvdW energies when varying membrane widths between 1 and 40 Å were applied. Different widths were modeled in the HDGB models by scaling the dielectric and non-polar profiles initially optimized for a 28.5 Å membrane width. For the HDGBvdW model, the density profiles were also scaled accordingly. Again, membrane-exposed residues were treated with the z-dependent dielectric, non-polar, and density profiles, whereas inward residues were assumed to be facing aqueous solvent and therefore implicit water parameters were applied.

It is necessary to define the exact meaning of the hydrophobic length to consistently compare the results with the experimental and other computational techniques. We took OPM energy calculations as reference since it is a well-established method. The midpoint of the energy curve in OPM gives the hydrophobic length, which corresponds approximately to the region between the glycerol backbone and the polar head groups, which is commonly used to delimit the hydrophobic region.⁵⁸ A comparison of the energy functions with HDGB and OPM for a membrane width of 28.5 Å is given in Figure 2. The OPM energy curve is calculated as the basic sigmoidal function reported in their work.¹⁹ The HDGB curve reflects the change in energy with different values of ε in the pre-factor of the generalized Born formula according to the HDGB profile.^{33, 38} Figure 2 also projects a DPPC bilayer generated using CHARMM-GUI server.⁵⁹ The energy curves in Figure 2 show that although both profiles are used to describe the same membrane in OPM and HDGB, respectively, their midpoint is shifted by 4 Å towards shorter distances in the HDGB model. The use of the midpoint rather than other features of the profiles is the most robust approach and therefore we used the midpoints of the optimized HDGB profiles and added 4 Å to obtain hydrophobic widths that are comparable to the OPM values (and the common definition of the hydrophobic width). We also compare with predictions from PDBTM. The hydrophobic length prediction of PDBTM is based on a hydrophobicity scale calculated by dividing the membrane exposed surface area of hydrophobic residues to the total membrane exposed surface area along the membrane normal. Therefore, the predicted lengths would correspond to a region below the interface of the lipid bilayer where nonpolar residues locate. Thus, PDBTM and OPM hydrophobic lengths are approximately defining a similar region located between the lipid head group and the glycerol backbone.

Figure 2.

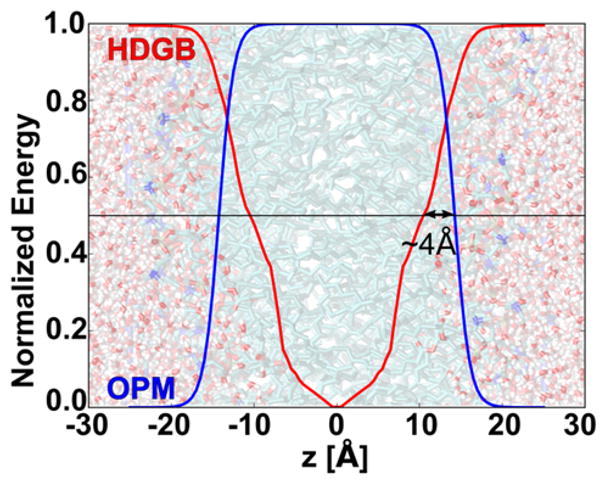
Normalized energy curves calculated by HDGB (red curve) and the OPM sigmoidal profile (blue curve). In the background, a DPPC bilayer is projected for reference with carbon, oxygen, and nitrogen atoms in green, red, and blue, respectively.

In the F-type Na⁺-ATPase protein (1yce), a glutamic acid residue (E65) was found to be outward-facing and in the middle of the membrane bilayer. Previous studies have suggested that the E65 residue is coordinated by a Na⁺ ion that reduces the energetic cost of the desolvation for this residue.⁶⁰ While we did not include Na⁺, we used instead the protonated glutamic acid during the orientation optimization and subsequent estimation of the hydrophobic length by HDGBv3 and HDGBvdW. This approach provided the expected positioning for the protein, with E65 located inside the membrane as predicted by previous experimental and computational studies.^{16, 54, 60}

Final membrane orientation and the hydrophobic length

The procedure for the optimization of orientations and prediction of hydrophobic widths using the HDGB models were repeated in a second iteration. In the second round, the orientation was optimized using the predicted membrane width in the first iteration to decrease the hydrophobic mismatch and obtain more reliable orientations. In the orientation optimization step, the protein was rotated at between −10 and 10˚ around the x and y axes with 1˚ intervals and a translation scan was also applied between −5 and 5 Å along the z-axis with an interval of 1 Å. Then, the final oriented structures were used for the hydrophobic length detection, which was carried out again as described above.

Software

All the calculations were performed with a modified version of CHARMM⁶¹, based on c41a1. The modifications involved the HDGB code to treat membrane-exposed and inward-facing residues differently. IMM1 and GBIM source codes in CHARMM were also modified to allow a separate treatment of inward-facing residues within the membrane bilayer and compare with the HDGB-based models. The Multiscale Modeling Tools for Structural Biology (MMTSB) Tool Set⁶² was used to facilitate the CHARMM energy calculations.

Statistical analysis

Correlations between models and experimental results were calculated from the linear regression curves and R², slopes and confidence intervals for the slopes were reported. F-tests were applied using the Python Scipy package⁶³ and p-values from F-tests were calculated to show the significance of the linear correlations, where the smallest p-values suggest the most significant correlations. The python module uses the cumulative distribution function for the calculation of two-sided p-value under the null hypothesis of zero slope of the linear correlation. Mean squared errors and mean residual differences were also calculated to present the deviations of the models from each other and from the experimental results.

MEMHLength web service

The protocol for predicting the length of the hydrophobic region in membrane proteins was implemented as the MEMHLength web server (http://feiglab.org/memhlength). The server orients the protein structure, uses HDGBv3 or HDGBvdW for the hydrophobic length calculation and provides an oriented structure and the predicted hydrophobic length as output. The output file also provides the inward and outward residues via the occupation column in the output PDB files where values larger than zero indicate exposed residues. Typical calculations are completed within a few minutes.

RESULTS

We developed a new protocol for predicting the length of the hydrophobic regions in membrane proteins assumed to match the hydrophobic widths of matching lipid bilayers. The protocol takes advantage of recent versions of the HDGB implicit membrane model. The protocol was tested on a set of membrane proteins for which experimental membrane widths are available. We further tested the protocol on another set of proteins containing ten α-helical and ten β-barrel membrane proteins for which we compared only with estimated lengths of the hydrophobic regions from the OPM and PDBTM databases.

Prediction of membrane-exposed residues

The algorithm for the detection of protein-inward and protein–outward residues was tested using a manually curated database.²⁴ We used ten proteins in our set which have manual results in the database. The database has structures from the PDBTM website and the detection of the membrane exposed residues was done for a membrane width of 30 Å. Following our protocol, we used the structures that were oriented by IMM1 and predicted inward-outward residues for each molecule. However, for validation, in order to make a fair comparison with the manually detected residues, we also used the same structures and pre-defined membrane widths upon which the manual prediction was based on. Furthermore, we compared our results with the recently reported results by Leman et al. that uses a concave-convex algorithm called mp_lipid_acc.²⁴ The results are shown in Table 1. Overall the accuracy with our method is high, predicting about 90% or more of the residues correctly for most structures. mp_lipid_acc gives slightly higher accuracies than our algorithm for most cases, but it should be noted that the mp_lipid_acc method was trained in part on the manual assessment results we are comparing against here. Furthermore, the manual assessments may not be completely reliable, since it is difficult to account for the van der Waals radii of protein and solvent atoms simply by looking at the 3D structures and therefore solvent accessibilities of certain residues could be overestimated.

Table 1.

Inward-outward residue prediction accuracies.

PDB ID	Accuracy 3D-grid	Accuracy mp_lipid_acc
1fep	0.95	0.97
1qd6	0.85	0.85
1qjp	0.90	0.95
1rzh	0.89	0.91
2x9k	0.93	0.95
3dzm	0.93	0.98
3wfd	0.90	0.86
4afk	0.93	0.97
4d5b	0.96	0.98
4fqe	0.89	0.97

Accuracy values were calculated by dividing the number of correctly predicted residues to the total number of the residues. The results for mp_lipid_acc were taken from Leman et al.²⁴ except for 1fep and 1qd6, for which accuracies were calculated using the PDB structures from their web server.^{24, 64}

Optimal orientation of membrane proteins

The orientation and positioning of membrane protein structures within a lipid bilayer is generally not available from the PDB structures but critical for correctly estimating their energetics within the membrane. Figure 3 shows the optimally oriented protein structures using the HDGBvdW model in the optimization protocol. Figure 3 shows that the hydrophobic regions of the proteins are generally matching the hydrophobic part of the implicit membrane models with the optimized widths. In some cases, there is noticeable tilting in the optimized structures suggesting that a titled configuration is preferable over a wider membrane width, as in 1qd6 for example. In other cases, the predicted membrane width appears to be less than the extent of what visually appears to be the hydrophobic region, as in 2oar, although the predicted width actually matches the experimental data reasonably well (see below), indicating that the HDGB model recognizes key features of the protein structure that favor a reduced membrane width.

Figure 3.

Positions and orientations of membrane proteins obtained after optimization using HDGBvdW. Shaded area show the hydrophobic region predicted by HDGBvdW. Residues are colored as follows: negatively charged, red; positively charged, blue; polar, green; non-polar, white.

Table 2 shows the tilt angles with the membrane normal and the center of mass positions along the z-axis (see Methods). Generally, the HDGBv3 model gives very similar orientations as with HDGBvdW, except for 1qj8, 1qjp, 1v55, 2qom and 4m48. The R² correlation between the two HDGB models is 0.66 with a slope of 0.89. There are larger differences between the tilt angles predicted by the HDGB-based method and the OPM and PDBTM results, although the differences rarely exceed 10˚. The correlations of OPM and PDBTM tilt angles with HDGBvdW predictions are 0.63 and 0.57 with slopes of 0.88 and 0.79, respectively. Based on the F-test for the linear regression between HDGBvdW and the other models, the results from the different models are highly correlated. In the absence of experimental data, it is difficult to determine, though, how realistic the predicted tilt angles are. There are also few MD simulation data that reported the average tilt angles of the proteins throughout the trajectory.^65–67 A comparison with those results shows that for 1qjp and 1gzm, HDGBvdW models tilted within the reported range, but, for 1qd6, the tilt angle is slightly higher than the range predicted by the MD simulations. We note that HDGB models were able to capture the tilt of single peptides in reasonable agreement with experiment in previous work.⁴⁰ The predictions can be improved further by using the dynamic HDGB (DHDGB) model,⁶⁸ which allows deformations of the membrane.

Table 2.

Tilt angle and the centers of mass relative to the membrane normal

PDB ID	HDGBv3		HDGBvdW		OPM		PDBTM		MD Simulations
	Tilt (˚)	Z (Å)	Tilt (˚)	Z (Å)	Tilt (˚)	Z (Å)	Tilt (˚)	Z (Å)	Tilt (˚)
1hxx	22.3	−4.0	22.9	−5.0	28.8	−6.6	28.8	−5.7	-
1fep	17.0	12.9	17.0	12.9	12.8	12.8	15.1	9.7	-
1nqe	42.1	8.7	40.7	8.8	39.5	9.8	36.5	8.1	-
1qj8	15.1	−6.8	27.6	−5.7	19.8	−7.3	7.4	−3.4	-
1qfg	14.5	−10.8	14.5	−11.8	20.1	−12.4	10.8	−8.9	-
1qd6	27.9	−1.6	27.8	−4.6	25.6	−5.2	25.6	−3.5	20–2567
1qjp	15.3	−5.9	6.7	−5.9	13.4	−3.8	8.4	−5.4	5–1065
1m0l	7.3	−1.1	6.3	−1.1	11.9	−1.7	11.9	0.3	-
1gzm	13.0	1.3	13.0	1.3	13.0	−0.4	7.2	−4.8	8–1666
1rzh	18.5	8.0	18.8	8.0	27.4	8.6	31.9	7.4	-
1v55	11.2	4.0	21.4	3.0	9.5	2.5	9.2	2.7	-
1r3j	2.0	2.1	2.0	3.1	0.0	2.1	0.0	2.4	-
2oar	4.1	4.8	4.0	4.8	1.4	9.5	0.0	11.9	-
1yce	1.4	−1.3	1.4	−1.3	0.0	−4.2	0.8	5.6	-
2cfp	3.1	−4.1	2.0	−4.1	9.3	−4.4	9.0	−2.1	-
1p4t	19.8	6.0	19.8	6.0	19.5	6.5	5.6	−1.5	-
2qom	4.4	6.0	22.0	3.9	18.0	7.7	18.7	4.1	-
2x9k	11.2	−3.7	11.2	−5.7	9.1	−7.6	6.4	−1.4	-
3aeh	5.0	−5.8	8.2	−7.8	10.5	−7.6	4.9	−4.8	-
3dzm	16.4	9.2	17.4	8.3	7.6	11.4	9.7	12.7	-
3syb	42.0	−5.7	42.0	−5.7	44.3	−6.8	39.6	−2.0	-
4afk	13.0	5.9	13.0	5.9	7.1	7.0	8.5	5.3	-
4d5b	5.7	9.2	5.0	9.2	8.3	10.6	1.4	3.5	-
4fqe	19.0	5.8	19.0	3.8	13.7	3.3	25.0	−1.4	-
4rl8	18.8	−3.4	16.4	−3.4	9.4	−6.2	16.4	−1.5	-
1okc	16.0	−3.0	16.0	−3.0	20.1	−4.4	8.8	−7.2	-
3wbn	9.2	−2.0	7.6	−1.0	16.7	−0.7	17.3	0.1	-
3wfd	13.9	1.8	13.9	0.8	11.6	−0.4	7.6	1.7	-
3wxv	23.2	−2.1	23.2	−4.1	25.1	−2.0	5.6	−2.6	-
4hyj	6.4	−1.2	5.8	−0.2	16.9	−1.5	8.8	1.3	-
4m48	43.2	0.7	16.5	1.7	33.1	1.9	21.5	0.4	-
4n6h	11.2	−5.6	15.2	−4.7	30.0	−9.1	10.7	−7.3	-
4uc2	13.0	3.9	12.1	3.9	9.8	4.6	8.9	3.1	-
4x5n	8.2	6.0	9.5	6.0	1.4	0.8	3.7	1.9	-
4yl3	2.0	−4.0	2.0	−4.0	0.0	−3.9	0.0	−5.1	-
avg.	14.8	0.69	14.9	0.35	15.6	0.08	12.3	0.39	-
R2	0.66	0.97	-	-	0.63	0.92	0.57	0.66
slope	0.89	0.97	-	-	0.88	1.11	0.79	0.76
95% CIa	0.22	0.06	-	-	0.23	0.11	0.23	0.19
pb	3·10−9	~0	-	-	1·10−8	~0	1·10−7	3·10−9
MRc	−0.16	0.34	-	-	0.65	−0.27	−2.6	0.04
MSEd	40.01	1.15	-	-	44.57	4.1	54.8	11.4

Tilt angles were calculated as the angle between the principal axis of the protein and the z-axis. For 1qd6, the average tilt angle of the two monomers was calculated to be able to compare with the MD simulation data. OPM and PDBTM structures were downloaded from the corresponding databases. For 1hxx, 1m0l and 1v55, chain A was used for the calculations since the monomer structures were used for these proteins in this work. For the calculated positions of the center of mass, the HDGB-based models were taken as the reference. In some cases, OPM and/or PDBTM models had to be flipped with respect to the membrane bilayer to compare equivalent orientations. Statistical analyses were applied to the pairs between HDGBvdW and each of the other models, HDGBv3, OPM and PDBTM. The F-test was applied to determine the probability that the results from two models are correlated via a linear relationship.

^aconfidence interval for slope;

^bp-value from the F-test for significance of a linear fit;

^cmean residuals;

^dmean squared error between predicted and experimental values.

Table 2 also shows the center of mass positions of the proteins along the membrane normal. Overall the positions obtained by HDGBv3 and HDGBvdW are close to each other and comparable with the OPM and PDBTM results, but, again, an experimental reference is not available. The average z position of the centers of mass is close to zero with the HDGB-optimized models, as well as with OPM models and PDBTM-optimized models. OPM and HDGBvdW-optimized models give more correlated center of mass positions compared to PDBTM (see Table 2).

Hydrophobic lengths of membrane proteins

Based on the minimal energies with the HDGB models using profiles for different membrane width we predicted hydrophobic lengths for membrane proteins as detailed in the Methods section. The results are compared against experimental data. While the experimental data is likely subject to significant uncertainties errors are generally not reported. However, for results from matching bilayer widths, we assumed errors of 1 Å based on a study by Lewis and Engelman⁶⁹. The values for 1qj8 and 2oar are potentially more problematic. For 1qj8, the experimental hydrophobic length was determined under the unverified assumption that the protein is aligned with the membrane normal without tilting.⁴⁴ For 2oar, the experimentally matching membrane width may not fully correspond to the hydrophobic part of the 2oar crystal structure as the protein structure may distort to relieve a hydrophobic mismatch.^{49, 50} Thus, the hydrophobic region of the 2oar structure could be longer than the experimentally detected lengths. Nevertheless, not knowing better, we used the values as reported.

The prediction of hydrophobic length was performed in two iterations as mentioned in the method section. The results after the first iteration are given in Table S1. In addition, Table S1 also shows results with the original HDGB codes along with results obtained by IMM1 and other GB-based models, namely the generalized Born with simple switching (GBSW) and generalized Born implicit membrane (GBIM) models. The results with the original versions for all the models, where inward-facing residues were not treated differently, were generally not able to reliably capture the hydrophobic lengths of the proteins. A modification for the treatment of the inside residues improved results significantly. The HDGB models performed best but the modified versions of IMM1 and GBIM also showed significant improvements.

Table 3 shows the predicted hydrophobic lengths of the proteins after the second iteration using the HDGBv3 and HDGBvdW variants as well as the modified IMM1 and GBIM versions in comparison with experimental values and predictions from OPM and PDBTM. IMM1 provides significantly shorter hydrophobic lengths than experimental values with a mean residual difference of −5.95 Å. On the other hand, GBIM provides longer hydrophobic lengths for most of the proteins with a mean residual difference of 3.14 Å. In contrast, the average hydrophobic lengths are only slightly underestimated with HDGBvdW by about 1 Å compared to the average over the experimental values. With HDGBv3, the predicted hydrophobic lengths are reduced further to about 2 Å less than the values from experiment. OPM predictions on the other hand overestimate the hydrophobic lengths by about 2 Å on average. In addition, HDGB models give the lowest mean squared errors among other methods suggesting that HDGB-based models provide smaller deviations from the experimental values than with the other models.

Table 3.

Hydrophobic lengths calculated using HDGBv3 and HDGBvdW models.

PDB ID	Exp.	IMM1	GBIM	HDGBv3	HDGBvdW	OPM	PDBTM
1hxx	20.3±1	10	23	17	19	24.0 ± 0.8	19.0
1fep	22.6	15	30	23	23	24.3 ± 1.1	20.3
1nqe	20	12	26	20	21	23.4 ± 1.0	20.0
1qj8	28	18	27	22	24	23.6 ± 2.8	28.5
1qfg	23	18	30	21	22	24.7 ± 1.0	25.5
1qd6	15–20	17	29	21	22	23.9 ± 1.0	22.5
1qjp	23	9	28	22	23	25.4 ± 1.5	20.0
1m0l	32	25	29	31	30	31.8 ± 1.1	24.5
1gzm	30	28	35	30	30	32.2 ± 1.5	32.5
1rzh	28	25	29	28	28	31.8 ± 0.8	24.0
1v55	27±1	27	32	20	22	28.0 ± 0.6	36.0
1r3j	34±1	25	34	30	30	34.8 ± 1.2	34.5
2oar	24±1	27	17	20	22	36.1 ± 2.2	32.5
1yce	34	31	40	36	36	37.0 ± 0.5	35.5
2cfp	31	25	35	31	31	31.1 ± 1.4	29.5
avge	26.5	20.8	29.6	24.8	25.5	28.8	27.0
R2		0.61	0.43	0.78	0.82	0.58	0.51
slope		1.11	0.72	1.00	0.89	0.76	0.88
95% CIa		0.48	0.45	0.29	0.22	0.35	0.47
pb		5.4·10−4	8.2·10−3	1.3·10−5	3.2·10−6	9.7·10−4	2.7·10−3
MRc		−5.66	3.14	−1.66	−0.93	2.35	0.53
MSEd		50.32	27.67	9.27	5.12	16.52	17.68
1p4t	-	18	28	24	24	24.9 ± 2.4	32.5
2qom	-	13	35	16	24	25.1 ± 1.6	27.5
2x9k	-	20	28	22	25	24.7 ± 1.2	31.5
3aeh	-	9	30	17	22	25.2 ± 1.1	30.0
3dzm	-	23	35	29	32	28.5 ± 2.6	21.0
3syb	-	13	28	19	19	23.6 ± 0.9	21.5
4afk	-	15	26	22	22	24.8 ± 0.9	28.5
4d5b	-	14	28	24	23	23.5 ± 1.0	33.9
4fqe	-	9	23	12	18	22.2 ± 1.5	25.0
4rl8	-	16	28	23	24	23.4 ± 1.1	32.5
1okc	-	22	28	25	25	29.5 ± 1.7	33.0
3wbn	-	23	27	26	25	31.8 ± 1.4	30.5
3wfd	-	26	34	22	24	31.7 ± 1.6	24.5
3wxv	-	24	29	24	29	32.8 ± 1.2	30.5
4hyj	-	21	21	25	25	30.0 ± 1.6	36.0
4m48	-	23	28	24	20	30.8 ± 1.6	27.5
4n6h	-	29	15	37	36	34.0 ± 2.3	36.0
4uc2	-	23	29	28	29	30.4 ± 0.9	31.0
4x5n	-	25	25	28	28	36.8 ± 1.1	32.5
4yl3	-	11	38	30	29	29.8 ± 0.7	26.5
avgf		19.7	28.8	24.3	25.3	28.4	28.5

Comparison with the experimental values (exp) and calculated values by OPM (PPM2 version) and PDBTM servers (PDBTM version: 2017-06-16) were presented. The OPM and PDBTM values were taken from the reported data for each PDB ID at the respective websites. Experimental hydrophobic lengths were taken from different studies; for 1fep, it is derived from the depth analysis; for 1nqe and 2cfp, it is calculated as the distances of Cα atoms of the membrane spanning residues along the z-direction (the membrane spanning region of 1nqe and the first principle axis of 2cfp were aligned along the z-axis for this calculation); for 1hxx, 1v55, 1r3j and 2oar, matching bilayer widths were extracted from the study of Lewis and Engelman⁶⁹ along with the experimental errors. For 1nqe and 1gzm, 10 Å was subtracted from head to head distances to obtain hydrophobic length.⁵⁸ For 1qd6, a range was reported and 20 Å was used as the experimental value for the statistical analysis. Because our protocol is deterministic, no statistical errors can be determined if only a single input structure is considered. R² and the slope were calculated from linear regression with respect to available experimental values.

^aconfidence interval for slope;

^bp-value from the F-test for significance of a linear fit;

^cmean residuals;

^dmean squared error between predicted and experimental values;

^eaverage over first set for which experimental values are available;

^faverage over all proteins.

The shifts in the average widths relative to the experimental values suggests that simply adding a constant to the predicted values could reduce the residuals and mean squared errors. From a systematic search to find minimal mean squared errors, we obtained optimal empirical corrections of +1.7 and +0.9 Å for HDGBv3 and HDGBvdW, respectively, leading to minimal mean squared errors of 6.5 Ų and 4.3 Ų. A similar analysis for OPM and PDBTM shows that the addition of −2.3 and −0.5 Å gives the smallest errors, 11.0 Ų and 17.4 Ų, respectively.

The predicted hydrophobic lengths with the HDGB models are highly correlated with the experimental values with R² values of around 0.8 and slopes near 1 based on linear regression fits with a 95% confidence interval of 0.29 and 0.22 for the slopes for HDGBv3 and HDGBvdW, respectively. HDGBv3 performs slightly worse than HDGBvdW in terms of correlation. In addition, HDGBvdW gives the lowest p-values from the F-test, indicating that the HDGBvdW predictions are statistically most similar to the experimental values. Both, OPM and PDBTM predictions as well as the results with GBIM and IMM1 are significantly less correlated with the experimental values than the HDGB predictions. In the additional set of proteins for which there is no experimental data available for comparison, the same trends are apparent. HDGBvdW and HDGBv3 are highly correlated with each other but with HDGBv3 giving somewhat smaller lengths whereas OPM (and PDBTM) predictions are overall larger than the HDGBvdW based predictions.

DISCUSSION AND CONCLUSIONS

In this work a new protocol is presented for determining the length of the hydrophobic regions of membrane proteins that would correspond to the width of the surrounding membranes after optimal positioning of the proteins. The two main purposes for applying such a method to a given membrane protein structure are the identification of the most likely physiological membrane, based on the predicted widths, and the choice of an optimal membrane width necessary for computational studies involving implicit or explicit lipid bilayers. In many cases, the native membrane composition is not known for a given membrane protein, and even when the type of membrane is known, information about hydrophobic mismatch is useful as such mismatches can significantly affect the function of membrane proteins.^{3, 4} The method presented here relies on the HDGB implicit membrane models and performs better than similar previous methods,^{15, 17, 19, 30, 31} in particular the method used as part of the widely used OPM server. With the HDGB-based method, we obtain higher correlations between the predicted hydrophobic lengths and experimental membrane widths. We believe that this reflects a more accurate energetic description of membrane bilayer with the HDGB-based implicit membrane models. The HDGB model is the latest representative of a broader class of GB-based implicit membrane models and we were pleased to find that the physically most accurate HDGBvdW model, that includes an additional dispersion term, also performed best. However, we expected that other variants such as the GBSW-based implicit membrane model³⁴, GBIM³⁵, or the related IMM1⁵⁷ method, would perform comparably. In this study, we could only test GBIM and IMM1 in modified versions where inward-facing residues within the membrane bilayer are treated differently. We did not pursue modifications of GBSW to accommodate inward-facing residues as that would involve extensive alterations of the source code. We find that GBIM and IMM1, even in the modified versions, significantly over- and underestimate the hydrophobic lengths of the proteins, respectively. However, both methods retain reasonable correlations with the experimental values that are about the same as with the PDBTM and OPM predictions. It is clear, though, that simply applying the unmodified GB models without considering inward-facing residues does not give reliable predictions of hydrophobic lengths within our protocol.

We noted that the OPM methods tend to overestimate the hydrophobic lengths, while the HDGB-based models slightly underestimate the experimental values. An exact comparison of the absolute value of the membrane width is problematic, however, as the definition of what exactly is measured experimentally as the membrane widths and how that corresponds to the criteria for determining the hydrophobic lengths from the computational profiles is not rigorous. Furthermore, although we did calibrate the OPM and HDGB profiles against each other as discussed above based on the midpoints in their profiles, this analysis neglects different shapes in the profiles in the intermediate region. Therefore, a more pragmatic approach is to adjust the offset of the predicted hydrophobic lengths with respect to the experimental membrane widths by simply adding the differences in the averages in Table 3 as discussed above. (+2 Å for HDGBv3, +1 Å for HDGBvdW and −2 Å for OPM). One could view such offsets as fitting parameters (the only such parameter in our model) but the physical interpretation is that they quantify the difference in the definitions of the membrane width between experiment and computational predictions. We note that the offsets do not affect correlation coefficients but only decrease mean squared errors.

The prediction of the hydrophobic lengths requires optimal positioning of the membrane proteins in the bilayer as well as reliable identification of which residues are outward-facing, in contact with the lipids, and which residues within the membrane bilayer are likely facing inward towards a water-filled cavity of channel. We also implemented these aspects as part of our protocol. The distinction between inward- and outward-facing residues is essential for the reliable application of implicit membrane models where the information about whether a given residue is in contact with lipids or water makes a critical energetic difference. Implicit membrane models, including HDGB, commonly vary energetic profiles as a function of z, the membrane normal, but ignoring the possibility of water-filled cavities of channels within the membrane bilayer. In order to consider such cavities, we modified the standard HDGB method here so that residues where not just distinguished by their z-positions along the membrane normal but also with respect to their annotation of being facing outward or inward. In the latter case, the membrane profiles were not applied, and the residues were treated as if in the bulk water phase. This approach greatly affects the energetics of membrane proteins with large internal cavities such as β-barrels. However, as these internal cavities and channels may be on the size of single water molecules, an implicit model that neglects the discrete molecular nature of water may not be entirely accurate for such conditions and further improvements, for example by filling such cavities with explicit water molecules may be possible.

Another possibility for further improvements in predicting optimal membrane widths is the consideration of membrane deformations in response to proteins inserted into a lipid bilayer.⁷⁰ This may also result in more reliable predictions of tilt angles. While an overall deformation due to a hydrophobic mismatch would be equivalent to predicting a larger or smaller optimal membrane width, there could be minor asymmetric membrane deformations to accommodate, for example, a polar or charged residue at the interface that are not considered here. The DHDGB model developed by us earlier⁶⁸ is in principle able to address such cases although further developments are needed to include the dispersion term in the DHDGB formalism and expand its use to arbitrarily large protein systems.

Finally, the assessment of our method presented here relies on comparisons with experimental data which is not very comprehensive and is likely limited in accuracy. The HDGB-based method presented here correlates well with the experimental data, but given the uncertainties in the experiments, it is likely that further methodological improvements, if they are possible, cannot be assessed reliably with the available data. Further experimental efforts to determine the hydrophobic lengths (and matching membrane widths) would therefore be highly desirable.

Our method offers a complete protocol for optimally positioning membrane proteins in the lipid bilayer and determining the length of the hydrophobic region that is expected to match the optimal lipid bilayer membrane width. The protocol was implemented as the MEMHLength web server (http://feiglab.org/memhlength) to serve the wider community. We also hope that our method can become integrated with other widely used services such as the OPM^{16, 29} or PDBTM^{17, 27, 28} databases or the CHARMM-GUI server⁵⁹ for setting up simulations of membrane proteins.

ABBREVIATIONS

ABNR

adopted-basis Newton-Raphson

CHARMM

Chemistry at Harvard Molecular Mechanics

DPPC

dipalmitoyl-phosphatidylcholine

EPR

electron paramagnetic resonance

GB

generalized Born

HDGB

heterogeneous dielectric generalized Born

HDGBvdW

heterogeneous dielectric generalized Born with van der Waals terms

IMM1

implicit membrane model 1

MMTSB

Multiscale Modeling Tools in Structural Biology

NMR

nuclear magnetic resonance

OMP

outer membrane protein

OPM

orientations of proteins in membranes

PB

Poisson-Boltzmann

PDB

Protein Data Bank

PDBTM

Protein Data Bank of Membrane Proteins

SASA

solvent-accessible surface area

SD

steepest descent