Summary
We study in this paper jointly testing the associations of a genetic variant with correlated multiple phenotypes using the summary statistics of individual phenotype analysis from Genome-Wide Association Studies (GWASs). We estimated the between-phenotype correlation matrix using the summary statistics of individual phenotype GWAS analyses, and developed genetic association tests for multiple phenotypes by accounting for between-phenotype correlation without the need to access individual-level data. Since genetic variants often affect multiple phenotypes differently across the genome and the between-phenotype correlation can be arbitrary, we proposed robust and powerful multiple phenotype testing procedures by jointly testing a common mean and a variance component in linear mixed models for summary statistics. We computed the p-values of the proposed tests analytically. This computational advantage makes our methods practically appealing in large-scale GWASs. We performed simulation studies to show that the proposed tests maintained correct type I error rates, and to compare their powers in various settings with the existing methods. We applied the proposed tests to a GWAS Global Lipids Genetics Consortium summary statistics data set and identified additional genetic variants that were missed by the original single-trait analysis.
Keywords: Correlated phenotypes, Fisher Method, Linear Mixed Models, Pleiotropy, Summary Statistics, Variance Component Test
1. Introduction
Genome-Wide Association Studies (GWASs) have identified thousands of genetic variants that are associated with hundreds of traits and diseases. The GWAS results showed that 4.6% of these disease-associated Single Nucleotide Polymorphisms (SNPs) and 16.9% of these genes are associated with multiple correlated phenotypes, indicating plausible biological pleiotropy (Solovieff et al., 2013). For example, a variant in the gene that codes phenylalanine hydroxylase affects multiple phenotypes of phenylketonuria, including mental retardation, eczema, and pigment defects (Paul, 2000). Purcell et al. (2009) found that schizophrenia and bipolar disorder shared a substantial proportion of heritability. There is an increasing interest in discovering novel biology of pleiotropy by jointly analyzing multiple phenotypes.
When individual level phenotype and genotype data are available, numerous multivariate methods that account for between-phenotype correlation have been proposed to study pleiotropy (Solovieff et al., 2013). Examples include Scaled Multiple-Phenotype Association Test (SMAT) (Schifano et al., 2013), and principal component analysis (PCA) (Aschard et al., 2014). However, individual-level phenotype and genotype data of many GWAS studies are often not accessible to researchers due to logistical and data confidentiality reasons. The summary test statistics of individual phenotypes of many GWAS studies are readily available. It is of substantial recent interest to study pleiotropy by jointly analyzing multiple phenotypes using the univariate GWAS phenotype analysis summary statistics while accounting for between-phenotype correlation. For example, in the large Global Lipids Genetics Consortium (Teslovich et al., 2010), the summary statistics of the GWAS analysis of each of the four individual lipid traits (HDL, LDL, TC and TG, see their definitions in Section 5) are publicly available. One is interested in using these results to study the pleiotropy of lipids without resorting to individual level data.
A challenge in the analysis of multiple phenotypes is that there is no uniformly most powerful (UMP) test. The power depends on signal directions and between-phenotype correlation. To boost analysis power, several methods have been proposed for GWAS multiple phenotype analysis besides the classical multivariate Wald test. The Fisher’s method of combining independent p-values has been extended to dependent unviariate tests (Li et al., 2014). However, the p-value approximations of these tests are not accurate for the small significance level often required by GWASs. The minimum of the p-values (MinP) of multiple phenotypes has been proposed as a testing statistic (Conneely and Boehnke, 2007). The MinP method is powerful when a SNP affects only a very small number of multiple phenotypes, but is less powerful in the presence of denser signals. Recently, Zhu et al. (2015) proposed two separate tests to detect homogeneous and heterogeneous effects respectively by aggregating the thresholded individual Wald-type Z statistics across multiple traits. These two tests lose power if the homogeneous or heterogeneous assumption is violated, and their p-values need to be calculated by Monte-Carlo simulations, which are computationally intensive when scanning the genome. As the association patterns between genetic variants and multiple phenotypes vary by SNPs across the genome, robust and computationally efficient tests need to be developed.
There are two objectives in this paper. First, we investigate the information contained in the summary statistics obtained from standard univariate phenotype GWAS analysis, and provide closed-form expressions of the means of the univariate Wald type statistics obtained from the underlying linear regression models that contain both genetic variants and covariates. We next show that the correlation matrix among the univariate Wald statistics is equal to the residual correlation matrix of the original quantitative phenotypes in single studies and meta-analysis of multiple studies under the null. We propose to estimate the between-phenotype correlation without individual-level data by using the univariate summary test statistics across the genome. Second, we propose robust and powerful tests for pleiotropy effets, which use data-adaptive procedures to combine the two independent score statistics for homogeneous and heterogeneous pleiotropy effects that are derived from testing a common mean of a variance component of a semiparametric linear mixed model for univariate GWAS summary statistics. We also propose Fisher’s and Tippett’s methods to combine the p-values of the two score statistics to robustly detect pleiotropy. All of our methods compute p-values analytically and hence are computationally efficient when scanning the genome in GWAS multiple phenotype analysis.
The rest of the paper is organized as follows. In Section 2, we investigate the information contained in univariate GWAS summary statistics. In Section 3, we introduce several Multiple Phenotype Association Tests (MPAT) using semiparametric linear mixed models for summary statistics. In Section 4, we perform simulation studies to evaluate the size and power of MPAT. In Section 5, we apply MPAT to analyze the global lipids GWAS summary statistics data set to study the pleiotropy of lipids, followed by discussions in Section 6.
2. The Means and Correlation Matrix of the Univariate Summary Test Statistics of Multiple Phenotypes
Consider K correlated phenotypes and assume for now that they are measured on the same study subjects in one study cohort, and this assumption will be relaxed later. In traditional GWAS analysis, one performs univariate phenotype analysis by analyzing each of the K phenotypes and each SNP separately. For simplicity, consider continuous phenotypes and assume univariate linear regression of the kth phenotype as
| (1) |
where for subject i (1 ≤ i ≤ n), Yik is the kth phenotype (1 ≤ k ≤ K) and Gi is the genotype of a SNP taking values 0, 1, 2 that counts the copy of the minor allele, and Ci is a vector of covariates, e.g., used for adjusting for population stratification.
For univariate analysis of phenotype k, to test for H0 : βk = 0 versus H1: βk ≠ 0, the univariate Wald-type statistic is often used , where is the MLE of βk and is its estimated standard error. Direct calculations show that the mean of Zk is
where is the coefficient of determination by regressing G on the covariates C, and under the Hardy-Weinberg equilibrium where MAF is the Minor Allele Frequency of G taking value in (0, 0.5), and βk/σk measures the genetic effect size on phenotype k. Therefore, inferring whether a particular SNP is associated with the kth phenotype can be done by inferring whether E(Zk) is zero or not.
Suppress the subscript i. Denote by Y = (Y1, ⋯, Yk)T and Z = (Z1, ⋯, Zk)T. We will first study the relationship of the correlation matrix of Z and the correlation matrix of Y conditional on the covariates C under H0. Let and be the design matrix of model (1), and . Standard linear regression gives
It follows that and its standard error is , where a2 denotes the second row of the matrix A. For two continuous phenotypes Yj and Yk of length n, under the null, direct calculations show that the correlation of Zj and Zk is
| (2) |
where σjk = cov(Yj, Yk|C) under the null.
This implies that for any SNP, under the null, the correlation matrix of the univariate summary test statistics Z = (Z1, ⋯, ZK)T is the same as the correlation matrix of the original multiple phenotyes Y = (Y1, ⋯, YK)T conditional on the covariates C, and the correlation matrix of Z does not depend on the genotype G. This implies that we can estimate the correlation matrix of the random vector Z = (Z1, ⋯, ZK)T by simply calculating the sample correlation matrix of the SNP-specific summary test statistics Z’s over a large number of independent null SNPs across the whole genome in a GWAS study, and the law of large numbers ensures that the estimated correlation matrix is consistent and accurate. The simulation results of Zhu et al. (2015) show that the correlation matrix can be accurately estimated using GWAS summary statistics in practice. Zhu et al. (2015) provided theoretical justifications for this result in the absence of covariates in model (1). Our theoretical justifications here allow for covariates, e.g., population stratification in GWAS.
If the two phenotpyes Yk and Yj are from different cohorts, then the correlation between Zj and Zk is induced if these two cohorts have overlapping study subjects. If these two cohorts are independent, then Zj and Zk are independent because Yk and Yj are independent to each other. Suppose phenotype Yk is from cohort A of sample size nA and phenotype Yj is from cohort B of sample size nB, where cohort A and B share ns study subjects. We have
If two cohorts have no overlapping samples (ns = 0), Zj and Zk are uncorrelated and thus independent. If two cohorts share all the subjects (the same cohort), the results are the same as given in (2). It follows that the correlation between two phenotype Z-scores does not depend on genotype but only depends on the correlation of the original two phenotypes, either measured in the same or different cohorts with possible overlapping subjects.
Now consider meta-analysis of the same set of multiple phenotypes across multiple studies. Suppose we perform univariate GWAS analysis of K phenotypes in cohort A of sample size nA and cohort B of sample size nB. Assume that the between-phenotype correlation is the same in the two studies, i.e., Cov(ZAj, ZAk) = Cov(ZBj, ZBk) = ρjk, 1 ≤ j ≠ k ≤ K, where ρjk denotes the covariance between these two summary statistics in both cohorts. Consider fixed-effect meta-analysis, which was used in the GWAS analysis of the global lipids consortium (Teslovich et al., 2010). Note that in meta-analysis, the cohort specific summary statistics are often not publicly available. One can easily show that the meta-analysis Z-score of the two cohorts for phenotype k (k = 1, ⋯, K) is , where . Hence cor(Zj, Zk) = ρjk. This result suggests that the correlation matrix of the summary statistics calculated from univariate fixed-effect meta-analysis of multiple phenotypes captures the correlation of the original multiple phenotypes conditional on covariates.
In practice, the GWAS summary statistics for multiple phenotypes are obtained in different settings. In the first setting, the K summary statistics of K phenotypes are from the same cohort. In the second setting, there are multiple cohorts, say J cohort. For each cohort, there are K phenotypes. We hence have K × J summary statistics for a particular SNP. This setting was considered by Zhu et al. (2015) and includes the first setting as a special case. The third setting is the same as the second setting, except that cohort-specific summary statistics are not available. One can only access the summary statistics based on meta-analysis performed for each phenotype across J cohorts. For instance, the global lipids GWAS summary statistics data set contains the meta-analysis results for each of the four lipids levels across 46 independent cohorts (Teslovich et al., 2010), but cohort-specific summary statistics are not available. The third case is more challenging than the second case, because cohort-specific summary statistics are not available. This case in common in practice, when GWAS results are published by large consortia. We discuss in this paper all the three settings.
If the summary statistics are obtained from logistic regressions for binary phenotypes, then under the null, the correlation matrix among the summary statistics still does not depend on genotype. We will show this in Web Appendix Section A. Hence our testing procedures to be introduced in Section 3 can be used broadly in many GWAS summary statistics settings.
3. Multiple Phenotype Association Tests (MPATs)
It is well known that there does not exist an uniformly most powerful (UMP) test for a multiple dimensional composite alternative hypothesis. As the genetic association patterns of multiple phenotypes vary from SNPs to SNPs across the genome, in this section, we propose robust and powerful tests for both homogeneous and heterogeneous genetic effects on multiple phenotypes in GWAS, using univariate summary test statistics by accounting for the correlation between them. Since the correlation matrix between the summary statistics Σ can be consistently and accurately estimated by as discussed in Section 2, for simplicity, we assume Σ is given. Based on summary statistics Z ∼ N(μ, Σ), the goal is to test H0 : μ = 0 versus H1 : μ ≠ 0.
3.1 Detection of Homogeneous Effects
If the means μk of the Zk’s (k = 1, ⋯, K) are the same as μk = μ0, then the distribution of Z is reduced to N(μ0J, Σ), where J = (1, 1, …, 1)T and μ0 is a scalar denoting the shared common effect size. To test for a common genetic effect on multiple phenotypes, we test H0: μ0 = 0 versus H1 : μ0 ≠ 0 and can use the following score statistic
which follows N(0, 1) under the null. It is essentially a weighted sum of the components of Z with the weights equal to JT Σ−1, which give higher weights to the phenotypes that are less correlated with the other phenotypes. It can be easily shown that the SUM test is the most powerful test when the effects are indeed homogeneous. The SUM test can be easily extended by using other weights, e.g., by replacing the ones in J with the square root of known phenotype-specific heritability, as suggested by a referee.
The between-phenotype correlation matrix Σ is held fixed when we scan the genome in multiple phenotype GWAS analysis. However, the true means μ’s of Z’s vary with SNPs and the assumption of homogeneous genetic effects on multiple phenotypes is likely to be violated. If the homogeneous effect assumption is violated, the SUM test can be subject to substantial power loss and even can be powerless if the genetic effects vector μ is orthogonal to Σ−1J because the ncp of SUM is JT Σ−1μ{JT Σ−1J}−1/2 = 0. For example, suppose Z is a standard bivariate normal vector with mean μ = (−100, 100)T, then JT Σ−1μ = 0 for any Σ in bivariate case and hence ncp = 0, i.e., the SUM test is powerless to detect this non-null mean μ = (−100, 100)T.
3.2 Detection of Heterogeneous Effects
As the SUM test has low power when the homogeneous effect assumption is violated, we propose in this section tests for heterogeneous genetic effects on multiple phenotypes. We formulate this problem using the following model for the univariate summary statistics
| (3) |
where μ = (μ1, …, μK)T. We further assume that μk (k = 1, …, K) follows an arbitrary common distribution F with mean 0 and variance τ. Then testing H0 : μ1 = … = μK = 0 is equivalent to testing H0 : τ = 0. Under this assumption, equation (3) becomes a linear mixed model. Following Lin (1997), one can derive the variance component score test statistic for τ given by
| (4) |
which is a quadratic function of Z. It can be easily shown that VC follows a mixture of chi-square distribution , where the weights λk are the eigenvalues of the matrix Σ−1. The p-value of VC can be calculated using the Davies method (Davies, 1980).
Compared to the classical Wald test ZT Σ−1Z, there is one more inverse covariance matrix in the middle of the expression of VC. A simple application of spectral decomposition gives and , where uk is the kth eigenvector of Σ. This says that the last eigenvector has the largest weight by noting that λK ≤ 1. Hence, both Wald and VC prefer the situations in which the mean vector μ of Z and the last eigenvector of Σ are in the same direction. However, VC performs even better than Wald in such cases. Since the last eigenvector of Σ usually contains elements of different signs and magnitudes in practical settings, so VC has more power than Wald to detect heterogeneous effects in such settings.
3.3 Robust Detection of Homogeneous and Heterogeneous Effects
Across the genome, the effects of genetic variants on multiple phenotypes vary by locus. Either SUM or VC test could lose substantial power under their non-favoring alternatives. Hence, we need to develop more robust and powerful testing procedures to detect both homogeneous and heterogeneous effects. Decomposing the effect vector μ = (μ1, ⋯, μK)T into the shared common effect across phenotypes and departures of individual effects from the common effect, we have the following linear mixed model for the summary statistics
| (5) |
where μ0 is a scalar denoting the shared common effect and bk = μk − μ0 denotes the departure of the effect of a genetic variant on the kth phenotype from the common effect, which is assumed to be mutually independent and follows an arbitrary distribution F with mean 0 and variance τ. If τ = 0, then this model reduces to the homogeneous effect model in Section 3.1. if μ0 = 0, then this model reduces to the heterogeneous effect model in Section 3.2. Therefore, model (5) is more general and includes the homogeneous and heterogeneous effect models as special cases.
Under Model (5), testing for the associations between a genetic variant and K phenotypes is equivalent to jointly testing H0 : μ = 0, τ = 0, i.e., jointly testing for the fixed effect and the variance component in mixed model (5). Under H0, the score of μ0 is
Following Sun et al. (2013), we derive the score for τ under H0 without restricting μ0 = 0
| (6) |
where is the MLE of μ0 under τ = 0, which is simply the sample mean of the Zk’s, i.e. . Because the second term in (6) does not depend on data, we could use the first term to construct the test statistic for H0 : μ = 0, τ = 0 as
It can be shown that and are statistically independent under H0. The proof is given in the Web Appendix B.1. The variance of is , where . The variance of is , where and . The score test is the same as the SUM test which can powerfully detect the homogeneous effect, while can detect heterogeneity effects. Therefore, a robust testing procedure can be obtained by combining and , which are both quadratic functions of Z.
We can use the following linear combination
| (7) |
where and ϕ ∈ [0, 1]. However, ϕ is usually unknown in practice and therefore needs to be chosen. We can use the inverse-variance weighting scheme which minimizes the variance of Tϕ with
The resulting Tϕ is refereed to as mixVar. We can also use inverse standard deviation weighting so that and are of equal variance,
This resulting Tϕ is refereed to as mixSD. These two weighting schemes only depend on the correlation matrix Σ and allocate more weight to the testing statistic that has smaller variance (SD). The relative magnitude of ϕVar and ϕSD can vary case by case. For example, for ρ = 0.1 in a bivariate correlation matrix, ϕVar ≈ 0.27 and ϕSD ≈ 0.38; however, for ρ = 0.6, ϕVar ≈ 0.8 and ϕSD ≈ 0.67. For any chosen ϕ, Tϕ follows a mixture of chi-squared distribution under the null, where θj are the eigenvalues of the matrix Σ1/2Λϕ1/2. Its p-value can be easily computed using the Davies’ method (Davies, 1980).
Both the inverse variance and inverse standard deviation weighting schemes determine the relative importance of and solely based on their corresponding variances or standard deviations under the null. However, under the alternative, the variances of and are different from their counterparts under the null. Therefore, both schemes might not provide the optimal weighting scheme that yields the best power. Inspired by the ideas originally proposed in the rare variant analysis settings (Lee et al., 2012, 2013), we propose to choose the optimal ϕ such that Tϕ has the minimal p-value,
where pϕ is the p-value computed based on Tϕ for any fixed value of ϕ ∈ [0, 1]. In practice, PAda could be obtained by grid searching over a range of possible values 0 = ϕ1 < ϕ2 < … < ϕB = 1, where B is the number of grid points in the interval [0, 1]. If the observed value of PAda is denoted as , then the p-value of PAda can be computed as
| (8) |
where and denotes the inverse cumulative distribution function of .
The B-dimensional integration in (8) requires the joint distribution of . One can show that Tϕ has the same distribution as the random variable τ(ϕ)S0 + (1−ϕ)S1, where τ(ϕ) = ϕJT Σ−1J and which follows a chi-squared distribution with one degree of freedom, , where the ηj are the non-zero eigen-values of the matrix . We can rwrite (8) as
| (9) |
where denotes the cumulative distribution function of S1 which is a mixture of chi-squared distributions defined above, is the probability density function of a standard random variable S0, and δ(x) is
So equation (9) could be easily computed using one dimensional numerical integration.
An alternative to combining the two testing statistics is to combine the two corresponding independent p-values of and using Fisher’s or Tippett’s procedure. Denote by and the p-values of and . Fisher’s p-value is
and the Tippett’s p-value is given by
We term these two methods as mixFisher and mixTippett respectively. Note that could be easily calculated based on the null distribution , while can be calculated from the mixture chi-square distribution , where the θj were defined above.
The Fisher method for combining p-values has asymptotic Bahadur efficiency in the sense that the resulting p-value converges to zero with the fastest rate under the alternative when the sample sizes goes to infinity (Littell and Folks, 1971). There is a subtle difference between mixFisher and mixTippett tests illustrated by comparing their rejection regions as shown in Web Figure S1. For example, suppose that and , then mixFisher gives p-value 0.024 while mixTippett gives p-value 0.116. However, if Pμ = 0.02 and Pτ = 0.8, then mixFisher has p-value 0.082 while mixTippett has p-value 0.04. Hence, mixFisher is more powerful when there exist both shared common effect and individual effects; while mixTippett is more powerful when there exists only the shared common effect or only individual effects. In practice, a causal genetic variant is more likely to have both shared common effect and individual heterogeneous effects on multiple phenotypes involved in a common disease process, one would expect that mixFisher is a better choice than mixTippett. We will illustrate this point in Section 5. We refer these mixed model based tests together as mix-type tests.
3.4 Graphical Comparison of the Rejection Boundaries of the Tests
We present in Figure 1 a graphical comparison of the rejection boundaries of our proposed tests (SUM, VC, mixSD and MixFisher) with those of the Wald and MinP test to gain a geometric insight of how these tests are related. The MinP test is defined as the minimum p-value among the K marginal p-values (Conneely and Boehnke, 2007). The results of the other proposed tests are given in Supplemental Figure S2. We considered a bivariate normal Z test statistics with correlation ρ = 0.6. The rejection boundaries of the tests under comparison are determined at the significance level 0.05 in the (Z1, Z2) space. The rejection boundary separates the acceptance region and the rejection region for each test. All the tests considered here have convex acceptance regions and therefore are all admissible (Birnbaum, 1954) and their powers however depend on alternatives.
Figure 1.
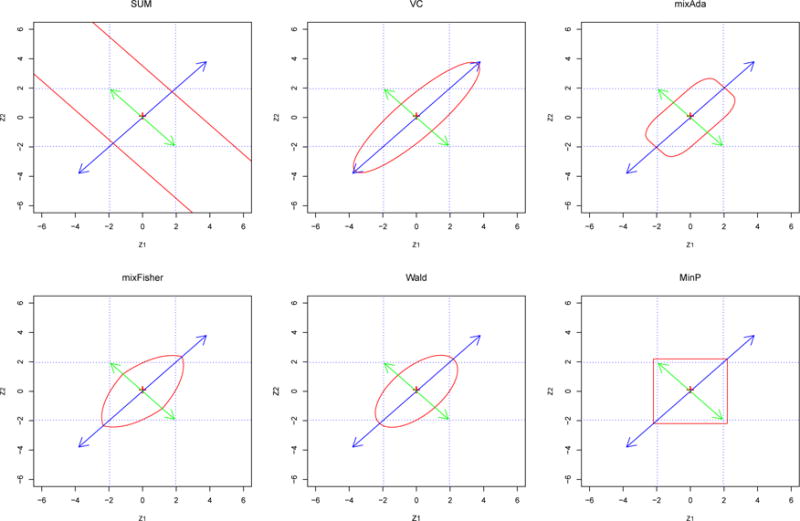
The rejection boundaries (solid lines without arrows or curves) of the six tests (SUM, VC, mixAda, mixFisher, Wald and MinP) at the significance level 0.05 for a bivariate normal Z = (Z1, Z2)T with correlation ρ = 0.6 under the null. The longer solid lines with arrows represents the direction where Z has the largest variation and the shorter solid lines with arrows represents the direction (orthogonal to the longer solid lines) where Z has the second largest variation under the null. The dotted lines mark the univariate critical values at ±1.96 for Z1 and Z2 respectively. This figure appears in color in the electronic version of this article.
This graphical representation clearly illustrates why the SUM test cannot detect any alternative μ on the direction spanned by vector (−1, 1) because such alternatives are parallel to its rejection boundaries. Compared to Wald, the ellipse of VC has a longer major axis but a shorter minor axis. Hence, if the alternative is on the direction of (−1, 1), then the rejection boundary of VC along this direction is closer to the null than that of Wald, so VC tend to be more powerful; while if the alternative is on the direction of (1, 1), then the rejection boundary of VC along this direction has a longer distance from the null than that of Wald, so VC tend to be less powerful than Wald.
Figure 1 also shows that both SUM and VC are not robust because their rejection boundaries have relatively long distance from the null along some directions. Our proposed mix-type tests are developed to overcome the limitations of SUM and VC tests, which can be seen graphically as well. Specifically, the rejection boundary of SUM has infinite distance from the null along the direction of (−1,1), while the rejection boundaries of the mix-type tests along this direction is much closer to the null. On the direction of (1, 1), the rejection boundary of the mix-type tests have a much shorter distance from the null compared to VC. Hence, the mix-type tests are more robust than both SUM and VC.
Figure 1 and Web Figure S2 show that the mix-type tests have similar but slightly different rejection boundaries, therefore their powers are generally similar in most cases but can be slightly different in special cases. Using rejection boundaries, we can easily explain the potential power gain of using multivariate tests compared to univariate ones. For example, suppose we observe Z = (−1.95, 1.95)T for a SNP, then we cannot detect this SNP using univariate analysis at significance level 0.05, but this Z point falls into the rejection regions of the VC, mixAda, mixFisher and Wald tests and hence can be detected by those tests.
4. Simulation Studies
4.1 Type I error rates
We first investigated the type I error rates of our testing procedures at various significance levels. We set K = 4 and the correlation matrix Σ to be exchangeable with ρ = 0.1, 0.3, 0.5. We generated 107 multivariate normal random samples with mean 0 and covariance matrix equal to Σ as summary statistics. We applied our proposed methods to obtain p-values for each sample. Table 1 shows that the type I error rates of the proposed methods (SUM, VC, mixAda, mixFisher) are well controlled at α = 0.05, 0.001 and even at more stringent thresholds 10−5 and 10−6. Similar results were found for mixVar, mixSD and mixTippet in Web Table S1.
Table 1.
Type I error estimates of the proposed methods. Each entry represents the type I error estimates as the proportions of p-values less than α under the null hypothesis based on 107 simulations. The correlation matrix is exchangeable with off-diagonal element equal to ρ.
| K | P | α | SUM | VC | mixAda | mixFisher | Wald | MinP |
|---|---|---|---|---|---|---|---|---|
| 4 | 0.1 | 0.05 | 0.049 | 0.049 | 0.049 | 0.050 | 0.050 | 0.049 |
| 4 | 0.3 | 0.05 | 0.049 | 0.050 | 0.049 | 0.050 | 0.049 | 0.049 |
| 4 | 0.5 | 0.05 | 0.049 | 0.049 | 0.050 | 0.049 | 0.049 | 0.049 |
| 4 | 0.1 | 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 |
| 4 | 0.3 | 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 |
| 4 | 0.5 | 10−3 | 9.9 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 1.0 × 10−3 | 9.8 × 10−4 |
| 4 | 0.1 | 10−5 | 8.4 × 10−6 | 8.8 × 10−6 | 8.8 × 10−6 | 9.6 × 10−6 | 9.5 × 10−6 | 9.3 × 10−6 |
| 4 | 0.3 | 10−5 | 9.1 × 10−6 | 8.1 × 10−6 | 9.2 × 10−6 | 9.8 × 10−6 | 9.6 × 10−6 | 9.0 × 10−6 |
| 4 | 0.5 | 10−5 | 9.3 × 10−6 | 6.6 × 10−6 | 9.5 × 10−6 | 9.4 × 10−6 | 9.2 × 10−6 | 9.2 × 10−6 |
| 4 | 0.1 | 10−6 | 8.0 × 10−7 | 7.0 × 10−7 | 8 × 10−7 | 6 × 10−6 | 6.0 × 10−7 | 8.0 × 10−7 |
| 4 | 0.3 | 10−6 | 8.0 × 10−7 | 8.0 × 10−7 | 9 × 10−7 | 8 × 10−6 | 7.0 × 10−7 | 9.0 × 10−7 |
| 4 | 0.5 | 10−6 | 7.0 × 10−7 | 6.0 × 10−7 | 7 × 10−7 | 6 × 10−6 | 8.0 × 10−7 | 8.0 × 10−7 |
4.2 Power
Since there is no single test that is uniformly most powerful for general alternatives, our simulation studies aim at illustrating the relative performance of the proposed methods under the alternatives of practical interest. In particular, we considered the following factors of practical interests: signal sparsity, effect heterogeneity and phenotype correlation structure. We included the MinP test and the Wald test for comparisons. All the empirical power is computed as the proportion of p-values that are less than significant level at 0.05.
We first considered K = 2, μ = (1, −1)T and three correlations ρ = 0.1, 0.5, 0.8 to illustrate how the correlation affects the power of multivariate tests. We simulate 104 bivariate normal random samples with mean vector equal to μ = (1, −1)T and correlation equal to ρ = 0.1, 0.5, 0.8 respectively. The power of univariate (marginal) analysis to detect μ1 = 1 or μ2 = −1 is about 0.2, and the result of multivariate testing procedures with correlation taken into account is summarized in Table 2 and Web Table S2. For example, the power of VC increases from 0.27 to 0.91 when the correlation increases from 0.1 to 0.8.
Table 2.
Power comparisons comparing SUM, VC, MixAda, MixFisher, Wald and MinP tests using simulation studies at the type I error rate α = 0.05 based on 104 replications for each configuration. When K = 2, Σ is specified by ρ = 0.1, 0.5, 0.8. When K = 3, Σ1 is exchangeable with the off-diagonal element ρ = 0.5 and Σ2 is unstructured and is specified in equation (10). When K = 100, Σ3 was set to be exchangeable with the off-diagonal element ρ = 0.2.
| K | μT | Σ | SUM | VC | mixAda | mixFisher | Wald | MinP |
|---|---|---|---|---|---|---|---|---|
| K = 2 | (1, −1) | 0.1 | 0.05 | 0.27 | 0.24 | 0.24 | 0.24 | 0.22 |
| (1, −1) | 0.5 | 0.05 | 0.54 | 0.45 | 0.44 | 0.44 | 0.24 | |
| (1, −1) | 0.8 | 0.05 | 0.91 | 0.84 | 0.81 | 0.82 | 0.25 | |
| K = 3 | (2.0, 2.0, 2.0) | Σ1 | 0.68 | 0.13 | 0.59 | 0.57 | 0.52 | 0.61 |
| (1.2, 1.2, 1.2) | Σ2 | 0.67 | 0.52 | 0.57 | 0.55 | 0.50 | 0.33 | |
| (1.63, −0.82, −0.82) | Σ1 | 0.05 | 0.70 | 0.62 | 0.60 | 0.65 | 0.34 | |
| (−1.21, 0.64, −1.46) | Σ2 | 0.48 | 0.74 | 0.63 | 0.68 | 0.62 | 0.33 | |
| (2.38, −1.72, −2.72) | Σ2 | 0.11 | 0.48 | 0.51 | 0.51 | 0.78 | 0.80 | |
| K = 100 | (1.4, …, 1.4, 1.4) | Σ3 | 0.87 | 0.05 | 0.80 | 0.79 | 0.15 | 0.64 |
We then considered K = 3, and two correlation matrices: Σ1 is a 3 × 3 exchangeable correlation matrix with off-diagonal element ρ = 0.5 and Σ2 is an unstructured correlation matrix estimated from the summary statistics from the lipids GWAS data (HDL, LDL and TG)
| (10) |
We considered the following five alternatives for K = 3: μ1 = (2, 2, 2)T with ℓ2-norm ‖μ1‖ = 3.46, μ2 = (1.2, 1.2, 1.2)T with ‖μ2‖ = 2.08, μ3 = (1.63, −0.82, −0.82)T with ‖μ3‖ = 2 (the third eigenvector direction of Σ1), μ4 = (−1.21, 0.64, −1.46)T with ‖μ4‖ = 2 (the third eigenvector direction of Σ2), μ5 = (2.38, −1.72, −2.72)T with ‖μ5‖ = 4 (the first eigenvector direction of Σ2).
Motivated by eQTL studies, where one is interested in studying the effect of a SNP on a genetic pathway or network, which often consist of not a small number of gene expressions, we also considered the case in which there are K = 100 phenotypes. For simplicity, we set the between-phenotype correlation matrix Σ3 to be exchangeable with off-diagonal element equal to ρ = 0.2, and the mean vector to be homogeneous: μ6 = (1.4, 1.4, …, 1.4, 1.4)T.
We generated 10, 000 multivariate normal random samples with mean vectors and covariance matrices specified by those six settings. We summarize the results in Table 2 where we compare SUM, VC, mixAda, mixFisher with Wald and MinP. The comparisons of these methods with all the other tests are given in Web Table S2.
As expected, the SUM test has the largest power for homogeneous effects μ1 and μ2, regardless of the correlation structures. The VC test has the largest power when the mean vectors are on the directions of the last eigenvectors of the correlation matrices as for alternatives μ3 and μ4. For the alternative μ3, the SUM test is almost powerless, indicating that there is no shared common effect. For the alternative μ4, the SUM test has decent power, suggesting that there exist both shared common effect and heterogeneous individual effects, and this well explains why mixFisher can be more powerful than Wald in this setting. For the alternative μ5, both SUM and VC perform poorly since the mean is neither homogeneous nor on the last eigenvector direction of Σ2. However, both mixAda and mixFisher have good power. MinP performs better than the others for μ5 because there exist a strong signal −2.72. In the last setting with not a small number of phenotypes (K = 100), the Wald test has very low power while mixFisher and mixAda remain to be powerful. Web Table S2 presents more simulation results.
We next considered the sparse signal settings where a genetic variant affects only one phenotype. For the exchangeable correlation matrix Σ1 and unstructured correlation matrix Σ2, we considered the following mean vectors for Z: μ = (2.5, 0, 0)T, (0, 2.5, 0)T, (0, 0, 2.5)T. The results are summarized in Figure 2 and Web Figure S3. The powers of each test for the three mean settings are the same when the correlation matrix is exchangeable but varies when the correlation matrix is unstructured, except for the MinP test. It was interesting to observe that, even in this sparse setting, the MinP test can be less powerful than VC, Wald and mix-type tests. This is because the non-signal phenotypes are correlated with the single signal phenotype and hence using non-signal phenotypes in constructing test statistics helps improve the power.
Figure 2.
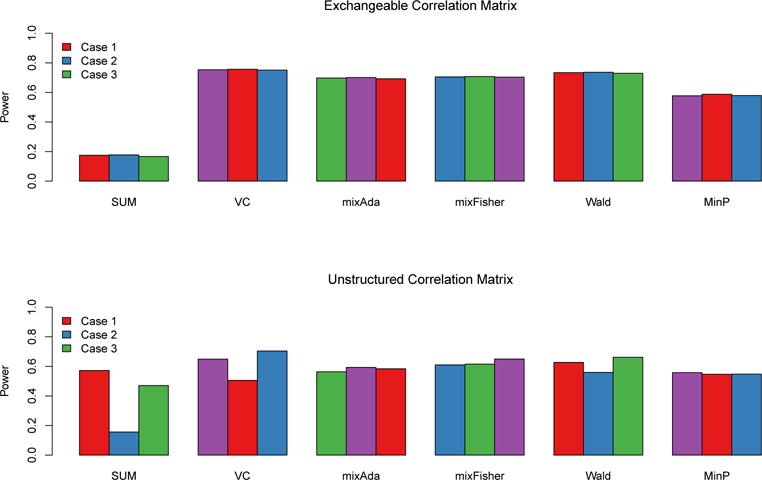
Powers of the tests when a genetic variant affects only one of the three phenotypes. Case j (j = 1, ⋯, 3) refers to the case where a genetic variant has effect only on the jth phenotype, i.e., the mean vector μ has a non-zero value in the jth position and 0 otherwise. The upper panel assumes an exchangeable correlation matrix with the non-zero mean value equal to 2.5, and the lower panel assumes the unstructured correlation matrix in (10) with the non-zero mean value equal to 2.5. This figure appears in color in the electronic version of this article.
5. Re-analysis of the Global Lipids GWAS Data
Coronary artery disease (CAD) is a leading cause of death in the United States and worldwide. Serum concentrations of high-density lipoprotein (HDL) cholesterol, low-density lipoprotein (LDL) cholesterol, total cholesterol (TC) and triglycerides (TG) are important risk factors for CAD and are therapeutic targets for drug development. The Global Lipids Genetics Consortium (GCLC) performed fixed-effects meta-analysis for each of the four lipids levels based on GWAS results from 46 cohorts comprising of more than 100,000 individuals of European ancestry. A total of 5395 SNPs reached the genome-wide significance level (P < 5 × 10−8) for at least one of the four lipids, and individually there are 2213,1769, 2593 and 1808 genome-wide significant SNPs for HDL, LDL, TC and TG respectively. Among those genome-wide significant SNPs, 95 of them were identified by Teslovich et al. (2010) after LD pruning. The meta-analysis summary statistics for the four lipids are publicly available at http://csg.sph.umich.edu//abecasis/public/lipids2010/, while cohort-specific summary statistics are not available. To compare with the multivariate analysis, the results of the univariate analysis are compared using the union of all the 5395 significant SNPs across the four lipids. Note that this univariate analysis approach did not correct multiple testing on the four lipids traits.
We performed multivariate analysis of the lipids data with a total number of 2691421 shared SNPs across the four traits using the proposed methods. Since LDL and TC are highly correlated (correlation=0.88), we restricted multivariate analysis of three phenotypes HDL, LDL and TG to illustrate the methods. The correlation matrix of the three Z-scores (HDL, LDL and TG) was estimated using the sample correlation matrix over all the SNPs after LD pruning, and the result is given in equation (10). We applied all the proposed tests to the lipids data and the numbers of significant SNPs are summarized in Figures 3(a) and Web Figure S4. As many of these SNPs are in LD with each other, and also in LD with the SNPs identified by univariate analysis, we thus performed LD pruning using Plink to obtain independent loci using very stringent LD threshold r2 < 0.01 in 500kb region (Purcell et al., 2007). After LD pruning, the numbers of independent loci are summarized in Figure 3(b) and Web Figure S5. We presented QQ plots for both univariate analysis and multivariate analysis results in Web Figures S6–S8 and found the genomic inflation factors are all close to 1 (0.98–1.1). The Manhattan plots in Web Figures S9–S16 show that the significant SNPs spread across many chromosomes, suggesting that the lipids traits are likely to be polygenic.
Figure 3.
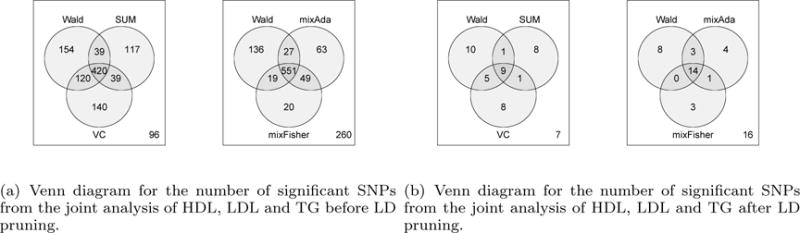
Joint Analysis of Global Lipids GWAS Summary Statistics. The genome-wide significance level is 5 × 10−8.
Overall, as expected, there is no single test that can dominate others, because there is no UMP test in multivariate settings. For example, there are nine independent SNPs that were detected by the VC test but not by the Wald test, because these nine SNPs correspond to the alternatives that favor VC more than Wald. To illustrate the effect of including TC, which is highly correlated with LDL, in multiple phenotype analysis, we compared the joint analysis results with and without TC in Table S4. These top SNPs remain significant or nearly significant after including TC, although the levels of significance change in different degrees. More details can be found in Supplementary Section D. In practice, we suggest that both biological knowledge and statistical consideration be taken into account when one decides which phenotype to include in joint multiple phenotype analysis in the presence of high correlation among some phenotypes.
We further used an online physical and functional annotation tool SCAN to annotate the detected SNPs (Gamazon et al., 2010). For illustration purpose, we only presented top SNPs ranked by the p-value of the mixFisher method in Table 3 and Web Table S3. For instance, SNP rs5167 is a coding missense variant located in gene APOC2 that was unable to be detected by univariate analysis (the p-value of TC is 3.91E-05), but our mixFisher by analyzing three phenotypes detected it with p-value=7.45E-16. A recent exome-wide study found that SNP rs5167 was associated with HDL (Tang et al., 2015). This result demonstrates that joint analysis using mixFisher test and other mix-type tests can be more powerful than univariate analysis in detecting novel SNPs for follow-up functional studies.
Table 3.
Top ten SNPs with gene annotation based on the P-value of mixFisher method in the joint analysis of HDL, LDL and TG. CHR refers to the chromosome number. NA represents not applicable. HDL, LDL and TG refer to high and low density lipoprotein cholesterol and triglycerides respectively.
| SNP | CHR | Gene | ZHDL | PHDL | ZLDL | PLDL | ZTG | PTG | PmixFisher |
|---|---|---|---|---|---|---|---|---|---|
| rs5167 | 19 | APOC2 | −4.81 | 1.51E-06 | −1.79 | 7.41E-02 | −4.20 | 2.68E-05 | 7.45E-16 |
| rs3095326 | 6 | NA | −3.08 | 2.10E-03 | −3.06 | 2.19E-03 | −4.85 | 1.22E-06 | 8.10E-13 |
| rs2777802 | 9 | ABCA1 | −4.88 | 1.06E-06 | −0.95 | 3.43E-01 | −2.73 | 6.35E-03 | 1.21E-11 |
| rs3786248 | 18 | LIPG | −5.33 | 9.99E-08 | −1.05 | 2.94E-01 | −2.23 | 2.56E-02 | 1.22E-11 |
| rs267733 | 1 | ANXA9 | −1.90 | 5.73E-02 | 5.40 | 6.52E-08 | −0.97 | 3.32E-01 | 5.18E-10 |
| rs17134601 | 10 | AKR1C4 | 1.78 | 7.59E-02 | 0.97 | 3.33E-01 | 4.95 | 7.56E-07 | 1.48E-09 |
| rs2278426 | 19 | DOCK6 | −5.08 | 3.87E-07 | −2.74 | 6.25E-03 | −1.07 | 2.86E-01 | 3.50E-09 |
| rs11216321 | 11 | PCSK7 | 5.34 | 9.12E-08 | 1.15 | 2.49E-01 | 1.05 | 2.95E-01 | 6.43E-09 |
| rs2304684 | 2 | CAD | 0.56 | 5.73E-01 | 0.15 | 8.81E-01 | 5.42 | 5.86E-08 | 1.05E-08 |
| rs13195279 | 6 | SLC17A2 | −4.87 | 1.13E-06 | 2.15 | 3.20E-02 | −0.41 | 6.82E-01 | 3.01E-08 |
6. Discussion
We proposed several testing procedures to detect genetic associations with multiple phenotypes using GWAS summary statistics of univariate phenotype analysis. We found that the correlation matrix between the summary statistics does not depend on the SNP genotype across the whole genome, and thus we can consistently and accurately estimate this correlation matrix by the sample correlation matrix across all the independent SNPs after LD pruning. This estimation procedure is valid if the GWAS summary statistics are obtained from one cohort, or multiple cohorts with possible overlapping subjects or phenotype-specific meta-analysis. Compared to univariate analysis, multivariate analysis can leverage the correlation among phenotypes to improve power.
It is known that there is no uniformly most powerful test for multiple phenotype analysis. The power of a particular test depends on signal directions and sparsity, as well as between-phenotype correlation structure. The SUM test can be more powerful than both Wald and VC when the effects are homogeneous. The VC test can be more powerful than SUM in the presence of heterogeneous effects, and is more powerful than the Wald test when the effect vector lies close to direction as the last eigenvector of the correlation matrix of multiple phenotypes. Our mix-type tests are more robust than both SUM and VC with respect to the effect directions and can identify a good number of SNPs that Wald fail to detect. As shown in our simulation studies, the Wald test is less powerful when there exists both the shared common effect and the heterogeneous effects while the mix-type tests, such as mixFisher, are robust to both homogeneous and heterogeneous effects. When the number of phenotypes is not small as in eQTL studies, the Wald test can be subject to very low power while the mix-type tests, such as mixFisher, remain powerful. Therefore, our proposed mix-type tests are complimentary to the Wald test by providing new findings for understanding the underlying genetic architecture in multiple phenotype studies, especially when the number of phenotypes is not small. The mix-type tests are computationally efficient since we can compute their p-values analytically. This feature is practically appealing in large-scale GWASs, where millions of genetic markers are analyzed.
There are several advantages of using summary statistics over using individual level data. First, the summary statistics are more accessible than individual level phenotype and genotype data. Second, the summary statistics within each study cohort have been controlled for study-specific confounders, such as study-specific population stratification. With the increasing availability of GWAS summary statistics, our methods provide a cost-effective way for analyzing multiple phenotypes. Future research is needed to compare the power and robustness of the proposed methods using cohort-specific phenotype-specific summary statistics versus using meta-analysis phenotype-specific summary statistics.
Our results show that the proposed mix-type tests, such as mixFisher, and the classical Wald test compliment each other for new discoveries by joint analysis of multiple phenotpyes. The results of the lipid GWAS indicate each test can identify additional SNPs that might be missed by others. If is of future research interest to develop an omnibus test to improve analysis by combining the evidence of different tests, e.g, combining the Wald test and the mixFisher test.
Our MPAT methods are applicable to GWAS studies where study subjects are unrelated. MPAT accounts for population structures, as it is based on summary statistics which have often adjusted for population structures using principal components (Price et al., 2006). Future research is needed to extend the proposed methods to account for familial and cryptic relatedness, e.g., using mixed models (Chen et al., 2016). Another area of future research is to develop multiple phenotype analysis of secondary phenotypes collected in case-control studies. The inverse probability weighted methods (Yung and Lin, 2016) can be extended to MPAT tests by accounting for the fact that case-control samples do not represent the general population in multiple secondary phenotype analysis. Extension of the proposed methods to analyzing multiple phenotypes in rare variant association studies is of great future interest.
Rare variant association tests usually need to be conducted using multiple SNPs in a SNP set. The methods in the paper are developed for single SNP analysis, and are based on normally distributed Z-scores. To extend the proposed methods to test for rare variants in a SNP set for multiple phenotypes, one needs to aggregate summary individual SNP-phenotype score statistics across multiple phenotypes and multiple SNPs in a SNP set. This requires accounting for both between-phenotype correlation and between-SNP correlaton, i.e., LD among SNPs, in a SNP set. Future research is needed.
Supplementary Material
Acknowledgments
The work is supported by NIH grants R35-CA197449, P01-CA134294, U01-HG009088, and R01-HL113338. The authors thank the reviewers for thoughtful and constructive comments that have helped improve the paper.
Footnotes
Supplementary Materials
Web Appendix referenced in Sections 3 to 5, and an R package implementing MPAT, are available with this paper at the Biometrics website on Wiley Online Library.
This paper has been submitted for consideration for publication in Biometrics
References
- Aschard H, Vilhjálmsson BJ, Greliche N, Morange PE, Trégouët DA, Kraft P. Maximizing the power of Principal-Component analysis of correlated phenotypes in genome-wide association studies. The American Journal of Human Genetics. 2014;94:662–676. doi: 10.1016/j.ajhg.2014.03.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birnbaum A. Combining independent tests of significance. Journal of the American Statistical Association. 1954;49:559–574. [Google Scholar]
- Chen H, Wang C, Conomos MP, Stilp AM, Li Z, Sofer T, Szpiro AA, Chen W, Brehm JM, Celedón JC, et al. Control for population structure and relatedness for binary traits in genetic association studies via logistic mixed models. The American Journal of Human Genetics. 2016;98:653–666. doi: 10.1016/j.ajhg.2016.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conneely KN, Boehnke M. So many correlated tests, so little time! rapid adjustment of p values for multiple correlated tests. Am J Hum Genet. 2007;81:1158–68. doi: 10.1086/522036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies RB. Algorithm as 155: The distribution of a linear combination of chi-squared random variables. Journal of the Royal Statistical Society. Series C (Applied Statistics. 1980;29:323–333. [Google Scholar]
- Gamazon ER, Zhang W, Konkashbaev A, Duan S, Kistner EO, Nicolae DL, Dolan ME, Cox NJ. Scan: Snp and copy number annotation. Bioinformatics. 2010;26:259–262. doi: 10.1093/bioinformatics/btp644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Teslovich TM, Boehnke M, Lin X. General framework for meta-analysis of rare variants in sequencing association studies. The American Journal of Human Genetics. 2013;93:42–53. doi: 10.1016/j.ajhg.2013.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee S, Wu MC, Lin X. Optimal tests for rare variant effects in sequencing association studies. Biostatistics. 2012;13:762–775. doi: 10.1093/biostatistics/kxs014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q, Hu J, Ding J, Zheng G. Fisher’s method of combining dependent statistics using generalizations of the gamma distribution with applications to genetic pleiotropic associations. Biostatistics. 2014;15:284–295. doi: 10.1093/biostatistics/kxt045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin X. Variance component testing in generalised linear models with random effects. Biometrika. 1997;84:309–326. [Google Scholar]
- Littell RC, Folks JL. Asymptotic optimality of fisher’s method of combining independent tests. Journal of the American Statistical Association. 1971;66:802–806. [Google Scholar]
- Paul D. A double-edged sword. Nature. 2000;405:515. doi: 10.1038/35014676. [DOI] [PubMed] [Google Scholar]
- Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D. Principal components analysis corrects for stratification in genome-wide association studies. Nature genetics. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- Purcell S, Neale B, Todd-Brown K, Thomas L, Ferreira MAR, Bender D, Maller J, Sklar P, de Bakker PIW, Daly MJ, Sham PC. Plink: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purcell SM, Wary NR, Stone JL, Visscher PM, O’Donovan MC, Sullivan PF, Sklar P, et al. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature. 2009;460:748–752. doi: 10.1038/nature08185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schifano ED, Li L, Christiani DC, Lin X. Genome-wide association analysis for multiple continuous secondary phenotypes. The American Journal of Human Genetics. 2013;92:744–759. doi: 10.1016/j.ajhg.2013.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovieff N, Cotsapas C, Lee PH, Purcell SM, Smoller JW. Pleiotropy in complex traits: challenges and strategies. Nature Reviews Genetics. 2013;14:483–495. doi: 10.1038/nrg3461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Zheng Y, Hsu L. A unified mixed-effects model for rare-variant association in sequencing studies. Genetic epidemiology. 2013;37:334–344. doi: 10.1002/gepi.21717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang CS, et al. Exome-wide association analysis reveals novel coding sequence variants associated with lipid traits in chinese. Nature communications. 2015;6 doi: 10.1038/ncomms10206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich TM, Musunuru K, Smith AV, Edmondson AC, Stylianou IM, Koseki M, Pirruccello JP, Ripatti S, Chasman DI, Willer CJ, et al. Biological, clinical and population relevance of 95 loci for blood lipids. Nature. 2010;466:707–713. doi: 10.1038/nature09270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yung G, Lin X. Validity of using ad hoc methods to analyze secondary traits in case-control association studies. Genetic Epidemiology. 2016;40:732–743. doi: 10.1002/gepi.21994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Feng T, Tayo BO, Liang J, Young JH, Franceschini N, Smith JA, Yanek LR, Sun YV, Edwards TL, et al. Meta-analysis of correlated traits via summary statistics from gwass with an application in hypertension. The American Journal of Human Genetics. 2015;96:21–36. doi: 10.1016/j.ajhg.2014.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


