Metabolic Trade-Offs Promote Diversity in a Model Ecosystem

Abstract

In nature, a large number of species can coexist on a small number of shared resources; however, resource-competition models predict that the number of species in steady coexistence cannot exceed the number of resources. Motivated by recent studies of phytoplankton, we introduce trade-offs into a resource-competition model and find that an unlimited number of species can coexist. Our model spontaneously reproduces several notable features of natural ecosystems, including keystone species and population dynamics and abundances characteristic of neutral theory, despite an underlying non-neutral competition for resources.

An astonishing characteristic of life on Earth is its great variety. In tropical rainforests, more than 300 tree species may be found on a single hectare [1], while in one gram of soil, the number of distinct microbial genomes has been estimated at ~2000–18, 000 [2]. Explaining this great biodiversity has been a main focus of research in ecology. One major conceptual challenge is embodied by the so-called “paradox of the plankton” [3]: in the framework of simple resource-competition models, it has been argued that the number of species indefinitely coexisting cannot exceed the number of resources [4–7]. Yet, in apparent contradiction to this theory, which is known as the competitive exclusion principle [8], some marine ecosystems host a hundred or more coexisting species of phytoplankton [9], competing for only a handful of abiotic nutrients [10].

The limit on diversity set by the competitive exclusion principle could be overcome in many possible ways. Even within simple resource-competition models, diverse populations may emerge from intrinsically oscillatory or chaotic dynamics [11,12], though the stability of such solutions in the face of long-term evolution has been challenged [13]. Looking beyond resource competition, there are many proposed mechanisms for diversity, generally falling into three (nonexclusive) categories: (1) systems never approach steady state due to temporal variation of the environment, e.g., weather changes [3,14] or seasonal cycles [15]; (2) real environments are heterogeneous in space, e.g., due to environmental gradients such as temperature, salinity, or exposure to light [16]; (3) ecosystems are limited by factors other than resources, e.g., predation [17,18] or self-limiting toxin production [19]. (For reviews see [20,21].)

While the above mechanisms are likely all broadly relevant, in the context of phytoplankton, it was recently suggested that diversity may also persist due to trade-offs between different traits or abilities [22]. With this in mind, we present a simple resource-competition model in which species are constrained by a trade-off between their different resource utilization abilities. In this model, organisms collectively shape the resource concentrations around them to produce a state equally favorable for all, and hence, an unlimited number of species can coexist. While the model is highly simplified, it highlights how both trade-offs and environmental shaping can contribute to ecological diversity.

We employ a classical resource-competition model [23] to investigate the population dynamics of m species competing for p types of nutrients. A “species” σ is specified by its metabolic strategy, namely the coefficients of its rate of utilization of each nutrient: α⃗_σ = (α_σ1, …, α_σp). Conceptually, α_σi is proportional to the number of enzyme molecules allocated by the organism to importing and processing nutrient i. We assume that enzymes for different nutrients may have different costs w_i, but to reflect “trade-offs,” all organisms have the same fixed enzyme budget: ${\sum }_{i=1}^p{w}_i{\alpha }_{\sigma i}=E$.

We further assume a well-mixed system such that the concentration of nutrients is homogeneous and is determined by the nutrient supply rates s⃗ = (s₁, …, s_p), by the uptake of nutrients by organisms, and by a degradation or loss rate μ_i. We denote the per-enzyme rate of consumption of nutrient i by r_i. A relevant choice for r_i is the Monod function c_i/(K_i + c_i), but it can be any monotone increasing, continuously differentiable function of c_i with r_i(0) = 0. The kinetics of nutrient concentration c_i is therefore given by

$$\frac{{\mathit{\text{dc}}}_i}{\mathit{\text{dt}}}=s_i-(\sum _{\sigma }{n}_{\sigma }(t){\alpha }_{\sigma i})r_i(c_i)-{\mu }_i{c}_i(t),$$ (1)

where n_σ is the population of species σ. Since metabolic reactions typically occur on a faster time scale than cell division, we assume a separation of these time scales. It follows that nutrient concentrations satisfy the flux-balance equations dc_i = dt = 0, and the quasi-steady-state nutrient concentrations c_i(t) are functions of the population sizes n_σ(t).

We assume that cell growth is resource limited, and that in principle, different nutrients have different “values” υ_i; i.e., they make different contributions to biomass production. The overall growth-rate function of a cell type σ is therefore given by

$$g_{\sigma }(c_1,\dots ,c_p)=\sum _{i=1}^p{\upsilon }_i{\alpha }_{\sigma i}{r}_i(c_i).$$ (2)

Finally, the population dynamics is given by a set of ordinary differential equations describing each species’ growth:

$$\frac{{\mathit{\text{dn}}}_{\sigma }}{\mathit{\text{dt}}}=\left[g_{\sigma }\right(c_1,\dots ,c_p)-\delta ]n_{\sigma },$$ (3)

where δ denotes a constant death rate. We see that the dynamics of different species are coupled through the nutrient concentrations c_i(t).

For clarity in what follows, we simplify some of the parameters, but our basic results hold for the general case presented above (see Supplemental Material [24]). First, since in physically relevant cases, the nutrient degradation or loss rate μ_i is several orders smaller than the influx rates at which nutrients are supplied, we set μ_i = 0. Using this and the separation of time scales, the quasi-steady-state perenzyme uptake rates r_i are fixed by (1) to be independent of the c_i, and hence, equation (2) does not depend on the specific form of r_i. Second, unless otherwise specified, we consider the symmetric case where all nutrients are equally costly to import and process (w_i = 1), equally accessible (K_i = 1), and equally valuable (υ_i = 1). With these simplifications, the growth equation (2) becomes

$$\frac{{\mathit{\text{dn}}}_{\sigma }}{\mathit{\text{dt}}}(\sum _{i=1}^p{\alpha }_{{\sigma }_i}\frac{s_i}{{\sum }_{\sigma \prime }{n}_{\sigma \prime }{\alpha }_{\sigma \prime i}}-\delta )n_{\sigma }.$$ (4)

If we add equations (4) together for all species σ, we find that the total population n_tot = Σ_σn_σ obeys ṅ_tot = S − δn_tot, where $S={\sum }_{i=1}^p{s}_i$ is the total nutrient supply. Therefore, at a steady state, the total population is always $n_{\text{tot}}^{\ast }=S/\delta$.

Within the framework of our model, we ask the following questions: starting from an initial mixed population of species, how diverse will the community be at long times? How does the outcome depend on the species present and the supply of nutrients? Finally, how stable will the outcome be if the populations are disturbed or the supply of nutrients is changed?

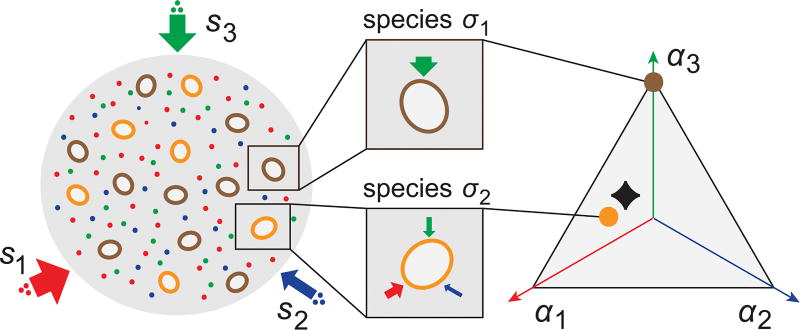
We tackle these questions using both analytics and numerical simulations, obtained by numerically solving the system of ordinary differential equations in (4). While the analytics pertain to an arbitrary number p of resources, the population dynamics simulations were performed for just three resources for clarity. As shown in Fig. 1, the latter allows for “simplex plots” that specify both the species σ (colored dots) and the nutrient supply conditions (black diamonds). This can be done because, due to the budget constraint ${\sum }_{i=1}^p{\alpha }_{\sigma i}=E$, the species occupy a p − 1 dimensional simplex in the space of uptake rates (α₁, …, α_p). To indicate the nutrient supply in this same simplex, we show s⃗_α = (E/S)s⃗ with a black diamond.

FIG. 1.

Schematic of model with two species competing for three resources. Resources are steadily and homogeneously supplied to the environment with rates s⃗ = (s₁, s₂, s₃). Different “species,” i.e., different metabolic strategies, are defined by their specific distributions of enzymes for resource utilization. Since the total number of enzymes a species produces is subject to the budget constraint ${\sum }_{i=1}^p{\alpha }_{\sigma i}=E$, each species can be represented by a point on the triangle in the space of resource utilization rates (α₁, α₂, α₃). To indicate the nutrient supply in the triangle, we show s⃗_α = (E/S)s⃗ with a black diamond.

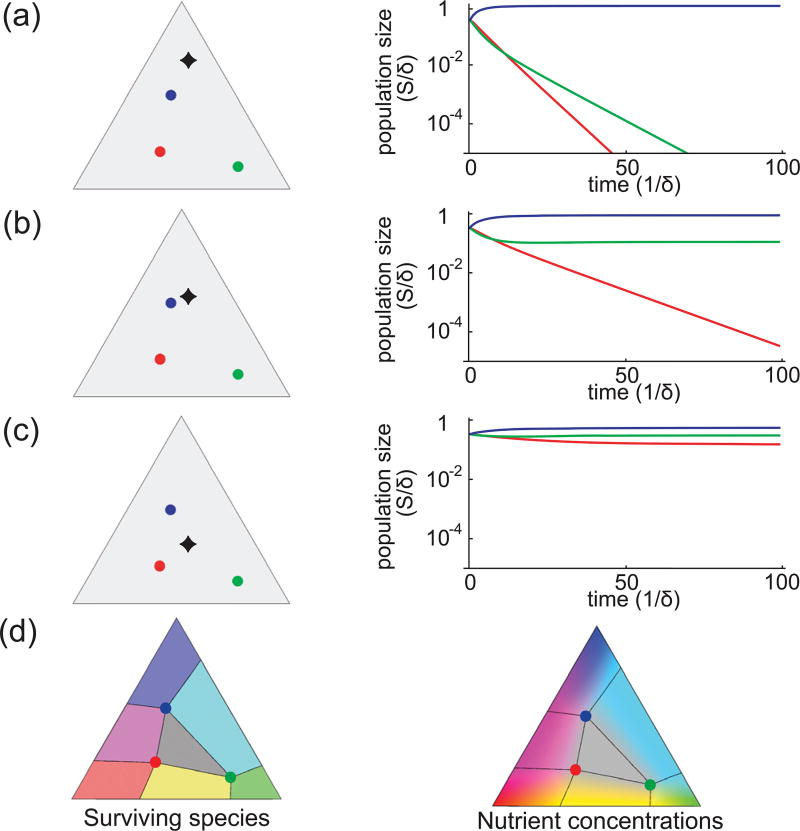
First, we consider starting with as many species as resources. From simulations, we find that any collection of the initial species may survive, depending on the nutrient supply, and that final populations are independent of initial populations. This is illustrated with examples in Fig. 2. To show final outcomes, the left panel of Fig. 2(d) was created by locating the population fixed points of (4). Since for each nutrient supply s⃗_α, there is exactly one stable fixed point, a color was assigned to s⃗_α based on which species comprise this stable steady state. Looking at the corresponding dynamics of nutrient concentrations, we observed that extinctions happen when particular nutrient concentrations become too low for particular species to survive, and their populations decay toward zero. For example, in Fig. 2(a), the system tends to uneven nutrient concentrations for which the growth rate (2) of both green and blue species is smaller than the death rate δ; hence, they die out. Alternatively, for supply conditions under which no extinctions occur, the system is driven to a state of balanced nutrient concentrations, $c_1^{\ast }=c_2^{\ast }=c_3^{\ast }$, where all species are equally fit by (2). The steady-state nutrient concentrations are displayed in the right panel of Fig. 2(d), where each s⃗_α is assigned an RGB color by adding together red, green, and blue, with intensities proportional to $c_1^{\ast },c_2^{\ast }$, and $c_3^{\ast }$, respectively.

FIG. 2.

Outcomes of a three-species competition, i.e., three distinct metabolic strategies compete for three steadily supplied resources. (a)–(c) Three illustrative examples of competition among the same three species, represented by the three colored points in all panels. Simulated population dynamics, starting from equal populations, is shown for three different steady nutrient supplies: the appropriately normalized supply rate of nutrients is indicated by the black diamonds. (d) The left triangle shows which of the three species survive for different values of the nutrient supply s⃗_α: the red/green/blue species drives both others to extinction if s⃗_α lies in the red/green/blue regions; the red & green/green & blue/blue & red species eradicate the third species if s⃗_α lies in the orange/cyan/purple region; all three species coexist if s⃗_α lies in the gray region. The right triangle shows the colormap of the corresponding steady-state concentrations of resources: the color is a mixture of red, green, and blue with proportions $c_1^{\ast }:c_2^{\ast }:c_3^{\ast }$. If s⃗_α lies outside the convex hull of the species, the steady-state nutrient concentrations mirror the proportions in which they are supplied. However, if s⃗_α lies within the convex hull of the species, the steady-state concentrations always reach $c_1^{\ast }=c_2^{\ast }=c_3^{\ast }$.

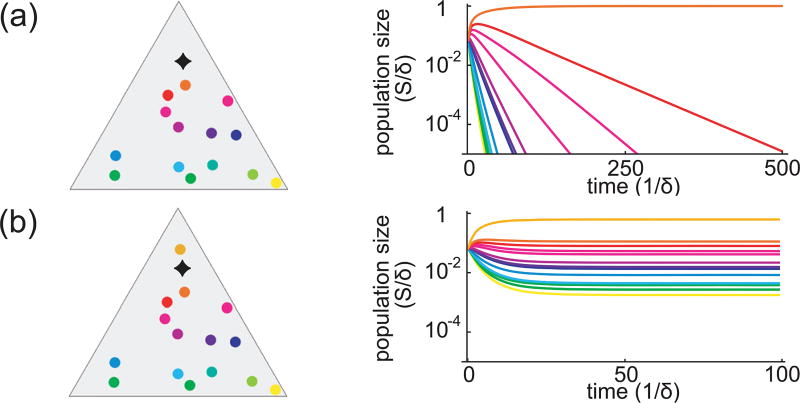
What happens when the number of initial species is greater than the number of resources? As before, we observe two very different behaviors of the system: nutrient concentrations are either driven to unequal values, in which case, extinctions occur and at most p − 1 species survive, or, alternatively, nutrient concentrations are balanced, $c_1^{\ast }=\cdots =c_p^{\ast }$, and all species coexist. Mathematically, the outcome depends on whether the nutrient supply s⃗_α is outside or inside the convex hull of the species α⃗_σ. (The convex hull of points in a plane can be visualized as a stretched rubber band that encloses all the points.) Interestingly, if the nutrient supply lies within this convex hull, competitive exclusion does not apply. Instead, the species “cooperate” in creating an environment equally favorable for all, and an unlimited number of species can coexist. An example is given in Fig. 3, where the appearance of a new species [from (a) to (b)] expands the convex hull of strategies to include the nutrient supply, and consequently, coexistence is achieved. Note that this new strategy acts as a “keystone” species, since its disappearance would entail a mass extinction. Its role in shaping the environment is essential to coexistence.

FIG. 3.

Outcomes of many species competing for three steadily supplied resources. (a) The triangle shows the competing species. The black diamond is the (appropriately normalized) supply rate of nutrients. The graph shows simulated population dynamics starting from equal populations of each species. The populations of all species except one decay to extinction. (b) Same as (a) but with one additional species (orange). All species now coexist, as the black diamond now lies within the convex hull of the metabolic strategies.

The convex hull condition for coexistence can be shown analytically (see Supplemental Material [24]). Moreover, if the nutrient supply s⃗_α is within the convex hull of the species α⃗_σ, then the nonempty set of populations

$$\{n_1^{\ast }>0,\dots ,n_m^{\ast }>0:n_1^{\ast }{\overrightarrow{\alpha }}_1+\cdots +n_m^{\ast }{\overrightarrow{\alpha }}_m=\frac{E}{\delta }\overrightarrow{s}\}$$ (5)

comprises fixed points of (4), and this set is an attractor (see Supplemental Material [24]). Hence, when there are more species than resources, the system converges to a point in (5) that depends on the initial populations.

How robust is the multispecies coexistence found in our model? In particular, we ask whether coexistence can withstand disturbances in populations or changes in nutrient supply. As mentioned, the set (5) is an attractor of the population dynamics (4): hence, if steady-state populations are perturbed, the system will return to (5), preserving coexistence (albeit the individual populations may differ if the number of species exceeds the number of resources, m − p > 0). Similarly, if the nutrient supply is changed, the community will survive, provided s⃗_α stays within the convex hull of strategies: the species present will establish a new equilibrium by adjusting their population sizes, and coexistence will be preserved.

What about more dramatic variations in nutrient supply? To test for coexistence in the face of strongly fluctuating resource availability, we imposed a time-dependent nutrient supply s⃗(t). Specifically, we simulated the population dynamics for a supply that regularly changes, at fixed time interval t_w, to a new, randomly selected s⃗, keeping the total nutrient supply constant, i.e., ${\sum }_{i=1}^p{s}_i(t)=S$. Each new s⃗ was chosen independently from a fixed sampling distribution (see Figs. S1 and S2 in Supplemental Material [24]). In analogy to the case of fixed nutrient supply, we find that a collection of species coexist if and only if the appropriately normalized mean nutrient supply 〈s⃗_α〉 lies within the convex hull of the species present. This can be proven for the case of two species competing for two nutrients and an arbitrary sampling distribution (see Supplemental Material [24]). Note that although, mathematically speaking, coexistence of species is independent of the length of the time interval t_w, as we increase t_w, fluctuations in population sizes increase, potentially crossing a practical extinction threshold (e.g., one organism) for very long time intervals t_w.

A central feature of our model is that when nutrient concentrations are driven to equal values, all species become equally fit. This motivates a comparison to the neutral theory of biodiversity [25]. In neutral theory, all species are identical in terms of fitness, and thus, biodiversity emerges not from niche differences, but from random births and deaths of individuals and random immigration of new species. To facilitate comparison, we therefore introduce a stochastic birth-death-immigration process: starting from a fixed initial population n⃗ such that n_tot = S and a fixed species immigration probability ν, at each time step, (1) a random individual dies according to the probabilities P(an individual from speciesσdies) = Δ_σ(n⃗), and (2) it is replaced by a new random individual according to the probabilities P(new individual is from a new species) = ν and P(new individual is from speciesσ) = (1 − ν)Γ_σ(n⃗). We compare the birth-death-immigration process corresponding to our resource-competition model, for which Γ_σ(n⃗) = g_σ(n⃗)n_σ/n_tot and Δ_σ(n⃗) = n_σ/n_tot, to the neutral birth-death-immigration process, for which Γ_σ(n⃗) = Δ_σ(n⃗) = n_σ/n_tot. For purposes of comparison, each new species is chosen randomly from the full simplex of species. (We note that due to the assumption n_tot = S, both sets of birth and death probabilities sum to 1.)

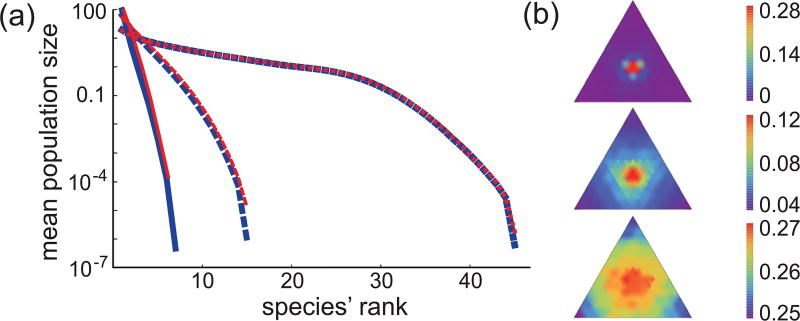
Fig. 4(a) shows a comparison of rank-abundance curves for our resource-competition model and the neutral model. The two models produce very similar rank-abundance curves, and the agreement is essentially perfect at high species immigration rate. However, there are still signatures in the data that the underlying resource-competition model is not neutral. For example, Fig. 4(b) shows color-coded histograms of the lifetime of species (as fractions of total simulation time) for the resource-competition model, revealing the greater average longevity of species that better match the evenly divided resource supply. However, even this signature of underlying competition is lost with increasing immigration rate.

FIG. 4.

Comparison of resource-competition model to neutral model. (a) Rank-abundance curves for the resource competition birth-death-immigration process (red) and the neutral birth-death-immigration process (blue), for a total population of 100, individuals competing for three resources (equally supplied for our model) and species immigration probabilities ν = 0.001 (solid curves), ν = 0.01 (dashed curves), and ν = 0.1 (dotted curves). The curves indicate the mean population size of the largest (rank 1), second largest (rank 2), etc., populations during simulations of 2⁶ × 10⁷, 2⁵ × 10⁷, and 2⁴ × 10⁷ time steps, respectively. The mean Shannon entropies of the distributions for the resource-competition and neutral models, in increasing order of ν, are H_{RC (N)} = 0.33(0.22), 1.6(1.4), 4.04(4.04); H = −Σ_σp_σ log₂(p_σ), where p_σ is the probability of an individual belonging to species σ. (b) The triangles show colormaps of the lifetime of species as fractions of the total simulation time, from top to bottom for ν = 0.001, 0.01, 0.1.

In the deterministic version of our model, variations in enzyme budgets or death rates lead to loss of diversity (see Fig. S3 in Supplemental Material [24]). However, in the stochastic version of the model defined above, diversity can be preserved even if species’ budgets and/or death rates are unequal. To see this, we allowed for variability in species’ budgets and death rates by specifying a species σ by a vector (max(α_σ1 + ξ_σ1, 0), …, max (α_{σ p} + ξ_σp, 0)) and a death rate δ + ξ_σ, where ${\sum }_{i=1}^p{\alpha }_{\sigma i}=E$, and the ξ_σi and ξ_σ are iid random variables with 𝒩(0, Σ²) distribution. If the standard deviation Σ = 0, we retrieve our original definition of species. We compared the rank-abundance curves corresponding to different values of Σ (Fig. S4) and found that the curves are very similar as long as Σ < Σ*, where Σ* is a threshold standard deviation which we estimate as Σ* ∝ log(S)/S for S ≫ 1 (see Supplemental Material [24]).

In summary, motivated by a recent study of the role of trade-offs in phytoplankton diversity [22], we investigated a minimal model ecosystem in which the population dynamics of a community is determined solely by competition for supplied nutrients. We implemented trade-offs between nutrient-utilization abilities via a simple sum rule. Depending on the composition of the nutrient supply, we observed two distinct behaviors of the system: either extinctions occur and the number of surviving species does not exceed the number of resources, as predicted by the competitive exclusion principle [8], or, surprisingly, no extinctions occur and an unlimited number of species can coexist, violating this principle. Importantly, the observed coexistence is robust: (1) if the populations are perturbed or the mean nutrient supply changes (within bounds set by the species present), the system always returns to a state of coexistence. (2) Within a stochastic version of the model, coexistence is maintained even if the enzyme budgets and/or death rates of species are unequal, up to a threshold set by species’ lifetimes.

There are two essential features of our model that allow for coexistence: organisms take part in shaping their environment, and all species are subject to the same trade-offs among metabolic abilities. The combined effect is that nutrient concentrations are robustly driven to unique values for which all species are equally fit and hence coexist. Both these essential features of the model are biologically well motivated. Organisms, particularly microbes [26], clearly affect their environments. The existence of trade-offs is widely cited [22,27], as is their importance for competition [7] and possible role in diversity [22,28], albeit modeling of the latter has been limited, e.g., to justifying chaotic population dynamics [29]. We chose to implement metabolic trade-offs via a simple sum rule. Other, possibly more realistic, choices and other types of trade-offs should be investigated in the future.

Remarkably, our simple trade-off model captures a number of nontrivial features of real ecosystems. First, the system has multiple steady states depending on the supply of nutrients [30]. Second, the rank-abundance patterns (Fig. 4) resemble the ones obtained from natural ecosystems [25], which are generally taken as signatures of neutral competition [25]. Indeed, within our model, niche and neutral theories of diversity are reconciled, as individuals occupy niches, whereas, the collective behaves neutrally. Third, single “keystone” species can play a crucial role in maintaining a diverse ecosystem, while other species’ effects on the environment may be redundant (e.g., species close to each other in the simplex representation may substitute for each other) [31–33].

Finally, since our minimal model closely describes a chemostat environment, we note that many chemostat experiments observe the coexistence of both phenotypically and genetically diverse microbes [34]. One way to test whether these microbes rely on each other (e.g., by jointly maintaining favorable nutrient concentrations, as in our model), would be to remove species one by one, similar to removal experiments in larger-scale ecosystems.