Abstract
Baricitinib is an oral inhibitor of Janus kinases (JAKs), selective for JAK1 and 2. It demonstrated dose‐dependent efficacy in patients with moderate‐to‐severe rheumatoid arthritis (RA) in a phase IIb study up to 24 weeks. Population pharmacokinetic/pharmacodynamic (PopPK/PD) models were developed to characterize concentration‐time profiles and dose/exposure‐response (D/E‐R) relationships for the key efficacy (proportion of patients achieving American College of Rheumatology 20%, 50%, or 70% response rate) and safety endpoints (incidence of anemia) for the phase IIb study. The modeling suggested that 4 mg q.d. was likely to offer the optimum risk/benefit balance, whereas 2 mg q.d. had the potential for adequate efficacy. In addition, at the same total daily dose, a twice‐daily regimen is not expected to provide an advantage over q.d. dosing for the efficacy or safety endpoints. The model‐based simulations formed the rationale for key aspects of dosing, such as dose levels and dosing frequency for phase III development.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Modeling‐based methodology is increasingly used to optimize drug development but published examples demonstrating its application in finding optimal doses for phase III evaluation are limited.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ We investigated the use of modeling‐based methodology to predict the performance of baricitinib doses and dosing frequency for the treatment of RA, to enable optimal phase III study design.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE
☑ Model‐based simulations on phase II efficacy (ACR20/50/70) and safety (incidence of anemia) data enabled quantitative assessment of risk‐benefit profiles across a range of baricitinib doses, not limited to the tested doses only. This assisted in selection of the optimal dose and dosing frequencies for inclusion in phase III studies of baricitinib in RA.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ Modeling exercises can optimize clinical trial design. They greatly informed the selection of the right dose of an important new treatment for patients with RA. At the same total daily dose, once‐daily and twice‐daily dosing provide similar efficacy and safety responses.
Baricitinib is an orally administered, potent, selective, and reversible inhibitor of Janus kinase (JAK)1 (half‐maximal inhibitory concentration = 5.9 nM) and JAK2 (half‐maximal inhibitory concentration = 5.7 nM).1 Inhibition of the JAK signaling pathway may modulate the activity of a number of cytokines implicated in the pathogenesis of rheumatoid arthritis (RA).2, 3, 4 In a phase IIb study, baricitinib demonstrated dose‐dependent improvements in the signs and symptoms of RA in patients with moderately‐to‐severely active disease despite treatment with methotrexate. Baricitinib seemed to be well tolerated through 24 weeks of treatment.5
In the phase IIb study, the impact of dose and dose frequency on key efficacy and safety parameters was examined to enable phase III study designs. Key efficacy parameters included a proportion of patients achieving American College of Rheumatology 20% (ACR20), 50% (ACR50), or 70% (ACR70) response through 24 weeks of treatment with baricitinib. An ACR20/50/70 response is defined as at least 20%, 50%, or 70% improvement in the ACR Core Set values.6 As erythropoietin (EPO) signals via a JAK2/JAK2 homodimer, hemoglobin (Hgb) levels were monitored as a key safety measure.7, 8
Few methods are available for linking discrete endpoints, especially ordered categorical variables, to the commonly used dose/exposure‐response (D/E‐R) model. As such, a latent variable approach was explored in conjunction with an inhibitory indirect response maximum effect (Emax) model to link the drug exposure to the efficacy endpoints of ACR20/50/70. To adequately describe the time course of change in Hgb with baricitinib treatment, simultaneous analysis of the time‐course data of red blood cells (RBCs), reticulocytes (RETs), and Hgb was conducted using a modified transit compartment model with a feedback describing the maturation and regulation processes in the EPO system.
The objectives of this study were: (i) to develop population pharmacokinetic/pharmacodynamic (PopPK/PD) models relating baricitinib exposure to the efficacy endpoint of ACR20/50/70 and safety endpoint of incidence of anemia; (ii) to evaluate the effects of subjects' demographic characteristics on the PK/PD of baricitinib; and (iii) to use model‐based simulations to quantitatively support certain elements of dosing regimens built into the registration trials.
METHODS
Patients
In this randomized, double‐blind, parallel‐group, placebo‐controlled, multicenter phase IIb study, a total of 301 patients with moderate‐to‐severe RA were randomized to q.d. baricitinib 1 mg (n = 49), 2 mg (n = 52), 4 mg (n = 52), 8 mg (n = 50), or placebo (n = 98) for 12 weeks of treatment.5 After 12 weeks of treatment, patients initially assigned to placebo or baricitinib 1 mg were re‐randomized to either baricitinib 2 mg b.i.d. (n = 61) or baricitinib 4 mg q.d. (n = 61) for an additional 12 weeks of blinded treatment. Patients initially assigned to baricitinib 2, 4, and 8 mg remained on the same treatment for an additional 12 weeks. The ACR responses were evaluated at weeks 2, 4, 8, 12, 16, 20, and 24. The Hgb was measured at baseline and weeks 2, 4, 8, 12, 14, 16, 20, and 24. Blood samples for pharmacokinetic (PK) analysis were collected for each patient at week 0 (15–30 minutes and 1–3 hours postdose), weeks 2, 4, and 8 (predose), week 12 (predose, 15–30 minutes, and 1–3 hours postdose), and weeks 14, 16, and 20 (one sample at a random time).
The study was conducted in accordance with the ethical principles of the Declaration of Helsinki and Good Clinical Practice guidelines. All patients provided written informed consent, and institutional review boards or ethics committees approved the protocol before the study started. Full details of the phase IIb study have been described previously.5
Population pharmacokinetic model
The PK data were available from 278 patients in the phase IIb study, contributing 2,272 measurable baricitinib concentration samples. The Monte Carlo importance sampling assisted by mode a posteriori estimation method with interaction in NONMEM version VII (ICON Development Solutions, Ellicott City, MD) was used to model baricitinib plasma concentrations.
The basic structure consisted of a two‐compartment model with zero‐order absorption (including lag time) and a semimechanistic partitioning of total apparent clearance into total apparent renal clearance (CLr/F) that is dependent on the estimated glomerular filtration rate (eGFR) and nonrenal clearance that is independent of the eGFR.9 The model is set up this way because baricitinib is primarily eliminated via renal excretion. The modification of diet in renal disease (MDRD; Eq. (1))10 was used to calculate eGFR, whereas Scr is serum creatinine concentration. Possible changes and fluctuations were accounted for by the inclusion of a time‐varying variable of MDRD‐eGFR.11 The CLr/F was estimated using Eq. (2), where θx is the typical CLr/F based on baseline MDRD‐eGFR (BeGFRMDRD) normalized to the median GFRMDRD of 93 mL/min/1.73 m2 from a previous analysis and θy is the time‐varying effect of MDRD‐eGFR.
| (1) |
| (2) |
The between‐subject variability (BSV) consisted of a log‐normal distribution for CLr/F, nonrenal clearance, apparent central volume of distribution (V1/F), intercompartmental clearance (Q), and apparent peripheral compartment volume of distribution. A Box‐Cox transformation for the distribution of the zero‐order absorption duration parameter (D1) was used where one parameter transforms a normal distribution into a left‐skewed or right‐skewed distribution.12
The PK of baricitinib had previously been modeled with data pooled from five early‐phase studies conducted in healthy subjects and patients with RA (phase I/IIa analysis). Estimates for PK parameters and covariates from this previous population pharmacokinetic (PopPK) analysis were adopted as priors for initiating the current PopPK model, and the model was further optimized through inclusion of concentrations from the phase IIb study. Covariates that were identified in the previous PK analysis (gender and body weight on V1/F and eGFR on CLr/F) were included in the current model and estimated with data from the phase IIb study. No additional covariates were tested.
ACR response model
All evaluable data comprising 2,299 observations of ACR20/50/70 from 299 patients in the phase IIb study were included for the ACR modeling. A sequential modeling approach, in which the individual post hoc PK parameters from the final PopPK model were fixed prior to modeling the ACR data, was used. Estimates of the ACR model parameters and associated error term were obtained using the general nonlinear model and Laplacian method in NONMEM.
Similar to a previously published approach,13 an indirect response model with drugs inhibiting the formation of the disease was used to describe the time course of the disease state, represented by a latent variable (ACR latent‐dependent variable (ACRL)) is shown in Eq. (3):
| (3) |
where Kin and kout are the formation and elimination rate constant of ACRL, Emax is the maximum inhibition by drug concentration (Cp), and EC50 is the half‐maximal response concentration. PBO(t) is the placebo effect over time:
| (4) |
where is the maximum placebo effect, t is the time after the first dose, and Tplb is the half‐life of the placebo effect in hours.
Logistic regression was used for fitting the categorical endpoint of ACR20/50/70. The logit function to attain each ACRr is described in Eq. (5):
| (5) |
where r = 20, 50, or 70 and ACRL spans values from 0 to 1. The logit value for a particular ACRr responder status and prob[ACRr = 1] is the likelihood of a patient achieving one of four possible responder states: nonresponder or responder to ACR20/50/70. At time = 0, ACRL was set at 1 such that the is 0 and translates to ACRr not achieved at the baseline. Because of the nature of , the model does not need to estimate the intercept values, which are fixed to
The likelihood of a particular responder status was calculated as follows:
| (6) |
where the logit from Eq. (5) was used to calculate the likelihood of achieving state r for responder status ), which are ACR20/50/70.
The probability of ACRr response was then calculated as follows:
| (7) |
where P0, P1, P2, and P3 are the probabilities of being a nonresponder or responder to ACR20, ACR50, and ACR70, respectively.
Patient factors tested included body surface area, height, weight, body mass index, age, gender, race, alcohol use, smoking status, C‐reactive protein, erythrocyte sedimentation rate, tender joint counts, and swollen joint counts.
Hemoglobin model
A total of 2,770 RET, 2,781 RBC, and 2,781 Hgb observations from 298 patients in the phase IIb study were used for the modeling of the Hgb level. Estimates of the parameters for the Hgb model and associated error terms were obtained by fitting these data in combination with individual Bayesian post hoc PK parameter estimates using the general nonlinear model with differential equations with NONMEM. Incidence of anemia (defined as Hgb <10 g/dL) was summarized from the modeled time course data of Hgb at steady‐state of dosing following various dosing regimens.
A transit compartment model14 was modified and applied to describe the time courses of RETs, RBCs, and Hgb simultaneously in the phase IIb study. Briefly, the model consists of a progenitor cell pool (Prol) that develops to form circulating RETs through a series of three transit compartments (T1–T3), followed by a maturation chain of four transit compartments representing maturation of the RETs (RETT4–T7), and a further maturation chain with four transit compartments for RBCs (RBCT9–T11). The change in Hgb levels was modeled using a proportionality scaling factor SHb, which represents the Hgb content per cell assumed based on the RET and RBCs (Ncells) at time t (Eq. (20)). Drug effect (Edrug) was evaluated as a linear (including a sigmoidal) function of drug concentration on the Prol and subsequent transit compartments prior to RETs. Key differential equations describing the model are shown in Eqs. (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20). Detailed model equations were included in a previous presentation.15
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
where ktr1, ktr2, and kcir are the transit rate constant for Prol, RET, and RBC, respectively. The total number of RET (RETT4, RETT5, RETT6, and RETT7) and RBC (RBCT8, RBCT9, RBCT10, and RBCT11) counts was the summation of each respective transit compartment at a given time. The transit compartments in the above equations are designated by their respective subscripts, where n represents the transit compartment number.
It was assumed that RET and RBC were at steady‐state prior to drug administration (i.e., dRET0/dt = 0 and dRBC0/dt = 0) and all baseline values were related to RET, as given by Eqs. (21), (22), (23), (24), (25), (26), (27), (28), (29), (30), (31), (32):
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
where RET0 and RBC0 are baseline RETs and RBCs.
A feedback mechanism is applied to characterize the effect of endogenous growth factors and cytokines on the Prol in response to changes in circulating cell counts.16, 17, 18 The feedback was assumed to be related to RETs and RBCs causing an increase of Prol by increasing the production rate of cells in the Prol compartment and equal to 1 at steady state.
| (33) |
where γ1 and γ2 are the feedback factors for RET and RBC, respectively.
The RET‐RBC‐Hgb of baricitinib had previously been modeled in the phase I/IIa analysis. Estimates for parameters and covariates from this analysis were adopted as priors for initiating the current model and the model was further optimized through inclusion of data from the phase IIb study. No additional covariates were tested.
The PopPK, ACR, and Hgb models were evaluated using the standard model diagnostic methods, which consisted of concordance plots, weighted residual error plots, weighted residual error distribution plots and random effects distribution plots, and simulation‐based diagnostics, such as posterior predictive check.
RESULTS
Pharmacokinetic profiles comparing dosing regimens
Model check via goodness‐of‐fit plots and visual predictive checks suggested reasonable agreement between predicted and observed plasma concentrations (data not shown). Estimates for key PK parameters together with BSV are summarized in Supplementary Table S1. The predicted median plasma concentration profiles over a dosing interval at steady‐state for dosing regimens of baricitinib 1 mg b.i.d., 2 mg q.d., 2 mg b.i.d., and 4 mg q.d. are compared in Figure 1. At the same total daily dose, the q.d. dosing produces slightly higher peak concentrations compared to the b.i.d. dosing, with the daily average concentrations over the 24‐hour interval at steady‐state being essentially the same for the b.i.d. and q.d. dosing regimens, as shown by the overlapping horizontal lines in Figure 1.
Figure 1.
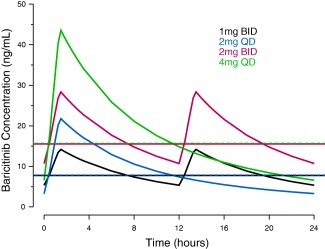
Model‐predicted median plasma concentration profiles over a dosing interval at steady‐state for 1 mg b.i.d., 2 mg q.d., 2 mg b.i.d., and 4 mg q.d. baricitinib. Blue, red, black, and green horizontal dashed lines indicate the mean concentrations over the 24‐hour interval at steady‐state for 1 mg b.i.d., 2 mg q.d., 2 mg b.i.d., and 4 mg q.d., respectively.
Dose‐response relationship for ACR20/50/70 for various dosing regimens
The predicted and observed ACR20 response rates over time following baricitinib treatment at various doses are shown in Figure 2. Similar plots for ACR50 and ACR70 are included in Supplementary Figure S1. Onset of action seemed more rapid with the 8 mg and 4 mg q.d. doses compared to the 2 mg q.d. dose (e.g., estimated ACR20 at week 2 is 38.0%, 32.7%, 25.0%, and 11.2% for 8 mg, 4 mg, 2 mg doses, and placebo, respectively). Overall, the observed response rates were largely within the prediction intervals (PIs), suggesting no obvious misfits to the data. A summary of the parameter estimates for the ACR20/50/70 model is presented in Table 1. The Emax for the ACRL was estimated to be 0.861 (standard error of estimate = 3.22%). This value translates to predicted maximum response rates (due to drug effect) of 87%, 64%, and 39% for the ACR20, ACR50, and ACR70 response rates, respectively.
Figure 2.
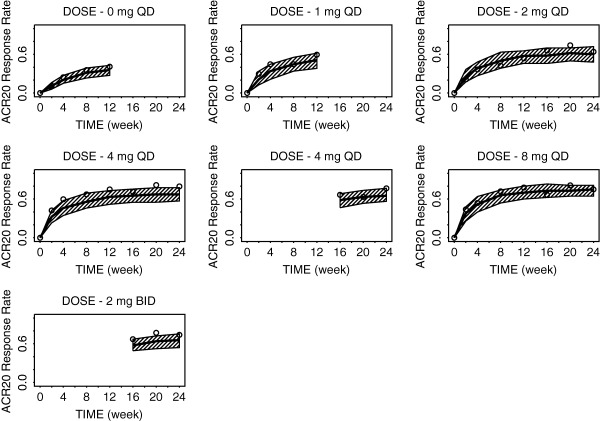
Model‐predicted and observed time course of American College of Rheumatology (ACR)20 response rates for various doses of baricitinib through week 24. The solid line is model‐predicted median response rate, the shaded area represents the 90% prediction intervals, and the open circles represent observed sample proportions.
Table 1.
Pharmacodynamic parameter estimates from the final population exposure‐response model for ACR20/50/70 in patients with rheumatoid arthritis on baricitinib
| Model parameter (units) |
Population mean (%SEE) |
95% Confidence interval from bootstrap analysis |
|---|---|---|
| Elimination rate constant Kout (week−1) | 0.171 (20.1) | (0.0839–0.450) |
| Half‐life for loss of placebo effect Tplb (hours) | 341 (56.3) | (5.99–6280) |
| Maximum ACRL effect Emax | 0.861 (3.22) | (0.264–0.897) |
| Concentration for half maximal ACRL effect EC50 (nM) | 68.0 (20.0) | (4.67–105) |
| Variance for BSV (logit scale) | 1.79 (11.5) | — |
ACR, American College of Rheumatology; ACR20/50/70 = 20%, 50%, and 70% improvement in ACR score, respectively; ACRL, ACR latent‐dependent variable; BSV, between‐subject variability; EC50, half‐maximal response concentration; Emax, maximal response; SEE, standard error of estimate; Tplb, half‐life of the placebo effect in hours.
The predicted mean with 90% PIs and observed dose‐response (D‐R) relationships for ACR20, ACR50, and ACR70 at week 12 are shown in Figure 3 a–c, respectively. The observed data for 2 mg b.i.d. are from week 24 after 12 weeks of dosing. The D‐R relationship was well captured within the dose range of 0–8 mg tested in the phase IIb study. A dose of 4 mg seemed to reach the plateau portion of the D‐R curve for ACR20/50/70 with incremental benefit over 2 mg, whereas a dose of 8 mg adds minimal benefit compared to 4 mg. The observed and estimated ACR20 response rates were 75.0% and 63.5% for 4 mg and 53.8% and 57.7% for 2 mg, respectively, at week 12, they were 79.6% and 67.3% for 4 mg and 64.0% and 60.0% for 2 mg, respectively, at week 24. The observed and predicted response rates were similar between the 2 mg b.i.d. and 4 mg q.d. doses. The model‐predicted ACR20/50/70 response rates for 1 mg b.i.d. (red symbols, Figure 3 a–c) were comparable to those for 2 mg q.d., and lower than those for 4 mg q.d.
Figure 3.
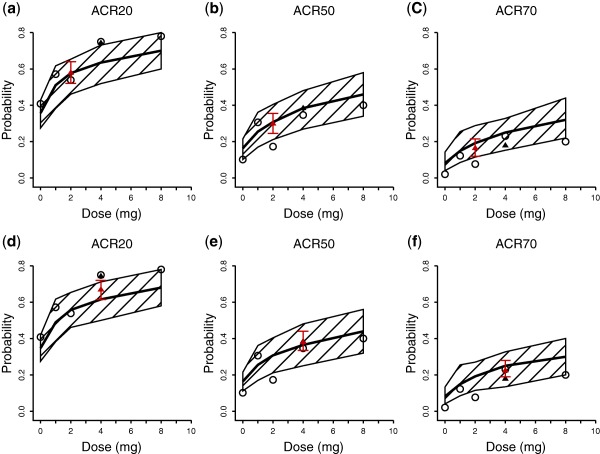
Estimated dose American College of Rheumatology (ACR)20/50/70 response relationship for baricitinib after 12 weeks of treatment based on all data (a–c) and based on observed data including only q.d. dosing regimens (d–f). The solid lines and the shaded area are model‐predicted median response with 90% prediction interval. Open circles and filled triangles are for observed data for q.d. and b.i.d. doses, respectively. The red triangle with error bar is for predicted data for 1 mg b.i.d. or 2 mg b.i.d.
To further evaluate the predictive performance of the model, the PopPK/PD model was fitted to a dataset that included only q.d. dosing, excluding data obtained from the 2 mg b.i.d. dosing group from weeks 12–24. The model was subsequently used to predict the ACR20/50/70 response rate of the 2 mg b.i.d. dosing group during the second 12 weeks in the phase IIb study (Figure 3 d–f). The predicted and observed responses were in reasonable agreement, suggesting that the model developed with q.d. data is capable of predicting responses of the b.i.d. dosing regimen.
None of the patient factors tested (age, gender, height, weight, body mass index, body surface area, race, alcohol use, smoking status, high sensitivity C‐reactive protein, erythrocyte sedimentation rate, tender joint counts, and swollen joint counts) were identified as a significant covariate on the ACR20/50/70 model.
Dose‐response relationship for incidence of anemia for various dosing regimens
The model diagnostics based on goodness‐of‐fit and visual predictive checks for the Hgb model are presented in Supplementary Figures S2 and S3, respectively. The random distribution of individual weighted residual and conditional weighted residual values suggests no apparent bias in the predicted Hgb concentrations. A summary of the parameter estimates for the Hgb model is presented in Table 2. Age, gender, and baseline Hgb levels were identified as significant covariates and were included in the final model.
Table 2.
Pharmacodynamic parameter estimates from the final population exposure‐response model for hemoglobin in patients with rheumatoid arthritis on baricitinib
| Model parameter | Unit |
Population mean (%SEE)a |
BSVb (%SEE)a |
|---|---|---|---|
| Baseline RETc, d | 109 cells/L | 16.3 (2.12) | 28.3 (10.4) |
| Transit rate constant from proliferation pool to RET (ktr1) | Hour | 0.0418 (7.51) | — |
| Feedback factor for RET | — | 0.352 (14.4) | — |
| Transit rate constant from RET to RBC (ktr2) | Hour | 0.0975 (1.82) | — |
| Drug effect on proliferation pool | — | 0.00534 (21.9) | — |
| Sigmoidal function for drug effect on proliferation pool | — | 0.586 (7.27) | — |
| Transit rate constant for RBC (kcir) | Hour | 0.00139 FIX | 27.4 (10.6) |
| Proportionality scaling factor (SHb) | pg/cell | 30.2 (0.0748) | — |
| Feedback factor for RBC | — | 0.925 (12.5) | — |
| Age effect on baseline RETd | — | −0.00164 (92.7) | — |
| Age effect on transit rate constant on RBCe | — | −0.00131 (115) | — |
| Gender effect on baseline RETd | — | −0.110 (9.27) | — |
| Covariance for baseline RET and kcir f | — | 0.0722 (10.7) | — |
| Proportional residual error for RETg | — | 0.219 (4.18) | — |
| Additive residual error for RETg | — | 11.2 (5.04) | — |
| Proportional residual error for RBCg | — | 0.0655 (4.55) | — |
| Additive residual error for RETg | — | 78.3 (60.8) | — |
| Additive residual error for Hgbg | — | 7.82 (1.99) | — |
BSV, between‐subject variability; FIX, fixed; Hgb, hemoglobin; RBC, red blood cell; RET, reticulocyte; SEE, standard error of estimate; SQRT, square root.
The standard errors were obtained by selecting the S matrix feature.
% coefficient of variation = (square root(SQRT)(exponential (EXP)(OMEGA(N)))−1) * 100%.
Estimate for each RET‐related compartment.
Baseline RET*EXP((Age‐48)*Age effect on baseline RET) * (1 + IND*Gender effect on baseline RET); where IND = 1 for women and 0 for men; age is age at study entry; 48 is the median age in years from the phase I/IIa analysis.
Transit rate constant for RBC*EXP((Age‐48)*Age effect on transit rate constant on RBC); where age is age at study entry; 48 is the median age in years from the phase I/IIa analysis.
Covariance between ω2.
Standard deviation.
The model‐predicted and observed incidence of anemia over the dose range of 0–8 mg during weeks 0–12 and weeks 12–24 are compared in Figure 4. Reasonable agreement is demonstrated between predictions and observations, suggesting that the model predicted the incidence of anemia within the dose range studied in the phase IIb study. From weeks 0–12, the D‐R curve is relatively flat from placebo (0 mg dose) through the 4 mg dose with a subsequent small increase from 4 to 8 mg. Similar findings were observed for the week 12–24 predictions and observations. For the comparisons shown in Figure 4, the actual baseline Hgb concentrations observed in the study were used in the simulations rather than a simulated distribution of baseline values.
Figure 4.
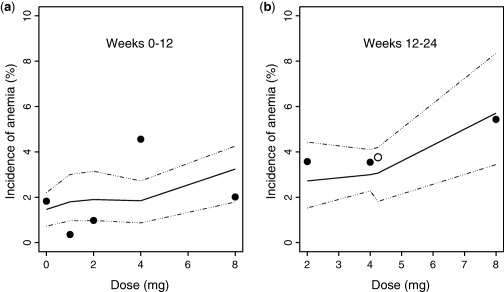
Comparison of predicted versus observed incidence of anemia (defined as hemoglobin <10 g/dL). Bold line represents model‐predicted median incidence, dashed lines correspond to the 95% prediction interval, and the observed incidence of anemia at particular dose levels for q.d. dosing (•) and 2 mg b.i.d. dosing (○) regimens, respectively.
Simulated Hgb levels and corresponding incidences of anemia for 1 mg b.i.d., 2 mg q.d., 2 mg b.i.d., and 4 mg q.d. from week 0 through week 24 are shown in Figure 5 a. There were no observed differences for either outcome between 1 mg b.i.d. and 2 mg q.d. or between 2 mg b.i.d. and 4 mg q.d. The impact of baseline Hgb levels on the incidence of anemia is shown in Figure 5 b,c (Figure 5 a,b seem similar because a majority of the patients had a baseline Hgb >12 g/dL). There is no apparent difference when comparing the incidence of anemia between the b.i.d. and q.d. dosing regimens at the same total daily doses.
Figure 5.
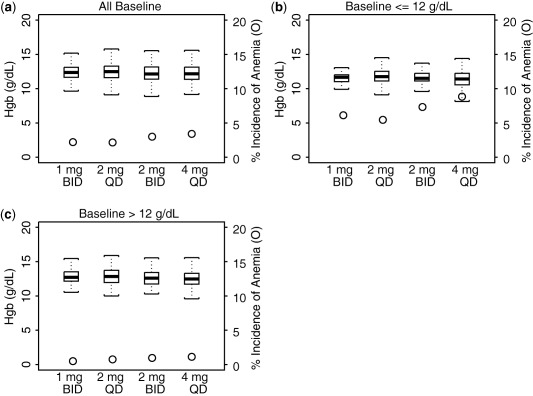
Model‐predicted absolute value of hemoglobin at steady‐state of dosing and corresponding incidence of anemia for all baseline hemoglobin (Hgb) (a), for baseline Hgb ≤12 g/dL (b), and for baseline Hgb >12 g/dL (c), for 1 mg b.i.d., 2 mg q.d., 2 mg b.i.d., and 4 mg q.d. dosing regimen. The box plots represent the absolute values of Hgb and were constructed with median, 25th and 75th percentiles, and the minimum and maximum values and uses y‐axis on the left. Circles represent incidence of anemia and uses y‐axis on the right.
DISCUSSION
Modeling‐based methodology is frequently used to understand the D/E‐R and to optimize future clinical study designs. Modeling and simulation incorporates prior knowledge,19, 20, 21 accounts for sources of variability,22, 23 and allows exploration of alternative dosing regimens without the need for costly additional clinical trials.24, 25 The analysis of the phase IIb study reported here exemplified the benefits of applying a modeling approach in drug development to aid clinical decision making. The integrated PopPK/PD models, by relating the doses as well as exposures over a broad range to the clinical endpoints, provided key insights about the doses with the optimal risk‐benefit profiles and whether lower individual doses given with greater frequency might provide a different risk‐benefit profile.
The PopPK model consisted of a two‐compartment model with zero‐order absorption. Use of a zero‐order absorption with a Box‐Cox BSV distribution more closely approximated the observed rapid absorption compared to a first‐order absorption with an exponential BSV distribution. The mean terminal half‐life of baricitinib was estimated to be ∼14 hours in patients with RA, consistent with a q.d. dosing strategy. The simulation suggested with the same total daily doses, b.i.d. and q.d. dosing, produced similar average daily concentrations over 24 hours, which is considered to be the driving force of efficacy and safety for baricitinib. Although the covariates of body weight and gender are statistically significant on V1/F, their effect sizes are generally small and within the BSV in the exposure estimates of baricitinib; therefore, they are not considered clinically relevant.
A latent‐variable approach in conjunction with an inhibitory indirect response model was used for describing the time course and D/E‐R for the ordered categorical endpoints of ACR20/50/70. This modeling approach represents several advantages. First, it links discrete endpoints to the mechanistic and physiologically plausible indirect response models. Baricitinib acts as a JAK1/2 inhibitor that inhibits the cytokine‐induced JAK/signal transducers and activators of transcription signaling pathway,26 and this model described baricitinib as having an inhibitory pharmacological effect on the disease condition. Second, the placebo effect was modeled to have a corresponding pharmacological effect via the same inhibitory mechanism as the active drug. The model for ACR20/50/70 is able to account for both baricitinib and the combined placebo and methotrexate effects. The placebo effect could be estimated based on the time‐course data from the placebo group, and the maximum achievable baricitinib effect was subsequently estimated through subtraction of the placebo effect from total effect. Last, the model allows simultaneous modeling of multiple endpoints that are categorically ordered. Modeling multiple endpoints (ACR20, ACR50, and ACR70) simultaneously has advantages over modeling a single endpoint alone because all information available is included and accounted for in the modeling, especially due to the correlation between these endpoints and the fact that all three ACR endpoints are derived from a progression of change in the ACR component measures. As a potential limitation, the intercepts for describing the ordinal relationship among ACR20/50/70 (in Eq. (5)) could not be reliably determined and were fixed. Further improvement of the model allowing estimation of the intercepts may be warranted for future studies. Nevertheless, the overall predictive performance of the current model was acceptably robust.
For a more complete evaluation of benefit‐risk profiles, the relationship between dose regimen and incidence of anemia was evaluated. It should be noted that baricitinib was well tolerated overall, with no unexpected safety findings across doses tested in the phase IIb study.5 An evaluation of Hgb was conducted because a dose‐dependent decrease in the Hgb level was observed and this decrease is considered mechanism‐related. Quantitative assessment for absolute neutrophil count as a putative mechanism‐related safety biomarker demonstrated a conclusion on the D‐R relationship similar to Hgb and, therefore, was not included in this presentation. Modeling for other laboratory parameters was not warranted given the small magnitude of changes and/or unknown mechanism.5 The semimechanistic Hgb model adequately characterized the time course of Hgb in a manner consistent with the mechanism of action of the inhibition of JAK by baricitinib, and the model structure is a reasonable approximation of the underlying biological processes related to EPO.27 The estimated D‐R curve showed a relatively flat relationship between the incidence of anemia and baricitinib dose with a small increase in the incidence of anemia from 4–8 mg. A difference in the incidence of anemia was observed between women and men. This can be largely attributed to the lower baseline Hgb levels in women compared to men and were accounted for in the model with the covariate effect of gender on baseline Hgb level.
The addition of a b.i.d. dosing regimen in the phase IIb study was based on data from early clinical studies that showed a relatively short half‐life in the range of 6–10 hours in healthy subjects. The 2 mg b.i.d. dosing data available from the second 12 weeks of treatment provided valuable information on an alternative dosing frequency to serve as a useful validation of the model prediction for b.i.d. dosing regimen. When only q.d. dosing data in the phase IIb study were included in the fitting of the ACR model, the model reasonably predicted the observed response rates for 2 mg b.i.d. in the second 12 weeks of treatment in the phase IIb study. The prediction of response for 1 mg b.i.d. was of particular interest, because this dosing regimen was never evaluated in a clinical study. The fact that the observed response rates were similar between 4 mg q.d. and 2 mg b.i.d. does not automatically allow the same conclusion to be drawn while comparing 2 mg q.d. and 1 mg b.i.d. The 4 mg q.d. (or 2 mg b.i.d.) and 2 mg q.d. (or 1 mg b.i.d.) doses reside on different parts of the D‐R curve, which are the plateau (4 mg q.d.) and ascending portions (2 mg q.d.) of the curve, respectively. Therefore, simulations based on data over a wide range of doses and various dosing regimens were essential to ensure an accurate prediction of the efficacy of the 1 mg b.i.d. dosing regimen. The associated data supported the clinically important conclusion that a b.i.d. dosing regimen does not offer advantages in terms of outcome over a q.d. dosing regimen, which would be anticipated as more convenient for patients.
In conclusion, this analysis of the phase IIb study was designed to adequately characterize the D/E‐R relationships for ACR20/50/70 and incidence of anemia following administration of baricitinib in patients with RA. The modeling integrated efficacy and safety data observed from phase IIb to conclude that a dose of 4 mg q.d. was likely to offer the optimum benefit‐risk balance, whereas 2 mg q.d. may potentially show some efficacy; thus, both doses had acceptable benefit‐risk profiles worthy of further exploration in confirmatory phase III trials. In addition, simulations were used to demonstrate that, at the same total daily dose, splitting the dose into a b.i.d. dosing regimen is unlikely to provide any efficacy or safety benefit over q.d. dosing regimen. In this case, modeling and simulation eliminated the need to conduct additional clinical studies to gain information on a b.i.d. dosing regimen.
Conflict of Interest
X.Z., L.C., C.S.E., W.M., T.R., and L.S.T. are employees of Eli Lilly and Company and also hold stock/shares in Eli Lilly and Company.
Supporting information
Supporting Information
Supplementary Figure S1A Model‐predicted and observed time course of American College of Rheumatology (ACR)50 response rates for various doses of baricitinib through week 24. The solid line is the model‐predicted median response rate, the shaded area represents the 90% prediction intervals, and the open circles represent observed sample proportions.
Supplementary Figure S1B Model‐predicted and observed time course of American College of Rheumatology (ACR)70 response rates for various doses of baricitinib through week 24. The solid line is the model‐predicted median response rate, the shaded area represents the 90% prediction intervals, and the open circles represent observed sample proportions.
Supplementary Figure S2 Goodness‐of‐fit plots for hemoglobin. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of g/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S3 Goodness‐of‐fit plots for red blood cells. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of cells^9/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S4 Goodness‐of‐fit plots for reticulocytes. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of cells^9/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S5 Visual predictive check for hemoglobin (Hgb) in the reticulocytes, red blood cells, and hemoglobin final model. The shaded area corresponds to the 95% confidence bounds. Hgb levels (•) for individuals are presented. PI, prediction interval.
Supplementary Table S1 Baricitinib pharmacokinetic parameter estimates from the final population pharmacokinetics model in patients with rheumatoid arthritis
Final_Model_Scripts
Acknowledgments
The authors wish to acknowledge the investigators and subjects who participated in the clinical study, as well as the following individuals: Michael Heathman and Stuart Friedrich, Eli Lilly and Company, for modeling consultations.
Source of Funding
This study was supported by Eli Lilly and Company and Incyte Corporation.
Author Contributions
X.J., L.C., C.S.E., W.M., T.R., and L.S.T. wrote the manuscript. X.J., W.M., and T.R. designed the research. X.J., L.C., C.S.E., W.M., T.R., and L.S.T. performed the research. X.J., L.C., C.S.E., and L.S.T. analyzed the data.
References
- 1. Fridman, J.S. et al Selective inhibition of JAK1 and JAK2 is efficacious in rodent models of arthritis: preclinical characterization of INCB028050. J. Immunol. 184, 5298–5307 (2010). [DOI] [PubMed] [Google Scholar]
- 2. O'Shea, J.J. , Holland, S.M. & Staudt, L.M. JAKs and STATs in immunity, immunodeficiency, and cancer. N. Engl. J. Med. 368, 161–170 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kremer, J.M. et al The safety and efficacy of a JAK inhibitor in patients with active rheumatoid arthritis: results of a double‐blind, placebo controlled phase IIa trial of three dosage levels of CP‐690,550 versus placebo. Arthritis Rheum. 60, 1895–1905 (2009). [DOI] [PubMed] [Google Scholar]
- 4. Williams, W. , Scherle, P. & Shi, J. A randomized placebo‐controlled study of INCB018424, a selective Janus kinase 1 & 2 (JAK1 & 2) inhibitor in rheumatoid arthritis (RA). Arthritis Rheum. 58, S431 (2008). [Google Scholar]
- 5. Keystone, E.C. et al Safety and efficacy of baricitinib at 24 weeks in patients with rheumatoid arthritis who have had an inadequate response to methotrexate. Ann. Rheum. Dis. 74, 333–340 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Villaverde, V. et al Activity indices in rheumatoid arthritis. J. Rheumatol. 27, 2576–2581 (2000). [PubMed] [Google Scholar]
- 7. Clark, J.D. , Flanagan, M.E. & Telliez, JB. Discovery and development of Janus kinase (JAK) inhibitors for inflammatory diseases. J. Med. Chem. 57, 5023–5038 (2014). [DOI] [PubMed] [Google Scholar]
- 8. O'Shea, J.J. , Kontzias, A. , Yamaoka, K. , Tanaka, Y. & Laurence, A. Janus kinase inhibitors in autoimmune diseases. Ann. Rheum. Dis. 72(suppl. 2), ii111–ii115 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Shi, J.G. et al The pharmacokinetics, pharmacodynamics, and safety of baricitinib, an oral JAK 1/2 inhibitor, in healthy volunteers. J. Clin. Pharmacol. 54, 1354–1361 (2014). [DOI] [PubMed] [Google Scholar]
- 10. Levey, A.S. , Bosch, J.P. , Lewis, J.B. , Greene, T. , Rogers, N. & Roth, D. A more accurate method to estimate glomerular filtration rate from serum creatinine: a new prediction equation. Modification of Diet in Renal Disease Study Group. Ann. Intern. Med. 130, 461–470 (1999). [DOI] [PubMed] [Google Scholar]
- 11. Wählby, U. , Thomson, A.H. , Milligan, P.A. & Karlsson, M.O. Models for time‐varying covariates in population pharmacokinetic‐pharmacodynamic analysis. Br. J. Clin. Pharmacol. 58, 367–377 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Petersson, K.J. , Hanze, E. , Savic, R.M. & Karlsson, M.O. Semiparametric distributions with estimated shape parameters. Pharm. Res. 26, 2174–2185 (2009). [DOI] [PubMed] [Google Scholar]
- 13. Hu, C. , Xu, Z. , Rahman, M.U. , Davis, H.M. & Zhou, H. A latent variable approach for modeling categorical endpoints among patients with rheumatoid arthritis treated with golimumab plus methotrexate. J. Pharmacokinet. Pharmacodyn. 37, 309–321 (2010). [DOI] [PubMed] [Google Scholar]
- 14. Hamrén, B. , Björk, E. , Sunzel, M. & Karlsson, M. Models for plasma glucose, HbA1c, and hemoglobin interrelationships in patients with type 2 diabetes following tesaglitazar treatment. Clin. Pharmacol. Ther. 84, 228–235 (2008). [DOI] [PubMed] [Google Scholar]
- 15. Ernest, C.S. II , Satterwhite, J.H. , Macias, W.L. , Hyslop, D.L. & Tham, L.S. A semi‐mechanistic model characterizing the time‐course of reticulocytes, red blood cells, and hemoglobin in rheumatoid arthritis patients on baricitinib. ASCPT Annual Meeting, March 5–9, 2013; Indianapolis, IN. [Google Scholar]
- 16. Friberg, L.E. , Henningsson, A. , Maas, H. , Nguyen, L. & Karlsson, M.O. Model of chemotherapy‐induced myelosuppression with parameter consistency across drugs. J. Clin. Oncol. 20, 4713–4721 (2002). [DOI] [PubMed] [Google Scholar]
- 17. Friberg, L.E. & Karlsson, M.O. Mechanistic models for myelosuppression. Invest. New Drugs 21, 183–194 (2003). [DOI] [PubMed] [Google Scholar]
- 18. Takatani, H. et al Levels of recombinant human granulocyte colony‐stimulating factor in serum are inversely correlated with circulating neutrophil counts. Antimicrob. Agents Chemother. 40, 988–991 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Lesko, L.J. , Rowland, M. , Peck, C.C. & Blaschke, T.F. Optimizing the science of drug development: opportunities for better candidate selection and accelerated evaluation in humans. Pharm. Res. 17, 1335–1344 (2000). [DOI] [PubMed] [Google Scholar]
- 20. Galluppi, G.R. et al Integration of pharmacokinetic and pharmacodynamic studies in the discovery, development, and review of protein therapeutic agents: a conference report. Clin. Pharmacol. Ther. 69, 387–399 (2001). [DOI] [PubMed] [Google Scholar]
- 21. van der Graaf, P.H. CPT: Pharmacometrics and Systems Pharmacology. CPT Pharmacometrics Syst. Pharmacol. 1, e8 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Holford, N. , Ma, S.C. & Ploeger, B.A. Clinical trial simulation: a review. Clin. Pharmacol. Ther. 88, 166–182 (2010). [DOI] [PubMed] [Google Scholar]
- 23. Bonate, P.L. Clinical trial simulation in drug development. Pharm. Res. 17, 252–256 (2000). [DOI] [PubMed] [Google Scholar]
- 24. Chien, J.Y. , Friedrich, S. , Heathman, M.A. , de Alwis, D.P. & Sinha V. Pharmacokinetics/pharmacodynamics and the stages of drug development: role of modeling and simulation. AAPS J. 7, E544–E559 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Zhang, L. et al Model‐based drug development: the road to quantitative pharmacology. J. Pharmacokinet. Pharmacodynam. 33, 369–393 (2006). [DOI] [PubMed] [Google Scholar]
- 26. Hsu, L. & Armstrong, A.W. JAK inhibitors: treatment efficacy and safety profile in patients with psoriasis. J. Immunol. Res. 2014, 283617 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lacombe, C. & Mayeux, P. The molecular biology of erythropoietin. Nephrol. Dial. Transplant. 14 Suppl 2, 22–28 (1999). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information
Supplementary Figure S1A Model‐predicted and observed time course of American College of Rheumatology (ACR)50 response rates for various doses of baricitinib through week 24. The solid line is the model‐predicted median response rate, the shaded area represents the 90% prediction intervals, and the open circles represent observed sample proportions.
Supplementary Figure S1B Model‐predicted and observed time course of American College of Rheumatology (ACR)70 response rates for various doses of baricitinib through week 24. The solid line is the model‐predicted median response rate, the shaded area represents the 90% prediction intervals, and the open circles represent observed sample proportions.
Supplementary Figure S2 Goodness‐of‐fit plots for hemoglobin. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of g/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S3 Goodness‐of‐fit plots for red blood cells. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of cells^9/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S4 Goodness‐of‐fit plots for reticulocytes. Lowess fit, a smoothed value given by a weighted linear least squares regression over the span of observations, for data presented (red line) in addition to a line of unity (black line). Data was in a unit of cells^9/L. CWRES, conditional weighted residuals; IWRES, individual weighted residuals.
Supplementary Figure S5 Visual predictive check for hemoglobin (Hgb) in the reticulocytes, red blood cells, and hemoglobin final model. The shaded area corresponds to the 95% confidence bounds. Hgb levels (•) for individuals are presented. PI, prediction interval.
Supplementary Table S1 Baricitinib pharmacokinetic parameter estimates from the final population pharmacokinetics model in patients with rheumatoid arthritis
Final_Model_Scripts


