Seeing real-space dynamics of liquid water through inelastic x-ray scattering

We directly observed time-dependent real-space atom-atom dynamic correlations in liquid water using inelastic x-ray scattering.

Abstract

Water is ubiquitous on earth, but we know little about the real-space motion of molecules in liquid water. We demonstrate that high-resolution inelastic x-ray scattering measurement over a wide range of momentum and energy transfer makes it possible to probe real-space, real-time dynamics of water molecules through the so-called Van Hove function. Water molecules are found to be strongly correlated in space and time with coupling between the first and second nearest-neighbor molecules. The local dynamic correlation of molecules observed here is crucial to a fundamental understanding of the origin of the physical properties of water, including viscosity. The results also suggest that the quantum-mechanical nature of hydrogen bonds could influence its dynamics. The approach used here offers a powerful experimental method for investigating real-space dynamics of liquids.

INTRODUCTION

The importance of water, H₂O, in our daily life and biological activity in general is beyond doubt. Water is also widely known as an atypical liquid because of its highly complex and anomalous behaviors in thermodynamic, structural, and transport properties, such as the high freezing/melting points and the maximum in density at 4°C (1–5). These anomalous properties of water are considered to be caused in large part by strongly directional hydrogen bonds (H-bonds). However, the nature of H-bonds remains elusive (6, 7), and how it affects the structure and collective dynamics of water molecules is unclear. Whereas the snapshot of atomic structure (the same-time atomic correlation function) is known through extensive studies by x-ray and neutron diffraction measurements (8–13), with a large variety of model waters [extended simple point charge (SPC/E), transferable intermolecular potential with three points (TIP3P), TIP4P, etc.] proposed to account for the experimental diffraction data (14), much less has been known about the real-space dynamics, surprisingly even for normal water. How water molecules move in the liquid state is actually a mystery, although elucidating its dynamics on a molecular level is the key to a fundamental understanding of the properties of water.

In crystalline solids, atomic and molecular dynamics is well described in terms of phonons. However, in liquids, short-wave phonons are strongly scattered and localized. Whereas acoustic phonons (15–19) and fast dynamics—such as intramolecular vibrations (20, 21)—in water have been widely studied by inelastic neutron scattering (INS), inelastic x-ray scattering, (IXS), and optical spectroscopy, local molecular dynamics—such as the H-bond lifetime and dynamic correlations—remains much less explored. Here, we report the first direct experimental observation of real-space, real-time motions of water molecules through the Van Hove function (VHF) determined by IXS measurement and show that they are directly tied to the origin of viscosity in water.

RESULTS

The VHF (22), g(r, t), describes the probability for an atom at the origin r = 0 at time t = 0 to find another atom at distance r and at time t and is given by

$$\mathit{g}(\mathit{r},\mathit{t})=\frac{1}{4\mathrm{\pi }\mathrm{\rho }\mathit{N}{\mathit{r}}^2}{\displaystyle \sum _{\mathit{i},\mathit{j}}}\mathrm{\delta }(\mathit{r}-|{\mathbf{r}}_{\mathit{i}}(0)-{\mathbf{r}}_{\mathit{j}}(\mathit{t})|)$$ (1)

where ρ is the average number density of atoms, N is the number of atoms in the system, and r_i(t) is the position of the ith atom at time t. It can be obtained by double Fourier transformation (FT) of the dynamic structure function, S(Q, E), over Q and E, where Q is the momentum transfer and E = ħω is the energy transfer in scattering, which can be determined by IXS or INS [see the Supplementary Materials for the definition of S(Q, E)]. Until recently, both IXS and INS measurements have been time-consuming, and it has been difficult to obtain S(Q, E) over a wide range of Q and E. For this reason, there is only one previous example of experimentally determining the VHF by INS with approximation for some simple metal liquids (23). However, with marked advances in the INS and IXS instrumentation (24, 25), it is becoming much more feasible. Here, we chose IXS, rather than INS, to probe the molecular dynamics of water, because hydrogen is nearly invisible to x-rays.

Although a large number of IXS measurements with synchrotron sources have already been reported for the study of water dynamics, most of them have focused on acoustic phonons (18, 19), observed in the Q range below 1 Å⁻¹, and real-space dynamics of water has never been directly probed. To extract real-space information, we carried out IXS measurements to determine S(Q, E) over wide ranges in Q (1.3 Å⁻¹ ≤ Q ≤ 9.5 Å⁻¹) and E (−10 meV ≤ E ≤ 100 meV) at ambient temperature (298 K). The energy resolution was 1.6 meV with the incident energy of 21.747 KeV. The measurement time required for the entire spectra was about 1 week. Details of the measurement are given in Methods. A related study was also performed earlier for water (26, 27) to determine the linear response function for a point charge, as discussed in the Supplementary Materials.

Figure 1 shows a two-dimensional (2D) plot of S(Q, E) for liquid water determined by IXS. It is evident that S(Q, E) is totally dominated by diffuse quasi-elastic scattering below 5 meV, and phonons (27 meV at Q = 1.3 Å⁻¹) (18) are invisible in this intensity scale. For this reason, we use smooth extrapolation for the portion of S(Q, E) below Q = 1.3 Å⁻¹, which includes phonons but contribute only weakly to g(r, t) at large r (>5 Å) upon FT. The measured S(Q, E) contains information about the dynamics of liquid water for picoseconds in time scale and up to 10 Å in length scale. The characteristic energies for intramolecular motion, such as OH stretching (420 meV) and HO bend vibration (200 meV), are out of this range, so that these intramolecular motions are not taken into account in our IXS experiment.

Fig. 1. Dynamic structure function, S(Q, E), for liquid water at ambient condition.

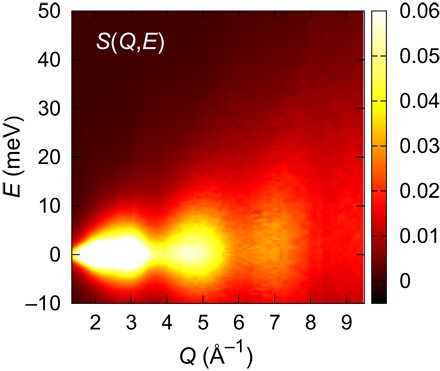
2D plot of the spectra obtained through the high-resolution (ΔE = 1.6 meV) IXS measurement.

The VHF can be obtained by double FT of S(Q, E) over Q and E (= ħω)

$$\mathit{g}(\mathit{r},\mathit{t})-1=\frac{1}{2\mathrm{\rho }{\mathrm{\pi }}^2\mathit{r}}{\displaystyle \int }\mathit{d}\mathit{Q}{\displaystyle \int }\mathit{d}\mathit{E} \text{exp}(\mathit{i}\mathrm{\omega }\mathit{t}) \text{sin}(\mathit{Q}\mathit{r}) \mathit{Q} \mathit{S}(\mathit{Q},\mathit{E})$$ (2)

The details of the procedure are presented in the Supplementary Materials. The results for g(r, t) are shown in Fig. 2. The VHF, g(r, t), consists of two parts: The first is the self-part up to 1.5 Å with the sharp peak around r = 0 that represents a single atomic self-motion, and the other is the distinct part that represents collective motions of two different atoms. The self-part suffers from strong termination noise, but the distinct part is much more noise-free, because termination noise is quickly reduced as r is increased (28). The VHF obtained by IXS mainly describes the correlation between oxygen ions, because hydrogens are much less visible to x-rays. The VHF at t = 0, g(r, 0), gives g(r), the snapshot pair distribution function (PDF). The PDF obtained here is in good agreement with the known PDFs obtained by x-ray diffraction (9–13), except for noise below 2 Å and small differences due to the limited ranges of Q and E in the current measurement.

Fig. 2. The VHF of liquid water determined by IXS.

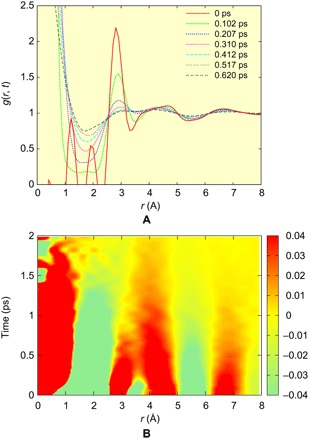
(A) g(r, t) at different times, and (B) 2D plot of g(r,t) – 1 for the IXS data. To show small changes in the second and third peaks, we used a narrow range (±0.04).

As shown in Fig. 2A, the distinct part of g(r, t) evolves toward unity with time as expected. Figure 2B shows a 2D plot of the measured g(r, t) – 1 for liquid H₂O. Surprisingly, we can see that as time is increased, the first peak (at 2.8 Å at t = 0) and the second peak (4 to 5 Å at t = 0) merge. This interesting behavior is in strong contrast to the case of metallic liquid (23), shown in fig. S4, for which g(r, t) decays monotonically and the peak positions remain largely unchanged with time, just as the behavior of the third peak in Fig. 2. In metallic liquids, the local coordination number (the number of nearest neighbors) is large (N_C ~12), because the structure of metallic liquids is governed by the principle of local packing (29). Thus, the local coordination number fluctuates greatly with time, and bond cutting and forming are not correlated in time and space (30). By contrast, water is highly covalent through H-bonds, and its coordination number is small (N_C ~ 4) (8–13). Consequently, the first and second neighbors of the VHF are dynamically coupled as seen in Fig. 2B, possibly because as soon as a molecule loses its neighbor, it is replaced by a second neighbor moving in to become the nearest neighbor. It is also possible that this dynamics reflects local fluctuations into the low-density water (LDW) (13, 31, 32), because the position of the second peak at t = 0 is close to that of LDW and is rather different from that of the high-density water (33). We plot the peak positions for the first and second peaks in Fig. 3A. The peak heights, g₁(t) − 1 and g₂(t) − 1, are shown in Fig. 3 (B and C). As shown in Fig. 3A, the two peaks merge around τ_MIX = 0.8 ps. This time scale is comparable with the earlier estimate of the structural relaxation time (6, 34). The height of the first peak decays much faster than the second peak, possibly corresponding to the short time scale observed by ultrafast spectroscopy (6).

Fig. 3. Peak position and intensity of the VHF.

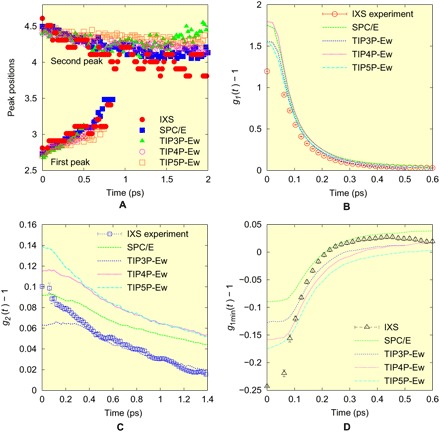
(A) The time evolution of the positions of the first and second peaks of the VHF, (B) the height of the first peak, g₁(t) − 1, (C) that of the second peak, g₂(t) − 1, and (D) that of the first minimum, g_1min(t) − 1, for the IXS experiment and for various models.

We compared the g(r, t) obtained by IXS with those obtained by atomistic simulations for various water models (SPC/E, TIP3P, TIP4P, and TIP5P), as discussed in Methods. The simulation results of g(r, t) are displayed in Fig. 4 (A and B) only for SPC/E as an example, and others are shown in the Supplementary Materials. It is found that the patterns of g(r, t) obtained by simulation qualitatively agree with the experimental result. Especially, the time dependence of the peak positions by simulation agrees reasonably well with those of the experimental result, as shown in Fig. 3A.

Fig. 4. Simulation of the VHF.

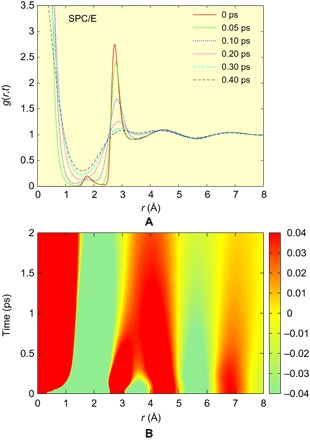
(A) g(r, t) at different times, and (B) 2D plot of g(r,t) – 1, both for the SPC/E model.

However, looking more closely, we find some differences. The peak heights for various models are shown in Fig. 3 (B and C). Note that only the portion beyond 0.1 ps can be meaningfully compared, because the experimental data of S(Q, E) were obtained only up to 9.5 Å⁻¹_, and significant termination effects are seen at time shorter than 0.1 ps, as discussed in the Supplementary Materials in detail. If we compare the time evolution of g(r, t) at the first peak, then the measured peak height is lower than that of the models and decays slightly faster than the simulation (Fig. 3B). For the second peak, TIP3P-Ew (Ewald) shows good agreement for t > 0.3 ps, but others overestimate the peak height. In addition, the models significantly underestimate the depth of the minimum between the first and second peaks corresponding to the interstitial site, g_1min(t) − 1, shown in Fig. 3D, although a part of this could be the termination effect. It is possible that this depth is also affected by fluctuations toward LDW (13, 31, 32). The experiment and models also disagree at long time, t > 0.4 ps. These comparisons suggest that the models cannot accurately describe the distribution of the lifetime of an H-bond, most probably because the quantum effect on the H-bond is not incorporated in the classical models. However, at the moment, accurate quantum-mechanical calculation of the dynamics of the H-bond, for instance by the quantum Monte-Carlo method, is beyond reach.

As discussed earlier, the dynamics of the first and the second peaks are strongly coupled. It appears that when an H-bond of the central molecule is broken, the second neighbor oxygen moves closer to form a new H-bond, as indicated in Figs. 2B, 3A, and 4B. This exchange of neighbors directly affects molecular transport. In the earlier simulation work on liquid metals, we found that the Maxwell relaxation time, τ_M = η/G_∞, where η is the viscosity and G_∞ is the instantaneous shear modulus, is equal to τ_LC, the time for an atom or a molecule to lose or gain one neighbor, above the viscosity crossover temperature T_A (30). For water, T_A ~ 60°C (35), so it is expected that the equality τ_M = τ_LC should hold approximately at room temperature. Although the fluctuations toward LDW set in below 60°C (13, 31, 32), these structural changes should have minimal effects on the equality. By inspecting the simulation results, we found that τ_MIX = 2τ_LC for all models, as shown in Fig. 5 (see the Supplementary Materials for more discussion). From this relationship, we obtain the average lifetime of the H-bond, τ_LC = 0.4 ps. Thus, the earlier attempts to determine the bond lifetime (6, 34) overestimate its value. Apparently, their results correspond to τ_MIX rather than τ_LC. The determination of τ_M is slightly problematic because of relaxation (see the Supplementary Materials), but the best estimate is τ_M ~ 0.34 ps at room temperature (298 K) (35, 36), which is close to τ_LC. The similarity of τ_LC and τ_M observed here is in strong support for our earlier finding that the topological excitations in the atomic connectivity are the origin of viscosity (30). In addition, the observation that the equality, τ_M = τ_LC, applies for two so vastly disparate liquids, water and metallic liquids, implies wide generality of this equality.

Fig. 5. The relationship between τ_LC and τ_MIX for several models.

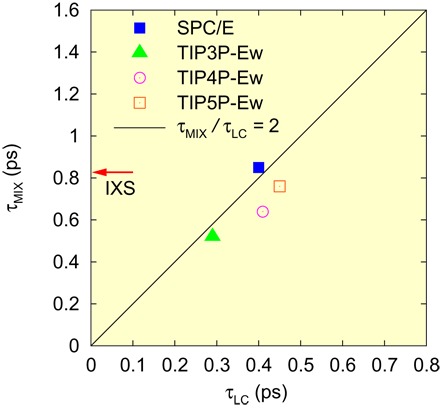
The line represents a linear line with a slope of two. The red arrow shows τ_MIX determined by IXS.

DISCUSSION

Here, we have determined the VHF of liquid water from the high-resolution IXS measurement over a wide range of momentum and energy transfer and succeeded in observing real-space, real-time motion of water molecules in the liquid state. We found that the evolution of the first and second nearest neighbors is strongly coupled to each other in space and time and showed that this local dynamics determines the viscosity and molecular transport. Although the simulation results largely agree with the measured VHF, there are some significant disagreements in detail, which suggest that classical models may not be fully capable of describing the quantum effects of the H-bond. Our new findings shed light on the microscopic mechanism in the real-space dynamics of liquid water and also provide an important reference point for dynamical modeling. The success of the method demonstrated here suggests that the VHF analysis is a powerful tool for the study of local dynamics in liquid in general.

METHODS

Experimental methods

The experiments on liquid water under ambient conditions (T = 298 K) were performed on the high-resolution IXS beamline (BL35XU) (37) at the SPring-8 facility. The incoming x-ray beam was monochromatized by backscattering using the Si (11 11 11) reflection. The energy of the incident beam was 21.747 keV, the Bragg angle was about 89.98°, and scattered x-ray was detected by an array of 12 backscattering Si-analyzers at the end of the 10-m horizontal arm. The spectrometer energy resolution was about 1.6 meV, and the Q resolution was set to be about 0.14 Å⁻¹. Liquid H₂O at room temperature was placed between two identical single-crystal diamond windows (5 mm × 5 mm × 0.3 mm). The sample thickness was 2 mm. The measurement was made by scanning energy at a fixed scattering angle, and data were collected over a wide range of Q and E (1.3 Å⁻¹ ≤ Q ≤ 9.5 Å⁻¹ and −10 meV ≤ E ≤ 100 meV).

Data reduction

The measured raw data, I_raw(Q, E), were corrected for various factors, such as background, sample absorption, multiscattering effects, efficiency of the analyzer and detector, and contribution from the container. The sample thickness of 2 mm was narrow enough to reduce sample absorption and multiple-scattering effects, and the absorption factor can be calculated as exp[−μl(θ)], where μ is the absorption coefficient for H₂O and l(θ) is a path length calculated in our setup. Phonon contributions from the diamond window were removed. In addition, the scattering spectrum with larger negative energy transfer was constructed through the principle of detailed balance, ${\mathit{I}}_{\text{raw}}(\mathit{Q},-\mathit{E})={\mathit{I}}_{\text{raw}}(\mathit{Q},\mathit{E}){\mathit{e}}^{-\mathit{E}/{\mathit{k}}_{\mathrm{B}}\mathit{T}}$, where 0 meV ≤ E ≤ 100 meV. Moreover, the corrected data had to be normalized to absolute intensity. Here, the scattering spectrum on absolute scale was given simply by $\mathit{I}(\mathit{Q}\mathit{E})={\mathit{I}}_{\mathit{X}}(\mathit{Q})\times \frac{{\mathit{I}}_{\text{raw}}(\mathit{Q},\mathit{E})}{{\displaystyle \int }\mathit{d}\mathit{E}{\mathit{I}}_{\text{raw}}(\mathit{Q},\mathit{E})}$, where I_X(Q) was the accurate x-ray diffraction data on liquid water measured by Hura et al. (9) and normalized to the molecular form factor. Then, the data were corrected for the efficiency of each analyzer. The dynamic structure function is given by S(Q, E) = I(Q, E)/〈F(Q)〉², where 〈F(Q)〉 is the molecular form factor for H₂O (38).

Molecular dynamics simulation

Molecular dynamics simulations for various water models were performed to make a comparison with the experimental data. Four typical water models, SPC/E, TIP3P-Ew, TIP4P-Ew, and TIP5P-Ew, were simulated in a cubic box with periodic boundary conditions. The temperature and pressure were fixed to be 300 K and zero under the NPT ensemble. The number of molecules N was 36,000 for SPC/E and 8640 for other models. In a simple ionic picture, all electrons are on oxygen ions, and protons are invisible to x-ray. However, in reality, protons were also weakly screened by electrons (12). We used the simplest picture (39) and assigned 1:3 electron to hydrogen in calculating the total VHF. Details of simulations are given in the Supplementary Materials.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/12/e1603079/DC1

section S1. Procedure of obtaining the VHF from the dynamic structure function.

section S2. The VHF of a simple liquid metal.

section S3. VHF of various models for ambient liquid water.

section S4. VHF and the Green function.

section S5. Effects of truncation over Q and E on VHF.

section S6. Local configurational excitations of liquid water.

section S7. Hydrogen dynamics.

fig. S1. Dynamic structure function S(Q, E) for liquid water at ambient condition.

fig. S2. Intermediate scattering function F(Q, t) for liquid water at ambient condition.

fig. S3. The low-Q part of F(Q, t).

fig. S4. The VHF, g(r, t) – 1, of liquid iron at 2500 K by simulation.

fig. S5. The calculated VHF for various water models.

fig. S6. 2D plot of g(r, t) – 1 for water models at 300 K.

fig. S7. The effect of a limited maximum Q in the Fourier transform of S_sim(Q, E) on the PDF g(r).

fig. S8. The effect of a limited maximum Q in the FT of F(Q, t) on the g(r, t).

fig. S9. The effect of a limited maximum Q in the Fourier transform of F(Q, t).

fig. S10. Comparison of the total and O-O VHF for the SPC/E model.

fig. S11. Correlation between τ_LC and τ_MIX for various models.

References (40–49)