Interactions between visual working memory representations

Abstract

We investigated whether the representations of different objects are maintained independently in working memory or interact with each other. Observers were shown two sequentially presented orientations and required to reproduce each orientation after a delay. The sequential presentation minimized perceptual interactions so that we could isolate interactions between memory representations per se. We found that similar orientations were repelled from each other whereas dissimilar orientations were attracted to each other. In addition, when one of the items was given greater attentional priority by means of a cue, the representation of the high-priority item was not influenced very much by the orientation of the low-priority item, but the representation of the low-priority item was strongly influenced by the orientation of the high-priority item. This indicates that attention modulates the interactions between working memory representations. In addition, errors in the reported orientations of the two objects were positively correlated under some conditions, suggesting that representations of distinct objects may become grouped together in memory. Together, these results demonstrate that WM representations are not independent but instead interact with each other in a manner that depends on attentional priority.

Introduction

An implicit assumption in many models of visual working memory (WM) is that items are represented as independent units that do not directly interact with each other (Alvarez & Cavanagh, 2004; Bays, Catalao, & Husain, 2009; Bays & Husain, 2008; Cowan, 2001; Fougnie, Suchow, & Alvarez, 2012; Luck & Vogel, 1997; van den Berg, Shin, Chou, George, & Ma, 2012; Wilken & Ma, 2004; Zhang & Luck, 2008). In other words, once the objects have been stored in WM, the specific information stored in one representation will have no effect on the other representations.

However, there are several reasons to doubt this assumption. First, the visual system tends to relate individual objects to each other using simple Gestalt rules (Kuboby & Pomerantz, 1981; Palmer, 1999). Indeed, there is ample evidence that perceptual grouping affects observers’ performance on WM tasks (Clevenger & Hummel, 2013; Jiang, Olson, & Chun, 2000; Woodman, Vecera, & Luck, 2003; Xu, 2006; Xu & Chun, 2007). Second, studies have found that interitem similarity improves observers’ performance on WM tasks (Jiang, Lee, Asaad, & Remington, 2016; Kahana & Sekuler. 2002; Lin & Luck, 2009; Sims, Jacobs, & Knill, 2012; Swan & Wyble, 2014; Viswanathan, Perl, Visscher, Kahana, & Sekuler, 2010). Third, recent studies have found evidence that WM contains group-level information – such as statistical summary information – along with item-level information (Brady & Alvarez, 2011; 2015; Orhan & Jacobs, 2012). Fourth, WM representations are vulnerable to inference from other simultaneously stored information (Huang & Sekuler, 2010; Radenmaker, Bloem, Weerd, & Sack, 2015; Oberauer & Lin, 2017). Together, these findings question the common assumption of independence and suggest that individual items might interact in WM.

However, these studies do not provide unambiguous evidence for interactions between WM representations. In particular, the interactions observed in most of these studies may have occurred during perception rather than reflecting interactions between WM representations per se. In other words, when multiple items are presented simultaneously, this might lead to distortions of perception or the extraction of summary properties, which are then carried forward into WM (e.g., Brady & Alvarez, 2011; 2015; Clevenger & Hummel, 2013; Orhan & Jacobs, 2013; Jiang, Olson, & Chun, 2000; Woodman, Vecera, & Luck, 2003; Xu, 2006; Xu & Chun, 2007; but see Huang & Sekuler, 2010; Kang & Choi, 2015; Rademaker et al., 2015). Little is known about whether and how visual WM representations interact with each other after the information has been encoded into WM. This is an important question for understanding the nature of the representations. For example, some neural network models of visual WM involve recurrent excitation and lateral inhibition, and these models predict that items with similar feature values will repel each other (Johnson, Spencer, Luck, & Schöner, 2009; Wei, Wang, & Wang, 2012). To test these models, it is necessary to examine interactions between the memory representations themselves, unconfounded by interactions that might change the perceptual representations prior to WM encoding.

Another issue is that many previous studies utilized non-circular visual feature dimensions (e.g., size, spatial frequency) that are prone to “edge effects” (Brady & Alvarez, 2011; Huang & Sekuler, 2010; Orhan & Jacobs, 2013; Wilken & Ma, 2004). Observers may avoid reporting extreme values (e.g., minimum or maximum sizes), and this could artificially produce the appearance of a bias toward the mean feature value.

In addition, some studies have focused on a narrow range of differences between feature values. For instance, Rademaker et al. (2015) studied distractor interference effects for orientation differences between a target and a distractor within a ±45° range, and Orhan and Jacobs (2013) used an even narrower ±15° range of orientation differences. Observers may learn the range of stimulus differences and adjust their reports accordingly, which could create a bias toward the mean of the learned stimulus range. For example, if participants learned that the orientation difference was always smaller than X° in the previous trials, then they may avoid reporting orientation difference larger than X° in the current trial. Indeed, a previous study hints that this is a possible scenario: Huang and Sekuler (2010) showed that WM reports of spatial frequency on a given trial are influenced by the average spatial frequency of the previous trials.

Here, the present study sought to investigate interactions between WM representations, overcoming some of the limitations of prior research. To focus on interactions between the WM representations themselves, and not perceptual interactions, we presented two orientated objects sequentially and examined the memory for each orientation (see Figure 1a). Specifically, we sought to find evidence that the second item influences the representation of the first item, because such an effect cannot be explained by a change in the perceptual encoding of the first item and must reflect a change in the memory itself. In addition, to investigate interitem interactions on a trial-by-trial basis, we assessed whether errors in the reports of the two items are correlated with each other. Moreover, because orientation is a circular dimension, and we used the entire range of possible orientations, our design minimized edge effects and stimulus range effects.

Figure 1.

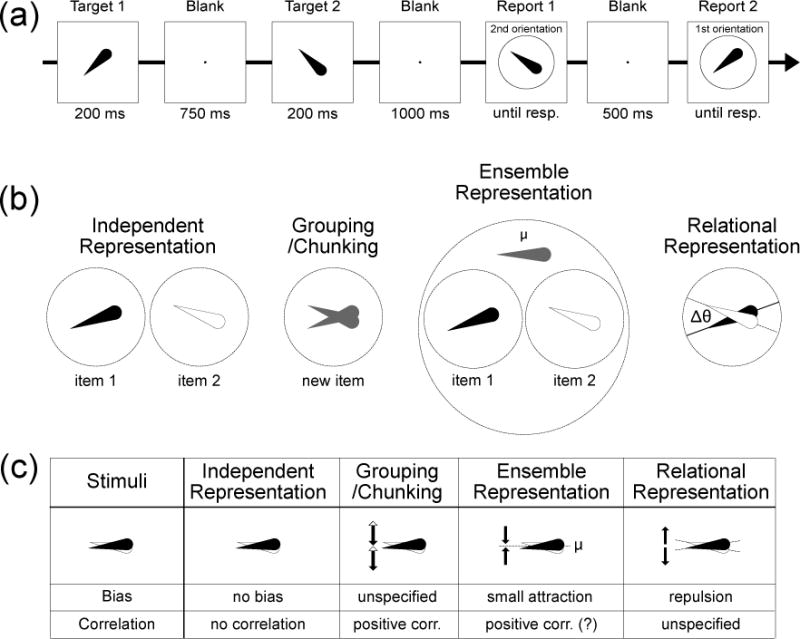
(a) Example of a single trial in Experiment 1. Observers remembered two serially presented target orientations and reproduced each orientation in a cued order. The second target is reported first in this example, but the order of report varied unpredictably across trials. (b) Four alternative models of the interactions between orientation memories. (c) Predictions of each model for the bias and correlation of the two orientation reports for a small difference in orientation between the two items being remembered. The independent representation models predict no bias or correlation in the memories. The grouping/chunking models predict that any noise in the memory of the group on a given trial will lead to errors in the same direction for both items, producing a positive correlation. The ensemble representation models predict that reports of the two items will be biased toward the mean of the two items and that the two reports will be positively correlated (because any noise in the mean will impact both reports in the same way). The relational representation models predict that nearby orientations will repel each other and that orientations differences near 180° will attract each other.

The present study took advantage of the fact that the perception and WM storage of orientation is strongly impacted by categorical boundaries (Huttenlocher, Hedges, & Duncan, 1991; Gibson & Rander, 1937; Girshick, Landy, & Simoncelli, 2011; Pratte, Park, Rosanne, & Tong, 2017; Wei & Stocker, 2015). Specifically, when individual orientations are perceived and remembered, their representations are repelled away from the cardinal axes (the 3 o’clock, 6 o’clock, 9 o’clock, and 12 o’clock positions on a clock face). For example, an orientation that is slightly clockwise from straight upward will be repelled away from the 12 o’clock position and be perceived and remembered as being farther clockwise from this axis than it actually was¹. We hypothesized that similar repulsion effects would be present for the relative orientations of two items that are stored in WM. For example, if the first item is at the 2 o’clock orientation and the second item is slightly clockwise from the first item, the representations of the two items will be repelled away from each other, causing the first item to be remembered as being counterclockwise from its original orientation and the second item to be remembered as being clockwise from its original orientation. Such an effect would indicate that WM representations are not independent but instead are coded relationally.

We contrasted this relational representation model with several other classes of models, which are illustrated in Figure 1b. These hypotheses differ from each other in terms of whether they predict repulsion or attraction between similar orientations (or neither), which we term the bias in the representations. They also differ in terms of whether the error in the observer’s report of one item should be correlated with the direction and magnitude of the error in the observer’s error of the other item (which can be directly assessed in this paradigm because both orientations are reported on every trial). The predictions of the different models are shown in Figure 1c.

The first model shown in Figure 1 is the independent representations model, which assumes that the two orientations are represented completely independently. This is what many current models of WM implicitly assume (Alvarez & Cavanagh, 2004; Bays et al., 2009; Bays & Husain, 2008; Cowan, 2001; Fougnie et al., 2012; Luck & Vogel, 1997; van den Berg et al., 2012; Wilken & Ma, 2004; Zhang & Luck, 2008). This model predicts no systematic bias in the representations (no repulsion or attraction) and no correlation between the errors of the two reports on a given trial.

The second class of models (grouping/chunking models) assume that the two orientations will be merged together into a single complex representation. This model makes no specific predictions about bias (repulsion or attraction), but it makes the strong prediction that any error in the report of one item will be positively correlated with the error in the other orientation. For example, if the memory of the grouped representation happens to drift clockwise on a given trial, then both of the individual items will be reported as being clockwise relative to their actual orientations on that trial.

The third class of models (ensemble representation models) posit that each item is represented individually, but that observers also store higher order ensemble information such as the mean of the feature values (Brady & Alvarez, 2011; Orhan & Jacobs, 2013; Sims, Jacobs, & Knill, 2012). At the time of report, the ensemble is used as a hierarchical Bayesian prior that constrains the conversion of the individual item representations into the actual reported values. A key prediction of these models is that the reported orientations of the two items should be shifted toward the mean of the two orientations (an attraction bias). Moreover, at least one of these models explicitly predicts that the amount of the attraction bias should be larger for “far” than “near” differences between the items being remembered (Orhan & Jacobs, 2013). This model also explicitly predicts a positive correlation between the reported orientations because the memory representations of both of the individual orientations contribute to the ensemble representation, which then impacts both of the reported orientations (Orhan & Jacobs, 2013). However, it would be possible to design an ensemble model that predicts no correlation or a negative correlation.

Our relational representation model makes a different set of predictions from these other classes of models. This model posits that each orientation serves as a reference for representing the other item. Reference points typically lead to repulsion of nearby features (Dick & Hochstein, 1989; Fisher, 1968; Gibson & Radner, 1937; Howe & Purves, 2005; Pratte et al., 2017; Wei & Stocker, 2015), so the relational representational model predicts that the reports of the two orientations will be repelled from each other, but only when they are similar (e.g., < 90° apart). This is the opposite of the prediction made by the ensemble representation models. The relational representation model does not make any strong predictions about correlations between the reports of the two orientations on a given trial.

In comparing these four classes of models in the context of the present experimental paradigm, it is important to note that very different results might be obtained if the stimuli were presented simultaneously rather than sequentially. With simultaneous presentation, perceptual factors such as grouping and texture perception might cause important interactions between the stimuli that then carry over into WM. In addition, ensemble models were originally developed for situations in when large numbers of objects are present, in which case parameters such as the mean and variance are more relevant than they would be in the present paradigm, in which only two objects were presented. Thus, the findings of the present study are narrowly relevant for the question of how WM representations of a small number of objects interact with each other when there is no opportunity for direct interactions between the sensory inputs. However, this narrow question is quite important, because it is likely that the human visual system is frequently called upon to represent discrete objects that are viewed sequentially. For example, as gaze moves among the objects in a complex scene, items that are acquired in different fixations may be stored simultaneously in WM (see, e.g., Hollingworth & Luck, 2009; Hollingworth, Richard, & Luck, 2008).

The predictions from the four classes of models implicitly assume that the two items are influencing one another with equal strength. However, there are at least two kinds of asymmetries that might be expected. First, whichever item is presented first may influence the representation of the second item more than the second item influences the first item. Second, it is possible that attentional mechanisms could be allocated to a given item to protect it from distortion by the other item (Matsukura, Luck, & Vecera, 2007; Makovski & Pertzov, 2015; Heuer & Schubö, 2016). Experiments 2 and 3 of the present study examined this issue by experimentally manipulating the attentional priority of each item.

The four models make different predictions about the consequences of this attentional priority manipulation. The independent representation model predicts no effects of attentional priority on bias or correlation, although the priority might impact the precisions of the representations (Bays & Husain, 2008; Zokaei, Ning, Manohar, Feredoes, & Husain, 2014). The grouping model does not make any obvious predictions about the effects of attentional priority on bias, but prioritizing one item and deprioritizing the other could result in a weaker correlation between the reports of the two items. The ensemble representation models could reasonably be expected to predict that the lower-priority item should exhibit greater attraction bias than the higher-priority item under the assumption that the higher-priority item will be given more weight in the average (Albrecht & Scholl, 2010). In the context of the relational representation model, one might expect that the higher-priority orientation would serve as a reference point for the lower-priority orientation, leading to a greater bias in the representation of the lower-priority item.

The same predictions can be made for comparisons of the first-presented orientation and the second-presented orientation under the assumption that the first-presented orientation will receive higher priority than the second-presented orientation. This is a reasonable assumption for three reasons. First, the first item should have higher priority than the second item during the initial encoding for the simple reason that the first item has no competition at this time whereas the second item is competing with the memory of the first item. Second, the first item must be given a high priority during the maintenance period so that it is not overwritten by the presentation of the second item. Third, the first item must be maintained for longer than the second item, so it may be given higher priority to yield approximately equivalent performance for the two items at the time of test.

Experiment 1

To investigate interitem interactions in WM, we used the task shown in Figure 1a, in which observers remembered two sequentially presented orientations and reproduced the orientation value of each item after a delay. If the two orientations interact in WM, then the reported orientation of one item should systematically vary with the orientation of the other item in one of the ways illustrated in Figure 1c. In addition, we investigated whether the error in the report of one item on a given trial was correlated with the error in the report of the other item, which would provide evidence of grouping.

Method

Participants

Sixteen college students (9 female; age range 18–30 years) with normal or corrected-to-normal visual acuity participated for course credit after providing informed consent. This sample size was selected a priori on the basis of our experience with previous experiments using delayed estimation procedures. Because no previous research has examined the specific effects that were the focus of this study, there was no way to estimate the likely effect size and perform a formal power analysis. However, the primary effects reported for Experiment 1 were replicated in every experiment we have performed with this paradigm, all of which have used 16 participants, suggesting that this sample size yields adequate statistical power.

Stimuli & Procedure

Stimuli were presented on a Dell U2412M LCD monitor with a gray background (31.2 cd/m²) at a viewing distance of 70 cm. A black fixation dot was continuously present except during the intertrial interval. Two target stimuli were presented on each trial (see Figure 1a). Each target was a teardrop shape (3° long, 1° maximum width) presented at the center of the display. The orientation of a given target was selected with equal likelihood from 16 equally spaced values (separated by 22.5°, starting at 11.25° from upright). The orientations of the two targets on a given trial were independently chosen with the constraint that they were never identical. Thus, the orientation difference between the two targets could be ±22.5°, ±45°, ±67.5°, ±90°, ±112.5°, ±135°, ±157.5°, or 180°. The data from trials with a 180° orientation difference will not be considered for the bias analysis because attraction and repulsion are not defined for a 180° difference. However, we included these trials in the correlation analysis.

Each trial began with the fixation dot. After 500 ms, the first target was presented for 200 ms, followed by a 750 ms blank interval. The second target was then presented for 200 ms, followed by a 1000 ms blank interval. A response ring then appeared along with the text “1^st orientation” or “2^nd orientation” at the top of the screen, indicating which target the observer should report first. Observers reproduced the specified target orientation using a computer mouse. The mouse pointer started at the fixation point at the beginning of the response period. Once the mouse started moving, a teardrop shape appeared at an orientation that matched the current position of the mouse. The observer then adjusted the mouse position until the teardrop matched the memory of the target shape and then pressed the mouse button to finalize the report. After one target’s orientation was reported, there was a 500-ms gap and then a second response ring appeared along with an instruction to report the other target. The order of report was randomized.

After 16 practice trials, each participant completed 4 blocks of 64 trials in a single one-hour session.

Analysis

The analyses focused on response error, the angular difference between the actual target orientation and the reported orientation on each trial. To determine whether the response to one target was attracted toward or repelled from the other target, the sign of the response error for the target being reported at a given moment was coded relative to the orientation of the target that was not being reported at that moment. The response error was given a positive sign if the reported orientation was away from the orientation of the other target, and it was given a negative sign if the reported error was toward the orientation of the other target. For example, consider a trial in which Target 1 had an orientation of 90° and Target 2 had an orientation of 112.5°. If the observer reported an orientation of 89° for Target 1, this would be coded as a response error of +1° (because it was 1° away from the true orientation of Target 1, in the direction away from Target 2). If the observer reported an orientation of 110.5° for Target 2, this would be coded as a response error of −2° (because it was 2° away from the true orientation of Target 2, in the direction toward Target 1).

The data were collapsed for mirror-image orientation differences, and the 180° orientation difference was excluded, producing 7 different orientation differences (±22.5°, ±45°, ±67.5°, ±90°, ±112.5°, ±135°, and ±157.5°). For each of these orientation differences, we computed the circular mean of the response errors to estimate the central tendency. Response errors larger than ±22.5° were excluded as outliers that likely reflect trials on which the reported target was not present in memory or on which the two targets were swapped in memory (Bays, Catalao, & Husain, 2009). This exclusion criterion removed 12.9% of trials. We present the raw response error distributions in Supplementary Materials (Figure S1).

We also fit a mixture model that takes into account both random guesses (which may occur if the observer was momentarily distracted) and swapping errors (Bays, Catalao, & Husain, 2009). The μ parameter of this model corresponds to our mean response error variable, and it showed the same pattern of results. The results from the mixture model are presented in the Supplementary Materials.

Results

Biases

Figure 2 shows the mean response error as a function of the orientation difference between the two targets, separated by the order in which the targets were presented (Target 1 versus Target 2; Figure 2a) and by the order in which the targets were reported (Report 1 versus Report 2; Figure 2b). When the orientations of the two targets were less than 90° apart, the reported orientation for a given target was biased away from the orientation of the other target (repulsion, indicated by positive report errors). When the orientations were more than 90° apart, the reported orientation for a given target was biased toward the orientation of the other target (attraction, indicated by negative report errors). The magnitude of the repulsion bias decreased gradually with the similarity between the two orientations. The transition from repulsion to attraction occurred at an orientation difference of approximately 90°, which may reflect the fact that a 90° difference forms an easily categorizable angle.

Figure 2.

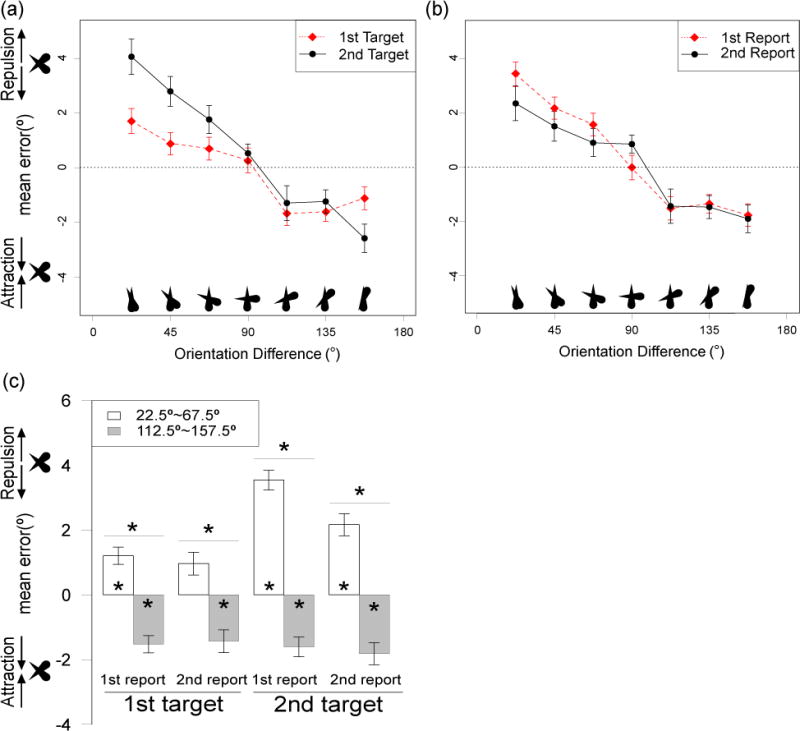
(a, b) Mean response error as a function of the orientation difference between the two items in Experiment 1. Data in a are plotted separately for the first and second targets on each trial, collapsed across order of report. Data in (b) are plotted separately for the first- and second-reported item on each trial, collapsed across the initial order of presentation. Dependent variable is the angular distance between reported orientation and actual orientation of the target being reported, reflected according to the direction of the other target. Positive error indicates bias away from the other target, and negative error represents bias toward the other target; the zero line indicates no bias. (c) Mean response error, collapsed into groups of trials with relatively small orientation differences (<90°) and groups of trials with relatively large orientation differences (>90°). Reported orientation of a given target was biased away from the orientation of the other target when the orientation difference was <90°, but biased toward the other item when the difference was >90°. This effect was larger for the second than for the first target, but was comparable for the first and second responses. Error bars show the within-subjects standard error of the mean (Morey, 2008). Asterisks over a pair of bars indicate significant difference between the means. Asterisks inside the bar indicate that the mean is significantly different from zero. *p < .05, FDR corrected

To simplify the statistical analysis, we collapsed the data into near orientations (orientation differences < 90°) and far orientations (orientation differences > 90° but excluding 180°). The collapsed values are shown in Figure 2d for each of the four combinations of presentation order and report order. The collapsed data were entered into a 3-way ANOVA with factors of orientation difference (near or far), presentation order (Target 1 or Target 2), and response order (Report 1 and Report 2). The finding of positive error values (repulsion) for near orientations and negative error values (attraction) for far orientations led to a significant main effect of orientation difference (F(1,15) = 73.08, p < .001, η_p² = 0.83). The repulsion was clearly stronger for the second target than for the first target, leading to a significant interaction between orientation difference and presentation order (F(1,15) = 8.83, p = .009, η_p² = 0.37). This effect was exaggerated when the second target was reported first, but neither the interaction between orientation difference and response order (F(1,15) = 2.15, p = .163, η_p² = 0.13) nor the three-way interaction was significant (F(1,15) < 1).

We conducted two sets of follow-up analyses, each using the false discovery rate (FDR) correction for multiple comparisons with an alpha level of 0.05 (Benjamini & Hochberg, 1995). The first analyses used paired t tests to compare the near and far orientations for each combination of presentation order and response order (see the four horizontal lines above each pair of bars in Figure 2c). A significant orientation difference effect was observed for all combinations. Thus, a difference in bias was observed between near and far orientations even for the first target when it was reported first; this is important because it shows that the second target changed the memory for the first target, which cannot be explained by an effect on perceptual encoding of the first target and must instead reflect a direct change in the working memory representation of this item. Experiments 2 and 3 will show that this effect is not produced by the mere presentation of the second target, but reflects the allocation of attention to this target. It is also important to note that substantial bias effects were observed for the first report (either of the first or the second target) and not just for the second report.

We also used FDR-corrected one-sample t tests to compare the bias to zero for each cell of the design (see asterisks inside the bars in Figure 2c). Significant attraction was observed at the far orientations for each case, and significant repulsion was observed at the near orientations for each case except when the first target was reported second.

Trial-by-Trial dependency

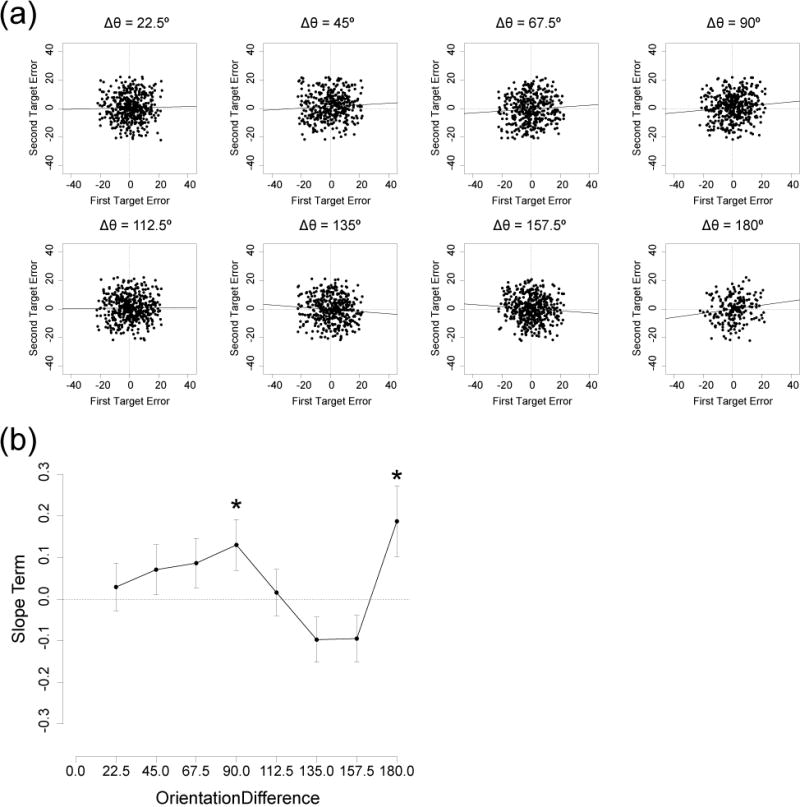
Figure 3a shows scatterplots of response errors for the first and second target on every trial for every observer, collapsed across order of report. These are raw error values (degrees from the true stimulus value), with positive values reflecting clockwise errors and negative values reflecting counterclockwise errors. Trials in which either response error was greater than 22.5° were excluded because these trials likely contained random guesses or swapping errors. We computed the slope of the relationship between the first- and second-report errors for each orientation difference using a linear mixed-effect model with observers as random effect (Faraway, 2016). None of the slopes was very large, but there was a systematic pattern of variation in slope across the orientation differences (Figure 3b). A significant positive slope (i.e., a significant positive correlation) was observed at the two cardinal orientation differences of 90° and 180° (Wald test, χ² (1) = 18.70, p < .001 and χ² (1) = 9.28, p < .01, respectively). A significant negative slope was observed at the two orientation differences that were closest to 0° and 180°, 22.5° and 157.5° (χ² (1) = 9.63, p < .01 and χ² (1) = 11.54, p < .01, respectively). All of these effects remained significant after FDR correction. These results show that the two reports were interdependent but that the direction of the dependency varied according to the particular relationship between the two orientations. A plausible explanation for this complex pattern of slopes is provided in the next section.

Figure 3.

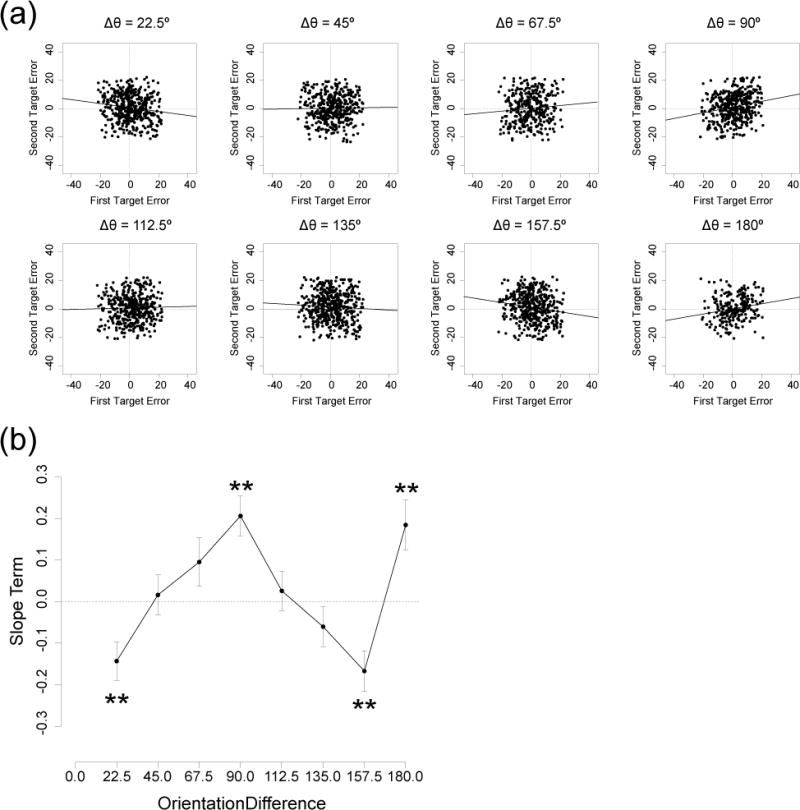
Trial-by-trial dependency between the two orientation reports in Experiment 1. (a) Scatterplots of response errors for the first (x-axis) and second (y-axis) targets on a given trial, with separate points for every trial in each observer, separated into the eight orientation differences. Trials with response errors larger than 22.5° were excluded to avoid contamination from random guesses and swapping errors. Solid line indicates maximum likelihood slope estimate from a linear mixed-effects model. (b) Slope term of the mixed-effects linear model obtained at each orientation difference. Error bars show standard error of each slope estimate. Asterisks indicate slopes that were significantly different from zero. **p < .01

Discussion

Experiment 1 provides two lines of evidence supporting the hypothesis that visual working memory representations interact with each other. First, the reported orientation of one target was biased by the orientation of the other target. Specifically, when the target orientations were similar, their working memory representations were repulsed away from each other, exaggerating the apparent differences between them. When the targets were highly dissimilar (e.g., > 90° apart), their working memory representations were attracted toward each other, reducing the apparent differences between them. Although the effects for the second target could be explained by a modulation of the perception of this item by the memory representation of the first target, the finding of repulsion/attraction biases for the first target cannot be explained in this manner, especially when it was reported first. However, the effects for the first target could reflect an influence of the perception of the second target (i.e., a memory-perception interaction). This possibility is further investigated in Experiment 3, in which the attentional priority for the two WM representations was manipulated after the stimuli were presented. Analogous effects have been reported in different task contexts (Gibson & Rander, 1937; Golomb, 2015; Kang & Choi, 2015; Marshak & Sekuler, 1979; Rauber & Treue, 1999). We discuss relationship between these studies and our results in the General Discussion.

The existence of these biases is incompatible with independent representation models, and the observed direction of the biases is opposite to the direction predicted by ensemble representation models. However, the repulsion bias observed for near orientation differences is consistent with the relational representation model. The relational representation model did not predict the attraction bias observed for far orientation differences. However, it is possible that these attraction effects are actually a result of repulsion between the sharp end of one teardrop and the rounded end of the other teardrop, which are quite close when the orientation difference between the two teardrops approaches 180°². Additional research would be needed to assess this explanation of the attraction effects. Nonetheless, the present findings provide evidence that WM is influenced by relational information.

A second source of evidence for interactions between WM representations was the finding that trial-by-trial variation in the report error for one target was associated with variation in the report error for the other target. The reports were positively related when the orientation differences were 90° and 180°, and they were negatively related when the orientation differences were 22.5° and 157.5°. As will be described later, the positive correlations observed at the 90° and 180° orientation differences were replicated in Experiments 2 and 3, but the negative correlations at the 22.5° and 157.5° orientations were not. We will therefore not speculate about the causes of the negative correlations and will instead focus on the positive correlations observed when the two items differed by 90° or 180°. For these angles, we speculate that it was easy for the observers to combine the two items into a single group (a right angle or a straight line). When the items were grouped in this manner, any variation in the representation of one of the two items would have carried over to the representation of the other item, producing the observed positive correlation. However, it is important to note that the magnitude of the observed correlations was small, suggesting that the grouping was weak or occurred on only a small fraction of trials.

Overall, Experiment 1 provides strong evidence that WM representations themselves interact in a manner that depends on the similarity of the items being represented. The pattern of observed biases and correlations are consistent with the relational representation model, with the addition of grouping/chunking when the two orientations form a clearly categorizable relationship. This is discussed in more detail in the General Discussion.

Experiment 2

In Experiment 1, the first target exhibited smaller bias effects than the second target. One possible explanation for this is a simple primacy effect: The first item on a trial may have a more stable representation than later items. However, an alternative explanation is that the first item receives greater attentional priority than the second item (for the simple reason that the first target can be encoded in WM without any competition from simultaneous WM representations). In other words, representations with higher attentional priority may be relatively protected from the biasing effects of representations with lower attentional priority, and representations with lower attentional priority may be more prone to exhibit attraction toward or repulsion from the higher-priority representation. Experiment 2 tested this hypothesis by using precues to manipulate the attentional priority of each item.

Specifically, a precue (a “1” or “2”) was presented at the beginning of the trial to indicate which of the two upcoming orientations should be given higher priority for that trial. We predicted that cued item would have a relatively strong impact on reported orientation of the uncued item, and the uncued item would have a relatively weak impact on report of the cued item.

Method

The methods were identical to those of Experiment 1, except as noted here. A new group of 16 college students (6 female; age range 18–30 years) participated for course credit after providing informed consent.

The procedure is illustrated in Figure 4a. Each trial started with a digit (either “1” or “2” with equal probability) presented at the center of the screen for 200 ms, indicating which item should be prioritized on that trial. After a 750 ms blank, the two orientations were presented serially with a duration of 200 ms and a 750-ms gap between them. After another 1000-ms blank, the observer was serially cued to reproduce each of the two orientations.

Figure 4.

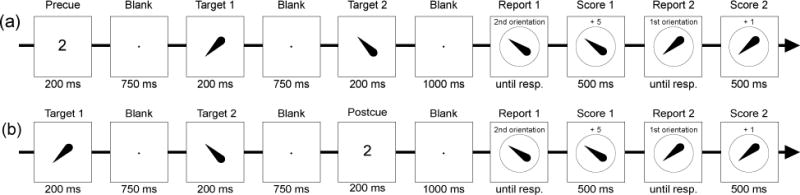
(a) Example of a single trial in Experiment 2. Each trial began with a precue indicating which of the two upcoming orientations should be prioritized. The two targets were then presented, followed by report of the two orientations. The cued orientation was always reported first. Observers received 5 points for an accurate report of the cued item and 1 point for an accurate report of the uncued item. In this example, the second target is cued and reported first. (b) Example of a single trial in Experiment 3. This experiment was identical to Experiment 2 except that the precue was replaced with a postcue that was presented after the second target.

Two methods were combined to motivate observers to give greater attentional priority to the cued target. First, the observer received 5 points for an accurate response (error ≦ 10°) to the cued target and only 1 point for an accurate response to the uncued target. Each response was followed by a 500-ms feedback screen showing the number of points received for that response. Second, the cued target was always reported first. This also had the advantage of reducing the total number of cells in the experimental design, thereby increasing the number of trials per cell. Note that Experiment 1 demonstrated that the order of report has little or no impact on performance (see Figure 2b), so the fact that the cued item was always reported before the uncued item should not have given the cued item any advantage (except insofar as this motivated participants to assign greater attentional priority to the cued item).

Results

Biases

Figure 5a shows mean response error as a function of the orientation difference between the two targets, separated by the order of target presentation (Target 1 versus Target 2) but collapsed across cued and uncued items. The results replicated the main finding of Experiment 1: When the two targets differed by less than 90°, the reported orientation for a given target was biased away from the orientation of the other target. However, when the orientation difference was larger than 90°, the reported orientation was biased toward the orientation of the other target. As in Experiment 1, this effect was larger for the second target than for the first target.

Figure 5.

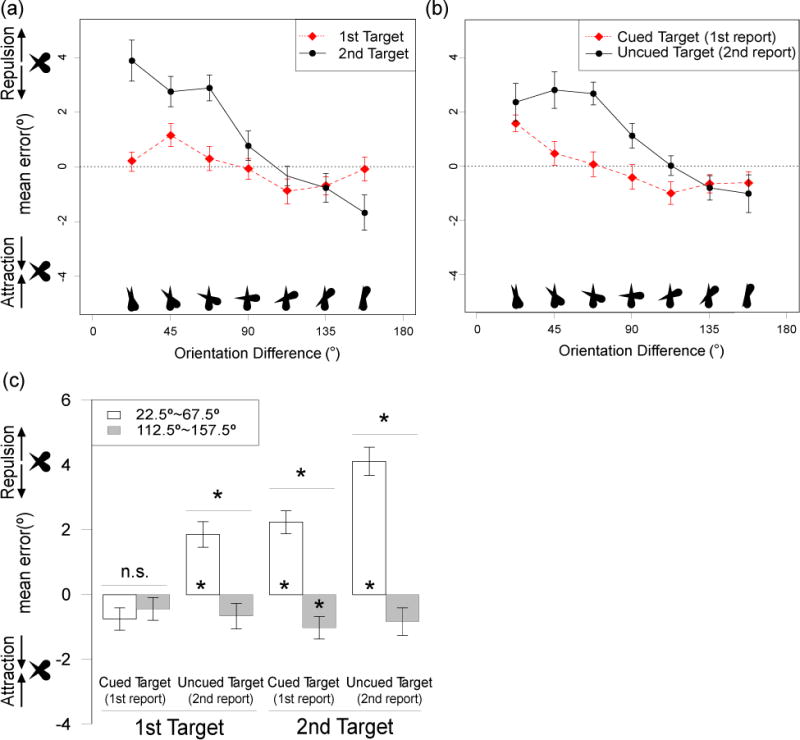
(a–b) Mean response error as a function of the orientation difference between the two items. Data in a are separated for the first and second targets on each trial, collapsed across which item was cued (and therefore collapsed across order of report). Data in (b) are separated according to which item was cued (and therefore reported first), collapsed across order of presentation. Positive error indicates bias away from the other target, and negative error represents bias toward the other target; the zero line indicates no bias. (c) Mean response error, collapsed into trials with relatively small orientation differences (<90°) and trials with relatively large orientation differences (>90°). Reported orientation of the reported target was biased away from the orientation of the other target when the orientation difference was <90°, but biased toward the other item when the difference was >90°. These repulsion and attraction effects were larger for the uncued target than for the cued target. Error bars show the within-subjects standard error of the mean (Morey, 2008). Asterisks over a pair of bars indicate significant difference between the means. Asterisks inside the bar indicate that the mean is significantly different from zero. *p < .05, FDR corrected

Figure 5b shows the data separated as a function of cuing (cued target vs uncued target), collapsed across order of presentation. The reported orientation of the uncued target was strongly biased away from the orientation of the cued target when the orientation difference was less than 90°. In contrast, the reported orientation of the cued target was only weakly biased away from the orientation of the uncued target, except for the 22.5° orientation difference, where the degree of repulsion was nearly as great for the cued item as for the uncued item.

As in Experiment 1, the orientation differences were collapsed into near orientations (orientation difference < 90°) and far orientations (orientation difference > 90°) for statistical analysis. The collapsed data (Figure 5c) were entered into a 3-way ANOVA with orientation difference (near versus far) and presentation order (Target 1 versus Target 2) as within-subject factors and precue condition (cued versus uncued) as a between-subject factor. The finding of a repulsion bias for the near orientations and an attraction bias for the far orientations led to a significant main effect of orientation difference (F(1,15) = 35.11, p < .001, η_p² = 0.70). The stronger repulsion/attraction bias for the second target led to a significant interaction between orientation difference and presentation order (F(1,15) = 9.50, p = .008, η_p² = 0.39). These findings replicated the results of Experiment 1.

The key new finding was that the repulsion/attraction effects were smaller for the cued target than for the uncued target, leading to a significant interaction between orientation difference and precue condition (F(1,15) = 7.49, p = .015, η_p² = 0.33). This interaction indicates that increased attentional priority protects a representation from being influenced by other representations, whereas decreased attentional priority makes a representation more prone to influence by other representations. The magnitude of this precue effect was comparable for Target 1 and Target 2, and the three-way interaction was not significant (F(1,15) = 1.63, p = 0.22).

To ensure that the interaction between orientation difference and cue condition was not merely due to the fact that the precued orientation was always reported first, we compared this experiment to Experiment 1, in which no cue was used. If the precue effect was solely a result of the order of report, then the effect of order of report in Experiment 1 should have been identical to the effect of cuing in the present experiment. However, the effects of cuing in Experiment 2 were very different from the effects of report order in Experiment 1 (compare Figures 2b and 5b). This was confirmed statistically with a separate 3-way ANOVA with factors of orientation difference (near versus far), report order/cuing (Report 1:precued versus Report 2:non-precued), and experiment (Experiment 1 versus 2), which yielded a significant three-way interaction (F(1,30) = 8.67, p = .006, η_p² = 0.22). This shows that the greater effect of orientation difference on uncued trials compared to cued trials in the present experiment was a result of attentional priority and not merely due to the fact that the cued item was always reported first and the uncued item was always reported second.

Follow-up analyses of the data from the present experiment tested the effect of orientation difference (near versus far) for each combination of presentation and cuing condition using FDR-corrected paired t-tests (see the four horizontal lines above each pair of bars in Figure 5c). No significant effect of orientation difference was observed for the first target when it was cued, indicating that the representation of the first target was protected from bias when it was the cued item. However, a significant effect was observed for the first target when it was uncued, which demonstrates that the representation of an object can be biased by an object presented later in time if the second object is given higher attentional priority. This provides very strong evidence that WM representations per se can be biased by the similarity between them, even when the effects cannot have occurred during perception. Significant effects of orientation difference were observed for the second target whether or not it was cued (although the effect was larger when it was uncued). Thus, the representation of a high-priority object can be influenced by a low-priority object under some conditions.

We also tested the repulsion and attraction effects separately for each cell of the design using FDR-corrected one sample t-tests (see asterisks inside each bar in Figure 5c). Significant repulsion effects were observed for the near orientations in every case except the first target when it was cued. Although there was a tendency toward an attraction bias in all four far orientation conditions, it was significant only for the second target when it was cued.

Trial-by-trial dependency

We analyzed the dependency between the two target reports on each trial, as in Experiment 1. Given that each trial contained one cued item and one uncued item, there was no way to analyze the effects of cuing on this dependency. We performed this analysis solely to assess the replicability of the effects observed in Experiment 1.

Figure 6a shows scatterplots of response errors for the first and second target on a given trial, collapsed across cuing condition, for all observers. Trial-by-trial dependency was analyzed via a linear mixed-effect model as in Experiment 1. Figure 6b shows the maximum likelihood estimate of the slope for each orientation difference. Significant positive slopes were obtained for orientation differences of 90° (χ²(1) = 4.57, p < .05) and 180° (χ²(1) = 4.88, p < .05), just as in Experiment 1. These two effects did not survive FDR correction for multiple comparisons, but such a correction is not essential given that this is a replication.

Figure 6.

Trial-by-trial dependency between the two orientation reports in Experiment 2. (a) Scatterplots of response errors for the first target (x-axis) and the second target (y-axis) on a given trial, with a separate point for every trial in each observer, separated in the eight orientation differences. Trials with a response error larger than 22.5° were excluded to avoid contamination from random guesses and swapping errors. Solid line indicates maximum likelihood slope estimate from a linear mixed-effect model. (b) Slope term of the mixed-effect linear model obtained at each orientation difference. Error bars show the standard error of each slope estimate. Asterisks indicate slopes that were significantly different from zero. *p < .05

In Experiment 1, significant negative slopes were observed for the 22.5° and 157.5° orientation differences. In the present experiment, there was no evidence of a negative slope in the 22.5° condition and only a non-significant trend for a negative slope in the 157.5° condition. Thus, only the positive correlations for the 90° and 180° orientation differences were replicated across experiments.

Discussion

Experiment 2 replicated the finding from Experiment 1 that orientation representations are biased away from each other when the two orientations are similar but are biased toward each other when they are dissimilar (although the attraction for dissimilar orientations was weaker in this experiment than in Experiment 1). This supports the main conclusion of Experiment 1, namely that WM involves the use of relational representations.

In addition, Experiment 2 demonstrated that attention modulates the magnitude of the bias effect. The high-priority item produced a large repulsion of the representation of the low-priority item, and the low-priority item produced only a weak repulsion of the representation of the high-priority item. This indicates that increasing the attention devoted to a given representation can increase the stability of that representation and increase its repulsion of lower-priority representations. Indeed, mixture model analyses showed that precision was higher for the cued item than for the uncued item, even when controlling for the fact that the cued item was always tested first (see the Supplementary Materials). If the repulsion effects reflect the operation of lateral inhibition (Johnson et al., 2009; Wei et al., 2012), this result suggests that the lateral inhibition originating from a given representation depends on the amount of attention allocated to that object.

In addition, Experiment 2 replicated the positive trial-by-trial dependencies observed in Experiment 1 at orientations differences of 90° and 180°. This provides additional evidence that grouping/chunking of representations occurs when the items have a salient categorical relationship, even when one of the representations is given a higher attentional priority than the other. The negative dependencies observed in Experiment 1 at orientation differences of 22.5° and 157.5° were not significant in the present experiment. It is not clear whether these are bona fide effects that differ across experimental contexts, whether the effects are too weak to replicate, or whether the negative correlations observed in Experiment 1 were Type I errors.

Experiment 3

In Experiment 2, observers knew what attentional priority to assign to a given item before the item was presented, creating the possibility that attention could be operating during perceptual processing. The fact that the first target was impacted by the orientation of the second target when the second target was cued indicates that a WM representation can be biased by subsequently presented information. However, this bias in the representation of the first target could have been a result in an attention-related change in the perceptual encoding of the second target.

To demonstrate an even purer interaction between WM representations, Experiment 3 presented the attention-directing cues after both stimuli had already been encoded in WM. In other words, Experiment 3 used postcues rather than precues. We predicted that the postcues in this experiment would produce the same pattern of bias observed for the precues used in Experiment 2. Such a finding would indicate that changing the attentional priority of a representation that is already in WM can impact the degree of relational interaction between that representation and another WM representation, even when attention has absolutely no opportunity to influence perceptual processing.

Method

The methods were identical to those of Experiment 2, except as noted here. A new group of sixteen college students (9 female; age range from 18–30) participated for course credit after giving informed consent.

The procedure is illustrated in Figure 4b. At the beginning of each trial, the two targets were presented serially with a duration of 200 ms and a 750-ms gap between them. After another 750-ms blank, a digit (“1” or “2” with equal probability) was presented at the center of the screen for 200 ms, serving as a postcue that indicated which of the two previously presented orientations should be prioritized on that trial. After another 1000-ms blank, the observer was serially cued to reproduce each of the two orientations.

Results

Biases

Figure 7a shows mean response errors as a function of the orientation difference between the two targets, separated by the order of presentation (Target 1 versus Target 2) but collapsed across cuing conditions. The results again replicated the main finding of Experiment 1. When the two targets differed by less than 90°, the reported orientation for a given target was biased away from the orientation of the other target. However, when the two targets differed by more than 90°, the reported orientation for a given target was biased toward the orientation of the other target. As in Experiments 1 and 2, this effect was larger for the second target than for the first target.

Figure 7.

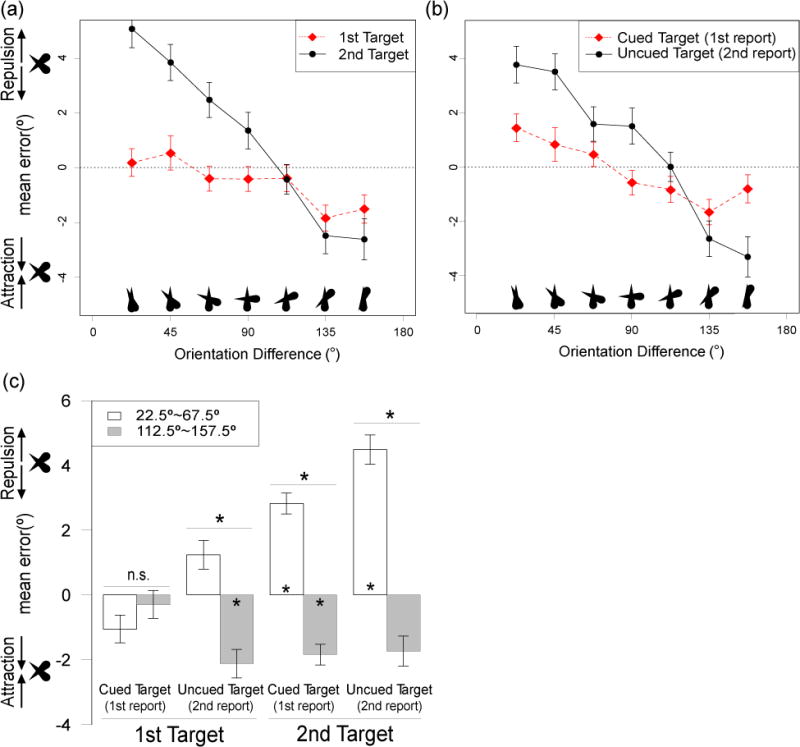
(a–b) Mean response error as a function of the orientation difference between the two items. Data in (a) are separated for the first and second targets on each trial, collapsed across which item was cued (and therefore collapsed across order of report). Data in (b) are separated according to which item was cued (and therefore reported first), collapsed across order of presentation. Positive error indicates bias away from the other target, and negative error represents bias toward the other target; the zero line indicates no bias. (c) Mean response error, collapsed into trials with relatively small orientation differences (<90°) and trials with relatively large orientation differences (>90°). Reported orientation of the reported target was biased away from the orientation of the other target when the orientation difference was <90°, but biased toward the other item when the difference was >90°. These repulsion and attraction effects were larger for the uncued than for the cued target. Error bars show the within-subjects standard error of the mean (Morey, 2008). Asterisks over a pair of bars indicate significant difference between the means. Asterisks inside the bar indicate that the mean is significantly different from zero. *p < .05, FDR corrected

Figure 7b shows the data separated as a function of cuing (cued target versus uncued target), collapsed across order of presentation. The pattern of postcue effects was qualitatively similar to the pattern of precued effects observed in Experiment 2. Specifically, the reported orientation of the uncued target was strongly biased away from the orientation of the cued target when the orientation difference was less than 90°, and this effect was much weaker for the cued target. In addition, attraction was observed for the largest orientation differences, and this effect was also stronger for reports of the uncued item than for reports of the cued item.

As in Experiments 1 and 2, orientation differences were collapsed into near orientations (orientation difference < 90°) and far orientations (orientation difference > 90°). The collapsed data (Figure 7c) were then entered into a 3-way ANOVA with orientation difference (near versus far) and presentation order (Target 1 versus Target 2) as within-subject factors and postcue condition (Cued versus Uncued) as a between-subject factor. The repulsion effect for the near condition and the attraction effect for the far condition led to a significant main effect of orientation difference (F(1,15) = 70.06, p < .001, η_p² = 0.82). The stronger repulsion/attraction bias for the second target led to a significant interaction between orientation difference and presentation order (F(1,15) = 30.50, p < .001, η_p² = 0.67).

The key result of Experiment 3 was that the weaker repulsion/attraction bias for the cued target led to a significant interaction between orientation difference and postcue condition (F(1,15) = 6.73, p = .02, η_p²¹ = 0.30). This interaction indicates that increasing the attentional priority of an internal WM representation protects that representations from being influenced by other simultaneously maintained WM representations, whereas decreasing the attentional priority makes a representation more prone to influence by other concurrent WM representations. The three-way interaction was not significant (F(1,15) = 4.11, p = .06, η_p² = 0.21). However, because the effect size was fairly large and the p value was close to .05, we cannot make a strong conclusion about the three-way interaction.

Follow up analyses tested the effect of orientation difference (near versus far) for each combination of presentation and report order using FDR-corrected paired t-tests (see the four horizontal lines above each pair of bars in Figure 7c). The effect of orientation difference was not significant for the first target when it was cued, indicating that the representation of the first target was protected from bias when it was given high attentional priority. However, a significant effect was observed for the first target when it was uncued and for the second target whether it was cued or uncued. Because the cue appeared after the two targets, these effects can be explained only by an effect of attention on the interaction between the WM representations, ruling out effects mediated by attention-related changes in target perception.

We also tested repulsion and attraction effects separately for each cell of the design using FDR-corrected one sample t-tests (see asterisks inside each bar in Figure 7c). Clear repulsion and attraction effects were visible for every cell except for the first target when it was cued, but the effects did not quite reach significance in each case.

The pattern of postcue effects in this experiment was qualitatively similar to the pattern of precue effects in Experiment 2 (compare Figures 5c and 7c), although the attraction effects were a little stronger in the present experiment and the repulsion effects were a little stronger in Experiment 2. To assess the differences between precue and postcue effects statistically, we repeated the main statistical analysis, but adding a between-subject factor of experiment (Experiment 2 versus Experiment 3) to the factors of orientation difference (near versus far), presentation order (Target 1 versus Target 2) and report order (Report 1: pre/postcued versus Report 2: non-pre/postcued). Consistent with the observation that the cuing effects were similar across experiments, we found no significant interactions involving the experiment factor (F < 1 for each relevant interaction term). Although it is impossible to prove that there were no subtle differences between the precue and postcue effects, the combination of a lack of an interaction with experiment in this statistical analysis and the presence of the same pattern of significant within-experiment effects for the two experiments provides strong evidence that precues and postcues produced qualitatively similar effects.

We also compared the results of the present experiment to Experiment 1 so that we could demonstrate that the interaction between orientation difference and postcue condition in the present experiment was not merely due to the fact that the postcued target was always reported first. If the postcue effect was a result of order of report, a similar effect should have been observed in Experiment 1. However, a 3-way ANOVA with orientation difference (near versus far) and report order (Report 1:postcued and Report 2:non-postcued) as within-subject factors and experiment (Experiment 1 and 3) as a between-subject factor showed a significant three-way interaction (F(1,30) = 5.99, p = .021, η_p² = 0.17). This shows that the cuing effect in the present experiment was not merely due to the fact that the cued item was always reported first.

Trial-by-trial dependency

To assess the replicability of the trial-by-trial dependency effects observed in Experiments 1 and 2, we analyzed these effects for the present experiment.

Figure 8a shows scatterplots of response errors for the first and the second target on a given trial, collapsed across cuing condition, for all observers. Trial-by-trial dependency was analyzed via a mixed-effect model, as in Experiments 1 and 2. Figure 8b shows the maximum likelihood estimate of the slope for each orientation difference. Significant positive slopes were obtained for orientation differences of 90° (χ²(1) = 17.48, p < .01) and 180° (χ²(1) = 9.62, p < .01), just as in Experiments 1 and 2. A significant positive slope was also observed for the 45° condition in the present experiment (χ²(1) = 16.91, p < .01), but this was not observed in Experiment 1 or Experiment 2.

Figure 8.

Trial-by-trial dependency between the two orientation reports in Experiment 3. (a) Scatterplots of response errors for the first (x-axis) and second (y-axis) targets on a given trial, with separate points for every trial in each observer, separated into the eight orientation differences. Trials with response errors larger than 22.5° were excluded to avoid contamination from random guesses and swapping errors. Solid line indicates maximum likelihood slope estimate from a linear mixed-effects model. (b) Slope term of the mixed-effects linear model obtained at each orientation difference. Error bars show standard error of each slope estimate. Asterisks indicate slopes that were significantly different from zero. **p < .01

A significant negative slope was obtained for the 157.5° orientation difference (χ²(1) = 11.11, p < .01); a negative slope was also observed for this condition in Experiments 1 and 2, although it did not reach significance for Experiment 2. There was no hint of a negative slope for the 22.5° condition in the present experiment; this slope was significant in Experiment 1 but was near zero in Experiment 2. Note that all of the significant slopes in the present experiment remained significant after FDR correction.

When the trial-by-trial dependency effects are examined across experiments, there was consistent evidence of positive dependencies at the 90° and 180° orientation differences, along with fairly consistent evidence of a negative dependency at the 157.5° orientation difference. None of the other orientation differences showed clear effects in more than one experiment.

Discussion

Experiment 3 again demonstrated that individual representations in working memory systematically interact with each other, consistent with relational representation models of WM. Specifically, as in Experiments 1 and 2, similar orientations exhibited repulsion and dissimilar orientations exhibited attraction. In addition, positive trial-by-trial dependencies were again observed for the 90° and 180° orientation differences, consistent with the hypothesis that grouping/chunking of representations occurs when the items have a salient categorical relationship.

Experiment 3 also replicated and extended the finding from Experiment 2 that WM interactions can be modulated by attentional priority, showing that these effects occur even when the priority is assigned by postcues after the perception of the target orientations. These results provide strong evidence that increasing the priority of a WM representation can make that representation more protected from bias and can increase the repulsion/attraction effects for lower-priority representations. To make this more concrete, consider a trial in which Target 1 and Target 2 are presented with similar orientations, followed by a postcue indicating that Target 2 should be given greater attentional priority. Even though both targets had already been stored in WM when the postcue appeared, the postcue led to a protection of the representation of Target 2 and an increase in the repulsion of the Target 1 representation away from the Target 2 orientation. In contrast, if Target 1 had been postcued, the Target 1 representation would have been protected, and the Target 2 representation would have exhibited greater repulsion away from the Target 1 orientation. Thus, this experiment demonstrates that attentional priority can influence interactions between WM representations per se, even when there is no opportunity for attention to impact perceptual processing.

We also tested whether attentional priority influenced the precision of the representations (see Supplementary Materials). Although the precision was higher for the postcued item than for the non-postcued item, this effect was not statistically distinguishable from simple response order effects. Thus, we did not find convincing evidence that postcues impact working memory precision.

General Discussion

Interactions Between Memory Representations

The present study sought to investigate how WM representations interact with each other. In three WM experiments, we presented two orientations sequentially to minimize the potential for perceptual interactions and focus on WM interactions. In all three experiments, we found that the representations of two orientations are systematically biased as a function of the similarity between them. When the two orientations were similar (i.e., < 90° apart), they were biased away from each other, but when they were dissimilar (i.e., > 90° apart), they were biased toward each other. Importantly, this bias effect could not be explained solely by perceptual interactions because the bias was observed for both the first and second orientations in the sequence. The present study also investigated the impact of attention on the interactions between the representations. Experiment 2 used a precue to manipulate the attentional priority of each orientation prior to stimulus encoding. Experiment 3 used a postcue to manipulate attentional priority after encoding and during WM maintenance. In both experiments, we found that the representation of the high-priority item was not influenced very much by the orientation of the low-priority item, but the representation of the low-priority item was strongly influenced by the orientation of the high-priority item. This indicates that increased attention can protect a WM representation from being influenced by other WM representations and decreased attention leaves a WM representation vulnerable to influence by other representations. Together, these results provide strong evidence that WM representations interact with each other and demonstrate that attention can modulate this interaction.

Of the four classes of models described in the Introduction (see Figure 1), only the relational representation model provides a natural explanation of the attention dependent WM interaction observed in the present study. The relational representation model assumes that individual items are represented in relation to each other, with each item serving as a reference for the other items. Just as perceptual representations are often biased away from reference points (Huttenlocher et al., 1991; Gibson & Rander, 1937; Pratte, Park, Rosanne, & Tong, 2017; Wei & Stocker, 2015), this model proposes that WM representations can be biased away from each other. Moreover, an attended item will be given greater weight as a reference point, so that it is not strongly biased but can more strongly bias lower-priority representations. This model does not directly predict the attraction effects we observed for dissimilar orientations but, as discussed earlier, this effect may reflect the repulsion of the narrow end of one teardrop away from the wide end of the other teardrop when these two ends are nearby.

A class of models that assume independent representations (Bays, et al, 2009; Bays & Husain, 2008; Fougnie et al., & Alvarez, 2012; Luck & Vogel, 1997; van den Berg et al., 2012; Zhang & Luck, 2008) clearly cannot explain the interactions observed in the present study, and grouping/chunking models also provide no obvious explanation. Existing ensemble-based models (Brady & Alvarez, 2011; Orhan & Jacobs, 2013) cannot account for these results because they predict that similar items will exhibit attraction, which is the opposite of what we observed. However, we note that the ensemble-based models were developed to explain cases in which large numbers of to-be-remembered items are presented simultaneously, as opposed to the sequential presentation of only two items used in the present study. Additional research is needed to determine whether and how ensemble-based representations might combine with the relational representations observed in the present study.

There are at least two subclasses of underlying mechanisms that could explain the repulsion effects observed for nearby orientations in the present study. One possibility is that WM representations exhibit lateral inhibition in feature space (Johnson et al., 2009; Wei et al., 2012). In other words, when an item is represented in WM, the neurons that represent that item send inhibitory connections to neurons that code similar orientations (which may be important for avoiding drift over time). When two nearby orientations are being represented, the excitatory representation of each item may fall partly within the zone of inhibition produced by the other item, leading the representations to shift away from each other in feature space. In this kind of explanation, the relationship between the feature values of the two items is not explicitly represented but affects the representations implicitly insofar as the two items are stored in a common set of neurons. A second possibility is that the relationship between the two feature values is explicitly coded, but in a categorical manner. For example, if an observer notes that the second item is clockwise relative to the first item (and the first item is therefore counterclockwise relative to the second item), this categorical knowledge may be combined with metric knowledge about the two orientations, leading to the first item being reported as more counterclockwise and the second item being reported as more clockwise than they actually were. Additional research will be needed to test these possibilities (which are not mutually exclusive).

Correlations Between Memory Representations

In addition to the attraction and repulsion effects, the present study found that trial-by-trial variations in the reports of the two orientations were correlated, but in a manner that varied as a function of the difference in orientation between the two items. None of the four classes of models completely predicted the observed pattern of trial-by-trial correlation. Grouping/chunking-based models and at least one version of the ensemble representation model predicted positive correlations, but the direction and magnitude of the correlation we observed varied with the difference between the two orientations. Some of this variation was inconsistent across the three experiments, but all three experiments showed a significant positive correlation when the two orientations differed by 90° or 180°. This may indicate that the WM representations of the two items became grouped only when they formed an easily categorizable pattern (i.e., a right angle or a straight line).

These correlations indicate that models of WM must combine relational representations with the ability to group items under some conditions. Note, however, that although the correlations were replicable for the 90° and 180° orientation differences, they were small in magnitude. This may indicate that the grouping was weak or occurred on a small proportion of trials.

Relationship With Other Tasks

It is important to ask how the present results are related to previous studies using other stimulus dimensions and other tasks. First, studies of motion perception have shown that representations of two motion directions are biased away from each other when the two motion directions are similar, a phenomenon called motion repulsion (Kang & Choi, 2015; Marshak & Sekuler, 1979; Rauber & Treue, 1999). In particular, using sequential presentation of two directions of motion, Kang and Choi (2015) found that the magnitude of motion repulsion was larger for the item retrieved later. They attributed this effect to retrieval processes, and did not assess interactions between the memory representations themselves. The present study demonstrates that interactions can also occur between the WM representations themselves in an attention-dependent manner, and this raises the possibility that the effects of retrieval observed by Kang and Choi were a result of the allocation of attention during the retrieval process.

Second, a study of selective attention found that the representation of a target color is biased either toward or away from a distractor color depending on the difference between them (Golomb, 2015). The direction of bias observed in the present study is consistent with this result, suggesting that these effects are general across stimulus dimensions. However, because Golomb (2015) used simultaneous presentation of multiple objects, it is difficult to draw strong conclusion about whether the observed effects in that study were purely driven by working memory interactions or were influenced by perceptual interactions.

Third, in the classic visual tilt illusion (Gibson & Rander, 1937), the perceived orientation of an object is attracted toward or repelled away from a reference orientation depending on the orientation difference. Again, this illusion consists of a perceptual interaction. Thus, in spite of several methodological differences, previous studies suggest that the general pattern observed in the present study can be generalized to other stimulus dimensions and other tasks.

Intriguingly, however, recent studies of serial dependence in perception have shown the opposite pattern of results. For example, Fischer and Whitney (2014) presented a series of orientations, each of which required an immediate response, and they found that the reported orientation of the current item was biased toward the orientation of the previous item, especially when the orientations were similar (analogous to what would be expected from ensemble-based WM models). Additional experiments would be needed to determine why the effects observed in the present paradigm were in the opposite direction. However, we speculate that the discrepancy may reflect the extent to which the task emphasizes the need to individuate the representations. In the study of Fischer and Whitney (2014), the task did not explicitly require more than one orientation to be maintained in memory, providing the observers with no reason to actively segregate the representation of the current orientation from the representation of the prior orientation. In contrast, our paradigm required participants to individuate two simultaneous representations, which may have encouraged the observers to actively contrast the two representations. Consistent with this proposal, Fritsche, Mostert, & de Lange (2017) showed that perceptual decisions about individual items lead to an attraction bias whereas perceptual comparisons lead to a repulsion bias. However, this is merely a speculation at this point.

Rademaker et al. (2015) found an attraction bias for small orientation differences, which is the opposite of the bias found in the present study. There are many differences between our study and Rademaker et al. (2015) which could potentially produce the discrepancy. Among several differences, we note that they used mixture model to quantify the direction and the magnitude of bias, but this model did not take into account the possibility that participants sometimes reported the other items (“swap errors” — see Bays et al., 2009), which would produce attraction-like bias effects. For this reason, it is difficult to know whether the attraction effect reported by Rademaker et al. (2015 – Experiment 3) truly reflected a shift in the representation.

The present results may also be helpful in explaining findings from tasks in which many items are presented simultaneously but only one item is reported (as in typical studies of visual working memory using delayed estimation tasks). In particular, the fact that the report of one item may vary systematically depending on its relationship to the other items stored in memory is a source of unexplained variance that will impact the distribution of error values if not explicitly modeled. For example, one influential model of visual WM storage assumes that the representational quality varies randomly from trial to trial as a result of attentional fluctuations (van den Berg et al., 2012), which provides an explanation for non-normalities in the shape of the error distribution. However, as pointed out in previous studies (Bae et al., 2014; 2015; Pratte et al., 2017), different stimulus values may be represented with different degrees of precision, and trial-by-trial variability in the specific feature values provides an alternative explanation of the non-normalities. In fact, when this stimulus-specific variability is taken into account, the data are better explained by a model that does not include trial-to-trial attentional fluctuations (Pratte et al., 2017). Here, the present study provides one more type of stimulus-specific variability— interitem interactions—that can impact the data and must be accounted for by models that attempt to explain the distribution of response errors (see also Brady & Alvarez, 2015).