Avoiding nerve stimulation in irreversible electroporation: a numerical modeling study

Abstract

Electroporation based treatments consist in applying one or multiple high voltage pulses to the tissues to be treated. As an undesired side effect, these pulses cause electrical stimulation of excitable tissues such as nerves and muscles. This increases the complexity of the treatments and may pose a risk to the patient. To minimize electrical stimulation during electroporation based treatments, it has been proposed to replace the commonly used monopolar pulses by bursts of short bipolar pulses. In the present study, we have numerically analyzed the rationale for such approach. We have compared different pulsing protocols in terms of their electroporation efficacy and their capability to trigger action potentials in nerves. For that, we have developed a modeling framework that combines numerical models of nerve fibers and experimental data on irreversible electroporation. Our results indicate that, by replacing the conventional relatively long monopolar pulses by bursts of short bipolar pulses, it is possible to ablate a large tissue region without triggering action potentials in a nearby nerve. Our models indicate that this is possible because, as the pulse length of these bipolar pulses is reduced, the stimulation thresholds raise faster than the irreversible electroporation thresholds. We propose that this different dependence on the pulse length is due to the fact that transmembrane charging for nerve fibers is much slower than that of cells treated by electroporation because of their geometrical differences.

1. Introduction

Electroporation is a biophysical phenomenon in which the cell membrane, when exposed to short, high electric field pulses, increases its permeability to ions and macromolecules. This effect can be either transient (reversible electroporation) or can result in cell death (irreversible electroporation) depending on the magnitude of the field, the duration of pulses, the number of pulses, and to a lesser extent, the pulse repetition frequency(Rols and Teissié 1990)(Silve et al 2014).

In vivo electroporation is the basis of multiple clinical treatment modalities. On the one hand, reversible electroporation is currently used in the treatment known as electrochemotherapy, in which electric pulses are applied to enhance the cellular uptake of a chemotherapeutic agent (Mir et al 1998, Gothelf et al 2003, Silve and Mir 2011), and it is also used for gene therapies as a transfection mechanism by facilitating the introduction of genes into the cytoplasm (Heller and Heller 2010, Bodles-Brakhop et al 2009). On the other hand, irreversible electroporation (IRE) is used as a non thermal ablation technique for treatment of solid tumors (Onik and Rubinsky 2010, Edd et al 2006, Jiang et al 2015), offering some advantages compared to other common ablation techniques.

Electroporation is considered to be a threshold-like phenomenon that depends on the cell transmembrane voltage (TMV) (Zimmermann et al 1974): the phenomenon takes place when the externally applied electric field induces a TMV higher than a certain threshold. This leads to an electric field magnitude threshold to achieve electroporation in tissues(Kotnik et al 2010, Ivorra 2010). In electroporation based treatments, treatment planning is performed under the assumption that all the cells exposed to an electric field higher than a certain value will experience the desired effect (either a reversible permeabilization level or cell death) (Zupanic et al 2012). The electric field threshold is estimated through experimental measurements and depends on the pulsing protocol (i.e. temporal features of the pulses) and the cells or tissues being treated.

In clinical applications, electroporation protocols usually consist in a series of monopolar pulses with a length in the order of 100 μs. For these pulses, the electric field thresholds to trigger action potentials in excitable cells are significantly lower than those for initiating electroporation. This implies that, in order to successfully perform electroporation, it is necessary to deliver high voltage pulses that can cause electrical stimulation of excitable tissues such as efferent and afferent nerves within the region of treatment or surrounding areas, even in distant regions, leading to muscle contractions and acute pain.

This electrical stimulation that appears as a side effect in electroporation based treatments may cause multiple clinical complications. Minimizing the risks associated to those complications leads to an increase in the complexity of the whole clinical procedure that may limit the applicability of electroporation based treatments because of the burden to benefit ratio or the risk to benefit ratio. First, to overcome acute pain, it is necessary to administer local anesthesia and, in some cases, it is even necessary to administer general anesthesia. Second, muscle contractions may displace the electrodes and change the outcome of the treatment by changing the distribution of the electric fields that are applied with respect to the prior planning. Furthermore, such electrode displacement may mechanically damage vital structures close to the region being treated. Therefore, sometimes it is necessary to administer muscle relaxants. Additionally, since the myocardium is a structure that contains excitable cells, the high currents that flow in the body during an electroporation based treatment may induce heart arrhythmias, including ventricular fibrillation.

Electrical stimulation has always been a concern among researchers and clinicians working in the field of electroporation (Arena and Davalos 2012). Fortunately, quite early it was identified a mechanism to prevent the risk of ventricular fibrillation: to synchronize the voltage pulses with the electrocardiogram signal to deliver the pulses when all myocardium cells are in the absolute refractory period (Okino et al 1992, Mali et al 2005). With the aim of reducing muscle contractions and acute pain, it has been proposed to confine the electric field the by placing a large number of electrodes surrounding the treated region (Golberg and Rubinsky 2012). This sort of approach, however, would be very challenging to implement in clinical settings, for instance, when treating deep seated tumors. Another sort of explored approach to minimize stimulation has consisted in modifying temporal features of the pulses. For instance, the use of bipolar pulses (Daskalov et al 1999) or the delivery of the electroporation pulses at different frequencies (Miklavčič et al 2005) were studied showing that electrical stimulation could be reduced.

Recently, a subset of the authors of the present study, has proposed a novel treatment protocol based on replacing the conventional 100 μs monopolar pulses by bursts of bipolar pulses with the same energized time and a short pulse length (1 or 2 μs) (Arena et al 2011). It has been demonstrated that this technique, coined “high-frequency irreversible electroporation” (H-FIRE), is able to successfully ablate regions of tissue while practically avoiding muscle contractions (Arena et al 2011, Siddiqui et al 2016). The promising results obtained in the first trials with the H-FIRE protocols led to a series of experiments to study the electroporation efficiency of high frequency bursts of bipolar pulses and their potential uses in clinical applications (Sano et al 2014, 2015, Sweeney et al 2016, Yao et al 2017).

The two main goals of the present study were: 1) to gain understanding on why bursts of bipolar pulses which are capable of inducing IRE do not cause neuromuscular stimulation and 2) to identify which pulsing protocols may be most suitable in order to minimize stimulation while maximizing IRE.

2. Materials and Methods

Figure 1.a illustrates the general scenario considered here: an electroporation treatment is delivered to tissue by applying high voltage pulses across two needle electrodes. Inside the tissue to be treated, or nearby, nerves and nerve terminations may be present.

Figure 1.

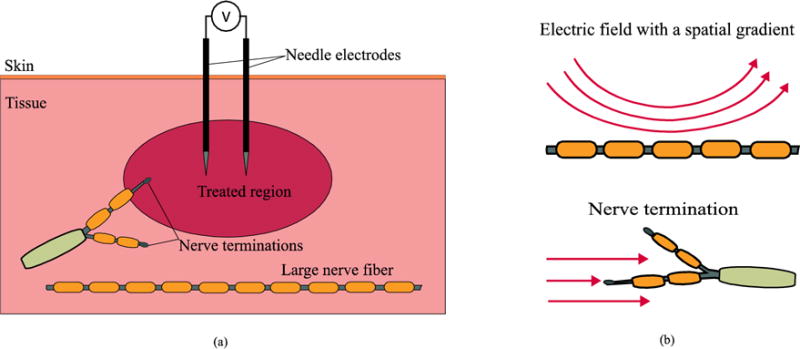
a) Schematic representation of the general electroporation scenario considered in the present study. b) Modeled excitation modes of a nerve.

Two nerve stimulation cases were modeled here (see figure 1.b): 1) a long nerve fiber propagating close to the treated region, and 2) a nerve termination close to the treated region. Under the assumption that the long nerve fiber corresponds to a motor neuron, the first case allowed comparison of different pulse protocols in terms of the maximum volume of tissue that can be ablated before an action potential is triggered in that nerve fiber and neuromuscular stimulation occurs. For performing such comparison, first it was modeled the response of a nerve fiber in the vicinity of the treated area to determine the maximum voltage across the needles that does not trigger an action potential. Then, this voltage was used to estimate the volume of tissue that could be ablated without initiating an action potential.

The second case would represent the activation of pain receptors (Reilly 1988). This case, unlike the long nerve fiber case, entails stimulation under the presence of a homogenous electric field. This scenario, despite not being strictly realizable (electric field will always present a spatial gradient in an electroporation clinical setup), is of interest to the present study as will be seen in the next sections.

2.1 Modeled Pulsing Protocols

In order to model the response of a nerve fiber or a nerve termination to different pulsing protocols, it was first modeled the electric potential distribution in tissue generated by two needle electrodes with a voltage difference between them. This was done using the physics simulation software platform COMSOL Multiphysics 4.4 (Stockholm, Sweden) which is based on the finite element method (FEM). The needle electrodes were modeled as cylinders with a 1 mm diameter and 1.5 cm of height at a separation of 1 cm between them. The tissue was modeled as a homogeneous conductive medium with an arbitrary conductivity of 1 S/m. The conductivity was arbitrarily set because, for the nerve fiber and nerve termination models, it is only relevant the voltage distribution in tissue and, since the medium is homogeneous, the conductivity value does not affect the voltage distribution. The dimensions of the simulation space were 10 cm × 10 cm × 10 cm and the complete model had 2581784 tetrahedral elements.

Voltage between the needles was arbitrarily set to 1 V and the electric potential at each point of the simulation space was computed through the steady state solution in the Electric currents mode of the AC/DC module of COMSOL (Stationary Study) using the linear system solver Pardiso.

The obtained voltage distribution was linearly scaled to assay the response of a nerve fiber to different voltage waveforms (figure 2) using the models described in the next section. For facilitating computation, the modeled pulses were not perfectly sharp; they included up and down linear ramps with a duration of 5% the pulse-length.

Figure 2.

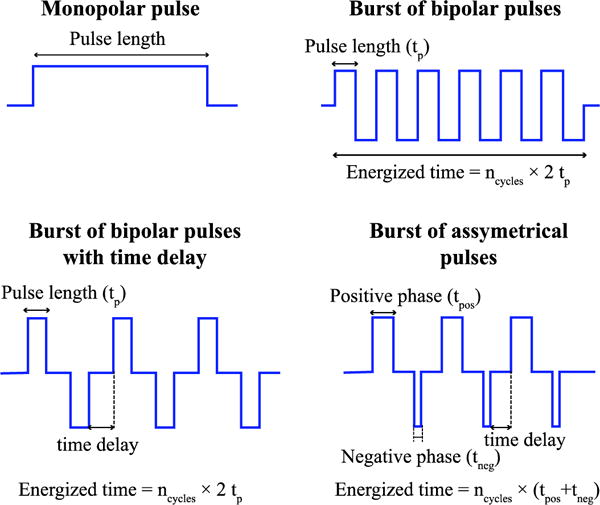
Waveforms considered in the present study.

2.2 Nerve fiber and nerve termination models

2.2.1 Nerve fiber model

The response of a nerve fiber to the voltage applied across the electrodes was determined using the cable model for a myelinated axon (McNeal 1976). Following this approach the TMV relative to the resting voltage (V_n =V_i,n − V_e,n − V_r) at the nth node of Ranvier can be calculated by solving the following equation:

$$\frac{d{V}_n}{dt}=\frac{1}{C_m}\left[G_a\left(V_{n-1}-2V_n+V_{n+1}+V_{e,n-1}-2V_{e,n}+V_{e,n+1}\right)-I_{i,n}\right]$$ (1)

where V_e,n is the extracellular voltage at each node, C_m is the membrane capacity, G_a is the axoplasmic conductance, and I_i,n is the ionic current across the membrane at each node. The ionic current was approximated as the sum of the current through 3 types of voltage gated ionic channels plus a leakage current as in (McIntyre et al 2002) (see Appendix A). Assuming that no axial current can exit at the end of the fiber (sealed end assumption) (Altman and Plonsey 1990, Reilly and Bauer 1987), the voltage at the extreme nodes is calculated as:

$$\frac{d{V}_1}{dt}=\frac{1}{C_m}\left[G_a\left(-V_1+V_2-V_{e,1}+V_{e,2}\right)-I_{i,1}\right]$$

$$\frac{d{V}_N}{dt}=\frac{1}{C_m}\left[G_a\left(-V_N+V_{N-1}-V_{e,N}+V_{e,N-1}\right)-I_{i,N}\right]$$ (2)

Equations (1) and (2) and the equations describing the evolution of the ionic currents were integrated by the implicit backward Euler method in MATLAB. The values of V_e, for each configuration were taken from the solution of the FEM model introduced in the previous section. Since the voltage at each point is proportional to the voltage difference between the needles, any voltage difference can be tested by multiplying the values extracted from the FEM model. The parameters used in the model are listed in table 1.

Table 1.

Parameters used in the nerve fiber model.

Symbol	Value	Definition, justification or source
ρa	70 Ω · cm	Axoplasmic resistivity, (Barrett and Crill 1974)
cm	2 μF/cm2	Nodal capacitance, (Frankenhaeuser and Huxley 1964)
L	1.15 mm	Internodal distance, (Berthold and Rydmark 1983)
G	1 μm	Nodal length, (Rydmark 1981)
D	10 μm	Fiber diameter
da	0.7 · D	Axon diameter, (Rydmark 1981)
dn	0.33 · D	Node diameter, (Rydmark 1981)
Cm	$c_m\pi d_n^{2}G$	Membrane capacity
Ga	$\frac{\pi d_a^2}{4{\rho }_{a}L}$	Membrane conductance
Vrest	−80 mV	Resting voltage

The position and orientation of the nerve fibers were chosen so as to maximize the second spatial derivative of the extracellular voltage as it has been identified that this value determines when stimulation occurs in the cable model of the nerve fiber (Rattay 1986). Two different locations were studied (see figure 3): first, a fiber parallel to the axis that joins the centers of the electrodes, placed at a small distance from them. Second, a fiber inside the plane containing the electrodes and at a small distance beneath the electrodes. These situations correspond to worst case scenarios as it is in these situations when lower excitation thresholds are expected for a given voltage amplitude across the electrodes.

Figure 3.

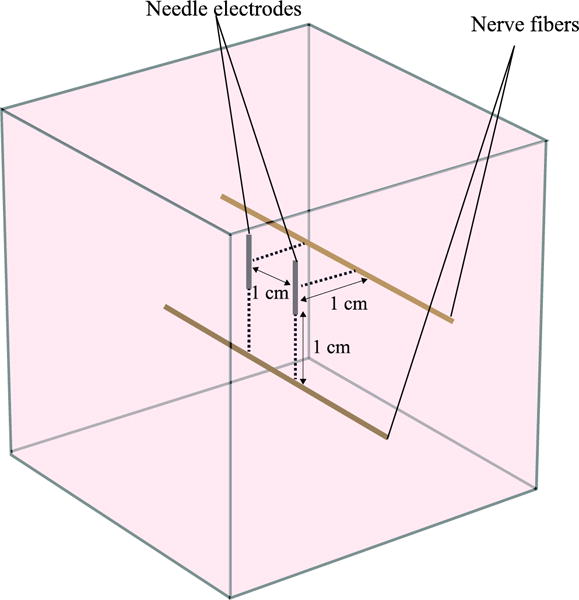
Model geometry used in the present study to simulate excitation of long nerve fibers (=myelinated axon). Two nerve fiber locations are analyzed: first, an axon parallel to the axis that joins the centers of the electrodes at a distance of 1 cm from them. Second, an axon inside the plane defined by the electrodes at a distance of 1 cm underneath them.

2.2.2 Nerve termination in a homogeneous electric field

To simulate the response of a nerve termination in a homogeneous field, it was modeled a terminated short fiber with only 6 nodes. By employing the following equation, it was modeled the case in which the nodes are equidistant and aligned in parallel the homogeneous electric field (Reilly 1988) :

$$V_{e,n}=V_{e,1}+\mathit{ELn}$$ (3)

where E is the electric field magnitude, L the distance between successive nodes and V_e,1 a reference voltage at the ending node. The value of voltage (V_e,1) has no impact on the response of the cable model and, for convenience, it was set to zero.

After defining the voltages in the nodes with the above equation, the procedure to determine the nerve termination response was the same as in the previous section. First, this voltage distribution was scaled to assay different field magnitudes and waveforms. Then, the same model, including the fiber parameters (see table 1), was used to model the ionic currents and the TMV. However, a smaller fiber diameter of 1 μm was defined in order to model sensory fibers, which have smaller diameters than motor fibers. Finally, the problem defined by equations (1), (2), and (3) was solved following the same methodology as in the previous section.

2.3 Determination of stimulation thresholds

The stimulation threshold for a given configuration was found through binary search until a maximum relative difference of 1% between a voltage that initiates an action potential and a voltage that does not was found. It was determined that an action potential had been triggered when the sodium current across the membrane showed a large and fast increase at in least one node. This increase was detected by monitoring the gating parameters that drive the fast sodium current, m and h (See appendix A).

The time step used to integrate the equations can have a significant influence in the stimulation threshold results, especially when simulating high-rate variation waveforms as is the case in the present study (Reilly 2016). To select the time step for each waveform type, simulations using the shortest pulse length were run and the time step was reduced until the relative difference on the excitation thresholds obtained in the subsequent simulations was negligible (taking into account that the search of the threshold is performed with a tolerance of a 1%). The largest time step that was found to provide stable results was 5 nanoseconds.

2.4 IRE model

Tissue ablation was modeled using experimental data from the in vitro experiments by Sano et al. (Sano et al 2015) (See table 2). In that study, measurements were performed in a 3D tumor mimic using PPT8182 murine primary pancreatic tumor cells. The treatments consisted on 120 bursts of bipolar pulses with an energized time of 100 μs a time delay of 2 μs and different pulse lengths.

Table 2.

IRE electric field threshold for a protocol consisting in 120 bursts with a total energized time of 100 μs and a time delay of 2 μs between pulses, as a function of pulse length, t_p. The data corresponds to measurements performed using PPT8182 murine primary pancreatic tumor cells in a tumor mimic (Sano et al 2015).

tp (μs)	EIRE (V/cm)
100	501
50	531
10	629
5	640
2	755
1	1070
0.5	1687
0.25	2022

For each configuration and pulse protocol, the voltage difference between the needles was set to the stimulation threshold and the electric field at each point of the simulation space was calculated through the FEM model introduced previously. To calculate the ablation volume, the volume of tissue exposed to an electric field above the IRE threshold was integrated using the volume integration tool of COMSOL.

3. Results

3.1 Long nerve fiber

For illustration and for validating our implementation of the cable model for a myelinated axon, we first compared stimulation when applying a single monopolar pulse and when applying a burst of bipolar pulses in a given geometry (figure 4.a). Figure 4.b shows the time courses of the TMV increase of the fiber at the node where an action potential is initiated when monopolar pulses and bursts of bipolar pulses are applied. It can be observed that, for the same voltage amplitude (100 V) and energized time (100 μs), a monopolar pulse easily triggers an action potential after about 70 μs whereas the equivalent burst of bipolar pulses is incapable of triggering an action potential as the membrane is charged and discharged repeatedly. Only after increasing the burst amplitude to 400 V it is possible to observe that an action potential is initiated. Figure 4.c displays the stimulation threshold results for the two types of waveforms. The stimulation thresholds in both cases follow a linear relationship with the pulse length in a log-log plot, which is consistent with neurostimulation literature (Reilly et al 1985, Boinagrov et al 2010, Dean and Lawrence 1985).

Figure 4.

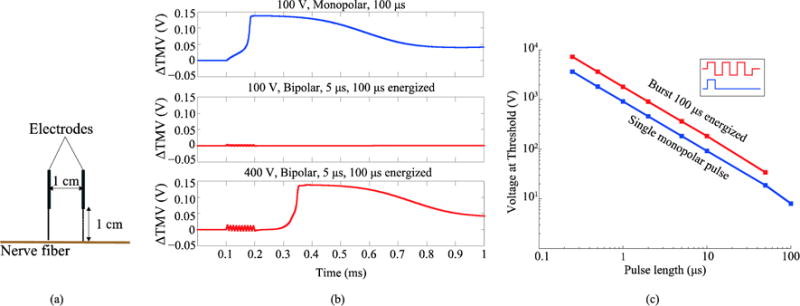
(a) Modeled geometry (b) Time evolution of the TMV increase with respect to the resting voltage when different pulses are delivered. Top, a 100 V monopolar pulse (starting at time = 0.1 ms) triggers an action potential. Middle, a burst of bipolar pulses with the same amplitude and energized time does not cause any response. Bottom, the same burst with a higher amplitude (400 V) triggers an action potential. (c) Minimum voltage amplitude across the electrodes able to trigger stimulation as a function of pulse length when a single monopolar pulse is applied and when a full burst of bipolar pulses with a 100 μs of total energized time is applied.

Note that the results in figure 4.c are presented as a function of the pulse length, meaning that a single monopolar pulse of a given pulse length is benchmarked against a full burst made up of bipolar pulses with that same pulse length reaching a total energized time of 100 μs. In other words, a single pulse is evaluated against a succession of equivalent positive and negative pulses that sum up a total energized time of 100 μs. The results show that the stimulation thresholds are significantly larger when a burst of bipolar pulses is applied compared to a single monopolar pulse. This occurs for all pulse lengths, even though at short pulse lengths the total energized time of the full burst is significantly longer than the duration of the monopolar pulse.

For the two axons locations and the electrode configurations in figure 2, figure 5.a shows the voltage stimulation thresholds when bursts of bipolar pulses with a 2 μs inter-pulse delay are delivered. The stimulation thresholds are presented as a function of the length of the pulses that make up the burst. In all cases the total energized time of the burst was set to 100 μs. The isolated points represent the stimulation thresholds for a conventional electroporation pulse (monopolar, 100 μs) and, unsurprisingly, deviate from the linear tendency that is seen for the rest of pulse lengths. In relative terms, the behavior of the stimulation thresholds does not depend significantly on whether the nerve fiber is beneath or beside the electrodes. Nevertheless, it is worth noting that the stimulation thresholds are lower when the nerve fiber is beside the electrodes.

Figure 5.

(a) Voltage stimulation thresholds versus pulse length for two different locations of the nerve fiber (see figure 2) when bursts of bipolar pulses with a total energized time of 100 μs and with a 2 μs inter-pulse delay are delivered. (b) For the same axon locations, simulated ablation volume that would be achieved by applying a voltage difference between the electrodes equal to the corresponding stimulation thresholds. (c) Voltage difference between the electrodes in order to produce a 2 cm³ ablation volume by means of IRE.

The stimulation thresholds in figure 5.a were used to estimate the maximum volume of tissue around the needles that could be ablated without initiating an action potential in the nerve fiber (figure 5.b). In both cases, the volume of tissue that theoretically could be ablated without stimulation greatly rises as the length of the pulses is shortened. As further explored in the next section and later discussed, this result can be explained as being the consequence of a steeper increase of the stimulation thresholds as the pulse length is reduced in comparison to the IRE thresholds increase. Indeed, it was computed the voltage necessary to produce a specific IRE ablation volume (2 cm³) using the bursts of bipolar pulses considered before (figure 5.c), and the voltage shows a significantly lower increase when the pulse length is reduced compared to the stimulation threshold voltages in figure 5.a.

3.2 Nerve termination

By modeling the response of the nerve termination under the action of a homogeneous electric field it is possible to directly benchmark IRE thresholds against stimulation thresholds for different pulsing protocols; for both phenomena it is possible to define an electric field magnitude threshold. Figure 6.a displays the simulated stimulation thresholds for the nerve termination and the experimental IRE thresholds from (Sano et al 2015) as a function of the pulse length. Nerve termination stimulation thresholds follow a linear relationship with pulse length in a log-log plot. IRE thresholds also exhibit a quite linear relationship with pulse length but, in this case, the slope is much more moderate. This result is aligned with the above observation: a steeper increase of the stimulation thresholds as the pulse length is reduced in comparison to the IRE thresholds increase.

Figure 6.

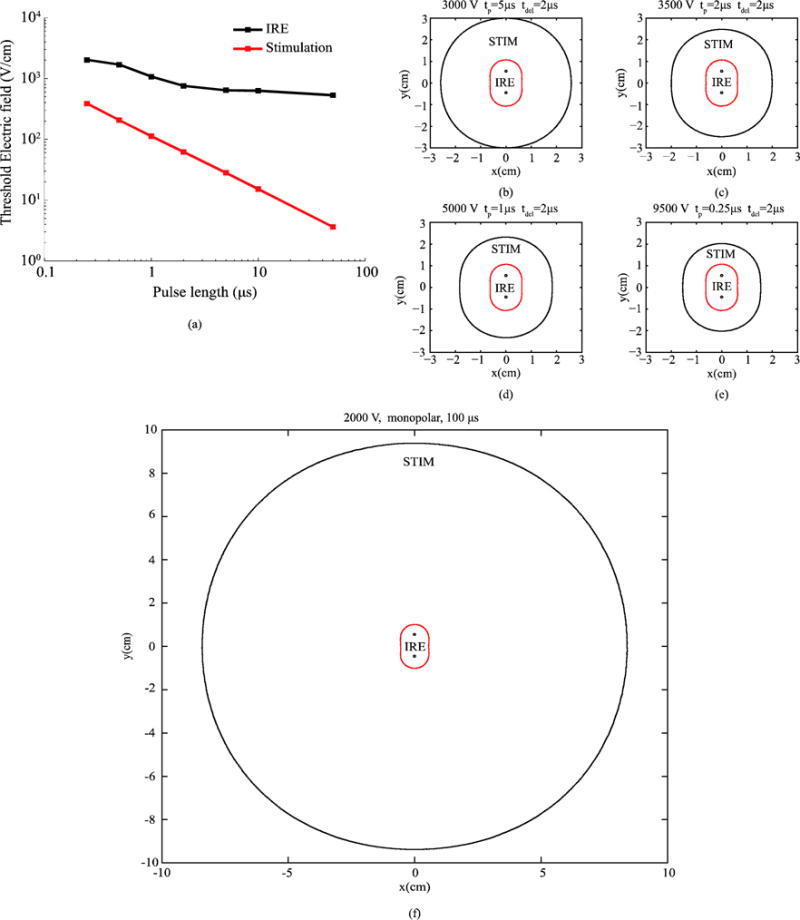
(a) IRE thresholds for PPT8182 cells (from (Sano et al 2015)) and stimulation thresholds for the modeled nerve termination when bursts of bipolar pulses with an energized time 100 μs and an inter-pulse delay of 2 μs are applied. (c)–(f) Simulated areas of ablation (IRE, red boundary) and of nerve termination stimulation (STIM, black boundary) for different pulse lengths and voltages across the needle electrodes. The voltage across the needles was adjusted to obtain a similar ablation area for each pulse length. The represented plane corresponds to the cross-section perpendicular to the electrodes which intersects their centers.

Since an electric field threshold can be defined both for stimulation and for IRE, it is possible to overlap the region that would be subjected to IRE to the region where existing nerve terminations would be stimulated. That is what is shown in figure 6.c–f. These plots show, for different pulse lengths and voltage amplitudes, the region where the FEM simulated field magnitude is above the IRE threshold (IRE) and the region where the electric field magnitude is above the stimulation threshold for the nerve termination (STIM). The represented plane corresponds to the cross-section perpendicular to the electrodes which intersects their centers. The amplitude of the voltage applied across the needles was heuristically adjusted in each case to obtain similar ablation areas. The results show that, by reducing the pulse length, the same ablation area can be achieved while reducing the area in which a nerve termination would be stimulated. In the case of a monopolar pulse (figure 6.f), the area above the stimulation threshold is much larger than in the bursts of bipolar pulses examples.

Using experimental data from (Sano et al 2017) for two cell lines, it was decided to test other pulsing protocols for IRE thresholds and nerve termination stimulation. The results are displayed in figure 7. Two additional protocols are compared: 100 bursts with an energized time of 100 μs and an inter-pulse delay of 1 μs (figure 7.b), and 100 bursts with 50 μs energized time and a delay between pulses of 1 μs (figure 7.c). For the reader’s convenience, it is represented again the case for 120 bursts with 100 μs energized time and an inter-pulse delay of 2 μs (figure 7.a). Again, it can be observed a steeper increase of the stimulation thresholds as the pulse length is reduced in comparison to the IRE thresholds increase.

Figure 7.

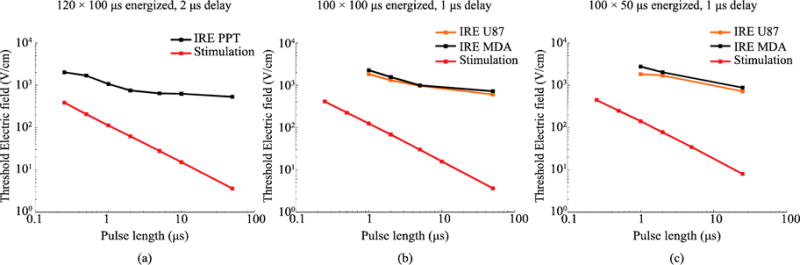
(a) Replica of figure 6.a, IRE thresholds for PPT8182 cells (from (Sano et al 2015)) and stimulation thresholds for the modeled nerve termination when bursts of bipolar pulses with an energized time 100 μs and an inter-pulse delay of 2 μs are applied. (b and c) The same plot for U87 and MDA-MB-231 BR3 cells (IRE data from (Sano et al 2017)) when bursts of bipolar pulses with an energized time of 100 μs and inter-pulse delay of 1 μs are applied (b) and when bursts of bipolar pulses with an energized time of 50 μs and an inter-pulse delay of 1 μs delay are applied (c).

Bipolar pulses are less effective in terms of electroporation than monopolar pulses (Ibey et al 2014). For this reason, the delivery of bursts consisting of asymmetric bipolar pulses has been proposed and it has indeed been experimentally shown that they significantly reduce the IRE thresholds compared to bursts of regular bipolar pulses (Sano et al 2017). However, due to the charge imbalance of the asymmetric pulses, the stimulation thresholds are also likely to be significantly reduced. This contingency was also tested here. Table 3 shows the modeled stimulation thresholds for a nerve termination in a homogeneous field and the IRE thresholds from (Sano et al 2017) for different waveforms. Although the IRE thresholds with asymmetric pulses are reduced about threefold compared to thresholds with symmetric pulses, the excitation thresholds are reduced in more than an order of magnitude. Therefore, these results suggest that the use of asymmetric bipolar pulses is not a worthwhile approach for minimizing unintended stimulation in electroporation protocols.

Table 3.

IRE and stimulation thresholds for assymmetric waveforms. Waveforms are defined as positive phase-delay-negative phase. IRE thresholds data extracted from (Sano et al 2017).

Waveform (μs)	Stimulation (V/cm)	IRE, U87 (V/cm)	IRE, MDA (V/cm)
5-1-5	30.0	967	998
5-1-0.5	1.0	541	826
5-1-0.25	1.5	484	812
2-1-2	68.4	1316	1563
2-1-0.5	2.2	700	885
2-1-0.25	1.8	594	818
1-1-1	124.4	1827	2271
1-1-0.5	4.1	1213	2000
1-1-0.25	2.0	780	945

4. Discussion

Our results indicate that, by replacing the conventional relatively long monopolar pulses by bursts of short bipolar pulses which achieve the same IRE efficacy, it is possible to avoid triggering action potentials in nearby nerve fibers or nerve terminations that otherwise would be stimulated. In other words, for the same ablation volume, less nerve fibers or nerve terminations would be recruited. This would have a positive impact on pain and neuromuscular stimulation during treatment, which is consistent with observations in previous in vivo studies (Arena et al 2011, Siddiqui et al 2016).

Our models indicate that the above is possible because, as the pulse length of the bipolar pulses is reduced, the stimulation thresholds raise faster than the irreversible electroporation thresholds.

The trends observable in figure 5 and figure 6 suggest that the ablation volumes that would be achieved without causing stimulation could be expanded with no limits by reducing the length of the delivered pulses. Nevertheless, in the present study we have not analyzed the thermal effects of the treatments, which are expected to be relevant, especially with short pulse lengths as very high electric fields would be required. Note that to produce a 2 cm³ ablation with the shortest pulse length in figure 5.c, the voltage difference between the electrodes was more than 5 kV. This voltage is higher than the clinically used values which usually do not exceed 3 kV. If an optimization study had to be performed for the pulsing protocol, our modeling framework would have to be upgrade to include thermal effects. This limitation of our study points out other limitations which are discussed below.

First, although electroporation protocols mostly consist in a sequence of several pulses (or bursts), stimulation in our study is simulated for a single pulse (or burst). This is a reasonable simplification taking into account that, in the vast majority of the clinical electroporation protocols, the delivery of the pulses is done with a 1 second delay between them. Hence, it is a safe assumption to consider that previous pulses have an insignificant effect on neuron’s excitability or at least on the threshold values.

Second, in the FEM model used to calculate the external voltage, we considered the medium to be homogeneous while in a real scenario this medium would be highly inhomogeneous, particularly around the nerve fibers. In addition the medium was considered to be purely conductive with a constant conductivity and it is agreed that electroporation alters the conductivity of tissues (Corovic et al 2013); although such alteration is not as remarkable in the case of high frequency bipolar bursts as it is in the case of conventional pulses (Bhonsle et al 2015). These circumstances significantly alter the electric field distribution and, normally, would have to be modeled in an electroporation study. Nevertheless, since the aim of the present study was to model the response of excitable cells in a general scenario in order to compare different pulsing protocols, for the sake of simplicity, these circumstances were ignored.

Third, the cable model only considers the TMV induced by the longitudinal component of the current (parallel to the axon) and neglects the transverse components (perpendicular to the axon). In long fibers, when the membrane charges to its steady state, the voltage induced by a longitudinal current is much higher than the voltage induced by a transverse current. Nevertheless, the membrane charging time is significantly longer for longitudinal currents (Meffin et al 2012). This means that, when delivering long pulses, longitudinal currents are more effective to excite long fibers. However, below a certain pulse length (≈ 100 ns) the transverse currents can become dominant and generate action potentials with a lower current. Therefore, although the cable model is appropriate in our study (pulse lengths > 100 ns), other approaches would be necessary to study shorter pulse lengths.

At this point it is worth discussing about the dependence of IRE and stimulation thresholds on pulse length. Electroporation and nerve stimulation are both threshold-like phenomena dependent on the induced TMV, meaning that they occur when the membrane reaches a certain TMV; higher in the case of electroporation. Although the mechanisms of cell death by means of IRE are complex and can vary among different treatment protocols, it is widely accepted that IRE can also be considered as a threshold-like phenomenon (Jiang et al 2015). This explains that, as observed in figure 6.a and figure 7.a–c, IRE and stimulation thresholds show both a linear relationship with pulse length in a log-log plot. The slopes of these plots are related to the membrane charging process, which, for a given pulse length, determines the electric field magnitude necessary to induce a TMV above the threshold. Therefore, one would expect both phenomena to show the same dependence on pulse length, but with higher electric field magnitudes in the case of IRE. However, the slopes described by our results and by the IRE experimental results are significantly different. What follows is an attempt to justify such difference.

The membrane charging process depends not only on membrane’s passive properties (e.g conductance and capacitance), but also on the geometry of the cell and the electric current paths (Kotnik and Miklavcic 2000, Cooper 1995, Meffin et al 2012, Reilly and Bauer 1987). A study on how several parameters affect the time constant when a fiber is exposed to the electric field created by a point electrode can be found in (Reilly and Bauer 1987). In a scenario like that presented in figure 3 — a long fiber exposed to the electric field created by two parallel needle electrodes—, the measured time constant will depend on the geometry of the fiber, the membrane’s passive properties, the electrode configuration, as well as the geometry of these electrodes. In these situations, where a nerve fiber is exposed to a non homogeneous electric field, the membrane charging is driven by the second spatial derivative. Therefore, besides the axon’s characteristics, the charging time will depend on the electrode configuration and will differ among different situations, such as, two parallel electrodes, two collinear electrodes or a single electrode and a distant grounding pad.

In the case of a nerve termination exposed to a homogeneous electric field (figure 6 and figure 7), the effects of the geometry and the spatial configuration of the electrodes do not exist. In this situation the charging time is determined by the membrane’s passive properties and the cell geometry. And, according to our results, in this scenario the IRE thresholds and the stimulation thresholds show a significantly different dependence on the pulse length in this case. Therefore, assuming similar passive properties, it can be concluded that the different behavior may be caused by the geometry of the cells.

In order to study to what extent the geometry of the cells could explain the different threshold evolution with pulse length, we have performed a brief study in which we compare the TMV induced by an external electric field in spherical cells and ellipsoidal cells. The spherical cells would represent the cells that were subjected to bursts in (Sano et al 2015). The ellipsoidal cells would account for a simplistic representation of the nerve terminations. The study is detailed in Appendix B.

From that brief study we conclude that cells with elongated shapes, such the neurons that form the nerve fibers, have significantly longer charging times than those with a lower eccentricity. As a consequence, reducing the pulse length has a stronger impact on the peak membrane voltage induced by an external alternating electric field in elongated cells than in small roundish cells. Therefore we propose that the difference in the dependence that the IRE thresholds and the stimulation thresholds show with the pulse length is closely related to the geometry of the involved cells.

5. Conclusion

Through a numerical study, we have shown that delivery of bursts of bipolar pulses instead of the conventional monopolar pulses, allows producing ablations by means of IRE while reducing or avoiding nerve fiber or nerve terminal stimulation. Our models indicate that this is possible because, as the pulse length of the bipolar pulses is reduced from 100 μs to 1 μs, the stimulation thresholds raise threefold faster than the irreversible electroporation thresholds. This suggests that, for treating the same volume of tissue, it will be possible to reduce the amount of recruited nerve fibers by reducing the length of the bipolar pulses.

We propose that the different dependence of the thresholds on the pulse length is due to the fact that transmembrane charging for nerve fibers is much slower than that of cells treated by electroporation because of their geometrical differences. Cells with elongated shapes, such the neurons that form the nerve fibers, have significantly longer charging times than those with a lower eccentricity. As a consequence, reducing the pulse length has a stronger impact on the peak membrane voltage induced by an external alternating electric field in elongated cells than in small roundish cells.

Although this study was focused on IRE based treatments, the results might be also valid for other electroporation based treatments. This reinforces the idea that working towards the use of bursts of bipolar pulses is a valid effort in order to improve electroporation based treatments in medicine.

The modeling framework employed in the present study, if complemented with thermal modeling and further experimental in vivo data on IRE thresholds for the bursts of bipolar pulses, could be used to optimize the pulsing protocols for safely performing IRE ablation with minimal neuromuscular stimulation.

Appendix A

The equations describing the ionic currents at the axon’s membrane were taken from (McIntyre et al 2002). The currents in this model are adjusted to represent the excitation of a mammalian motor neuron at 36 °C and consist of 3 types of ionic channels and a leakage current. The total ionic current at each node is calculated as the sum of 4 different currents:

$$I_i=I_{\mathit{Naf}}+I_{\mathit{Nap}}+I_{Ks}+I_{Lk}$$

The equations driving the time evolution of these currents and their dependence with the transmembrane voltage are as follow (expressed in mV and ms):

• Fast sodium current

  $$I_{\mathit{Naf}}=g_{\mathit{Naf}}{m}^{3}h\left(V_m-E_{Na}\right)$$

  $$\frac{dm}{dt}={\alpha }_m\left(1-m\right)-{\beta }_{m}m$$

  $${\alpha }_m=6.57\frac{V_m+20.4}{1-\exp \left[-\left(V_m+20.4\right)/10.3\right]}$$

  $${\beta }_m=0.304\frac{-\left(V_m+25.7\right)}{1-\exp \left[\left(V_m+25.7\right)/9.16\right]}$$

  $$\frac{dh}{dt}={\alpha }_h\left(1-h\right)-{\beta }_{h}h$$

  $${\alpha }_h=0.34\frac{-\left(V_m+114\right)}{1-\exp \left[\left(V_m+114\right)/11\right]}$$

  $${\beta }_h=\frac{12.6}{1+\exp \left[-\left(V_m+31.8\right)/13.4\right]}$$
• Persistent sodium current

  $$I_{\mathit{Nap}}=g_{\mathit{Nap}}{p}^3\left(V_m-E_{Na}\right)$$

  $$\frac{dp}{dt}={\alpha }_p\left(1-p\right)-{\beta }_{p}p$$

  $${\alpha }_p=0.0353\frac{V_m+27}{1-\exp \left[-\left(V_m+27\right)/10.2\right]}$$

  $${\beta }_p=0.000883\frac{-\left(V_m+34\right)}{1-\exp \left[\left(V_m+34\right)/10\right]}$$
• Slow potassium current

  $$I_{Ks}=g_{Ks}s\left(V_m-E_K\right)$$

  $$\frac{ds}{dt}={\alpha }_s\left(1-s\right)-{\beta }_{s}s$$

  $${\alpha }_s=\frac{0.3}{1+\exp \left[-\left(V_m+53\right)/5\right]}$$

  $${\beta }_s=\frac{0.03}{1+\exp \left[-\left(V_m+90\right)/1\right]}$$
• Leakage current

  $$I_{Lk}=g_{Lk}\left(V_m-E_{Lk}\right)$$

Values of the parameters used to model the ionic currents: g_Naf = 3 S/cm², g_Nap = 0.01 S/cm², g_Ks = 0.08 S/cm², g_Lk = 0.007 S/cm², E_Na = 50 mV, E_K = −90 mV, E_Lk = −90 mV.

Appendix B

We computed in COMSOL the maximum transmembrane voltage respect to the resting voltage induced by an external electric field, ΔTMV, for three different cell geometries. Maximum ΔTMV was obtained following the procedure described in (Mercadal et al 2016). Cell volume and dielectric properties were equal in the three assayed cell geometries (see table B.1). We considered a sphere with a radius of 5 μm and two ellipsoids, having two equal semi-axes and a longer semi-axis with relationships of R₂=20R₁ and R₂=5R₁ between the length of these semi-axes and the length of longest one. In order to maintain the same volume in the three geometries, the lengths of the semi-axes were: 2.9 μm and 14.6 μm in the ellipsoid with R₂=5R₁ and 1.8 μm and 36.8 μm in the ellipsoid with R₂=20R₁. The longest semi-axis was aligned with the direction of the electric field. Therefore this situation would resemble the geometry of the nerve termination model in this study.

The time course of the maximum ΔTMV in the three cell geometries is displayed in figure B1.a when a relatively long pulse of 100 μs is applied. Although the sphere reaches the steady state faster, the ellipsoids reach significantly higher ΔTMV values. The ellipsoid with the largest ratio between semi-axes (R₂=20R₁) reaches the highest ΔTMV, nevertheless, it also has the longest charging time. Cooper discussed this same effect for cylinders using a cable model and comparing different lengths (Cooper 1995). When bursts of bipolar pulses are applied (figure B1.b), due to this difference in the charging and discharging times, if short pulses such as the ones considered in our study are applied, the difference in the maximum ΔTMV induced at the sphere and at the most elongated ellipsoid is reduced, down to sign inversion. Indeed, below a certain pulse length, the induced ΔTMV is larger in the sphere than in the ellipsoid.

It has been suggested that the difference in membrane charging times can be explained as being the consequence of the fact that there are two separate mechanisms by which an external electric field induces a TMV. First, the current that crosses the membrane creates an ohmic voltage drop. Second, a difference in the external and internal electric field induces a TMV. According to Rall (Rall 2011), in short cylinders the difference in electric field strengths between inside and outside the cell is the dominant process. In this case, most of the current flows alongside the surface of the cell and very few current flows across the membrane. Therefore, the steady state is reached through a redistribution of charges at the surface of the cell, which is a faster process than the ohmic potential. On the other hand, as the cylinder length increases, a larger amount of current must flow across the membrane to reach the steady state, making the charging time longer.

Based on the above, we also performed a COMSOL study aimed to reproduce the behavior observed in figure 6.a. We assumed that the spherical cells (radius = 5 μs) were the cells to be electroporated and assigned to them an IRE ΔTMV threshold of 1 V. And we assumed that the ellipsoidal cells (R₂ = 20 R₁) were the excitable cells and assigned to them a stimulation threshold of 50 mV. Then, using the same waveforms as in figure 5 and figure 6 (100 μs energized time and 2 μs inter-pulse delay), we calculated the electric field magnitude necessary for each pulse length in order to reach a peak ΔTMV equal to the thresholds defined above. To do so, we simulated the induced ΔTMV when the cell is exposed to an arbitrary 100 V/cm electric field for each geometry and pulse length. Finally, these results were used to scale the electric field magnitude in order to reach the desired peak ΔTMV in all cases. Figure B2 displays the obtained results, which show a similar trend to the results in figure 6 and figure 7. The sphere shows a flat dependence with the pulse length up to the shortest lengths due to its small charging time (≈0.2 μs). The ellipsoid on the other hand, has a longer charging time and as a consequence it shows a linear dependence in a log-log plot that starts at about 10 μs of pulse length.

Table B1.

Dielectric properties of the model: electrical conductivity, σ, and relative permittivity, ε_r. The modeled thickness of the cell mebrane was 5 nm.

Extracellular medium	σ	1.5 (S/m)
	εr	80
Cell membran	σ	2.5×10−7 (S/m)
	εr	5
Intracellular medium	σ	0.5 (S/m)
	εr	80

Figure B1.

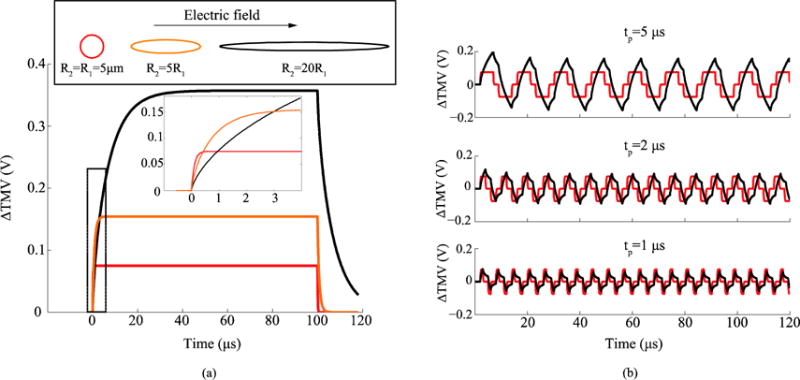
(a) Simulated time evolution of the maximum ΔTMV induced in a spherical cell and in two ellipsoidal cells when these are subjected to an electric field pulse of 100 V/cm and 100 μs. The two ellipsoidal cells have two equal semi-axes and the other semi-axis has a length 20 times and 5 times the length of those axes respectively (R₂=20R₁ and R₂=5R₁). The volume and the dielectric properties were the same in the three geometries (See table B.1). (b) Simulated maximum ΔTMV in a spherical cell and in an ellipsoidal cell with R₂=20R₁ when a burst of bipolar pulses with a delay of 2 μs and an amplitude 100 V/cm is applied, for different pulse lengths.

Figure B2.

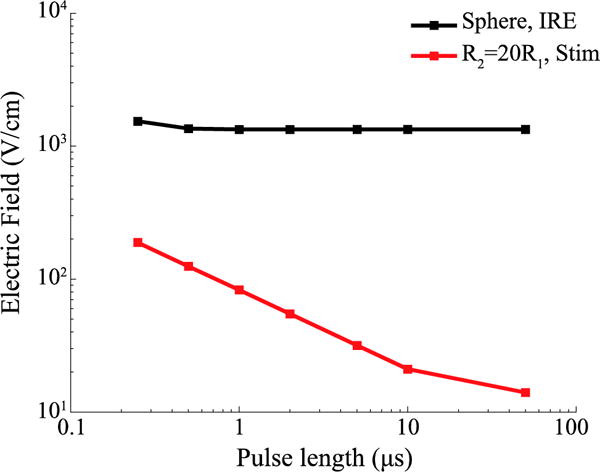
Hypothetical electric field magnitude that, when delivering bursts of bipolar pulses, would be necessary to induce IRE in a spherical cell (black line) and that would initiate an action potential in an elongated ellipsoid (red line). An arbitrary ΔTMV of 1 V was used as IRE threshold, and 50 mV were used as stimulation threshold. For different pulse lengths, the electric field magnitude necessary to reach a peak ΔTMV equal to the defined thresholds was calculated. The geometries and dielectric properties were the same in both geometries and the same as in figure B1.