Acute Toxicity of Ternary Cd–Cu–Ni and Cd–Ni–Zn Mixtures to Daphnia magna: Dominant Metal Pairs Change along a Concentration Gradient

Abstract

Multiple metals are usually present in surface waters, sometimes leading to toxicity that currently is difficult to predict due to potentially non-additive mixture toxicity. Previous toxicity tests with Daphnia magna exposed to binary mixtures of Ni combined with Cd, Cu, or Zn demonstrated that Ni and Zn strongly protect against Cd toxicity, but Cu–Ni toxicity is more than additive, and Ni–Zn toxicity is slightly less than additive. To consider multiple metal–metal interactions, we exposed D. magna neonates to Cd, Cu, Ni, or Zn alone and in ternary Cd–Cu–Ni and Cd–Ni–Zn combinations in standard 48 h lethality tests. In these ternary mixtures, two metals were held constant, while the third metal was varied through a series that ranged from nonlethal to lethal concentrations. In Cd–Cu–Ni mixtures, the toxicity was less than additive, additive, or more than additive, depending on the concentration (or ion activity) of the varied metal and the additivity model (concentration-addition or independent-action) used to predict toxicity. In Cd–Ni–Zn mixtures, the toxicity was less than additive or approximately additive, depending on the concentration (or ion activity) of the varied metal but independent of the additivity model. These results demonstrate that complex interactions of potentially competing toxicity-controlling mechanisms can occur in ternary-metal mixtures but might be predicted by mechanistic bioavailability-based toxicity models.

Graphical abstract

1. INTRODUCTION

Metals are ubiquitous, even in pristine environments, and their concentrations can become considerably elevated in freshwater and saltwater systems as a result of industrial, municipal, mining, and agricultural discharges.¹ Metals almost never occur alone in surface waters and instead usually are in mixtures of several metals, each of which is present as various chemical forms (e.g., “free” metal ions and charged and uncharged complexes with other ions and dissolved organic matter (DOM)). Despite the prevalence of metal mixtures in surface waters, most regulatory approaches and risk-assessment procedures for metals are largely based on results of individual-metal aquatic toxicity tests and the assumption that when more than one metal is present, the metals will behave in a way than can be predicted by simple interaction of each metal, referred to generally as additive interaction.²

Currently, there are two general models for predicting additive mixture effects: independent action (IA, also referred to as the response-addition model) and concentration addition (CA).^2,3 The CA model is generally assumed to be appropriate when the chemicals have the same mechanism of toxic action (e.g., Cd and Zn both impair Ca homeostasis⁴), while the IA model is generally assumed to be appropriate when the chemicals have different mechanisms of action (e.g., impairment of Na homeostasis versus impairment of Ca homeostasis⁴).⁵ However, additive toxicity does not appear to occur in most metal-mixture systems.^6–9 For example, Norwood et al.¹⁰ and Vijver et al.¹¹ conducted literature reviews in which decades of metal-mixture data were analyzed, and they determined that only approximately 20 to 25% of metal-mixture tests resulted in additive toxicity, whereas approximately 30% of mixtures resulted in more-than-additive toxicity, and approximately 45 to 50% resulted in less-than-additive toxicity.²

The inability to accurately predict mixture toxicity based on an assumption of additivity stems from the use of dissolved-metal concentrations as predictors of toxicity. Factors such as aqueous metal speciation, metal–metal competition for binding to dissolved ligands, and metal–metal interactions within an organism can complicate this system to an extent that metal-mixture toxicity cannot be accurately explained using either a CA or an IA assumption.² Thus, it is not currently well-understood how the interactions of binary metals, water chemistry parameters, and aquatic organisms affect the toxicity of metal mixtures based only on dissolved-metal concentrations.² Compounding this conundrum, an even-greater challenge is to predict the outcome when multiple metal– metal interactions may contribute to toxicity in a mixture. For example, if the toxicity of a mixture containing metal 1 and metal 2 was less than expected, but the toxicity of a mixture with metal 2 and metal 3 was generally greater than expected, a ternary mixture containing metals 1, 2, and 3 could exhibit a complicated combined effect of those interactions.

In this study, our goal was to explore possible competing interactions among metals in ternary mixtures. To do this, we used Cd and Ni (two metals that, when combined, had been previously determined to result in a less-than-additive toxicity)⁹ in all the metal-mixture toxicity tests, while the third metal in the ternary mixture was either Cu or Zn. In previous studies with Daphnia magna analyzed using the IA model, Cd–Ni and Cu–Ni mixtures produced less-than-additive and more-than-additive acute toxicity to D. magna, respectively.⁹ In addition, Cd–Cu mixtures caused less-than-additive acute toxicity when Cu was titrated into a constant background concentration of Cd but more-than-additive toxicity when the roles of the two metals were reversed.⁶ Because the effects of the binary mixtures differed greatly depending on the metals in the mixture, ternary Cd–Cu–Ni mixtures were chosen to test which effect would prevail in a ternary mixture in which both types of interactions (i.e., less-than-additive and more-than-additive toxicity) might occur. In contrast, Cd–Ni and Cd–Zn mixtures caused less-than-additive toxicity that was qualitatively similar for the two binary-metal mixtures,^6,9 and less-than-additive toxicity also occurred in Ni–Zn mixtures, although to a much-lesser extent.⁹ Therefore, we also tested ternary Cd–Ni– Zn mixtures to determine if the toxicity remained less-than-additive at all concentration combinations. For both ternary sets of metals, the null hypothesis was additive toxicity despite the less-than-additive toxicity of the Cd–Cu, Cd–Ni, Cd–Zn, and Ni–Zn pairs and the more-than-additive toxicity of the Cu–Ni pair; the alternative hypothesis was non-additive toxicity (upper right-hand corner of Figure 1).

Figure 1.

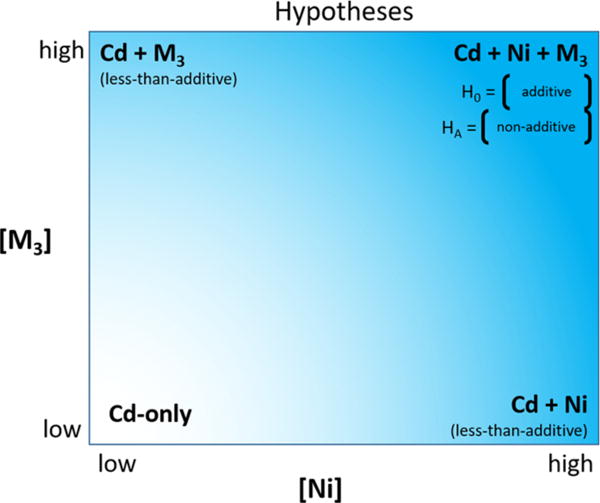
Hypothesized additivity of acute toxicity of ternary Cd–Cu– Ni and Cd–Ni–Zn mixtures to Daphnia magna neonates (shown in upper right-hand corner of the diagram), where metal 3 (M₃) is either Cu or Zn. Previously reported toxicity of binary Cd–M₃ and Cd–Ni mixtures is shown in the upper left and lower right corners, respectively,^6,9 and Cd-only toxicity occurs when the concentrations of both Ni and M₃ are low (lower left corner). H₀ is the null hypothesis; H_A is the alternative hypothesis.

For several reasons, these results will help to advance the understanding and prediction of metal-mixture toxicity. To our knowledge, this is the first systematic study of the potential for non-additive toxicity across a wide range of concentrations in two ternary-metal mixtures (Cd–Cu–Ni and Cd–Ni–Zn) expected to have different types of metal–metal toxicity interactions. Additionally, we analyze the results using two different mixture-additivity models (CA and IA) and using two different forms of the metals as predictors of toxicity (metal concentrations and ion activities). Finally, we use a relatively new method to test for statistically significant deviations from additive mixture toxicity, which uses a randomization approach that incorporates both the uncertainty in the observed toxicity and the uncertainty on the CA- and IA-model-predicted toxicity. This differs from approaches used in most statistical analyses of the additivity of mixture toxicity, which only incorporate the uncertainty in the observed toxicity. Together, these features produce a novel insight into previously undescribed gradients of mixture-toxicity additivity and non-additivity that is enhanced by strong statistical inference.

2. EXPERIMENTAL SECTION

2.1. Test Organisms

D. magna neonates were used in all toxicity tests and were obtained from Aquatic Biosystems, Inc., in Fort Collins, CO in moderately hard reconstituted water (MHRW)¹² that contained the green alga Pseudokirchneriella subcapitata as food. The neonates were sent via same-day shipping to ensure that all organisms were less than 24 h old at the start of the toxicity tests. Because the tests were started as soon as a shipment arrived and lasted only 48 h, the D. magna were not fed again.

2.2. Exposure Water

The exposure water in the toxicity tests was MHRW to which organic carbon was added at 3 mg/L as Suwannee River fulvic acid (obtained from the International Humic Substances Society; http://www.humicsubstances.org/). Metal salts [Ni(NO₃)₂, Cd(NO₃)₂, Cu(NO₃)₂, and Zn(NO₃)₂ (reagent-grade, Mallinckrodt Chemical (Ni) and Baker Chemical Company (Cd, Cu, and Zn))] were used to prepare concentrated stock solutions that were added to the exposure matrix. Exposure solutions were prepared 24 to 36 h before the start of a toxicity test to allow equilibration of the metals with the organic carbon.¹³

2.3. Acute Toxicity Tests

The toxicity of individual metals and ternary mixtures was determined in 48 h static, nonrenewal lethality tests, following procedures recommended by the U.S. Environmental Protection Agency.¹² The ternary-metal tests comprised a series of either 6 or 12 metal concentration combinations in a gradient designed to produce mortalities ranging between 0 and 100%. Series with only six metal concentrations were used in ternary mixtures that contained high metal concentrations, in which nearly 100% mortality was expected to occur at all concentrations. In the ternary mixtures, the concentrations of Cd and Ni were held constant throughout an entire series, while the concentration of the third metal (M₃; either Cu or Zn) was increased incrementally in the series (i.e., a “titration” experimental design), and then the roles of Ni and M₃ were reversed in separate tests (i.e., the former M₃ became a constant-concentration metal along with Cd, and Ni became the varied-concentration metal). The concentration of Cd was held constant at 9 × 10⁻⁷ M (0.1 mg/L) throughout all of the ternary-metal toxicity tests. This concentration was selected because, in our previous toxicity tests with Cd as the only contaminant, 9 × 10⁻⁷ M Cd caused approximately 50% mortality. That baseline of approximately 50% mortality allowed equal opportunity to observe less-than-additive toxicity (i.e., less than 50% mortality) or more-than-additive toxicity (i.e., more than 50% mortality) as the other two metals were added to the exposure waters. Individual-metal toxicity tests were conducted concurrently with each ternary mixture and comprised a dilution series of six concentrations (including a control that contained no added metals) for each metal, and these controls also served as the no-added-metal controls for the concurrent metal-mixture tests. For example, concurrent with the ternary Cd–Cu–Ni tests, individual-metal toxicity tests were conducted with Cd, Cu, and Ni.

In all tests, each metal concentration or mixture was tested in four replicate chambers, each containing 25 mL of exposure water and five organisms. Therefore, a total of 20 organisms were exposed to each concentration in the individual- or ternary-metal gradient. The number of dead organisms was recorded at 24 and 48 h, with immobilization as the indicator of mortality.¹²

The ternary-metal tests were conducted during an 8 month period. All tests were conducted in incubators (VWR International) at a temperature of 20 ± 2 °C, with a 16 h–8 h light–dark cycle. To test for variability in responses, each set of a metal-mixture series and its associated individual-metal toxicity tests was repeated on a different week during the study (i.e., duplication of each set of tests).

2.4. Chemical Analyses

Water samples from all controls and exposure concentrations were analyzed at the beginning of the toxicity tests for total concentrations of metals (including Cd, Cu, Ni, and Zn), major inorganic cations (Ca²⁺, Mg²⁺, Na⁺, and K⁺), and sulfur (reported as sulfate after stoichiometric conversion) using an Optima 5300 inductively coupled plasma optical emission spectrophotometer (ICP-OES) (PerkinElmer). The exposure waters were not filtered before analysis because particles were unlikely in this synthetic laboratory water and because preliminary tests demonstrated that commercial filters either sorb metals from, or leach metals into, initial volumes of water that are passed through the membranes.⁶ Consequently, the small volumes (<100 mL) of exposure waters used in these D. magna toxicity tests were not sufficient to adequately rinse the filters or exceed their sorption capacity. Additional preliminary tests, in which sufficient sample was used to saturate the filter membrane, demonstrated that the metals added to MHRW were >90% dissolved.⁶ Therefore, the total-metal concentrations were assumed to closely approximate the dissolved-metal concentrations.

Temperature and dissolved oxygen were measured using a YSI 55 probe (YSI Incorporated), and pH was measured using an Orion ROSS electrode and Orion 2 STAR meter (Thermo Fisher Scientific) calibrated with pH 4, 7, and 10 buffers. Alkalinity was analyzed in the MHRW that was used to prepare all the exposure waters by titration with H₂SO₄ (Hach) to the bromo-cresol green end point.¹⁴ Total organic carbon (TOC) concentrations were analyzed by UV-catalyzed persulfate oxidation using a Sievers Model 900 TOC Analyzer (GE Analytical Instruments). Chloride concentrations were calculated by assuming the molar Cl⁻ concentration equaled the measured molar K⁺ concentration (because the only Cl⁻ in the MHRW recipe was added as KCl).¹²

In all ICP-OES analytical runs, a Sc internal-calibration standard was continuously introduced into the plasma along with each sample, and samples were analyzed in triplicate. Quality assurance and quality control (QA/QC) samples included deionized water blanks (Barnstead Nanopure system, Thermo Fisher Scientific) that contained 2% trace-metal-grade HNO₃ (Thermo Fisher Scientific) and certified continuing calibration verification (CCV) standards (PerkinElmer). The QA/QC samples were analyzed immediately after instrument calibration, after every 10 samples, and at the end of each set of samples. Additionally, NIST certified standard reference materials 1640a and 1643e¹⁵ were analyzed for trace elements before and at the end of each set of samples. All samples were reanalyzed in any analytical run in which acceptable QA/QC results were not obtained. Those unacceptable results could include: deviations of the internal Sc standard greater than 20% from the known concentration, deviations of the CCV samples greater than 10% from the known concentrations, or relative standard deviations (RSDs) of triplicate analyses of a sample greater than 10%. The ranges of instrument detection limits for the metals, major cations, and sulfur during the 8 month study were (in μg/L): 4.7–7.0 Ca, 0.1–0.3 Cd, 0.3–0.4 Cu, 3–40 K (equivalent to 2.7–36.3 Cl), 0.1–0.4 Mg, 6–8 Na, 5.8–6.5 S (equivalent to 17.4–19.5 SO₄), 0.1–0.4 Ni, and 0.5–0.7 Zn.

Unfiltered water samples for analysis of TOC concentration were collected from the control and the highest metal concentration at the beginning of a test, the latter sample being taken to confirm no changes occurred due to addition of the metals. The TOC samples were preserved by addition of H₃PO₄ to pH < 2. The alkalinity of each batch of MHRW was determined before its use in toxicity tests. At the beginning of each test, unfiltered water from each treatment in the metal-concentration series was acidified to pH ≤ 2 with 2% Optima HNO₃ and analyzed by ICPOES.

2.5. Data Analyses

We used both types of additivity models (IA and CA) to evaluate the additivity of toxicity in the ternary metal mixtures because the exact mechanism of toxic action of Ni, which was included in each ternary-metal mixture, is not known.⁴ Additionally, we used both metal concentrations and the chemical activities of the “free” metal ion plus the monohydroxide ion (M²⁺ + MOH⁺) to predict toxicity with each additivity model because those two ions are assumed to be potentially bioavailable¹⁶ and are included as predictors in some individual-metal biotic ligand models (e.g., http://www.windwardenv.com/biotic-ligand-model/).¹⁷ Ion activities take into account metal–metal competition for binding to DOM and thus might help to explain apparently more-than-additive toxicity results predicted by dissolved-metal concentrations that do not take into account the metal–metal competition. The chemical-speciation software WHAM VII (The Centre for Ecology and Hydrology) was used to compute chemical activities of the ions of each metal in each individual-metal and each ternary-metal toxicity data set.

Although it is traditional to compare median effect concentrations (EC50 values) determined from two or more concentration–response series to quantitatively characterize and compare toxicity results, this approach was not adopted for the present study because such an analysis does not have the resolution to evaluate multiple metal–metal interactions that may occur at various portions of a concentration–response curve. Instead, we calculated the ratio of the observed mixture mortality to the predicted mortality. In this analysis, an observed-to-predicted mortality ratio less than 1 indicates less-than-additive toxicity, a ratio of 1 indicates additive toxicity, and a ratio greater than 1 indicates more-than-additive toxicity.

We tested for statistically significant non-additive toxicity with both the IA and CA models using modifications of the randomization tests described in Meyer et al.² The computer software @RISK (Palisade Corporation) was used to compute Monte Carlo-type randomizations in which the uncertainty associated with the observed mortality and the uncertainty in the predicted mortality in each combination of metal concentrations were combined to test for nonadditivity on a point-by-point basis. In each randomization run, 100 000 iterations were performed.

In each @RISK iteration for the IA model, random concentration–response curves were generated for each of the three metals by randomly drawing EC50 and log–logistic slopes from normal distributions defined by the average and standard error associated with each of those variables. Those EC50 values, slopes, and their standard errors were calculated from results of the individual-metal toxicity tests conducted concurrently with each ternary-metal toxicity test. Due to high age-dependent variability of EC50 values for D. magna neonates exposed to some of these metals,¹⁸ it was important to calculate the predicted toxicity based on the individual-metal tests that had been conducted on the same day as a given mixture test (instead of consolidating all of the individual-metal data to obtain a central-tendency concentration–response curve for each metal).

Each concentration–response curve was a log–logistic relationship in the form:

$$M=\frac{1}{1+{\left(\frac{\text{EC}50}{C}\right)}^{\text{slope}}}$$ (1)

where M is the mortality proportion (0 to 1), and C is the metal concentration or ion activity (in the same units as the EC50). To avoid randomly selecting unrealistic zero or negative values for the EC50 and slope, the lower tail of each of those normal distributions was truncated at 1 × 10⁻²⁰. Then, the predicted mortality in the ternary mixture for the IA model was calculated as

$$\text{IA Predicted Mixture Mortality Proportion}=1-\left(S_{\text{Cd}}\times S_{\text{Ni}}\times S_{\mathrm{M}3}\right)$$ (2)

where S_Cd, S_Ni, and S_M3 are the survival proportions (= 1 – M) that are predicted from the randomly generated individual-metal concentration–response relationships for Cd, Ni, and M₃ at the measured concentrations of those metals in the Cd–Ni– M₃ mixture.

Concurrently, a random value of the observed mortality was drawn from a beta distribution defined by the average and standard error of the observed mortality. The lower and upper limits imposed on the β distribution were 0.0 (0% mortality) and 1.0 (100% mortality). We chose a β distribution bounded by 0 and 1 for this randomization parameter because, by definition, a mortality proportion can only range from 0 to 1. Use of a normal distribution (which by default is bounded by –∞ < x < ∞) or any other applicable distribution (e.g., logarithmic, Poisson, γ) would have required truncation of the distribution in one or both tails, thus producing a biased distribution of mortality probabilities. After a random value of the observed mortality was drawn, the ratio of observed mixture mortality to predicted mixture mortality was calculated. This process was repeated for each of the 100 000 iterations, and the 2.5 and 97.5 percentiles of the distribution of 100 000 ratios were calculated as the 95% confidence limits. If the resulting 95% confidence interval on that ratio did not include 1 (which is the value of the mortality ratio assuming the null hypothesis of additive toxicity), the mixture toxicity was inferred to be non-additive at the 95% confidence level.

To avoid overly sensitive statistical inferences about non-additive toxicity (e.g., to avoid having a 2% difference between observed and predicted mortality declared statistically significant), we did not consider a less than 10% difference between the average observed and average predicted mortalities significant. This is analogous to the U.S. Environmental Protection Agency’s guideline of allowing the control mortality in an acute toxicity test to be up to 10%, as an acknowledgment of random variability in mortality.¹²

The same procedure was used in each @RISK iteration for the CA model except (1) the metal exposures were converted to potency-normalized toxic units of the metal concentrations and the ion activities, and (2) the concentration–response relationships based on the toxic units were combined for all three metals in each ternary mixture to generate one composite slope-and-intercept pair (instead of generating a separate slope-and-intercept pair for each metal). The toxic-unit concentration (TU) of each metal was calculated as TU = C/EC50, where C and EC50 were based on metal concentrations or ion activities. The sum of the toxic units (ΣTU) in a given mixture was calculated as

$${\displaystyle \sum \text{TU}}=\frac{C_{\text{Cd}}}{\text{EC}{50}_{\text{Cd}}}+\frac{C_{\text{Ni}}}{\text{EC}{50}_{\text{Ni}}}+\frac{C_{{\mathrm{M}}_3}}{\text{EC}{50}_{{\mathrm{M}}_3}}$$ (3)

where C_Cd, C_Ni, and C_M3 are the metal concentrations or the ion activities that are predicted from the randomly generated individual-metal concentration–response relationships for Cd, Ni, and M₃ at the measured concentrations or ion activities of those metals in the Cd–Ni–M₃ mixture. Then, the predicted mortality in the ternary-metal mixture for the CA model was calculated as

$$\text{CA Predicted Mixture Mortality Proportion}=\frac{1}{1+{\left(\frac{\text{TU}\text{EC}50}{{\displaystyle \sum \text{TU}}}\right)}^{\text{TU}\text{slope}}}$$ (4)

In this study, the EC50 values and the slopes of the associated concentration–response curves in the individual-metal exposures were calculated using the logit-regression method in OriginPro 9.1 (OriginLab Corporation). Microsoft Excel was used to calculate the 95% confidence intervals on the averages of several EC50 values or slopes and to perform a one-way analysis of variance (ANOVA) with Tukey HSD posthoc comparisons to test for significant differences in the EC50 values and slopes for the individual metals.

3. RESULTS AND DISCUSSION

Water chemistry parameters measured in all individual-metal and metal-mixture toxicity tests and the calculated log–logistic regression slopes and intercepts (EC50s) are tabulated in the Supporting Information. Average measured concentrations of the constant-concentration metals in the metal-mixture tests are reported in the captions and legends of Figures 2–5, but the measured concentrations for each trial are tabulated in the Supporting Information. Average measured concentrations of the varied-concentration metals in each replicate metal-mixture toxicity test are plotted on the horizontal axes in Figures 2–5 and are also tabulated in the Supporting Information. The average observed:predicted mortality ratio of the two replicate tests in each metal-mixture concentration combination is plotted on the vertical axes in Figures 2–5. Survival in all controls during the 8 month study was greater than or equal to 90%.

Figure 2.

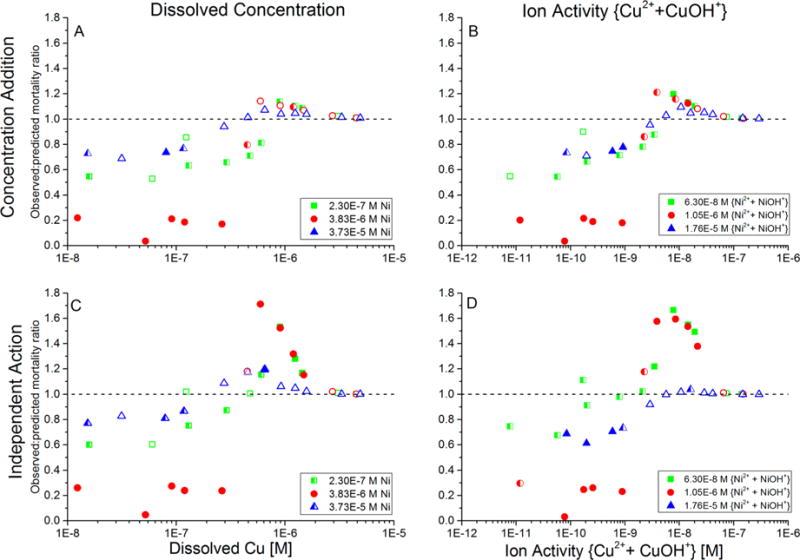
Additivity of toxicity of Cd–Cu–Ni mixtures that contained constant concentrations of Cd (9 × 10⁻⁷ M Cd in all exposure waters) and Ni (separate concentrations in each of the three sets of tests shown in the legend), while Cu was varied along a concentration gradient within each of the three sets of tests. Additivity of toxicity was evaluated by the observed-to-predicted mortality ratio, for which predicted mortality was calculated using either a concentration-addition (CA) or independent-action (IA) model. (A) CA model with predicted toxicity based on metal concentrations; (B) CA model with predicted toxicity based on ion activities; (C) IA model with predicted toxicity based on metal concentrations; and (D) IA model with predicted toxicity based on ion activities. Each data point is the average of duplicate runs of each combination of metal concentrations. Closed symbols: statistically significant non-additive toxicity (p ≤ 0.05) in both replicate trials; open symbols: not-significant non-additive toxicity in both replicate trials; half-filled symbols: significant non-additive toxicity in only one of the two replicate trials. Ratios less than 1 indicate less-than-additive toxicity; ratios greater than 1 indicate more-than-additive toxicity.

Figure 5.

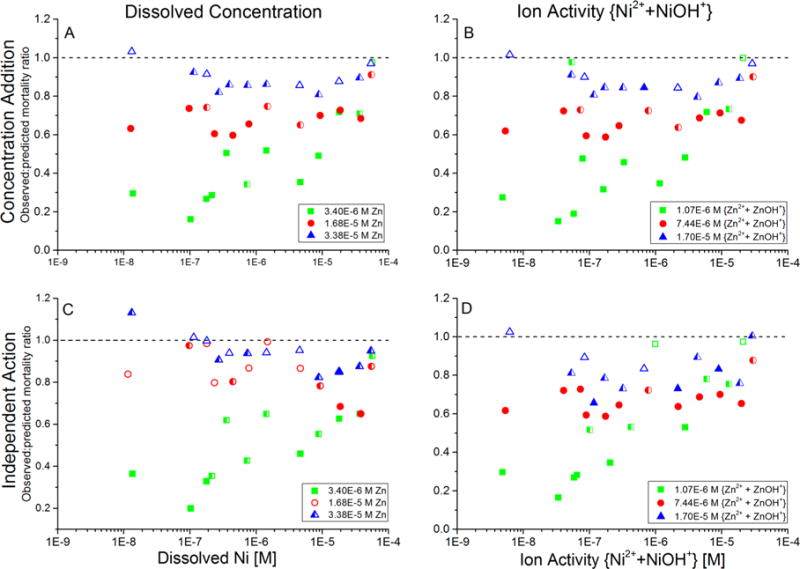
Additivity of toxicity of Cd–Ni–Zn mixtures that contained constant concentrations of Cd (9 × 10⁻⁷ M Cd in all exposure waters) and Zn (separate concentrations in each of the three sets of tests shown in the legend), while Ni was varied along a concentration gradient within each of the three sets of tests. Additivity of toxicity was evaluated by the observed-to-predicted mortality ratio, for which predicted mortality was calculated using either a concentration-addition or independent-action model. (A) CA model with predicted toxicity based on metal concentrations; (B) CA model with predicted toxicity based on ion activities; (C) IA model with predicted toxicity based on metal concentrations; and (D) IA model with predicted toxicity based on ion activities. Each data point is the average of duplicate runs of each combination of metal concentrations. Closed symbols: statistically significant non-additive toxicity (p ≤ 0.05) in both replicate trials; open symbols: not significant non-additive toxicity in both replicate trials; half-filled symbols: significant non-additive toxicity in only one of the two replicate trials. Ratios less than 1 indicate less-than-additive toxicity; ratios greater than 1 indicate more-than-additive toxicity.

3.1. Individual Metals

Based on the molar metal-concentration EC50 values in the individual-metal toxicity tests, Ni was the least toxic (i.e., it had the highest EC50) of the four metals tested in this DOM-supplemented MHRW, followed by Zn, Cu, and Cd in sequence of increasing toxicity (Table 1). These results are consistent with previously reported results for the same exposure-water recipe.^6,9 When the toxicity of the individual metals was analyzed using ion activities, Cu was the most toxic, followed by Cd, Zn, and Ni in sequence of decreasing toxicity (Table 1).

Table 1.

Individual-Metal Toxicity Data for Metal Concentrations and Ion Activities (M²⁺ + MOH⁺) for Cd, Cu, Ni, and Zn^a

metal	metal concentration		ion activity		n
	EC50 (M) (95% CI)	slope (95% CI)	EC50 (M) (95% CI)	slope (95% CI)
Cd	8.36 × 10−7 A (5.80–10.91 × 10−7)	1.68 A (1.21–2.15)	2.98 × 10−7 A (2.67–3.30 × 10−7)	1.47 A (1.34–1.59)	8
Cu	1.41 × 10−6 B (1.21–1.70 × 10−6)	6.29 B (3.44–9.15)	1.74 × 10−8 B (1.40–2.09 × 10−8)	3.92 B (2.99–4.85)	5
Ni	3.14 × 10−5 C (2.34–3.95 × 10−5)	2.85 C (2.30–3.40)	9.92 × 10−6 C (8.92 × 10−6–1.09 × 10−5)	3.04 B (2.77–3.31)	8
Zn	1.21 × 10−5 D (0.69–1.74 × 10−5)	1.70 A (1.25–2.16)	3.65 × 10−6 D (3.12–4.19 × 10−6)	1.38 A (1.26–1.50)	5

^aThe average 48 h median effect concentration (EC50), slope of log–logistic concentration–response curve, and number of toxicity tests conducted (n) is reported for the immobilization of Daphnia magna neonates exposed to each of the metals in repeated static, non-renewal lethality tests. Numbers in parentheses are the 95% confidence interval (CI) on the EC50 or slope. Different capital letters within a column indicate statistically significant (p ≤ 0.05) differences among the metals.

3.2. Cu–Cd–Ni Mixtures

When the Cd concentration was held constant at 9 × 10⁻⁷ M, the Ni concentration of Ni was held constant at 2.3 × 10⁻⁷, 3.8 × 10⁻⁶, or 3.7 × 10⁻⁵ M, and Cu was increased from sublethal to lethal concentrations, the toxicity ranged from less-than-additive at very low Cu concentrations to approximately additive or even substantially more-than-additive toxicity at higher concentrations, depending on the additivity model used to analyze toxicity (Figure 2). At low Cu concentrations in the mixture, the predicted mortality was greater than the observed mortality (i.e., the observed-to-predicted mortality ratio was less than 1, indicating less-than-additive toxicity) regardless of whether the toxicity was modeled as CA or IA and whether metal concentrations or ion activities were used to predict the toxicity. This result is consistent with the less-than-additive toxicity in Cd–Ni binary mixtures⁹ because the Cu concentrations and ion activities contributed little to the toxicity in the low-Cu ternary mixtures (less than approximately 1 × 10⁻⁷ M Cu (1 × 10⁻⁹ M ion activity), which is less than 0.1 times the average Cu-only EC50). However, as the Cu concentration was increased to approximately 3–4 × 10⁻⁷ M Cu (3–4 × 10⁻⁹ M ion activity), the observed-to-predicted mortality ratio increased to approximately 1, indicating approximately additive toxicity. Similar to the less-than-additive trends at low concentrations, the additive effect in the midrange Cu concentrations was evident regardless of (1) whether the toxicity was modeled as CA or IA and (2) whether metal concentrations or ion activities were used to predict the toxicity.

At high metal concentrations and ion activities of Cu, the predictions of the additivity models diverged. The observed-to-predicted mortality ratio using the CA model remained close to the additive-toxicity ratio of 1, regardless of whether metal concentrations or ion activities were used to predict the toxicity (Figure 2A,B). In contrast, the IA model produced observed-to-predicted mortality ratios substantially greater than 1 at Cu concentrations greater than approximately 5 × 10⁻⁷ M (5 × 10⁻⁹ M ion activity), indicating more-than-additive IA-predicted toxicity (Figure 2C,D).

Even in the IA analyses, the highest concentration of Ni tested (3.73 × 10⁻⁵ M) exhibited the least extent of less-than-additive toxicity at Cu concentrations less than 2 × 10⁻⁷ M, as well as the generally least extent of more-than-additive toxicity (or even merely additive toxicity) at Cu concentrations greater than 2 × 10⁻⁷ M (Figure 2C). This is likely due to the high “background” concentration and ion activity of Ni in this series, for which high “background” mortality would be predicted based on results of the Ni-only tests. Because the predicted and observed mortality cannot exceed 100%, those mortality percentages converged and the ratio of observed-to-predicted mortality did not differ greatly from 1. Similarly, at the highest Cu concentrations and ion activities tested, the observed-to-predicted mortality ratio approached 1 because both the observed and predicted mortality percentages approached their maxima of 100%. Therefore, the ability to resolve non-additive toxicity disappears at very high metal concentrations, as it also disappears at very low metal concentrations that cause little to no toxicity.

When the roles of Cu and Ni were reversed (i.e., the Cd and Cu concentrations were held constant, while Ni was increased from sublethal to lethal concentrations), the responses again varied from less-than-additive, to approximately additive and, in some cases, to more-than-additive toxicity (Figure 3). In general, the lower Cu concentrations (4.6 × 10⁻⁷ and 6.3 × 10⁻⁷ M Cu, equivalent to 1.7 × 10⁻⁹ and 5.3 × 10⁻⁹ M ion activity) exhibited predominately less-than-additive or additive toxicity for the Cu concentrations as well as the Cu ion activities at every Ni concentration with both the CA and IA models. In contrast, the next two higher Cu concentrations (9.1 × 10⁻⁷ and 1.37 × 10⁻⁶ M Cu, equivalent to 9.6 × 10⁻⁹ and 2.3 × 10⁻⁸ M ion activity) ranged from approximately additive toxicity predicted by CA (Figure 3A,B) to substantially more-than-additive toxicity (i.e., observed-to-predicted mortality ratio was significantly greater than 1) predicted by IA (Figure 3C,D). As expected from Cd–Cu binary mixture tests with no added Ni,⁶ the ratio of observed-to-predicted mortality that occurred in the 9 × 10⁻⁷ M Cd–3.6 × 10⁻⁶ M Cu–3 × 10⁻⁸ M Ni ternary mixture (i.e., the left-most black data point in every panel of Figure 3) was less than 1; however, this ratio was not statistically different than 1. At all higher Ni concentrations combined with those Cd and Cu concentrations (i.e., at the highest background Cu concentration), the observed-to-predicted mortality ratio was equal to or approximately 1 because both the observed and predicted mortality percentages approached their maxima of 100%.

Figure 3.

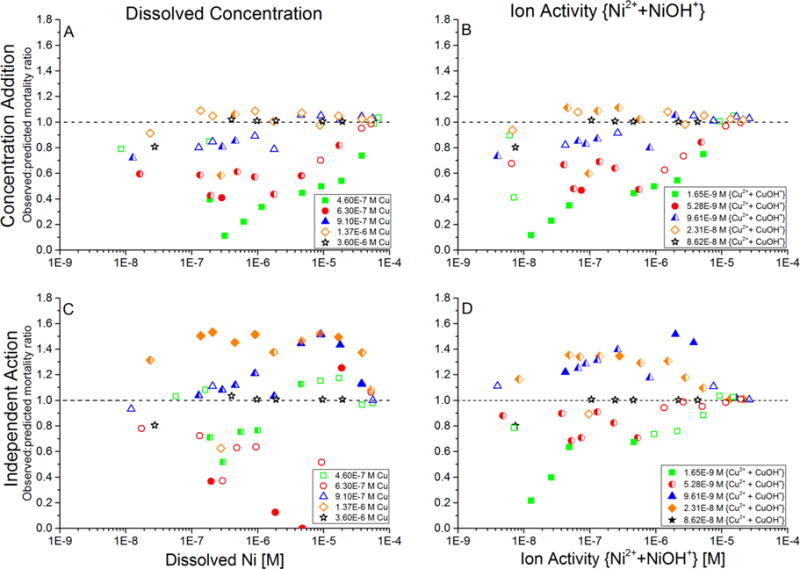
Additivity of toxicity of Cd–Cu–Ni mixtures that contained constant concentrations of Cd (9 × 10⁻⁷ M Cd in all exposure waters) and Cu (separate concentrations in each of the five sets of tests shown in the legend), while Ni was varied along a concentration gradient within each of the five sets of tests. Additivity of toxicity was evaluated by the ratio of observed-to-predicted mortality ratio, for which predicted mortality was calculated using either a concentration-addition or independent-action model. (A) CA model with predicted toxicity based on metal concentrations; (B) CA model with predicted toxicity based on ion activities; (C) IA model with predicted toxicity based on metal concentrations; and (D) IA model with predicted toxicity based on ion activities. Each data point is the average of duplicate runs of each combination of metal concentrations. Closed symbols: statistically significant non-additive toxicity (p ≤ 0.05) in both replicate trials; open symbols: not significant non-additive toxicity in both replicate trials; half-filled symbols: significant non-additive toxicity in only one of the two replicate trials. Ratios less than 1 indicate less-than-additive toxicity; ratios greater than 1 indicate more-than-additive toxicity.

The more-than-additive toxicity at high Cu or Ni concentrations and ion activities in Cd–Cu–Ni mixtures using the IA model is similar to the more-than-additive toxicity in Cu–Ni binary mixtures analyzed using the IA model,⁹ and it almost entirely overshadows any less-than-additive toxicity that would be expected from either Cd–Ni or Cd–Cu binary interactions at these concentrations and ion activities.^6,9 Although the results of these ternary Cd–Cu–Ni tests support the existence of the less-than-additive toxicity that has been demonstrated in Cd–Cu and Cd–Ni binary mixtures, the IA model suggests the more-than-additive Cu–Ni interaction can overshadow those protective effects at high Cu or Ni concentrations and ion activities.

If metal–metal competition for binding to DOM is an important cause of apparently more-than-additive toxicity when metal concentration is used to predict mortality, predicting toxicity using ion activities should reconcile the more-than-additive toxicity. According to this hypothesis,^6,9 the ion activity of at least one of the three metals in the ternary mixture would be higher than its ion activity at the same metal concentration in the absence of the other metals. In general, the WHAM VII speciation calculations supported this hypothesis but only at the highest Ni concentrations tested. Therefore, the observed-to-predicted mortality ratios using the IA model did not differ considerably (i.e., the more-than-additive toxicity conclusions did not change considerably) at the majority of the metal-concentration combinations in Figures 2C,D and 3C,D. However, the mortality ratios tended to decrease when metal–metal competition for binding to the DOM increased the ion activity of at least one metal.

For example, in Figure 2C,D, at the two lowest background Ni concentrations (2.3 × 10⁻⁷ and 3.8 × 10⁻⁶ M, both of which are less than the Ni EC50), the observed-to-predicted mortality ratios remained approximately constant because the Cd and Cu ion activities did not increase when combined with those Ni concentrations. However, at the highest background Ni concentration (3.7 × 10⁻⁵ M, which is approximately 4 times the EC50), the observed-to-predicted mortality ratios at intermediate Cu concentrations decreased to approximately 1 or lower because the WHAM-calculated Cd and Cu ion activities increased by approximately 2-fold when combined with that background Ni concentration and thus caused increased ion-activity-predicted mortality. Similarly, in Figure 3C,D, the observed-to-predicted mortality ratios decreased from as high as 1.4 down to approximately 1 at the highest Ni concentrations (>1 × 10⁻⁵ M) because the Cd and Cu ion activities were approximately 2- to 4-fold higher than in the absence of Ni. In addition, the lack of major changes in ion activities at low-to-intermediate Ni concentrations (when combined with most of the background Cu concentrations) resulted in minimal changes in the ion-activity-predicted mortality and, thus, in the observed-to-predicted mortality ratio. These results support our hypothesis that geochemical interactions could have contributed to more-than-additive mixture toxicity in some of the combinations of metal concentrations, but residual IA-predicted more-than-additive toxicity in other combinations of metal concentrations might also have been caused by other factors.

Because the observed-to-predicted mortality ratios approximately equaled 1 using the CA model at high concentrations and ion activities of Cu and Ni, but some of the ratios significantly exceeded 1 using the IA model, CA was a better predictor of toxicity at high-end concentrations in these Cd– Cu–Ni mixtures (i.e., the CA-predicted mortality approximately equaled the observed mortality). This result is interesting because, based on metal concentrations, the slopes of the concentration–response curves differ significantly among these three metals (which suggests different mechanisms or sites of action), thus indicating a priori that the IA model might be more appropriate than the CA model.² In contrast, based on ion activities, the slopes of the individual-metal curves for Ni and Cu no longer differed significantly from each other, but they remained significantly different from Cd (Table 1). These Cd–Cu–Ni toxicity results suggest that at least Cu and Ni might have the same mechanism and sites of toxicity instead of having separate mechanisms and sites of toxicity, at least for acute lethality to D. magna. However, it also is possible that Cu and Ni have separate mechanisms or sites of toxicity despite having similar concentration–response slopes, and a physiological interaction that is not accounted for by the bulk exposure-water chemistry causes the IA-predicted more-than-additive toxicity. More-extensive investigation would be needed to differentiate between these possibilities.

Because both the CA and IA models resulted in apparently less-than-additive toxicity at low-end metal concentrations and ion activities, chemical speciation of the metals in the bulk exposure water does not explain the protectiveness of the Cu and Ni against Cd toxicity in these concentration ranges. Instead, it appears that a different negative-feedback process or processes might dominate at those concentrations. Possible mechanisms include metal–metal competition for binding to the biotic ligand(s) and as-yet-unidentified physiological interactions after the metals are internalized by D. magna, as hypothesized elsewhere.^2,6,9

3.3. Cd–Ni–Zn Mixtures

Mixtures in which the combination of Cd, Ni, and Zn was tested largely exhibited similar results regardless of whether metal concentrations or ion activities were used to predict toxicity and regardless of the specific additivity model (CA or IA) that was used to analyze the data. When Ni and Cd concentrations were held constant while Zn was increased through an exposure-concentration series (Figure 4) and when Cd and Zn concentrations were held constant while Ni was increased through an exposure-concentration series (Figure 5), the observed mortality was almost always less than the CA- or IA-predicted mortality (i.e., the observed-to-predicted ratio was less than 1 for nearly all mixture concentrations). In Figure 4, at low concentrations of Zn, only one data point had an observed-to-predicted mortality ratio greater than 1, and it did not differ significantly from 1 in any of the analyses and occurred at the lowest tested concentrations of both Ni and Zn in the ternary mixture. Therefore, these data effectively represent a Cd-only toxicity test. When the same Cd concentration was tested with higher concentrations of Ni, Zn, or both Ni and Zn, in all instances, these metals protected against the Cd toxicity (the observed-to-predicted mortality ratio was less than 1). At high Zn concentrations (greater than 2–4 × 10⁻⁵ M, i.e., 1–2 × 10⁻⁵ M ion activity), the curves approach a ratio of 1 because of nearly 100% observed and predicted mortalities.

Figure 4.

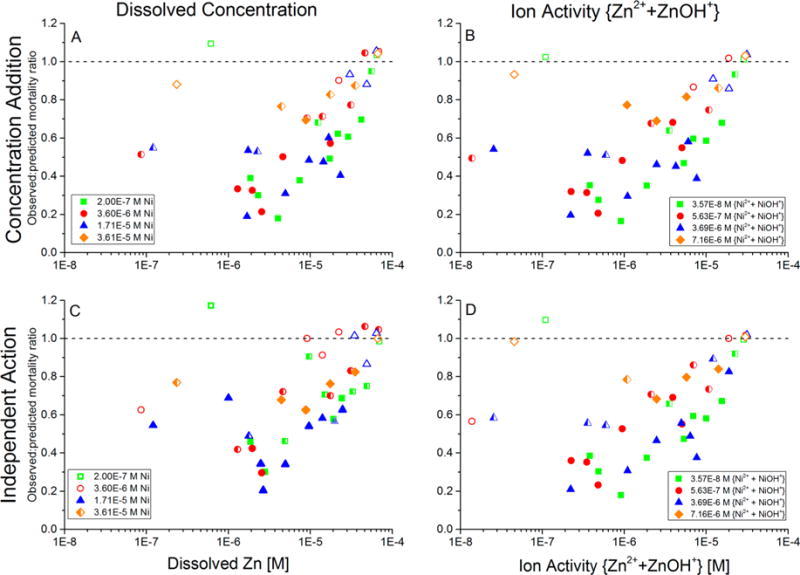
Additivity of toxicity of Cd–Ni–Zn mixtures that contained constant concentrations of Cd 9 × 10⁻⁷ M Cd in all exposure waters) and Ni (separate concentrations in each of the four sets of tests shown in the legend), while Zn was varied along a concentration gradient within each of the four sets of tests. Additivity of toxicity was evaluated by the observed-to-predicted mortality ratio, for which predicted mortality was calculated using either a concentration-addition or independent-action model. (A) CA model with predicted toxicity based on metal concentrations; (B) CA model with predicted toxicity based on ion activities; (C) IA model with predicted toxicity based on metal concentrations; and (D) IA model with predicted toxicity based on ion activities. Each data point is the average of duplicate runs of each combination of metal concentrations. Closed symbols: statistically significant non-additive toxicity (p ≤ 0.05) in both replicate trials; open symbols: not significant non-additive toxicity in both replicate trials; half-filled symbols: significant non-additive toxicity in only one of the two replicate trials. Ratios less than 1 indicate less-than-additive toxicity; ratios greater than 1 indicate more-than-additive toxicity.

In Figure 5, when Zn and Cd concentrations were held constant and Ni was varied across a gradient, the lowest constant concentration of Zn (3.4 × 10⁻⁶ M, equivalent to 1.1 × 10⁻⁶ M ion activity) initially caused the largest less-than-additive effect at very low Ni concentrations. This result is consistent with the previously reported less-than-additive interaction between Zn and Cd.⁶ At the intermediate constant Zn concentration (1.6 × 10⁻⁵ M, equivalent to 7.4 × 10⁻⁶ M ion activity), the toxicity was also less less-than-additive. At the highest constant Zn concentration (3.4 × 10⁻⁵ M, equivalent to 1.7 × 10⁻⁵ M ion activity), the observed-to-predicted mortality ratio was approximately 1, and thus, the mixture toxicity usually did not differ significantly from additivity. This latter result may be partially due to a “limit of detection” because the concentrations of Zn that were tested exceeded the EC50 of Zn (approximately 1.2 × 10⁻⁵ M concentration and 3.6 × 10⁻⁶ M ion activity; Table 1). As a result, multiple competing less-than-additive mechanisms did not combine to form a more-than-additive interaction in the Cd–Ni–Zn mixtures.

3.4. Synthesis

In our previous studies of binary-metal mixtures that contained various combinations of Cd, Cu, Ni, and Zn,^6,9 the wide range of additive and non-additive toxicity demonstrated why a predictive model that can account for the various chemical interactions of metals with each other in a mixture, with various components of the exposure water (e.g., pH, alkalinity, major cations, and DOM), and with biotic ligands would help to improve water-quality criteria and guidelines instead of continuing to regulate on a metal-by-metal basis in most jurisdictions. The same conclusions can be drawn from the results of the current ternary-metal toxicity tests. The additivity and nonadditivity of the mixture toxicity differed considerably when the concentrations of two of the metals were held constant, but the identity and concentration of the third metal were varied. Additional coordinated data sets with complete water chemistry and acute (for U.S. regulations) and chronic (for European regulations) toxicity data for these and other metal mixtures will be needed to improve the mechanistic basis for predictive models.

Our results for ternary-metal mixtures are similar to results of other studies of metal mixtures that included Cd, Cu, Ni, and Zn, in which a wide range of less-than-additive, additive, or more-than-additive toxicity was observed, depending on the combinations of metals, their concentrations, and the type of additivity model chosen to evaluate and predict the mixture toxicity. In general, less-than-additive effects are some of the most commonly observed interactions in ternary-metal mixtures involving Cd.^6,11,16 Xu et al.¹⁹ conducted toxicity tests on binary, ternary, and quaternary metal mixtures and also observed less-than-additive toxicity in binary mixtures of Cd and Zn but approximately additive toxicity in all ternary- and quaternary-metal mixtures. However, most of the mixture-toxicity studies to date either do not have a robust set of binary-mixture toxicity data to which ternary-mixture results can be compared, or the experiments were not conducted in a way in which consistency or discrepancies between the binary- and ternary-mixture results can be determined.

Our results indicate that the less-than-additive toxicity displayed at low-end concentrations in the ternary-metal mixtures is independent of the model chosen to determine additivity and that taking into account speciation of the metals does not eliminate the apparent less-than-additive toxicity. Based on these results and assuming the WHAM VII speciation results are relatively accurate, we conclude that the less-than-additive toxicity was caused by processes occurring at the surface of or inside the organism instead of being caused by physical-chemical processes controlled by the bulk exposure-water chemistry. Those processes at or inside the organism might include metal–metal competition for binding to the biotic ligand(s) and as-yet-unidentified physiological interactions of the metals.^2,6,9

Several geochemical processes can contribute to non-additivity of metal-mixture toxicity. We previously hypothesized that metal–metal competition for binding to DOM and inorganic ligands in the exposure water could potentially increase the free-ion concentration of one or more of the metals in the mixture, therefore contributing to either more-than-additive (if the less-toxic metal is competing for binding to nonbiotic ligands) or less-than-additive mixture toxicity (if the more toxic metal is competitively binding to the nonbiotic ligands) when expressed on a dissolved-metal basis.^6,9 However, our results for Cd–Cu–Ni mixtures demonstrate that the apparently more-than-additive effect using the IA model was equally evident in the analyses using both the Cu concentration and the ion activity. If Ni had been competing with Cd and Cu for binding to the DOM (thus resulting in a higher Cd, Cu, or Ni ion activity in the exposure water than would have been present in Cd-only, Cu-only, or Ni-only exposures at the same Cd, Cu, or Ni concentration), using the Cd, Cu, and Ni ion activities instead of the metal concentrations to predict the mixture toxicity should have accounted for this interaction and thus eliminated the apparently more-than-additive toxicity. As a result, we would have expected the observed-to-predicted mortality ratio to decrease from significantly greater than 1 to a value of approximately 1. Instead, based on the results in Figures 2 and 3, any increase in the ion activity of a more-toxic metal as a result of Ni being titrated into the solution did not increase enough to substantially increase the IA-predicted mortality. Therefore, we have concluded that the ion activity analysis did not help reconcile the mechanism influencing the more-than-additive toxicity.

Alternatively, nongeochemical processes such as metal–metal induced physiological interactions within the organism (potentially decreasing or increasing the toxicity of the metal mixture, thus contributing to less-than-additive or more-than-additive mixture toxicity) may be the cause of non-additive toxicity.^6,9 All of these geochemical and physiological processes can occur concurrently when an organism is exposed to a metal mixture, and the dominant effect will depend on the metals and their concentrations in the mixture. The contrast between Figures 2 and 4 presents an excellent example in which the mixture toxicity progressed from less-than-additive to more-than-additive as the concentration and ion activity of Cu was increased in a given combination of Cd and Ni concentrations (Figure 2), but the mixture toxicity was always less-than-additive (or at most only additive), as the concentration and ion activity of Zn was increased in a given combination of Cd and Ni concentrations (Figure 4).

The CA model predicted mortality in the Cd–Cu–Ni mixtures better than the IA model (i.e., the observed-to-predicted mortality ratio based on the CA model never exceeded 1.2, whereas the ratio based on the IA model considerably exceeded 1; see Figures 2 and 3). Because of that result and because the CA and IA models predicted mortality in the Cd–Ni–Zn mixtures approximately equally well and never predicted observed-to-predicted mortality ratios greater than 1.1 (Figures 3 and 4), the CA model appears to be preferred if only one model had to be chosen for predicting mortality in these two ternary mixtures. However, based on our results, we cannot exclude the possibility that an as-yet-unidentified greater-than-additive metal–metal interaction occurs at high-end concentration in Cd–Cu–Ni mixtures, thus making the IA model more “accurate”. Additionally, an apparent preference for the CA model based on the results with these two ternary-metal mixtures does not preclude the IA model from being more appropriate with other metal mixtures.

Although using observed-to-predicted mortality ratios made it easier to quantitatively demonstrate complex patterns of additive or non-additive toxicity than a simple comparison of observed and predicted EC50 values would allow, the resolving power of this method is limited when the metal concentrations considerably exceed the EC50 for one of the varied metals (i.e., at greater than 1.4 × 10⁻⁶ M Cu, 3.1 × 10⁻⁵ M Ni, or 1.2 × 10⁻⁵ M Zn in these D. magna tests). At concentrations greatly exceeding the EC50 of Cu or Ni, both the observed and predicted mortalities approach 100%, thus forcing the observed-to-predicted mortality ratio to approach a value of 1 and thereby making nonadditivity nondetectable. Nonetheless, this analysis of observed-to-predicted toxicity ratios is instructive when either the observed or predicted mortality in a mixture is greater than 0% and less than 100%.

Another limitation of using observed-to-predicted mortality ratios with our “titration” experimental design is that an upper detection limit on the extent of nonadditivity is automatically imposed. That upper detection limit is determined by the initial mortality caused by the “background” metals in the mixture. For example, if the combined mortality predicted for the constant “background” concentrations of Cd and Ni is 50%, the highest observed-to-predicted mortality ratio possible is 2 (because the highest more-than-additive observed mortality possible after addition of Cu to the mixture is 100%). Therefore, it might erroneously be concluded that a Cd– Cu–Ni mixture never under-predicts the toxicity by a factor of more than 2 if all the calculated observed-to-predicted mortality ratios are between 1 and 2, and that might be considered a satisfactory fit by some modelers or other practitioners. However, that result might simply have been an artifact of the experimental design because observed-to-predicted mortality ratios greater than 2 could in concept occur if the predicted mortality due to the constant “background” metal concentrations is less than 50%. In fact, this situation occurred in the current study because we purposely chose a constant “background” Cd concentration that would result in a predicted “background” mortality of 50% (thus leaving the most room to simultaneously detect either less-than-additive or more-than-additive toxicity). Had we wanted to determine whether extremely high observed-to-predicted mortality ratios were possible in our metal mixtures, we would have had to use “background” metal concentrations that would have resulted in approximately 20% predicted mortality (thus allowing us to detect observed-to-predicted mortality ratios as high as 5). The disadvantage to this choice of an EC20 (or any other low ECx concentration) for the “background” metal(s) would have been a decreased ability to infer statistically significant less-than-additive toxicity (i.e., decreased ability to detect observed-to-predicted mortality ratios of significantly less than 1).

Overall, testing binary, ternary, and quaternary mixtures is a useful start to help understand mechanisms and build preliminary models. However, metal combinations in natural systems often contain more than only a few metals and thus have almost unlimited possible combinations of metals and their concentrations. Additionally, the types and extents of interactions among metals might vary as water chemistry varies. Because testing a large number of combinations of metals and their concentrations in a wide variety of water chemistries would be expensive and time-consuming, many combinations of metals and water chemistry likely will never be evaluated. To this end, incorporating mechanistic models that include both geochemical interactions among metals and differences between the bioavailability of metals in mixtures could improve the prediction of metal-mixture toxicity.

Because the understanding of mechanisms underlying metal-mixture toxicity and the ability to predict those effects are still being developed, it is important to test interactions in mixtures that contain a relatively small number of metals before progressing to mixtures containing many metals. Based on the results of this study of ternary-metal mixtures, and similar to studies with binary-metal mixtures, more-than-additive, less-than-additive, and additive toxicity can all be observed in metal mixtures containing more than two metals, depending on the metals in the mixture and their concentrations. Because none of our results was inconsistent with the interactions expected from results of binary-metal mixtures (Figure 1), predictive models that can accurately describe a binary-metal system may be sufficient for predicting the toxicity of mixtures that contain more than two metals. Because the results were consistent with metal–metal competition for binding to dissolved ligands and biotic ligands, bioavailability-based models that incorporate these types of biogeochemical interactions might be useful for predicting multiple-metal toxicity.