Complexity analysis of cortical surface detects changes in future Alzheimer's disease converters

Abstract

Alzheimer's disease (AD) is a neurological disorder that creates neurodegenerative changes at several structural and functional levels in human brain tissue. The fractal dimension (FD) is a quantitative parameter that characterizes the morphometric variability of the human brain. In this study, we investigate spherical harmonic‐based FD (SHFD), thickness, and local gyrification index (LGI) to assess whether they identify cortical surface abnormalities toward the conversion to AD. We study 33 AD patients, 122 mild cognitive impairment (MCI) patients (50 MCI converters and 29 MCI nonconverters), and 32 healthy controls (HC). SHFD, thickness, and LGI methodology allowed us to perform not only global level but also local level assessments in each cortical surface vertex. First, we found that global SHFD decreased in AD and future MCI converters compared to HC, and in MCI converters compared to MCI nonconverters. Second, we found that local white matter SHFD was reduced in AD compared to HC and MCI mainly in medial temporal lobe. Third, local white‐matter SHFD was significantly reduced in MCI converters compared to MCI nonconverters in distributed areas, including the medial frontal lobe. Thickness and LGI metrics presented a reduction in AD compared to HC. Thickness was significantly reduced in MCI converters compared to healthy controls in entorhinal cortex and lateral temporal. In summary, SHFD was the only surface measure showing differences between MCI individuals that will convert or remain stable in the next 4 years. We suggest that SHFD may be an optimal complement to thickness loss analysis in monitoring longitudinal changes in preclinical and clinical stages of AD. Hum Brain Mapp 38:5905–5918, 2017. © 2017 Wiley Periodicals, Inc.

INTRODUCTION

The fractal dimension (FD) is a quantitative parameter that has been used in neuroimaging to analyze structural patterns of the human brain. Metrics of FD are able to characterize the complexity of a wide range of objects of interest by assessing how a fractal structure occupies their geometrical target space [Mandelbrot, 1983]. The versatility of FD analysis has enabled the development of a remarkable number of applications in structural neuroimaging [Di Ieva et al., 2015], mostly using the MRI modality, such as in multiple sclerosis [Esteban et al., 2009], amyotrophic lateral sclerosis [Rajagopalan et al., 2013], schizophrenia [Tae et al., 2005], mild cognitive impairment (MCI) [Yuan et al., 2013], or Alzheimer's disease (AD) [King et al., 2010]. Although some pioneer studies of FD analysis used single FD values to characterize the whole brain or hemisphere shape, new methods have arisen to evaluate FD from a higher resolution framework. As neurodegenerative disorders present distinctive structural changes along the cortical mantle, it seems optimal to evaluate them separately and not in combination with the rest of the cerebral tissue. In this sense, King [2014] has proposed a modification of the classic box‐counting method to estimate local FD values for regions of the cerebral cortex with sizes of from 15 to 60 isotropic voxels mm. Moreover, Yotter and collaborators [Nenadic et al., 2017, 2014; Yotter et al., 2011] have presented a new method to quantify local FD using spherical harmonic reconstructions [Shen et al., 2009] (SHFD). The SHFD method calculates FD complexity maps from a cerebral cortex surface at different scales: (1) global: a single value for the whole brain hemisphere; (2) regional: a set of values for regions of interest; and (3) local: a value for each surface vertex. This approach presents a high test–retest reliability [Madan and Kensinger, 2017] and has two main advantages compared to the box‐counting method [Yotter et al., 2011]: (1) as this method does not need to down‐sample the cortical surface, it delivers high‐resolution results; (2) moreover, it is able to obtain FD estimations independently of the orientation of the surface, which is a typical caveat of the box‐counting method.

Previous studies have analyzed the FD of the cerebral cortex in aging [Madan and Kensinger, 2016; Zhang et al., 2007] and MCI/AD individuals [King et al., 2010, 2009; King, 2014; Yuan et al., 2013], particularly using global and local box‐counting FD analysis of the cortical surface in both 2D [King et al., 2009] and 3D [King et al., 2010; King, 2014]. In general, the FD of the cortical surface of AD subjects is lower than controls—particularly in the medial temporal lobes and parietal lobes—and it correlates well with other brain surface measures such as local gyrification index (LGI) [Schaer et al., 2008] but not with thickness [Fischl and Dale, 2000]. In this study, we aimed to characterize the cortical surface complexity of AD and MCI individuals using a high‐resolution SHFD approach and two other well‐known surface analytical approaches, namely thickness and LGI. Thickness is associated to tissue lost or atrophy and LGI is a good descriptor of cortical development. On the other hand, the SHFD of the cortical surface measures the folding pattern, so more convoluted cortical surfaces or white matter structures with a more complicated branched pattern present higher SHFD values. Thus, SHFD can complement thickness and LGI metrics for the study of structural changes in AD by measuring the topological complexity of the cortex and providing a sensitive measure of subtle brain structural changes, even locally at vertex level. Furthermore, given that structural changes are thought to be close to cognitive decline [Jack et al., 2013], SHFD metric may be specially relevant for the identification of MCI at risk of conversion to AD. We directed our analysis to detecting the structural surface features that identify future conversion to Alzheimer's disease, particularly focused on differentiating MCI converters (MCIc) and MCI nonconverters (MCIn) in the next 4‐year follow‐up period. Thus, we used an SHFD method [Yotter et al., 2011] to analyze the shape of the cerebral surface (pial surface and gray/white surface) in a local cohort of 187 subjects. Despite the potential advantages of using fractal analysis to detect complex structural changes in AD stages, little is known about the differences between MCI subjects that convert to AD and MCI that remain stable [Yuan et al., 2013], and no information has been reported regarding high‐resolution SHFD changes in these populations.

METHODS

Subjects

We included 187 subjects in this study (see Table 1 for demographics): 32 elderly healthy control (HC) subjects (16 males, 16 females, mean age: 72.7 ± 5.9), 33 subjects with AD (10 males, 23 females, mean age: 75.7 ± 3.7), and 122 subjects suffering MCI (58 males, 64 females, mean age: 73.2 ± 5.7). All individuals with AD and MCI diagnosis were recruited by experienced neurologists from dementia units of the Valencian community healthcare system in Spain. Control participants were recruited from patient's relatives and/or friends without any notable medical illnesses; history of drug or alcoholic abuse; or a family history of AD. Participants were informed of the nature of the research and provided written informed consent prior to their participation in the study. The Institutional Review Board of the Universitat Jaume I of Castellón approved this research study and all of the study procedures conformed to the Code of Ethics of the World Medical Association.

Table 1.

Demographic data

	HC	MCI	AD
N	32	122	33	p‐value
Age (y)	72.7 ± 5.9	73.2 ± 5.7	75.7 ± 3.7	F = 2.82, P = 0.062a
Gender (M:F)	16:16	58:64	10:23	χ 2 = 5, P = 0.025b
MMSE	29.6 ± 0.7	27.3 ± 2.3	22.3 ± 3.3	F = 93.47, P = 1.64 × 10−17 c
FAQ	0.5 ± 0.56	3.74 ± 3.47	14.5 ± 6.55	F = 159.66, P = 1.7 × 10−25 c
Boston	11.96 ± 0.17	9.53 ± 1.94	7.35 ± 3.37	F = 22.20, P = 5.5 × 10−6 c
Phon. Flu.	13.69 ± 2.32	8.13 ± 2.55	5.37 ± 2.27	F = 28.37, P = 3.67 × 10−7 c
Sem. Flu.	17.60 ± 3.91	11.06 ± 3.22	7.96 ± 2.37	F = 23.64, P = 2.9 × 10−6 c
Imm. Recall	8.53 ± 0.98	4.04 ± 1.19	2.22 ± 1.45	F = 52.06, P = 2.43 × 10−11 c
Del. Recall	6.53 ± 0.94	1.13 ± 1.05	0.09 ± 0.39	F = 28.63, P = 3.20 × 10−7 c
FDS	7.18 ± 0.69	5.62 ± 1.32	4.70 ± 1.71	F = 10.34, P = 0.0016c
BDS	6.25 ± 1.07	3.69 ± 1.21	2.54 ± 1.26	F = 21.83, P = 6.5 × 10−6 c

Values expressed as mean ± standard deviation.

^aAnalysis of variance: HC, AD, and MCI.

^b χ ² test: HC, AD, and MCI.

^cAnalysis of variance: AD and MCI.

MMSE, Mini‐Mental State Examination; FAQ, Functional Activities Questionnaire; Phon. Flu., Phonemic Fluency; Sem. Flu., Semantic Fluency; Imm. Recall, Immediate Recall; Del. Recall, Delayed Recall; FDS, Forward Digit Span; BDS, Backward Digit Span.

The AD group was composed of patients that met revised criteria for probable AD [McKhann et al., 2011] and showed a Clinical Dementia Rating (CDR) score of 1 (mild AD). For the MCI group, the inclusion criteria included (1) memory complaints (autoinformed or confirmed by an informant); (2) objective memory impairment assessed with the long delay free recall subtests of the Verbal auditory memory subtest from the Barcelona's test [Peña Casanova, 2005]; (3) essentially intact activities of daily living; (4) no evidence of dementia; and (5) a CDR score of 0.5. Cognitively normal subjects were included in the control group if they had no memory complaint, normal performance (within ±1.5 SD corrected by age) in the tests included in the neuropsychological assessment (see below) and a CDR score of 0. None of the participants of the study had any of the following clinical characteristics: (1) other nervous system diseases such as a brain tumor, cerebrovascular disease, encephalitis, epilepsy, or met the criteria for other dementias different from AD or MCI in the case of impaired individuals; (2) Geriatric Depression Scale score ≥ 6 [Aguado et al., 2000; Yesavage et al., 1982]; (3) visible abnormalities reported by an experienced radiologist in magnetic resonance images, such as leukoaraiosis or infarction; (4) current psychiatric disorder or use of psychoactive medication.

All participants underwent a structured clinical interview and a neuropsychological assessment which included MMSE [Folstein et al., 1975; Lobo et al., 2002], Functional Activities Questionnaire (FAQ; [Pfeffer et al., 1982]), short form of Boston naming test [Serrano et al., 2001], Verbal fluency test, Verbal auditory memory subtest from the Barcelona test [Peña Casanova, 2005], and Digit subtest (forward and backward) from the Wechsler memory scale‐III (WMS‐III; [Wechsler, 1997]). The MCI patients were followed up clinically with periodic neuropsychological assessment and clinical interviews (every 6 months) for a period of 4 years, although the MR data was acquired only once in the first clinical visit. These patients were classified into two groups depending on the conversion to AD in any moment of the clinical follow‐up period (see Table 2 for demographics). MCI subjects were considered converted to AD when they met the AD criteria exposed previously in any of the clinical follow‐up evaluations by trained neurologist. The MCIn group consists of those subjects that showed no change during the time of follow‐up. The participants who abandoned the study before a year of follow‐up were included in the analyses involving the whole MCI group but were not included in the MCIc or MCIn groups. Thus, the follow‐up period for the MCI subjects ranged from 1 to 4 years (mean: 1.68 ± 1.08). Of note, MCIc (N = 50, 20 males, 30 females, mean age: 74.4 ± 5.3) and MCIn (N = 29, 14 males, 15 females, mean age: 71.9 ± 5.7) are subsamples of the baseline MCI population of 122 individuals. The baseline MCI group is referred to as MCI in figures and results.

Table 2.

Demographic data of MCI subjects

	MCIn	MCIc	P value
N	29	50
Time (y)a	2.34 ± 1.09	1.30 ± 0.90
Age (y)	71.96 ± 5.7	74.42 ± 5.3	F = 3.66, P = 0.06b
Gender (M:F)	14:15	20:30	χ 2 = 2, P = 0.15c
MMSE	28.8 ± 1.1	26.3 ± 2.4	F = 27.33, P = 1.42 × 10−6 b
FAQ	3.17 ± 1.62	5.04 ± 4.34	F = 4.93, P = 0.029b
Boston	10.10 ± 1.31	8.82 ± 1.61	F = 13.22, P = 4.97 × 10−4 b
Phon. Flu.	8.78 ± 2.23	8.11 ± 2.02	F = 1.86, P = 0.17b
Sem. Flu.	11.49 ± 2.28	10.31 ± 2.58	F = 4.11, P = 0.046b
Imm. Recall	4.03 ± 1.08	3.74 ± 1.09	F = 1.30, P = 0.25b
Del. Recall	1.24 ± 0.68	0.95 ± 0.88	F = 2.15, P = 0.14b
FDS	5.20 ± 0.81	5.28 ± 1.37	F = 0.06, P = 0.79b
BDS	3.58 ± 0.73	3.42 ± 1.14	F = 0.49, P = 0.48b

Subjects in MCIn group are those nonconverter MCI subjects with a follow‐up time >1 year. Values expressed as mean ± standard deviation.

^aTime to conversion for MCIc (AD diagnosis date–first MR date) and follow‐up time for MCIn (years).

^bAnalysis of variance.

^c χ ² test.

MMSE, Mini‐Mental State Examination; FAQ, Functional Activities Questionnaire; Phon. Flu., Phonemic Fluency; Sem. Flu, Semantic Fluency; Imm. Recall, Immediate Recall; Del. Recall, Delayed Recall; FDS, Forward Digit Span; BDS, Backward Digit Span.

MR Acquisition

MRI data acquisition was performed on a 3 T MR scanner (Siemens Magnetom Trio, Erlangen, Germany) using a 12‐channel head coil. Whole‐brain 3‐D images were collected using sagittal T1‐weighted images (MP‐RAGE sequence, 176 slices, 256 × 256 matrix, TR = 2300 ms, TE 2.98 ms, flip angle 9°, spatial resolution 1 × 1 × 1 mm).

Cortical Surface Reconstruction

Cortical reconstruction and volumetric segmentation of the images were performed using FreeSurfer v. 5.3 (http://surfer.nmr.mgh.harvard.edu/). The main processing steps in FreeSurfer consist of motion correction and averaging of multiple volumetric T1‐weighted images [Reuter et al., 2010], removal of nonbrain tissue [Ségonne et al., 2004], segmentation of the white matter and gray matter volumetric structures [Fischl et al., 2002], tessellation of the gray matter–white matter boundary [Fischl et al., 2001], and surface deformation to place the gray/white and gray/cerebrospinal fluid borders [Dale et al., 1999]. Once the cortical models are complete, two additional procedures were performed for further data processing and analysis: surface inflation [Fischl et al., 1999a] and registration to a spherical atlas to match cortical geometry across subjects [Fischl et al., 1999b].

Cortical thickness and LGI are two cortical measures widely used to detect structural complexity in the human brain. Following previous studies that have compared these two measures with the FD [Im et al., 2006; Jiang et al., 2008; King et al., 2010], we included them in our investigation. Cortical thickness is calculated in FreeSurfer as the closest distance from the gray/white boundary to the gray/CSF boundary at each vertex on the tessellated surface [Fischl and Dale, 2000]. The Gyrification index quantifies the amount of cortex buried within the sulcal folds as compared with the amount of cortex on the outer visible cortex. A cortex with extensive folding has a large gyrification index, whereas a cortex with limited folding has a small gyrification index. The method incorporated into FreeSurfer [Schaer et al., 2008] computes local measurements of gyrification at thousands of points over the whole cortical surface, generating a map called the LGI. Figure 1A–E shows an example of a T1‐weighted image, the corresponding pial (gray/cerebrospinal fluid border) and white (gray/white border) tessellated surfaces and the thickness and LGI maps for that image, all obtained by the FreeSurfer pipeline through the command recon‐all with the localGI option. As each individual map corresponds to a tessellated surface that is not equal between subjects, a preprocessing step is needed to smooth and reparameterize each individual map to a common space. These reparameterized and smoothed maps were computed in FreeSurfer through the commands mris_preproc, targeting the average subject provided by FreeSurfer, and mri_surf2surf with a default FWHM value of 10 mm. Finally, the average map for each group was calculated with the FreeSurfer command mri_concat. Global values of thickness and the gyrification index for each hemisphere were obtained as the average of the values at each vertex in the corresponding local map for that hemisphere. These global values were obtained by using the FreeSurfer command mris_anatomical_stats.

Figure 1.

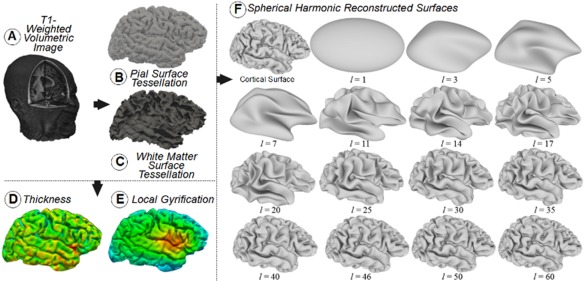
3D visualization of a T1‐weighted volumetric image (A). Surfaces and maps obtained from image A through the FreeSurfer pipeline: pial surface with overlapped tessellation (B); white surface (C); thickness map (D); and local gyrification index (LGI) map (E). The original cortical surface of a right hemisphere as was obtained from FreeSurfer and the reconstructed surfaces obtained with SPHARM for the SH functions with degree l ranging from 1 to 60 (F). [Color figure can be viewed at http://wileyonlinelibrary.com]

Fractal Dimension Computation Based on Spherical Harmonics

To obtain a precise local value of FD for each vertex of the pial and white tessellated surfaces, we implemented the SHFD method developed by Yotter et al. [2011]. Spherical domains or genus‐zero surfaces, as the surface representing a brain hemisphere, can be naturally decomposed into a set of spherical harmonics (SH) [Zhou et al., 2004]. The SH functions $\{Y_l^m\left(\theta ,\hspace{0.17em}\phi \right):\hspace{0.17em}\left|m\right|\le l\in \mathbb{N}\}$ are orthornormal functions defined on the unit sphere as

$$Y_l^m\left(\theta ,\hspace{0.17em}\phi \right)=k_{l,m}{P}_l^m\mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right)e^{im\phi }$$

where $\theta \in [0,\pi ]$, $\phi \in \left[\mathrm{0,2}\pi \right[$, $k_{l,m}$ is the constant $\sqrt{\frac{2l+1}{4\pi }\frac{\left(l-m\right)!}{\left(l+m\right)!}}$, and $P_l^m$ is the associated Legendre polynomial. A spherical function $g:{\mathbb{S}}^2\to \mathbb{R}$ can be expanded in terms of SH as

$$g\left(\theta ,\hspace{0.17em}\phi \right)=\sum _{l=0}^{\infty }\sum _{\left|m\right|\le l}{c_{l,m}Y}_l^m\left(\theta ,\hspace{0.17em}\phi \right)$$

where the coefficients $c_{l,m}$ are the amplitudes of the corresponding SH functions.

A genus‐zero triangulated 3D surface can be re‐parameterized to spherical coordinates [a spherical parameterization is a bijective mapping between (x, y, z) and ( $\theta ,\hspace{0.17em}\phi$)] and then described by three spherical functions $x\left(\theta ,\hspace{0.17em}\phi \right)$, $y\left(\theta ,\hspace{0.17em}\phi \right)$, and $z\left(\theta ,\hspace{0.17em}\phi \right)$. These three spherical functions can be expressed in terms of SH functions, and their corresponding coefficients c_{l , m} can be computed using standard least‐squares estimation up to a user‐specified maximum degree L _max. From these estimated coefficients, we can reconstruct the original function, where the larger L _max is used, the more accurate the reconstruction is.

We used the software package SPHARM (http://www.enallagma.com/SPHARM.php) to obtain the spherical parameterization of the triangulated surface describing the brain hemisphere [Shen and Makedon, 2006] and then to estimate the coefficients of the SH functions up to a degree of L _max = 60. From these coefficients, by using SPHARM, we obtained a set of reconstructions of the original triangulated surfaces of the hemisphere provided by FreeSurfer, from l = 1 to l = L _max [Shen et al., 2009]. This set of reconstructions is the base element used to calculate the SHFD value of the hemisphere and the SHFD map at local level. A limit of L _max = 60 was established based on the fact that the reconstructed surface quickly converges to the original surface when l increases and therefore, as we will show below, the reconstructions actually needed to calculate the SHFD value have a degree l rather lower than 60.

We show in Figure 1F the original triangulated cortical surface of a right hemisphere and a set of reconstructed surfaces from SH functions with degrees ranging from l = 1 to l = 60. The reconstructed surfaces have the same number of triangles as the original surface, 221,481 triangles in the case of Figure 1F, and each vertex in each surface reconstruction has the same vertex index. This figure also shows how quickly the reconstructed surface approximates the original surface when l increases, and therefore, the difference between consecutive reconstructions is very small for high values of l.

The classical box‐counting method for calculating the FD is based on counting the number of boxes covered by the object for different box sizes and then obtaining the slope of the log–log plot of (1/box size) versus number of covered boxes [Hou et al., 1990]. The algorithm used to obtain the SHFD [Yotter et al., 2011] follows a similar strategy, but the degree l of the reconstructed surfaces and the surface areas are used instead of considering the box sizes and the number of covered boxes, respectively. This allows us to obtain not only a global SHFD value for the entire hemisphere surface but also a local SHFD value for each vertex of the triangulated surface.

The global SHFD value for each hemisphere surface was calculated as follows: (1) The total area of each reconstructed surface was calculated by adding the area of all their triangles. (2) A log–log plot of degree l versus surface area was obtained from all reconstructed surfaces. In this plot, the areas of the reconstructed surfaces were normalized regarding the area of the original surface. (3) The global SHFD value was calculated as the slope of the regression line for the linear fragment of the log–log plot obtained in Step (2). Previous studies [Nenadic et al., 2014, ; Yotter et al., 2011] have demonstrated that a range of reconstructions with l from 11 to 29 provides the best approximation of this linear fragment for the case of the surface of a brain hemisphere obtained from FreeSurfer, so this was the range of l we used. This range of reconstructions supposes an approximate total area of 40% (l = 11) to 80% (l = 29) of the original surface area. Figure 2A shows the log–log plot and the regression line for the values obtained from the hemisphere in Figure 1F.

Figure 2.

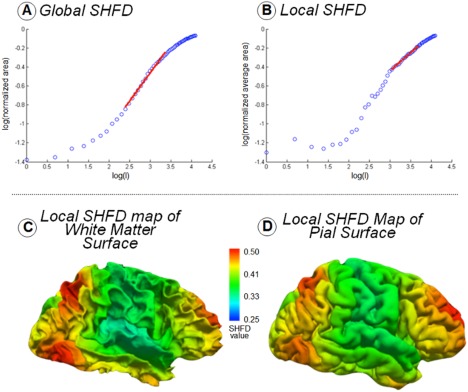
(A) Global SHFD computation as the slope of the regression line of the log–log plot of surface area versus degree l of the reconstruction. Surface areas of reconstructions were normalized by the original surface area. The linear approximation shown in red corresponds to reconstructions with degrees l from 11 to 29. (B) Local SHFD computation for a vertex as the slope of the regression line of the log–log plot of average area versus degree l of the reconstruction. Average areas for the vertex in each reconstruction were normalized by the original average area for that vertex. The linear approximation shown in red corresponds to reconstructions with degrees l from 21 to 40. (D) Local SHFD map of the pial surface shown in Figure 1. (C) Local SHFD map of the white surface shown in Figure 1. [Color figure can be viewed at http://wileyonlinelibrary.com]

The local SHFD value for each vertex of the hemisphere surfaces was calculated as follows: (1) An area value was associated to each vertex in each reconstruction calculated as the average area of the triangles of the reconstruction that share that vertex [Yotter et al., 2010]. (2) The set of average areas for the vertices in each reconstruction was smoothed through a 30 mm Gaussian heat kernel [Chung et al., 2005] by using the software provided by Dr Chung at http://brainimaging.waisman.wisc.edu/~chung/lb/. A distance of 30 mm was selected to enhance features in the range of the distance between sulci and gyri, which is about 20–30 mm [Luders et al., 2006]. (3) For each vertex, a log–log plot of degree l versus average area was obtained from all reconstructed surfaces. In this plot, the average areas associated to the vertex for each reconstructed surface were normalized regarding the average area associated to the vertex in the original surface. (4) The local SHFD value was then calculated as the slope of the regression line for the linear fragment of the log–log plot obtained in Step (3). Owing to the fact that the linear fragment is quite variable among the tens of thousands of vertices present in each surface, we selected the range of degrees l that maximized the correlation and minimized the error of the linear regression for the majority of the vertices. We made an exhaustive search testing all the intervals from l = 1 to l = 60 which have a size ranging from 15 to 20, and the selected interval corresponded to degrees l from 21 to 40. As an example, Figure 2B shows the log–log plot and the regression line for the values obtained for a vertex (the vertex number 20,034 out of 221,481) in the cortical surface shown in Figure 1F. Figure 2C,D respectively shows the local SHFD maps obtained visualizing the local SHFD values for all the vertices in the pial and white surfaces of the hemisphere shown in Figure 1B,C.

All SHFD algorithms were implemented in C++ and global SHFD values and local SHFD maps were obtained from the SH reconstructions of pial and white surfaces for all subjects in the study. To perform group comparisons at local level, average local SHFD maps for each group were obtained following the same steps described above for the case of thickness and LGI maps.

Statistical Analysis

Statistical differences between groups in global values for thickness, gyrification index, and SHFD were assessed using an analysis of covariance (ANCOVA) with age as covariate to remove the effect of age. The resulting values were thresholded at a P value of P < 0.05. Regression coefficients were computed using the Pearson partial correlation method controlling for the effect of age. Analyses at global level were performed using statistical functions within MATLAB R2013a (The MathWorks Inc., Natick, MA).

Vertex‐wise comparisons between each pair of groups at local level were performed using the general linear model (GLM) in FreeSurfer by using the mri_glmfit tool. In each group comparison, the measure (thickness, LGI, local SHFD—pial, and Local SHFD—white) was the dependent variable, and the diagnostic group was the independent variable, including age as a nuisance covariate. Surface maps showing significant differences between groups were then generated. Correlations of surface measures with MMSE were performed establishing the measure as the dependent variable and MMSE as the independent variable. All the results obtained were corrected for multiple comparisons using the false discovery rate (FDR) method [Benjamini and Hochberg, 1995] with a q rate of 0.05.

RESULTS

Alzheimer's Disease Versus Elderly Healthy Controls Comparisons

After comparing the global scores of SHFD, thickness, and LGI, we found that AD display significant reductions in their SHFD global values (Fig. 3A,B) and in thickness and LGI average scores (Fig. 3C,D). Particularly, SHFD was statistically significantly reduced in AD compared to HC in both cerebral hemispheres for the white matter SHFD and in the right hemisphere for the pial SHFD (Fig. 3A,B). Thickness was reduced in the AD group compared to HC in both hemispheres (Fig. 3C), and LGI was reduced in the AD group compared to HC unilaterally in the right hemisphere (Fig. 3D). All F‐statistics and exact P values of group comparison of Figure 3 are presented in Supporting Information, Table I. Moreover, for methodological comparison purposes, we show the Pearson correlation scores between SHFD, thickness, and LGI within each study group in Supporting Information, Table II. White‐matter SHFD and pial SHFD displayed r values ranging from 0.85 to 0.92. Both SHFD metrics were also correlated with LGI, with r values ranging from 0.50 to 0.78. The thickness score did not achieve significant positive correlation with any of the remaining metrics.

Figure 3.

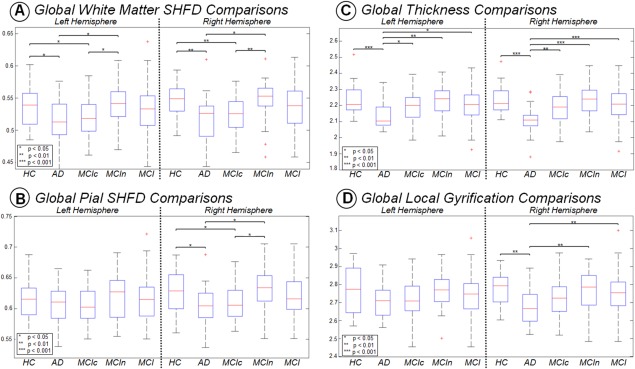
Boxplot with differences between groups for each hemisphere in Global SHFD ‐ white (A), Global SHFD ‐ pial (B), average thickness (C), and average LGI (D). P values correspond to ANCOVA analyzes with age as covariate. Only P values below 0.05 are displayed. [Color figure can be viewed at http://wileyonlinelibrary.com]

At local level, we found that white‐matter SHFD, thickness, and LGI analysis, but not pial SHFD, were able to detect significant vertex‐wise changes in the AD group compared to HC (Fig. 4). AD displayed significant decreases in white matter SHFD in the insula, temporal pole, medial temporal lobe—including the entorhinal, hippo/parahippocampus areas—and the posterior cingulate cortex (PCC) (Fig. 4A). AD displayed significant reductions of cortical thickness in the lateral temporal, anterior/medial temporal lobe—including the entorhinal, hippo/parahippocampus areas—and PCC (Fig. 4B). As for LGI, the AD group showed a more distributed pattern but with a particular contribution of the posterior‐medial temporal lobe (Fig. 4C). All comparisons between AD and HC were more prominent in the right hemisphere.

Figure 4.

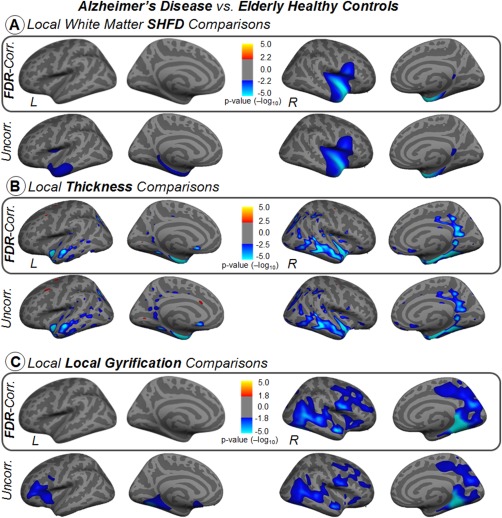
Vertex‐wise comparisons of white‐matter SHFD, thickness, and local gyrification index between Alzheimer's disease and elderly healthy control groups in inflated surface. Statistical analysis was controlled for age. Results were corrected for multiple comparisons using false discovery rating with q rate of 0.05. Uncorrected results are also displayed in the second row for references purposes. The color bars show the logarithmic scale of P values (−log 10). [Color figure can be viewed at http://wileyonlinelibrary.com]

Mild Cognitive Impairment Comparisons

At global level, SHFD was the only measure displaying significant reductions in MCIc group compared to HC and MCIc compared to MCIn. SHFD was also statistically significantly reduced in AD compared to MCIn and MCIc compared to HC, all presented in both cerebral hemispheres for the white matter SHFD and in the right hemisphere for the pial SHFD (Fig. 3A,B). Thickness was reduced in the AD group compared to MCIn, MCIc, and MCI in both hemispheres (Fig. 3C), and LGI was reduced in the AD group compared to MCIn and MCI unilaterally in the right hemisphere (Fig. 3D).

At local level, similar to comparisons involving healthy controls, the AD group showed reductions when compared to the baseline MCI group. Although some extension differences are observable in the maps, all three metrics display changes in equivalent cortical locations (Fig. 5A–C). Significant reductions in equivalent but smaller zones were found when compared AD to MCIn in thickness and LGI (maps not shown). No significant differences were found between HC and MCI in any measure.

Figure 5.

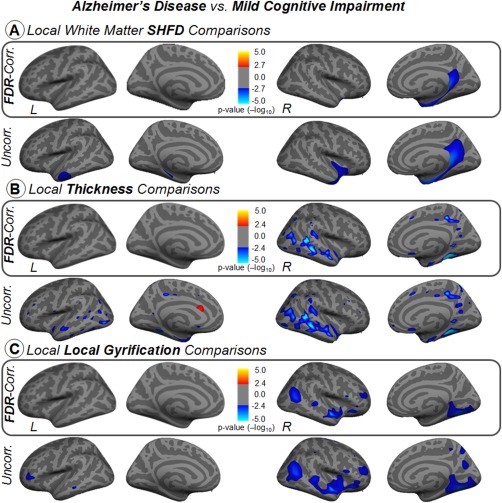
Vertex‐wise comparisons of white‐matter SHFD, thickness, and local gyrification index between Alzheimer's disease and mild cognitive impairment groups in inflated surface. Statistical analysis was controlled for age. Results were corrected for multiple comparisons using false discovery rating with q rate of 0.05. Uncorrected results are also displayed in the second row for reference purposes. The color bars show the logarithmic scale of P values (−log 10). [Color figure can be viewed at http://wileyonlinelibrary.com]

Importantly, we observed that only white‐matter SHFD and thickness were able to detect changes in the group of individuals that clinically convert to AD within the 4 years' follow‐up period (Fig. 6). The white matter SHFD metric showed cortical differences in distributed areas—including an extended area in the medial frontal lobe—between MCIc and MCIn (Fig. 6A). This metric also presented similar regions with cortical differences in the frontal lobe between MCIc and HC (Fig. 6B). On the other hand, the thickness approach captured differences in the entorhinal cortex, lateral temporal, and PCC between MCIc and HC (Fig. 6C). No significant differences were found between AD and MCIc in any measure. Of note, Supporting Information, Figures 1 and 2 show the average maps of the three cortical surface metrics per group.

Figure 6.

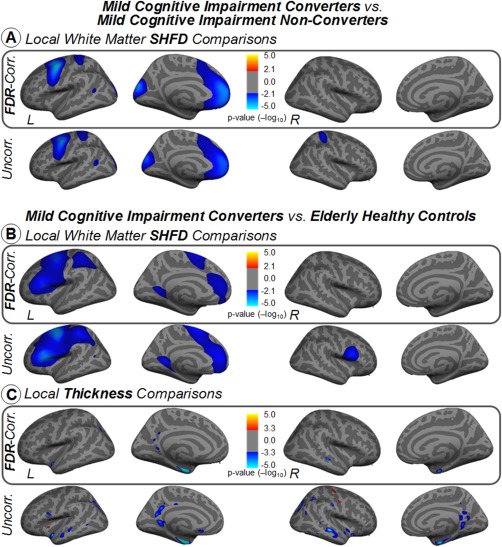
Vertex‐wise comparisons between mild cognitive impairment converters and mild cognitive impairment nonconverters groups for white‐matter SHFD (A), and vertex‐wise comparisons between mild cognitive impairment converters and elderly healthy control groups for thickness in inflated surface (B). Statistical analysis was controlled for age. Results were corrected for multiple comparisons using false discovery rating with q rate of 0.05. Uncorrected results are also displayed in the second row for reference purposes. The color bars show the logarithmic scale of P values (−log 10). [Color figure can be viewed at http://wileyonlinelibrary.com]

Association Between Local Cortical Complexity and Cognition (MMSE)

We investigated whether cognitive impairment was associated to the SHFD, thickness, and LGI metrics. No significant correlation was found between MMSE and any of the metrics in each group separately; nevertheless, we observed that MMSE correlates with cortical surface changes among the impaired individuals of our sample in all three approaches (Fig. 7). MMSE displayed significant correlations with white‐matter SHFD in distributed areas such as the left medial/superior frontal lobe, left intraparietal sulcus, and bilateral limbic areas—including the entorhinal and hippo/parahippocampus areas (Fig. 7A). MMSE displayed significant correlations with cortical thickness in the left lateral temporal, bilateral entorhinal and inferior temporal cortex, and right PCC (Fig. 7B). MMSE displayed significant correlations with LGI in distributed areas such as the bilateral posterior‐medial and lateral temporal lobe, insula, and dorsolateral prefrontal cortex (Fig. 7C). We have also investigated MMSE association in the group composed of AD plus MCIc (Supporting Information, Figure 3). Compared to the previous results (AD plus MCI), we observed that some FDR‐corrected correlations on the left hemisphere disappear, while cortical areas with significant correlation in the right hemisphere remain present.

Figure 7.

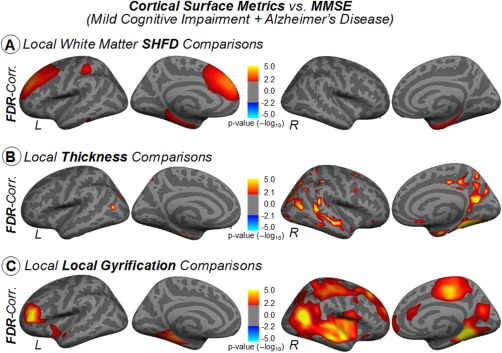
Vertex‐wise partial correlations, with age as nuisance covariate, between cortical measures and MMSE for AD plus MCI. Results were corrected for multiple comparisons using false discovery rating with q rate of 0.05. The color bars show the logarithmic scale of P values (−log 10). [Color figure can be viewed at http://wileyonlinelibrary.com]

We also computed all partial correlations controlling for the age between the other neuropsychological measures (Table 1) and the three structural metrics for each group. However, no significant correlation was found in any of these measures.

Association Between Local Cortical Complexity and Age

Finally, given that age is one of the most important factors for brain structural changes in elderly, we also investigated whether age was associated with cortical surface metrics. We found that thickness in the HC group was the only measure displaying significant correlations with age. At global level, correlation coefficients r = −0.49 (left hemisphere) and r = −0.44 (right hemisphere) were obtained. Vertex‐wise correlations shown in Supporting Information, Figure 4 indicate that thickness decreases with age in some small areas of the anterior/superior temporal lobe, supramarginal gyrus, and superior frontal gyrus.

DISCUSSION

AD involves neurodegenerative changes that alter the structural complexity of the human brain. As these structural alterations begin years before the clinical manifestations and conversion to AD, there is a critical need for developing and implementing neuroimaging biomarkers that can detect changes in the normal shape of the cerebral gyri. In the past, cortical‐related assessments such as thickness and LGI analysis, and more recently, FD quantifications have been proposed as sensitive approaches to detecting early fingerprints of neurodegeneration due to their ability to characterize small morphometric deformations at the surface level. Using a large sample of individuals, we found that FD, thickness, and LGI metrics display distinctive capabilities for describing cortical complexity changes in impaired populations (AD, MCI, MCIc, and MCIn) compared to healthy controls.

In our study, we included three surface‐related methods belonging to two different categories: one aimed to investigate the cortical thickness, therefore, with little ability to assess shape‐related properties, and two focused on detecting changes in cortical folding patterns (FD and LGI). In agreement with these categories, we observed that global white matter SHFD, pial SHFD, and LGI approaches display strong correlations among themselves within all studied groups, while the thickness approach did not show significant positive associations with the other two methods. Other studies have shown similar findings, where significant correlations between global FD measurements based on box‐counting or regional FD assessments and gyrification index have also been described in control groups [King et al., 2010; Madan and Kensinger, 2016]. Moreover, King et al. [2010] reported no correlations between thickness and FD of pial and white matter surface, although other significant correlations were found between the FD of the pial surface and thickness in healthy subjects [Im et al., 2006; Jiang et al., 2008; Madan and Kensinger, 2016]. Interestingly, King et al.'s study also obtained better estimations for FD differences between studied groups using the white surface rather than the pial surface. Our results fully agree with this observation, where the white‐matter SHFD approach seems to be more sensitive to detecting bilateral changes at the global level and statistically corrected changes at the local level than the pial SHFD.

Despite the potential advantage of detecting complex structural changes, it is still poorly understood whether cortical surface‐based methods are useful for characterizing populations at risk of conversion to AD. Thus, we designed our study to investigate the structural surface features that may identify future conversion to Alzheimer's disease in MCI subjects. In this sense, several recent studies have analyzed and compared the local thickness between healthy controls and patients suffering MCI and AD [Blanc et al., 2015; Delli Pizzi et al., 2014; Julkunen et al., 2009; Li et al., 2011; Mak et al., 2015; Wang et al., 2016; Zhao et al., 2015] (in Wang et al., 2016, LGI is also analyzed). In general, they reported significant differences between HC and AD in similar regions as our findings, including the bilateral temporal cortex, and distributed regions in the parietal and frontal lobe [Blanc et al., 2015; Delli Pizzi et al., 2014; Li et al., 2011; Zhao et al., 2015]. The study presented in Mak et al. [2015] is a longitudinal analysis involving the percent change of thickness over 12 months (longitudinal cortical thinning). Although their results are not directly comparable to ours, they found significantly greater percent change of thickness in the AD group compared with HC in similar bilateral regions, where we found significant differences between HC and AD: the temporal pole, lateral and medial temporal lobe, and PCC. Moreover, small parietal and temporal regions with significant differences between HC and amnestic MCI were found in Wang et al. [2016] in both thickness and LGI. Julkunen et al. [2009] found that MCIc displayed significantly reduced thickness bilaterally in the superior and middle frontal, superior, middle and inferior temporal, fusiform, and parahippocampal regions and the cingulate and retrosplenial cortices and also in the right precuneal and paracentral regions compared to MCIn subjects. As for FD‐related studies, there is only one previous investigation that applies a local FD approach to AD or MCI individuals [King, 2014]. Unfortunately, that study uses a box‐counting local FD method on only two subjects: one healthy control and one AD patient, and it is difficult to draw conclusions about any similarities with ours. Another study used a longitudinal FD (box‐counting) approach to study the atrophy of several regions of interest (ROI) in MCI [Yuan et al., 2013]. Although the box‐counting FD of ROIs is not exactly equivalent to a local vertex‐wise FD analysis such as ours, their results revealed lower FD values for MCIc compared to MCIn after 12 months (hippocampus), 18 months (temporal lobe), and 24 months (cingulate gyrus) of follow‐up.

As supported by our findings, all three surface‐based metrics (white‐matter SHFD, thickness, and LGI) are able to detect cortical changes in the AD group compared to HC and MCI. However, they perform distinctively. White‐matter SHFD FD identifies changes in limbic structures, particularly in the temporal lobe and PCC. Thickness also distinguishes limbic regions in the medial temporal lobe and PCC, but additionally detects alterations in the lateral temporal. LGI is able to capture local changes in the posterior‐medial temporal lobe.

In any case, one of the most interesting target populations in AD research is the MCI converter. As AD stages may be too late to introduce therapeutic interventions, the study of MCI individuals that remain stable or not over time may be more interesting to understand the underlying mechanisms of progression. Thus, we investigated the three surface‐based metrics in MCI individuals with information about future conversion within 4 years. When comparing MCIc and MCIn, only white‐matter SHFD showed significant differences both at the global and local vertex‐wise level. Moreover, white‐matter SHFD displayed changes between HC and MCIc in similar regions as white‐matter changes between MCIc and MCIn. On the other hand, the thickness approach detected changes between HC and MCIc and between HC and AD in analogous regions. In this sense, white‐matter SHFD and thickness analysis may complement each other to cover the preclinical spectrum of AD, in which thickness analysis seems to be sensitive to detecting early conversion in the entorhinal and limbic system and white‐matter SHFD in the medial prefrontal system, a prominent area of the default mode network. No known previous studies have examined the biological mechanism of the FD changes in AD or MCI. It is hypothesized that FD reductions in the brain WM could be mainly due to axonal loss, although other factors such as an increased water content, a decreased myelin content, and other inflammatory events can also contribute to a more amorphous tissue that may lead to the decrease of FD [Esteban et al., 2007; Zhang and Yue, 2016].

Finally, our study supports the association between cortical surface‐based metrics, including white‐matter SHFD, and cognitive impairment measured by MMSE. In the past, the correlation between thickness, LGI, and MMSE in AD and aMCI has been analyzed in several studies [Blanc et al., 2015; Fjell et al., 2009; Wang et al., 2016; Yao et al., 2012]. Results shown in Blanc et al. [2015] and Fjell et al. [2009] revealed significant correlations between thickness and MMSE in an AD group in distributed areas including parietal and temporal entorhinal cortices. In Wang et al. [2016], the aMCI group shows small regions with significant correlation between thickness and MMSE (left post central, left inferior parietal, left precuneus, right supra marginal, and right fusiform), although in Yao et al. [2012], only a region on the left‐middle and superior temporal gyrus presented a positive correlation between thickness and MMSE in aMCI. In Wang et al. [2016], LGI and MMSE presented a positive correlation for the aMCI group in a small zone of the right superior temporal gyrus. Similar to our previous comparison results, white‐matter SHFD, thickness, and LGI display patterns of cortical associations in which different cortical systems correlate with MMSE.

CONCLUSIONS

Our results suggest that white‐matter SHFD may be a sensitive measure for characterizing complex cortical folding changes in populations at risk to convert to AD. SHFD results complement known findings about thickness loss in AD and MCI samples. In this sense, SHFD appears to be a promising tool for obtaining a deeper understanding in morphological changes of cortex present in AD, MCI, and possibly other neurodegenerative diseases. The main study limitation is the relatively small sample size of the HC group (N = 32).

Supporting information

Supporting Information