Abstract
Due to the correlated nature of diffused light, the problem of reconstructing optical properties using diffuse optical tomography (DOT) is ill-posed. US-, MRI- or x-ray-guided DOT approaches can reduce the total number of parameters to be estimated and improve optical reconstruction accuracy. However, when the target volume is large, the number of parameters to estimate can exceed the number of measurements, resulting in an underdetermined imaging model. In such cases, accurate image reconstruction is difficult and regularization methods should be employed to obtain a useful solution. In this manuscript, a simple two-step reconstruction method that can produce useful image estimates in DOT is proposed and investigated. In the first step, a truncated Moore-Penrose Pseudoinverse solution is computed to obtain a preliminary estimate of the image that can be reliably determined from the measured data; subsequently, this preliminary estimate is incorporated into the design of a penalized least squares estimator that is employed to compute the final image estimate. By use of phantom data, the proposed method was demonstrated to yield more accurate images than those produced by conventional reconstruction methods. The method was also evaluated with clinical data that included 10 benign and 10 malignant cases. The capability of reconstructing high contrast malignant lesions was demonstrated to be improved by use of the proposed method.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.1610) Clinical applications, (170.3010) Image reconstruction techniques, (170.3660) Light propagation in tissues, (170.3880) Medical and biological imaging, (170.6935) Tissue characterization
1. Introduction
Diffuse optical tomography (DOT) and spectroscopy (DOS) have been explored for diagnosis of breast cancers [1–12]. Utilizing DOT or DOS alone to perform breast cancer diagnosis has been reported in many studies [1–4,8,13]. However, due to intensive light scattering in tissue, lesion localization and light quantification accuracy may not be fully demonstrated [4,13]. Because of the correlated nature of diffused light measured at multiple optical source and detector positions and also measurement noise, the DOT reconstruction problem is ill-posed and often underdetermined.
A variety of image reconstruction methods have been employed to improve target reconstruction accuracy in DOT. This includes the algebraic reconstruction technique (ART) [14], nonlinear iterative gradient based optimization methods [15–17], and Newton-like methods that requires the direct calculation and inversion of the Jacobian or weight matrix [18,19]. Reconstruction methods using a prior information determined from co-registered high resolution MRI [9, 20–24], x-ray imaging [10,11], and ultrasound imaging (US) [5,6,12, 21] have been investigated extensively. These methods segment the lesion and background regions or different tissue types seen by a high resolution modality, and therefore reduce voxels with unknown optical properties and improve the ill-posed and underdetermined DOT reconstruction problem.
Another means of incorporating a prior information into an iterative image reconstruction method is through the initial image estimate. Behnoosh and Zhu proposed a two step reconstruction using Genetic Algorithm (GA) to find a suitable initial image estimate that was subsequently refined by use of a conjugate gradient (CG) method, which showed improved target quantification as compared to CG with zero initial estimate [25]. However, GAs are time-consuming and an optimal CG stopping criterion for use with experimental data is difficult to specify.
In this manuscript, a simple two-step reconstruction method that can produce useful image estimates in DOT is proposed and investigated. In the first step, a truncated Moore-Penrose Pseudoinverse (MPP) solution is computed to obtain a preliminary estimate of the target image that can be reliably determined from the measured data; subsequently, this preliminary estimate is incorporated into the design of a penalized least squares estimator that is employed to compute the final image estimate. The MPP was employed to compute the initial estimate of the target image for several reasons. Firstly, the MPP pseudoinverse, by definition, produces the least-squares estimate of the image that possess the minimum norm. This yields a solution that can be interpreted as an orthogonal projection of the true target image onto a subspace that is the orthogonal complement to the null space of the imaging operator. Therefore, the MPP solution describes the estimate of the target that is closest to the true target but contains no component in the null space. This is a reliable strategy for image reconstruction when no reliable a priori information about the target is available. Secondly, the MPP pseudoinverse solution can be easily regularized by excluding contributions that correspond to small values. Therefore, there is little ambiguity in how to choose the regularization parameter. Thirdly, the MPP pseudoinverse operator for our system can be explicitly stored in memory, which leads to near real-time image reconstruction. By use of phantom data, the proposed method was demonstrated to yield more accurate images than those produced by conventional reconstruction methods. The method was also evaluated with clinical data that included 10 benign and 10 malignant cases. The capability of reconstructing high contrast malignant lesions was demonstrated to be improved by use of the proposed method.
2. Methods
2.1 Constrained optimization
The propagation of diffused light through tissue can be described by photon diffusion approximation as [26]:
| (1) |
where S(r) is the equivalent isotropic source and, U(r) is the photon density wave, D is the diffusion coefficient, and are the absorption and reduced scattering coefficients, respectively. The inverse problem is typically linearized by Born approximation [26]. By digitizing the imaging space into N voxels, the resulted integral equations are formulated as following:
| (2) |
where is the measured scattered photon density wave, M is the number of measurements, denotes the unknown changes of absorption coefficient at each voxel. The weight matrix, W, describes the distribution of diffused wave in the homogenous medium and characterizes the measurement sensitivity to the absorption and scattering changes. At the end, the inverse problem can be formulated as an unregularized optimization problem as:
| (3) |
In our ultrasound-guided DOT image reconstruction, a dual-zone mesh scheme is used to segment the imaging volume into a lesion region identified by co-registered US and a background region with fine and coarse voxel sizes, respectively [27]. This scheme effectively reduces the total number of voxels with unknown optical properties. The conjugate gradient (CG) method is utilized to iteratively solve the inverse problem. As a result, the target quantification accuracy can be significantly improved. However, when the lesions are larger, the total number of finer voxels and coarse voxels, N, can be much larger than the total measurements, M, which is the number of sources × the number of detectors × 2 = 14 × 9 × 2 = 252 counting for both amplitude and phase data. Due to the correlated nature of diffused light measured at closely spaced source and detector positions and also measurement noise, increasing the number of sources and detectors does not effectively mitigate the ill-conditioned nature of the DOT inversion problem.
In this manuscript, we formulate the inverse problem as:
| (4) |
where is a preliminary estimate of the optical properties that can be reliably determined from the measured data and λ is a regularization parameter. A Newton-like or conjugate gradient optimization method will be employed to approximately solve Eq. (4). No spatial or temporal filters were used on solution of
2.2 Truncated pseudoinverse as an initial estimate
We propose to employ a truncated pseudoinverse (PINV) operator of to form the preliminary estimate of as , which appears in the second term in Eq. (4). According to singular value decomposition (SVD) theory, can be decomposed as:
| (5) |
and are left and right singular vector of W or orthonormal eigenvector of , are nonzero eigenvalues of or and R is the number of nonzero singular values.
MPP of W is,
| (6) |
From system of linear equations, Eq. (2),
| (7) |
Since our measurement contains noise, we assume additive noise n, Then the reconstructed absorption is given as:
| (8) |
For very small singular values , may contain image artifacts.
In the truncated MPP approach, a threshold is set for singular values and the initial solution using MPP is:
| (9) |
In the phantom and clinical data, we have chosen as 10% of as a cut off value. From the truncated pseudoinverse, a preliminary estimate of unknown optical properties can be obtained. A simple projection operation is used to suppress pixels outside the region of interest identified by a sphere B obtained from measurements of co-registered ultrasound image. This projected absorption map is used as an initial solution for Newton or Conjugate gradient search method.
2.3 Newton method
The Newton method uses 2nd derivative of objective function (known as hessian) to calculate a 2nd order search direction resulting in quadratic convergence rate. We reformulate our penalized least square problem as a quadratic optimization problem,
| (10) |
Clearly, the hessian is positive definite when . Our solution is iteratively updated using following equations,
| (11) |
The iteration process is terminated when change of objective function between successive iterations become smaller than a preset tolerance. Choice of the regularization parameter is a critical part of solution design. Based on tumor size measured from ultrasound image and largest singular value of weight matrix, we empirically chose our regularization parameter as , where p is proportional to tumor size.
2.4 Conjugate gradient method
The Conjugate gradient (CG) method is a well-known iterative technique for solving symmetric positive definite linear systems of equations. We investigated this method both with regularization and without regularization. For the unregularized optimization formulation as given in Eq. (3), is only positive semi-definite because it possesses singular values that take on zero values. From phantom experiments using absorbers with known optical properties, we determined 3 iterations as a stopping criterion because the reconstructed absorption coefficients are close to known values. For the regularized least square formulation , and is, by construction, symmetric and positive semi-definite. For any choice of , will be a positive definite matrix since the lower bound for the singular values of is . Again, is chosen with p proportional to the target size measured from US. The algorithm for implementing the CG method is adapted from Ref.28.
2.5 Comparison of five reconstruction methods
Five reconstruction methods have been compared using phantom and clinical data. Using zero as an initial estimate of target optical properties and regularized Newton optimization (Newton Zero initial) and regularized CG optimization (CG Zero initial); using PINV as an initial estimate of target optical properties and regularized Newton optimization (Newton PINV initial), regularized CG optimization (CG PINV initial), and using zero initial estimate and unregularized CG. Additionally, target centroid error i.e. the absolute difference between the center of a phantom target measured by co-registered US and the centroid of corresponding reconstructed target absorption map, is calculated as a measure of reconstruction quality.
2.6 US-guided DOT system, data acquisition
Our US-guided DOT system has been reported earlier [28]. Briefly, it consists of a commercial US system and a NIR imager. Four laser diodes of wavelength 740, 780, 808 and 830 nm respectively are used to deliver light modulated at 140 MHz carrier frequency to tissue. Each laser diode is multiplexed to 9 positions on a hand-held probe and 14 photomultiplier detectors (PMT) detect reflected light via light guides. A custom A/D board samples detected signals from each patient at both lesion and contralateral normal breast and stores it in PC. Multiple data sets acquired from contralateral normal breast are used to compute a composite reference [29]. We consider a composite reference as homogeneous reference and use fitted optical absorption and reduced scattering to calculate for each wavelength. Lesion absorption maps of 4 wavelengths were reconstructed and total hemoglobin map was calculated from the absorption maps using extinction coefficients from these four wavelengths [30].
3. Methods
3.1 Phantom experiments
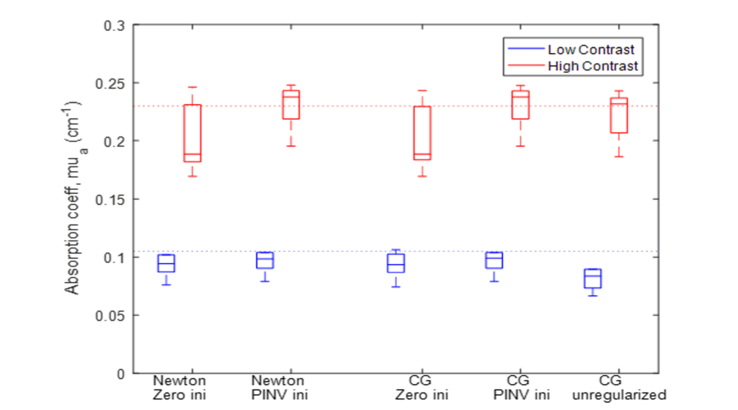
Phantom experiments were performed with solid ball phantoms of different sizes and different optical contrasts emulating tumors. These targets were submerged in 0.08% intralipid solution of in the range of 0.02-0.03 and in the range of 7 to 8 emulating homogeneous background tissue. We used 3 different sized solid balls with diameters of 1, 2 and 3 cm submerged at depths of 1.5 cm to 3 cm in 0.5 cm step in depth. The calibrated high and low contrast phantoms were and mimicking malignant and benign lesions, respectively. An absorption map for each target location, size and contrast was reconstructed and maximum is obtained for quantitative comparison. Average reconstructed maximum from all target conditions using five reconstruction methods are given in Table 1 and shown in Fig. 1. Errors of both high and low contrast targets reconstructed using different methods are given in Table 2. As seen from the Table, Newton and CG with PINV as an initial accurately estimate absorption coefficient while Newton and CG with a zero initial produce larger errors. Unregularized CG gives a better estimate for high contrast phantoms but results in under reconstruction for low contrast ones.
Table 1. Maximum reconstructed absorption (cm−1) (mean ± standard deviation) for phantom.
|
Newton with
zero Ini |
Newton with PINV ini |
CG with
zero ini |
CG with
PINV ini |
CG unconstrained | |
|---|---|---|---|---|---|
| Reconstructed μa (low contrast) | |||||
| Reconstructed μa (high contrast) |
Fig. 1.
Box plot of phantom data obtained from 1 to 3 cm size absorbers of high contrast (red) and low contrast (blue) located at different depths (1.5-3.5 cm center depth) using zero and PINV as an initial guess and Newton as optimization, respectively (first and second columns), zero and PINV as initial guess and CG, respectively (third and fourth columns), and unregularized CG (last column).
Table 2. Errors (mean ± standard deviation) in reconstructed absorption coefficient using different method.
|
Newton with
zero Ini |
Newton with PINV ini |
CG with
zero ini |
CG with
PINV ini |
CG unconstrained | |
|---|---|---|---|---|---|
| Error (low contrast) | 11.6 ± 13.8% | 0.04 ± 9.1% | 11.8 ± 13.2% | 0.1 ± 9.0% | 3.5 ± 9.9% |
| Error (high contrast) | 12.0 ± 16.1% | 9.6 ± 14.6% | 15.6 ± 10.9% | 8.8 ± 15.8% | 26.5 ± 8.5% |
3.2 Patient data
Performance of proposed method is demonstrated using clinical data obtained from 20 patients [12]. Based on biopsy results, 10 patients had benign lesions and 10 patients had cancers. The study was approved by the local Institution Review Boards (IRB) and was compliant with the Health Insurance Portability and Accountability Act (HIPPA). Informed consent was given by each patient. Data used in this study have been de-identified.
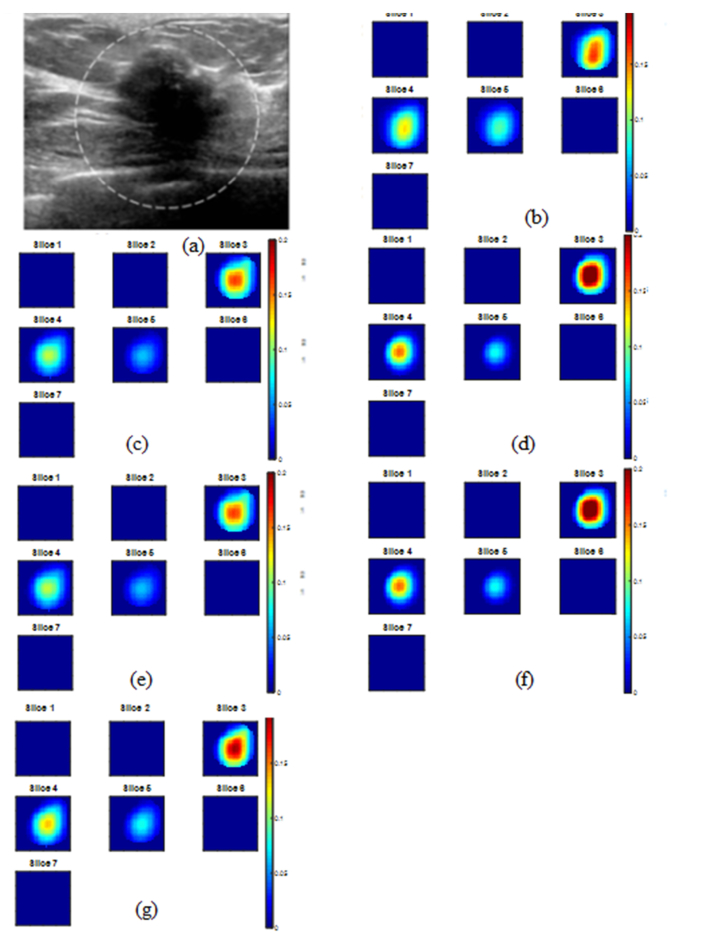
An example of a cancer case is shown in Fig. 2. Figure 2(a) is the co-registered US image with the suspicious lesion marked by a circle. Absorption maps of PINV initial image from truncated PINV (b) and reconstructed images using Newton with zero initial (c), PINV initial (d), CG with zero initial (e), CG with PINV initial (f) and unregularized CG (g) have shown similar lesion position and shape, however, the Newton’s method with PINV initial yields highest reconstructed µa = 0.268 cm−1. An example of a benign lesion is shown in Fig. 3. Figure 3(a) is the co-registered US image with the suspicious lesion marked by a circle. Absorption map of MPP estimated image is shown in Fig. 3(b), reconstructed images using five corresponding reconstruction methods are given in Fig. 3(c)-3(g) and reconstructed maximum µa are quiet similar.
Fig. 2.
Reconstructed absorption map at 780 nm of a malignant case. (a) co-registered US image, (b) PINV initial image, Max µa = 0.194 cm−1 (c) Newton with zero initial, Max µa = 0.179 cm−1 (d) Newton with PINV initial, Max µa = 0.268 cm−1 (e) regularized CG with zero initial, Max µa = 0.179 cm−1 (f) regularized CG with PINV initial, Max µa = 0.267 cm−1 and (g) unregularized CG, Max µa = 0.216 cm-1. Each map shows 7 sub-images marked as slice 1 to 7 and each sub-image shows spatial x and y distribution of absorption coefficients reconstructed from 0.5 cm to 3.5 cm depth range from the skin surface. The spacing between the sub-images in depth is 0.5 cm. The color bar is absorption coefficients in cm−1. We chose the µa display range from 0 to 0.2 cm−1 because most of the reconstructed absorption values fall within this range. Each subfigure dimension is 8cm x 8cm with scales from −4 cm to 4 cm in both X and Y axis.
Fig. 3.
Reconstructed absorption map at 780 nm of a benign case. (a) co-registered US image, (b) PINV reference image, Max µa = 0.076 cm−1 (c) Newton with zero initial, Max µa = 0.078 cm−1 (d) Newton with PINV initial, Max µa = 0.087 cm−1 (e) regularized CG with zero initial, Max µa = 0.077 cm−1 (f) regularized CG with PINV initial, Max µa = 0.088 cm−1 and (g) unregularized CG, Max µa = 0.092 cm−1. The absorption maps have the same scale as Fig. 2.
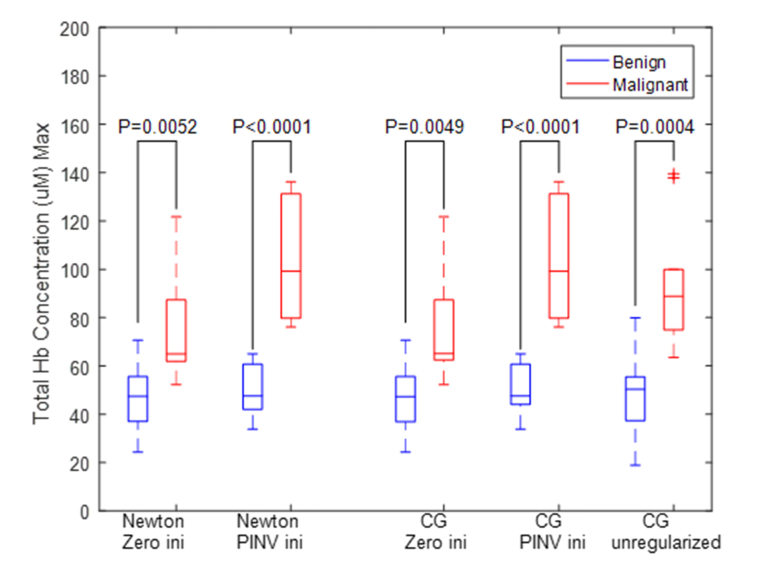
Box plot of maximum total hemoglobin (tHb) of all clinical cases is shown in Fig. 4. The two sample t test was performed between malignant and benign groups of each method. Newton’s method and CG with PINV as an initial provide highest statistical significance.
Fig. 4.
Box plot of total hemoglobin concentration of 20 patients (malignant (red), n = 10, benign (blue) n = 10) using five methods. PINV as an initial guess and Newton as optimization (first and second columns), zero and PINV as initial guess and CG (third the fourth columns), and unregularized CG (last column).
Additionally, the malignant to benign contrast ratios are 1.61, 2.11, 1.61, 2.07, 1.93, for Newton’s with zero initial, PINV initial, CG zero initial, PINV initial and unregularized CG respectively. The average and standard deviation of maximum tHb concentration obtained from each method is given in Table 3. For benign cases, reconstructed tHb are comparable using five methods, however, for malignant cases the total Hb contrast is much higher when Newton’s and CG are used with PINV initial estimate.
Table 3. Total Hb concentration (μM) for clinical cases using different methods.
|
Newton with
zero Ini |
Newton with PINV ini |
CG with
zero ini |
CG with
PINV ini |
CG unregularized | |
|---|---|---|---|---|---|
| Total Hb conc. (Benign) | 47.5 ± 14.2 | 49.4 ± 10.6 | 47.5 ± 14.3 | 50.4 ± 9.8 | 48.5 ± 16.3 |
| Total Hb conc. (Malignant) | 76.4 ± 23.9 | 104.2 ± 23.6 | 76.5 ± 23.8 | 104.2 ± 23.6 | 93.5 ± 26.9 |
3.3 Convergence speed analysis
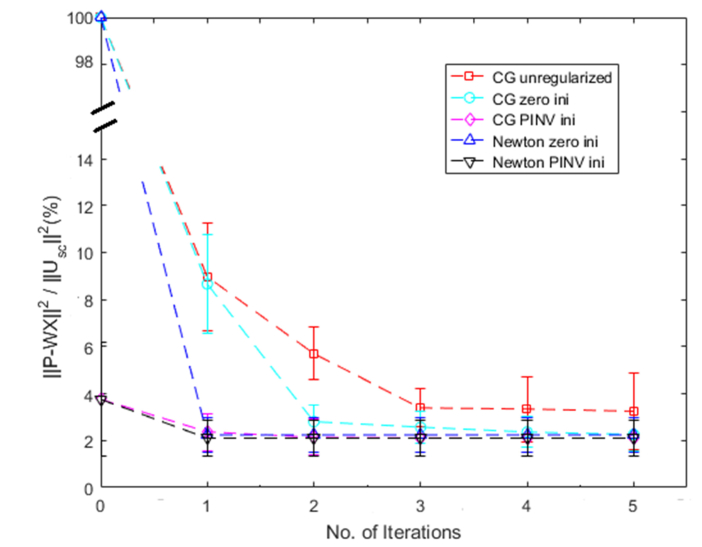
It is important for an iterative image reconstruction algorithm to converge quickly and therefore to provide images needed for on-site diagnosis by physicians. To compare the convergence of differenrt reconstruction methods, we normalize the Least Square Error (LSE), for each method to the power of the scattered field, , which is the initial objective function for unregularized CG method. Shown in Fig. 5 is the mean and standard deviation of normalized LSE of five methods using phantom data. Truncated pseudoinverse provides a good initial guess which reduces the initial LSE, , to 4% of the power of the scattered field, . Newton and CG with PINV as an initial estimate converge in 1 and 2 iterations, respectively. Newton and CG with zero initial converges in 1 and 3 iterations, respectively, and the residual LSE of CG is slightly higher than that with PINV as an initial. Unregularized CG converges in 3 ietrations. Note that for our early studies using unregularized CG, the iteration was stopped at 3 ietrations because it provided optimal performance for phantom data.
Fig. 5.
Normalized LSE of five different methods using phantoms data.
3.4 Target centroid error analysis
To compare different reconstruction methods, the target centroid error i.e. the absolute difference between the center of a phantom target measured by co-registered US and the centroid of corresponding reconstructed target absorption map, is calculated as a measure of reconstruction quality. Phantom data of both low and high contrast targets of 1 cm diameter located at different depths and measured at 780 nm were used to estimate the centroid error and results are shown in Table 4. MATLAB function ‘regionprop’ is used to estimate the centroid of target absorption map and the difference between the estimated centroid and the measured target center from corresponding co-registered US is calculated. As seen from Table 4, the target centroid error which is less than one voxel size of 0.25 cm does not depend on reconstruction method. Thus, all reconstruction methods provide the same target centroid.
Table 4. Object centroid error (mean ± standard deviation) for phantom data.
|
Newton with
zero ini |
Newton with PINV ini |
CG with
zero ini |
CG with
PINV ini |
CG unregularized | |
|---|---|---|---|---|---|
|
Object centroid
Error (Δx) |
0.157 ± 0.093 | 0.157 ± 0.093 | 0.157 ± 0.093 | 0.157 ± 0.093 | 0.163 ± 0.091 |
|
Object centroid
Error (Δy) |
0.225 ± 0.101 | 0.225 ± 0.101 | 0.225 ± 0.101 | 0.225 ± 0.101 | 0.190 ± 0.069 |
4. Discussion and summary
Choice of regularization parameter, λ, is an important part of reconstruction. If λ is too small, then the penalty may not have any effect on reconstruction, however, a larger λ heavily penalizes data fidelity term and solution may not converge near true minimum of unregularized objective function. In our approach, λ is chosen as which decreases with and increases with background .Thus for higher background , the λ regulates more to improve the conditioning of the Q matrix. Additionally, because the huge difference between the first and the rest of the eigenvalues, the increases with n and therefore λ regulates more for smaller eigenvalues and further improves the conditioning of Q matrix.
Choice of regularization parameter is always a difficult problem and mathematical techniques like L-curve and U-curve are not often useful. We have determined regularization parameter by trial and error using phantom data to ensure convergence, reconstruction accuracy and lower image artifacts. In further study, we will apply machine learning techniques to automatically select regularization parameter to minimize the reconstruction error. The ultimate clinical use of ultrasound-guided diffused light imaging is to maximize the separation of benign and malignant lesions.
In the past two decades, researchers in DOT community have tried to simultaneously reconstruct target absorption coefficient, , and diffusion coefficient, D (, see Eq. (1)). However, since the lesion diffusion coefficient is much smaller than the absorption coefficient, correctly reconstructing the scattering coefficient is a challenge. Also, simultaneously reconstructing the absorption and diffusion coefficients doubles the number of unknown optical parameters to estimate. Therefore, the reconstruction becomes more ill-posed and under-determined. However, with a better initial estimate and an appropriate choice of regularization parameter λ, it is possible to explore simultaneous reconstruction of both parameters. This has been demonstrated in reference 25 using GA as an initial estimate and unregulated CG to iteratively reconstruct target absorption and scattering maps. In this manuscript, our objectives were to 1) evaluate the performance of the proposed simple, robust, two-step reconstruction algorithm; and 2) compare this algorithm with a group of four algorithms including the unregulated CG algorithm that we have used in the past. Therefore, we did not attempt to simultaneously reconstruct both parameters but focused on absorption coefficient, , which is the most important parameter to reveal tumor angiogenesis. Thus, our phantoms have similar reduced scattering coefficient as the background medium. In future study, we will evaluate the performance of the proposed novel algrothm in simultaneously recovering both target absorption and scattering maps.
In summary, a simple, robust, two-step reconstruction algorithm has been proposed and its performance has demonstrated using phantom and clinical data. Using a truncated pseudoinverse as a preliminary estimate of target optical properties and regularized Newton and CG optimization search methods to iteratively reconstruct target optical properties within region of interest identified by co-registered US gave best results. The truncated pseudoinverse as a preliminary estimate and regularized Newton optimization converges in one iteration. This two-step reconstruction technique is generally applicable to x-ray-guided and MRI guided DOT imaging reconstruction.
Funding
The authors thank the funding support of this work from the National Institute of Health (R01EB002136).
Disclosures
QZ is the inventor of the patents related to ultrasound-guided near-infrared tomography technologies and patents owned by the University of Connecticut. The other authors declare there are no conflicts of interest related to this article.
References and links
- 1.Tromberg B. J., Cerussi A., Shah N., Compton M., Durkin A., Hsiang D., Butler J., Mehta R., “Imaging in breast cancer: diffuse optics in breast cancer: detecting tumors in pre-menopausal women and monitoring neoadjuvant chemotherapy,” Breast Cancer Res. 7(6), 279–285 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Choe R., Konecky S. D., Corlu A., Lee K., Durduran T., Busch D. R., Pathak S., Czerniecki B. J., Tchou J., Fraker D. L., Demichele A., Chance B., Arridge S. R., Schweiger M., Culver J. P., Schnall M. D., Putt M. E., Rosen M. A., Yodh A. G., “Differentiation of benign and malignant breast tumors by in-vivo three-dimensional parallel-plate diffuse optical tomography,” J. Biomed. Opt. 14(2), 024020 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Poplack S. P., Tosteson T. D., Wells W. A., Pogue B. W., Meaney P. M., Hartov A., Kogel C. A., Soho S. K., Gibson J. J., Paulsen K. D., “Electromagnetic breast imaging: results of a pilot study in women with abnormal mammograms,” Radiology 243(2), 350–359 (2007). [DOI] [PubMed] [Google Scholar]
- 4.Athanasiou A., Vanel D., Balleyguier C., Fournier L., Mathieu M. C., Delaloge S., Dromain C., “Dynamic optical breast imaging: a new technique to visualise breast vessels: comparison with breast MRI and preliminary results,” Eur. J. Radiol. 54(1), 72–79 (2005). [DOI] [PubMed] [Google Scholar]
- 5.Zhu Q., Cronin E. B., Currier A. A., Vine H. S., Huang M., Chen N., Xu C., “Benign versus malignant breast masses: optical differentiation with US-guided optical imaging reconstruction,” Radiology 237(1), 57–66 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zhu Q., Hegde P. U., Ricci A., Jr, Kane M., Cronin E. B., Ardeshirpour Y., Xu C., Aguirre A., Kurtzman S. H., Deckers P. J., Tannenbaum S. H., “Early-stage invasive breast cancers: potential role of optical tomography with US localization in assisting diagnosis,” Radiology 256(2), 367–378 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ueda S., Nakamiya N., Matsuura K., Shigekawa T., Sano H., Hirokawa E., Shimada H., Suzuki H., Oda M., Yamashita Y., Kishino O., Kuji I., Osaki A., Saeki T., “Optical imaging of tumor vascularity associated with proliferation and glucose metabolism in early breast cancer: clinical application of total hemoglobin measurements in the breast,” BMC Cancer 13(1), 514 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chance B., Nioka S., Zhang J., Conant E. F., Hwang E., Briest S., Orel S. G., Schnall M. D., Czerniecki B. J., “Breast cancer detection based on incremental biochemical and physiological properties of breast cancers: a six-year, two-site Study 1,” Acad. Radiol. 12(8), 925–933 (2005). [DOI] [PubMed] [Google Scholar]
- 9.Mastanduno M. A., Xu J., El-Ghussein F., Jiang S., Yin H., Zhao Y., Michaelsen K. E., Wang K., Ren F., Pogue B. W., Paulsen K. D., “Sensitivity of MRI-guided near-infrared spectroscopy clinical breast exam data and its impact on diagnostic performance,” Biomed. Opt. Express 5(9), 3103–3115 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fang Q., Selb J., Carp S. A., Boverman G., Miller E. L., Brooks D. H., Moore R. H., Kopans D. B., Boas D. A., “Combined optical and X-ray tomosynthesis breast imaging,” Radiology 258(1), 89–97 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Krishnaswamy V., Michaelsen K. E., Pogue B. W., Poplack S. P., Shaw I., Defrietas K., Brooks K., Paulsen K. D., “A digital x-ray tomosynthesis coupled near infrared spectral tomography system for dual-modality breast imaging,” Opt. Express 20(17), 19125–19136 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhu Q., Ricci A., Jr, Hegde P., Kane M., Cronin E., Merkulov A., Xu Y., Tavakoli B., Tannenbaum S., “Assessment of functional differences in malignant and benign breast lesions and improvement of diagnostic accuracy by using US-guided diffuse optical tomography in conjunction with conventional US,” Radiology 280(2), 387–397 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Collettini F., Martin J. C., Diekmann F., Fallenberg E., Engelken F., Ponder S., Kroencke T. J., Hamm B., Poellinger A., “Diagnostic performance of a Near-Infrared Breast Imaging system as adjunct to mammography versus X-ray mammography alone,” Eur. Radiol. 22(2), 350–357 (2012). [DOI] [PubMed] [Google Scholar]
- 14.Intes X., Ntziachristos V., Culver J. P., Yodh A., Chance B., “Projection access order in algebraic reconstruction technique for diffuse optical tomography,” Phys. Med. Biol. 47(1), N1–N10 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Arridge S., Schweiger M., “A gradient-based optimisation scheme foroptical tomography,” Opt. Express 2(6), 213–226 (1998). [DOI] [PubMed] [Google Scholar]
- 16.Hielscher A. H., Bartel S., “Use of penalty terms in gradient-based iterative reconstruction schemes for optical tomography,” J. Biomed. Opt. 6(2), 183–192 (2001). [DOI] [PubMed] [Google Scholar]
- 17.Hielscher A. H., Klose A. D., Hanson K. M., “Gradient-based iterative image reconstruction scheme for time-resolved optical tomography,” IEEE Trans. Med. Imaging 18(3), 262–271 (1999). [DOI] [PubMed] [Google Scholar]
- 18.Dehghani H., Srinivasan S., Pogue B. W., Gibson A., “Numerical modelling and image reconstruction in diffuse optical tomography,” Philos Trans A Math Phys Eng Sci 367(1900), 3073–3093 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Schweiger M., Arridge S. R., Nissilä I., “Gauss-Newton method for image reconstruction in diffuse optical tomography,” Phys. Med. Biol. 50(10), 2365–2386 (2005). [DOI] [PubMed] [Google Scholar]
- 20.Zhang L., Zhao Y., Jiang S., Pogue B. W., Paulsen K. D., “Direct regularization from co-registered anatomical images for MRI-guided near-infrared spectral tomographic image reconstruction,” Biomed. Opt. Express 6(9), 3618–3630 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Althobaiti M., Vavadi H., Zhu Q., “Diffuse optical tomography reconstruction method using ultrasound images as prior for regularization matrix,” J. Biomed. Opt. 22(2), 026002 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brooksby B., Jiang S., Dehghani H., Pogue B. W., Paulsen K. D., Weaver J., Kogel C., Poplack S. P., “Combining near-infrared tomography and magnetic resonance imaging to study in vivo breast tissue: implementation of a Laplacian-type regularization to incorporate magnetic resonance structure,” J. Biomed. Opt. 10(5), 051504 (2005). [DOI] [PubMed] [Google Scholar]
- 23.Azar F. S., Lee K., Khamene A., Choe R., Corlu A., Konecky S. D., Sauer F., Yodh A. G., “Standardized platform for coregistration of nonconcurrent diffuse optical and magnetic resonance breast images obtained in different geometries,” J. Biomed. Opt. 12(5), 051902 (2007). [DOI] [PubMed] [Google Scholar]
- 24.Zhang L., Zhao Y., Jiang S., Pogue B. W., Paulsen K. D., “Direct regularization from co-registered anatomical images for MRI-guided near-infrared spectral tomographic image reconstruction,” Biomed. Opt. Express 6(9), 3618–3630 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tavakoli B., Zhu Q., “Two-step reconstruction method using global optimization and conjugate gradient for ultrasound-guided diffuse optical tomography,” J. Biomed. Opt. 18(1), 016006 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fishkin J. B., Gratton E., “Propagation of photon-density waves in strongly scattering media containing an absorbing semi-infinite plane bounded by a straight edge,” J. Opt. Soc. Am. A 10(1), 127–140 (1993). [DOI] [PubMed] [Google Scholar]
- 27.Zhu Q., Chen N., Kurtzman S. H., “Imaging tumor angiogenesis by use of combined near-infrared diffusive light and ultrasound,” Opt. Lett. 28(5), 337–339 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xu C., Vavadi H., Merkulov A., Li H., Erfanzadeh M., Mostafa A., Gong Y., Salehi H., Tannenbaum S., Zhu Q., “Ultrasound-guided diffuse optical tomography for predicting and monitoring neoadjuvant chemotherapy of breast cancers: recent progress,” Ultrason. Imaging 38(1), 5–18 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Vavadi H., Zhu Q., “Automated data selection method to improve robustness of diffuse optical tomography for breast cancer imaging,” Biomed. Opt. Express 7(10), 4007–4020 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Zhou F., Mostafa A., Zhu Q., “Improving breast cancer diagnosis by reducing chest wall effect in diffuse optical tomography,” J. Biomed. Opt. 22(3), 036004 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]