Fast label-free microscopy technique for 3D dynamic quantitative imaging of living cells

Abstract

The refractive index (RI) is an important optical characteristic that is often exploited in label-free microscopy for analysis of biological objects. A technique for 3D RI reconstruction of living cells has to be fast enough to capture the cell dynamics and preferably needs to be compatible with standard wide-field microscopes. To solve this challenging problem, we present a technique that provides fast measurement and processing of data required for real-time 3D visualization of the object RI. Specifically, the 3D RI is reconstructed from the measurement of bright-field intensity images, axially scanned by a high-speed focus tunable lens mounted in front of a sCMOS camera, by using a direct deconvolution approach designed for partially coherent light microscopy in the non-paraxial regime. Both the measurement system and the partially coherent illumination, that provides optical sectioning and speckle-noise suppression, enable compatibility with wide-field microscopes resulting in a competitive and affordable alternative to the current holographic laser microscopes. Our experimental demonstrations show video-rate 3D RI visualization of living bacteria both freely swimming and optically manipulated by using freestyle laser traps allowing for their trapping and transport along 3D trajectories. These results prove that is possible to conduct simultaneous 4D label-free quantitative imaging and optical manipulation of living cells, which is promising for the study of the cell biophysics and biology.

1. Introduction

Living biological cells constantly vary their shapes, sizes and other biophysical characteristics which analysis results crucial for their study, detection and diagnosis of disease, etc. Tracking the cell motion in real time as well as observing intracellular phenomena in 3D require optical microscopic techniques able to achieve high data acquisition and processing rates while providing enough spatial and temporal resolution. Since the cell is mostly transparent its analysis often relies on marking specific cellular structures by using labeling agents such as fluorescent dyes requiring a high level of illumination intensity, that chemically affect and might damage the cell due to photo-damage. The field of quantitative phase imaging (QPI) emerged as a possible alternative to provide quantitative cell analysis without using labeling agents. It involves computational retrieving of a 2D phase image that reveals the cell topography from an interferometric measurement of the laser field scattered by the object, recorded as a hologram by a digital camera. Numerous variants of such a digital holographic microscopy (DHM) technique have been developed in the last decades demonstrating nearly real-time 2D phase imaging of different transparent objects including living cells, see for example [1, 2]. However, the retrieved phase provides incomplete information of the object. In contrast, the 3D reconstruction of the object refractive index (RI) indeed allows obtaining full quantitative information about the cell structure, shape, mass, volume and other relevant biophysical characteristics required for thorough analysis of the object.

Several research groups have demonstrated the feasibility of 3D mapping of RI for label-free imaging of cells by extending DHM with computerized tomography [3] or with optical diffraction tomography [4–6]. Specifically, the coherent optical diffraction tomography (C-ODT) allows for the computational reconstruction of the 3D RI by sequentially measuring multiple holograms with varying angles of illumination (e.g. by using moving mirrors). The illumination angle is limited by the numerical aperture of the microscope condenser lens and therefore the collection of scattered fields is incomplete leading to missing-angle artifacts. To overcome this limitation, the C-ODT can be combined with mechanical rotation of the object that in turn provides complete 3D reconstruction with isotropic spatial resolution [4, 7]. However, this significantly increases the data acquisition time making challenging real-time 3D imaging. Note that C-ODT is able to reconstruct the object RI by computing hundreds of digital holograms and then performing 3D deconvolution with the complex optical transfer function of the microscope. This approach is computationally demanding and requires processing of a big amount of data. In addition, the interferometric setup makes necessary specially designed holographic microscopes that suffer from speckle-noise and parasite interference due to the coherent laser illumination. In spite of these difficulties, several commercially available holographic microscopes based on C-ODT have been recently developed providing reliable 3D RI at low video rates typically at 0.5 – 2.5 fps (thus in the range 400 – 2000 ms according to manufacturer data, Nanolive SA and Tomocube Inc.) suited for long-term cell observation. An option for increasing the acquisition rate in C-ODT is to reduce the number of illumination angles achieving rates up to 60 fps, but at expense of the spatial resolution and quality of the 3D RI reconstruction [8] due to increased missing-angle artifacts. Nevertheless, real-time 3D reconstruction and visualization of the object RI is still a challenging problem that requires high speed in both the measurement and processing of data.

Here, we exploit a completely different label-free microscopy technique that is compatible with conventional microscopes (equipped with halogen or LED lamps providing spatial and temporal partially coherent illumination) and significantly simplifies the reconstruction of the object RI enabling fast video-rate (in the range of 50 – 100 ms) 3D quantitative imaging of living cells. It is based on a recently developed partially coherent ODT (PC-ODT) technique [9] that takes into account the non-paraxial OTFs and only needs the measurement of a single stack of bright-field intensity images, axially scanned by a high-speed focus tunable lens (optical refocusing module) mounted in front of a digital camera. This kind of electrically-controlled tunable lens enables a fast axial scan such that the acquisition time of the proposed PC-ODT technique is only limited by the camera frame rate. Moreover, in contrast to other PC-ODT methods [10–12] developed for static 3D RI imaging, our technique exploits the high numerical aperture (NA) of the objective lens NA_o and condenser NA_c providing the low spatially coherent illumination required for high transverse and axial resolution similar to C-ODT [6]. As a result, here, we have been able to achieve 3D RI imaging of living cells at 10 fps (temporal resolution of 100 ms) for a XYZ region of volume 40 × 40 × 12 μm³ (spatial resolution of 200 × 200 × 500 nm³) combining the benefits of optical sectioning and speckle-noise free imaging provided by partially coherent illumination. Both the measurement system and illumination source enable compatibility with conventional microscopes resulting in a competitive alternative to the current holographic C-ODT microscopes. Indeed, the optical refocusing module can be easily incorporated into wide-field microscopes even into those including optical tweezers. To experimentally demonstrate the performance of the proposed technique, we have considered living yeast cells (Schizosaccharomyces pombe bacteria dispersed in aqueous solution) that exhibit swimming motion and have fine cellular features.

Another relevant achievement is that this technique is fast enough to exploit label-free quantitative imaging (4D RI visualization) together with optical manipulation tools (e.g., optical tweezers) for the study of the cell biophysics. Thus, our experimental demonstrations also include optical manipulation of living bacteria by using freestyle laser traps providing confinement and transport of the cells to optically control their motion along arbitrary 3D trajectories. Note that optical manipulation of bacteria is often performed by using the familiar point-like laser traps, see for example [13]. Here, we show for the first time the use of freestyle laser traps to achieve light-driven transport of living bacteria along reconfigurable trajectories. The considered examples prove the practical capabilities of the combined application of the proposed optical manipulation and PC-ODT techniques.

2. Experimental technique

The considered bright-field microscope comprises an objective lens with NA_o = 1.4 (Olympus UPLSAPO, 100×, oil immersion, n_imm = 1.518) and an Abbe condenser lens with NA_c = 0.95 collecting the light of a quasi-monochromatic LED source (central wavelength λ₀ = 470 nm). The diaphragm of the condenser lens is fully open yielding the low spatially-coherent illumination over the sample (coherence ratio S = NA_c/NA_o ~ 0.7). Such an illumination together with the high NA of the lenses provide the optical sectioning capability required for 3D imaging as well as reasonably good trade-off between transverse Δx = Δy = λ₀/(NA_o + NA_c) ≈ 200 nm and axial $\mathrm{\Delta }z={\lambda }_0/(n_{imm}-{(n_{imm}^2-{\text{NA}}_{\mathrm{o}}^2)}^{1/2})\approx 500$ nm spatial resolution limits [9]. Note that the bright-field microscope (with fully opened condenser aperture) transmits the same object spatial-frequency content that the C-ODT is able to achieve from multiple illuminations [9]. To measure the Z-stack of intensity images, the high-speed focus tunable lens (ETL, Optotune EL-10-30-C) and the sCMOS camera (Hamamatsu, Orca Flash 4.0, 16-bit gray-level, pixel size of 6.5 μm) have been synchronized. Specifically, the ETL has been configured to perform a repetitive bidirectional Z-scanning by setting a periodic triangular electrical signal in the lens micro-controller while the sCMOS camera continuously acquired the images during the entire optical scanning process. The measurement process is fully automatic because the ETL triggers the camera acquisition (the first rising edge of the triangular signal serves as an external start trigger for the camera) enabling their synchronization. In our case, each stack of intensity images (400 × 400 × 50 voxels) corresponding to a 3D region of 40 × 40 × 12 μm³ (XYZ) has been measured in 100 ms by using an exposure time of 2 ms, thus achieving an acquisition rate of 10 fps for 3D stacks. Note that the considered sCMOS camera is able to acquire 16-bit images of 400 × 400 pixels at a rate of 500 fps (exposure time t_exp = 2 ms). The frequency of the triangular electrical signal of the ETL, ν_ETL, is given as a function of the exposure time of the camera and number N of intensity images of the 3D stack to be measured as it follows: ν_ETL = 1/2Nt_exp. Thus, in our case this frequency is ν_ETL = 5 Hz (varying between 40 mA and 160 mA in amplitude) providing a proper focal length shift to scan the required N = 50 images [9]. Let us underline that a higher acquisition frame rate is possible just by reducing the size of the field of view (size of the 3D stack). See Appendix for further details about the experimental setup.

The described optical scanning process allows for the acquisition of the 3D intensity image $I\left(\overrightarrow{r}\right)$ that for weak scattering objects, in the first-order Born approximation, can be written as a linear superposition of the real and imaginary parts of the object scattering potential $(V\left(\overrightarrow{r}\right)=P\left(\overrightarrow{r}\right)+\mathrm{i}A\left(\overrightarrow{r}\right))$ convolved with the point spread functions (PSFs) $h_P\left(\overrightarrow{r}\right)$ and $h_A\left(\overrightarrow{r}\right)$ as it follows [10]:

$$I\left(\overrightarrow{r}\right)=B+P\left(\overrightarrow{r}\right)\otimes h_P\left(\overrightarrow{r}\right)+A\left(\overrightarrow{r}\right)\otimes h_A\left(\overrightarrow{r}\right),$$ (1)

with B being the background intensity (unscattered light) and $\overrightarrow{r}=(x,y,z)$ Note that $h_P\left(\overrightarrow{r}\right)$and $h_A\left(\overrightarrow{r}\right)$ are the microscope response functions to a point scatter $(V\left(\overrightarrow{r}\right)=\delta \left(\overrightarrow{r}\right))$ and to a point absorber $(V\left(\overrightarrow{r}\right)=\mathrm{i}\delta \left(\overrightarrow{r}\right))$, respectively. As pointed out in [9], in the case of weak absorption objects corresponding to biological cells one can assume $A\left(\overrightarrow{r}\right)=\epsilon P\left(\overrightarrow{r}\right)$ with ε ≪ 1. Thus, the expression Eq. (1) can be rewritten in the Fourier domain as

$$\hat{I}\left(\overrightarrow{\rho }\right)=B\delta \left(\overrightarrow{\rho }\right)+\hat{P}\left(\overrightarrow{\rho }\right)H_E\left(\overrightarrow{\rho }\right),$$ (2)

from which the reconstruction of the 3D-RI distribution $n\left(\overrightarrow{r}\right)$ results straightforward by using a regularized Wiener deconvolution algorithm:

$$\hat{P}\left(\overrightarrow{\rho }\right)=\frac{\hat{I}\left(\overrightarrow{\rho }\right)H_E^{*}\left(\overrightarrow{\rho }\right)}{{\left|H_E\left(\overrightarrow{\rho }\right)\right|}^2+\beta },$$ (3)

where the regularization parameter β depends on the signal to noise ratio (typically β ~ 10^–2 – 10^–4). Indeed, since $n^2\left(\overrightarrow{r}\right)=P\left(\overrightarrow{r}\right)k_0^{-2}(1+\mathrm{i}\epsilon )+n_m^2$ the real and imaginary part of the object RI can be easily obtained from Eq. (3) [9], where k₀ = 2π/λ₀ and n_m is the refractive index of the surrounding medium. The term $H_E\left(\overrightarrow{\rho }\right)=H_P\left(\overrightarrow{\rho }\right)+\epsilon H_A\left(\overrightarrow{\rho }\right)$ is the effective non-paraxial OTF including both phase-only OTF $(H_P\left(\overrightarrow{\rho }\right))$ and absorption OTF $(H_A\left(\overrightarrow{\rho }\right))$ of the microscope [14], see also [9] for further details. In this work, we use ε = 0.05 (ideal phase-only specimens correspond to ε = 0) that has been experimentally proved successful for the RI reconstruction of different biological specimens such as diatoms and blood cells [9]. Note that in the weak absorption approximation the real part of the RI, $n_{\mathrm{Re}}\left(\overrightarrow{r}\right)=\sqrt{(\left|n^2\left(\overrightarrow{r}\right)\right|+\mathrm{Re}\left\{n^2\left(\overrightarrow{r}\right)\right\})/2}$, is significantly larger than the imaginary counterpart and therefore only $n_{\mathrm{Re}}\left(\overrightarrow{r}\right)$ provides relevant structural information of the object.

3. Results and discussions

To test the performance of the proposed technique and measurement setup for dynamic 3D quantitative imaging, we have considered a sample of yeast cells (Schizosaccharomyces pombe, further referred to as S. pombe) dispersed in aqueous solution (sugared water). The S. pombe bacteria are rod-shape cells particularly interesting in genetics [15] and well suited for testing quantitative imaging techniques [16]. Figure 1 shows the reconstructed 3D RI $(n_{\mathrm{Re}}\left(\overrightarrow{r}\right) \text{henceforth})$ of S. pombe bacteria. This corresponds to one 3D frame of the 4D RI reconstruction provided as a video file in Visualization 1 ^{(274.2KB, mp4)} , which shows their natural motion for a recording time of 1 s as an example. Note that the reconstructed 3D RI has been rendered as a volume by using open source software, Fiji imaging suite (ImageJ) [17]. Briefly, this kind of bacterium divides itself by fission yielding two identical daughter cells separated by a medial wall or septum [18, 19]. The daughter cells present a cleavage point in the septum, then they divide and each one subsequently repeat the fission process. The septum is clearly distinguishable in Fig. 1 (see the cells located at the center, they have a size of ~ 3.5 μm long and ~ 1.5 μm wide) because the bacteria were going through their reproductive cycle that can be of several hours. Furthermore, small features such as endoplasmatic organelles (tiny intracellular structures of 250 – 350 nm indicated by arrows in Fig. 1) are also observed into the cytoplasm and the cell membrane is clearly bounded. In particular, the RI of the membrane (n_Re = 1.40 ± 0.01) is higher than that of the cytoplasm (n_Re = 1.38 – 1.39). These RI values are in good agreement with the literature [16] and support the weak object approximation given that the refractive index of the sugared water is close to n_m = 1.37 (see Appendix), thus the RI contrast between surrounding medium and bacteria is about Δn_Re = 0.03 – 0.04. The S. pombe bacteria exhibit wobbling and swimming motion [13], see Visualization 1 ^{(274.2KB, mp4)} .

Fig. 1.

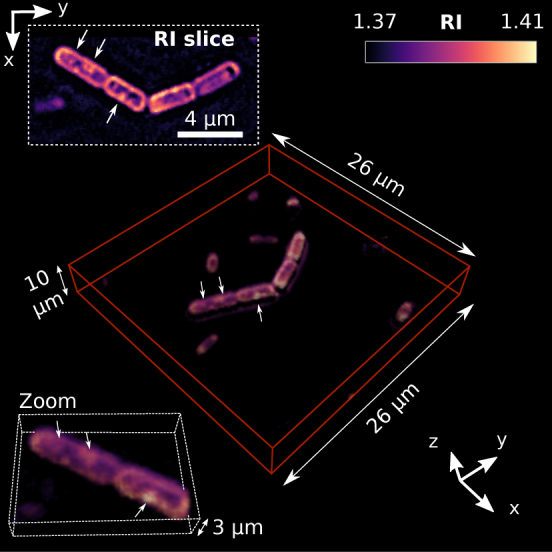
3D RI reconstruction of multiple S. pombe bacteria. The inset displaying a RI XY-slice shows four cells (~ 3.5 μm long and ~ 1.5 μm wide) with well-defined membrane and exhibiting small intracellular structures of 250 – 350 nm indicated by the arrows. It is also observed tiny bacteria freely swimming in the scanned sample volume, see Visualization 1 ^{(274.2KB, mp4)} .

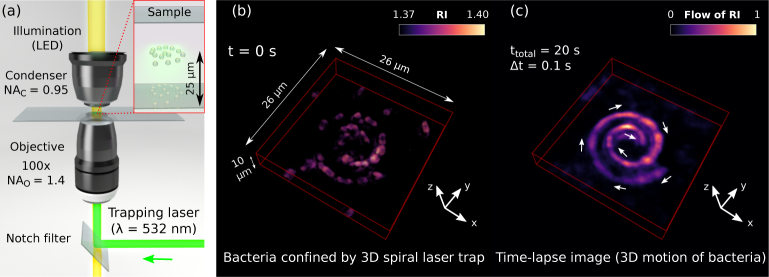
To further testing the proposed 4D label-free imaging technique, we have used an optical manipulation tool which is able to induce pre-designed bacteria motions. Specifically, we have used freestyle laser traps [20] to optically confine and transport the bacteria along arbitrary 3D curves. Such freestyle laser traps have been experimentally demonstrated for optical manipulation of inorganic samples such as dielectric micro-spheres of 1 μm (silica) and metallic nanoparticles (e.g., gold and silver particles of 100 nm), see [20–22]. Here, for the first time, it is proved that this new kind of laser trap allows for optical confinement and transport of living bacteria cells along trajectories that can be easily designed according the considered application. Let us underline that the optical trapping and transport of multiple living cells are challenging by using conventional optical tweezers. In contrast, freestyle laser traps optically control the motion of multiple living bacteria even deep within the sample far away from the chamber walls [e.g. up to 25 μm in depth, see Fig. 2(a)], which has been previously demonstrated only for the case of silica micro-spheres [20, 21]. To introduce the working principle of the freestyle laser trap and illustrate its performance in manipulating living bacteria, let us first consider a 3D spiral laser trap as the example shown in Fig. 2(b). The trapping laser beam (wavelength of 532 nm) has been strongly focused in form of 3D spiral and its high-intensity gradients exert 3D trapping forces confining the bacteria along the curve. While, the phase gradient of the trapping laser beam has been designed to exert an optical propelling force [20–22] that is responsible for the transport of bacteria along the curve. Indeed, as observed in the reconstructed 4D RI provided in Visualization 2 ^{(393KB, mp4)} , multiple bacteria have been transported from the spiral tail towards its center. The time lapse image displayed in Fig. 2(c) has been made by summing all the recorded 3D frames of RI and it reveals the trajectory followed by the trapped bacteria, which coincides with the spiral shape of the optical trap as expected. Note that this kind of time lapse image shows the trajectory followed by the bacteria in form of accumulated RI (normalized at its maximum value) that can be understood as a flow of RI along the curve.

Fig. 2.

(a) Sketch of the bright-filed microscope used for 4D RI reconstruction and optical manipulation experiments: A trapping laser beam is focused into the sample by using the same objective lens imaging the sample. The bacteria have been optically trapped up to 25 μm deep within the sample. (b) A freestyle laser trap in form of 3D spiral is used to optically confine and transport the bacteria along the spiral, see Visualization 2 ^{(393KB, mp4)} . (c) The trajectory followed by the transported bacteria along the spiral is revealed in the displayed time-lapse image, which has been made by combining all the recorded video frames of Visualization 2 ^{(393KB, mp4)} .

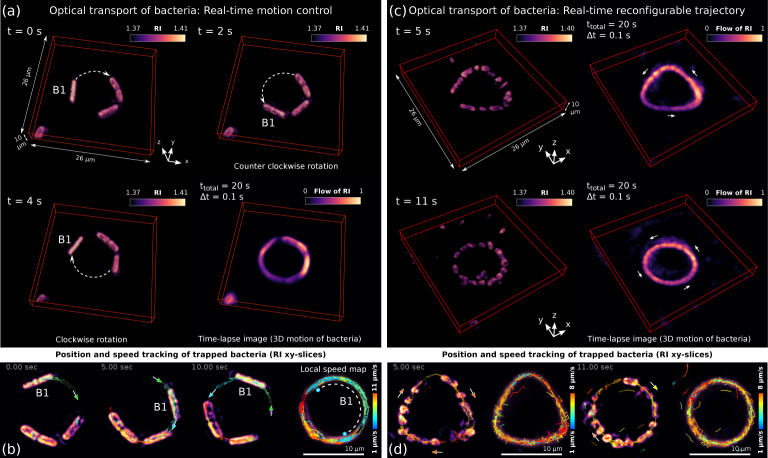
The speed and motion direction of the trapped bacteria can be also optically controlled along 2D curves in real time if needed. For example, Fig. 3(a) and Visualization 3 ^{(537KB, mp4)} show three bacteria (about 6 μm long and 2 μm wide) confined in a ring trap that sets them into rotation in a programmable way. Note that S. pombe cells grow in the longitudinal direction while remaining at almost constant width [23], as it is observed in Fig. 3(a). Another advantage of reconstructing the RI in 4D is that this permits tracking the cell and estimating its speed as displayed in Fig. 3(b), see also Visualization 3 ^{(537KB, mp4)} . In particular, the local speed map shown in Fig. 3(b) reveals that the cell labeled as B1 follows a pendulum-like movement along the ring trap reaching a maximum speed of 6 μm/s and a minimum speed of 1 μm/s at the recoil points where its motion has been optically switched [20, 21] from clockwise to counter-clockwise rotation and vice versa. Such a speed map also confirms that the bacteria are stably trapped in the ring trap as expected. The rest of cells also follow a prescribed pendulum-like movement but along a shorter distance. These tracking results have been obtained by using a particle tracking software included in Fiji, Trackmate plug-in [24], which is well suited for monitoring of the cell motion.

Fig. 3.

(a) Experimental results demonstrating 4D RI reconstruction of three bacteria (S. pombe, ~ 6 μm long and ~ 2 μm wide) while they have been optically manipulated by using a laser ring trap. This example shows real-time motion control achieved by simultaneously exploiting trapping and propelling optical forces. The cell labeled as B1 optically transported along the ring follows a pendulum-like motion (due to switching the rotation direction) as observed in Visualization 3 ^{(537KB, mp4)} . The time-lapse image confirms stable 3D confinement of the cells in the ring. (b) The positions of the confined cells have been tracked revealing their trajectory and velocity distribution during this experiment, see the corresponding local speed map. Note that some of these cells are undergoing division cycle with a clearly visible medial cavity. (c) Experimental 4D RI results demonstrating real-time reconfiguration of the transport trajectory, switching between triangle and ring laser trap. The time-lapse images reveal the corresponding flows of cells transported along the curves while their tracking confirm a nearly uniform velocity distribution for each case as shown in (d), see also Visualization 4 ^{(842.2KB, mp4)} . In these experiments the recording time was 20 s with rate of 10 fps (100 ms each 3D frame).

This optical confinement and transport tool results promising for contactless guiding of living cells. To further illustrate its versatility, Fig. 3(c) and Visualization 4 ^{(842.2KB, mp4)} show how the trajectory can be reconfigured in real time while keeping the transported cells well confined. In this case the bacteria have been confined in a triangle-shaped trapping laser beam that sets them into rotation along the triangle. After a few seconds the triangular trap has been rapidly switched to a ring trap and consequently the rotating flow of bacteria immediately gets confined in the new trap geometry, as observed in Visualization 4 ^{(842.2KB, mp4)} . The corresponding speed maps displayed in Fig. 3(d) indicate stable confinement as expected. Moreover, the velocity distribution is almost uniform along both curves because in both kind of traps the phase gradient prescribed along the curve is uniform [21], that yields an optical force that continuously propels the bacteria. Nevertheless, there also exist hydrodynamic interactions and collisions events between the trapped bacteria responsible for the variations in the velocity distribution observed in Fig. 3(d). We recall that in the case of Fig. 3(a) and 3(b) the sign of the phase-gradient force propelling the bacteria has been switched in real time to change the rotation direction of the bacteria along the ring trap. While, in Fig. 3(c) and 3(d) a constant clockwise rotating flow of bacteria has been generated by using an uniform phase-gradient propelling force in two different trap geometries.

The considered examples demonstrate video rate 3D label-free quantitative imaging that is fast enough even for study 3D optical manipulation of unstained cells, thus resulting in a promising tool for biophysics and biomedicine applications. Such a 4D visualization of the cell RI is well suited to study its dynamics while facilities tracking the position, speed, and orientation of the cell in 3D. For example, this allowed us observing the natural wobbling motion of freely swimming bacteria (1 – 3 μm long) as well as characterizing the motion of bacteria optically trapped and transported along 3D curved trajectories. As shown in Fig. 3(c) and Visualization 4 ^{(842.2KB, mp4)} , the trapped bacteria can exhibit continuous reorientation: The elongated cell body lies contained into the XY plane (laser curve) but also tends to align along the propagation direction of the trapping beam (Z-axis). This reorientation seems to be conditioned by random wobbling motion, collisions and hydrodynamic effects apart from complex interactions between the cell body and the laser beam. Nevertheless, more elongated bacteria (~ 6 μm long) as the ones studied in Fig. 3(a) do not exhibit significant wobbling motion and they remained stably aligned along the laser curve (contained in the XY plane) during the entire optical manipulation process. These results illustrate the importance of dynamic 3D label-free quantitative imaging for observing and studying the changes in the structure of cells and their motions in vivo. We underline that in the considered experiments the prepared sample of bacteria has been diluted to reach a concentration of about 5 % in sucrose aqueous solution, see Appendix. Further research is required to determine how a higher concentration of cells affects the performance of the laser traps and reconstruction of the sample RI.

4. Conclusions and outlook

Dynamic 3D RI visualization at video rates results promising in optical manipulation experiments, which often relay in basic imaging methods (e.g., the 2D bright-field or phase contrast ones) to study the manipulated object. Here, we have shown that video-rate 3D RI visualization at 10 fps (region of 40 × 40 × 12 μm³ and exposure time of 2 ms) can be sufficient to study optical transport of living cells but it could also be suited for other demanding applications as for example tomographic microscopy in micro-fluidic conditions [25–28], etc. Let us underline that in the considered examples the measurement of a single stack of intensity images has been performed in 100 ms while the corresponding 3D RI reconstruction was achieved in 1.5 s by using Matlab R2016a and Intel Xeon E5-1620v3 CPU (8 GB DDR4-RAM). Nevertheless, the exposure time can be reduced or alternatively a smaller region can be measured if faster video rate visualization is needed. While, the computation time of the described direct reconstruction method (Eq. (3) involving the Fast Fourier Transform) can be significantly reduced from 1.5 s to a few milliseconds by harnessing the power of the current graphics processing unit (GPU, e.g. NVIDIA’s CUDA parallel computing architecture) available in personal computers and workstations.

The developed system is inherently robust, affordable and compatible with conventional microscopes providing a high-speed optical scanning only limited by the acquisition rate of the sCMOS camera, whose incessant technological development produces even faster devices. Such a high-speed optical scanning together with a direct and fast deconvolution method, as the ones used here, facilitate the challenging problem of real-time reconstruction and visualization of the object’s RI in 3D. Therefore, we envision that this technique will serve for 4D label-free quantitative study of living cells in future real-time applications.

5. Appendix

5.1. Experimental setup

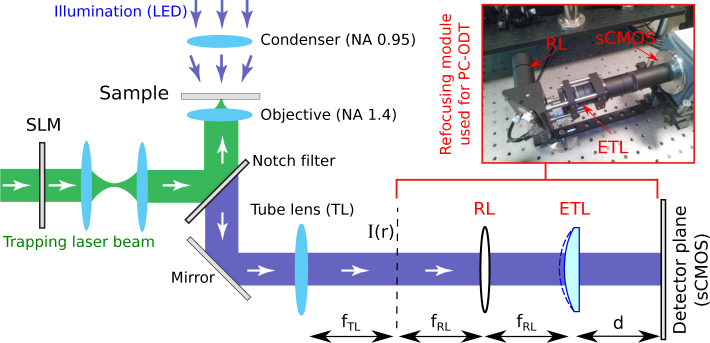
The experimental setup used for simultaneous 4D label-free quantitative imaging (based on partially coherent optical diffraction tomography, PC-ODT) and optical trapping and manipulation of living cells is sketched in Fig. 4. It consists of a bright-field microscope – including an objective lens Olympus UPLSAPO, 100× NA_o = 1.4 (oil immersion, n_imm = 1.518) and an Abbe condenser lens with NA_c = 0.95 collecting the light of a quasi-monochromatic LED source (central wavelength λ₀ = 470 nm) – in which it has been incorporated two systems: the optical refocusing module used for PC-ODT and the setup required for shaping the laser traps (comprising a laser device and a programmable spatial light modulator SLM).

Fig. 4.

Sketch of the experimental setup used for simultaneous 4D label-free quantitative imaging (based on PC-ODT) and optical trapping and manipulation of living cells. In the bright-field microscope (comprising the condenser and objective lenses) has been incorporated two systems: The measurement setup required for PC-ODT and the setup for shaping the laser traps (SLM and the laser device). The laser beam modulated by the SLM is relayed onto the back aperture of the objective lens by using a set of two identical convergent lenses (focal length of 150 mm) working as a ×1 Keplerian telescope. Both the microscope’s tube lens (with focal length f_TL = 150 mm) and the relay lens RL (f_RL = 150 mm) are achromatic convergent lenses (Thorlabs AC254-150-A-ML).

5.1.1. Refocusing module used for PC-ODT

The measurement of the stack $I\left(\overrightarrow{r}\right)$ of intensity images, needed in PC-ODT to reconstruct the 3D object’s refractive index, is performed by using a sCMOS camera (Hamamatsu, Orca Flash 4.0, 16-bit gray-level, pixel size of 6.5 μm) synchronized with an optical refocusing module comprising a high-speed focus tunable lens (ETL, Optotune EL-10-30-C). The ETL has been configured to perform a repetitive bidirectional Z-scanning by setting a periodic triangular electrical signal in the lens micro-controller while the sCMOS camera continuously acquired the images during the entire optical scanning process. Let us underline that the measurement process is fully automatic because the ETL triggers the camera acquisition (the first rising edge of the triangular signal serves as an external start trigger for the camera) enabling their synchronization. The light scattered by the sample is collected by the microscope’s lenses and then it is redirected to the optical refocusing module comprising a relay lens (RL) and the ETL, which provides the required axial scanning by changing its focal length (f_ETL) according to the applied electrical current (I_ETL), see also Fig. 5(a). In our case, the focal length of RL is f_RL = 150 mm and the distance between the ETL and sCMOS detector of the camera is d = 116 mm. The shift of the imaged plane is given as a function of the focal length f_ETL, the effective magnification of the objective-tube lenses (M = 83 in our case) and f_RL as it follows [29]:

$$\mathrm{\Delta }{z}_{defocus}=\frac{n_m{\mathrm{f}}_{\text{RL}}^2}{M^2{\mathrm{f}}_{\text{ETL}}d}({\mathrm{f}}_{\text{ETL}}-d),$$ (4)

where n_m is the refractive index of the surrounding medium of the sample (e.g. water). The latter expression is derived by calculating the ray transfer ABCD-matrix T of the optical refocusing module sketched in Fig. 4:

$$\begin{array}{l}\mathbf{T}=\left[\begin{array}{cc}1& d\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ \frac{-1}{{\mathrm{f}}_{\text{ETL}}}& 1\end{array}\right]\left[\begin{array}{cc}1& {\mathrm{f}}_{\text{RL}}\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ \frac{-1}{{\mathrm{f}}_{\text{RL}}}& 1\end{array}\right]\left[\begin{array}{cc}1& z\\ 0& 1\end{array}\right]\\ =\left[\begin{array}{cc}\frac{-d}{{\mathrm{f}}_{\text{RL}}}& \left(1-\frac{d}{{\mathrm{f}}_{\text{ETL}}}\right){\mathrm{f}}_{\text{RL}}+d\left(1-\frac{z}{{\mathrm{f}}_{\text{RL}}}\right)\\ \frac{-1}{{\mathrm{f}}_{\text{RL}}}& \left(1-\frac{z}{{\mathrm{f}}_{\text{RL}}}\right)-\frac{{\mathrm{f}}_{\text{RL}}}{{\mathrm{f}}_{\text{ETL}}}\end{array}\right],\end{array}$$ (5)

that for the imaging condition, f_RL(1 – d/f_ETL) + d(1 – z/f_RL) = 0, gives the distance

$$z={\mathrm{f}}_{\text{RL}}\left[1+{\mathrm{f}}_{\text{RL}}\left(\frac{1}{d}-\frac{1}{{\mathrm{f}}_{\text{ETL}}}\right)\right],$$ (6)

between the corresponding imaging plane of $I\left(\overrightarrow{r}\right)$ (at the focal plane of the tube lens) and the object focal plane of the relay lens. Therefore, from the expression

$$\mathrm{\Delta }z\prime =z-{\mathrm{f}}_{\text{RL}}={\mathrm{f}}_{\text{RL}}^2\left(\frac{1}{d}-\frac{1}{{\mathrm{f}}_{\text{ETL}}}\right)=\frac{{\mathrm{f}}_{\text{RL}}^2}{{\mathrm{f}}_{\text{ETL}}d}({\mathrm{f}}_{\text{ETL}}-d),$$ (7)

the defocus distance is found by taking into account the magnification M and refractive index n_m as it follows: Δz_defocus = n_mΔz′/M².

Fig. 5.

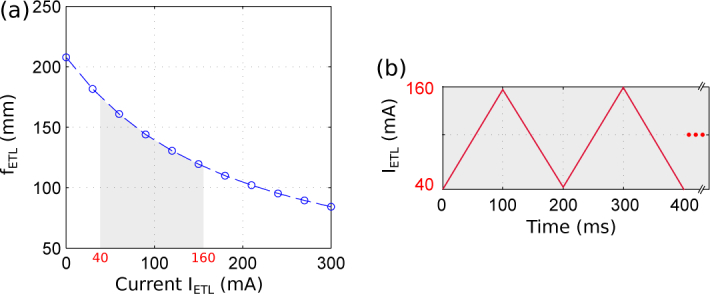
(a) Focal length variation of the ETL. (b) Electrical signal addressed into the ETL required for optical axial scan.

In the considered experiments a stack $I\left(\overrightarrow{r}\right)$ of intensity images (stack of 400 × 400 × 50 voxels corresponding to a XYZ region of 40 × 40 × 12 μm³) has been measured in 100 ms by using an exposure time of 2 ms, thus achieving an acquisition rate of 10 fps. Since the considered sCMOS camera is able to acquire 16-bit images of 400 × 400 pixels at a rate of 500 fps (exposure time of 2 ms), which might change depending on the camera manufacturer, the frequency of the triangular electrical signal of the ETL has been set at 5 Hz [I_ETL varying between 40 mA and 160 mA, see Fig. 5(b)] providing a proper focal length shift to axially the region Δz_defocus = 12 μm recording 50 images. Let us recall that a higher acquisition frame rate is possible just by reducing the size of the field of view (size of the 3D stack).

5.1.2. Optical trapping and manipulation setup

To generate the laser traps allowing for optical confinement and transport of the cells along arbitrary 3D curves, we have considered the same beam shaping approach reported in [20, 21]. It requires a computer generated hologram addressed into a programmable SLM (Holoeye PLUTO device with pixel size of 8 μm). The laser beam modulated by the SLM was relayed onto the back aperture of the objective lens by using a set of two identical convergent lenses (focal length of 150 mm) working as a ×1 Keplerian telescope. See [20, 21] for further details about the design and generation of the considered laser trapping beams and their optical forces that allow confining and propelling the particles. As depicted in Fig. 4, a Notch filter (Semrock, dichroic beam splitter for wavelength of 532 nm) has been used to redirect the trapping laser beam (Laser Quantum, Ventus, wavelength of 532 nm, 170 mW, linearly polarized) towards the objective lens. This filter also avoids imaging the backscattered laser light into sCMOS camera. Note that each cell confined in the considered laser traps receives an optical power of a few mW during a time of about 20 s, thus preventing the cell from being damaged.

5.2. Sample preparation

To experimentally demonstrate the performance of the proposed technique, we have considered living yeast cells (Schizosaccharomyces pombe bacteria dispersed in aqueous solution) that exhibit swimming motion and have fine cellular features. Specifically, a 1 gr of the yeast sample are poured into a test tube containing 100 ml of sucrose solution (20 %) in distilled water. This sucrose dilution acts as a surrounding medium with n_s = 1.37 (see [30]). Then, the dilution is stirred and heated at $35° \mathrm{C}$ for 10 minutes. Finally, it has been incubated 12 hours at room temperature$(25° \mathrm{C})$. S. pombe bacteria undergo aerobic fermentation in the presence of excess sugar, so 48 hours after the preparation the bacteria population has grown exponentially.

Funding

The Spanish Ministerio de Economía y Competitividad is acknowledged for the project TEC2014-57394-P.

Disclosures

The authors declare that there are no conflicts of interest related to this article.