Abstract
Quantification of tissue optical properties with optical coherence tomography (OCT) has proven to be useful in evaluating structural characteristics and pathological changes. Previous studies primarily used an exponential model to analyze low numerical aperture (NA) OCT measurements and obtain the total attenuation coefficient for biological tissue. In this study, we develop a systematic method that includes the confocal parameter for modeling the depth profiles of high NA OCT, when the confocal parameter cannot be ignored. This approach enables us to quantify tissue optical properties with higher lateral resolution. The model parameter predictions for the scattering coefficients were tested with calibrated microsphere phantoms. The application of the model to human brain tissue demonstrates that the scattering and back-scattering coefficients each provide unique information, allowing us to differentially identify laminar structures in primary visual cortex and distinguish various nuclei in the midbrain. The combination of the two optical properties greatly enhances the power of OCT to distinguish intricate structures in the human brain beyond what is achievable with measured OCT intensity information alone, and therefore has the potential to enable objective evaluation of normal brain structure as well as pathological conditions in brain diseases. These results represent a promising step for enabling the quantification of tissue optical properties from high NA OCT.
OCIS codes: (170.6935) Tissue characterization, (170.4500) Optical coherence tomography, (290.0290) Scattering, (170.3660) Light propagation in tissues, (170.3880) Medical and biological imaging
1. Introduction
Optical coherence tomography (OCT) has been widely used to investigate tissue microstructure in both clinical and scientific studies due to its high resolution and 3D imaging capability. OCT image intensities originate from back-scattered light and provide distinctive contrasts for various tissue types such as structural landmarks, pathological alterations, and varied physiological states. The depth profiles (A-lines) created with OCT are generally prescribed by four factors: the sample refractive index, attenuation coefficient, back-scattering coefficient, and the numerical aperture (NA) of the focusing optics. The attenuation coefficient, sum of the absorption and scattering coefficients, is an intrinsic property of the tissue independent of system optics and incident power. The attenuation coefficient has been routinely extracted from OCT measurements based on Beer’s law, which is appropriate for low NA measurements. This simple model has proven to be useful in detecting cancerous tissues in skin, bladder and brain [1–3], monitoring blood glucose concentration [4], characterizing atherosclerosis plaques [5,6] and correlating collagen content with histological staining [7]. Recently, quantification of the attenuation coefficient has been adopted in brain imaging [8] to follow neurological development in mouse models [9], to detect borders of brain tumors in human specimens [3,10], and to examine the physiological alterations in edema [11]. At imaging depths up to ~1mm, typically only a few scattering lengths deep in the tissue, it is generally valid to assume the single scattering Beer’s law where detected photons only scattering once within the tissue. For highly scattering samples, particularly with a large scattering anisotropy, a multiple-scattering model was introduced to investigate the effect of multiple scattering on the estimated attenuation coefficient, axial resolution and signal to noise ratio [12,13]. It has been reported that for the majority of biological tissues, the contribution of multiple scattering in the OCT image is fairly small, usually less than 10% [14].
The single-scattering exponential model describing signal attenuation versus depth is appropriate for low NA OCT systems where the lateral resolution is typically greater than 10 µm and the depth of focus (2 x Rayleigh range) is comparable to the effective imaging range [5,15]. For high NA OCT in which the lateral resolution approaches a few micrometers or less, the shape of the axial point spread function (PSF) becomes an important factor in modulating the signal depth profiles, and the effect of the confocal parameter in deriving the optical properties of tissue has to be considered [15,16]. We have shown that OCT with 3.5µm lateral resolution is able to differentiate laminar structures in the neocortex of human brain samples by using the average intensity projection (AIP) over the effective depth range [17]. To extend the previous study, our goal is to test the hypothesis that quantifying the intrinsic optical properties of the tissue would provide additional information to better differentiate the structures within the brain. However, to-date, the optical properties of tissue have not been quantitatively characterized with high NA OCT. Models including the impact of the confocal parameter have only been theoretically proposed and validated by uniform phantom samples [18,19]. In this work, we set out to extend the prior modeling of high NA OCT signal profile to quantify tissue optical properties. We find that in addition to extracting the attenuation coefficient, that we can also estimate the back-scattering property of the tissue, thus providing another dimension of information for the characterization [5,20]. We test the accuracy of the model fit in samples of microsphere solutions with varied concentrations, and analyze factors affecting the uncertainty of the estimates. We developed an iterative fitting approach that derives the optimal parameters for estimating the axial PSF that is subsequently used to estimate the tissue optical properties. We then investigate the optical properties of the human brain in two regions: the primary visual cortex and the midbrain. The results confirm that the combined features of attenuation coefficient and back-scattering showed an advantage over AIP in characterizing various structures in the human brain.
2. Methods
2.1 Theoretical model
Considering the shallow depth range we are interested in for ex-vivo brain imaging, we assume that the effect of multiple scattering is negligible on the measured signal. Using the single scattering model derived from Schmitt [15] and Izatt [16], the OCT signal can be expressed as
| (1) |
where is the incident power, is the quantum efficiency of the camera sensor, is the electron charge, is the integration time of the line-scan camera, and is the photon energy. R(z) is the reflectance from the sample at the depth of z, and z = 0 is the tissue surface. The reflectance is affected by two factors: the back-scattering coefficient () and the total attenuation coefficient () which is the sum of the scattering coefficient and the absorption coefficient . In the near-infrared spectral range, light attenuation within the tissue is dominated by scattering () and is negligible. Therefore, we use to represent the attenuation coefficient in the following sections. Both and are assumed constant over depth in one A-line.
| (2) |
is the axial PSF, which depends on the refractive index (), the focus depth () and the Rayleigh range (). In a single mode fiber based OCT system, the light beam in the sample approximately follows a Gaussian distribution [18]. We used a simplified PSF model that ignored the effect of refractive index differences at the tissue-air interface.
| (3) |
is the effective Rayleigh range which depends on the refractive index of the sample and the Rayleigh range obtained from the optics ( where is the beam waist at the focus, is the center wavelength, and NA is the numerical aperture of the optics). However, in highly scattering medium, the effective Rayleigh range has been observed to deviate from the theoretical expression [18,21], which is likely a result of the longer path lengths of the oblique rays attenuating more strongly than the on-axis rays and thus the NA of the focusing optics is effectively reduced [21]. Therefore, we introduced an effective Rayleigh range in the medium () and used empirical fitting to estimate for each experimental condition and sample. We also fit the model to estimate the empirical , as visually setting the focus depth at the exact location during experiment was not easy to achieve. As will be seen in the results, the actual obtained with fitting can slightly deviate from the experimental settings by a few tens of microns.
The back-scattering coefficient can be quantified with known and ; however, this would require careful calibration of the optical system because of optical losses from all of the optical components. We thus utilize the variable as a relative back-scattering coefficient for a specific OCT setup. We can measure relative changes in between different spatial regions and thus get an estimate of the relative changes in as the system specific parameters remain constant and cancel in the ratio.
The ratio of back-scattering coefficient and scattering coefficient indicates a back-scattering ratio (), which can be used as another feature to distinguish tissue types. In the model, we introduce a relative back-scattering ratio term () that is proportional to the absolute back-scattering ratio .
2.2 Spectral domain OCT system
We used a spectral domain OCT system to measure the optical properties of the sample [17], [22]. The light source was a broadband superluminescent diode with a center wavelength of 1300 nm and a full width half maximum bandwidth of 170 nm, yielding an axial resolution of 3.5 μm in tissue. The spectrometer consisted of a 1024 pixel InGaAs line scan camera operating at an A-line rate of 47kHz. The total imaging depth was estimated to be 1.5 mm. In the sample arm, two objective lenses were used in the experiment, including a 10x air coupled objective (Mitutoyo, NIR) and a 10 × water immersion objective (Zeiss, N-Achroplan), both yielding a lateral resolution of 3.5 μm with an expected depth of focus of 40 μm in a non-scattering medium. The volumetric imaging covered a field of view (FOV) of 1.5 × 1.5 × 1.5 mm3. The voxel size, which was defined by the stepping size of galvo mirror scanning laterally and obtained by the total imaging depth divided by the number of pixels axially, was isotropic 2.9 μm. The sensitivity of the system was 105 dB.
2.3 Sensitivity roll-off characterization
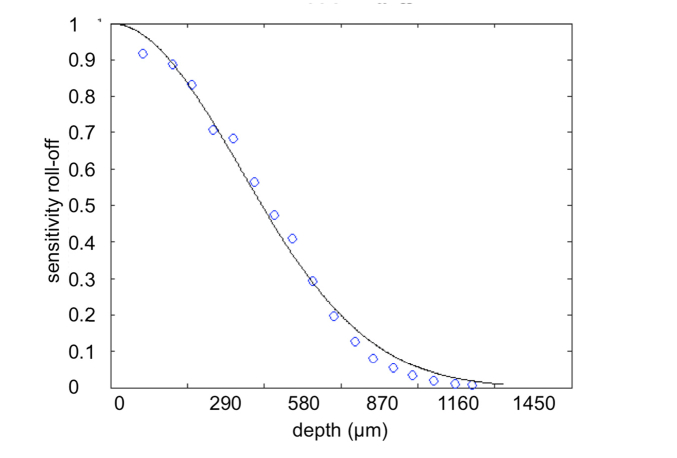
In spectral domain OCT, the sensitivity drops with imaging depth due to a limited resolution of the spectrometer and the discrete sampling by the line-scan camera. This sensitivity roll-off () was obtained by locating a reflective surface at a series of imaging depths and characterizing the peak reflectance accordingly. The measurements of the peak reflectance were fit as a function of [23], where is the relative depth normalized to the maximum imaging depth, represents the ratio of the spectrometer resolution () and the wavelength spacing between camera pixels ().
We characterized the sensitivity roll-off of the system using a silver mirror and plotted the fit with the measured data together in Fig. 1. The estimated function of was used throughout the study to compensate for the signal decay of the depth profiles before evaluating the optical properties.
Fig. 1.
Normalized sensitivity roll-off of the SD-OCT system (blue circles) together with the fitting function (solid black line). Note that each pixel on the x-axis corresponds to a depth of 2.9 μm in water.
2.4 Phantom test
Phantom preparation
Suspensions of monodisperse polystyrene microspheres with 1 µm mean diameter (Polysciences Inc.) were prepared for the phantom test. At the wavelength of 1300 nm, the refractive index of the microspheres is 1.57. The original solution was diluted in distilled water for five different concentrations, resulting in a volume fraction ranging from 0.22% to 1.10%. We used a Mie scattering calculator to derive the scattering coefficient for each sample, which was distributed between 2.1 mm−1 and 10.7 mm−1 for the concentrations used. The scattering anisotropy was 0.81. Table 1 summarizes the specifications of the samples.
Table 1. Specifications of the phantom samples.
| scattering coeff. (mm−1) | concentration (spheres/µm3) | volume fraction (%) |
|---|---|---|
| 2.1 | 0.0042 | 0.22 |
| 4.3 | 0.0084 | 0.44 |
| 6.4 | 0.0126 | 0.66 |
| 8.5 | 0.0168 | 0.88 |
| 10.7 | 0.021 | 1.1 |
Measurement
We imaged the five phantom samples with a 10x air objective. Each sample was measured at 8 different focus depths, starting from the surface where we defined and incremented by 50 µm up to a depth of 350 µm in the sample. The samples were slightly tilted with respect to the incident beam to reduce the specular reflection from the surface. Each measurement consisted of 5000 repeated A-lines at the same location, with a total acquisition time of 106.4 ms.
The raw data was resampled in k-space, compensated for dispersion and Fourier transformed to obtain the depth profile (). The depth profile was divided by the sensitivity roll-off function and then the noise floor (), defined as the average intensity at the imaging depth between 0.9 mm and 1.1 mm, was deducted. After this preprocessing, the data was fitted by the model Eqs. (2)-(3) for parameter estimations.
2.5 Curve fitting
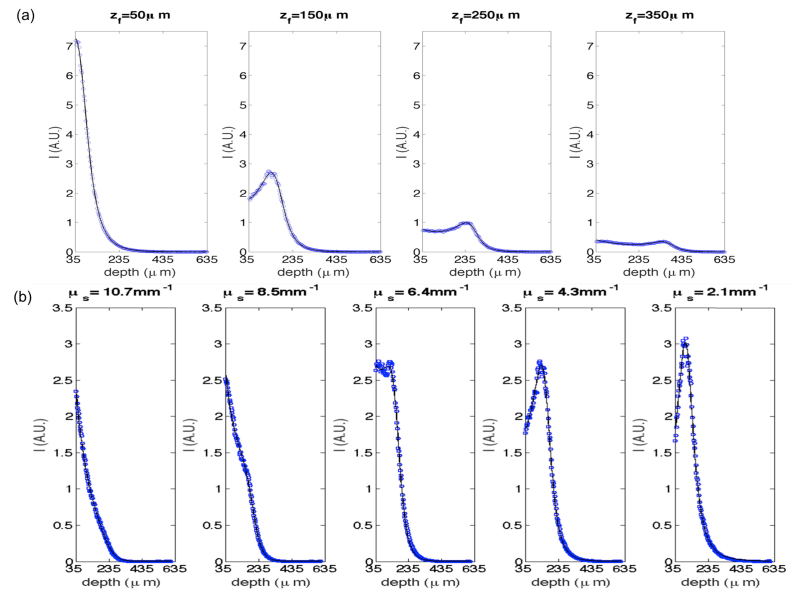
The expected Rayleigh range with the 10x air objective is 40 μm in air. In this study, we determined the effective Rayleigh range for individual sample measurements using parameter fitting. We also estimated the model parameter and compared the estimation with the experimental settings. A nonlinear least-squares cost function was used to obtain the optimization for , , , and . Recall that is a relative variable that is proportional to the back-scattering coefficient . Figure 2 shows the average depth profiles (blue dots) overlaid with the fitting (solid curves in black) for one microsphere suspension imaged at different focus depths (a) and the five samples with varied concentrations imaged at a certain focus depth (b). To minimize the effect of specular reflection, data from the top 35 μm depth of the microsphere samples was excluded from the fitting and the plots.
Fig. 2.
Depth profiles of the microsphere phantom at different focus depths (a) and with different concentrations (b). a) = 4.3mm−1, the focus depths at 50 μm, 150 μm, 250 μm and 350 μm, respectively. b) = 150 μm, expected scattering coefficients are 10.7 mm−1, 8.5 mm−1, 6.4 mm−1, 4.3 mm−1, and 2.1 mm−1, respectively. The dashed blue curves are averaged depth-profile from 5000 A-lines, and the solid black curves are the fitting functions.
2.6 Tissue imaging
Materials
A human brain was obtained from the Massachusetts General Hospital Autopsy Suite. The brain was neurologically normal without previous diagnosis of neurological deficits. The sample was fixed with 10% formalin for at least two months. The post-mortem interval did not exceed 24 h. The brain was cut into smaller blocks. Then the blocks of interests were embedded in oxidized agarose and covalently cross-linked with the agarose using borohydride borate solution. The surface of the embedded sample was flattened using a vibratome slicer before OCT imaging [24].
Data acquisition and analysis
Two experiments were conducted for the human brain imaging: one in the primary visual cortex and the other in the midbrain. The goal of the first experiment was to investigate the laminar structures of the visual cortex in human samples. A 3 × 3 mm2 section of primary visual cortex (BA17) was imaged with a 10x water immersion objective (Zeiss, N-Achroplan). The sample was flat faced with the vibratome to reveal the cortical layers and the adjacent white matter on the face of the sample. The volumetric imaging spanned a FOV of 1.5 x 1.5 x 1.5 mm3, with a voxel size of 2.9 x 2.9 x 2.9 μm3. The focus of the light beam was located 150 μm below the surface. The face of the sample was imaged with three overlapping tiles in order to cover all of the cortical layers and the adjacent white matter. There was a 33.3% overlap between adjacent tiles to ensure reliable registration. Motorized xyz stages were integrated under the sample arm to automatically translate the sample between image tiles. In the second experiment, we examined the structures of the midbrain. A 2 x 1.5 cm2 section of a midbrain tissue block was imaged with the same microscope objective. The focus of the light beam was directed 100 μm below the surface. The whole section was imaged in 260 tiles following the same scanning procedures as for the primary visual cortex. The total acquisition time was 45 min. We used Fiji software to stitch the tiles and create the mosaic images [25].
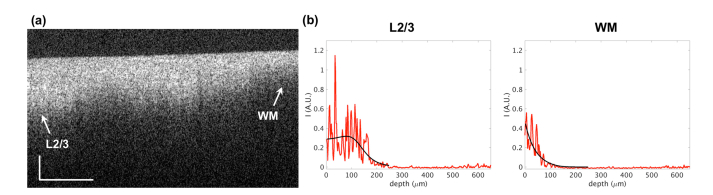
Before fitting the depth-profiles and estimating the optical properties, pre-processing was performed in two steps. The volumetric images were filtered with a 4x4 moving average window to reduce the speckle noise. The location of the tissue surface was determined on cross-sectional images, using a threshold to mask out the non-tissue region followed by an edge detector [26]. The start position for fitting was selected 35 μm below the tissue surface, in order to reduce the impact of specular reflection from the surface. The depth range used for profile fitting was 200 μm. Figure 3 demonstrates a cross sectional image for the primary visual cortex sample including the laminar structures and the white matter. The depth profiles for the layer 2/3 and the white matter are shown together with the corresponding fitting curves. We obtained the scattering coefficient map () and the back-scattering map () for the individual image tiles, and used the same Fiji software to stich the tiles together. To compare with conventional OCT contrast, the average intensity projection (AIP) and maximum intensity projection (MIP) maps within the same depth range were computed as well.
Fig. 3.
An example of cross sectional image for the primary visual cortex (a) and the curve fitting for the depth profiles (b). Scale bar: horizontal, 300 μm; vertical, 100 μm. The arrows in (a) indicate the position of the depth profiles (red) and fitting (black) shown in (b). L2/3: layer 2/3; WM: white matter. The zero depth in (b) indicates the location of the tissue surface.
To compare the scattering coefficient quantified with the proposed high NA model to the conventional low NA method of an exponential model , we repeated the measurement using a low NA objective in one experiment. The primary visual cortex sample was imaged with a 5x air objective, which yields a lateral resolution of 15 μm and an expected depth of focus of 280 μm in the tissue. The volumetric imaging covered a FOV of 3 x 3 x 1.5 mm3 with a voxel size of 5.8 x 5.8 x 2.9 μm3. The logarithmic depth-profile was fit with a linear function and the slope was used for estimation.
3. Results
3.1 Optical property characterization for the phantom samples
Estimation of and
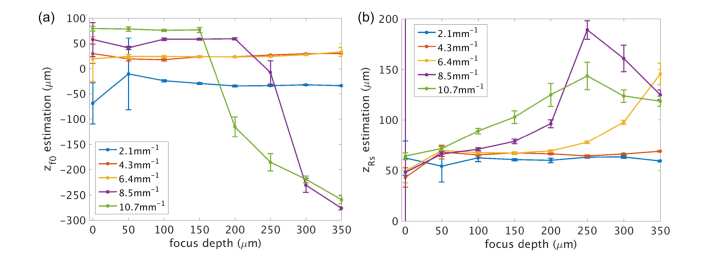
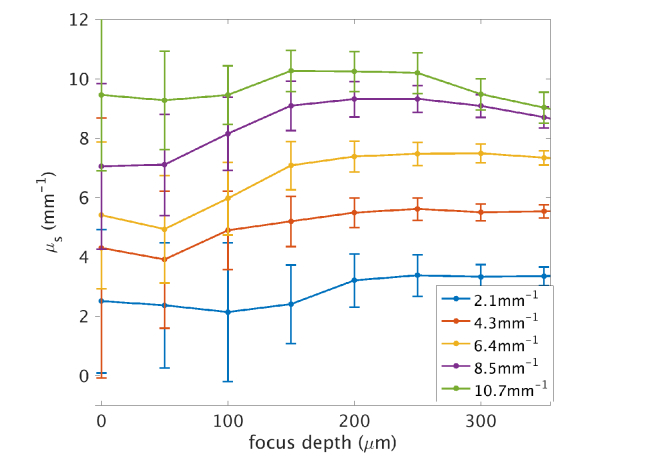
We first fit a 4 parameter model to estimate , , and for five microsphere samples measured at eight focus depths. For each measurement, the 5000 A-lines were divided into 25 observations with 200 A-lines in each block. The average of the 200 A-lines was used as the input data for each observation, and the median of the 25 observations was used as the prediction for each parameter. For estimation, we assumed that the 50 μm increment of the focus depth set in each measurement was precisely controlled by a manual translation stage, whereas the localization of the first at the sample surface was to be determined. Therefore, we fit the parameter of initial location of focus () where , (). Figure 4a plots the median ( ± S.E.M) of estimations from the 25 observations as a function of experimentally set focus depth for 5 phantom samples with varied concentration. The positive sign indicates below the tissue interface, while the negative sign indicates above the interface. Note that the initial focus was set independently for each sample and thus variation in between samples is expected. In general, the experimental setting slightly underestimated the initial focus depth (focus above surface) for low concentration medium ( = 2.1 mm−1) and overestimated the initial focus depth (focus below surface) for high concentration medium ( = 8.5 mm−1 and 10.7 mm−1). It is noticed that for the two highest concentrations, the estimation of > 200 μm significantly deviates from the expected depth, probably because the signal is greatly attenuated to the noise floor and the contribution of the axial PSF is diminished in the depth profile, which is indicated by the profiles of = 8.5 mm−1 and 10.7 mm−1 in Fig. 2b. We used the average of the first 5 focus depths (the first 4 for = 10.7 mm−1) as the initial focus depth (Table 2) for each sample measurement.
Fig. 4.
Estimation of a) the initial focus depth () and b) the effective Rayleigh range () as a function of experimentally set focus depth for 5 sample phantoms.
Table 2. Estimated focus depth set at the sample surface for the phantom samples.
| μs | 2.1 mm−1 | 4.3 mm−1 | 6.4 mm−1 | 8.5 mm−1 | 10.7 mm−1 |
|---|---|---|---|---|---|
| zf0 | −57.48 μm | −6.33 μm | −5.33 μm | 22.68 μm | 48.71 μm |
The effective Rayleigh range was fit using the five microsphere concentrations measured at differed focus depths. Figure 4(b) plots the median ( ± S.E.M) of the effective Rayleigh range from the 25 observations as a function of experimentally set focus depth, which is ~1.28 – 1.4 times greater than the theoretical expectation () in the scattering media. is comparable for all the microsphere suspensions measured at shallow focus depths, but distinctly increases with the focus depth for high scattering medium ( = 8.5 mm−1 and 10.7 mm−1). The rate of increase is more pronounced at higher concentration and scattering, leading to an almost doubling of for the highest concentration when the focus was set 200 μm deep compared to that at the surface. The results suggest that the effective Rayleigh range is both impacted by the scattering coefficient and the focus depth. Similar problem is present for the two highest scattering coefficients at deeper focus depth, where prediction of was severely underestimated.
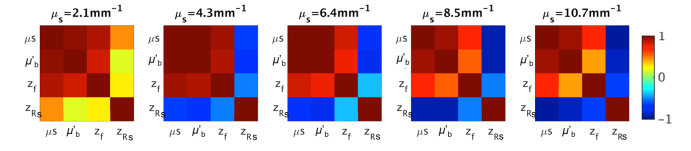
One problem of the nonlinear fitting is the inter-dependency of the estimated parameters. Figure 5 shows the correlation coefficient amongst pairs of the fitting parameters , , , and obtained from the phantom samples with five different microsphere concentrations. The strong covariance of and with and yields a large uncertainty in predicting the optical properties of the samples and makes the quantitative characterization of tissue optical properties ( and ) less reliable when applied to intricate biological systems. To minimize the problem, we applied a second round fitting of and using a fixed and , taken as the mean value for each sample using the first five focus depths (the first four for = 10.7 mm−1) and the first five effective Rayleigh ranges in Fig. 4. As a result, the error of estimation was significantly reduced (Fig. 6), despite the fact that the inter-dependency of and are still present. In principle, with careful experimental calibration, and can always be known a priori.
Fig. 5.
Correlation coefficient of the fitting parameters , , and for the microsphere suspensions at five concentrations.
Fig. 6.
The scattering coefficients estimated for the microsphere samples with five different concentrations. The curve shows the mean of the 250 observations and the error bar indicates the standard deviation. The expected scattering coefficients calculated by Mie theory are 2.1 mm−1, 4.3 mm−1, 6.4 mm−1, 8.5 mm−1, and 10.7 mm−1.
Estimation of
The scattering coefficient derived with fixed and is shown in Fig. 6. The solid dot and the error bar represent the mean and the standard deviation, respectively, for a specific focus depth and microsphere concentration. In each measurement, 5000 A-lines were divided into 250 blocks. The average of the 20 A-lines was used as the model input and the standard deviation was estimated across the results for the 250 blocks. The number of averages was selected to match the extent of spatial averaging for tissue imaging, so that the expected noise and the uncertainty of estimation were comparable for phantom and biological evaluations. The mean prediction ( ± S.E.M.) of the eight focus depths for the five samples is 2.9 ( ± 0.17) mm−1, 5.1 ( ± 0.21) mm−1, 6.7 ( ± 0.33) mm−1, 8.4 ( ± 0.30) mm−1, and 9.5 ( ± 0.20) mm−1, respectively, indicating an agreement with the expected values of 2.1 mm−1, 4.3 mm−1, 6.4 mm−1, 8.5 mm−1, and 10.7 mm−1 respectively. At high concentration and scattering ( = 10.7mm−1), the prediction tends to underestimate the scattering coefficient at increasing focus depths, possibly due to the contribution of multiple scattering. As we assumed the same for all the focus depths, the underestimation of for the deeper focus at higher scattering coefficients could also lead to a further underestimation of . It is notable that the uncertainty decreases with increasing focus depth for all the samples, and a desirable focus depth was observed below 100 μm that realized the most reliable prediction and a favorable precision to differentiate the scattering samples. The larger uncertainty at the shallower focus depths might be explained by the incomplete axial PSF, as the first 35 μm of the depth profile was excluded from the fitting (Fig. 2(a)). The contribution of the PSF shape was thus weakened in the profile formation for these shallower focus depths and fitting was heavily influenced by noise.
3.2 Optical properties of the human brain
We followed the two-step procedures introduced in the phantom characterization to investigate the optical properties of the human brain samples. We fit the 4 parameter model (,, and ) to the experimental data and obtained an average and for each brain sample. Then we repeated the fitting with fixed and to estimate the spatially varying optical properties of and for the brain samples. We also investigated the coefficient of determination (R2) for the parameter estimation.
Laminar structures in the primary visual cortex
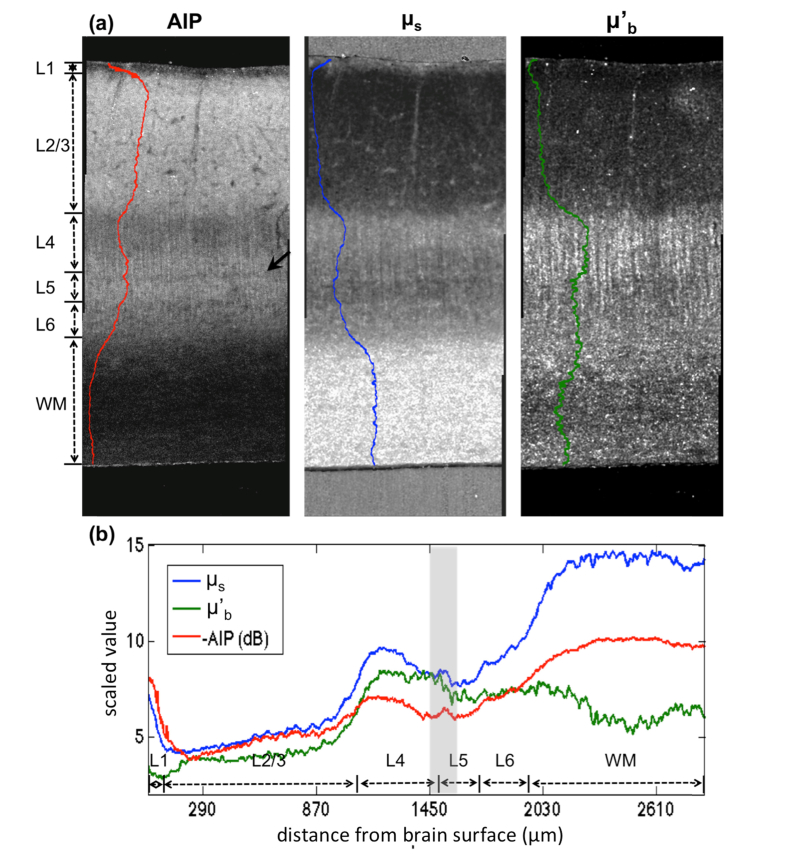
The laminar structures of primary visual cortex are evident in AIP, scattering coefficient (), and back-scattering () as shown in Fig. 7(a) along with the corresponding signal profiles. The and images illustrate remarkable features of the primary visual cortex. is significantly higher in the white matter compared to the cortex. Within the cortex, the scattering coefficients are higher in layer 1, 4 and 6 where vast tangential or vertical fiber tracts are present. Layer 2/3 bears the lowest scattering where cell bodies such as pyramidal neurons are dominantly concentrated. Layer 5 displays an intermediate brightness. The average for the six cortical layers and the white matter is 6.99 mm−1 and 14.09 mm−1, respectively. The back-scattering () exhibits a distinctive characteristic, in which the supragranular layers (layer 1-3) are significantly lower than the infragranular layers (layer 4-6). The vertical fibers in layer 4, which are axons extending from layer 2/3 pyramidal cell bodies are also highlighted by . For the tissue presented, is lower in the white matter than the adjacent cortical layers, probably because of the through-plane orientation of the fiber tracts.
Fig. 7.
The optical contrast maps of AIP, and demonstrate the laminar structure of the primary visual cortex in the human brain sample (a). The corresponding laminar profiles were obtained by the averaging the image intensity along the x-axis and plotted on the left side of individual images in (a), and overlaid in a single plot in (b). L1-L6 indicates the six cortical layers and WM indicates the white matter region. The black arrow in (a) and the gray shadow in (b) indicate the location of a novel structure shown by the optical contrasts.
To correlate the optical properties and with the OCT AIP image, we show the AIP map on the left. In general, the AIP is negatively correlated with across the laminar structures of the cortex. For example, the highest AIP is observed in layer 2/3, while the lowest is in the white matter. However, AIP is attributed to the combined factors of light attenuation and back scattering. Therefore, characterization of the cortical layers by pure intensity could be challenging, such as differentiating layer 2/3 and layer 5 in the primary visual cortex. In contrast, the optical properties and manifest distinctive characteristics between those layers. It is also noticeable that the high and low together contribute to the dark appearance of the white matter on the AIP image.
To further compare the signal profiles across the laminar structures, the inverted AIP (i.e. -AIP), and are plotted together in Fig. 7(b). It is interesting to note that both and AIP manifest a very narrow band with high scattering and low intensity between layer 4 and layer 5 in the primary visual cortex (arrow in Fig. 7(a) and the band between two gray lines in Fig. 7(b)), which is not well documented in the histological literature. In contrast, this band is not observed in , instead, an interface indicating a transition of brightness from high to low is shown.
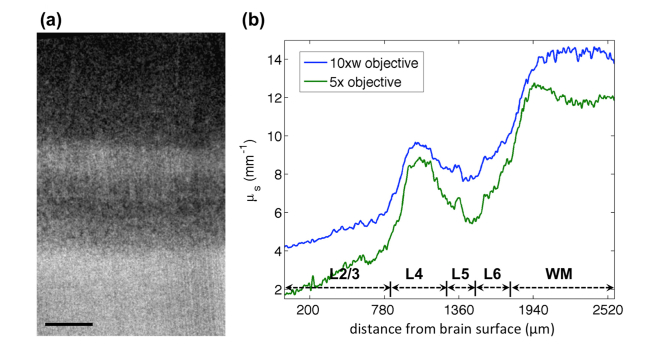
To compare the quantification results of the proposed model with the conventional method using a single exponential model, the same sample was imaged with a low NA objective, where the impact of the axial PSF was excluded due to the extended depth of focus. Figure 8(a) shows the scattering coefficient map of the laminar structures in the primary visual cortex (layer 1 excluded) using a 5x objective lens. The map exhibits similar contrast to that obtained with the higher resolution OCT (Fig. 7(a)). However, detailed features such as the vessels in layer 2/3 and the vertical fibers in layer 4 are only noticeable with the high NA OCT. We overlaid the profiles for the laminar structures obtained by the two models (Fig. 8(b)). The profiles demonstrate a general agreement in describing the layer specific characteristics. The estimation with the proposed model including the axial PSF appears to be slightly higher, with a difference ranging between 0.5 mm−1 and 1.8 mm−1. The different depth of focus for the 10x and 5x objectives might contribute to the discrepancy in the estimation.
Fig. 8.
Comparing the scattering coefficient map of the laminar structures in the primary visual cortex imaged by a low NA 5x and higher NA 10x objective. (a) The scattering coefficient map with a 5x objective lens. Scale bar: 400 μm. (b) Overlaid laminar profiles of the scattering coefficient obtained by the 10x water immersion objective (higher NA) and the 5x objective lens (lower NA).
The midbrain structures
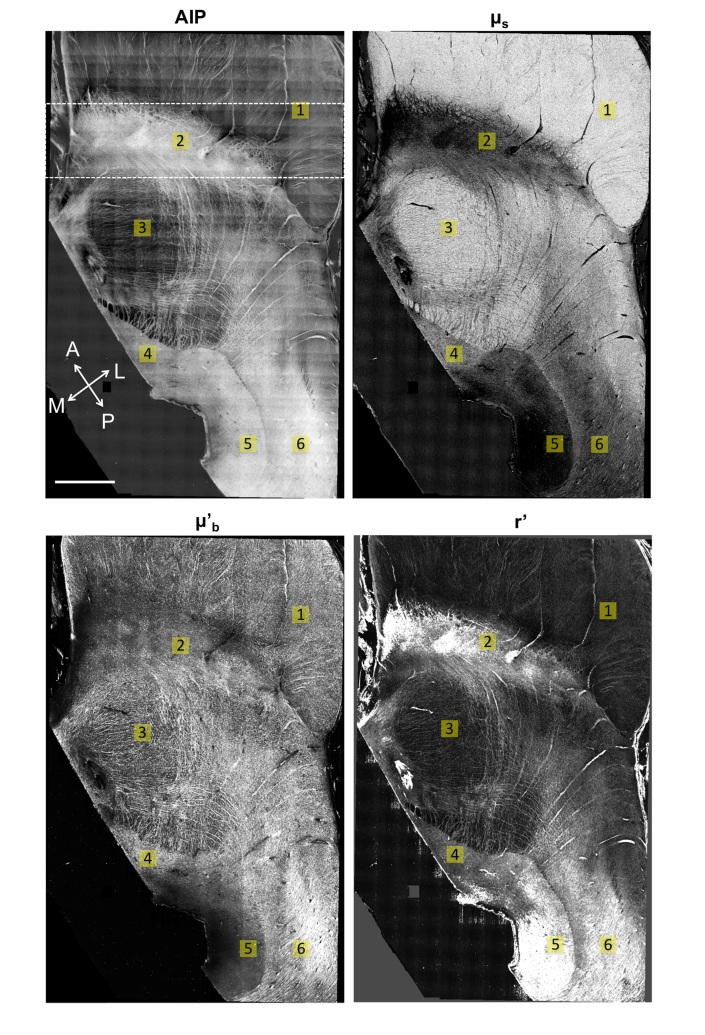
The human midbrain is a complex region that is compact in size while containing mixed structures of fiber tracts and various nuclei. The AIP, scattering coefficient and back-scattering maps in Fig. 9 demonstrate a 2 x 1.5 cm2 horizontal section of the midbrain (rotated by 30° counter-clockwise), with 6 labeled structures (cerebral peduncles, substantia nigra, red nucleus, oculomotor nucleus, periaqueductal gray and fasciculus) of the human brain anatomy [27]. The grid appearance on AIP is a stitching artifact introduced by the inhomogeneous intensity of the FOV. Consistent with the observations in the primary visual cortex, the contrasts of and AIP are negatively correlated. White matter regions such as the cerebral peduncles (ROI 1) manifest the highest scattering, followed by the highly myelinated nuclei mixed with intricate fibers, such as the red nucleus (ROI 3). The lightly myelinated nuclei such as substantia nigra (ROI 2) and periaqueductal gray (ROI 5) display the lowest scattering. The prominent contrast of facilitates the identification of these anatomical structures, particularly where the AIP map has less discrimination in spatially neighboring regions such as the oculomotor nucleus and the lateral periaqueductal gray. In addition, the white matter consistently exhibits a higher compared to the gray matter and the highly myelinated nuclei, indicating that the scattering coefficient is a reliable measure to distinguish the gray and white matter in the human brain. The grid appearance on AIP is a stitching artifact introduced by the inhomogeneous intensity of the FOV. However, this artifact is not visible on the map, indicating that the attenuation coefficient purely represents a tissue optical property independent of incident light intensity. Therefore, the quantification of provides an objective measure to characterize the brain structures.
Fig. 9.
The AIP, scattering coefficient (), back-scattering () and relative back-scattering ratio (r’) maps of a horizontal human midbrain section rotated by 30° counter-clockwise. ROIs: 1, cerebral peduncles; 2, substantia nigra; 3, red nucleus; 4, oculomotor nucleus; 5, periaqueductal gray; 6, fasciculus. Coordinates: A, anterior; P, posterior; M, medial; L, lateral. Scale bar: 2.5 mm. Note that the scales for and g’ are arbitrary as the backscattering coefficient units are not calibrated.
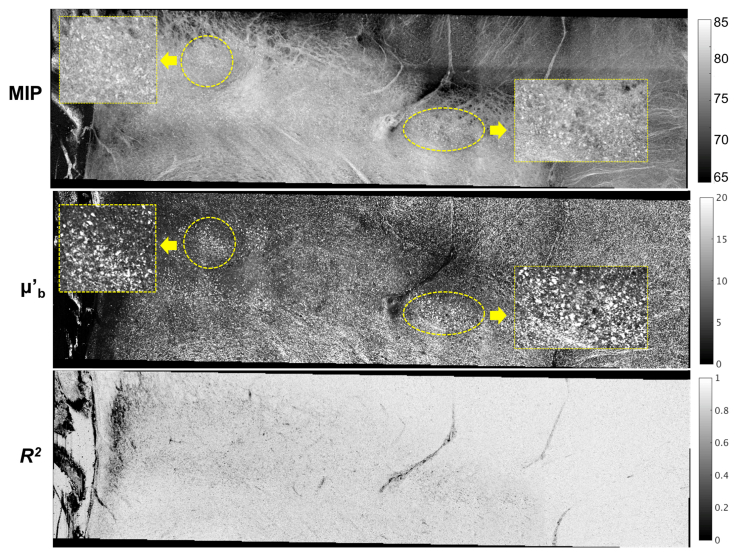
In addition to the scattering coefficient map, the back-scattering map offers another feature dimension to discriminate different tissue types. It is noticeable that highlights the small fiber tracts across the midbrain (right panel of Fig. 9). In a zoomed region (Fig. 10 with the location indicated by the dashed box on AIP of Fig. 9), the large neuromelanin pigmented neurons forming clusters in the substantia nigra are sensitively captured by as well (the yellow circles and zoomed in rectangle in Fig. 10), which are implied by MIP but with less pronounced contrast. Therefore, and each provide unique information and enhances the ability of OCT to distinguish intricate structures in the human brain beyond what is achievable with conventional OCT intensity information alone. The R2 map indicates how well the model fits the data. The average R2 of 0.84 for the midbrian sample indicates a good fit using the model to characterize the depth profiles in the high resolution OCT images. Because the model assumes a single scattering coefficient and back-scattering coefficient in one A-line without accounting for the depth-wise differences, we expect a lower R2 in fitting where highly scattered components are present at certain localized depths, such as individual neurons or fiber tracts.
Fig. 10.
Zoomed-in maps of , and R2 for the regions of cerebral peduncles and substantia nigra in the midbrain. The location of the regions is indicated by the dashed rectangular box on AIP of Fig. 9. The yellow circles indicate the clustered neuromelanin pigmented neurons in the substantia nigra manifested on the and MIP map. The rectangle boxes show zoomed-in clusters.
The back-scattering coefficient is proportional to the scattering coefficient, where the proportionality is dependent on the back-scattering ratio. Thus, variation in the ratio between the back-scattering and scattering coefficient provides another useful feature to distinguish structures in the brain. The relative back-scattering ratio () image for the midbrain is demonstrated in Fig. 9 as well. The map highlights the fasciculus (ROI 6) next to the periaqueductal gray (ROI 5) and the reticular fiber meshes across the midbrain region, which might indicate fibers running parallel to the imaging plane. The substantia nigra (ROI 2) also shows a high relative back-scattering ratio possibly contributed by the neuromelanin pigmented neurons. It is noticeable that in the posterior part of periaqueductal gray is excessively high, which might be an artifact introduced by an error in the fitting (indicated by a low R2).
4. Discussion
Previous studies investigating the optical properties of biological tissues with OCT primarily adopted a simple exponential model based on Beer’s law. For high-resolution OCT, models including the impact of the confocal parameter have only been theoretically proposed and validated by uniform phantom samples [18,19]. In this study, we established a method to systematically investigate the scattering coefficient and the back-scattering of tissue using a 3.5 μm resolution OCT system, in which the axial PSF contributes significantly to the formation of the depth profiles. We developed a procedure to quantify the parameters of the axial PSF and the optical properties of the tissue in two consecutive steps. Applying the model in human brain imaging demonstrates that additional information can be extracted about the tissue from this quantitative analysis versus from the conventional AIP image alone. In particular, the recovered scattering and back-scattering coefficients improve the ability to distinguish various brain structures. The objective characterization is potentially helpful to explore new structures that are largely unknown in the human brain. The quantitative information may benefit the pathological evaluations at an early stage before the vast structural alteration occurs. In addition, a further implementation of real-time optical property estimation may be used for intraoperative examination.
4.1 Optical properties of the human brain
We applied the models in two human brain samples including primary visual cortex and the subcortical regions in the midbrain. The quantitative properties have proven to be capable of distinguishing laminar structures in the cortex, as well as white matter tracts and subcortical nuclei. We obtained an average scattering coefficient of 7.54 mm−1 for the gray matter and 17.72 mm−1 for the white matter, which are roughly comparable with previous reports in brain tissues [28]. As cell density and myelin content are much higher in the human, we expect an overall higher scattering coefficient in the human compared to rodents [9], [29]. Another factor influencing the optical property is the ex vivo tissue preparation. Overall, tissue dehydration increases scattering probably due to more dense packing of the intercellular and intracellular components, and the crosslink of proteins during fixation is likely to change the scattering property as well [30,31]. There is a general negative correlation between the scattering coefficient and the AIP, as expected as the greater light attenuation results in a lower average intensity in the OCT images. However, the scattering coefficient offers a better signature for distinguishing the anatomical structures, especially for those that are densely packed and spatially adjacent. Our results suggest that the differences in the scattering coefficient are more pronounced between layer 2/3 and layer 5 in the primary visual cortex, and the gray matter of oculomotor nucleus and lateral periaqueductal gray in the midbrain; whereas, the AIP yields less distinct contrast measures among those structures. Another advantage of using the scattering coefficient to characterize the brain is that the quantification releases the dependency on the optics and the incident power, and hence serves as an objective measure of tissue property. As shown in Fig. 9, the map completely gets rid of the stitching artifact observed on AIP due to inhomogeneous light intensity across the imaging field of view.
The biological factors modulating the scattering coefficient may include cellular/molecular size, cell density, arrangement of axons and myelin content. We found that the highest both in the primary visual cortex and the midbrain is displayed in the white matter, which is mainly composed of myelinated fibers. Highly myelinated nucleus or cortical layers (layer 4) also exhibit high scattering. We hypothesize that the myelin content is the most important factor contributing to a high scattering coefficient. The is low in regions where cell bodies are primarily present, such as layer 2/3 in the primary visual cortex and the substantia nigra in the midbrain. Therefore, light scattering by cell bodies is much weaker compared to the myelinated axons. We did observe a trend for increasing in the transition from layer 2 to layer 3, which possibly implied a difference in cell size and density and the number of connections between the two layers.
The model supports extraction of the scattering coefficient and the back-scattering property separately, allowing each to provide unique information. In the white matter region, depends on the orientation of the fiber with respect to the incident angle of the light source. For fibers running through the plane, could be significantly lower than the gray matter, as shown in the primary visual cortex tissue. This low also contributes to the dark appearance on the OCT intensity image. The variations of the OCT intensity in the white matter have been shown both in ex vivo rodent and human brain imaging [8], [17], and the extraction of in the current study provides a further explanation for the observations. Another example is the substantia nigra of the midbrain, where illustrates generally a low light attenuation; however, adds on the feature dimension that indicates the localization of big neuron clusters within the structure. As a result, the 2 parameter quantifications dramatically enhance the power of using OCT to distinguish intricate structures in the human brain over what is achievable with conventional OCT intensity information alone. The combination of the scattering coefficient and the back-scattering supports the identification of novel structures that only show subtle differences in a single feature. In this study, we found an intriguing architectural feature in the primary visual cortex that is not well documented by histology. The map reveals a narrow band, ~80μm wide, between layer 4 and layer 5 that exhibits high brightness, whereas the map shows it as an interface transition between high and low brightness. Immunohistochemistry staining supports the presences of different chemical zones between layer 4C and layer 5 of BA 17 [32,33]. In addition, a thin line of myelin at the border of layer 4 and 5 has been reported [34]. It is possible that the two optical properties represent distinctive biological processes spatially co-aligned in the primary visual cortex. These findings by tissue optical property characterization may trigger new explorations of the cellular biology for neuronal type screening of the human brain.
4.2 Factors affecting the model performance
There are four parameters in the model for constructing an OCT depth profile, including , , , and . The first two are important in high-resolution OCT to determine the axial point spread function. Leeuwen et al. developed a model to simplify the point spread function with the two parameters of and [18]. However, the values of and were either pre-determined by experimental settings or estimated with known and in phantom samples [19]. In our study, parameter fitting suggests that the exact could easyly deviate from the anticipated settings by tens of microns, which is on the order of the Rayleigh range. Although the Rayleigh range in air can be determined by the optics, the effective Rayleigh range alters in scattering media. Leeuwen’s study tested a phantom sample with OCT and used empirical fitting to investigate the Rayleigh range in the scattering medium and reported a factor of two compared to the Rayleigh range in air [18]. Theer et al. investigated the fundamental limitation of the imaging depth in two-photon imaging due to the deterioration of resolution, and proposed a model to quantify the effect of imaging depth on the Rayleigh range with high NA objective [21]. In this study, we found that the effective Rayleigh range is affected by the scattering coefficient and the focus depth. The effect of focus depth is more pronounced in highly scattering medium, as dramatically increases as the imaging focus goes deeper results in stronger attenuation of the large angle light rays versus the on-axis light rays [21]. It is indicating that for highly scattered tissue, the transverse resolution becomes rapidly deteriorated as the focus goes deeper into the tissue. As a result, it is useful to obtain the actual and by using model predictions in tissue imaging.
The nonlinear model results in an inter-parameter dependency in the predictions. As Table 2 suggested, and are positively correlated, and both of them are highly correlated with and . This correlation becomes stronger as the scattering coefficients increases. Therefore, the estimation of the tissue optical properties could be compromised by a biased estimation of or , although the overall goodness of fitting appears reasonable. Fitting all the parameters at the same time leads to large uncertainty, which reduces the precision and makes the quantification less reliable for distinguishing subtle differences in the optical properties. In this study, we developed a two-step approach to quantify the optical properties, where the parameters for the axial PSF were derived first using an average value of the fitting results, and then the scattering coefficients and the back-scattering were obtained with the axial PSF parameters fixed. The results from phantom characterization suggested that with pre-estimated or , the scattering coefficients were reliably obtained and matched with the theoretical expectations.
The characterization of in the phantom samples suggested a desirable focus depth resulting from the tradeoff between resolution loss and prediction uncertainty. Our study indicates that the most favorable focus is to be set between 100 to 200 μm in the tissue with a 10x microscope objective, in order to obtain a reliable and precise prediction for the optical properties. With a more shallow focus, the specular reflection from the tissue surface could bias the fitting. In addition, the shape of the axial PSF was not fully revealed in the depth profile and hence makes the parameter estimations heavily affected by the superficial noise. A deep focus appears to significantly reduce this variability; however, the resolution and signal to noise ratio are severely deteriorated by the scattering. With a focus below 200 μm the effect of multiple scattering becomes more influential and can result in an underestimation of from the expected value.
There are several limitations in the current model. The refractive index difference at the tissue interface was not considered in the axial point spread function. This might be a minor effect using a water immersion objective as we did, however it could significantly influence the estimation with an air objective. Both the Schmitt model [15] and Izatt model [16] included the factor of refractive index. However, the model required more parameters to be estimated and the dependency between parameters in the nonlinear fitting could introduce a greater bias in the prediction. We tested the Izatt model in the microsphere samples and did not find a significant difference for the estimation. Characterization of the additional parameters in advance may help to improve the model performance for optical property estimation in tissue. The refractive index differences between different tissue types were not considered in the model. It was known from mouse brain imaging that the refractive index for the white matter is greater than the gray matter [35,36]. This difference could account for a varied and among brain structures. The current model assumed a single refractive index in the tissue and dismissed the effect on the parameters related to the point spread function. This may provide an explanation for the observed difference of estimations between the single exponential model and the model used in this study, especially in the white matter regions. The empirical fitting suggested that the effective Rayleigh range changes with the scattering coefficient especially in high scattering media. In the current study, a uniform effective Rayleigh range was assumed in tissue imaging. Future models establishing the relationship between the effective Rayleigh range and the scattering coefficient should be developed for heterogonous tissue imaging such as the human brain. Finally, it is desirable to develop the depth-solved model for characterizing the optical properties ( and ) of tissue because of the inherent 3D capability of OCT. The current assumption of constant scattering and back-scattering coefficients for one A-line restricts the ability of OCT to quantify small features located at certain depths, such as neuronal cell bodies, small fiber tracts and vessels in the human brain. Depth-resolved models have been proposed for low NA OCT with validations by phantom samples and demonstrations in retinal, colon and bladder imaging [37], [38]. In the future, adaptation of the depth-resolved model for high NA OCT will enable OCT to map 3D optical properties of tissues with higher than ever resolution.
5. Conclusion
High NA OCT has shown the ability to enable investigation of the human brain structures at cellular level resolution. However, models for quantifying the optical properties of biological tissues with high NA OCT have only been theoretically proposed and validated by uniform phantom samples. In this study, we established a method to systematically characterize the optical properties of the human brain for high NA OCT with a 3.5 μm lateral resolution, in which the factor of confocal parameter was included. The results show that the scattering and back-scattering coefficients each provide unique information to differentially identify laminar structures in primary visual cortex and various nuclei in the midbrain. Therefore the objective quantification significantly enhances the power of OCT to investigate the intricate human brain beyond the measured OCT intensity.
Funding
Support for this research was provided in part by the National Institute of Biomedical Imaging and Bioengineering (P41EB015896, R01EB021018, 1R01EB023281, R01EB006758, R21EB018907, R01EB019956), the National Institute on Aging (5R01AG008122, R01AG016495), the National Institute of Diabetes and Digestive and Kidney Diseases (R21DK108277-01), the National Institute of Neurological Disorders and Stroke (R01NS0525851, R21NS072652, R01NS070963, R01NS083534, 5U01NS086625, R01NS091230, P01NS055104), and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by the NIH Blueprint for Neuroscience Research (5U01-MH093765), part of the multi-institutional Human Connectome Project.
Disclosures
BF has a financial interest in CorticoMetrics, a company whose medical pursuits focus on brain imaging and measurement technologies. BF’s interests were reviewed and are managed by Massachusetts General Hospital and Partners HealthCare in accordance with their conflict of interest policies.
References and links
- 1.Coleman A. J., Richardson T. J., Orchard G., Uddin A., Choi M. J., Lacy K. E., “Histological correlates of optical coherence tomography in non-melanoma skin cancer,” Skin Res. Technol. 19(1), 10–19 (2013). [DOI] [PubMed] [Google Scholar]
- 2.Cauberg E. C. C., de Bruin D. M., Faber D. J., de Reijke T. M., Visser M., de la Rosette J. J., van Leeuwen T. G., “Quantitative measurement of attenuation coefficients of bladder biopsies using optical coherence tomography for grading urothelial carcinoma of the bladder,” J. Biomed. Opt. 15(6), 066013 (2010). [DOI] [PubMed] [Google Scholar]
- 3.Kut C., Chaichana K. L., Xi J., Raza S. M., Ye X., McVeigh E. R., Rodriguez F. J., Quiñones-Hinojosa A., Li X., “Detection of human brain cancer infiltration ex vivo and in vivo using quantitative optical coherence tomography,” Sci. Transl. Med. 7(292), 292ra100 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Larin K. V., Eledrisi M. S., Motamedi M., Esenaliev R. O., “Noninvasive Blood Glucose Monitoring With Optical Coherence Tomography: A Pilot Study In Human Subjects,” Diabetes Care 25(12), 2263–2267 (2002). [DOI] [PubMed] [Google Scholar]
- 5.Xu C., Schmitt J. M., Carlier S. G., Virmani R., “Characterization of atherosclerosis plaques by measuring both backscattering and attenuation coefficients in optical coherence tomography,” J. Biomed. Opt. 13(3), 034003 (2008). [DOI] [PubMed] [Google Scholar]
- 6.van der Meer F. J., Faber D. J., Baraznji Sassoon D. M., Aalders M. C., Pasterkamp G., van Leeuwen T. G., “Localized measurement of optical attenuation coefficients of atherosclerotic plaque constituents by quantitative optical coherence tomography,” IEEE Trans. Med. Imaging 24(10), 1369–1376 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Yang Y., Wang T., Biswal N. C., Wang X., Sanders M., Brewer M., Zhu Q., “Optical scattering coefficient estimated by optical coherence tomography correlates with collagen content in ovarian tissue,” J. Biomed. Opt. 16(9), 090504 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang H., Zhu J., Akkin T., “Serial optical coherence scanner for large-scale brain imaging at microscopic resolution,” Neuroimage 84, 1007–1017 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chong S. P., Merkle C. W., Cooke D. F., Zhang T., Radhakrishnan H., Krubitzer L., Srinivasan V. J., “Noninvasive, in vivo imaging of subcortical mouse brain regions with 1.7 μm optical coherence tomography,” Opt. Lett. 40(21), 4911–4914 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Vuong B., Skowron P., Kiehl T. R., Kyan M., Garzia L., Sun C., Taylor M. D., Yang V. X., “Measuring the optical characteristics of medulloblastoma with optical coherence tomography,” Biomed. Opt. Express 6(4), 1487–1501 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rodriguez C. L. R., Szu J. I., Eberle M. M., Wang Y., Hsu M. S., Binder D. K., Park B. H., “Decreased light attenuation in cerebral cortex during cerebral edema detected using optical coherence tomography,” Neurophotonics 1(2), 025004 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Levitz D., Thrane L., Frosz M., Andersen P., Andersen C., Andersson-Engels S., Valanciunaite J., Swartling J., Hansen P., “Determination of optical scattering properties of highly-scattering media in optical coherence tomography images,” Opt. Express 12(2), 249–259 (2004). [DOI] [PubMed] [Google Scholar]
- 13.Wang R. K., “Signal degradation by multiple scattering in optical coherence tomography of dense tissue: a Monte Carlo study towards optical clearing of biotissues,” Phys. Med. Biol. 47(13), 2281–2299 (2002). [DOI] [PubMed] [Google Scholar]
- 14.Almasian M., Bosschaart N., van Leeuwen T. G., Faber D. J., “Validation of quantitative attenuation and backscattering coefficient measurements by optical coherence tomography in the concentration-dependent and multiple scattering regime,” J. Biomed. Opt. 20(12), 121314 (2015). [DOI] [PubMed] [Google Scholar]
- 15.Schmitt J. M., Knuettel A. R., Gandjbakhche A. H., Bonner R. F., “Optical characterization of dense tissues using low-coherence interferometry,” Proc. SPIE 1889, 197–211 (1993). [Google Scholar]
- 16.Izatt J. A., Hee M. R., Owen G. M., Swanson E. A., Fujimoto J. G., “Optical coherence microscopy in scattering media,” Opt. Lett. 19(8), 590–592 (1994). [DOI] [PubMed] [Google Scholar]
- 17.Magnain C., Augustinack J. C., Reuter M., Wachinger C., Frosch M. P., Ragan T., Akkin T., Wedeen V. J., Boas D. A., Fischl B., “Blockface histology with optical coherence tomography: A comparison with Nissl staining,” Neuroimage 84, 524–533 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.van Leeuwen T. G., Faber D. J., Aalders M. C., “Measurement of the axial point spread function in scattering media using single-mode fiber-based optical coherence tomography,” IEEE J. Sel. Top. Quantum Electron. 9(2), 227–233 (2003). [Google Scholar]
- 19.Faber D., van der Meer F., Aalders M., van Leeuwen T., “Quantitative measurement of attenuation coefficients of weakly scattering media using optical coherence tomography,” Opt. Express 12(19), 4353–4365 (2004). [DOI] [PubMed] [Google Scholar]
- 20.Schmitt J. M., Knüttel A., Yadlowsky M., Eckhaus M. A., “Optical-coherence tomography of a dense tissue: statistics of attenuation and backscattering,” Phys. Med. Biol. 39(10), 1705–1720 (1994). [DOI] [PubMed] [Google Scholar]
- 21.Theer P., Denk W., “On the fundamental imaging-depth limit in two-photon microscopy,” J. Opt. Soc. Am. A 23(12), 3139–3149 (2006). [DOI] [PubMed] [Google Scholar]
- 22.Srinivasan V. J., Jiang J. Y., Yaseen M. A., Radhakrishnan H., Wu W., Barry S., Cable A. E., Boas D. A., “Rapid volumetric angiography of cortical microvasculature with optical coherence tomography,” Opt. Lett. 35(1), 43–45 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yun S., Tearney G., Bouma B., Park B., de Boer J., “High-speed spectral-domain optical coherence tomography at 1.3 μm wavelength,” Opt. Express 11(26), 3598–3604 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ragan T., Kadiri L. R., Venkataraju K. U., Bahlmann K., Sutin J., Taranda J., Arganda-Carreras I., Kim Y., Seung H. S., Osten P., “Serial two-photon tomography for automated ex vivo mouse brain imaging,” Nat. Methods 9(3), 255–258 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Preibisch S., Saalfeld S., Tomancak P., “Globally optimal stitching of tiled 3D microscopic image acquisitions,” Bioinformatics 25(11), 1463–1465 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Canny J., “A Computational Approach to Edge Detection,” IEEE Trans. Pattern Anal. Mach. Intell. 8(6), 679–698 (1986). [PubMed] [Google Scholar]
- 27.Naidich T., Duvernoy P., Delman H. M., Sorensen B. N., Kollias A. G., Haacke S. S., “Internal Architecture of the Brain Stem with Key Axial Section,” in Duvernoy’s Atlas of the Human Brain Stem and Cerebellum (Springer Vienna, 2009). [Google Scholar]
- 28.Jacques S. L., “Optical properties of biological tissues: a review,” Phys. Med. Biol. 58(11), R37–R61 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Wang H., Black A. J., Zhu J., Stigen T. W., Al-Qaisi M. K., Netoff T. I., Abosch A., Akkin T., “Reconstructing micrometer-scale fiber pathways in the brain: Multi-contrast optical coherence tomography based tractography,” Neuroimage 58(4), 984–992 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hsiung P. L., Nambiar P. R., Fujimoto J. G., “Effect of tissue preservation on imaging using ultrahigh resolution optical coherence tomography,” J. Biomed. Opt. 10(6), 064033 (2005). [DOI] [PubMed] [Google Scholar]
- 31.Pitzschke A., Lovisa B., Seydoux O., Haenggi M., Oertel M. F., Zellweger M., Tardy Y., Wagnières G., “Optical properties of rabbit brain in the red and near-infrared: changes observed under in vivo, postmortem, frozen, and formalin-fixated conditions,” J. Biomed. Opt. 20(2), 25006 (2015). [DOI] [PubMed] [Google Scholar]
- 32.Leuba G., Kraftsik R., Saini K., “Quantitative distribution of parvalbumin, calretinin, and calbindin D-28k immunoreactive neurons in the visual cortex of normal and Alzheimer cases,” Exp. Neurol. 152(2), 278–291 (1998). [DOI] [PubMed] [Google Scholar]
- 33.Garcia-Marin V., Ahmed T. H., Afzal Y. C., Hawken M. J., “Distribution of vesicular glutamate transporter 2 (VGluT2) in the primary visual cortex of the macaque and human,” J. Comp. Neurol. 521(1), 130–151 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Braak P. D. H., “The Three Standard Techniques Used in Architectonics,” in Architectonics of the Human Telencephalic Cortex (Springer; Berlin Heidelberg, 1980). [Google Scholar]
- 35.Binding J., Ben Arous J., Léger J.-F., Gigan S., Boccara C., Bourdieu L., “Brain refractive index measured in vivo with high-NA defocus-corrected full-field OCT and consequences for two-photon microscopy,” Opt. Express 19(6), 4833–4847 (2011). [DOI] [PubMed] [Google Scholar]
- 36.Sun J., Lee S. J., Wu L., Sarntinoranont M., Xie H., “Refractive index measurement of acute rat brain tissue slices using optical coherence tomography,” Opt. Express 20(2), 1084–1095 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Vermeer K. A., Mo J., Weda J. J. A., Lemij H. G., de Boer J. F., “Depth-resolved model-based reconstruction of attenuation coefficients in optical coherence tomography,” Biomed. Opt. Express 5(1), 322–337 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Smith G. T., Dwork N., O’Connor D., Sikora U., Lurie K. L., Pauly J. M., Ellerbee A. K., “Automated, Depth-Resolved Estimation of the Attenuation Coefficient From Optical Coherence Tomography Data,” IEEE Trans. Med. Imaging 34(12), 2592–2602 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]