Abstract
A uniformly diffusing applicator can be advantageous for laser treatment of tubular tissue. The current study investigated various conical angles for diffuser tips as a critical factor for achieving radially uniform light emission. A customized goniometer was employed to characterize the spatial uniformity of the light propagation. An ex vivo model was developed to quantitatively compare the temperature development and irreversible tissue coagulation. The 10-mm diffuser tip with angle at 25° achieved a uniform longitudinal intensity profile (i.e., 0.90 ± 0.07) as well as a consistent thermal denaturation on the tissue. The proposed conical angle can be instrumental in determining the uniformity of light distribution for the photothermal treatment of tubular tissue.
OCIS codes: (140.3390) Laser materials processing, (120.6810) Thermal effects, (170.1610) Clinical applications, (170.3660) Light propagation in tissues, (230.1980) Diffusers
1. Introduction
For decades, laser systems have widely been developed for medical applications such as tumor ablation, blood coagulation, cancer treatment, surgical resection, and optical imaging [1–3]. However, these applications have often been limited by short optical penetration depths due to the intrinsic turbidity of biological tissue. Thus, optical fiber technologies are typically incorporated to deliver high-power laser light in an endoscopic manner. Depending on the geometry of the targeted disease, a number of fibers have been developed and fabricated including end-firing fibers, side-firing fibers, spherical fibers, and diffusing fibers [4]. The designed tip can determine the direction and spatial distribution of the emitted light, eventually achieving an effective treatment for the targeted tissue with minimal injury to the surrounding healthy tissue.
Recently, diffusing optical applicators have been developed and investigated for the treatment of tubular tissue such as photodynamic therapy, nasopharyngeal carcinoma treatment [5], laser lipolysis [6], endovenous laser ablation [7], and tracheal stenosis treatment [8]. However, these developments are partly finished and their availability on the market is still unsatisfactory. In addition, the precise delivery of the amount of optical energy from the fiber is one of the main factors in determining favorable therapeutic outcomes. Thus, non-uniform light irradiation can hardly predict a temperature distribution in tissue, which may cause unpredictable coagulation and even carbonization during thermal treatment. Thermal injury or incomplete treatment can also lead to complications such as discomfort, pain, and risk of recurrence. For light diffusers, a number of fabrication techniques have been developed, including acid-etching [9, 10], melt-drawing [9, 11], scattering media [12, 13], CO2 laser polishing [14], long period gating (LPG) [15, 16], and UV micro-drilling [10, 17]. However, both the acid-etching and melt-drawing techniques are limited to using small core diameters (33–125 µm), and external impact is often employed to roughen the fiber tip surface, causing physical damage to the fiber surface [9, 11]. Depending on the TiO2 concentration, the addition of scattering media can lead to unpredictable light diffusion from the tip [12, 13]. In spite of creating a conical tip for radial emissions, a CO2 laser was able to fabricate a short range of the active element for the diffusing tip [14]. In the case of the LPG technique using a KrF excimer laser, the fabricated fibers are protected by coating a mixture of clear epoxy and TiO2. However, the use of TiO2 usually limits the input power and wavelength (i.e., 600–1064 nm) [16]. Recently, another feasible method was developed to directly modify the end of the optical fiber by implementing laser processing [17, 18]. Multiple arrays of microholes were drilled and scanned across the fiber by using a galvanometer scanner combined with a UV laser [17]. The UV micro-drilling technique still accompanied multiple complex procedures and required lengthy fabrication times (at least a few hours). Alternatively, helical patterns were created along the fiber with a CO2 laser [18]. Although the CO2 laser can provide a simple machining process, the emission profile still yielded an intensity peak at the proximal end of the diffuser [18]. In addition, to minimize the laser light leakage at the distal end of the diffuser, several options have been introduced such as the addition of a reflector at the distal end tip (i.e., micro-gold mirror, right conical end, corner cube retro-reflector, and high diffuse backscattering layer) [12, 13, 16] and tapered fiber tip (i.e., acid, mechanical polishing, or laser) [9, 11, 14, 18]. Yet, with the proposed options, it is still complex to attain the uniform light emissions from the diffusing tip with minimal energy loss in a forward direction. Thus, the optimal method to fabricate diffusing applicators is still required to yield the uniform light irradiation as well as deliver a wide range of powers and wavelengths. The aim of the current study was to evaluate the function of various conical angle tips as a critical factor to accomplish the uniformly distributed light emissions for the diffusing applicators. The etched fiber surface was engraved to diffuse the transmitted light and to minimize any light leakage at the tip. A customized goniometer was employed to characterize the spatial uniformity of the light propagation. Additionally, the diffusing fibers with various conical angle tips were quantitatively compared in terms of temperature distribution and irreversible tissue coagulation.
2. Materials and methods
2.1 Design of diffusing elements
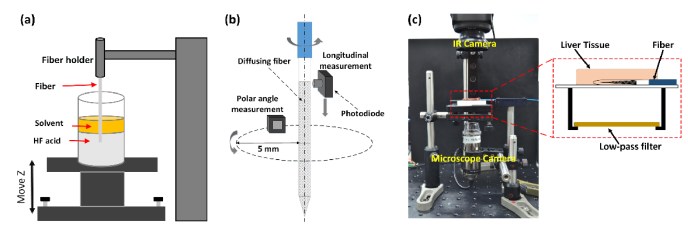
Figure 1(a) illustrates the experimental setup for the fiber tip tapering using the dynamic meniscus etching method [19–21]. Multimode 600-µm fibers (NA = 0.5, FT600EMT, Thorlabs, Newton, New Jersey) were used for the fabrication of a diffusing fiber. Prior to the etching, the Tefzel jacket of each fiber was removed with a mechanical stripper, and the tip was cleaned for three minutes to completely remove the polymer buffer with 99.7% - Acetone liquid (SamChun pure chemical Co., Ltd, Gyeoggi-do, Korea). Then, 7-mm tip of the fiber was initially put in a Teflon tank containing two layered etching solutions: hydrofluoric acid (48% - HF acid, Duksan pure chemicals Co., Ltd, Kyunggi, Korea) and 99% - p-xylene (Yakuri pure chemicals Co., Ltd, Tokyo, Japan). As an organic solvent, the p-xylene was used to create an immiscible protection layer to prevent HF vaporization into the air environment [20]. A translation stage (SLS6H-108, Science town, Incheon, Korea) was employed to vertically move the position of the tank (moving distance = 0 ~4500 µm) at various fiber pulling speeds (0 ~25 µm/min) in conjunction with LabView software (National Instrument Corp., Austin, Texas, USA). After three hours of the etching process, each fiber was pulled out of the solution, neutralized by using a 0.5 M solution of NaOH, and cleaned in deionized water by using an ultrasonic cleaner (SH-1025, Saehan ultrasonic Co. Ltd., Seoul, Korea) to prevent any further etching by the residual acid. Each condition was conducted four times (N = 4). Scanning Electron Microscopy (SEM) was utilized to qualitatively characterize the fabricated tip shape, and the conical angle of the etched tip was measured by using Image J (National Institute of the Health, Bethesda, MD). A software (Origin 8.0, OriginLab, Northampton, Massachusetts, USA) was then employed to curve-fit the measured conical angles as a function of fiber pulling speed.
Fig. 1.
Experimental setup for (a) fiber tapering using dynamic meniscus etching method, (b) customized goniometer, and (c) ex vivo 980-nm laser coagulation on porcine liver tissue.
After the etching process, a 60-W, CO2 laser system (λ = 10.6 µm, vi60, Synrad, Mukilteo, Washington, USA) was employed to fabricate each etched fiber. A lens system with concave and convex lenses was prepared to focus the CO2 laser beam onto the fiber surface with a spot diameter of ~30 µm. The fiber was fixed onto a motorized-stage system consisting of both translational and rotational stages. A pressurized air system was used to remove melting particles from the micro-machined areas with a pressure ranging from 50 psi to 70 psi. A laser power of 4 W was employed (stability = ± 7%) to reliably control the depth of each groove on the fiber surface (~20 µm) and eventually achieve hexagonal patterns with high uniformity. SEM images of the fiber surface were acquired to confirm the patterns created by the laser micro-machining, and groove dimensions were estimated by using Image J. A customized glass cap (closed end, length = 15 mm, inner diameter = 1.1 mm, and thickness = 0.15 mm) was then glued to the fabricated tip by sealing with epoxy for mechanical protection. A customized goniometer was implemented to validate the spatial light distribution of each manufactured fiber in terms of the longitudinal and polar angle emissions as shown in Fig. 1(b). Based on the method by Vesselov [22], the measurement setup used a photodiode head (PD-300-3W, Ophir, Jerusalem, Israel) and power meter (Nova II, Ophir, Jerusalem, Israel). A He–Ne laser (λ = 632 nm, Thorlabs Inc., Newton, New Jersey, USA) was coupled to the fibers as a light source for the measurements. For longitudinal emission measurements, the photodiode detector with a sensing area of 1 cm2 was moved at 0.05 mm/s along the fiber. To limit the diffusive light and to achieve high spatial resolution, a pinhole tube (1-mm inner diameter and 3-mm length) was created by using PCNC machine (PCNC 440, Tormach Inc, Waunakee, WI, USA). For the measurement, the tube was situated in front of the detector surface and was moved with the detector along the fiber. The distance from the diffuser surface to the tube was 0.5 mm. Four different angular positions (i.e., 0, 90, 180, and 360°) of the fiber were measured to assess the overall beam profile. For polar emission measurements, the photodiode with a limitedly sensing area of 1.5 × 1.5 mm2 was rotated around the fiber axis at the middle point of the diffusing segment (5 mm away from proximal end) with a radius of 5 mm. The normalized intensities were then analyzed by using Excel software. All the measured intensities were normalized to minimize the effect of laser power fluctuations on the emission measurements. The coefficients of variation (CV = mean value / standard deviation) was also calculated to assess the data repeatability. Three diffusers were made with each conical angle to validate the reliability of the fabrication procedure (N = 3). Based on the preliminary screening (i.e., conical angles at various pulling speeds), three different conical angles (9, 25, and 45°) were selected and tested for the rest of the comparative tests.
2.2 Ex vivo experiment
Figure 1(c) illustrates an experimental setup for ex vivo laser experiments on porcine liver tissue. A 980-nm laser system (S60-980-0, Apollo Instruments, Irvine, California, USA) was employed to interstitially coagulate the tissue samples with three different diffusing fibers (conical angle = 9, 25, and 45°) at 4 W and irradiation times (0 to 90 s). For sample preparation, the porcine liver tissue was procured from a local slaughterhouse and was initially frozen at −80 °C. Each frozen sample was then cut into a 2-mm thin layer of 2 × 2 cm2 in size and was stored in saline at 4 °C prior to the testing. For the ex vivo experiments, each fiber was placed on top of a microscope slide and carefully covered with the prepared tissue specimen to minimize air entrapment at the tissue-fiber-slide interface as shown in Fig. 1(c). An infrared (IR) thermal camera (4 × lens, 320 × 240 pixels, 60 Hz acquisition rate; A325sc, FLIR, Inc., Oregon, USA) was used to record the temperature from the sample surface during laser irradiation in order to indirectly assess the temperature development in the tissue. The distance between the IR camera and the sample surface was 80 mm. A transient temperature change was then evaluated by dividing the relative temperature increase by the total treatment period. In addition, a digital microscope camera (AM413ZT, Dino-Lite, New Taipei City, Taiwan) was positioned 50 mm below the microscope slide to record the real-time process of tissue coagulation. A low-pass filter (wavelength = 750 nm and diameter = 2.54 cm; FF750-SDi02, Semrock, Inc., New York, USA) was placed between the camera and the microscope slide to filter out the incident 980-nm wavelength during the irradiation. For all the fibers, two thermal images were captured at 0 (pre-irradiation) and 90 s after irradiation from the recorded movies to reconstruct 2D and 3D temperature profiles of the tissue surface. In addition, spatial distribution of the temperature along the fiber axis was measured to compare temperature variations at various axial positions of each diffuser. According to the previous study [18], irreversible tissue coagulation was vividly observed as discoloration in the treated tissue. Thus, Image J was later employed to measure the discolored area from the images captured by the microscope camera for comparative analysis. The measured areas represent the regions of longitudinal tissue coagulation along the diffuser. To identify any correlation between the beam profile and the extent of the tissue coagulation, the coagulation thickness (distance between diffuser and margin of coagulated region) was measured from the fiber axis to the margin of the coagulated region in a perpendicular direction at various fiber positions. The measured thickness values were then normalized by the maximum thickness value from each fiber for quantitative comparison. Each fiber was tested three times (N = 3).
In an attempt to evaluate the degree of radial coagulation along each fiber, porcine liver tissue was prepared in a volume of 3 × 6 × 3 cm3 and placed in a rectangular plastic holder, which was fabricated by using a 3D printer (Replicator Z18TM, Makerbot, New York, USA). The holder was prepared to firmly position each tissue sample as well as each fiber during the laser irradiation. Three 2-mm holes (distance between two adjacent holes = 2 cm) were created on the side of the plastic holder for the fiber insertion, so each fiber was tested three times in a sample (N = 3). After the irradiation (4-W 980-nm for 90 s) at room temperature, the sample was frozen at –80 °C for three hours. Then, each frozen sample was manually cut into seven 2-mm-thick slices (along diffuser axis). After the experiments, the cross-sections of the tissue slices were photographed by using a digital camera (D5100, Nikon Corporation, Tokyo, Japan). Image J was used to measure the degree of the radial coagulation (i.e., total width of discolored region) at various cross-sectional positions of each fiber. All the fabricated diffusers were examined in terms of light distribution before and after each testing (i.e., temperature and radial coagulation) by using a customized goniometer to confirm the consistent performance of the diffusing elements. The fibers were replaced with the new ones when the distribution profiles became changed by more than 15%. For non-parametric statistical analysis, Mann–Whitney U Test (two groups) and ANOVA (three groups) were performed with p < 0.05 being significant.
3. Results
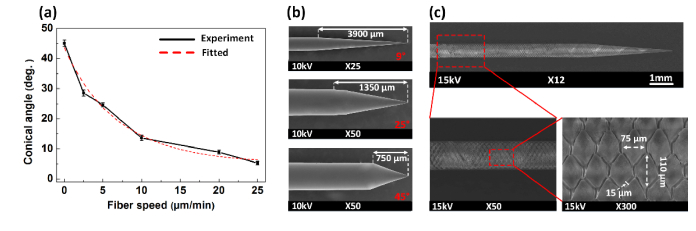
Figure 2(a) presents the conical angles of the etched tips as a function of vertical fiber-pulling speed (v). The corresponding moving distances ranged from 0 at 0 µm/min to 4500 µm at 25 µm/min. The experimental data were curve-fitted with an exponential function (i.e., red dashed line) by using Origin software. Overall, the conical angles (θ) exponentially decrease with the fiber speed due to the decreased meniscus force that occurred at the interface between the fiber surface and the applied solvent (i.e.,; regression = 0.98). The stationary etching (i.e., fiber speed = 0 μm/min and moving distance = 0 μm) yields the largest angle of 45.1 ± 2.2°, whereas the highest speed (25 μm/min and 4500 μm) results in the smallest angle of 5.8 ± 0.6° (eight-fold decrease; p < 0.001). Based on the current findings, three different conical angles were selected and tested for the rest of the comparative analysis: 45° (0 μm/min), 25° (5 μm/min), and 9° (20 μm/min). Figure 2(b) shows the SEM images of the fiber tips after the etching process at 20 (top), 5 (middle), and 0 µm/min (bottom). Regardless of the fiber speed, the etching achieved a smooth surface at the distal end. The speed increase led to a sharper fiber tip (i.e., smaller conical angle). In fact, as the speed increases by a factor of four, the conical angle decreases by 180% (i.e., 25 and 9° for 5 and 20 µm/min, respectively; p < 0.001). Conversely, the tapering length increases with fiber speed (i.e., 750, 1350, and 3900 µm for 0, 5, and 20 µm/min, respectively). The repeated tests also confirmed the reproducibility of both the conical angle and the tapering length for each fabrication procedure (i.e., CV < 10%). Figure 2(c) displays SEM images of the fabricated fiber after the etching at 20 µm/min. It is observed that the laser micro-machining created uniform hexagonal groove patterns on the surface along the 10-mm fiber tip. The image also indicates no overlapping between the patterns on the fiber surface. The groove width between the two consecutive patterns is measured to be about 15 µm, and the groove depth is estimated to be about 20 µm. Each pattern exhibits a hexagonal shape (110-µm long and 75-µm wide).
Fig. 2.
Characterization of fabricated fiber tips: (a) conical angle as a function of fiber speed and SEM images of (b) etched fiber tips at different angles and (c) fabricated fiber tips.
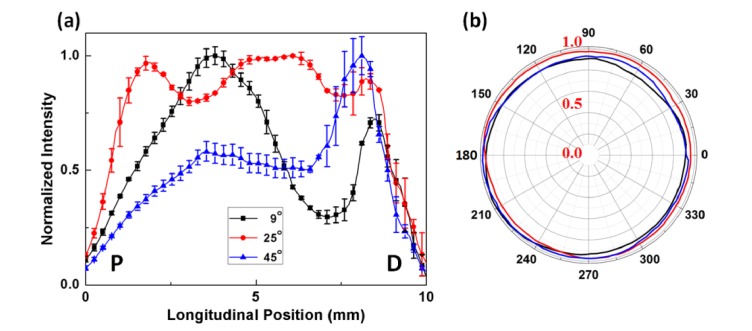
Figure 3(a) displays the longitudinal distributions of the normalized intensity estimated from three diffusing applicators. Each line represents the mean value measured from four angular positions for each fiber. The fiber with the smallest conical angle (9°) is associated with a slightly right-skewed profile, and the peak intensity (global maximum) is positioned at 4 mm away from the proximal end. Then, the intensity rapidly drops to 70% at 7 mm but increases again at 8 mm (i.e., local minimum at 7 mm and local maximum at 8 mm). The fiber with a conical angle of 25° results in a relatively uniform and even light distribution along the fiber in a rectangular shape (i.e., deviation < 10%), and most of the transmitted power is emitted from between 0.5 and 9.5 mm. The fiber with a conical angle of 45° exhibits an almost left-skewed profile with the peak intensity positioned 8 mm away from the proximal end. The overall longitudinal intensities along the 10-mm whole length of the diffusing tip are estimated to be 0.65 ± 0.23, 0.90 ± 0.07, and 0.57 ± 0.17 for 9, 25, and 45°, respectively. The corresponding CVs are 0.36, 0.08, and 0.30; thus, the conical angle of 25° yields more uniform distribution along the fiber axis, compared with the others. It should be noted that the repeated measurements on different fibers with the same conical angle confirmed a similar tendency in the emission profile. Figure 3(b) displays the normalized polar emissions from all the fibers with various conical angles over 2π. The overall normalized intensities seem quite uniform with a deviation of less than 5%, and no significant difference can be found in the polar emissions among the fibers (i.e., 0.92 ± 0.03, 0.96 ± 0.02, and 0.94 ± 0.05 for 9, 25, and 45°, respectively; p = 0.12). It is also confirmed that both wavelengths of 632 and 980 nm yield the comparable emission profiles [23].
Fig. 3.
Evaluations of spatial light distribution at various conical angles: (a) longitudinal and (b) polar angle emissions (P = proximal and D = distal ends; λ = 632 nm).
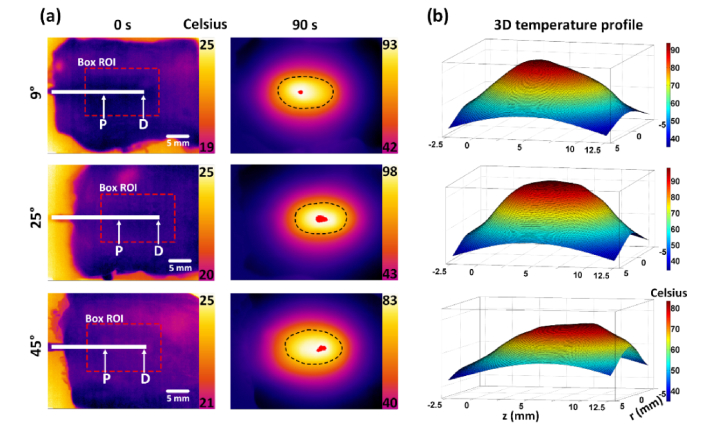
Thermal profiles of the tissue surface were measured during irradiation of 4-W 980 nm light with three diffusing fibers. Figure 4(a) displays the 2D temperature distributions of the surface of the 2-mm thick tissue before (0 s; left column) and 90 s after (right column) irradiation. The red dots in the center and the dotted lines in the right column represent 99 and 70% of the peak temperature, respectively. Regardless of the conical angle, the overall thermal profile is elliptical. The conical angle of 25° shows that the temperature is almost symmetrically distributed with the peak temperature in the center. Conversely, the other angles (9 and 45°) yield the deviation of the peak temperatures from the center, representing a relatively asymmetrical temperature distribution. Figure 4(b) shows the 3D thermal mapping from the captured IR images in Fig. 4(a) for stereoscopic evaluations of the temperature distribution. Similarly, the conical angle of 25° yields a relatively symmetric temperature distribution with the flat peak temperature along the fiber axis, while the other angles are associated with the right-skewed (9°) or slightly left-skewed (45°) distribution.
Fig. 4.
Thermal profiles of fiber tips with various conical angles (9, 25, and 45°): (a) 2D thermal imaging (before and 90 s after laser irradiation) and (b) 3D temperature profile. Note that the red color and dotted lines represent 99 and 70% of the peak temperature, respectively.
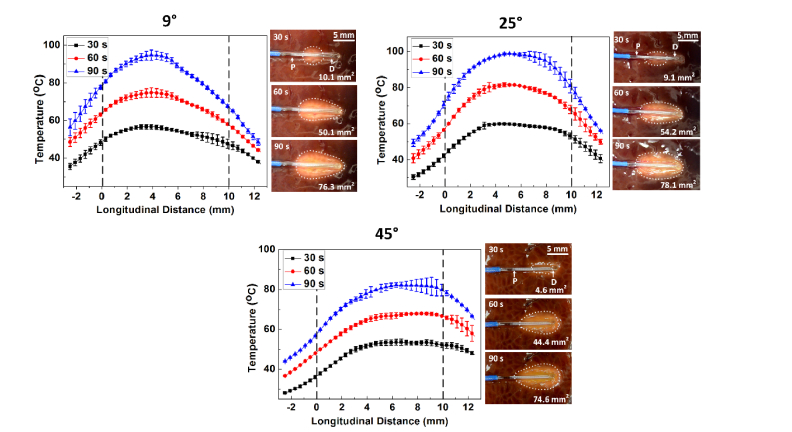
Figure 5 presents the temporal development of the surface temperature (left graph) and the denatured areas around the fibers (right images) at various irradiation times (i.e., 30, 60, and 90 s) captured by using a microscope camera. The initial temperature of the tissue was 20 ± 1 °C (N = 3). Irrespective of conical angle, the overall temperature profile along the diffusing applicator is comparable for all the irradiation times. After 90 s of irradiation, the peak temperatures are measured to be 94.7 ± 2.9, 98.3 ± 1.2, and 82.1 ± 1.9 °C for 9, 25, and 45°, respectively (i.e., rate of transient temperature change = 0.63, 0.65, and 0.48 °C/s, respectively). The corresponding coagulated areas are 76.8, 78.1, and 74.6 mm2. It is observed that the thermal distribution corresponds to the degree of irreversible coagulation of the tissue surface (i.e., whitish color). In addition, the right images demonstrate that the coagulated area from the 25° reflects an elliptical shape, whereas the other angles (9 and 45°) are associated with the right-skewed (9°) or left-skewed (45°) distribution relative to the center of the diffuser tip length.
Fig. 5.
Temporal development of temperature (left graph) and denatured area (right images) at various irradiation times (30, 60, and 90 s under 4-W, 980 nm irradiation) for three different conical angles (P = proximal and D = distal ends).
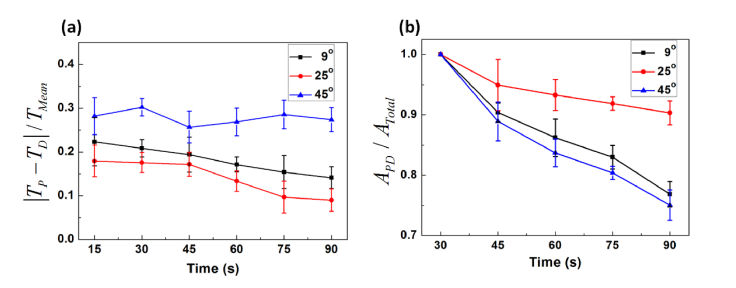
Figure 6 quantitatively compares the variations in temperature (|TP – TD|; Fig. 6(a)) and coagulated area (APD; Fig. 6(b)) between the proximal (P) and the distal (D) ends as a function of irradiation time during 4-W 980 nm irradiation (N = 3). The mean temperature along the diffuser (TMean; mean value measured along fiber axis) and the total coagulated area in the entire tissue (ATotal) were used to normalize |TP – TD| and APD, respectively, to demonstrate the relative change in both the temperature and the coagulation region. The conical angle of 45° presents almost constant (0.27 ± 0.03 in arbitrary units, a.u.) but up to three-fold larger temperature variations, compared with those from the other conical angles (i.e., 0.14 ± 0.04 and 0.09 ± 0.03 a.u. for 9 and 25°, respectively). Both the angles of 9° and 25° yield an apparent decrease in the temperature change. However, the conical angle of 25° is associated with the smaller ratio of the temperature variation (up to 40% than that of 9°), implicating that the conical angle of 25° displays a more symmetrical temperature distribution along the diffusing applicator. Figure 6(b) shows the ratio of the denatured area (APD) between the proximal and distal ends to the total coagulated area (ATotal). The coagulated area within the diffusing element (APD) was quantitatively compared with the total coagulated region (ATotal) in order to assess the effect of the light distribution on thermal distribution in tissue. Overall, the conical angle of 25° displays a relatively slower decrease in the area ratio than that of the other angles. After the 90 s of irradiation, the 25° fiber yields a 15% and 17% higher denatured ratio than those of the 9° and 45° fibers, respectively (i.e., 0.77 ± 0.02, 0.90 ± 0.02, and 0.75 ± 0.03 a.u. for 9, 25, and 45°, respectively; p < 0.05). In turn, the active length (i.e., between proximal and distal ends) of the 25° fiber diffusing tip covered more than 90% of the tissue surface for the irreversible thermal coagulation. Conversely, both the 9 and 45° fibers coagulated the tissue surface even beyond the active parts.
Fig. 6.
Comparison of normalized variations in (a) temperature and (b) denatured area between proximal (P) and distal (D) ends for various conical angles.
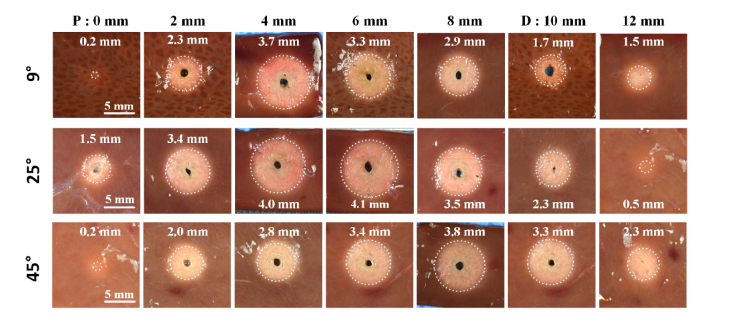
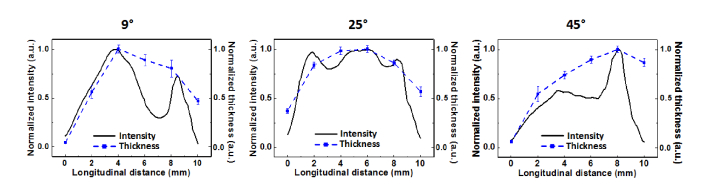
Figure 7 presents the irreversible thermal responses of porcine liver tissue after 90 s of laser irradiation with various conical angles. A compilation of cross-sectional images was acquired along the diffusing fiber. Overall, the coagulation profile is circular, reflecting the polar emission, as shown in Fig. 3(b). The 9° fiber generated the largest coagulation thickness of 3.7 ± 0.2 mm at 4 mm (slightly skewed to the right). The 25° fiber created the maximum coagulation area in the middle (4 and 6 mm), with a corresponding coagulation thickness of 4.1 ± 0.3 mm. In the case of the 45° fiber, the maximum denatured region occurred at 8 mm (left-skewed) along with a coagulation thickness of 3.8 ± 0.2 mm. It is noted that both the angles of 9 and 45° yield more distinctive tissue coagulation on the tissue surface at 12 mm than that of 25°, which is beyond the active length (i.e., 1.6 ± 0.2 mm for 9° and 2.3 ± 0.2 mm for 45° vs. 0.5 ± 0.1 mm for 25°; p < 0.001). Figure 8 compares the normalized longitudinal light intensity (solid black line) with the normalized coagulation thickness (dotted blue line) along the fibers with various conical angles. Compared to the fibers of 9 and 45°, it is observed that the 25° fiber yields a uniform spatial distribution of both the light and the coagulation from the active length of the diffusing tip.
Fig. 7.
Compilation of cross-sectional images of tissue after laser irradiation with different conical angle tips (P = proximal and D = distal ends). The dotted lines represent the denatured tissue regions.
Fig. 8.
Quantitative comparison between normalized light intensity (black) and coagulation thickness (blue) along diffuser axis (i.e., longitudinal distance) after 90 s of photocoagulation at 4 W for various conical angles.
4. Discussion
Uniformly diffusing fibers are often desirable to deliver laser energy with a homogeneous intensity distribution for interstitial coagulation. The thermal distribution inside the tissue typically depends on the spatial emissions (both longitudinal and angular) of the fibers. The uniform light distribution along the diffuser can precisely control the extent of the denatured area with no or minimal injury to the adjacent tissue. The goal of the current study was to develop and validate various conical fiber tips to improve the circumferential light distribution. According to Figs. 2(a) and 2(b), the conical angles of the etched tips decreased with fiber pulling speed. The height of the meniscus at the interface between fiber surface and solvent can be given by the Young–Laplace Eq. (1)/R1 + 1/R2 = Δρ/σ, where R1 and R2 are the principal radii of curvature, Δρ is the pressure difference, and σ is the surface tension) [21, 24]. According to this equation, the surface tension difference between the HF acid and p-xylene can determine the final height of the meniscus at the fiber tip. Along with the meniscus height, the pulling speed increased the tapering length of the fiber (i.e., 750, 1350, and 3900 µm for 0, 5, and 20 µm/min, respectively). In turn, both the chemical and physical conditions could be crucial in defining the eventual geometry of the fiber tip for light diffusion.
According to Fig. 3(a), the overall longitudinal intensities along the fibers were estimated to be 0.64 ± 0.23, 0.90 ± 0.07, and 0.57 ± 0.17 for 9, 25, and 45°, respectively. A conical angle of 25° yielded a relatively symmetric spatial light distribution along the fiber axis, whereas the other angles were associated with the right-skewed (9°) or slightly left-skewed (45°) distribution. The selection of laser parameters can be responsible for the degree of the light distribution. The laser fabrication process involves two critical factors to determine the quality of the fiber surface: focused beam size ([4λM2f]/[πD]) and depth of focus (DOF; [8λf2]/[πD2], where λ is the wavelength (10.6 µm), M2 mode quality (≤ 1.2), f focal length (25 mm), and D beam diameter at the lens surface (10 mm) [25]. A smaller focused beam size is typically accompanied by a reduction in DOF. For the current method, the CO2 energy was focused on the fiber surface with a focused beam of approximately 30 µm and DOF of about 160 µm. However, when the focused beam was moved to the distal end tip that had been etched, different conical angles could slightly misalign the focal spot. In fact, a part of the etched tip was difficult to be fabricated due to the misalignment of the focused beam (i.e., fabricated length / total length of etched tip = 200/750 µm for 45°, 500/1350 µm for 25°, and 1200/3900 µm for 9°). Thus, the optimized laser parameters could be essential to achieve the uniformity and symmetry of the emission profiles from the diffusing applicators.
The current study used multimode fibers (NA = 0.5, acceptance half-angle θacc = 30°, ncore = 1.459, ncladding = 1.365). Due to the conical angles after fiber preparation, the incident light could be internally reflected at the core-to-air interface on the tip according to Snell’s law (critical angle θcri = sin–1 [nair / ncore] = 43.3°). In turn, the incidence angle of the light on the conical surface can be limited to be θinc = 90° – (θacc + θcone/2), where θacc is the acceptance half-angle of the fiber and θcone the conical angle after the tip-etching. The calculated θinc is thus 37.5, 47.5, and 55.5° for 45, 25, and 9°, respectively. Accordingly, the smaller the conical angle is, the greater total internal reflection can occur at the fiber tip. In fact, among the three fabricated fibers in the current study, the spatial light emission of the 9° fiber was strongly distributed at the proximal end, whereas the profile from the 45° fiber was considerably skewed to the distal end. Therefore, the 25° fiber can generate relatively moderate and acceptable light distributions for diffusive emissions.
Compared with previous studies [10, 15, 17], the proposed fabrication proved to be a reliable process because of the direct patterning on the fiber surface. In fact, after etching, less than 3 min were required to create hexagonal patterns with high uniformity on the entire fiber surface. Therefore, based on the acquired light distribution and tissue responses, the additional etching method could not only improve the quality of the spatial emission (Fig. 3), but also minimize the loss of optical energy propagating in the forward direction from the distal end tip (Fig. 7) [16, 18]. The current study demonstrated that both longitudinal and polar emission profiles with the 25° fiber yielded a normalized intensity of 0.96 ± 0.02 (polar) and 0.90 ± 0.07 (longitudinal) as shown in Fig. 3. Conversely, the diffusers in previous studies showed various intensity profiles: for instance, they showed the peak intensity at the proximal diffuser along with 0.94 of polar emission and 0.8 of longitudinal emission [18] or 0.95 of polar emission and 0.75 of longitudinal emission [26], peak intensity at the distal end of the diffuser [9, 22], decreasing intensities [22, 26, 27], increasing intensities [9, 12], or various peak intensities [10, 12, 22]. Furthermore, the etching technique provided almost no optical energy leaking at the distal end tip compared with the previous diffuser (18% power loss) [18]. Thus, the currently proposed diffusers can achieve better homogeneity in both emission directions and can achieve better fabrication reliability.
According to Figs. 4 and 5, the temperature distributions from both the 9 and 45° fibers hardly reflected the light distribution displayed in Fig. 3. In fact, the fiber with a conical angle of 9° exhibited a right-skewed profile along with the peak intensity at 4 mm and a second peak at 8 mm from the proximal end (Fig. 3). Conversely, the thermal distribution exhibited a single peak temperature between 4 and 5 mm on the diffuser (Fig. 5). A mismatch between the light and the temperature distributions might have resulted from the conductive heat diffusion upon the irreversible thermal coagulation in the tissue, leading to the accumulation of thermal effects. The variations in optical properties during the irradiation could also have contributed to the changes in the photon distribution inside the tissue (i.e., absorption coefficient = 0.64 cm–1 for native liver vs. 0.41 cm–1 for coagulated liver) [28]. Compared to 25°, both the conical angles of 9 and 45° yielded more distinctive tissue coagulation on the tissue surface at 12 mm than the angle of 25° did (Figs. 7 and 8), which was beyond the active diffusing length (i.e., 1.5 ± 0.2 mm for 9° and 2.3 ± 0.2 mm for 45° vs. 0.5 ± 0.1 mm for 25°; p < 0.001). In fact, even the 25° fiber showed a slightly faint thermal coagulation at 12 mm (Fig. 7). Thus, the excessive thermal coagulation could be associated with the forward light leakage. To minimize the unwanted light loss, a glass cap will be coated with reflective materials at the cap tip, which can contain all the photons emitting in a forward direction from the fiber tip. For more effective and predictable temperature distributions, the new fabrication patterns (zig-zag, modulation, and zebra-lines) will also be tested on the fiber surface, and numerical simulations will be conducted to estimate the degree of tissue coagulation during/after laser irradiation. Furthermore, to translate the proposed technique to clinical applications such as photodynamic therapy and endovenous laser ablation, in vivo animal models should be tested and evaluated in terms of acute/chronic efficacy and safety of the diffuser-based laser treatment.
5. Conclusion
The current study demonstrated that the degree of conical angle tips was a deterministic factor in uniformly distributing the light emission from diffusing applicators. A conical angle of 25° with a 10-mm diffusing element achieved radial light distribution as well as circumferential coagulation in tissue. Further investigations will test the proposed fibers in in vivo animal models to evaluate treatment efficacy, acute/chronic tissue responses, and wound healing for clinical translation.
Funding
This research was supported by a grant from Marine Biotechnology Program (20150220) funded by Ministry of Oceans and Fisheries, Korea.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Azadgoli B., Baker R. Y., “Laser applications in surgery,” Ann. Transl. Med. 4(23), 452 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kolkman R. G., Steenbergen W., van Leeuwen T. G., “In vivo photoacoustic imaging of blood vessels with a pulsed laser diode,” Lasers Med. Sci. 21(3), 134–139 (2006). [DOI] [PubMed] [Google Scholar]
- 3.Tripathi M. M., Hajjarian Z., Van Cott E. M., Nadkarni S. K., “Assessing blood coagulation status with laser speckle rheology,” Biomed. Opt. Express 5(3), 817–831 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Welch A. J., Van Gemert M. J., Optical-thermal response of laser-irradiated tissue (Springer, 1995). [Google Scholar]
- 5.Nyst H. J., van Veen R. L., Tan I. B., Peters R., Spaniol S., Robinson D. J., Stewart F. A., Levendag P. C., Sterenborg H. J., “Performance of a dedicated light delivery and dosimetry device for photodynamic therapy of nasopharyngeal carcinoma: phantom and volunteer experiments,” Lasers Surg. Med. 39(8), 647–653 (2007). [DOI] [PubMed] [Google Scholar]
- 6.Hwang J., Hau N. T., Park S. Y., Rhee Y.-H., Ahn J.-C., Kang H. W., “Ex vivo laser lipolysis assisted with radially diffusing optical applicator,” J. Biomed. Opt. 21(5), 058001 (2016). [DOI] [PubMed] [Google Scholar]
- 7.Ahn M., Chae Y., Hwang J., Ahn Y., Kang H. W., “Endoluminal application of glass‐capped diffuser for ex vivo endovenous photocoagulation,” J. Biophotonics 10(8), 997–1007 (2017). [DOI] [PubMed] [Google Scholar]
- 8.Lee H. S., Kim S. W., Oak C., Kang H. W., Oh J., Jung M. J., Kim S. B., Won J. H., Lee K. D., “Rabbit model of tracheal stenosis using cylindrical diffuser,” Lasers Surg. Med. 49(4), 372–379 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Kosoglu M. A., Hood R. L., Rossmeisl J. H., Jr, Grant D. C., Xu Y., Robertson J. L., Rylander M. N., Rylander C. G., “Fiberoptic microneedles: Novel optical diffusers for interstitial delivery of therapeutic light,” Lasers Surg. Med. 43(9), 914–920 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Volkov V. V., Loshchenov V. B., Konov V. I., Kononenko V. V., “Fibreoptic diffuse-light irradiators of biological tissues,” Quantum Electron. 40(8), 746–750 (2010). [Google Scholar]
- 11.George R., Walsh L. J., “Performance assessment of novel side firing safe tips for endodontic applications,” J. Biomed. Opt. 16(4), 048004 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Ripley P., MacRobert A., Mills T., Bown S., “A comparative optical analysis of cylindrical diffuser fibres for laser therapy using fluorescence imaging,” Lasers Med. Sci. 14(4), 257–268 (1999). [Google Scholar]
- 13.Sroka R., Beyer W., Krug M., Noack A., Unsöld E., Ell C., “Laser light application and light monitoring for photodynamic therapy in hollow organs,” Lasers Med. Sci. 8(1), 63–68 (1993). [Google Scholar]
- 14.Şimşek E. U., Şimşek B., Ortaç B., “CO2 laser polishing of conical shaped optical fiber deflectors,” Appl. Phys. B 123(6), 176 (2017). [Google Scholar]
- 15.Vesselov L., Whittington W., Lilge L., “Design and performance of thin cylindrical diffusers created in Ge-doped multimode optical fibers,” Appl. Opt. 44(14), 2754–2758 (2005). [DOI] [PubMed] [Google Scholar]
- 16.Peshko I., Rubtsov V., Vesselov L., Sigal G., Laks H., “Fiber photo-catheters for laser treatment of atrial fibrillation,” Opt. Lasers Eng. 45(4), 495–502 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.M. Domke, J. Gratt, and R. Sroka, “Fabrication of homogeneously emitting optical fiber diffusors using fs-laser ablation,” in SPIE LASE (International Society for Optics and Photonics, 2016), pp. 97400–97401. [Google Scholar]
- 18.Nguyen T. H., Rhee Y. H., Ahn J. C., Kang H. W., “Circumferential irradiation for interstitial coagulation of urethral stricture,” Opt. Express 23(16), 20829–20840 (2015). [DOI] [PubMed] [Google Scholar]
- 19.Haber L. H., Schaller R. D., Johnson J. C., Saykally R. J., “Shape control of near-field probes using dynamic meniscus etching,” J. Microsc. 214(Pt 1), 27–35 (2004). [DOI] [PubMed] [Google Scholar]
- 20.Hoffmann P., Dutoit B., Salathé R.-P., “Comparison of mechanically drawn and protection layer chemically etched optical fiber tips,” Ultramicroscopy 61(1–4), 165–170 (1995). [Google Scholar]
- 21.Muramatsu H., Homma K., Chiba N., Yamamoto N., Egawa A., “Dynamic etching method for fabricating a variety of tip shapes in the optical fibre probe of a scanning near-field optical microscope,” J. Microsc. 194(Pt 2-3), 383–387 (1999). [DOI] [PubMed] [Google Scholar]
- 22.Vesselov L. M., Whittington W., Lilge L., “Performance evaluation of cylindrical fiber optic light diffusers for biomedical applications,” Lasers Surg. Med. 34(4), 348–351 (2004). [DOI] [PubMed] [Google Scholar]
- 23.Pham N. T., Lee S. L., Park S., Lee Y. W., Kang H. W., “Real-time temperature monitoring with fiber Bragg grating sensor during diffuser-assisted laser-induced interstitial thermotherapy,” J. Biomed. Opt. 22(4), 045008 (2017). [DOI] [PubMed] [Google Scholar]
- 24.Squire P., “Axisymmetric meniscus formation: a viscous-fluid model for cones,” J. Fluid Mech. 129, 91–108 (1983). [Google Scholar]
- 25.Powell J., CO2 laser cutting (Springer, 1993). [Google Scholar]
- 26.Nguyen T. H., Park S., Hlaing K. K., Kang H. W., “Temperature feedback-controlled photothermal treatment with diffusing applicator: theoretical and experimental evaluations,” Biomed. Opt. Express 7(5), 1932–1947 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Small W., Buckley P. R., Wilson T. S., Loge J. M., Maitland K. D., Maitland D. J., “Fabrication and characterization of cylindrical light diffusers comprised of shape memory polymer,” J. Biomed. Opt. 13(2), 024018 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ritz J. P., Roggan A., Isbert C., Müller G., Buhr H. J., Germer C. T., “Optical properties of native and coagulated porcine liver tissue between 400 and 2400 nm,” Lasers Surg. Med. 29(3), 205–212 (2001). [DOI] [PubMed] [Google Scholar]