Momentum transfer Monte Carlo for the simulation of laser speckle imaging and its application in the skin

Abstract

Due to its simplicity and low cost, laser speckle imaging (LSI) has achieved widespread use in biomedical applications. However, interpretation of the blood-flow maps remains ambiguous, as LSI enables only limited visualization of vasculature below scattering layers such as the epidermis and skull. Here, we describe a computational model that enables flexible in-silico study of the impact of these factors on LSI measurements. The model uses Monte Carlo methods to simulate light and momentum transport in a heterogeneous tissue geometry. The virtual detectors of the model track several important characteristics of light. This model enables study of LSI aspects that may be difficult or unwieldy to address in an experimental setting, and enables detailed study of the fundamental origins of speckle contrast modulation in tissue-specific geometries. We applied the model to an in-depth exploration of the spectral dependence of speckle contrast signal in the skin, the effects of epidermal melanin content on LSI, and the depth-dependent origins of our signal. We found that LSI of transmitted light allows for a more homogeneous integration of the signal from the entire bulk of the tissue, whereas epi-illumination measurements of contrast are limited to a fraction of the light penetration depth. We quantified the spectral depth dependence of our contrast signal in the skin, and did not observe a statistically significant effect of epidermal melanin on speckle contrast. Finally, we corroborated these simulated results with experimental LSI measurements of flow beneath a thin absorbing layer. The results of this study suggest the use of LSI in the clinic to monitor perfusion in patients with different skin types, or inhomogeneous epidermal melanin distributions.

1. Introduction

Laser speckle imaging (LSI) enables visualization and quantitation of blood flow in biological tissues [1–6]. The dynamic intensity interference pattern provides information about the movement of scattering particles within tissue. The pattern fluctuates at a rate proportional to the speed of the moving scatterers. With use of a camera with an exposure time longer than the time period between speckle fluctuations, acquired images of dynamic regions of the interference pattern have diminished speckle visibility [7]. This visibility, or speckle contrast, is quantified with calculation of the local standard deviation of intensity values over the local mean intensity within a sliding structuring element of pixels (typically 5x5 or 7x7 in size) [8, 9]. The contrast is inversely proportional to the speed of the moving scatterers.

Research groups have utilized LSI for a variety of medical applications. We reported on LSI as a real-time approach to image perfusion during laser treatment of port-wine stain birthmarks [3,10–12]. Other groups reported on the use of LSI during neurosurgery [13–16]. In preclinical studies, LSI was used to visualize blood-flow dynamics following ischemic stroke [4] and in response to phototherapies [17, 18].

Due to its simplicity and low cost, LSI has achieved widespread use, especially in the field of neurobiology. However, interpretation of the blood-flow maps remains ambiguous. LSI enables only limited visualization of vasculature below scattering layers such as the epidermis and skull [19, 20]. Such layers often are described as having “static” scattering, to differentiate them from regions with optical scattering events by “dynamic” red blood cells moving within blood vessels. For LSI in general, researchers typically are interested in mapping speckle contrast perturbations associated with these dynamic scatterers, but the static scattering components compromise the ability of LSI to quantify blood flow [21–24].

In addition, several optical imaging modalities are affected by the presence of absorption, such as epidermal melanin absorption [25–28]. For example, techniques such as diffuse optical spectroscopic imaging and spatial frequency domain imaging have difficulty decoupling absorption events associated with melanin versus hemoglobin [29, 30]. This presents challenges for in vivo clinical imaging, in which patients have varying skin types and different concentrations of epidermal melanin [31, 32].

Here, we describe a computational model that enables flexible in silico study of the impact of these factors on LSI measurements. The model uses Monte Carlo methods to simulate light and momentum transport in a heterogeneous tissue geometry. With the model, we studied the depth sensitivity of LSI by tracking the precise location of dynamic scattering events. We also applied the model to study the spectral dependence of speckle contrast as well as the impact of epidermal melanin content. Many of these questions would be difficult to address using traditional experimental LSI, but can be easily explored with our model.

2. Theory

Wang et al. described the seminal Monte Carlo model that has achieved widespread use to model light transport within multi-layered tissue [33]. Here, we used a modified version of the C# Command Line Monte Carlo model developed by the Virtual Photonics Initiative at Beckman Laser Institute to track photon scattering using a discrete absorption weighting scheme [34–38]. We calculate the momentum transfer that occurs at each scattering event of a simulated photon [39–41]. All photons have a momentum (ρ), described by ρ = ħk, where ħ is the reduced Planck’s constant and k the wavenumber, which has both a magnitude and a direction. Momentum transfer (q) occurs with each scattering event, and is quantified by the change in direction of the wavevector, or q = k_final-k_initial. The magnitude |q| is given by |q| = (2k)sin(θ/2), where θ is the scattering angle of the photon [39].

By tracking momentum transfer, we estimate the field correlation function g₁(τ) for each simulated photon as [39, 40]:

$$g_1\left(\tau \right)=\exp \left[-\frac{1}{6}{{\displaystyle \sum }}^{\text{}}{q}_i^2\text{Δ}{r}^2\left(\tau \right)〉\right]$$ (1)

We sum “q” for each scattering event “i” (static or dynamic) associated with a mean-squared displacement (<Δr²(τ)>) described either by Brownian motion (6D_bτ) or directed flow (vτ²), where “D_b” is the Brownian diffusion coefficient and “v” the speed of directed flow. We integrate Eq. (1) over all photon path histories generated by the Monte Carlo simulation, to obtain the total electric field correlation:

$$g_1\left(\tau \right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}P\left(Y\right)\text{exp}\left[\frac{-Y{k}^2\text{Δ}{r}^2\left(\tau \right)〉}{3}\right]dY$$ (2)

where “Y” is the dimensionless momentum transfer (Y = 1-cos(θ)) and “P(Y)” the normalized probability distribution of momentum transfer [39, 40]. The simulation computes “Y” for each scattering event and its corresponding summation along the total photon pathlength. With this information, we generate a histogram of normalized photon weight “P(Y)” versus dimensionless momentum transfer “Y” for each simulated photon.

Equations (1) and (2) are valid for a sample with a single mean-squared displacement value (i.e., <Δr²(τ)> is uniform throughout the entire simulated geometry). We previously reported on modification of these equations to properly account for two different flow types or speeds, such as a static top layer overlying a dynamic layer, or a blood vessel within a medium [41]. For a two-flow system, the field correlation function is:

$$g_1\left(\tau \right)=\underset{0}{\overset{\infty }{{\displaystyle \int }}}P(Y)\underset{0}{\overset{1}{{\displaystyle \int }}}P(y)\exp \left[\frac{-Y{k}^2\left(y\right)〈\text{Δ}{r}_1^2\left(\tau \right)〉+(1-y)〈\text{Δ}{r}_2^2(\tau )〉}{3}\right]dydY$$ (3)

where “P(y)” is the normalized probability distribution of total momentum transfer associated with one flow type, and <Δr₁²(τ)> and <Δr₂²(τ)> are the mean-squared displacements associated with each of the two flow types [41]. The equations for a two-flow system are readily adapted to a simulation of blood-flow dynamics in a layered skin model (described below). In this simulation, we use the blood volume fraction of each layer and a random number generator to categorize each scattering event as either dynamic or static.

We then use the Siegert relation (g₁ = <I²> + β|g₁(τ)|²dτ) to calculate the intensity correlation function “g₂(τ)” and subsequently speckle contrast “K” as:

$$K^2=\frac{2\beta }{T}\underset{0}{\overset{T}{{\displaystyle \int }}}\left(1-\frac{\tau }{T}\right){|\frac{g_1\left(\tau \right)}{g_1\left(0\right)}|}^{2}d\tau$$ (4)

where “T” is the exposure time of the camera and β an empirical constant which accounts for experimental factors such as detector pixel size and laser coherence length [7, 42–46]. Here, we set β to unity to represent the maximum theoretical dynamic range of speckle contrast.

3. Virtual detectors of the momentum transfer Monte Carlo (MTMC) model

Our Monte Carlo model uses virtual detectors to track quantities such as the reflectance and transmittance, or the weight and location of simulated photons exiting the simulated geometry. The absorbance, or weight of absorbed photons, and fluence, or weight of photons passing through each spatial location within the sample geometry, is tracked in three dimensions.

To calculate speckle contrast, we used data from the reflected or transmitted momentum transfer detectors. These detectors quantify both total momentum transfer and the fraction of momentum transfer that occur within each region. The latter quantity is further separable into the fraction that occur from dynamic versus static scatterers. The histogram of the fractional momentum transfer events that occur in dynamic versus static scatterers is used in the two-region calculation of field correlation (Eq. (3)).

We created a detector to track momentum transfer as a function of depth within the sample. For each scattering event, the momentum transfer is multiplied by the final reflected or transmitted photon weight, and tabulated at the z-position of the event [47]. With this detector, we studied the depth over which dynamic scattering events affect speckle contrast values.

We used custom-written MATLAB software (The Mathworks, Natick, MA) to perform the numerical integration of Eqs. (2)-(4).

4. Experimental methods

4.1 Validation experiments

To test our MTMC model, we performed several in-vitro LSI experiments. The LSI device consisted of a CMOS camera (1280x1024 pixel resolution) (HotShot 1280, NAC Imaging Technology, Simi Valley, CA) equipped with a macro lens (Nikon, Melville, NY) and a long-coherence 808nm laser diode (Ondax, Monrovia, CA). An aspheric lens and a ground-glass diffuser (ThorLabs, Newton, NJ) expanded the collimated diode output to achieve uniform illumination of the sample.

For the samples, we used both solid and liquid tissue-simulating phantoms. Solid phantoms consisted of a polydimethylsiloxane (PDMS) base with titanium dioxide added to achieve a reduced scattering coefficient (μ_s’) of ~1mm⁻¹ at 650nm [48]. To create liquid phantoms, we diluted Intralipid (Baxter Healthcare, Deerfield, IL) to a concentration of 1% or 1.7%, resulting in μ_s’ = 1mm⁻¹ or 1.7mm⁻¹, respectively. To vary solution viscosity and hence the Brownian diffusion coefficient, we added 28% and 43% solutions of glycerol to the Intralipid dilution, similar to experiments reported by Rice et al [40]. For some experiments, we increased phantom absorption by adding a concentration of 0.005mg/ml (μ_a = 0.005mm⁻¹) of Nigrosin. To achieve directed flow, we used a syringe infusion pump (Harvard Apparatus, Holliston, MA) to inject Intralipid through a glass microchannel (inner diameter of 650μm) embedded within the surface of one of the PDMS phantoms described above (Fig. 1(a)).

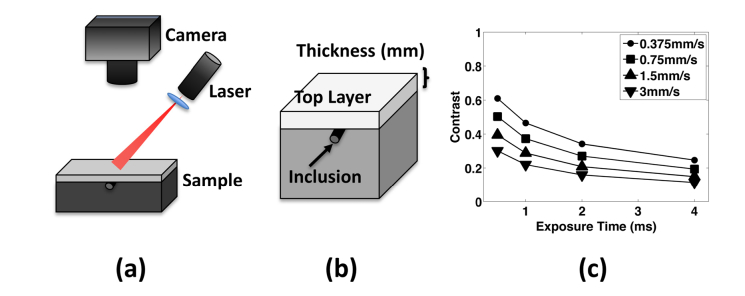
Fig. 1.

(a) Laser speckle imaging set-up. The laser projects a diffuse speckle pattern onto the sample which is imaged using a CMOS camera. (b) Sample geometry for validation experiments (experimental and computational). The sample consisted of a variable thickness (0.75-4.0mm) top layer above a 5cm bottom layer. For experiments with flow present, a glass microchannel inclusion was placed at the surface of the second layer and Intralipid infused through the tube with a syringe pump. (c) Results from simulated flow in a subsurface inclusion. We modeled speckle contrast for flow through the inclusion at different speeds and exposure times. As expected, speckle contrast decreased with increasing flow speed and exposure time. The results closely matched previous work by Rice et al [41].

4.2 Creation/characterization of thin, flexible, absorbing phantoms

To mimic absorption due to epidermal melanin, we created flexible, absorbing static phantoms using gelatin and Nigrosin. With continuous stirring, we dissolved 10g of powdered gelatin (Type A, 300g bloom, G1890, Sigma-Aldrich, St Louis, MO) in 100ml of water heated on a hot plate. We made a 10mg/ml solution of Nigrosin (Sigma-Aldrich, St Louis, MO) by dissolving 500mg Nigrosin in 50ml of water and sonicating (Branson 1510 Ultrasonic Cleaner, Emerson Electric Co, St Louis, MO) for two hours. We created phantoms with five different final concentrations of Nigrosin. Each phantom consisted of 0.4ml glycerol (Sigma-Aldrich, St Louis, MO), 10ml of the dissolved gelatin mixture, and 4.5ml of a Nigrosin dilution (Table 1). We spread 3.5ml of the gelatin-Nigrosin solution into a 6cm diameter Petri dish and let it set overnight. The resulting phantoms were measured with calipers in five random locations, and were found to be ~80μm thick. To characterize the absorption coefficient (μ_a) of each phantom, we measured the transmittance using an integrating sphere (4P-GPS-033-SL, Labsphere, North Sutton, NH), and computed μ_a using Beer’s law (Table 1).

Table 1. Absorption properties of the thin flexible phantoms used to simulate epidermal melanin.

Phantom	Nigrosin (mg)	μa (mm−1)	Kmeasured (T = 10ms)	% Diff. vs A0	% Diff. vs A1	Ksimulated (T = 10ms)	% Diff. vs A0 Simulated	% Diff. vs A1 Simulated
A0	0	0	0.1079	-	4.51%	0.2216	-	0.2%
A1	0.25	1.5	0.1130	4.73%	-	0.2541	0.2%	-
A2	2.5	5.3	0.1184	9.73%	4.78%	0.2663	6.14%	5.93%
A3	5.0	9.5	0.1165	7.97%	3.1%	0.2748	9.53%	9.31%
A4	7.5	13.5	0.1203	11.54%	6.5%	0.2680	6.82%	6.6%
A5	12.5	20.6	0.1224	13.44%	8.32%	0.2749	9.57%	9.35%

Experimental and simulated contrast values (10ms exposure time). Percent difference (% Diff.) between contrast determined with a top layer, and contrast with no top layer (A0) or with the least-absorbing phantom (A1), for both in vitro and in silico results.

4.3 LSI of absorbing phantoms

In vitro experiments were conducted using the LSI setup described above. We imaged flow of 20% Intralipid (Baxter Healthcare, Deerfield, IL) in the PDMS phantom containing a microchannel described above. The thin, absorbing phantoms were placed over the microchannel (Fig. 1(a)). A sequence of 30 images was collected with the aperture at f/8, acquisition rate of 30fps, and exposure time of 10 or 30ms. To prevent pixel saturation associated with imaging of samples with low absorption, neutral density filters (ThorLabs, Newton, NJ) were used to attenuate the laser. Spatial contrast was computed using a 7x7 sliding window algorithm, and contrast values in a region of interest were averaged over the 30 contrast images. The region of interest was chosen as a 25x480 pixel area centered on the microchannel.

5. Validation of the MTMC model

We compared data calculated with a single-layer model with those from Rice et al, who developed and worked with a similar model for spatial frequency domain laser speckle imaging [40]. We imaged mixtures of Intralipid, water, Nigrosin dye, and glycerol, to test the sensitivity of LSI to samples with different D_b values (Table 2). To decrease D_b, we added glycerol to the phantom, and observed the expected, and previously demonstrated, trend of increasing contrast with increasing viscosity. The percent difference in contrast arising from measurements of 28% and 43% glycerol solutions, and simulations using the same glycerol solutions, was higher than expected. One potential explanation arises from selection of the value of β used in this study. We used a previously reported value of β in Eq. (4) to reduce the dynamic range of the simulated results to be similar to the experimental range, but it is well known that this value can vary due to differences in the imaging hardware [7].

Table 2. Simulated contrast for model validation in homogenous samples with varying optical properties (μ_s’ and μ_a) and diffusion coefficients (D_b).

Sample	μa (mm−1)	μs’ (mm−1)	Db (mm2/s)	Ksimulated	Kexperimental	Percent Error
0% glycerol	5x10−3	1	2x10−6	0.121	0.118	2.5%
28% glycerol	5x10−3	1	0.86x10−6	0.172	0.148	16.5%
43% glycerol	5x10−3	1	0.5x10−6	0.223	0.182	22.3%
800nm microspheres	5x10−3	1	6.1x10−7	0.200	-	-
1% Intralipid	3.3x10−4	1	2x10−6	0.103	0.100	2.8%
1.7% Intralipid	3.3x10−4	1.7	2x10−6	0.097	0.103	5.6%

We also modified the diffusion coefficient using 0.3% weight per volume of 800nm polystyrene microspheres, and found the simulated contrast value of 0.200 matched the simulated value used by Rice et al [40].

To compare sample measurements with our simulated results, we collected LSI data from samples with different quantities of Intralipid and scattering microspheres and obtained less than 6% error between the simulated and experimental results (Table 2).

Additionally, we compared data from our two-region model with data from Rice et al [41]. We simulated 1) a geometry consisting of a variable-thickness dynamic top layer above a 5cm thick static bottom layer, and 2) a variable-thickness static top layer above a dynamic second layer (Table 3). We observe a trend of decreasing contrast with increasing thickness of the dynamic top layer, and conversely increasing contrast with increasing thickness of the static top layer. These trends agree with our expectations – an increase dynamic scattering events will occur as the thickness of a dynamic top layer is increased, resulting in increased momentum transfer from moving scatterers. Similarly, as the thickness of the static top layer increases, the number of detected photons that reach the dynamic second layer decreases, resulting in a decrease in momentum transfer from moving scatterers and a corresponding increase in contrast. Our values follow the same trend reported by Rice et al [41].

Table 3. Simulated contrast for model validation in two-layer geometry.

Top Layer	Thickness of Top Layer (mm)	Ksimulated
Dynamic	0.75	0.463
Dynamic	1.5	0.381
Dynamic	2.25	0.335
Dynamic	3.0	0.312
Dynamic	3.75	0.295
Static	0.4	0.301
Static	1.3	0.452
Static	2.2	0.580
Static	3.1	0.684
Static	4.0	0.769

We also used the two-region model to compare simulated flow in a vessel-like inclusion placed below the surface of a liquid phantom (Fig. 1(a)). We varied the simulated flow speed and computed contrast for different exposure times (Fig. 1(b)). As expected, the contrast decreased as exposure time increased because a longer exposure time allows for more blurring of the speckle pattern. The contrast decreased as flow speed increased, which is consistent with the fact that faster flow results in a more rapid decorrelation of the speckle pattern. The data for flow at 0.375mm/s was in close agreement with simulation data by Rice et al [41].

6. Effect of optical properties and imaging geometry on speckle contrast

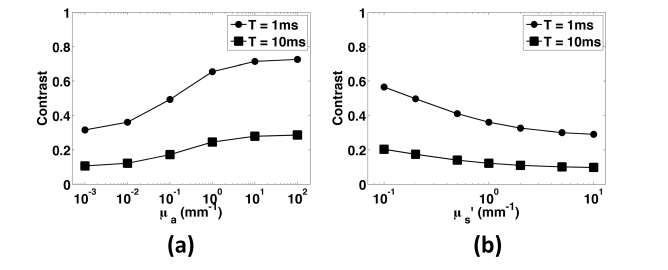
With a homogeneous, semi-infinite tissue geometry, we assessed the effect of optical properties on speckle contrast (Fig. 2). We used a uniform, square illumination source (30x30mm) to mimic the wide-field illumination scheme commonly used with LSI. To compute speckle contrast with Eq. (4), we assigned to the homogeneous layer a D_b of 2x10⁻⁶mm²/s, which is representative of Intralipid in water [40]. We varied μ_a over five orders of magnitude, from 10⁻³mm⁻¹ to 10²mm⁻¹, covering a range of absorption values associated with different combinations of tissue type (i.e., skin, skull, blood) and illumination wavelength [49, 50]. We held the μ_s’ constant at 1mm⁻¹. We computed the simulated speckle contrast at exposure times of 1 and 10ms, which are frequently used experimentally (Fig. 2(a)).

Fig. 2.

Simulated data from samples with varying optical properties and camera exposure times. (a) Speckle contrast as a function of absorption coefficient, with μ_s’ held at 1mm⁻¹ for two commonly used exposure times, 1ms (circles) and 10ms (squares). Speckle contrast increased with increasing absorption due to a reduction in the number of scattering events per remitted photon. Contrast is higher for shorter exposure times. (b) Speckle contrast as a function of μ_s’, with μ_a held constant at 0.01mm⁻¹. Contrast decreased as scattering increased due to the increase in momentum transfer associated with longer photon pathlengths.

Overall, speckle contrast increased with an increase in tissue μ_a, in agreement with the trend observed in previous studies [26,27]. As μ_a is increased, the number of scattering events per simulated photon is decreased, resulting in a decrease in momentum transfer and hence a slower decorrelation of the speckle signal.

We next performed a similar set of simulations, but instead held absorption constant at 0.01mm⁻¹ and the scattering anisotropy (g) at 0.8. We varied μ_s’ over two orders of magnitude, from 0.1mm⁻¹ to 10mm⁻¹ (Fig. 2(b)). As μ_s’ increased, contrast decreased. With an increase in the number of scattering events for each simulated photon, an increase in the total momentum transfer and hence a more rapid decorrelation of the speckle signal occurred, which led to a decrease in speckle contrast.

7. Spectral dependence of speckle contrast in the skin

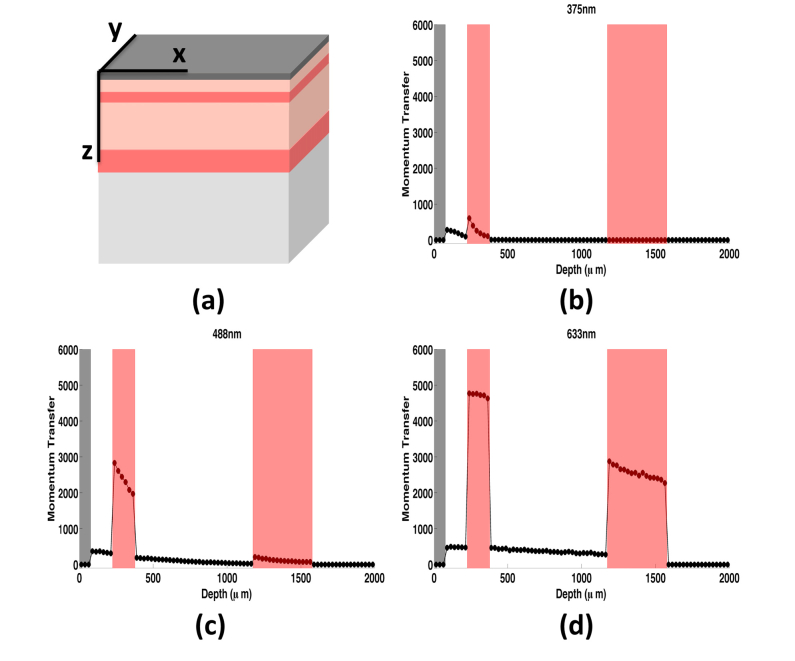
To study the spectral dependence of speckle contrast, and the depth localization of dynamic momentum transfer events, we simulated light and momentum transfer in a model of human skin. We simulated skin as a layered geometry consisting of a bloodless epidermis with 3% melanin content, which is representative of fair skin; and four dermal layers with varying blood-volume fractions representative of the papillary and reticular dermis and the upper and lower capillary blood nets (Fig. 5(a)). The blood-volume fraction and thickness of each layer are given in Table 4 [51]. We modeled a semi-infinite geometry with a static-scattering lipid layer below the skin [52]. We used the spectral library and “makeTissue” function by Jacques to estimate optical properties for each layer at 21 wavelengths (375nm to 980nm) [53].

Fig. 5.

(a) Layered skin geometry used in simulations. The model of skin consisted of a static epidermis (dark gray), two highly perfused capillary beds (upper and lower blood nets, red), and two dermal layers (papillary and reticular dermis, light pink). A semi-infinite lipid layer (light gray) was added below the skin. (b)-(d) Dynamic momentum transfer as a function of depth for three wavelengths: (b) 375nm, (c) 488nm, and (d) 633nm. The upper and lower blood nets (highlighted in red) contribute most to the overall contrast signal due to the tenfold higher blood fraction than the dermal layers. As wavelength increases, the contribution of deeper tissue layers to the speckle signal increases.

Table 4. Six-layer skin model with corresponding layer thickness and blood volume fraction of each layer.

Layer	Thickness (μm)	Blood Volume Fraction (%)
Epidermis	75	0.0
Papillary Dermis	150	0.4
Upper Blood Net	150	4.0
Reticular Dermis	800	0.4
Lower Blood Net	400	4.0
Lipid	up to 10mm	0.0

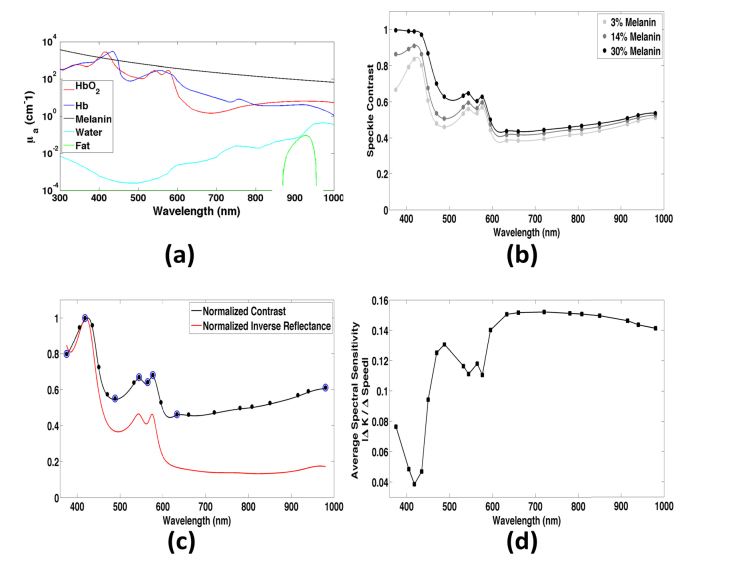
The wavelengths corresponded to features and key inflection points of the absorption spectrum of hemoglobin (Fig. 3(a)), and common wavelengths used for LSI. For each simulation, we used 10⁶ simulated photons distributed evenly over a 15x15mm square. To avoid any inconsistencies near the edges of the illuminated region, we calculated an average contrast over a central 7x7mm region of interest. We assigned the dynamic scatterers a flow speed of 0.36mm/s, which is representative of healthy tissue perfusion [54]. We simulated LSI with an exposure time of 10ms, which is common for LSI.

Fig. 3.

(a) Absorption spectra of chromophores in the skin. (b) Speckle contrast as a function of wavelength and epidermal melanin concentration for fair (3% melanin), tan (14% melanin), and dark (30% melanin) skin. Contrast increases slightly with increasing epidermal melanin, especially at lower wavelengths where the combined absorption of melanin and hemoglobin greatly shorten the photon pathlength. However, contrast values between the three cases are very similar in the optical window, and there is no significant difference in average contrast. (c) Normalized speckle contrast as a function of wavelength (black) compared to the normalized inverse reflectance (red). Both curves exhibit features of the hemoglobin absorption spectra, however, contrast is not as flat in the optical window. Blue circles indicate wavelengths where there is an inflection point in the contrast curve, which are used for the spectral analysis of momentum transfer. (d) Spectral sensitivity to changes in flow of contrast in skin with 3% melanin content. Contrast is most sensitive to changes in flow around 650-700nm.

We ran each simulation twice, using different seeds to the random number generator. For each pair of runs, we determined that both reflectance and contrast varied by less than 1%, suggesting that we used a sufficient number of simulated photons.

The spectral speckle contrast curve (Fig. 3(b)) had a shape similar to that of the absorption spectrum of hemoglobin (Fig. 3(a)). We next studied whether the observed changes in speckle contrast are due solely to the spectral variations in hemoglobin absorption. We calculated the normalized inverse reflectance values resulting from the Monte Carlo simulations. We observed a difference between inverse reflectance and hemoglobin absorption (Fig. 3(c)). In the 380-576nm wavelength region, over which hemoglobin absorption is high, contrast was less than 1.5 times the inverse reflectance. At wavelengths longer than 576nm, the contrast increased to two to four times the inverse reflectance. These data suggest that the spectral speckle contrast curve does not merely replicate the spectral absorption curve.

To study the spectral sensitivity of speckle contrast to changes in flow speed, we calculated contrast for speeds from 0.01 to 5.085mm/s, in 0.175mm/s increments, for each of the 21 wavelengths. We calculated spectral sensitivity at each wavelength as the average of the absolute value of the change in contrast (ΔK) divided by the change in speed (ΔSpeed). The sensitivity of contrast was inversely proportional to the hemoglobin absorption. The sensitivity peaked around 700nm (Fig. 3(d)), suggesting that this wavelength achieves the best sensitivity to flow changes in the simulated skin geometry.

8. Depth dependence of momentum transfer in the skin as a function of wavelength

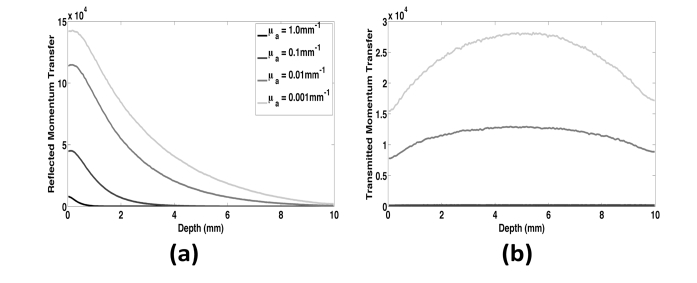
To study the origins of speckle contrast, we developed a virtual detector to track the weighted reflected momentum transfer as a function of depth. The detector tracks the dynamic momentum transfer events that occur at each depth. These events are then weighted by the final reflectance or transmittance value associated with each simulated photon [47].

We tested this detector by varying μ_a (0.001, 0.01, 0.1 and 1.0mm⁻¹) in a 10mm thick homogeneous block of tissue with μ_s’ of 1mm⁻¹. For each simulation, we estimated a characteristic penetration depth of light and a characteristic speckle origination depth as the depths over which 95% of the total fluence and reflected momentum transfer occurred, respectively (Table 5). As the absorption increased over three orders of magnitude, the average penetration depth of the light decreased by a factor of 5.6. Over the same range of μ_a values, the speckle origination depth increased by a factor of 8.4 (Fig. 4(a)). For a given μ_a value, the penetration depth of light was greater than the speckle origination depth. This is due to the fact that the light captured by the reflected momentum transfer detector must reach a particular depth, then return back to the surface. This results in a higher probability of absorption due to the longer pathlength compared to light quantified by the fluence detector, which only measures where in the tissue the light has passed. These data suggest that even if light reaches a certain depth in a tissue, information about blood flow at the depth may not be contained in the reflected speckle contrast measurement.

Table 5. Characteristic depth over which 95% of the fluence or reflected momentum transfer occurred for homogeneous samples with μ_s’ = 1mm⁻¹ and μ_a values varied over three orders of magnitude.

Absorption Coefficient (mm−1)	95% Fluence Depth (mm)	95% Reflected Momentum Transfer Depth (mm)
1.0	1.48	0.78
0.1	4.97	2.58
0.01	7.88	5.68
0.001	8.24	6.58

Fig. 4.

(a) Weighted reflected momentum transfer as a function of depth for a homogeneous sample with μ_s’ held at 1mm⁻¹ and absorption varied over three orders of magnitude. The majority of the reflected speckle contrast signal originates near the surface of the sample, however as absorption decreases there is more information contributing to the signal from deeper within the tissue. (b) Weighted transmitted momentum transfer as a function of depth for the same optical properties as (a). The transmitted contrast signal consists of information from throughout the entire depth. At very low absorption, the majority of the transmitted signal comes from the center of the sample. For tissues with μ_a values of 0.1 and 1mm⁻¹, the plots of transmitted momentum transfer overlap and are negligible on this scale.

We next compared epi-and trans-illumination LSI by computing the weighted momentum transfer versus depth for transmitted light (Fig. 4(b)). With trans-illumination LSI, we observed a decrease in total momentum transfer due to a decrease in the number of photons exiting the geometry. The depth distribution of momentum transfer was more uniform, with lower contributions from the tissue regions closer to air. The decreased contributions near the upper surface were due to remittance of photons scattered at superficial depths.

We then applied this detector to simulations performed on the layered model of skin described above (Fig. 5(a)). Figures 5(b)-5(d) show plots of weighted reflected dynamic momentum transfer as a function of depth for three wavelengths representative of different optical regimes. For each of the wavelengths, we observed an increase in dynamic momentum transfer in the upper blood net (shaded in red). With a longer wavelength, the dynamic momentum transfer increased at deeper depths and especially in the lower blood net.

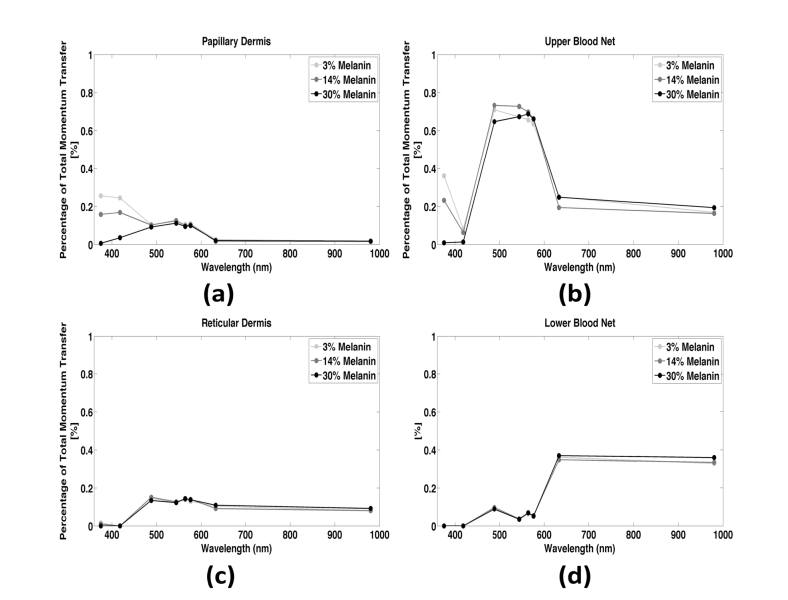
We studied the relative contribution of momentum transfer at different depths to the speckle contrast signal at eight wavelengths associated with inflection points of the absorption spectrum in Fig. 3(c) (blue circles). We calculated the percentage of the total reflected momentum transfer arising from different layers of the simulated tissue (Fig. 6, light gray). This percentage represented the dynamic momentum transfer integrated over each dermal layer, divided by the total momentum transfer in the entire tissue geometry. At wavelengths between 488 and 576nm, the percentage was highest (~0.67%) from the upper blood net (Fig. 6(b)), due to the relatively low penetration depth of those wavelengths. At wavelengths below 600nm, dynamic scattering within the papillary dermis contributed to the signal (~0.10-0.26%) (Fig. 6(a)). At longer wavelengths, the contribution from the papillary dermis was negligible (<0.03%) and the majority (~0.35%) of the speckle contrast signal arose from the lower blood net (Fig. 6(d)). This finding is consistent with the increased penetration depth at these longer wavelengths.

Fig. 6.

Percentage of the total momentum transfer contributing to the speckle contrast signal versus wavelength and epidermal melanin content for each of the dermal layers. There is no significant difference in the percent contribution between tissues with different melanin contents. (a) Very little of the signal comes from the papillary dermis, especially at wavelengths typically used for LSI (above 600nm). (b) Most of the contrast signal originates from the upper blood net at lower wavelengths (below 600nm) (c) The proportion of signal coming from the reticular dermis is relatively uniform across different wavelengths. (d) The majority of our speckle contrast signal originates in the lower blood net for wavelengths typically used in LSI (>600nm) supporting the potential for rough depth sectioning using dual-wavelength LSI.

Collectively, these simulated data show the potential of the model to improve our understanding of the contribution of tissue architecture to the speckle contrast signal. At red and near infrared wavelengths, which are typically used for LSI, the primary contribution to speckle contrast is from the lower blood net. With use of shorter wavelengths, the contribution is predominantly from the upper blood net. This result suggests the potential for two-wavelength LSI (i.e., 543nm HeNe and a 785nm laser diode) to perform coarse depth sectioning of blood-flow measurements in skin.

9. Impact of epidermal melanin content on speckle contrast in layered skin model

In a homogeneous scattering medium, speckle contrast correlates with μ_a (Fig. 2). This trend is in agreement with previous findings [26]. Next, we studied the effects of a thin, statically scattering, absorbing top layer (i.e., epidermis) on speckle contrast. We used the layered skin geometry described above (Fig. 5(a)). The epidermal melanin concentration was set at 3, 14, and 30%, which is representative of fair, tan, and dark skin, respectively. Speckle contrast increased with melanin content, as increasing epidermal μ_a decreased the number of dermal dynamic scattering events. The difference is greatest at wavelengths shorter than 500nm, at which melanin absorption is very strong (>20mm⁻¹ for 30% melanin), but the mean contrast for each of the three concentrations is not significantly different (1-way ANOVA, p>0.05).

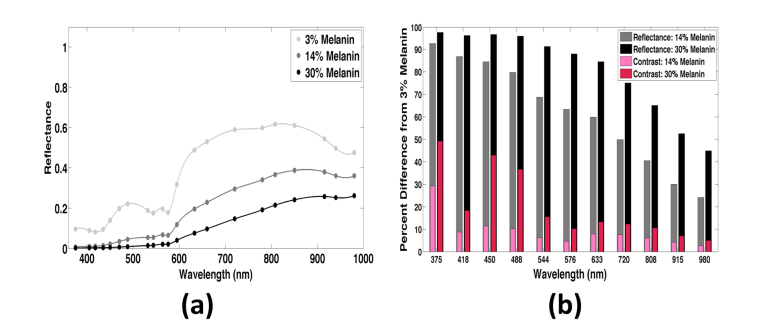
We also determined the normalized reflectance spectrum for each of the three melanin distributions (Fig. 7(a)). As melanin content increased, the spatial features of the hemoglobin absorption spectrum became less prominent. The reflectance values calculated with 3% melanin differed significantly from those at higher melanin contents (one-way ANOVA, p = 2.6x10⁻⁵).

Fig. 7.

(a) Reflectance versus wavelength and epidermal melanin content. At 3% melanin content (light gray) the reflectance curve contains features of the hemoglobin absorption curve. As epidermal melanin increases (dark gray, black), the reflectance curve flattens and is dominated by features of the melanin absorption curve. (b) Percent difference in speckle contrast (pink/red) and reflectance (gray/black) between light skin (3% melanin) and tan/dark skin (14% / 30% melanin). The percent difference in contrast is significantly less than the difference in reflectance, indicating the potential for clinical use of LSI over other optical reflectance techniques.

We compared speckle contrast and reflectance values associated with the three epidermal melanin content skin types. Specifically, we calculated the percent difference between the contrast or reflectance value for skin with 14 or 30% melanin and the respective value for skin with 3% melanin (Fig. 7(b)). The percent difference in reflectance ranges from 24 to 93% for tan skin and 44 to 98% for dark skin. At each wavelength, the impact of epidermal melanin content is greater for reflectance than for speckle contrast. At 808nm, we observed only a ~6% difference in contrast between tan (14% melanin) and fair (3% melanin) skin. At 633nm, we observed only a 13% difference in contrast between dark (30% melanin) and fair (3% melanin) skin. These percent differences are less than the changes in speckle contrast that were observed in previous in vivo studies. For example, a 20 to 60% change in contrast was reported during laser therapy of port-wine stain birthmarks, and a 20 to 55% change in contrast was associated with burn wounds [3, 55]. With analysis of the depth distribution of dynamic momentum transfer (Fig. 6), we determined that the average percentage of dynamic momentum transfer did not significantly differ among skin with different epidermal melanin content (ANOVA, p>0.05) for any of the four dermal layers (p = 0.1747, 0.9315, 0.9998, and 0.9972). Collectively, these data suggest that the impact of epidermal melanin content on speckle contrast values and the depth sensitivity of LSI is unexpectedly small.

To test this in silico observation, we next performed experiments involving flow of Intralipid in a 650μm tube beneath thin absorbing phantoms that simulated epidermal melanin absorption. We computed the spatial speckle contrast in a region of interest within the tube. The exposure time was set at 10ms, which matched the time used in the simulated data described above.

We fabricated five thin (~80μm) absorbing phantoms using gelatin for structure and Nigrosin dye for absorption (Table 1). We selected a gelatin concentration to ensure fabrication of flexible phantoms that were neither sticky nor brittle. The absorption of phantom A₁ (μ_a = 1.5mm⁻¹) matched that of fair skin at wavelengths longer than ~550nm and tan skin at wavelengths longer than ~870nm. The absorption of phantom A₅ (μ_a = 20.6mm⁻¹) matched that of dark skin at 495nm and tan skin at 395nm. Hence, we achieved epidermal μ_a values that spanned the range of values reported in the literature over the visible and near-infrared spectral region for melanin concentrations of 3-30%.

We calculated the percent difference in contrast among each of the five phantoms and the contrast when no top layer was present. We also calculated the percent difference in contrast measured using phantoms A₂-A₅ and that measured with the least absorbing phantom (Phantom A₁, μ_a = 1.5mm⁻¹) (Table 1). The percent difference in contrast ranged from ~4 to 13% when compared to the contrast measured with an absorbing layer, and ~3 to 8% compared with Phantom A₁. These measurements support the findings from the layered simulation data (Fig. 6), that the impact of epidermal melanin content on speckle contrast values is relatively small.

10. Impact of epidermal melanin content on speckle contrast in subsurface inclusion

We next ran simulations in which 20% Intralipid was present in a tube placed beneath a static absorbing top layer. We used a rectangular inclusion geometry, with an 800x800μm cross-section. This inclusion was at the surface of a static scattering layer (μ_s’ = 1mm⁻¹), with an 80μm thick static absorbing layer positioned above. We selected the μ_a values of the absorbing layer to match those of our in vitro phantoms (Table 5). We calculated contrast based on reflected momentum transfer values from a region of interest directly above the inclusion. We used a Brownian diffusion constant of 2x10⁻⁶mm²/s, an exposure time of 10ms, and an excitation wavelength of 808nm.

We computed the corresponding percent difference among contrast values associated with the different absorbing top layers and those with either a clear, non-absorbing top layer (A₀) or the least absorbing top layer (A₁) (Table 5). These values ranged from ~0.2 to 10% when compared to a clear top layer, and ~6 to 9% when compared to top layer A₁. Similar to the layered simulation data (Fig. 6), these in silico and in vitro data demonstrate that LSI measurements of subsurface flow are only minimally impacted by large differences in epidermal melanin content.

11. Conclusions

In conclusion, we developed a Monte Carlo model to simulate LSI in a heterogeneous tissue geometry. The virtual detectors of the model track several important characteristics of light, including the absorbance, reflectance, transmittance, fluence, and momentum transfer. This model enables study of LSI aspects that may be difficult or unwieldy to address in an experimental setting. The model can account for different skin geometries and other tissue types (i.e., brain), to enable detailed study of the fundamental origins of speckle contrast modulation in tissue-specific geometries.

With trans-illumination of the tissue, modulation of the speckle contrast signal occurs in a more uniform fashion than with epi-illumination (Fig. 4). The speckle contrast spectrum contained similar features to the absorption of hemoglobin (Fig. 3(b)), and the spectral sensitivity was inversely proportional to hemoglobin absorption (Fig. 3(d)). In a representative model of skin, shorter wavelengths characterize blood flow primarily within the upper blood net and papillary dermis, and longer wavelengths characterize blood flow primarily from the lower blood net (Fig. 6). This result suggests the potential for segmenting perfusion information from different depths by using multiple wavelengths to perform LSI.

We also determined that epidermal melanin concentration has a smaller effect on speckle contrast than on reflectance (Figs. 3(b), 6). This finding has implications for clinical applications of LSI in patients with different skin types, especially for patients with darker skin (Fig. 7, Table 5). Other reflectance-based optical imaging technologies have limitations when imaging patients with darker skin types. In contrast, our data suggest that the relative insensitivity of LSI measurements to melanin content enables LSI to measure blood flow in any patient regardless of skin type. One such potential clinical application is during skin flap surgery, in which doctors need to identify if tissue is perfused following the procedure. Another potential dermatological application is for identifying cancerous skin lesions in which there is increased blood flow beneath regions of high melanin content.

Funding

National Institutes of Health (R01 DE022831, P41 EB015890); National Science Foundation BEST IGERT Program (DGE 1144901); Roche/ARCS Scholar Awards

Disclosures

The authors declare that there are no conflicts of interest related to this article.