Observation of live chromatin dynamics in cells via 3D localization microscopy using Tetrapod point spread functions

Abstract

We report the observation of chromatin dynamics in living budding yeast (Saccharomyces cerevisiae) cells, in three-dimensions (3D). Using dual color localization microscopy and employing a Tetrapod point spread function, we analyze the spatio-temporal dynamics of two fluorescently labeled DNA loci surrounding the GAL locus. From the measured trajectories, we obtain different dynamical characteristics in terms of inter-loci distance and temporal variance; when the GAL locus is activated, the 3D inter-loci distance and temporal variance increase compared to the inactive state. These changes are visible in spite of the large thermally- and biologically-driven heterogeneity in the relative motion of the two loci. Our observations are consistent with current euchromatin vs. heterochromatin models.

1. Introduction

Tightly regulated gene expression is critical in cell development and disease progression [1]. During interphase, DNA in the form of chromatin is extensively compacted when a gene is inactive, but becomes accessible for transcription when a gene is activated. Most studies investigating gene regulation rely on epigenomic methods [2,3], where the regulatory DNA is extracted outside of its native environment of the cell nucleus. These methods provide only static snapshots of the local spatial organization of the genome and typically show data from an ensemble of cells, and they do not provide information about the complex spatio-temporal organization in single cells. To further our understanding of gene regulation, tools are required that allow measurements of the dynamics of the genome in all three spatial dimensions (3D) in real time in live single cells. Fluorescence microscopy is an excellent match with the challenge of live chromatin studies on the single cell level, thanks to its specificity, high precision, and typically high SNR capability.

Elucidating the full 3D behavior of fluorescent objects inside a living cell requires a method for 3D spatiotemporal tracking. Several such methods have been developed and used in fluorescence microscopy – these include confocal scanning microscopy [4], multi-plane imaging [5,6], light sheet microscopy [7–9], and point spread function (PSF) engineering [10–15]. In PSF engineering, the PSF of a microscope, namely, the image that is detected on the camera when imaging a point source, is modified optically, such that its shape encodes the depth position of the source [15]. In this way, multiple fluorescent loci in each widefield 2D image reveal their x, y, and z positions. PSF engineering is a powerful tool used both for nanoscale 3D super-resolution localization microscopy [16,17] and for single particle tracking, in which it provides 3D precision on the order of ten to tens of nanometers over a depth range of several microns [18–20].

Here, we use PSF engineering for 3D tracking of DNA loci in order to investigate time-dependent behavior of chromatin in living systems. Recently, three-dimensional tracking of DNA loci in yeast, using the double-helix PSF, has been performed to study the correlation of motion between the two copies of the GAL gene locus in diploid cells in activating and repressive conditions [18]. In the current work, we focus on the conformational state of chromatin in the single GAL gene locus in haploid cells. The GAL locus in S. cerevisiae comprises three genes, GAL7, GAL10, and GAL1, which code for proteins that are required for the metabolism of galactose. Importantly, in the presence of galactose, the GAL locus becomes actively transcribed [21], whereas in the presence of dextrose, the preferred yeast carbon source, transcription is inhibited [22]. Therefore, controlling the growth and imaging environment of the yeast cells (galactose vs. dextrose) is a simple and effective way to affect the transcription status of the GAL locus. Fluorescent protein label arrays of two different colors are placed near the GAL locus using well-known DNA targets and fluorescently labeled DNA binding proteins (LacO/LacI-GFP and TetO/TetR-mCherry [18]).

In this work, to detect the 3D position of the tracked loci, we use a Tetrapod PSF designed to have a depth range of 6 µm [19], comparable to the size of a whole yeast cell. In previous experimental measurements, the Tetrapod PSF has only been implemented using a liquid-crystal spatial light modulator (SLM) for phase modulation. Such an implementation is inefficient in terms of photon conservation: since in our implementation the SLM modulates only one polarization of the light, typically ~50% of the precious emitted fluorescence photons are lost. In the current work, we use a specially fabricated dielectric transmittance mask for phase modulation. This dramatically increases photon efficiency, which is of great importance due to the challenging conditions of live-cell imaging (high background), and the large lateral extent of the Tetrapod PSF, which spreads photons over many camera pixels.

2. Optical setup

In order to track two different loci in 3D, we use a dual-color imaging setup, employing PSF engineering in each color channel. The experimental arrangement used in this work is similar to a dual-channel setup used previously [18,23] utilizing a double-helix phase-mask [13]. Here we use the Tetrapod PSF, which is designed for information-optimal precision over a 6 µm depth range [14,19], and employ a longer focal length tube lens (400 mm) to optimize the size of the Fourier plane image. The setup is depicted in Fig. 1(a). At the emission side of an inverted microscope (Nikon Diaphot 200), the light passes through a multi-band pass dichroic mirror (ZT405/488/561rpc, Chroma), a dual-bandpass filter (FF01-523/610, Semrock), and a 561 nm notch filter (NF03-561E), before it is split into two color channels (‘green’ and ‘red’) by a dichroic mirror (FF560-FDi01, Semrock). The red channel contains an additional long pass filter (HQ605LP, Chroma), to minimize cross-talk GFP signal.

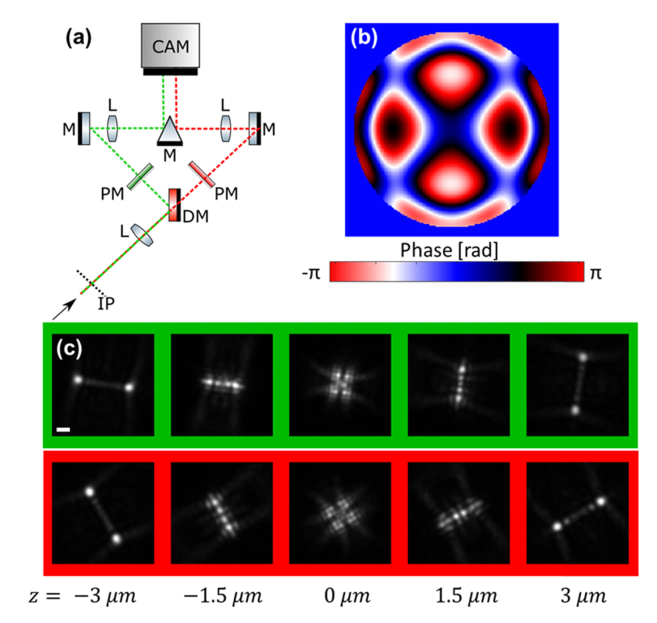
Fig. 1.

Dual-color Tetrapod imaging. (a) Optical setup (main components). A split-color 4f system is added to a standard inverted microscope, starting from the image plane (IP), yielding a dual-color image illuminating two corners of the camera (CAM). L = lens, DM = dichroic mirror, M = mirror, PM = phase mask. (b) A 6 µm Tetrapod phase pattern, implemented by photo-lithographically etched dielectric phase-masks placed in the Fourier plane, one for each color channel. (c) Experimental calibration measurements of a fluorescent microsphere imaged over a 6 µm range in the green channel (top) and red channel (bottom). Lateral orientation angle of the PSF is calibrated in the fitting procedure. Scale bar = 1 µm.

Each channel contains a 4f optical system with a dielectric phase mask in the Fourier plane, with the Tetrapod phase pattern [19] (Fig. 1(b)). The Tetrapod phase mask is a key component in the optical system. It is a specially fabricated slab of quartz, etched at varying depths in order to impose a specific phase delay pattern. See Section 10 for fabrication details. Due to its positioning conjugate to the back-focal plane, its effect is a modification of the PSF of the microscope. Specifically, the Tetrapod PSF has been designed such that its shape encodes the depth of the point source with optimal precision over a preselected axial range [14,19].

The resulting PSF, as measured by axially scanning fluorescent microspheres (F8800, Invitrogen) over 6 µm is shown in Fig. 1(c). The two color channels are imaged onto two corners of an EM-CCD camera (Andor Ixon DU-897E) [18,23].

3. PSF calibration and multichannel registration

The localization of fluorescent loci with Tetrapod PSFs is performed using an imaging model based on the scalar diffraction approximation developed by Gibson and Lanni [24]. In our model, the PSF resulting from an in-focus, on-axis point source, is calculated from the pupil plane electric field, which has the form:

$$P(x\text{'},y\text{'})=\frac{circ(\rho )}{{\left\{1-{[(\mathrm{NA}/{\mathrm{n}}_1)\rho ]}^2\right\}}^{1/4}}\exp \left[i\mathcal{M}\left(\rho ,\phi \right)\right],$$ (1)

where $\rho \in (0,1]$ is the normalized radial coordinate in the pupil plane, $\phi$ is the azimuthal coordinate, NA and n₁ are the numerical aperture and immersion medium of the objective, respectively, and $\mathcal{M}\left(\rho ,\phi \right)$ is the Tetrapod phase pattern. The denominator in Eq. (1) is an apodization factor due to the compression of the spherical wavefront onto the pupil plane [25], and the circle function truncates the field at the limiting spatial frequency collected by the objective.

Importantly, the fluorescent protein images (the spots) arise from emitters which are often located several microns above the coverslip, which requires accounting for the mismatch between the refractive indices of the coverslip (n₁ ≈ 1.518) and the sample (n₂ ≈ 1.33). We do this by parameterizing each PSF with two depth terms: the distance of the emitters above the coverslip $z_0$, and the distance of the nominal focal plane of the objective above the coverslip, $f_n$. The latter term corresponds to the physical distance the objective is moved from perfect focus at the sample-coverslip interface. Each depth term carries its own phase factor based on the corresponding phase lag incurred by a ray with a given spatial frequency. The total depth factor is given by

$${\psi }_{depth}\left(\rho ,\phi \text{|}{z}_0,f_n\right)=-k{n}_1{f}_n\sqrt{1-{\left(\frac{NA}{n_1}\rho \right)}^2}+k{n}_2{z}_0\sqrt{1-{\left(\frac{NA}{n_2}\rho \right)}^2}.$$ (2)

With the inclusion of Eq. (2) in the imaging model, the calculated PSFs closely resemble those observed in our experiments. However, optical aberrations compromise the precision and accuracy of the Tetrapod PSF over some parts of the axial range [26]. In order to account for the aberrations present in the experimental setup, we use a phase retrieval algorithm [26] to estimate an additional phase aberration term,${\psi }_{aberr}$, which is added to the imaging model. Briefly, axial scans of a fluorescent bead are acquired over the 6 µm range of the Tetrapod PSF and used to determine the phase aberration to append to the imaging model via maximum likelihood estimation. The phase aberration is a weighted sum of Zernike polynomials which improves the PSF model by maximizing its similarity to the experimentally observed Tetrapod PSF. The final pupil plane electric field is given by:

$$P_{aberr}\left(\rho ,\phi \right)=P\left(\rho ,\phi \right)\exp \left\{i\left[{\psi }_{depth}\left(\rho ,\phi \text{|}z,f_n\right)+{\psi }_{aberr}\left(\rho ,\phi \right)\right]\right\}.$$ (3)

A final consideration is the calibration of slight lateral and axial localization biases. Due to the low symmetry of certain aberrations [27], as well as outstanding discrepancies between the observed and calculated PSFs, the position estimates obtained from super-localization (as described in Section 5) can be offset from their known values. To compensate for this, we fit a calibration scan in which the lateral position of a fluorescent bead is held constant while the axial position is varied by scanning the objective over the axial range of the Tetrapod. A polynomial fit to the position estimate in each axis as a function of nominal focus position f_n is used to adjust the localizations to their known values. Subsequently, localizations of Tetrapod PSFs in our experiments are adjusted similarly, using the same calculated polynomial curves.

Dual channel registration is performed by imaging ~20 static fluorescent microspheres adhered to a coverslip and randomly scattered throughout the field of view, in both color channels, while scanning axially (z) over 6 µm with 250 nm increments. Consequently, mapping of the coordinates of both channels is performed by calculating a global affine transformation at each z value, such that at the end of the process there are 24 affine transformations. The specific affine transformation used in registering the experimental data is the one that is closest to the z position of each locus. The process of taking registration calibration data takes a few minutes and is repeated every day data is taken.

Typical registration precision using this method, quantified by calculating the target registration error (namely, removing a test group of fluorescent beads from the calculation of the affine transformation and calculating their registration error) [28] is <10 nm.

4. Data acquisition

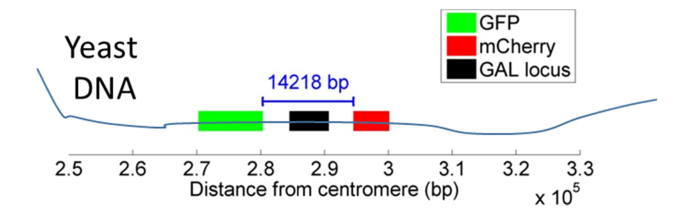
The samples imaged in this work are budding yeast (S. cerevisiae) cells mounted on agarose pads. Sample preparation and strain details are given in Section 9. Two S. cerevisiae strains are used in this study, KWY5028 and KWY4067. In both strains, two loci are labeled by integrating into the yeast genome: a sequence of at most 256 LacO repeats, to which freely diffusing LacI-GFP binds (producing a green spot), and a sequence of at most 112 TetO repeats, to which freely diffusing TetR-mCherry proteins bind (producing a red spot) (Fig. 2).

Fig. 2.

Yeast labeling scheme. Engineered yeast strain (KWY5028) contains two fluorescently labeled loci on opposite sides of the GAL locus. Dual color labeling is achieved using the LacO/LacI-GFP system (green) and TetO/TetR-mCherry system (red).

The difference between the two strains is that in KWY5028, the green and red spot are on opposite sides of the GAL locus, whereas KWY4067 serves as a control strain, in which both spots are downstream of the GAL locus.

Data acquisition consists of time-lapse imaging of single yeast cells, interleaved between the two channels, to minimize inter-channel cross-talk. This is performed by a high-throughput imaging method based on custom built Matlab code. First, candidate yeast cells on the coverslip are identified by screening the sample using white-light illumination, and their positions, as determined by a piezo linear drive XY stage (Physik Instrumente M-687) are recorded. The candidate cells are those who appear to be in a non-budding stage in the cell cycle, and they are positioned in the center of the field of view, in order to avoid field-dependent aberrations to the PSF which may degrade localization performance [29]. One cell is imaged per field of view.

Once a list of ten candidate cell positions has been compiled, the automated imaging sequence is initiated. The stage is periodically moved between the positions on the list, where at each position two pump lasers (488 nm and 561 nm, ~400 W/cm² and ~800 W/cm² at the sample plane, respectively) are activated sequentially and a pair of consecutive 30 ms frames are captured, effectively imaging both color channels sequentially, using the Tetrapod PSF. The motion of the stage is synchronized such that each cell is imaged with a time-lapse interval of 6 seconds.

The output of the automated imaging method is a series of movies, one movie per cell, each containing one time-lapse sequence per color channel. The limitation of the obtained trajectory length is set by photobleaching of the fluorescent proteins (typically the mCherry spot bleaches before the GFP spot). Typically, it is possible to obtain fifty 30 ms frames spaced by 6 s with satisfactory signal-to-noise ratio.

5. Image analysis

Obtaining time dependent inter-loci distances from a raw movie consists of localizing each emitter in each frame in each color-channel in 3D, followed by channel registration.

In order to extract the 3D position of each locus in each channel (green and red), we use maximum-likelihood estimation (MLE). Specifically, we numerically minimize the negative log likelihood function given the imaging model and noise model (Poisson), given by [30]:

$$NLL={\displaystyle \sum }_m\left({\mu }_m+b\right)-I_m\text{log}\left({\mu }_m+b\right),$$ (4)

where m is the pixel index, $I_m$is the measured image, b is the mean background level per pixel, and $\mathit{\mu }$ is the pixelated imaging model, sampled from the scalar imaging model (Eq. (1), with an additional linear phase term corresponding to the lateral position of the emitter:

$$\hat{\mu }\propto {\left|F\left\{P_{aberr}\left(\rho ,\phi ;z_0,f_n,n_1,n_2\right)\cdot \exp \left[ik\frac{NA}{\sqrt{M^2-N{A}^2}}\rho \left(x_0\cos \text{φ}+{\mathrm{y}}_0\sin \phi \right)\right]\right\}\right|}^2,$$ (5)

where (x₀,y₀,z₀) denotes the 3D position of the point source in object space, $0<\rho <1$, denotes normalized pupil plane radial coordinates, k represents the wavenumber $k=2\pi /\lambda$,$n_1$ and $n_2$are the refractive indices of glass and imaging medium, respectively, NA is the numerical aperture of the system, and $P_{aberr}$ represents the pupil-plane phase pattern, which includes the phase mask and experimentally calibrated aberrations (see Section 3).

Since our imaging model takes into account refractive index mismatch between the imaging medium (n ≈ 1.33) and the coverslip (n ≈ 1.518) Eq. (5), it requires knowledge of the nominal focus of the microscope $f_n$, which corresponds to the physical distance the objective is moved from perfect focus on the coverslip. This is obtained by imaging and localizing a fiducial microsphere adhered to the coverslip in every field of view that is imaged. Notably, using a Tetrapod PSF with a 6 µm depth range enables simultaneous imaging of the fiducial microsphere and the DNA loci at any position in the yeast cell, without need for refocusing. This is unlike previous loci tracking work using the shorter-range (<3 µm) double-helix PSF, in which data could be taken only for loci near the bottom of the cell. Note that the fiducial bead is used only for focus estimation. Channel registration is performed using the registration procedure described in Section 3

Background fluorescence is a major source of noise in our data, mostly due to unbound fluorescently labeled proteins (LacI-GFP and TetR-mCherry) within the cell nucleus. We account for the high background by including the cellular fluorescence in our imaging model used for MLE as follows. Specifically, the cellular background is modeled as a two-dimensional (2D) elliptical Gaussian which is added to the image of the PSF, with the same lateral orientation as the PSF. While in reality, the background is the outcome of 3D convolution of each diffuse emitter with the Tetrapod PSF, its modeling as a 2D Gaussian seems to be a reasonable approximation. A high-background example taken from our raw data is given in Fig. 3.

Fig. 3.

Fitting with strong background: example. (a) Raw data: yeast measurement with strong cellular background (red channel). (b) Model used for fitting, consisting of the Tetrapod PSF (c) combined with cellular background modeled as a 2D Gaussian (d). Scale bar = 1 µm. Color scales are normalized per figure.

After 3D localization is performed in each channel, the final step is channel-registration. This is performed by applying the affine transformation derived by calibration measurements (see Section 3) on the red channel. Determining which of the 24 affine transformation to use is done by finding an emitter depth (z₀) that produces a maximally similar (by correlation) PSF to the measured PSF, given a nominal focus of f_n = 0.

6. Data analysis and results

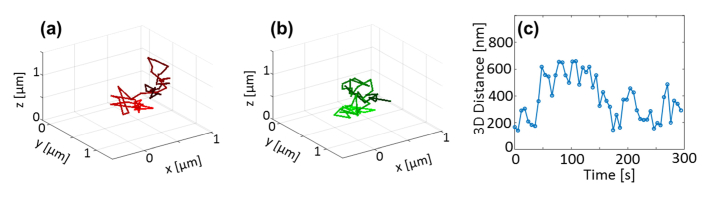
The image analysis step described in the previous section yields a list of 3D positions as a function of time (trajectories), per color channel, per cell. An example pair of trajectories is shown in Fig. 4, showing the trajectories of the two loci (Fig. 4(a), 4(b)) and the obtained 3D distance between them as a function of time (Fig. 4(c)). The precision associated with determining the 3D distance is approximated to be ~41 nm (standard deviation) (see Section 8 for details of this estimate). Notably, the inter-locus distance varies over a range of hundreds of nm in this and essentially all cells, likely due both to constant thermally driven agitation as well as biologically driven motions.

Fig. 4.

3D trajectories and co-localization trace: example. 3D trajectories of red (a) and green (b) loci, taken from a KWY5028 cell in galactose, over five minutes, in a time-lapse video with 6 second intervals. Time is encoded in color-value (dark = start, light = end). (c) The obtained 3D distance trace.

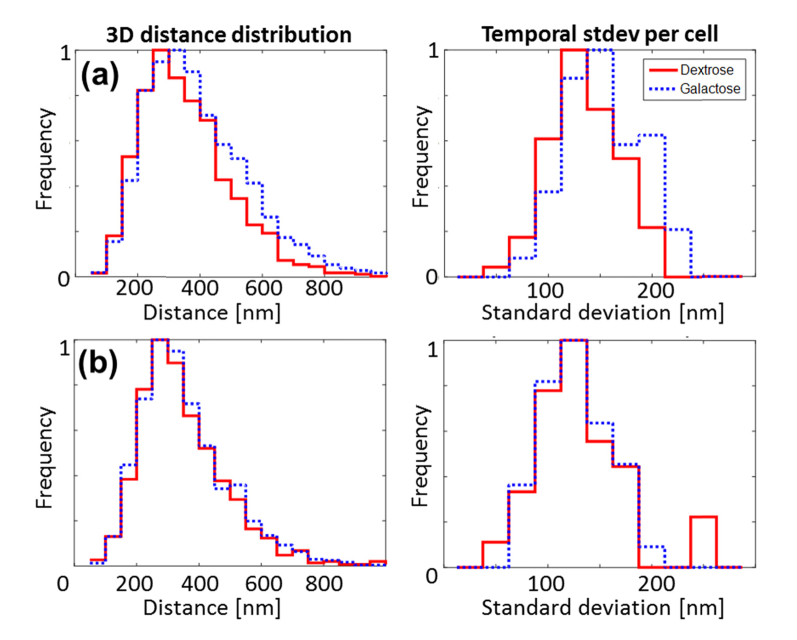
Observing many trajectories and analyzing the statistics of the motion reveals the picture depicted in Fig. 5. A total of 198 KWY5028 cells and 68 KWY4067 (control) cells were analyzed. When comparing cells that are grown and imaged in galactose (gal) rich environment with cells that are grown and imaged in dextrose (dex), gal cells exhibit larger 3D distance (mean distance of 344 nm vs. 307 nm). This effect is consistent with the open/closed chromatin model and with recent 2D bulk distance measurements of the same system [31]. Furthermore, a larger temporal standard deviation per cell (Fig. 5(a)) is observed in gal cells compared to dex cells (mean std. of 141 nm vs. 122 nm). These effects are not apparent in the control strain (Fig. 5(b)), which exhibit a mean distance of 307 nm (galactose) vs. 301 nm (dextrose), and a mean temporal standard deviation of 115 nm (galactose) vs. 120 nm (dextrose).

Fig. 5.

3D co-localization results. (a) Statistical comparison between galactose and dextrose conditions, in KWY5028, where the two labeled loci are on opposite sides of the GAL locus. 3D distance distribution using all data points (left) and temporal standard deviation per cell, derived from co-localization traces such as in Fig. 4(c). (b) Control: 3D distance distribution (left) and temporal standard deviation per cell (right) for control strain KWY4067, where the two labeled loci are on same side of GAL locus.

7. Discussion

We have presented 3D, dual color DNA-loci tracking measurements in living yeast cells using the 6 µm Tetrapod PSF. The large depth range of the PSF allowed us to simultaneously track fiducial microspheres adhered to the coverslip as well as the cellular loci which can be practically at any depth inside the cells. This is unlike previous work using the DH-PSF in which only loci near the bottom of the cells could be imaged due to limited (<3 µm) depth range [18].

These 3D tracking measurements allowed us to observe an overall larger inter-locus distance in the activated regime (galactose conditions) compared to the inactivated state (dextrose conditions). Importantly, using many single-cell tracks, we could measure the single cell temporal fluctuations (temporal distance fluctuations for one locus pair), and by measuring many single-cell tracks we could also quantify the cell-to-cell heterogeneity in these fluctuations. Despite the considerable variation from cell to cell, we were able to directly observe larger fluctuations in the active chromatin state compared to the inactive state.

More generally, the capability to measure the 3D distance between DNA loci in a live cell is an important step towards the elucidation of conformational and dynamical aspects of chromatin structure in the relevant biological environment. While such aspects play a fundamental role in gene regulation and thus are highly important, they are extremely difficult to study experimentally. Three-dimensional tracking of fluorescently labeled loci with high spatio-temporal resolution offers a powerful technique for direct observation of chromatin dynamics, complementary to in vitro chromatin conformation capture techniques [2,3]. These methods, as well as related ones using multicolor PSF engineering [32], may be used generally in future explorations of the detailed motions in chromatin which employ additional labels and biological perturbations to examine binding partners or other modulators of dynamical state.

8. Precision estimation

In this section we quantify the precision to which the magnitude of the 3D distance between the two loci, which we denote as R, can be determined. The overall error in determining R consists of two error sources: 1. Localization precision per channel, and 2. Channel-registration precision.

8.1 Localization precision

Localization precision per channel was estimated experimentally, using the following method: Using the same experimental conditions as in the locus tracking experiment, a yeast cell (KWY4067) was imaged continuously: 30 ms frames over 50 frames (total time: 1.5 s), and each frame was localized. This was repeated in both color channels.

The motion of each locus is assumed to be small during the acquisition time, and therefore a low-order (4^th) polynomial fit is performed on the trajectory in each axis, and subtracted from the data. All fluctuations after this subtraction are interpreted as localization error, and hence the standard deviation is used as the estimate of localization precision.

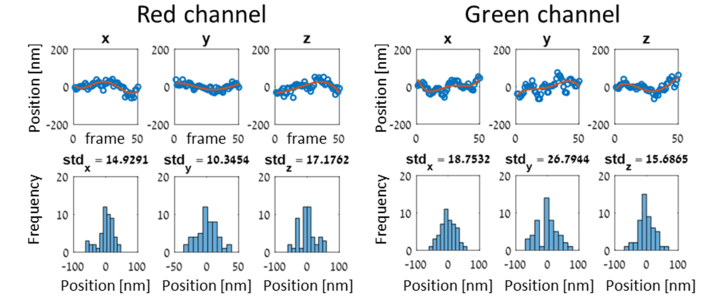
This procedure was repeated in both channels, and example traces are shown in Fig. 6. Three different cells were used in the red channel and two different cells in the green channel. The mean precisions obtained in the two channels are: $\Delta r_{re{d}_{loc}}=$ (26, 18, 22) nm and $\Delta r_{gree{n}_{loc}}=$(18, 33, 19) nm.

Fig. 6.

Localization precision estimates per channel. Two example cells are shown - one in each color channel. Localization traces are shown in the top panel, along with low-order polynomial fits in red. The bottom panel shows the localization histograms after subtracting the polynomial fits.

8.2 Registration precision

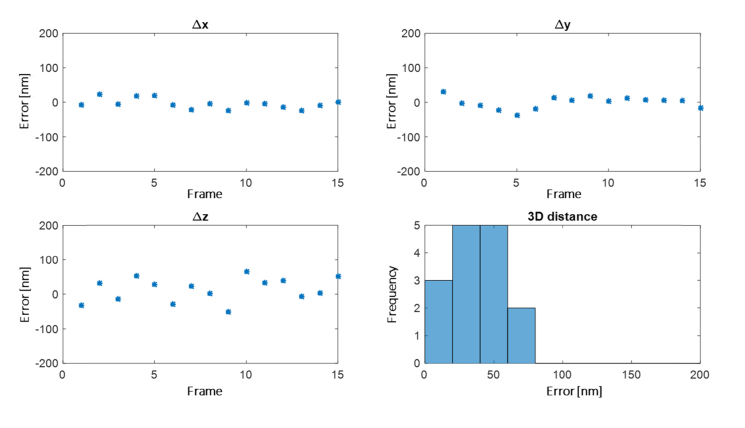
Registration precision is determined experimentally by the following method. A static fluorescent microsphere positioned ~2 µm above the coverslip, embedded in agarose, was imaged in both channels, while axially scanning the objective over a range of 3.75 µm, and co-localized using our affine registration procedure explained earlier. We used a bead embedded in agarose rather than on the surface of the coverslip in order to account for the effect of refractive index mismatch, to some extent, on our localization and registration methods. Differences in x,y,z between the information from the two channels were plotted vs. time, and the standard deviations of those is taken as precision. Figure 7 shows the measured errors. The localization precision (x,y,z), obtained by the standard deviation of those errors is (15,18,35) nm.

Fig. 7.

Experimental determination of registration error. A fluorescent bead embedded in agarose (~2 µm deep) is scanned axially over a 3.75 µm range, imaged in both color channels and co-localized using our depth dependent affine registration procedure. The resulting localization errors in x,y,z and a 3D error histogram are shown.

8.3 Overall inter-locus distance precision

The magnitude of the 3D distance vector between the two loci is given by:

$$R=\sqrt{{\left(x_{green}-x_{red}\right)}^2+{\left(y_{green}-y_{red}\right)}^2+{\left(z_{green}-z_{red}\right)}^2},$$ (6)

where x,y,z denote the positions of each locus. The error in estimating x,y,z is determined by combining the localization precision in each channel with the registration precision.

$$\begin{array}{l}x=x_{green}-x_{red}={\hat{x}}_{green}-{\hat{x}}_{red}+\text{Δ}{x}_{green}+\text{Δ}{x}_{red}+\text{Δ}{x}_{reg}\\ y=y_{green}-y_{red}={\hat{y}}_{green}-{\hat{y}}_{red}+\text{Δ}{y}_{green}+\text{Δ}{y}_{red}+\text{Δ}{y}_{reg}\\ z=z_{green}-z_{red}={\hat{z}}_{green}-{\hat{z}}_{red}+\text{Δ}{z}_{green}+\text{Δ}{z}_{red}+\text{Δ}{z}_{reg}\end{array}$$ (7)

Here for simplicity we denote by (x,y,z) the measured inter-locus distance in each axis, where $\hat{x}$ denotes the true position, $\text{Δ}{x}_{green}$ and $\text{Δ}{x}_{red}$ denote the error in determining x for green and red, respectively, and $\text{Δ}{x}_{reg}$ denotes the error contributed by channel registration. The other axes (y,z) are denoted equivalently.

The error in estimating x is: $\text{Δ}x=\sqrt{{\left(\text{Δ}{x}_{green}\right)}^2+{\left(\text{Δ}{x}_{red}\right)}^2+{\left(\text{Δ}{x}_{reg}\right)}^2}$, and similarly for y,z. These quantities, obtained from our precision measurements described above, are: $\text{(Δ}x,\text{Δ}y,\text{Δ}z)=$(35, 42, 45) nm. Finally, the error in determining $R$(Defined as $R=\sqrt{x^2+{\mathrm{y}}^2+{\mathrm{z}}^2}$), can be approximated using propagation of error [33] assuming the errors are uncorrelated. Specifically:

$$\begin{array}{l}\Delta (R^2)=\sqrt{(\Delta {(x^2)}^2+\Delta {(y^2)}^2+\Delta {(z^2)}^2)}=2\sqrt{{(x\Delta x)}^2+{(y\Delta y)}^2+{(z\Delta z)}^2)}\\ \Delta (R^2)=\Delta (R\cdot R)\approx 2R\Delta R\end{array}$$ (8)

Leading to:

$$\Delta R\approx 1/R\sqrt{{(x\Delta x)}^2+{(y\Delta y)}^2+{(z\Delta y)}^2}.$$ (9)

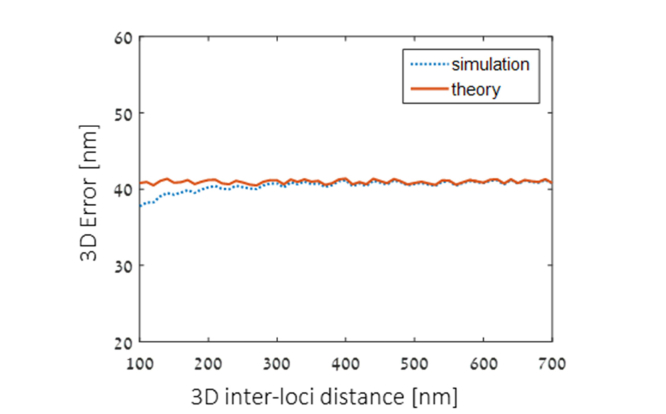
Note that the magnitude of the error depends to some extent on the distance itself. To quantify and validate the error approximation we simulate random inter-locus distances over the relevant distance-ranges in our experiment (~100-700 nm): For each distance value, a pair of random locus positions are chosen. For each position, the “measured” position is simulated by adding localization error with our experimental error distribution (35, 42, 45 nm – standard deviation in x,y,z), and this is repeated 10⁶ times. The precision per distance value (R) is then defined as the standard deviation of the obtained “measured” distances, since all of the ground-truth simulation instances per distance are defined in the simulation to be identical.

The result of the simulation is shown in Fig. 8, compared with the theoretical calculation using Eq. (9). The resulting inter-distance co-localization precision (standard deviation) is ~38-42 nm, and the numerical error calculation is a good fit with the theoretical approximation, with some improvement with increasing inter-locus distances.

Fig. 8.

Numerical simulation of inter-locus distance precision.

Another effect to be considered when analyzing localization precision is the effect of locus motion during acquisition time. Our numerical simulations, based on previously reported diffusion characteristics of yeast loci [18] suggest that the effect of this diffusion on the deviation of the reported locus position from a static locus is minimal (within ~1 nm). Nevertheless, during an acquisition time of 30 ms, the locus diffuses under fractional Brownian motion. Such high-frequency motion is not measured by our setup, but our simulations indicate that high-frequency distances exhibit a wider distance distribution by ~10 nm (std).

9. Sample preparation

Cells were grown semi-aerobically in vials covered with aluminum foil at 30°C on a rotary shaker for 24-36 h in a synthetic drop-out medium comprising 6.7 g/l yeast nitrogen base (YNB, BD Difco), 0.74 g/l complete supplementary mixture without tryptophan (CSM-Trp, MP Biomedicals, LLC), and 2 g/l raffinose (Fisher Scientific). The cells were then diluted between 1:500 and 1:2000 in medium as described above but where raffinose was replaced by either 2 g/l dextrose (BD Difco) or 2 g/l galactose (Sigma-Aldrich) as indicated, and the cells were allowed to grow for at least 12 h in this new culture medium. Cells were harvested at an OD₆₀₀ of 0.4-0.8 by centrifugation at 15000 g for 2 min, and subsequently concentrated by a factor of 50 by removal of supernatant. Concentrated cell solution was added to a pad comprising 1.5% (w/w) agarose (Invitrogen) in the same culture medium as the cell solution, and the pad was inverted onto a plasma-etched coverslip spun coat with a 1% (w/v) polyvinyl alcohol (PVA, Sigma) layer containing orange fluorescent microspheres (F8800, Invitrogen). The cells were imaged within 40 min from addition to the agarose pad. (Table 1)

Table 1. Yeast strains used in this study. Both KWY strains listed are derived from S288c and are of the BY varieties BY4742 (MATα his3Δ1 leu2Δ0 lys2Δ0 ura3Δ0) and BY4741 (MATa his3Δ1 leu2Δ0 met15Δ0 ura3Δ0), respectively [34].

Strain #	Genotype	Source
KWY5028	MATα POA1:TetO112:URA3 his3::GFP-LacI;TetR-3xmCherry;HIS3 YBR016W:LacO256;LEU2	This study
KWY4067	MATa POA1:TetO112:URA3 his3::GFP-LacI;TetR-3xmCherry;HIS3 YPK3:LacO256;LEU2	This study

10. Phase mask fabrication

The transmissive phase masks were fabricated using standard photolithography methods at the Stanford Nanofabrication Facility. First, 4-inch amorphous quartz wafers (~475 µm in thickness, WRS Materials) were cleaned in a chemical bath of Piranha solution (90% sulfuric acid, 10% hydrogen peroxide) at 70°C for 20 min. Next, the wafers were rinsed with clean water in an automatic dump rinser and a spin/rinse dryer. Then, the wafers were dehydrated at 150°C before being primed with hexamethyldisilazane (HDMS) at 70°C for 20 min in a Yield Engineering Systems (YES) oven. After the priming step, the wafers were spin-coated with a 1.6 µm thick layer of Shipley 3612 positive photoresist with 5-mm edge bead removal by using a Silicon Valley Group (SVG) resist coat system. The wafers were then pre-baked on a hot plate at 90°C for 120 seconds to drive off excess solvent. The photoresist film was patterned by exposing it to ultraviolet (UV) illumination with a KarlSuss MA-6 aligner for 1.6 seconds. The patterns on the binary masks used in this step were designed by converting the tetrapod phase mask into 3 different binary masks (3 bits = 8 equally spaced levels) with diameters of 2.7 mm.

The binary mask patterns were printed by a vendor. After exposure, the wafers were baked on a hotplate at 110°C for 90 seconds to set the photoresist. The positive photoresist in the UV-exposed regions were then removed by using a SVG developer. Next, the wafers were placed in a 90°C oven for 20 min to drive off moisture and harden the photoresist. Finally, the quartz wafers were etched in an Applied Materials Precision 5000 Etcher with the magnetically-enhanced reactive ion etch (MERIE) system. The durations of the etching period were calibrated and adjusted for each of the three etch steps. After the etch step, the photoresist left on the wafers was stripped with a Gasonics aura plasma asher. To further ensure that the photoresist was removed, the wafers were placed in a chemical bath of PRS-3000 at 60°C for 20 min. The wafers were then rinsed with clean water in an automatic dump rinser and a spin/rinse dryer. After the photoresist was stripped, the surface profiles of the quartz wafers were characterized with a Sensofar S Neox 3D optical profiler. This tool uses white-light vertical scanning interferometry to measure the step heights. After confirming the step heights, the entire process is repeated again starting at the HDMS priming step until all three etch steps were completed with the three different binary masks.

Funding

This work was supported in part by the National Institute of General Medical Sciences Grant No. R35GM118067 (to W.E.M.), by the National Institute of Biomedical Imaging and Bioengineering Grant No. U01EB021237 (to W.E.M.) and by the Swiss National Science Foundation Grant No. SNF159731 (to K.W.). A.-K.G. acknowledges partial financial support from the Swedish Research Council (2016-00130), and from The Foundation BLANCEFLOR Boncompagni-Ludovisi, née Bildt. Y.S. is supported in part by a Career Advancement Chairship from the Technion. M.Y.L. is supported by a National Science Scholarship (PhD) from A*STAR, Singapore.

Disclosures

The authors declare that there are no conflicts of interest related to this article.