Abstract
Pore volume is one of the main properties for the characterization of microporous crystals. It is experimentally measurable, and it can also be obtained from the refined unit cell by a number of computational techniques. In this work, we assess the accuracy and the discrepancies between the different computational methods which are commonly used for this purpose, i.e, geometric, helium, and probe center pore volumes, by studying a database of more than 5000 frameworks. We developed a new technique to fully characterize the internal void of a microporous material and to compute the probe-accessible and -occupiable pore volume. We show that, unlike the other definitions of pore volume, the occupiable pore volume can be directly related to the experimentally measured pore volumes from nitrogen isotherms.
Introduction
The internal void volume is an important characteristic of microporous materials, as it will determine their permeability to guest molecules, the adsorption capacity, and many other properties that can be engineered for the industrial applications that involve the use of these material, such as gas separation,1 gas storage,2 catalysis,3 or drug delivery.4 The field of microporous materials used to be dominated by zeolites, but recently, studies on new classes of microporous materials have been published. Examples include metal organic frameworks (MOFs),5 covalent organic frameworks (COFs),6 zeolitic imidazolate frameworks (ZIFs),7 porous polymer networks (PPNs),8 etc. For each of these classes, a large number of different materials can be obtained by combining different ligands and nodes, leading to millions of frameworks, each with different topologies, pore shapes, and chemistries. For example, at present, over 10000 MOFs and related porous materials have been synthesized,9 and large databases of computationally predicted structures are rapidly expanding.10−12 All the main applications for porous materials involve the adsorption of guest molecules in the pores. For this reason, it is of critical importance to correctly characterize the pore volumes of these materials as this is the first, and often the only, step to characterize a material.
The internal void volume of a porous material can be determined computationally from the crystal structure.13,14 This theoretical value of the pore volume can be compared with the experimental pore volume derived, for example, from the nitrogen uptake at low temperature.15 The comparison of the two values can give some insight into the characteristics of the synthesized crystal. For example, if the experimentally measured void volume is smaller than the computed one, this can be symptomatic of an incomplete desolvation (solvent molecules still trapped inside the pore), limited permeability at the surface, or defects in the crystal. In addition, deviations of the theoretical pore volume from the experimental one can also indicate that the synthesized material is a poor representation of the ideal crystal structure.
In this paper, we review a number of different methods employed to compute the void fraction.13,14,16−18 We show that, because of the different assumptions, each method computes a (slightly) different portion of the volume. For some particular cases, these differences can be large and, more importantly, the theoretical pore volume cannot be compared with the experimental pore volume. One of the reasons for these differences is that the definition of pore volume depends on the type of probe that is used to compute it. To address this issue, we introduce the “probe-accessible and -occupiable volume”. It represents the internal free space of the material where a spherical probe can have access and that it can occupy. We will highlight why this measurement can be meaningfully compared with experimental data.
To illustrate the importance of this concept of probe-occupiable volume, we introduce a simple but representative model of a microporous material to test our algorithm. Then we investigate the discrepancies in the values of the volume as computed by different methods for a set of more than 5000 three-dimensional MOFs from the Cambridge Structure Database (as refined in the CoRE MOF database19). Finally, we demonstrate some of the practical consequences by considering a sample of 10 structures, for which we can directly compare the computed pore volume with available experimental data.
Methods
Experimental Measurement of the Pore Volume
The internal free volume of a microporous material can be experimentally measured by determining the maximum loading of a gas in the pores of the material. Nitrogen is commonly used for this purpose because of its small size and because it weakly interacts with the framework. In addition, its normal boiling point is sufficiently low (77 K) that condensation at the exterior of the pores is avoided before the full saturation inside the pores. The pore volume is obtained under the assumption of validity of the Gurvich rule:20,21 the density of the saturated nitrogen in the pores is assumed equal to its liquid density regardless of the shape of the internal void network and, because of the weak interactions, regardless of the chemistry of the framework. The pore volume (vpore) and the void fraction (θ) are computed from
| 1 |
| 2 |
where vpore is commonly expressed in cubic centimeters per gram of crystal, nN2ads,satd is the specific amount of nitrogen adsorbed (g of nitrogen/g of crystal), and ρN2 and ρcryst are the densities of the liquid nitrogen (0.808 g/cmliq3) and of the material, respectively. The commonly used protocol to determine the pore volume involves measuring the nitrogen uptake just before it starts to condense outside the material, i.e., 0.9P/P0,21 with P0 being the saturation pressure of the probing gas (1 atm for pure N2). To compare this pore volume with a theoretical value obtained from the crystal structure, it is important to realize that this experimentally measured value does not consider all the small interstices between the atoms where the nitrogen molecule cannot fit, nor the nonaccessible pores, i.e., the pores connected only by channels too narrow for a nitrogen molecule to enter.
Computational Methods To Assess the Pore Volume from the Unit Cell
To compute the pore volume of a microporous crystal from the knowledge of the atomic structure of the unit cell, there are a number of different methods that are currently employed.13,14,16−18 Each one computes slightly different portions of the full internal volume, as shown in Figure 1.
Figure 1.
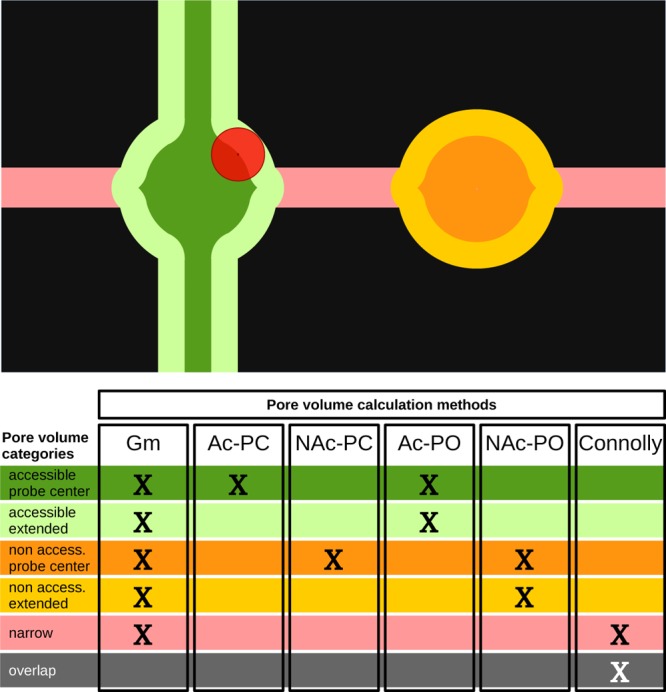
Qualitative two-dimensional model of the unit cell of a microporous material, permeable to a spherical probe (red). Each color corresponds to a different category of volume. In the table, the color coding is explained and a summary of which portions of the volume are considered for each method is given: geometric pore volume (Gm), accessible and nonaccessible probe center pore volume (Ac-PC, NAc-PC), accessible and nonaccessible probe-occupiable pore volume (Ac-PO, NAc-PO), and solvent-free Connolly volume.
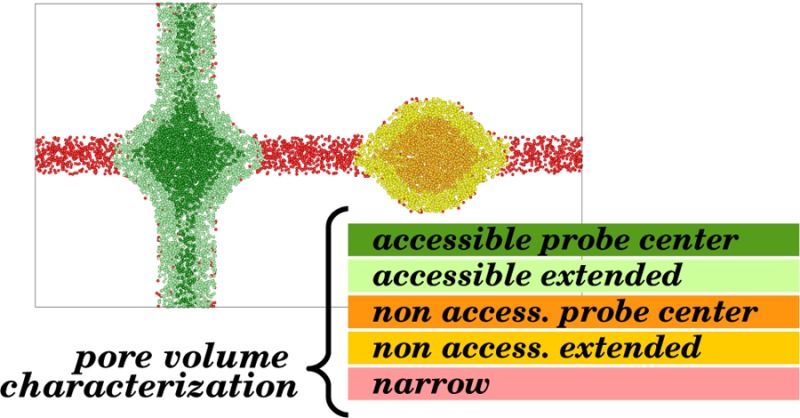
Here we propose a list of precise definitions to distinguish the volume computed with each method. For all these definitions, the pore volume can be further characterized either as accessible (Ac, part of an accessible network) or as nonaccessible (NAc, isolated pocket).
(1) Geometric pore volume (Gm). The Gm is defined as all the volume of the unit cell which is not overlapping with the atoms of the crystal. In Figure 1, this is the nonblack area.
(2) Probe center pore volume (PC). The PC is defined as the volume that the center of a spherical probe can occupy. In Figure 1, this is the sum of the dark green area (for pores that are accessible from the outside) and dark orange area (for pores that are nonaccessible from the outside).
(3) Helium pore volume (He). In the definition of the PC volume, we assume hard-sphere interactions between the probe atoms and the atoms of the pore. In the definition of the helium pore volume, these hard-core interactions are replaced by a more realistic intermolecular potential, which makes this volume dependent on the temperature assumed for the calculation. In Figure 1, the He volume is represented by the same colors as the PC volume (dark green and dark orange).
(4) Probe-occupiable pore volume (PO). This is a definition which we introduce here to ensure that the theoretical pore volume matches the pore volume obtained experimentally from the nitrogen isotherms. The experimental definition assumes that we can take the bulk density of the gas and compute the volume from the number of adsorbed gas molecules per unit volume. This volume, however, has no notion of atoms and should be defined as the entire volume enclosing all the adsorbed gas atoms. Therefore, in Figure 1, this volume has to include the light green (for accessible pores) and light orange (for nonaccessible pores) areas in addition to the dark green and dark orange areas. If we have a system with large pores, the difference between the Gm and PO volumes is small, but for micropores, however, this difference can be significant.
These pore volumes can be multiplied by the density of the material to be converted to the corresponding void fractions. The frameworks are assumed rigid, i.e., considering the atoms frozen in their crystallographic positions.
For the geometric pore volume (Gm), we assume that the atoms can be approximated as spheres with a conventional radius, depending on the atom type and which represents their electron cloud, i.e., the van der Waal (vdW) radius. The analytical calculation of the Gm pore volume needs to consider all the many-body overlaps between the atoms. Consequently, the most efficient solution to obtain the geometric pore volume is to perform a Monte Carlo test. A number of points, randomly displaced in the unit cell or taken on a 3D grid, are evaluated: if a point is overlapping with an atom, i.e., the distance of the point with that atom is less than its vdW radius, then a value of 0 is assigned to that point. A value of 1 is assigned otherwise. Therefore, the Gm void fraction θGm of the crystal from N sample points is obtained as
| 3 |
Consequently, the geometric pore volume can be obtained by dividing the void fraction by the density of the framework (eq 2). In this measurement, the volume inside the large pores is summed together with all the small interstices in the framework, which are too narrow to be effectively occupied by a guest molecule. Hence, the value computed in this way will always be an upper bound for the volume that a probe can effectively access.
The probe center pore volume (PC), often named simply “pore volume”,14,17 considers the shape of the probe used for the measurement, conventionally spheres with a radius of 1.32 Å for helium and 1.86 Å for nitrogen.19,22 In this definition, it is important to recall that even the nitrogen molecule is treated as a spherical probe, as shown in Figure 2.
Figure 2.
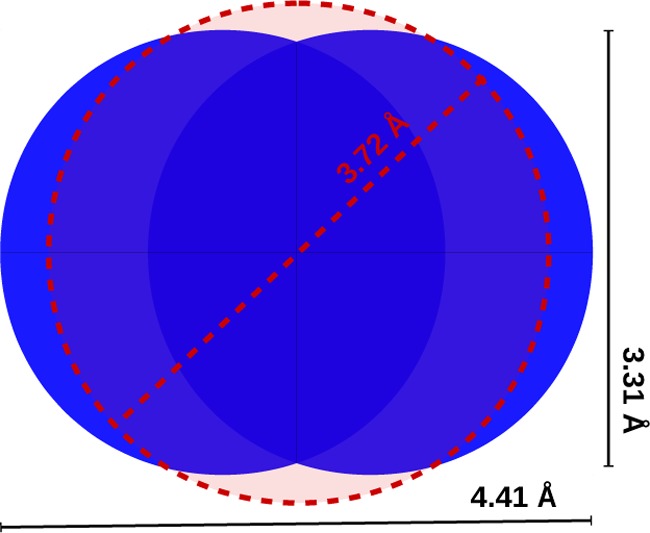
N2 spherical model of radius 1.86 Å (3.72 Å diameter) compared to the van der Waals representation of the same molecule (using the Lennard-Jones σ value and the N–N distance of the TraPPE model).23
For this calculation, the same Monte Carlo test is performed, but this time the radius of the framework’s atoms is taken as the sum of the atomic radius plus the probe radius. The obtained void fraction then represents the portion of the volume which is occupiable by the centers of the probe (Figure 3).
Figure 3.
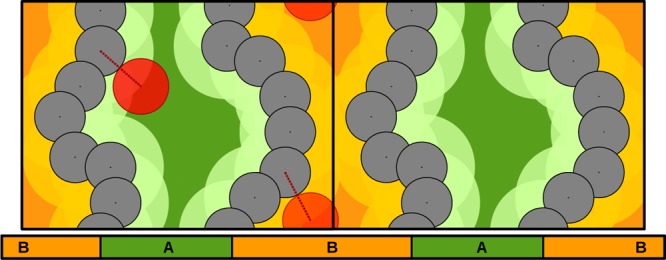
Two-dimensional example of the probe center pore volume calculation. The periodic unit cell is duplicated in the x directon. The radius of the framework’s atoms (black) is expanded by the radius of the red probe (light green and light orange). The remaining area is what we define as the probe center pore volume (dark green and dark orange). The framework is composed by two channels: channel A (green), which is accessible, and channel B, which is nonaccessible (orange). Channel B is too narrow for the probe to pass from one side to the other and can be referred to as an isolated pocket.
It is also important to note that the PC pore volume for a probe of zero radius corresponds to the Gm pore volume.
A third solution is to compute the helium pore volume (He). Similarly to the Gm pore volume, a collection of sampling points are considered, but instead of assigning a value of 0 or 1 depending on the overlap with atoms, this time the Boltzmann factor (BF), related to the insertion of a helium atom, is computed:
| 4 |
Eint is the energy of interaction of the helium atom with the atoms of the framework, as computed using, for example, the Lennard-Jones potential (see the Supporting Information). Similarly to the previous cases, the void fraction θHe (and therefore the pore volume) is computed as the average over all the sample points:
| 5 |
It is worth noting that this measurement is influenced by the force field and the temperature used. It is therefore important to use a consistent choice to compare different sets of results.17 We need to stress that the He void fraction, in the way it is measured, does not correspond to the amount of helium that can saturate in the pores. The physical meaning of the He void fraction is linked to the probability of a single helium atom to be adsorbed in the framework at a certain temperature, which is chosen to be 298 K by convention.17
At this point, it is important to recall that none of the previously summarized methods to compute the pore volume exactly match with the pore volume we obtain from the nitrogen isotherms. To arrive at a definition of pore volume that can be directly compared to experiments, we introduce the probe-occupiable pore volume (PO), and we propose an algorithm to compute it. We use the term “occupiable” to define the portion of the space that can be spanned by the probe, which should not be confused with the term “accessible” (Ac), which defines the pores where the probe can have access.
Accessible versus Nonaccessible Channels
In these Monte Carlo simulations, we are probing a number of points within the unit cell to measure the void fraction (and therefore the pore volume) of the bulk material. However, it is also important to know if the detected free space is accessible from the outside, i.e., if a cavity forms a multidimensional network where a guest molecule can enter at the solid/gas interface and diffuse. The same analysis allows detection of whether a solvent molecule is able to exit the pores and a synthesized crystal can be effectively desolvated.
This concept of accessibility is obviously related to the size of the molecule, represented as a spherical probe, which we are interested to evaluate. Once we compute the PC volume, we can further categorize this internal space as accessible (Ac-PC) or nonaccessible (NAc-PC) by considering whether it composes a multidimensional network along the periodic boundaries. This is illustrated in the two-dimensional example of Figure 3: the central channel (A) is accessible to the probe, while the other one (B) is not, because the PC pore volume does not form a continuous path. The accessibility test can be performed by doing a percolation analysis along the edges obtained from the Voronoi decomposition24 or analyzing a grid of points.25,26
The same concept can be applied to compute the Ac-PO (as presented in the next section) or the Ac-He pore volume. In the second case, one needs to first assume an energy cutoff for the helium–framework interactions, which defines the regions that are diffusively inaccessible on an experimental time scale (e.g., 15 kbT). Then one must consider the regions of the volumes where the interaction energy is lower than the cutoff to perform a percolation analysis.27 For what concerns the Gm volume, the calculation considers a dimensionless probe, and therefore, we do not have any practical interest in analyzing its accessibility.
Algorithm To Compute the Occupiable Pore Volume
In this section, we propose an algorithm to obtain the experimental pore volume from our definition of the accessible and occupiable volume (Ac-PO) and in general to fully characterize the internal volume of a microporous material.
(1) Let us consider a set of N sample points, randomly selected within the unit cell.
(2) For each point, we compute its distance to the framework’s atoms: if this distance is smaller than the atomic radius, the sample point is categorized as ”overlap”; if it is larger than the sum of the atomic and probe radii, it is categorized as PC. For each point assigned to the PC volume, we compute the distance δ between the point and the surface of the PC volume, defined as
| 6 |
with d being the distance to the closest atom, rprobe the radius of the spherical probe, and ratom the vdW radius of the closest atoms of the framework (Figure 4). In addition, we use a percolation algorithm14 to further classify the sample point as Ac-PC or NAc-PC.
Figure 4.
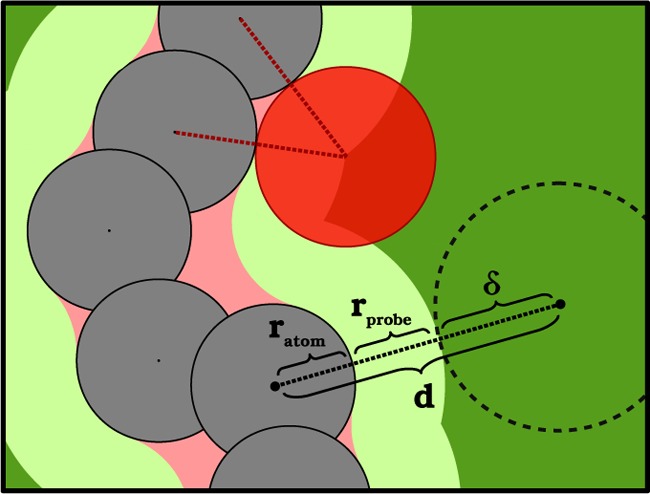
Calculation of δ from eq 6 shown in a two-dimensional model. The color coding is consistent with that reported in Figure 1: the atoms (which correspond to the overlap volume) in black, the probe in red, the accessible probe center volume in dark green, the accessible extended volume in light green, and the narrow volume in pink.
(3) For each sample point left, we compute the distance for all the Ac-PC marked points, and if one of these distances is closer to the Ac-PC surface than the probe radius, or
| 7 |
the uncategorized point will be considered as part of the now defined “accessible extended volume” (light green in Figure 1). The inclusion of δ in eq 7 improves the speed and the accuracy of the algorithm (at the same number of sample points), because in this way also the internal points of the Ac-PC volume give some information on the position of its surface.
(4) The same test is performed for the NAc-PC points: in the case of success, uncategorized points will be marked as belonging to the “nonaccessible extended volume” (light orange in Figure 1).
(5) If none of the previous tests are true, the sample point belongs to what we define as the “narrow volume” (pink in Figure 1).
It follows that the PO volume is given by the summation of the probe center and the extended volume. Figure 1 presents all the different categories of volume with color coding for an illustrative two-dimensional model.
With these definitions, we marked as “narrow” the entire volume that cannot be touched by the probe because it is hindered by the framework. This can be the case for a narrow channel (pink, Figure 1) or the small interstices between the atoms of the crystal (pink, Figure 4). Moreover, the overlap volume added to the narrow volume gives what is commonly defined in biochemistry as the ”solvent-free volume” or ”Connolly” volume18 (Figure 1).
Computational versus Experimental Pore Volumes
Now that we have fully characterized the pore volume inside a microporous framework, we can couple the computational results with experimental measurements. Under the assumption of the Gurvich rule, the experimental 77 K nitrogen’s pore volume can be compared with the Ac-PO pore volume computed from the unit cell, using a spherical N2 probe. The nitrogen’s NAc-PO pore volume could also be measured experimentally with smaller probing molecules, e.g., helium,28 or with positron annihilation lifetime spectroscopy (PALS).29 The measurements with these techniques are not as frequently used. An alternative to nitrogen is argon as the probing molecule at 87 K. Despite the higher cost of Ar, it can be preferred due to the smaller size and the enhanced diffusion rate at 10 K higher temperature.30 By selecting for the calculations a probe radius that corresponds to the gas used in the experiments, we are able to directly compare our theoretical calculations with the experimental data.
We stress once more that for these methods the thermal vibrations of the atomic positions are not taken into account, and for the Ac-PO calculation, we use hard-sphere potentials for which the effective volume does not depend on the temperature. These assumptions hold for the experimental conditions (i.e., 77 K for nitrogen adsorption). Moreover, we do assume that the crystal structure does not change upon adsorption of nitrogen (e.g., pore swelling or ligand rotation). For cases where the diameter of the channel is very similar to the diameter of the probe, further investigations are needed.31 A small distortion of the framework or a different choice of the parameters can drastically change the amount of Ac and NAc volume detected, an effect which has similarly been shown in the context of noble gas uptake.32
Software and Parameters
In this section, we illustrate how the different pore volumes are determined in the different software packages that compute pore volumes.
The Poreblazer package13 computes the Gm and He pore volumes using sample points lying on a grid with a 0.2 Å bin size.
The Zeo++ package14 gives the Gm and PC volumes, the first one being obtained by setting the radius of the spherical probe to 0. In this software, the number of sample points specified in the input is randomly displaced in the unit cell.
The PLATON package16 computes the PO volume using a grid of points. Points belonging to the PC pore volume are first detected, and then their neighbor points are considered. Contrary to Zeo++, this software does not distinguish between Ac and NAc volumes. Also, one should pay attention to the terminology: in this software, the authors define as “accessible” volume what here we define as “occupiable” volume.
The Raspa package33 (which is mainly used for Monte Carlo and molecular dynamics simulations) provides the He pore volume considering a specified number of sample points in random positions of the unit cell.
The algorithm we proposed in this work to compute the Ac-PO volume and fully characterize the internal pore volume has been implemented as an extension of Zeo++.14
In our calculations, the He volume is computed at 298 K (25 °C), which is the typical temperature condition of most previous calculations.17 We used the Lennard-Jones potential to describe the dispersion interactions, applying the Lorentz–Berthelod mixing rules and considering a cutoff distance of 12.8 Å; beyond that, the potential is set to 0. Parameters for the framework and for helium were taken from the universal force field (UFF)34 and from Hirschfelder,35 respectively. Concerning the ”hard sphere” calculations (Gm, PC, and PO) and for all the software packages (Poreblazer, Zeo++, and PLATON), the Lennard-Jones σ values from UFF were used as the diameter of the framework atoms, to be consistent with the He calculations. A kinetic radius of 1.86 Å was considered for nitrogen.22
Results and Discussion
3D Model for the Full Characterization of the Pore Volume
To illustrate the difference between the various approaches, we applied our algorithm on a three-dimensional model which is able to represent qualitatively the characteristics of a microporous material, inspired by the two-dimensional example reported in Figure 1. The model has one accessible pore and one nonaccessible pore, with a narrow channel (i.e., with a diameter smaller than the probe’s diameter) connecting the two. The model is built with a large number of spheres lying on a grid to represent the framework, leaving free space that corresponds to pores and channels (Figure 5, top).
Figure 5.
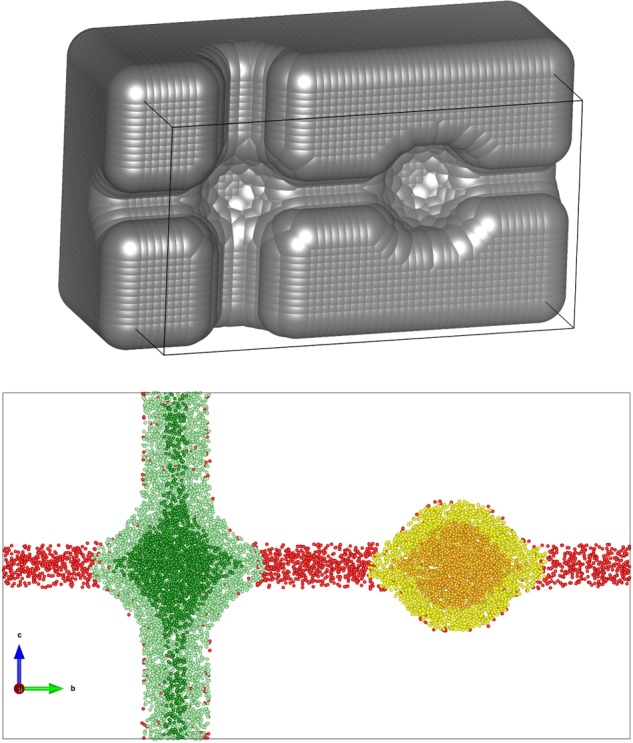
Section of the 3D model (top) and analysis of the pore volume using 500000 points (bottom). For the color coding, refer to Figure 1; overlap points were omitted. The probe has a diameter of 2 Å. The diameters of the accessible and narrow channels are 3 and 1.5 Å, respectively.
In this simplified model of a porous framework, we can really distinguish between all the different categories of internal volume listed in Figure 1: the result from the analysis with 500000 sample points is shown in Figure 5 (bottom) using the same color coding for the points.
To assess the convergence of the method, we run our algorithm for different numbers of sample points. From the results shown in Figure 6, it is immediately evident how the conventionally computed void fraction based on the Ac-PC method is considerably smaller than the void faction computed with the Ac-PO method. The Ac-PO calculation is converged to 0.1% of the void fraction with 10 points per cubic angstrom. Within our algorithm, to measure the PO void fraction, we need first to accurately locate the surface of the PC volume and expand this volume by the length of the probe radius. To minimize the error associated with a poorly sampled PC surface, one should increase the number of sample points, albeit with a significant computational cost. Nevertheless, in real frameworks, we can consider it reasonable to use a convergence within 1% of the void fraction to compare the calculated values with experimental data.
Figure 6.
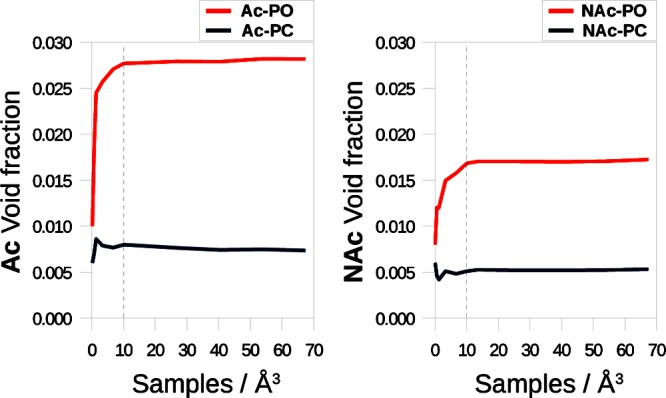
Assessment of the Ac-PC, NAc-PC, Ac-PO, and NAc-PO void fractions in the three-dimentional model presented in Figure 5 for an increasing number of sample points per cubic angstrom. Numerical data are provided in Table S2 (Supporting Information).
Comparison of Different Pore Volume Definitions with Experimental Data for HKUST-1
The triclinic unit cell structure of HKUST-1 (CSD code FIQCEN) was considered to compute the void fraction with the different methods. Water solvent molecules were removed from the original deposited structure.19 No NAc volume was detected. The resulting void fraction and computational time are reported as a function of the number of samples per cubic angstrom that were used for the calculation (Table 1).
Table 1. Assessment of the Ac-PC and Ac-PO Void Fractions in the FIQCEN Structure (HKUST-1 with a Triclinic Unit Cell) for an Increasing Number N of Sample Pointsa.
| Ac-PC | Ac-PO | N | N/Å3 | CPU time (s) |
|---|---|---|---|---|
| 0.240 | 0.606 | 4571 | 1 | 2 |
| 0.250 | 0.649 | 22851 | 5 | 9 |
| 0.250 | 0.656 | 45702 | 10 | 28 |
| 0.249 | 0.658 | 68553 | 15 | 55 |
| 0.250 | 0.660 | 91404 | 20 | 90 |
| 0.248 | 0.663 | 228510 | 50 | 475 |
| 0.248 | 0.664 | 342765 | 75 | 998 |
| 0.249 | 0.665 | 457020 | 100 | 1702 |
The CPU time refers to a 3.60 GHz Intel processor: for this framework the time needed for the calculation is proportional to ∼N1.5.
We use as the experimental value for the void fraction 0.678,21 which is the highest value we could find in the literature for the desolvated crystal. Lower values were reported in the literature, from 0.590 to 0.660.36−40 The computed Ac-PO void fraction converges to a value which is close to the experimental result, while the Ac-PC void fraction is significantly smaller. The PO void fraction computed with the CALC_SOLV routine in PLATON is 0.654: this result was obtained in 165 s with a minimum grid spacing (0.14 Å). These settings give 365 samples per cubic angstrom, and it is the most accurate sampling that the program can manage. The Gm void fraction of 0.708 is similar to the Ac-PO value, meaning that the percentage of narrow volume is negligible. On the other hand, the He calculation gives a value of 0.764, which overestimates the experimental void fraction. It is surprising to note that using a different parametrization for the Lennard-Jones interactions, i.e., UFF’s34 instead of Hirschfelder’s35 parameters for helium, we obtain an He void fraction of 0.947, which disagrees with the experimental and Ac-PO values. This evidence motivated a deeper analysis of the physical and mathematical meaning of the He calculation.
Helium Void Fraction
The He calculation is very commonly used to compute the void fraction.41,42 As we demonstrated in the previous section, its value depends strongly on the force field parameters used to model the helium–framework interactions, and it can lie far off the experimental value. Therefore, we analyze the underlying mathematical reason for this variability. First, we study the case of a helium atom interacting with a carbon atom, using the Hirschfelder–UFF parameters to represent their interaction at different distances. The potential and the Boltzmann factor (BF) for different He–C distances are shown in Figure 7.
Figure 7.

One-dimensional representation of the Lennard-Jones potential and the associated Boltzmann factor as a function of the C–He distance (system shown on the top). The Boltzmann factor (blue solid line) function is compared to the factor associated with the occupiability of the space, i.e., 1, everywhere outside the carbon’s van der Waals radius (blue dashed line). In the bottom figure, the sensitivity of the Boltzmann factor to the arbitrary value of the temperature is investigated. Notice that doubling or halving the temperature corresponds to respectively halving or doubling the value of ε for the Lennard-Jones interaction.
We can now compare the He calculation to the Gm calculation (in this diatomic model, the Gm and Ac-PO volumes are equivalent). For the He calculation, the BF is the value assigned for every He–C distance, while, for the Gm calculation, we assign a value of 0 for a He–C distance inferior to the carbon’s radius (equivalent to half the Lennard-Jones’s σ for carbon) and a value of 1 elsewhere (see the dashed blue line in Figure 7). Therefore, the void fraction is the integration of these values over the entire volume considered. He and Gm coincide exactly in the case when the two integrals are equal, i.e., when there is a match between the cyan and purple areas in Figure 7. The BF depends on the set of parameters used and on the temperature assumed in the calculation. Indeed, the common choice of the temperature of 298 K is just a convention, and its variation can drastically affect the He calculation, as shown in Figure 7. Moreover, the He void fraction is not strictly restricted to be smaller than 1, since also the BF can take values larger than 1, especially for the framework’s atom with a large Lennard-Jones ε parameter. In UFF, for example, the ε values for aluminum, silicon, and phosphorus are ca. 5, 4, and 2.5 times the carbon’s value, which may give unrealistic contributions larger than 1 for part of the pores.
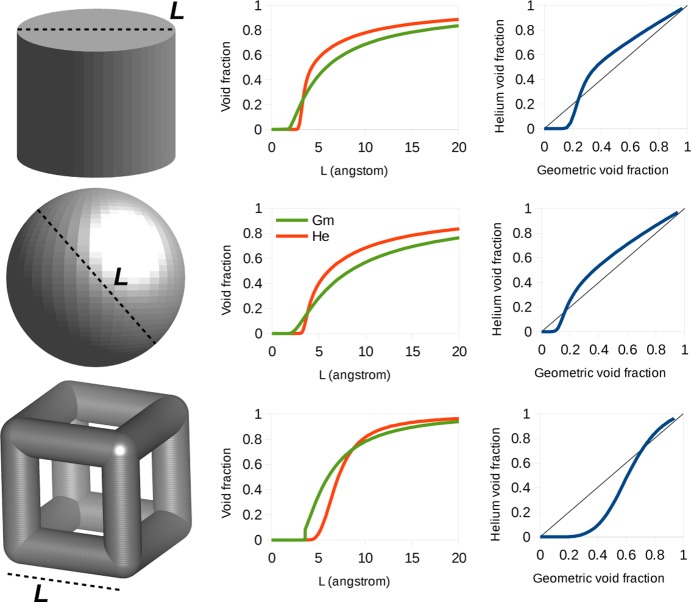
To see for which types of pores the Gm and He void fractions show the largest differences, we extended our analysis to cylindrical and spherical pores and a reticular structure. We modeled the framework with a smeared continuous distribution of carbon atoms. The details are reported in the Supporting Information. Figure 8 shows the comparison between the Gm and He void fractions in these models. We observe for all three pore shapes that the Gm void fraction is greater than the He void fraction for small pores, while for bigger pores the He void fraction becomes greater. This is due to the fact that for smaller pores the BF for helium is always less than 1, because of the unfavorable interaction between the particle and the framework. For bigger pores, the BF can assume values larger that 1, and in such cases, the He void fraction systematically overestimates the experimental void fraction. A similar trend for the He vs Gm curve is observed for the three types of pores in Figure 8, with the main difference being the value of the intersection with the bisector, which is therefore dependent on the geometry of the pore.
Figure 8.
Geometry of the pore for the different three-dimensional models: comparison of the Gm (green) and He (red) void fractions versus the characteristic length L of the pore and direct comparisons of the two values of the void fraction for pores with different dimensions.
The Ac-PO volume is expected to be similar to the Gm volume, with the notable difference that it collapses to 0 for small pores, i.e., for
| 8 |
CoRE MOF Screeening
Our model calculations show that the differences between the He and the Gm void fractions are not negligible and can be interesting to see how these model calculations compare with the void fractions for the experimental MOF structures. A set of 5109 MOF structures were investigated from the CoRE MOF database: 4764 frameworks were modified by the authors (solvent removal and other adjustments described in the paper),19 and the remaining 345 frameworks were downloaded directly from the Cambridge Structural Database,43 without any further manipulation. The results of computing the He and Gm void fractions for these structures are shown in Figure 9.
Figure 9.
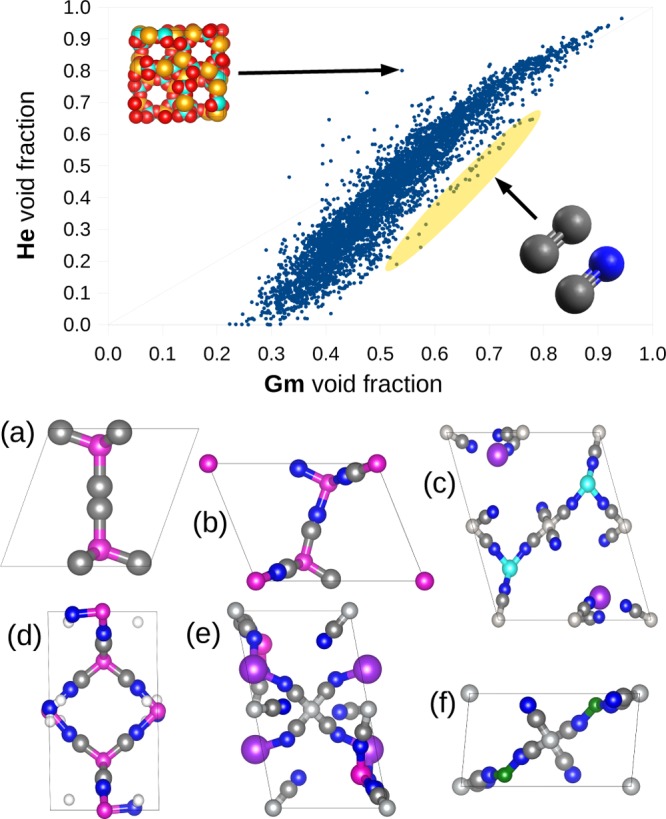
Comparison of the Gm and He void fractions for the materials from the CoRE MOF database.19 Some out-trend materials are highlighted. LOFZUB has a remarkably higher value for the He void fraction compared to the Gm void fraction (upper inset: Al, orange; P, cyan; O, red). Other structures show a high porosity combined with a systematic underestimation of the void fraction by the He calculation. These frameworks, characterized by C≡N- and C≡C-based ligands (C, gray; N, blue), are highlighted in yellow. Some of them are shown: PIYZAZ (a), KECRAL10 (b), YEQRER (c), YARYEV (d), YEQRER (e), EBEMEF (f).
For most materials, the trend is mostly similar to the reticular model presented in the previous section. One can notice that for many materials the void fraction computed using the He method is higher than the Gm void fraction, when the Gm method should compute an upper bound value for the void fraction. The most extreme example for this overestimation is the structure LOFZUB:44 this framework contains aluminum and phosphorus, which have a particularly high Lennard-Jones ε. On the other side, a few frameworks appear to have the opposite trend, showing a moderate Gm void fraction but a lower He void (highlighted in yellow in Figure 9). Interestingly, all of them have a similar chemistry; i.e., the ligands of these structures are based on C≡N and C≡C bonds. These kinds of ligands are particularly thin and simple, resulting in weaker dispersion forces, which explains the low He void fraction.
Using our algorithm, we computed the Ac-PO void fraction for all the frameworks considering a probe of 1.86 Å (N2) and using 100000 sample points. The results are compared with the Gm and He void fractions in Figure 10.
Figure 10.
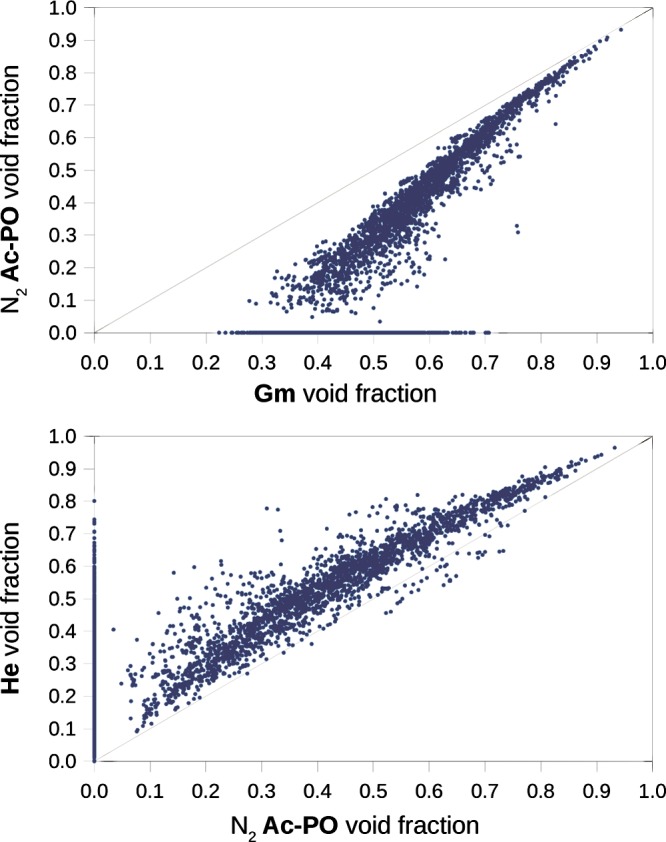
(Top) Gm void fraction compared with the Ac-PO void fraction for a 1.86 Å nitrogen probe. For the materials nonpermeable to the probe, the Ac-PO void fraction collapses to 0. (Bottom) Comparison of the He and Ac-PO void fractions.
As expected, the value of the Ac-PO void fraction is always smaller than that of the Gm void fraction. This behavior is more pronounced for very dense materials, where the atoms of the framework create many small interstices (narrow volume) that are excluded for the calculation of the Ac-PO void fraction. Also, for many structures, the void fraction collapses to 0, meaning that, under the assumption of a rigid framework, these crystals are completely impermeable to the probing sphere. The material labeled SETPEO is a prominent example: the 0.71 geometric void fraction of this material can be decomposed to a 7% narrow volume, with 64% of the volume nonaccessible to the nitrogen probe (the 29% remaining is the volume occupied by the atoms). For this material, we can expect, if not a complete impermeability, a slow diffusion of nitrogen inside the activated crystal. Moreover, methanol is used as the solvent for the synthesis, and given the size of methanol, we can expect the impossibility of a complete desolvation, as effectively reported.45
If we compare the He and nitrogen Ac-PO volume fractions, it is interesting to note the systematic overestimation of the pore volume which affects the He method. There are three reasons for this: the helium probe is smaller, the nonaccessible volume is not excluded, and, most important, it is possible for the BF to be higher than 1. The structures with the opposite trend, where the void fraction is underestimated by the He method, are again the ones characterized by C≡N and C≡C ligands (shown in Figure 9) .
Comparison with Experimental Data for 10 MOFs
We studied in detail 10 different MOFs (including HKUST-1) to obtain some insights into the practical consequences of the differences in pore volume that are computed by the different methods and their agreement with experimental data.21,46−54 All the frameworks investigated have accessible channels for nitrogen, and no NAc pore volume was detected. Figure 11 shows that the PO method leads to the best agreement among the different methods. These results emphasize that the value for the PC pore volume (sometimes simply defined as “pore volume”) leads to a significant underestimation of the experimental pore volume. Another consideration is that for these 10 structures the total Gm void fraction is close to the PO void fraction, meaning that in these samples the narrow volume is a negligible percentage of the Gm pore volume.
Figure 11.
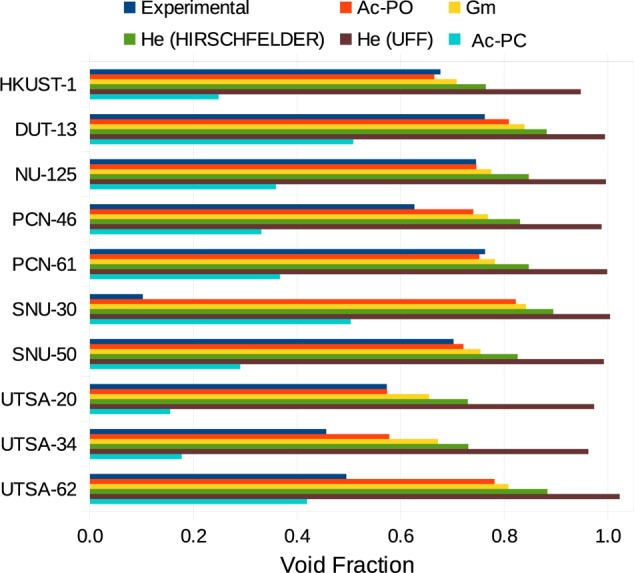
Void fraction as computed with the different methods shown and compared with experimental data. The structures were computationally desolvated as reported in the CoRE MOF database.19 A list with the references for the experimental values is provided in the Supporting Information.
The He void fraction is close to the experimental value if we use Hirschfelder’s Lennard-Jones parameters for helium, noticing however a systematic but relatively small overestimation. Nevertheless, the same calculation employing the He parameters from UFF shows a much larger overestimation of the void fraction, even with nonphysical values greater than 1 for SNU-30 and UTSA-62.
In four materials, the experimental volume is more than 10% lower than the computed value (PCN-46, SNU-30, UTSA-34, and UTSA-64). We attribute this difference to some incomplete desolvation or pore shrinking after the removal of the solvent. At this point, it is important to note that the computational pore volumes are based on structures from the CoRE MOF database in which solvent molecules are removed computationally, keeping the rest of the crystal structure unchanged.19 In some cases, this procedure is unrealistic, and the most evident example is SNU-30, where the computed void fraction is 8 times the measured value. The authors of its synthesis already reported a big discrepancy between the experimental and computed surface areas, which was attributed to the shrinking of the evacuated pores.
Conclusions
In the present work, we compared different methods that are used to compute the pore volume of a crystalline microporous material from its crystal structure. We show that these methods use different definitions of the pore volume, and we show that in particular for micropores these differences can be quite significant. These volumes are referred to in this work using a consistent nomenclature, i.e., the geometric (Gm), the helium (He), the probe center (PC), and the probe-occupiable (PO) methods. For the last two, it is meaningful to further identify the volume as accessible (Ac) or nonaccessible (NAc).
The main conclusion of this work is that the accessible probe-occupiable (Ac-PO) pore volume gives the closest representation of the experimentally measured pore volumes for all types of pores. The other methods show systematic deviations. The geometric (Gm) calculation leads to a value for the pore volume which is an upper limit for this quantity, while the probe center (PC) calculation considerably underestimates the experimental value. The helium (He) void fraction was shown to be very dependent on the parameters and on the reference temperature assumed for the calculation.
In addition, we have presented a novel algorithm to fully characterize the internal volume of a crystal and assess its Ac-PO pore volume. This extension is now implemented in the freely available Zeo++ code (www.zeoplusplus.org). The algorithm takes into account both the solvent accessibility and solvent occupability of the internal pore cavity, and therefore, its result can be meaningfully compared with the measurement of the pore volume, as obtained from the nitrogen uptake. The comparison between the experimental data and the Ac-PO void fraction allows detection of discrepancies due to low crystallinity, poor desolvation, and pore shrinking in the real material.
Acknowledgments
The research of D.O. and P.G.B. was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 666983, MaGic). S.B. was supported by the National Center of Competence in Research (NCCR), Materials’ Revolution: Computational Design and Discovery of Novel Materials (MARVEL), of the Swiss National Science Foundation (SNSF). M.W. was supported by the Center for Gas Separations Relevant to Clean Energy Technologies, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0001015 for development of the analytical models used to compare helium and geometric void fractions. M.H. was supported by the Center for Applied Mathematics for Energy Research Applications (CAMERA), funded by the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b01682.
Description of the 3D spherical, cylindrical, and reticular models, references of the experimental measurement for the 10 MOF structures, with CSD refcodes, Lennard-Jones parameters used for the atoms in this study (PDF)
Screening data for 5109 MOFs and the structures of the three-dimensional models are available at www.materialscloud.org/archive/2017.0005/v1/
The authors declare no competing financial interest.
Supplementary Material
References
- Li J.-R.; Kuppler R. J.; Zhou H.-C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. 10.1039/b802426j. [DOI] [PubMed] [Google Scholar]
- Morris R. E.; Wheatley P. S. Gas storage in nanoporous materials. Angew. Chem., Int. Ed. 2008, 47, 4966–4981. 10.1002/anie.200703934. [DOI] [PubMed] [Google Scholar]
- Corma A. From microporous to mesoporous molecular sieve materials and their use in catalysis. Chem. Rev. 1997, 97, 2373–2420. 10.1021/cr960406n. [DOI] [PubMed] [Google Scholar]
- Horcajada P.; Chalati T.; Serre C.; Gillet B.; Sebrie C.; Baati T.; Eubank J. F.; Heurtaux D.; Clayette P.; Kreuz C.; et al. Porous metal-organic-framework nanoscale carriers as a potential platform for drug delivery and imaging. Nat. Mater. 2010, 9, 172–178. 10.1038/nmat2608. [DOI] [PubMed] [Google Scholar]
- Long J. R.; Yaghi O. M. The pervasive chemistry of metal–organic frameworks. Chem. Soc. Rev. 2009, 38, 1213–1214. 10.1039/b903811f. [DOI] [PubMed] [Google Scholar]
- Feng X.; Ding X.; Jiang D. Covalent organic frameworks. Chem. Soc. Rev. 2012, 41, 6010–6022. 10.1039/c2cs35157a. [DOI] [PubMed] [Google Scholar]
- Park K. S.; Ni Z.; Côté A. P.; Choi J. Y.; Huang R.; Uribe-Romo F. J.; Chae H. K.; O’Keeffe M.; Yaghi O. M. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 10186–10191. 10.1073/pnas.0602439103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu W.; Yuan D.; Zhao D.; Schilling C. I.; Plietzsch O.; Muller T.; Bräse S.; Guenther J.; Blümel J.; Krishna R.; et al. Porous polymer networks: synthesis, porosity, and applications in gas storage/separation. Chem. Mater. 2010, 22, 5964–5972. 10.1021/cm1021068. [DOI] [Google Scholar]
- Furukawa H.; Cordova K. E.; O’Keeffe M.; Yaghi O. M. The chemistry and applications of metal-organic frameworks. Science 2013, 341, 1230444. 10.1126/science.1230444. [DOI] [PubMed] [Google Scholar]
- Wilmer C. E.; Leaf M.; Lee C. Y.; Farha O. K.; Hauser B. G.; Hupp J. T.; Snurr R. Q. Large-scale screening of hypothetical metal-organic frameworks. Nat. Chem. 2012, 4, 83–89. 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
- Martin R. L.; Simon C. M.; Smit B.; Haranczyk M. In silico design of porous polymer networks: high-throughput screening for methane storage materials. J. Am. Chem. Soc. 2014, 136, 5006–5022. 10.1021/ja4123939. [DOI] [PubMed] [Google Scholar]
- Martin R. L.; Simon C. M.; Medasani B.; Britt D. K.; Smit B.; Haranczyk M. In Silico Design of Three-Dimensional Porous Covalent Organic Frameworks via Known Synthesis Routes and Commercially Available Species. J. Phys. Chem. C 2014, 118, 23790–23802. 10.1021/jp507152j. [DOI] [Google Scholar]
- Sarkisov L.; Harrison A. Computational structure characterisation tools in application to ordered and disordered porous materials. Mol. Simul. 2011, 37, 1248–1257. 10.1080/08927022.2011.592832. [DOI] [Google Scholar]
- Willems T. F.; Rycroft C. H.; Kazi M.; Meza J. C.; Haranczyk M. Algorithms and tools for high-throughput geometry-based analysis of crystalline porous materials. Microporous Mesoporous Mater. 2012, 149, 134–141. 10.1016/j.micromeso.2011.08.020. [DOI] [Google Scholar]
- Sing K. The use of nitrogen adsorption for the characterisation of porous materials. Colloids Surf., A 2001, 187-188, 3–9. 10.1016/S0927-7757(01)00612-4. [DOI] [Google Scholar]
- Spek A. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. 10.1107/S0021889802022112. [DOI] [Google Scholar]
- Myers A.; Monson P. Adsorption in porous materials at high pressure: theory and experiment. Langmuir 2002, 18, 10261–10273. 10.1021/la026399h. [DOI] [Google Scholar]
- Connolly M. L. Computation of molecular volume. J. Am. Chem. Soc. 1985, 107, 1118–1124. 10.1021/ja00291a006. [DOI] [Google Scholar]
- Chung Y. G.; Camp J.; Haranczyk M.; Sikora B. J.; Bury W.; Krungleviciute V.; Yildirim T.; Farha O. K.; Sholl D. S.; Snurr R. Q. Computation-ready, experimental metal-organic frameworks: A tool to enable high-throughput screening of nanoporous crystals. Chem. Mater. 2014, 26, 6185–6192. 10.1021/cm502594j. [DOI] [Google Scholar]
- Gurvich L. J. Phys. Chem. Soc. Russ. 1915, 47, 49–56. [Google Scholar]
- Mason J. A.; Veenstra M.; Long J. R. Evaluating metal–organic frameworks for natural gas storage. Chem. Sci. 2014, 5, 32–51. 10.1039/C3SC52633J. [DOI] [Google Scholar]
- Bae Y.-S.; Yazaydın A. O.; Snurr R. Q. Evaluation of the BET method for determining surface areas of MOFs and zeolites that contain ultra-micropores. Langmuir 2010, 26, 5475–5483. 10.1021/la100449z. [DOI] [PubMed] [Google Scholar]
- Potoff J. J.; Siepmann J. I. Vapor–liquid equilibria of mixtures containing alkanes, carbon dioxide, and nitrogen. AIChE J. 2001, 47, 1676–1682. 10.1002/aic.690470719. [DOI] [Google Scholar]
- Van der Marck S. Network approach to void percolation in a pack of unequal spheres. Phys. Rev. Lett. 1996, 77, 1785. 10.1103/PhysRevLett.77.1785. [DOI] [PubMed] [Google Scholar]
- Hoshen J.; Kopelman R. Percolation and cluster distribution. I. Cluster multiple labeling technique and critical concentration algorithm. Phys. Rev. B 1976, 14, 3438. 10.1103/PhysRevB.14.3438. [DOI] [Google Scholar]
- Martin R. L.; Prabhat; Donofrio D. D.; Sethian J. A.; Haranczyk M. Accelerating analysis of void space in porous materials on multicore and GPU platforms. Int. J. High Perform. Comput. Appl. 2012, 26, 347–357. 10.1177/1094342011431591. [DOI] [Google Scholar]
- Kim J.; Martin R. L.; Rübel O.; Haranczyk M.; Smit B. High-throughput characterization of porous materials using graphics processing units. J. Chem. Theory Comput. 2012, 8, 1684–1693. 10.1021/ct200787v. [DOI] [PubMed] [Google Scholar]
- Setoyama N.; Kaneko K.; Rodriguez-Reinoso F. Ultramicropore characterization of microporous carbons by low-temperature helium adsorption. J. Phys. Chem. 1996, 100, 10331–10336. 10.1021/jp960467p. [DOI] [Google Scholar]
- Thornton A.; Jelfs K.; Konstas K.; Doherty C.; Hill A.; Cheetham A.; Bennett T. Porosity in metal-organic framework glasses. Chem. Commun. 2016, 52, 3750–3753. 10.1039/C5CC10072K. [DOI] [PubMed] [Google Scholar]
- Thommes M.; Kaneko K.; Neimark A. V.; Olivier J. P.; Rodriguez-Reinoso F.; Rouquerol J.; Sing K. S. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. 10.1515/pac-2014-1117. [DOI] [Google Scholar]
- Chokbunpiam T.; Fritzsche S.; Chmelik C.; Caro J.; Janke W.; Hannongbua S. Gate opening, diffusion, and adsorption of CO2 and N2 mixtures in ZIF-8. J. Phys. Chem. C 2016, 120, 23458–23468. 10.1021/acs.jpcc.6b05506. [DOI] [Google Scholar]
- Witman M.; Ling S.; Jawahery S.; Boyd P. G.; Haranczyk M.; Slater B.; Smit B. The Influence of Intrinsic Framework Flexibility on Adsorption in Nanoporous Materials. J. Am. Chem. Soc. 2017, 139, 5547–5557. 10.1021/jacs.7b01688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubbeldam D.; Calero S.; Ellis D.; Snurr R. RASPA 2.0: Molecular software package for adsorption and diffusion in (flexible) nanoporous materials. Mol. Simul. 2016, 42, 81–101. 10.1080/08927022.2015.1010082. [DOI] [Google Scholar]
- Rappé A. K.; Casewit C. J.; Colwell K.; Goddard W. A.; Skiff W. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. 10.1021/ja00051a040. [DOI] [Google Scholar]
- Hirschfelder J.; Bird R. B.; Curtiss C. F.. The Molecular Theory of Gases and Liquids; Wiley-Interscience: Hoboken, NJ, 1964. [Google Scholar]
- Cavenati S.; Grande C. A.; Rodrigues A. E.; Kiener C.; Müller U. Metal organic framework adsorbent for biogas upgrading. Ind. Eng. Chem. Res. 2008, 47, 6333–6335. 10.1021/ie8005269. [DOI] [Google Scholar]
- Wiersum A. D.; Chang J.-S.; Serre C.; Llewellyn P. L. An adsorbent performance indicator as a first step evaluation of novel sorbents for gas separations: application to metal-organic frameworks. Langmuir 2013, 29, 3301–3309. 10.1021/la3044329. [DOI] [PubMed] [Google Scholar]
- Moellmer J.; Moeller A.; Dreisbach F.; Glaeser R.; Staudt R. High pressure adsorption of hydrogen, nitrogen, carbon dioxide and methane on the metal–organic framework HKUST-1. Microporous Mesoporous Mater. 2011, 138, 140–148. 10.1016/j.micromeso.2010.09.013. [DOI] [Google Scholar]
- Senkovska I.; Kaskel S. High pressure methane adsorption in the metal-organic frameworks Cu 3 (btc) 2, Zn 2 (bdc) 2 dabco, and Cr 3 F (H 2 O) 2 O (bdc) 3. Microporous Mesoporous Mater. 2008, 112, 108–115. 10.1016/j.micromeso.2007.09.016. [DOI] [Google Scholar]
- Chowdhury P.; Mekala S.; Dreisbach F.; Gumma S. Adsorption of CO, CO2 and CH4 on Cu-BTC and MIL-101 metal organic frameworks: Effect of open metal sites and adsorbate polarity. Microporous Mesoporous Mater. 2012, 152, 246–252. 10.1016/j.micromeso.2011.11.022. [DOI] [Google Scholar]
- Sarkisov L.; Kim J. Computational structure characterization tools for the era of material informatics. Chem. Eng. Sci. 2015, 121, 322–330. 10.1016/j.ces.2014.07.022. [DOI] [Google Scholar]
- Talu O.; Myers A. L. Molecular simulation of adsorption: Gibbs dividing surface and comparison with experiment. AIChE J. 2001, 47, 1160–1168. 10.1002/aic.690470521. [DOI] [Google Scholar]
- Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge structural database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72, 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright P. A.; Maple M. J.; Slawin A. M.; Patinec V.; Aitken R. A.; Welsh S.; Cox P. A. Cation-directed syntheses of novel zeolite-like metalloaluminophosphates STA-6 and STA-7 in the presence of azamacrocycle templates. Dalton Trans. 2000, 1243–1248. 10.1039/a909249h. [DOI] [Google Scholar]
- Heine J.; Hołyńska M.; Reuter M.; Haas B.; Chatterjee S.; Koch M.; Gries K. I.; Volz K.; Dehnen S. In (SAr) 3 as a building block for 3D and helical coordination polymers. Cryst. Growth Des. 2013, 13, 1252–1259. 10.1021/cg301724v. [DOI] [Google Scholar]
- Prasad T. K.; Hong D. H.; Suh M. P. High gas sorption and metal-ion exchange of microporous metal-organic frameworks with incorporated imide groups. Chem. - Eur. J. 2010, 16, 14043–14050. 10.1002/chem.201002135. [DOI] [PubMed] [Google Scholar]
- He Y.; Furukawa H.; Wu C.; O’Keeffe M.; Krishna R.; Chen B. Low-energy regeneration and high productivity in a lanthanide-hexacarboxylate framework for high-pressure CO 2–CH 4–H 2 separation. Chem. Commun. 2013, 49, 6773–6775. 10.1039/c3cc43196g. [DOI] [PubMed] [Google Scholar]
- Grünker R.; Senkovska I.; Biedermann R.; Klein N.; Lohe M. R.; Müller P.; Kaskel S. A highly porous flexible metal-organic framework with corundum topology. Chem. Commun. 2011, 47, 490–492. 10.1039/C0CC02273J. [DOI] [PubMed] [Google Scholar]
- He Y.; Zhang Z.; Xiang S.; Wu H.; Fronczek F. R.; Zhou W.; Krishna R.; O’Keeffe M.; Chen B. High separation capacity and selectivity of C2 hydrocarbons over methane within a microporous metal-organic framework at room temperature. Chem. - Eur. J. 2012, 18, 1901–1904. 10.1002/chem.201103927. [DOI] [PubMed] [Google Scholar]
- Zhao D.; Yuan D.; Yakovenko A.; Zhou H.-C. A NbO-type metal-organic framework derived from a polyyne-coupled di-isophthalate linker formed in situ. Chem. Commun. 2010, 46, 4196–4198. 10.1039/c002767g. [DOI] [PubMed] [Google Scholar]
- Guo Z.; Wu H.; Srinivas G.; Zhou Y.; Xiang S.; Chen Z.; Yang Y.; Zhou W.; O’Keeffe M.; Chen B. A metal–organic framework with optimized open metal sites and pore spaces for high methane storage at room temperature. Angew. Chem., Int. Ed. 2011, 50, 3178–3181. 10.1002/anie.201007583. [DOI] [PubMed] [Google Scholar]
- Wilmer C. E.; Farha O. K.; Yildirim T.; Eryazici I.; Krungleviciute V.; Sarjeant A. A.; Snurr R. Q.; Hupp J. T. Gram-scale, high-yield synthesis of a robust metal-organic framework for storing methane and other gases. Energy Environ. Sci. 2013, 6, 1158–1163. 10.1039/c3ee24506c. [DOI] [Google Scholar]
- Park H. J.; Cheon Y. E.; Suh M. P. Post-synthetic reversible incorporation of organic linkers into porous metal-organic frameworks through single-crystal-to-single-crystal transformations and Modification of Gas-Sorption Properties. Chem. - Eur. J. 2010, 16, 11662–11669. 10.1002/chem.201001549. [DOI] [PubMed] [Google Scholar]
- Yuan D.; Zhao D.; Sun D.; Zhou H.-C. An isoreticular series of metal-organic frameworks with dendritic hexacarboxylate ligands and exceptionally high gas-uptake capacity. Angew. Chem., Int. Ed. 2010, 49, 5357–5361. 10.1002/anie.201001009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.