Order and gelation of cellulose nanocrystal suspensions: an overview of some issues

Abstract

Cellulose nanocrystals (CNCs) are polydisperse rod-shaped particles of crystalline cellulose I, typically prepared by sulfuric acid hydrolysis of natural cellulose fibres to give aqueous colloidal suspensions stabilized by sulfate half-ester groups. Sufficiently dilute suspensions are isotropic fluids, but as the concentration of CNC in water is increased, a critical concentration is reached where a spontaneously ordered phase is observed. The (equilibrium) phase separation of the ordered chiral nematic phase is in competition with a tendency of the CNC suspension to form a gel. Qualitatively, factors that reduce the stability of the CNC suspension favour the onset of gelation. The chiral nematic structure is preserved, at least partially, when the suspension dries. Solid chiral nematic films of cellulose are of interest for their optical and templating properties, but the preparation of the films requires improvement. The processes that govern the formation of solid chiral nematic films from CNC suspensions include phase separation, gelation and also the effects of shear on CNC orientation during evaporation. Some insight into these processes is provided by polarized light microscopy, which indicates that the relaxation of shear-induced orientation to give a chiral nematic structure may occur via an intermediate twist-bend state.

This article is part of a discussion meeting issue ‘New horizons for cellulose nanotechnology’.

1. Cellulose nanocrystal preparation

Colloidal dispersions of cellulose crystallites, produced by careful sulfuric acid hydrolysis of natural cellulose fibres, self-assemble into a chiral nematic phase above a critical concentration in water [1]. The critical concentration depends primarily on the axis ratio of the rod-like cellulose particles, which typically have widths of a few nanometres, and lengths of tens of nanometres [2]. Aqueous suspensions of what are now referred to as cellulose nanocrystals (CNCs) are electrostatically stabilized by the presence of sulfate half-ester groups on the cellulose surface. Above the critical concentration, the suspension forms a two-phase system, with the isotropic phase in equilibrium with the chiral nematic phase, until at high concentrations, the suspension is almost completely liquid crystalline. The critical concentration and the width of the biphasic region depend on the dimensions of and charge on the CNCs [3] and on the ionic strength of the aqueous medium [4].

The CNC dimensions and surface charge depend in turn on the source of the crystalline cellulose, and on the hydrolysis conditions. For the usual process, where the amorphous regions of pre-purified natural cellulose from wood or cotton are removed by reaction with concentrated sulfuric acid, leaving the crystalline CNCs, tight control of the sample pre-treatment, acid concentration, hydrolysis temperature and reaction time is required [5]. Unless otherwise stated, the discussion below assumes that the CNCs are stabilized by sulfate half-ester surface groups.

2. Colloidal stability and desulfation

Formation of a chiral nematic phase from CNC suspensions requires that the suspensions remain stable as the concentration is increased. A key factor governing the stability is the sulfate half-ester content on the surface. A decrease in sulfate half-ester group content leads to aggregation and gelation through a decrease in electrostatic stabilization [3,6]. Beck et al. [7] have recently provided a protocol for the analysis of the sulfate half-ester content, and detailed the conditions under which the autocatalysed acidic desulfation of CNC suspensions and films occurs [8]. One important point is that the cation associated with the sulfate half-ester anion is an important variable in colloid and thermal stability of CNC suspensions and films; the autocatalytic nature of the desulfation process means that the acid form of the CNC half-esters is less stable than, for example, the sodium form.

3. Effect of desulfation on order and gelation

The extent of desulfation governs the concentration of CNCs at which the ordered phase forms, and also the optical properties of CNC suspensions and films. The optical properties in turn depend on three key concentration-dependent factors: (i) the chiral nematic pitch, (ii) the liquid crystalline texture of the suspensions and films, and (iii) the concentration at which (i) and (ii) become frozen in during drying [9,10]. The first two factors have been intensively investigated, but the third factor, the competition between concentration-driven changes in pitch and concentration-driven gelation, is difficult to quantify. The competition between nematic liquid crystal formation and gelation for suspensions of sterically stabilized boemite rods led to the observation of two different nematic phases [11]. Qualitatively, for CNC films, the importance of kinetic factors in governing the optical properties has been recognized [12,13]. Gel formation can slow the normally steep decrease in chiral nematic pitch with increasing concentration (kinetic impairment), but the gel volume can still decrease by evaporation, giving a slower decrease in pitch until a glassy solid forms, with no significant further decrease (kinetic arrest). As CNC applications as optical or templating materials involve evaporation to a chiral nematic solid, the role of gelation during evaporation needs to be better understood.

4. Concentration dependence of gelation onset

Measurement and prediction of the onset of gelation in both anisotropic and ordered suspensions of rods are challenging. To approach this problem in a very oversimplified manner, consider the static packing of rigid rod-like particles, modelled as spherocylinders, length L + d, diameter d and axial ratio (L + d)/d. The average excluded volume, v_ex, for a pair of randomly oriented spherocylinders, was first calculated by Onsager [14]

4.1

Starting with equation (4.1), Philipse [15] proposed a random contact model, which considered an assembly of (on average) randomly oriented particles with independent mechanical contacts between particles. Suppose there is an average number density, ρ, of such randomly distributed particles. Philipse showed that the average number of contacts experienced by a given particle, 〈γ〉, is simply related to the number density and the orientationally averaged excluded volume, v_ex, for a pair of particles:

4.2

This is Philipse's mechanical equation of state (the ‘random contact equation’) for a system of fixed random particles with uncorrelated mechanical contacts. For rigid spherocylinders, substituting equation (4.1) and the spherocylinder volume into equation (4.2) gives, for spherocylinders or rods with high aspect ratios,

4.3

Philipse used experimental data for a variety of macroscopic rods to show that shaking rods with sufficiently long axis ratios gave solid-like stiff structures of fairly reproducible ‘random close packing density’ (or random close packed rod volume fraction, ϕ_rcp) that depended only on the rod axis ratio, L/d. He concluded that the experimental data for rods with L/d > 15 fitted the relationship

4.4

From equations (4.3) and (4.4), the random close rod packing corresponds to around 11 contacts on any given rod, or, because this counts each contact twice, about 5–6 total contacts per rod. This number of contacts fixes the positions of the rods.

The random close packed rod volume fraction, ϕ_rcp, is the maximum density attained by long randomly oriented and positioned rods. Rod–rod interactions will of course start to occur at lower volume fractions. Philipse & Verbermoes [16] considered the statistical geometry of random thin-rod packing. In their static model, thin rigid rods are placed one by one in fixed, random orientations and positions, subject only to the condition that the rods cannot penetrate each other. They calculate a volume fraction, ϕ_t, at which sideways translational motion of a given rod is caged by γ_t contacts with neighbouring rods. (Translation parallel to the rod axis is not blocked.) The probability of forming a translational cage obviously increases with the volume fraction of rods. The authors showed that the average number of contacts with a caged rod, 〈γ_t〉 = 5. Hence, from equation (4.3), the corresponding rod volume fraction at which rods are translationally caged, ϕ_t, is simply

4.5

It is tempting to assign ϕ_rcp (equation (4.4)) to the onset of kinetic impairment, and ϕ_t (equation (4.5)) to kinetic arrest. However, note that equations (4.4) and (4.5) are derived for randomly oriented rods, so they only apply to the situation where gel formation occurs at concentrations below that at which ordered suspensions form. It is of interest to compare the concentrations predicted for static packing of rigid spherocylinders with Onsager's predictions for the onset of nematic ordering [14]. For hard core interactions (where excluded volume is the only interaction between rods), a first-order transition to an ordered (anisotropic) phase would occur at some critical volume fraction, ϕ_i. The ordered phase has a somewhat higher concentration than the randomly oriented rods in the initial isotropic phase, and both phases coexist until the overall concentration exceeds a second critical concentration, ϕ_a. The phase formation again depends only on the axial ratio of the rods. The following equations hold for axial ratios above approximately 15:

4.6

and

4.7

Thus, the volume fractions of spherocylinders where static packing reaches limiting values overlap the volume fractions at which ordered phase formation is observed. For example, the onset of ordered phase formation for spherocylindrical rods with axial ratio 15 is predicted to occur at ϕ_i = 0.22, where, for the same axial ratio, the static packing densities are ϕ_t = 0.17 and ϕ_rcp = 0.36. In other words, the physical jamming of the rods is predicted to occur in the same concentration range as ordered phase formation. This will be true for all sufficiently large axial ratios.

However, in the above, the effect of electrostatic charge on the phase separation of charge has been ignored. One approach to dealing with the electrostatic repulsion between charged rods is to replace L and d by L_eff and d_eff, where the effective dimensions are enlarged to compensate for the double layer repulsion [17]. For spherocylinders with L_eff ≫ d_eff, the effective axial ratio will decrease because of charge, but if L_eff and d_eff are used in equations (4.6) and (4.7), the resultant effective volume fractions must reflect the enlarged dimensions, and for comparison must be converted to the volume fraction of the uncharged rods:

4.8

and

4.9

The result is that the electrostatic repulsion decreases the concentration (volume fraction) at which the ordered phases form to below the volume fraction where the geometry-driven static packing causes kinetic arrest.

Equations (4.8) and (4.9) are very crude approximations, and ignore the electrostatic repulsion between rods that generates an achiral twisting force [17]. A comparison between theories of static packing (equations (4.4), (4.5)) and phase separation (equations (4.8), (4.9)) rationalizes the observed importance of charge in the competition between gelation and liquid crystal formation. CNCs are far from ideal uniform spherocylinders, and also display marked polydispersity in dimensions and surface charge. Obviously more work is required. Experimentally, gelation rather than ordered phase formation is observed when the initial sulfation conditions are too mild [5], when surface sulfate half-ester groups have been removed [18,19], or when the axial ratio of the CNC is close to the limit for ordered phase formation [20].

5. Observations of drying process by polarized light microscopy

The above approach assumes that the gel is isotropic and that the ordered phase is nematic, so it can at best be a guide to structure development during evaporation. However, for CNCs the observed ordered phase is normally chiral nematic, and for sufficiently stabilized suspensions, the chiral nematic structure can form a gel during evaporation, eventually drying to a chiral nematic film. The process is complex, as the evaporating CNC suspension may pass through isotropic, biphasic, and chiral nematic phases, and may form a thixotropic gel on its way to forming a stable solid with chiral nematic order. The progression is conveniently followed by polarized light microscopy [21]. The most straightforward process is the evaporation of concentrated CNC suspensions from shallow flat containers into an atmosphere at a controlled humidity: this helps to minimize defect and multidomain formation, and gives relatively uniform films [22]. At the other extreme, evaporation of a small droplet on a flat surface generates iridescent rings with a rich variety of textures. Profilometric measurements across the rings show that the outer edge of the films is much thicker than the region in the centre. This is ascribed to a ‘coffee-stain’ effect; the CNCs are transported to the outer edge for droplets where the contact line is pinned during evaporation [23]. The gradient in concentration across the ring results in a colour gradient, with the longer wavelengths at the edge decreasing towards the centre of the sample, in accord with the hypothesis of a two-stage process for CNC chiral nematic colour formation. Weaker pinning of the contact line during evaporation leads to a series of rings, thin at the edge and thicker towards the centre, each with a distinctive texture [21]. A polarized light image of part of a dry film cast from a 6 wt% droplet of CNC suspension is shown in figure 1. In this image, the black lines between bands are cracks through the film, presumably due to shrinkage on drying.

Figure 1.

Polarized light image (crossed polars, 530 nm red wave plate) of film cast from 6 wt% CNC suspension on glass. Adapted from [21, fig.15].

6. Twist-bend structure

The rich textures displayed by simple evaporation of CNC suspensions depend on factors such as the initial CNC concentration, on the effects of shear applied intentionally or unintentionally during preparation of the microscope sample, and on relaxation time for these very concentrated suspensions. To attempt to investigate the slow relaxation at a given concentration, the textures of some sealed samples were observed for up to 18 h after preparation. A transitory texture characteristic of nematic order was observed, leading to a novel proposal [24] regarding the mechanism by which a shear oriented nematic-like organization relaxes to the normal chiral nematic phase. The transition between nematic (shear induced) and chiral nematic states (and vice versa) is often viewed as a simple twisting or untwisting around the chiral nematic axis. This process requires elastic distortion over a length scale of the order of the pitch, and singularities arise each half-pitch, where the orientation of the nanocrystals is orthogonal to the x–z plane. Rather than a twisting and untwisting of layers along the chiral nematic axis, it was proposed that the samples passed through an intermediate structure analogous to that found in the twist-bend phase of some bent-molecule liquid crystals [25]. For a conical helicoidal structure with axis along the z direction of a right-handed Cartesian coordinate frame (figure 2), the director of a twist-bend structure, , is defined by

6.1

where Θ_o is the constant oblique angle (the tilt angle) of the director with the helix axis, z, and φ is the azimuthal angle of the oblique helicoid. φ = 2π(z/P) = tz where t = 2π/P and P is the pitch of the conical helicoid. Equation (4.1) also describes a nematic phase when Θ_o = 0, and a chiral nematic phase when Θ_o = π/2.

Figure 2.

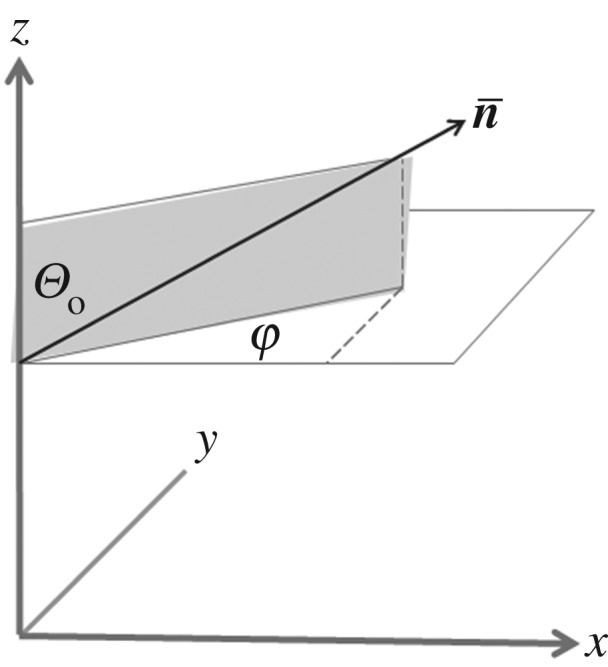
Coordinate system showing twist-bend director, , as function of azimuthal angle, φ, and tilt angle, Θ_o.

The proposed route between nematic and chiral nematic starts with the nematic director along the z axis. This corresponds to a tilt angle Θ_o = 0 relative to the helix axis along the z direction. Increasing the tilt angle gives a twist-bend type of CNC orientation (equation (6.1)) until at tilt angle Θ_o = 90°, the equilibrium chiral nematic structure is restored. Conversely, starting with a chiral nematic, the twist-bend type of intermediate structure might explain the relative ease with which the suspension orients along the shear direction.

It must be stressed that the proposed twist-bend structure is transitory, and not an equilibrium phase. The evidence from polarized light microscopy for a twist-bend intermediate [24] is weak, and more microscopy and scattering experiments are required. In particular, the mechanism for relaxation from a nematic to a chiral nematic organization could be distinguished by noting that for a twist-bend mechanism the helicoidal axis should be parallel to the original nematic director, but for the usually assumed twist–untwist mechanism the chiral nematic axis should be orthogonal to the nematic director.

7. Conclusion

Despite recent progress, some basic problems remain regarding the formation of ordered films from suspensions of CNCs. The role of nanocrystal geometry and surface charge in ordered phase separation of CNC suspensions is at least qualitatively understood, but the interplay between gelation and liquid crystalline ordering at high CNC concentrations remains experimentally and theoretically challenging.

Data accessibility

This article has no additional data.

Competing interests

I declare I have no competing interests.

Funding

Support from the Natural Sciences and Engineering Research Council of Canada is gratefully acknowledged.