Spontaneous mirror symmetry breaking and origin of biological homochirality

Abstract

Recent reports on both theoretical simulations and on the physical chemistry basis of spontaneous mirror symmetry breaking (SMSB), that is, asymmetric synthesis in the absence of any chiral polarizations other than those arising from the chiral recognition between enantiomers, strongly suggest that the same nonlinear dynamics acting during the crucial stages of abiotic chemical evolution leading to the formation and selection of instructed polymers and replicators, would have led to the homochirality of instructed polymers. We review, in the first instance, which reaction networks lead to the nonlinear kinetics necessary for SMSB, and the thermodynamic features of the systems where this potentiality may be realized. This could aid not only in the understanding of SMSB, but also the design of reliable scenarios in abiotic evolution where biological homochirality could have taken place. Furthermore, when the emergence of biological chirality is assumed to occur during the stages of chemical evolution leading to the selection of polymeric species, one may hypothesize on a tandem track of the decrease of symmetry order towards biological homochirality, and the transition from the simple chemistry of astrophysical scenarios to the complexity of systems chemistry yielding Darwinian evolution.

1. Introduction

In spite of the claims that chemistry should dedicate more efforts to study the origins of life [1,2] and the fact that the number of research groups working on this topic is increasing, there is a lack of work compared to that generated in other chemical fields, the latter being arguably far less significant for the advancement of knowledge. Organic synthesis should be the experimental bench on which to test hypotheses on the emergence of life in abiotic terrestrial scenarios. However, such as has been quoted [2], in the study of the chemical evolution towards life processes, physical chemists have already paved the way for organic chemists, but have not succeeded in this task psychologically.

Homochirality is ubiquitous and ever present in biological chemistry from its very start, but there is a most curious absence of the chirality question in the studies concerning the abiotic stage of formation of the instructed polymers and replicators leading to the onset of Darwinian evolution, which is a striking paradox. Models of mutualism and cooperative effects in autocatalytic sets, on quasi-species, the protein world and the RNA world (see for example, [3–6]) all assume tacitly the homochirality of the implied species. The origin of biological homochirality is thus considered as a separate and disjoint event: the formation of enantiomerically pure polymers is assumed to occur by starting from enantiomerically pure mixtures of their monomers. This, from a chemical point of view, is an unlikely scenario because it implies vast pools of enantiomerically pure mixtures of amino acids and sugars, and does not take into account the fact that racemization is likely to occur, at least to a certain degree, on the long timescales of evolution and for the experimental conditions necessary for the formation of the condensation of polymers.

In the last few years, the role and mechanisms of natural chiral forces and chemical polarizations, able to lead to biases from the racemic composition, have been so well clarified that it is no longer a mystery that an important bias from the racemic composition can be obtained starting from achiral compounds. Especially important is the fact that the fundamental difference between simple asymmetric inductions and reactions taking place with spontaneous mirror symmetry breaking (SMBS) is now clear [7–9] from a theoretical point of view, and this in spite of the fact that the specific reaction mechanisms of the few experimental examples on spontaneous mirror symmetry breaking (SMSB) are, until now, not well described [10–13]. However, it is still not understood in which abiotic scenarios of chemical evolution the emergence of homochirality could have taken place, and of the relevance of this symmetry reduction for the emergence of life.

SMSB can take place, and occur within certain enantioselective autocatalytic networks and for specific reaction parameters: the bias from the racemic composition is not achieved by kinetic control but is rather a consequence of non-equilibrium stable stationary states. This is because the racemic state becomes metastable along a thermodynamic branch and fluctuations allow the system to evolve to one of two energetically degenerate chiral states (a bifurcation scenario to ordered states). Note that this phenomenon does not correspond to chiral amplifications nor to simple nonlinear induction deviations, but to an absolute asymmetric synthesis in the absence of any chiral polarization.

Autocatalysis is a necessary condition for life [2,14] and emerges during the evolutionary stage of the onset of replicator molecules and template mechanisms of self-reproduction. The emergence of primordial replicators is simulated in systems leading to steady state dynamics, such as those of the living cell, as was already quoted by Oparin [15] and later, subsequently formulated on a physical chemistry basis (see for example [16–18]). In this respect, the chemical analogies of SMSB processes with those of replicators are surely significant: both concern the ability of enantioselective autocatalysis to exhibit growth dynamics leading to enantiomeric selection and occurs in thermodynamic systems leading to non-equilibrium steady states (NESS). Regarding the chemical characteristics of SMSB, we discuss here the hypothesis that biological homochirality would emerge in tandem with those supramolecular species possessing catalytic and replicative functionalities. This hypothesis implies that these SMSB processes occurred during the advanced stages of chemical evolution (terrestrial chemical evolution). We also discuss that such SMSB requires initial, albeit small, enantiomeric excess (ee) values, that originate from asymmetric inductions in the formation of simple chiral monomeric species during the early stages (as in astrophysical or terrestrial scenarios), which are needed to convert the SMSB stochastic distribution of chiral signs between experiments into an imperfect bifurcation leading deterministically to only one of the two chiral signs.

2. Chemical conditions leading to biases from the racemic composition

Enantioselectivity is an extreme limiting case of chemical selectivity because enantiomer pairs are energetically degenerate. Notice that we do not take into account, any chemical consequence of the extremely feeble energy difference between enantiomers due to the charge-parity or CP violation [19–21]. This energy difference is orders of magnitudes lower than the k_BT values of the thermal bath. Therefore, no detectable bias of the racemic composition can be obtained in enantioselective syntheses, either by kinetic or by thermodynamic control. The law of large numbers determines that, in the absence of any chiral polarization, the racemic composition will always be obtained. This holds for any enantioselective reaction with a finite rate for the inverse reaction pathways in a closed system that can achieve thermodynamic equilibrium with its surroundings. In the case of SMSB systems, the stochastic chiral fluctuations originated in enantioselective reactions very probably will overcome any effect of this weak interaction symmetry violation.

The question of biological homochirality requires the understanding of the conditions that may lead to stable biases about the racemic composition. In this respect, the recent reports on the characteristics of enantioselective autocatalytic networks able to lead to SMSB (absolute asymmetric synthesis in the absence of any chiral polarization) underscore the fundamental differences between these systems and those leading to common asymmetric synthesis [9].

2.1. Asymmetric induction on enantioselective reactions

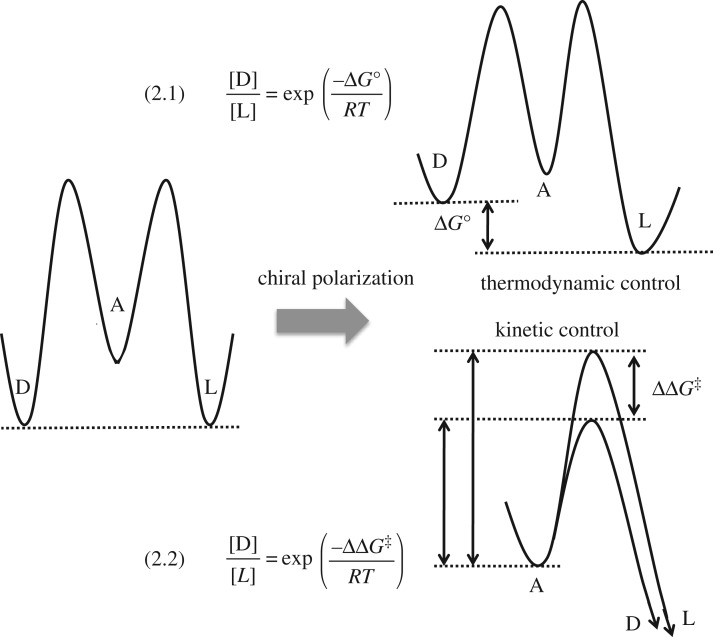
The effect of a chiral polarization on a racemic mixture exerts a chiral recognition on the enantiomers, leading to a differentiation of their free energies and therefore when they are connected directly or indirectly by a chemical transformation. The racemic composition is biased according to the free energy difference generated by this chiral recognition. This is the case of the equilibrium between enantiomers (i.e. racemization) and also of the reactions implying chiral species yielding outputs via the so-called thermodynamic control (i.e. by chiral polarization of the reaction surroundings) (figure 1).

Figure 1.

Thermodynamic and kinetic control in an enantioselective reaction 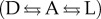, where A is achiral and D/L is an enantiomeric pair.

Applied organic synthesis can assume the approximation of irreversible reactions in the case of relatively high exergonic reactions and for reaction times that are not too long; this is the case of the so-called kinetically controlled reactions. In this case the selectivity is determined by the free energy differences between the transition states. The paradigm of asymmetric synthesis is to convert enantiomeric reaction paths into diastereomeric ones by the interaction with chiral species at the activated complex of the transition state (figure 1).

Chiral polarizations acting either by thermodynamic or kinetic control yield biases from the racemic composition with values that depend on the free energy difference induced by the chiral polarization upon initial and final products (equation (2.1) in figure 1 and table 1) or upon the activated complexes (equation (2.2) when, at the timescale of the experiment, racemization is not detected), respectively.

Table 1.

Dependence of the enantiomeric excess (ee) on the free energy difference, exerted by a chiral polarization on the enantiomers (see figure 1): thermodynamic control, equation (2.1); kinetic control, equation (2.2).

[D]/[L] at 300 K	ee (%) at 300 K	–ΔG° or –ΔΔG‡ (KJ mol–1)
1.0	0.0	0.00
1.1	4.8	0.24
1.5	20.0	1.01
3.0	50.0	2.74
10.0	81.8	5.74
100	98.0	11.49
500	99.6	15.50

From an applied chemical point of view, large free energy differences are more easily obtained by using chiral recognition interactions at the transition states and reaction paths than on the initial and final reaction compounds themselves.

Notice, that in the first stages of abiotic chemistry (e.g. astrophysical scenarios) in the emergence of ee values the chiral polarization exerted by a chiral compound must be excluded and that only the action of natural chiral forces should be taken into account. In this respect, the number of natural chiral forces is rather small [22,23] and their effect on the reactions of applied chemistry is also small, but in astrophysical scenarios very large chiral natural forces could be operative.

2.2. Enantioselective autocatalytic reaction networks which may lead to spontaneous mirror symmetry breaking

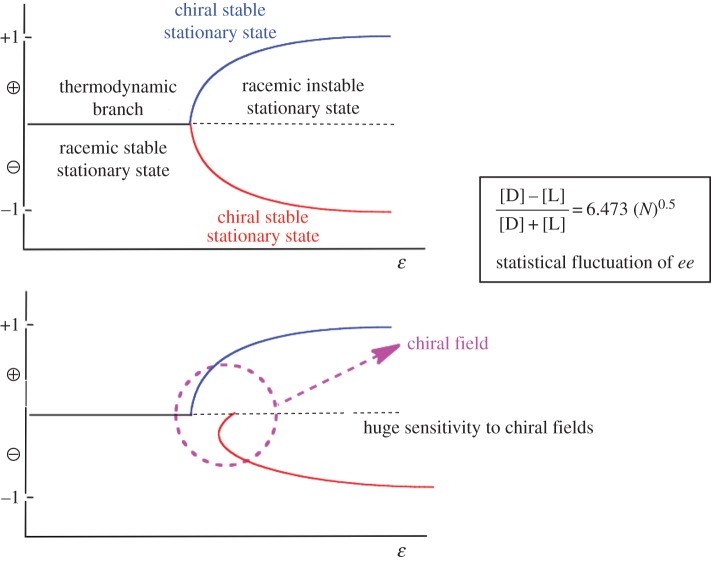
Absolute asymmetric synthesis is understood here as a conversion of achiral starting materials into chiral products that takes place under SMSB. This corresponds to an enantioselective transformation that, for specific reaction parameters, transits to a bifurcation scenario (chapter 19 of ref. [24]) where the racemic composition becomes metastable. Therefore, small chiral statistical fluctuations suffice to destabilize the system away from the racemic state towards one of two stable enantiomeric states. Furthermore, in such a bifurcation scenario, very weak chiral polarizations may transform the perfect bifurcation into an imperfect one (figure 2). This means, that instead of the stochastic distribution of final chiral signs between experiments, the same final chiral sign will be obtained for all experiments. The free energy difference, between enantioselective paths, necessary to transform the stochastic distribution of chiral signs into a deterministic one, is orders of magnitude lower than the free energy values required to achieve chiral inductions in common asymmetric synthesis. Such low chiral polarizations in SMSB systems do not change significantly the final ee value and their effect is to select one of the two enantiomeric branches at the bifurcation point. Therefore, in order to avoid current misunderstandings with classical chiral asymmetric inductions, these chiral effects in SMSB systems should be called chiral sign selections instead of chiral inductions. The experimental results using cryptochiral species in the Soai reaction (see for example ref. [25]) must be understood in the framework of such a chiral sign selection.

Figure 2.

Bifurcation enantioselective scenario. The racemic state may become unstable and chiral statistical fluctuations drive the racemic stationary state towards one of two degenerate enantiomeric stable stationary states. Weak chiral polarization acting at the bifurcation point transforms the stochastic bifurcation into a deterministic one.

Reaction networks able to lead to SMSB require, as a necessary but not sufficient condition, nonlinear kinetic dependences of enantioselective autocatalysis [26]. This is a rare reaction in chemistry, but rather more significant in life, because it sustains self-reproduction (replicators) in the nucleic acids/protein domain.

Autocatalysis is a basic property of life [4,5,14]. Therefore, the autocatalysis emerging at the formation of the first replicators represents a crucial stage of chemical evolution. Biological replication is in fact enantioselective, therefore an SMSB scenario of enantioselective autocatalysis occurring at the same stage of abiotic evolution, rather than at the stage of the emergence of replicators (pre-RNA- or RNA-world), would be reasonable. To the best of our knowledge, this has been pointed out [27] only recently.

The lack of any discussion of the chirality question in the models for the transition from the diversity of organic compounds to the complexity of systems chemistry is, in our opinion, a consequence of the misunderstanding of the characteristics of SMSB. In this respect, before the formulation of a basic speculation of the role of chirality in the different stages of chemical evolution, we first review, and from a conceptual point of view, how SMSB may arise.

In the consideration of systems able to lead to SMSB, two different issues must be taken into account: namely (i) the enantioselective autocatalytic reactions or reaction networks which may lead to SMSB, thanks to their kinetic nonlinear dependences on the enantiomer concentrations; and (ii) the thermodynamic systems where the above reaction networks may lead to non-equilibrium stable stationary states of final homochiral compositions.

2.2.1. Reaction networks able to lead to spontaneous mirror symmetry breaking

The simplest reaction network able to lead to biases in the racemic mixture is enantioselective autocatalysis (2.3) that, by virtue of the nonlinear kinetic dependence on enantiomer concentrations, may exhibit exponential growth leading to the selection of one of the two enantiomers.

2.3

Obviously, for finite values of the inverse rate reaction constant (k₋₁ > 0) and in closed systems, which achieve thermodynamic equilibrium with their surroundings (isolated state approximation), the final fate of the system is the racemic mixture. Such reaction networks in closed systems may in fact show large temporary biases in the racemic composition, and before achieving thermodynamic equilibrium. This may be of interest in applied chemistry, but not for chemical evolution scenarios, where the enormous geological timescales of the chemical reactions must be taken into account. However, in thermodynamic systems able to yield NESS, SMSB may occur (see the next section) in (2.3) for n ≥ 2 in the case of elementary reaction steps as in the case of reaction (2.3). It is necessary to stress this, because for first order, also called quadratic autocatalysis (n = 1), racemic initial conditions always lead to final racemic outputs, this also occurs in open systems. Only for initial scalemic or homochiral conditions can the final state show, and in certain open systems, a bias from the racemic composition that, in any case, cannot be larger than that of the initial ee values. Quadratic autocatalysis alone does not lead to chiral amplification. By contrast, autocatalytic orders of n ≥ 2 (n = 2, second order or cubic autocatalysis) may lead to SMSB. The physical chemistry basis of the autocatalytic order necessary to achieve species selection (survival/extinction) is a well-established issue [28–30]. However, old reports containing errors regarding the ability of isolated quadratic autocatalysis to achieve SMSB are still being cited to the present day.

However, autocatalytic orders higher than that corresponding to enantiomeric bimolecularity are so rare that they very probably did not play a significant role in the emergence of replicators. Furthermore, actual chemical systems can show the direct transformation (2.4), in addition to (2.3):

2.4

This determines that SMSB for cubic autocatalysis, where also k₁ > k₀, the absolute rate of (2.3) can only overcome the racemizing role of (2.4) at high enantiomeric concentrations. Obviously, this is not a desirable scenario in chemical evolution. Therefore, the question is how quadratic enantioselective autocatalysis, when coupled to other reactions implying enantiomeric chiral recognition between enantiomers/catalysts, is able to lead to the growth dynamics [28–30] necessary to achieve selection between the enantiomers.

Quadratic autocatalysis, when coupled to other enantioselective reactions, may show a dynamic signature of growth similar to those of higher order autocatalysis, i.e. able to perform species selection. Notice that signatures of autocatalytic growth in more complex reaction networks than that of elementary reaction steps akin to that of reaction (2.3) may imply a non-integer value of n [30]. In this case, the rule for species selection (survival/extinction) applies for n > 1, and the so-called survival of all holds for n ≤ 1. It is worth noting that in complex reaction networks and certain reaction mechanisms, the actual enantiomeric species in the autocatalytic transformation may be distinct from the final reaction products.

In the following we discuss which reaction networks, composed of a first order enantioselective autocatalysis (the common expected one), when coupled to other reactions, may show SMSB. The networks described are a reductionistic description of the basic types of such reaction networks, that in actual systems, can be much more complex. In the reactions networks discussed here the reversibility of all chemical reaction steps is always assumed. Notice that the reversibility/irreversibility aspects are the fundamental difference between the chemical species selection and the Darwinian selection of living beings [31]. As commented this point must be taken into account to obey the microreversibility principle, i.e. the expression of the second thermodynamic principle at the molecular reaction level.

2.2.1.1. Frank-like reaction networks

The reaction model derived from Frank's seminal report [32] is composed of a first order autocatalytic reaction [reaction (2.3) for n = 1] coupled to a heterochiral reaction between enantiomers that leads to an optically inactive compound (P),

2.5

The system may contain other related reactions, such as direct synthesis (2.4) and non-enantioselective autocatalysis (2.6)

2.6

provided these are much slower reactions than the enantioselective autocatalysis. Note that (2.4) and (2.6) contribute to racemization; this means that they reduce the parameter space region for SMSB, but they do not prevent SMSB.

Frank-like reaction network mechanisms can be clearly distinguished via the coupling of the enantioselective quadratic autocatalysis to a mutual inhibition reaction, such as in (2.5), between the enantiomers/catalysts. Notice that Frank-like reaction networks imply that, in the chiral recognition between enantiomers, the heterochiral interaction is much stronger that the homochiral one. In this respect, most chiral organic compounds show preferential heterochiral interactions, but some show preferential homochiral interactions [33,34], which is highly significant in a biological context. As a consequence, for these latter types of compounds, Frank-like reaction networks cannot be taken into account or invoked as possible SMSB systems.

2.2.1.2. Limited enantioselectivity reaction network

The limited enantioselectivity (LES) model was proposed for SMSB as an alternative to avoid the mutual inhibition between enantiomers/catalysts [35]. The minimal set of the LES model is composed of enantioselective autocatalysis (2.3) and non-enantioselective autocatalysis (2.6). Mathematically, SMSB may be obtained for such systems, but it was demonstrated that under the constraints implied by the principle of micro-reversibility, SMSB is not at all possible [36]. These thermodynamic constraints are simply applied by considering that the two autocatalysis and the direct transformation, (2.3), (2.6) and (2.4) respectively, have the same equilibrium constant. This determines that the ratios between the forward and backward reaction rate constants of these three reactions must be the same. The conditions for SMSB in LES can only occur under violation or breaking of this constraint, i.e. by violation of the microreversibility principle. However, when properly taken into account, viable LES-like networks able to yield SMSB have been proposed. For example, when reactions (2.3) and (2.6) have different equilibrium constants, which can be the case when one of them is promoted or driven by an additional chemical reagent.

It is worth noting that the correct application of the pertinent thermodynamic constraints, derived from the first and second principles of thermodynamics, to models of SMSB is not a specific problem of the LES scheme, but is a frequently repeated error made within the SMSB topic itself [37,38]. In this respect, the recognition of reaction cycles between initial achiral products and the final enantiomers is important, where the application of the microreversibility constraints to the rate reaction constants is made under the consideration of the so-called Wegscheider condition [39]. This states that the products of the rate reaction constants in both cyclic directions must be the same. Unidirectional cycles can be established by coupling some of the reactions to reagents that are subject to input and output flows, or by applying external physical energy (mechanical, photons, etc.) to only some of the species in the network.

2.2.1.3. Enantioselective hypercyclic autocatalysis

The so-called hypercyclic model [16] solves the problem of how to perform replicator selection, i.e. to achieve exponential growth dynamics based on quadratic autocatalysis. Recently, it has been shown that the model is also able to yield SMSB, and this means enantiomeric selection in the case of chiral replicators [27]. The simplest reaction network of hypercyclic enantioselective autocatalysis is that involving two chiral replicators:

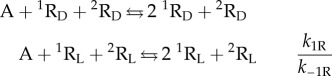2.7

and

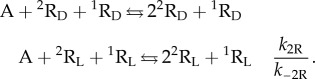2.8

Species A represents the achiral resources to form the chiral replicators, ¹R and ²R, which show additional homochiral cross-catalysis between them. Notice, that the model assumes enantiospecific growth arising from the replicating reaction mechanism (template mechanism). There is also the key stereochemical question prior to SMSB: that is, how are homochiral polymer chains formed instead of the diastereomeric polymers formed by heterochiral building blocks? This is a consequence of the template mechanism of polymer formation. In this respect, there is experimental evidence that the formation of racemic mixtures of homochiral polymers results the stereospecificity of the template mechanism [40–43].

2.2.1.4. Viedma deracemization mechanisms

Deracemization of enantiopure crystal mixtures (racemic conglomerates) of compounds, which are achiral or racemize in solution, occur under the action of crystal grinding of their saturated solutions [11], or temperature gradients [39,40]. Viedma deracemization is a paradoxical phenomenon of not only theoretical interest (see for examples refs. [44,45]) but also when applied to the preparation of enantiopure organic compounds [46]. Furthermore, it probably also occurs in the self-assembly of achiral compounds to chiral aggregates [47], and theoretically may also occur in polymerizations [48].

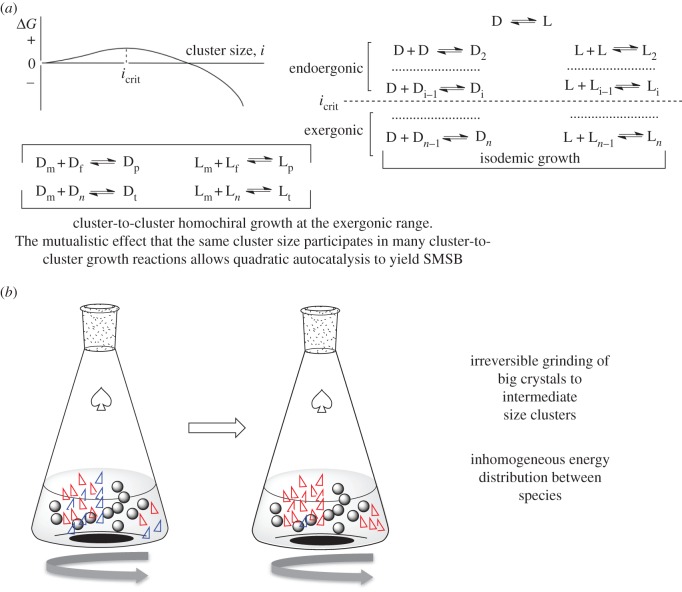
The mechanisms of the Viedma phenomenon are the subject of ongoing controversial discussions. In our opinion, this is due to the fact that the mechanisms of crystal growth (modelled as reaction networks) are discussed jointly with other features (thermodynamic system), such as grinding and permanent temperature gradients, which are responsible for keeping the system in non-equilibrium stationary states, and are therefore subject to misinterpretation. In this respect we consider here the fundamental Viedma reaction network (figure 3a) and discuss later the thermodynamic system that finally leads to SMSB (figure 3b). A Viedma reaction network contains the following three elements [44] (figure 3a):

• (a) A growth process that is endergonic during its initial steps, but that from a critical size of the aggregates onward (clusters in crystallization), transforms into exergonic by virtue of cooperative effects.

• (b) In addition to isodesmic ‘polymerization’, homochiral cluster-to-cluster growth must be present. Only the latter gives nonlinear kinetic dependences capable of yielding SMSB.

• (c) The cluster-to-cluster growth mechanism involves a range of sizes. Therefore, the product of a cluster-to-cluster aggregation contributes as well to the formation of other homochiral clusters. Most likely, this mutualistic effect creates an exponential growth greater than that of the quadratic dependence of a single cluster-to-cluster step. This is an important point that requires further detailed study, principally because it bears some analogies with the role of cross-catalysis in hypercyclic replicators.

Figure 3.

Scheme of the reaction network and thermodynamic system of Viedma deracemization [11]. (a) Viedma reaction network: free-energy aggregation diagram, according to the classical theory of primary nucleation showing a free energy profile of cooperative polymerization with the existence of critical cluster/oligomer size (i_crit). Cluster-to-cluster mechanisms of growth give a quadratic nonlinear kinetic dependence. The mutualistic effect that a specific size be formed by different cluster sizes may lead to exponential growth dynamics for SMSB [44]. (b) Thermodynamic system: crystal grinding in their saturated solution yields small clusters which are more soluble that the bigger ones, i.e. it maintains the crystal growth in a stationary state. The unidirectional cycle of matter flux through the crystal growth mechanisms reveal the potentiality of the reaction network for SMSB. The same effect can be created by the different supersaturations provided by permanent temperature gradients [49,50]. (Online version in colour.)

Notice that in the former reaction network it only exists in supersaturated solutions. In saturated solution there are only fluctuations between the crystal and the monomeric species occurring by the isodesmic growth mechanism, i.e. the ee of any crystal mixture showing similar crystal sizes (same solubility for all crystals) cannot change. This provides an additional fascinating element to the Viedma deracemization: the stabilization of final crystal outcome once the grinding ceases or a homogeneous temperature distribution is achieved.

2.2.2. Characteristics of the thermodynamic systems versus reaction networks leading to spontaneous mirror symmetry breaking

The final fate of all enantioselective reaction networks able to yield SMSB (2.2.1) in closed systems with homogeneous distributions of energy and mass, and because the backward reactions rates are non-zero, is thermodynamic equilibrium (racemic composition). A necessary condition for SMSB is a thermodynamic system unable to achieve thermodynamic equilibrium with its surroundings, such as in an open system to matter or a closed system with an inhomogeneous distribution of energy, temperature or matter. The condition of a system unable to achieve thermodynamic equilibrium with its surroundings is a current scenario in chemical synthesis. Most of the synthetic procedures, including those of the so-called thermodynamic controlled reactions, correspond to final NESS. For example, a reaction under reflux shows a permanent temperature gradient between the heated walls of the flask and the dropping liquid phase returning to the reacting solution, therefore the final state is non-equilibrium.

The architecture of the thermodynamic system with respect to the components of the reaction network (species and/or reactions) is crucial for achieving SMSB or not: for example a specific reaction network in an non-adequate thermodynamic system will lead to stable stationary states of racemic composition, but can lead to SMSB in thermodynamic systems of different configurations [8,9].

In the following, we describe theoretical and experimental examples of the role of the thermodynamic system with respect to the reaction network able to achieve SMSB.

2.2.2.1. Open flow systems

Continuous stirred tank reactors (CSTR) and tubular open flow reactors (OFR) imply the entry of a specific volume of reactant solutions and the exit of the same volume of the actual concentrations (those within the tank reactor) of all reaction network species. In the approximation of perfect mixing, the dynamics in CSTR and OFR are easily simulated by differential rate equations: constant inflow of a solution volume with specific concentrations of the initial reagents (zero order rate constants) and the outflow of the same volume of the actual species of the solution (first order rate constants).

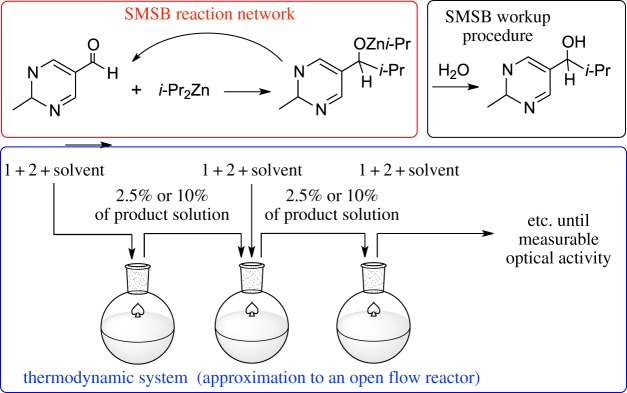
The Soai reaction [10] (figure 4) shows a complex reaction mechanism, but its reaction network, in our opinion, can be reduced to a Frank-like reaction scheme [52,53], where the autocatalytic species of homochiral oligomers is the zinc alkoxyde, and the mutual inhibition species are the optically inactive species. The high exergocity of the reaction avoids the detection of racemization on the timescale of the synthetic bench reactions. However, SMSB in the Soai reaction is revealed by using a multistage reaction step methodology [51] where, in each step, the reactants are added to the reaction output from the previous experiment: as previously noted [7] such a procedure is an approximation of a CSTR.

Figure 4.

Differentiation between reaction network and thermodynamic system in the case of the Soai reaction [10]. Adapted with permission from ref. [51]. (Online version in colour.)

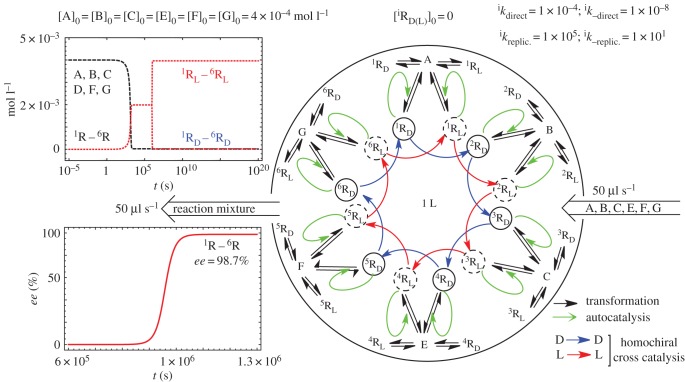
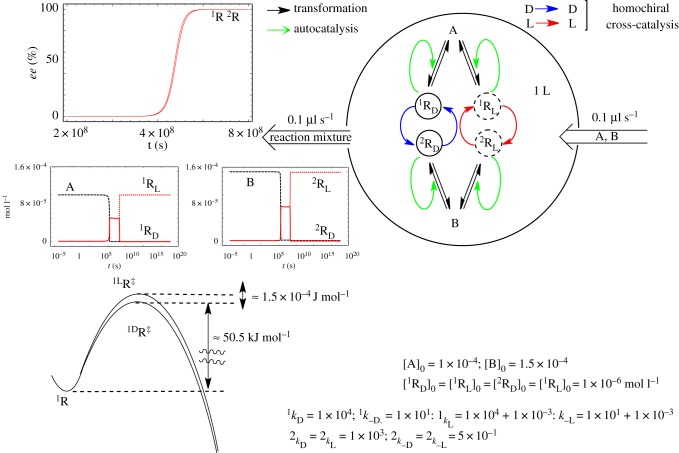
SMSB has been simulated in CSTR and OFR for several reaction networks using the numerical integration of ordinary differential equations (e.g. refs. [27,44,53]) and stoichiometric network analysis (SNA) for the stability analysis of the final stationary states [54]. Figure 5 shows the SMSB in the simulation of a hypercyclic autocatalytic reaction network in a CSTR.

Figure 5.

Simulation of SMSB in a CSTR of a six-member hypercycle, where A, B, C, E, F and G are the achiral resources of the replicators. The reaction network also includes the presence of the much slower direct non-catalytic replicator synthesis. Reproduced with permission from ref. [27].

2.2.2.2. Net flux reaction cycles

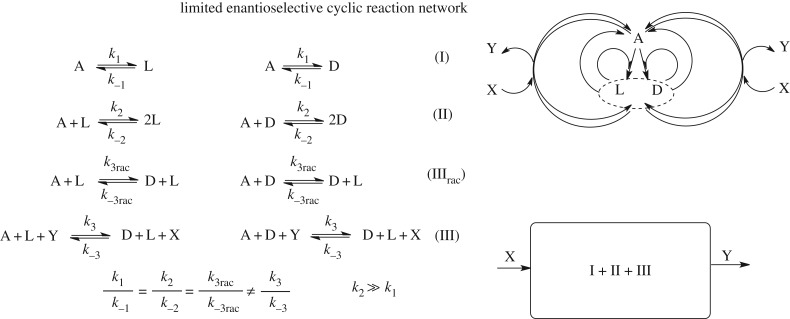
Simulation of chemical transformations in living cells must take into account the permeability and active transport through the cell membrane of only some species of the reaction network. This is a formidable task in applied synthesis, but a common scenario in living cells. A theoretical example of this is how SMSB may occur in the LES model. The LES model can overcome the microreversibility principle constraint (2.2.1.2) when additional reagents drive either enantioselective or non-enantioselective autocatalysis and when the thermodynamic system is open to these reagents (figure 6). Such a LES network creates a unidirectional flux in the cycles between initial compounds and enantiomers that, for certain reaction parameters, leads to SMSB [55,56] (figure 6).

Figure 6.

Limited enantioselective (LES) reaction network, which obeys the thermodynamic constraints of microreversibility. SMSB may be obtained in a system open to the reagents X and Y, by the formation of net unidirectional fluxes between the reactants (A, achiral) and the final enantiomeric products (D and L) [55].

2.2.2.3. Closed systems with inhomogeneous energy distribution

The energy input to an SMSB reaction network located within a closed system when transferred by an achiral force cannot lead to any bias about the racemic when the energy is distributed homogeneously to all species of the reaction network. This also occurs in a closed system, in which thermodynamic equilibrium with the surroundings may or may not be achieved. For example, heating leading to a homogeneous temperature increase merely leads to the increase of all the reaction rate constants, i.e. to a new thermodynamic equilibrium, when the system equilibrates thermodynamically with its surroundings leads inexorably to a racemic stationary state and when the system is unable to equilibrate with its surroundings to give a stable racemic NESS. In some discussion on the topic of SMSB, the energy input to a closed system is correlated with a possible achievement of SMSB, however a chiral stationary state can only be obtained when the external energy input is absorbed by only some of the reaction species, if so, then SMSB might occur.

The paradigm of SMSB by selective energy uptake is the Viedma deracemization experiment [11] by means of the mechanical grinding of the crystals in their saturated solutions (figure 3b). The elements of the thermodynamic system that reveal the potentiality of the reaction network (figure 3a) for SMSB are:

• (a) the mechanical force of grinding is provided only to the visible crystals;

• (b) the higher solubility of the smaller crystals and the crystallites created by grinding determine that for the crystal of larger sizes, the solution is supersaturated;

• (c) the former effects create a unidirectional flow of matter from the visible crystals to the smaller clusters and back to the larger crystals.

Viedma deracemization can also occur via the effect of permanent temperature gradients (for example [49,50]). In this case, with effective mass transport and perfect mixing, different temperature regions show different critical cluster sizes, i.e. different saturation values and free energy profiles of the cluster size distribution, that determine the formation of unidirectional flux through the SMSB autocatalytic cycle.

A theoretical case of SMSB by means of specific energy uptake is that of the LES reaction network in a scenario of deep ocean hydrothermal vents [56]: the different energy uptakes between the enantioselective autocatalysis and the non-enantioselective autocatalysis takes place due to the compartmentalization, at different sites held at very different temperatures, of each one of the two types of autocatalysis.

2.2.3. Relationships between reaction network and thermodynamic system for spontaneous mirror symmetry breaking

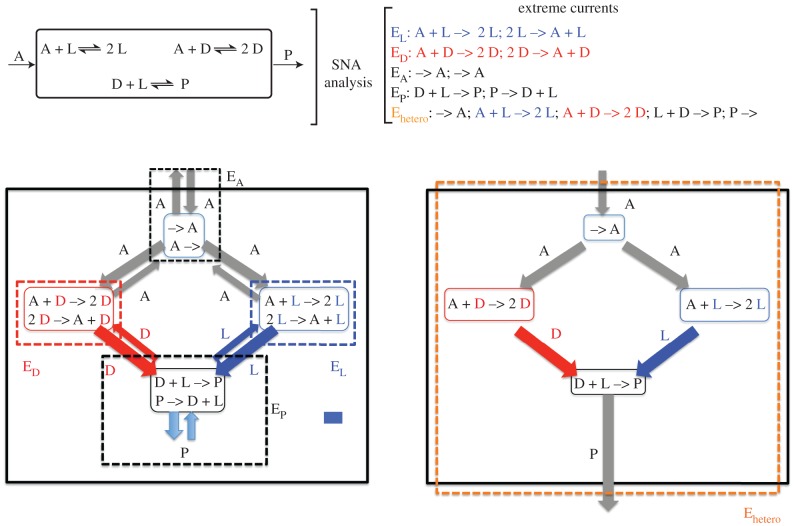
Stoichiometric network analysis (SNA) indicates the role of non-zero fluxes for achieving SMSB. Figure 7 shows the irreducible combinations of the network reactions, the so-called extreme currents from an SNA analysis, in a simple Frank-like reaction network working in a flow reactor with the entry of the achiral initial species A and exit of the mutual inhibition compound P [32]. The pair of enantiomeric fluxes (E_L/E_D) of the quadratic autocatalysis, the achiral flow E_A, and the mutual inhibition reaction (E_P) drive the system towards the racemic composition. However there is an extreme current (E_hetero), corresponding to the flux transiting through the reaction network from the entry of the initial product A to the exit of the mutual inhibition compound P, that will lead to maximum entropy production for the racemic composition and a decrease of the entropy production when the ee increases (SMSB). Therefore, the transition from an unstable racemic stationary state to one of the two degenerate but stable chiral ones, i.e. the bifurcation scenario, will arise from the competition between the irreducible currents leading to a stationary state of minimum entropy production [8,57,58]. More work is in progress on this fundamental role of the extreme current flows for achieving the transition from the thermodynamic branch to the branch of organized states.

Figure 7.

Stoichiometric flux analysis of the extreme currents of a simple Frank reaction network working in an open system with entry of the initial achiral reagent (A) and the exit of the mutual inhibition achiral compound P. The competition between extreme currents for a minimum entropy production (racemic composition for the currents on the left, and homochiral composition for the current on the right) may lead to the bifurcation scenario. Adapted with permission from ref. [54].

The results also shown that the thermodynamic system may reveal the SMSB potential of the reaction network only when net fluxes exist between the compounds in the net reaction network. In this respect, the net reaction in figure 7 is A → P, therefore the thermodynamic system able to show SMSB must imply the entry of A to the reactor and the exit of P. For example, the entry and exit of only A or the entry and exit of A, D and L cannot lead to SMSB. However, the entry and exit of all species A, D, L and P may lead to SMSB, because then the necessary current crossing the reaction network from A to P is present.

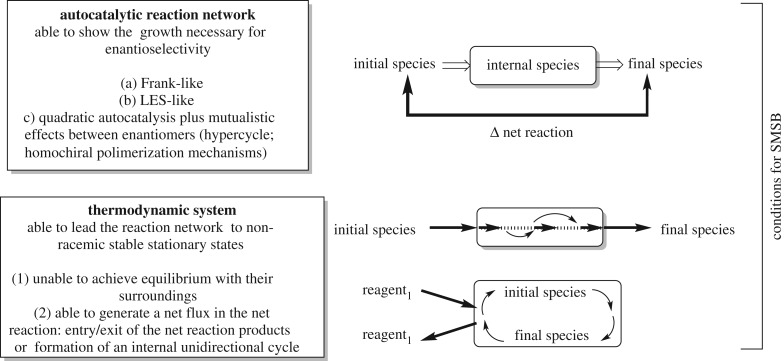
In summary, a qualitative description of a thermodynamic system able to yield SMSB, in an adequate reaction network, is:

• (a) The system must be unable to achieve thermodynamic equilibrium with the surroundings. This is a necessary condition for NESS but not a sufficient condition for SMSB.

• (b) For SMSB, a net directional flux between the initial and final products of the reaction compounds of the reaction network (see figure 8) must be formed. This flux can be established either by creating a flux crossing the reaction operative within a OFR or CSTR system, or in the case of a reaction network forming enantioselective cycles, when the energy is input to only some of the species of the reaction network, thereby creating a unidirectional net flux in the cycle.

Figure 8.

Necessary elements for yielding SMSB. The reaction network should be able to show enantiomeric nonlinearity capable of achieving the hyperbolic growth necessary for the selection between enantiomers. The thermodynamic structure of the system able to reveal SMSB of a reaction network must generate a net flux between the ‘initial and final species’ of the transformation, either by the entry and exit of specific species in the reactor, or by creating a unidirectional flux in the case of enantioselective autocatalytic cycles. These features of unidirectionality or irreversibility in the cycles/flows are what lead to the generation of entropy.

3. Abiotic track towards biological homochirality

The current models on the abiotic emergence of homochirality are based on the formation of enantiopure monomers from achiral compounds, which subsequently condensate to form homochiral polymers. Such a scenario is hampered by the problems of how to achieve such pools of enantiopure reagents in extended regions, and the assumption that racemization processes do not occur. Racemization is likely to occur to a certain degree, because of the long geological timescales and the experimental conditions where polymerizations could have occurred [59]. The hypothesis of the emergence of homochirality as a punctuated and accidental event is a deus ex machina for solving these valid criticisms. However, such a singular event scenario lacks the competitive and mutualistic effects characteristic of evolution. In summary, the present models on the transition from a diversity of organic compounds to the systems chemistry complexity of catalytic sets, quasi-species, the pre-RNA world, etc., avoid the tricky question of the emergence of homochirality assuming, either explicitly or implicitly, that it was achieved in a prior stage. This of course does not solve the problem, but merely sweeps it aside. However, the necessary role of a stochastic transition towards homochirality at the stage of formation of replicating polymers has been previously proposed [60].

Life seems to be free of racemization processes, which are first detected with the transit to death [61]. In this respect, the resilience to racemization of life's chiral machinery is presently assumed to occur thanks to 100% enantioselectivity in biological transformations, and that the crucial transformations occur under kinetic control. This latter condition assumes the approximation of the absence of reverse reaction paths. However, this overlooks that:

• (a) the free energy differences between significant chiral biological compounds are small and that the high exergonicity of most of biological reactions, where the approximation of the absence of the inverse reaction can be applied, is a consequence of the substrate transformation into an activated intermediate. Notice, that such an activation process does not change the free energy differences of the racemization/epimerization reactions between non-activated initial and final products, and;

• (b) the experimental conditions of many of the abiotic scenarios do not exclude, but even favour, racemization/epimerization reactions.

The approximation of the absence of inverse reaction paths is the root cause of many of the controversial discussions of the SMSB topic. A principle case in point is when the methodologies used from systems biology, where irreversible transformations of complex species occur, are translated to chemical reactions [62]. We may say that living species are born and die, but chemical compounds in a reaction network are born, can die and can also be ‘resurrected’ thanks to inverse reaction pathways.

To justify the resilience to racemization, in other words, the healing or repairing of the racemization/epimerization errors introduced in biopolymers, and to give a reasonable hypothesis for the formation of enantiopure polymers in abiotic evolution, we hypothesize that the present chiral machinery of life is an evolutive consequence of primordial SMSB processes which occurred during the evolutionary stages of the emergence of polymers with catalytic and replicating functionalities.

Autocatalysis is a basic property of life [9,14,15,63,64]. Furthermore, the catalytic functionalities and self-reproduction processes of life are supported in intrinsically chiral systems: this means that there is experimental evidence that life is based on enantioselective autocatalysis [65]. Furthermore, Darwinian evolution in nucleic acid polymer selection requires hyperbolic growth dynamics [28–30]. In summary, there is a strong analogy between SMSB and RNA polymer selection mechanisms. Therefore, it is a reasonable hypothesis that the emergence of autocatalysis (e.g. replicators) and polymer selection would have occurred simultaneously with the emergence of biological homochirality. Nevertheless, the abiotic evolution towards biological homochirality cannot be reduced to SMSB processes in the evolution stages of the formation of condensation polymers and replicators (terrestrial scenarios). Asymmetric inductions exerted by natural chiral forces at the first stages of chemical evolution (for example in astrophysical scenarios) would also be necessary for the emergence of biological homochirality. This is because of the stochastic character of the chiral sign distribution in a perfectly symmetric unbiased SMSB bifurcation. In this respect, we note that the emergence of replicators and condensation polymers might have taken place under compartmentalization or under heterophase interactions with catalytic supports (e.g. clays). This implies a very large number of reacting sites, so that the stochastic distribution of chiral signs of SMSB would lead to a globally racemic outcome. However, the chiral sign selection exerted by external chiral forces, acting over a spatially extended region, or when the resources of the replicators (amino acids and sugars) show a permanent albeit low bias about the racemic, the SMSB bifurcation becomes an imperfect one, thus leading deterministically to one unique chiral sign (figure 9). Despite the fact that the ee obtained during monomer formation of amino acids and sugars, via racemization processes, would evolve strongly diminished at the initiation of the subsequent stages of emergence of replicators, they would nevertheless suffice to determine the final sign of the SMSB processes. Such chiral sign selection between two enantiomeric polymers could be rightly interpreted as a primordial Darwinian phenotype selection at the emergence of genotypic replicators: the chiral manifold that adapts better to the surroundings survives.

Figure 9.

Example of the sensitivity of a SMSB system (enantioselective hypercyclic autocatalysis in an open flow reactor). A weak change on the enantioselective reaction constants of one replicator (seven orders of magnitude lower in the example) suffices to select the final chiral sign. The same effect is achieved when, instead of a chiral polarization, the enantiomeric reaction rate constants have an extremely low initial ee value. Adapted with permission from ref. [27].

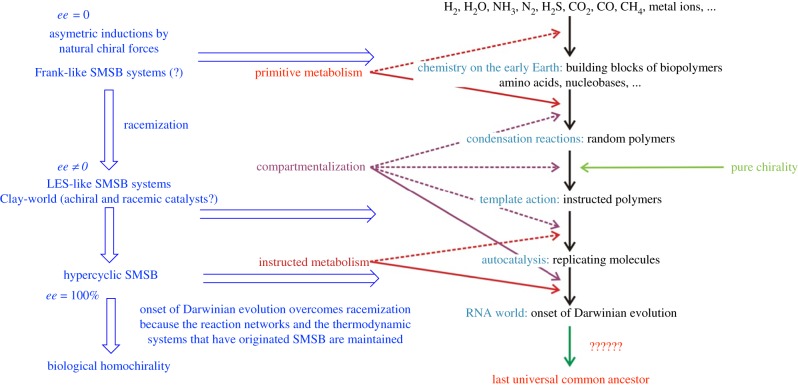
Figure 10 depicts the current description of the hierarchical stages of abiotic evolution, starting from the synthesis of simple compounds in the interstellar media, to the formation of the last universal common ancestor (LUCA) in planetary evolution. There, the current hypothesis concerning the formation of homochiral biopolymer precursors by the synthesis of condensation polymers from enantiopure pools of their building blocks is shown in green colour on the right-hand side of figure 10. Figure 10 left (in blue colour) schematizes the hypothesis presented here on the role of chirality, as a decrease in the symmetry order arriving to homochirality by SMSB during the stages of instructed polymer and replicator formation.

Figure 10.

Scheme for chemical evolution from simple molecules (astrophysical scenarios) to the systems chemistry complexity of proto-cellular systems (terrestrial scenarios) indicating their relationship with the chirality question. Adapted with the author's permission from [66]. On the right (green colour) the current hypothesis that the formation of primordial biopolymers requires enantiopure pools of building blocks. On the left (blue) the hypothesis presented here on the role of chirality during the different stages of chemical evolution: SMSB appears at the onset of polymer formation and replicator selection and, due to residual ee values coming from former simple asymmetric inductions or singular SMSB syntheses, the stochastic chiral sign distribution transforms into a deterministic final chiral sign.

3.1. Type of reaction network

Biopolymers probably have a higher preference for homochiral interactions as opposed to heterochiral ones. Furthermore, heterochiral interactions between RNA chains, such as those necessary for a Frank-like reaction network, are undesirable chemical interactions for RNA polymer selection [67]. Therefore, Frank-like reaction networks are not a reasonable chemical hypothesis for SMSB during the stages of polymer formation. Therefore, for SMSB at the formation of condensation polymers, homochiral mutualistic reaction networks are the possible reaction networks; Viedma-like for condensation polymers [48] and then hypercyclic at the replicator level, after the emergence of other catalytic functionalities [27]. Frank-like networks would be reasonable only during the early stages of chemical evolution, for example in amino acid synthesis, based on Strecker-like processes [56], or in sugar synthesis, based on the autocatalytic formose reaction [68]. However, the large ee values obtained in these initial SMSBs must be expected to survive after being rather strongly diminished at the decisive stages of biopolymer formation.

3.2. Type of thermodynamic system

The scenarios for SMSB in hypercyclic replicators should be the same as those of the pre-RNA or RNA world. This means protocell compartmentalization of small reactors open to matter exchange of some species with their surroundings.

In the previous stage of the formation of condensation polymers, reasonable chemical scenarios are those of heterophase catalysis, as thoroughly proposed but without taking into account the role of chirality, by the action of clays [69]. Such scenarios imply not only compartmentalization, but also a different site location of some of the reactions of the overall SMSB reaction network, and/or inhomogeneous energy/temperature distributions. In this respect, it is surely significant that some clays show chiral structures [70]. These clays, although present in racemic mixtures, provide excellent justification for enantioselective catalytic mechanisms. Theoretical examples of SMSBs in a LES reaction network siting both of the above-mentioned autocatalysis at two different sites at different temperatures, have been reported for the scenario of deep ocean hydrothermal vents [48].

3.3. Homochirality as a driving force?

The hypothesis presented here implies a progressive decrease of the symmetry order and the corresponding increase of ee values along the abiotic chemical evolution pathway: achiral → racemic → homochiral. Furthermore, living system catalysts are not only chiral but are also asymmetric (point symmetry group, C₁). Enzymes and nucleic acid tertiary structures are not only chiral, but asymmetric (C₁) they belong to the lowest symmetry order, as they are composed of structurally related, but non-identical building blocks. In this respect biopolymers formed by a unique chiral building block yield chiral tertiary structures of higher symmetry order than C₁ (e.g. C₂ helices), which exhibit a tendency towards enantioselective interactions hindering polymer selection processes. By contrast when the chains are formed by homochiral but non-identical building blocks polymer selection is possible (compare the results of ref. [67] with those of ref. [43]). This suggests an advantage of asymmetry in evolution leading to the chemical systems constituting protocells. Such an advantage of asymmetry for the emergence of efficient catalysis should be a consequence of entropic/information theoretic aspects concerning not only the potential information of complex asymmetric structures, but also to entropy production changes in the free energy profile of the reaction coordinate of catalytic processes.

Data accessibility

This article has no additional data.

Authors' contributions

All the authors participated equally in the review work and participated in the interdisciplinary discussions on the basis of their expertise, which lead to the concepts and critical points reported here. J.M.R. wrote and edited the manuscript which was corrected by D.H. and A.M.

Competing interests

We declare we have no competing interests.

Funding

Financial support was provided by MINECO (Project CTQ2013-47401-C2-1/2). The work forms part of the COST Action CM1304 ‘Systems Chemistry’ (European Union) and of the project no. 2014SGR10 (Generalitat de Catalunya).