Sub-10 Nanometer Feature Size in Silicon Using Thermal Scanning Probe Lithography

Abstract

High-resolution lithography often involves thin resist layers which pose a challenge for pattern characterization. Direct evidence that the pattern was well-defined and can be used for device fabrication is provided if a successful pattern transfer is demonstrated. In the case of thermal scanning probe lithography (t-SPL), highest resolutions are achieved for shallow patterns. In this work, we study the transfer reliability and the achievable resolution as a function of applied temperature and force. Pattern transfer was reliable if a pattern depth of more than 3 nm was reached and the walls between the patterned lines were slightly elevated. Using this geometry as a benchmark, we studied the formation of 10–20 nm half-pitch dense lines as a function of the applied force and temperature. We found that the best pattern geometry is obtained at a heater temperature of ∼600 °C, which is below or close to the transition from mechanical indentation to thermal evaporation. At this temperature, there still is considerable plastic deformation of the resist, which leads to a reduction of the pattern depth at tight pitch and therefore limits the achievable resolution. By optimizing patterning conditions, we achieved 11 nm half-pitch dense lines in the HM8006 transfer layer and 14 nm half-pitch dense lines and L-lines in silicon. For the 14 nm half-pitch lines in silicon, we measured a line edge roughness of 2.6 nm (3σ) and a feature size of the patterned walls of 7 nm.

Mask-less techniques are required for prototyping of ultimately scaled devices and to fabricate the masters and mask for nanoimprint and for high-volume lithography such as deep ultraviolet lithography (DUV) and extreme ultraviolet lithography (EUV). Whereas water immersion DUV has reached its physical limits at approximately 75 nm pitch, EUV theoretically reaches in the current implementation 13 nm half-pitch according to the manufacturer. The technology, in principle, scales to resolutions below 10 nm, as shown by extreme ultraviolet interference lithography.¹ Also several mask-less techniques such as electron beam lithography (EBL) in ultrathin resist layers,^2,3 electron beam induced deposition (EBID),⁴ and helium ion beam lithography (HIBL)⁵ have demonstrated sub-10 nm resolution capabilities in patterning dense lines with tight pitch. Using EBL, the transfer of sub-15 nm half-pitch patterns into silicon was demonstrated and used for subsequent nanoimprint and metal lift-off.⁶

Scanning probe lithography (SPL) provides similar resolution with minimal substrate interference and proximity effects. It operates in ambient conditions and allows in situ nondestructive inspection and on the fly correction of the patterning parameters.⁷ Application examples include the fabrication of semiconductor nanoscale devices,⁸ the chemical activation of polymer surfaces to create protein gradients,⁹ and the patterning of 10 nm wide chemical guiding patterns for block copolymers.¹⁰ SPL has also been used to directly pattern novel materials such as graphene¹¹ and 2D WeS₂ layers.¹² In addition, thermal SPL (t-SPL) has demonstrated an overlay accuracy of better than 5 nm¹³ and the capability to fabricate 3D depth profiles with nanometer scale accuracy.¹⁴

The resolution in t-SPL is highest for shallow patterns because of the conical shape of the tip. Consequently, the transfer of such patterns into functional structures on a substrate is challenging. In recent work, we introduced¹⁵ and optimized¹⁶ a versatile three-layer stack that is able to transfer sub-20 nm lateral and 5 nm vertical amplitude t-SPL patterns into a substrate by etch transfer or into metal features by a lift-off process. At such dimensions, little is known about the mechanisms controlling pattern formation. Whereas for deep patterns the shape of the pattern is similar to the tip shape,¹⁷ this is less obvious for nanoscale patterns. Moreover, for highly cross-linked materials and thermomechanical indentations, a mechanical interaction between neighboring indents limits the resolution,¹⁸ but it is not clear whether this mechanism also holds for non-cross-linked and self-amplified depolymerization resist material.¹⁹

Here, we present a detailed study of the t-SPL parameters that influence high-resolution patterning on the transfer stack and demonstrate that sub-15 nm half-pitch resolution patterning and transfer by t-SPL are feasible. First, we examine the critical etch step in the transfer process and determine the minimum thickness of the imaging layer as well as the minimum pattern geometry needed for a successful transfer. Benchmarking against these limiting values, we then investigate pattern formation in the optimized stack as a function of the patterning temperature and applied force. For the optimized conditions obtained, we study the pattern geometry as a function of the distance between neighboring lines, identifying plastic deformation as the major factor limiting resolution. The transferred patterns are studied using scanning electron microscopy (SEM) and scanning transmission electron microscopy (STEM), revealing ∼7 nm feature size in 14 nm half-pitch patterns. Finally, the mechanisms governing the line shape and limiting the resolution are discussed.

Results

In t-SPL, we use a hot tip to pattern lines into the polyphthalaldehyde (PPA) layer of a pattern transfer stack, as shown in Figure 1a. In ref (16), we demonstrated a successful pattern transfer for 5 nm deep patterns in a 9 nm thick PPA layer on 3 nm SiO₂. The thinning step for the PPA film (first step in Table 1; see Methods) was identified to be the critical part of the etch transfer process. In this study, we changed the patterning stack by placing an additional 2 nm thick poly(methyl methacrylate) (PMMA) layer between the SiO₂ hard mask and the PPA layer, keeping a total thickness of 8–9 nm. As the etch characteristics of PMMA in the O₂/N₂ plasma are similar to those of PPA, the total etch behavior has not changed significantly. However, the PMMA layer is not consumed in the patterning process and thus provides a soft landing layer for the hot tip reducing tip wear. Moreover, it adds additional thermal isolation to the transfer stack, as is evident from the lower tip heater temperatures required for successful patterning in this study.

Figure 1.

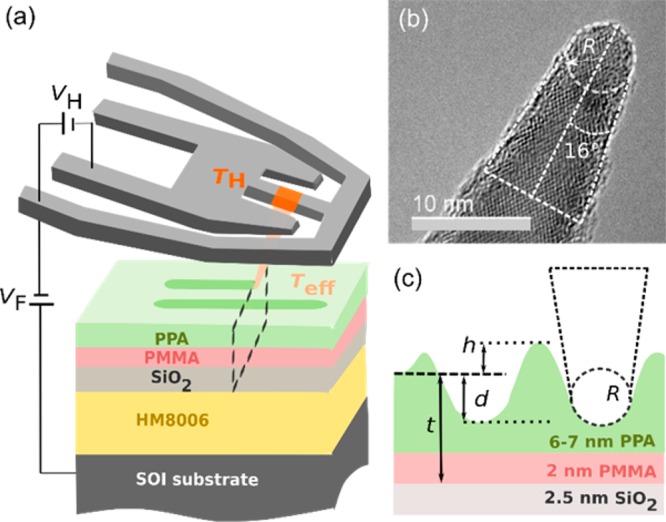
(a) Schematic of the t-SPL patterning mechanism on the pattern transfer stack. The tip resting at a distance of 250 nm is heated to a temperature T_H by applying the voltage V_H to the resistive heater. A voltage V_F is applied between the substrate and the cantilever to pull the tip into contact with the PPA surface for each patterning pixel. After contact, the polymer temperature is elevated to T_eff < T_H. (b) TEM image of an unused tip. The apex radius R is ∼3 nm. The estimated half-angle of the tip cone is 16°. (c) Schematic line shape profile for two consecutive lines. Between trenches of depth d a rim of height h is formed. The total thickness t of the polymeric PMMA and PPA layers is 8–9 nm.

Table 1. Etch Details in the Transfer Process.

etched layer	gases	power (W)	set pressure (mTorr)	etch time (s)
PPA+PMMA	1:4 O2/N2	10	15	4–6
SiO2	CHF3	100	15	12
HM8006	O2	20	15	75
Si	1:3.3 SF6/CHF3	200	15	16

Key for high-resolution patterning is the sharpness of the tip (see Figure 1b). Six randomly selected tips were imaged with atomic resolution in the TEM, as described in ref (20). We measured tip radii in the range of 2.5 to 3.5 nm with a 1–2 nm thin native oxide covering the crystalline silicon. A typical profile of dense lines patterned into a PPA layer of thickness t is shown in Figure 1c. The pattern depth d and the height h of the profile between consecutive lines are the parameters relevant for the pattern transfer. This profile has to be thinned by an O₂/N₂ reactive ion etching (RIE) step in order to reliably open the SiO₂ hard mask. For this critical step, we formulate the following three criteria. First, the remaining film thickness (including roughness) after thinning of the PPA layer needs to be sufficiently thick to protect the SiO₂ mask from being etched in the subsequent pattern transfer steps. Second, the residual material in the trenches needs to be completely removed for a reliable opening of the SiO₂ membrane. Third, the thinning process needs to be stable in the plasma etch tool.

We first investigate the plasma etch behavior of the PPA and PMMA polymer layers on the pattern transfer stack see Figure 2a). We find that the etch rate is high for the first 5–10 s. We attribute this behavior to the increased pressure in the chamber (strike pressure = 60 mTorr) which settles to the final pressure of 15 mTorr in roughly 7 s. Once the base pressure has been reached, etching slows down significantly, approaching an etch rate of approximately 10 nm/min in thicker films.^16,21 In addition, we found that the last two nanometers close to the hard substrate were much harder to remove (see Figure 2a). Clearly, the etch time has to be timed precisely in order to obtain reproducible results. However, the etch tool does not account for the variability of the plasma ignition after pressing the start button. This would add uncertainties on the order of fractions of a second to the time measurement. Therefore, we observed the ignition of the plasma by eye and controlled the total etch time manually. We chose to etch for a duration of nominally 6 s, for which we expect from the graph that a variation in etch time by 1 s leads to a difference in thinning of 0.5 nm. In these 6 s, 5–6 nm of the polymer is consumed, which sets the total film thickness of the polymer layers to 8–9 nm to provide a sufficient protection of the unpatterned surface of 3 nm.

Figure 2.

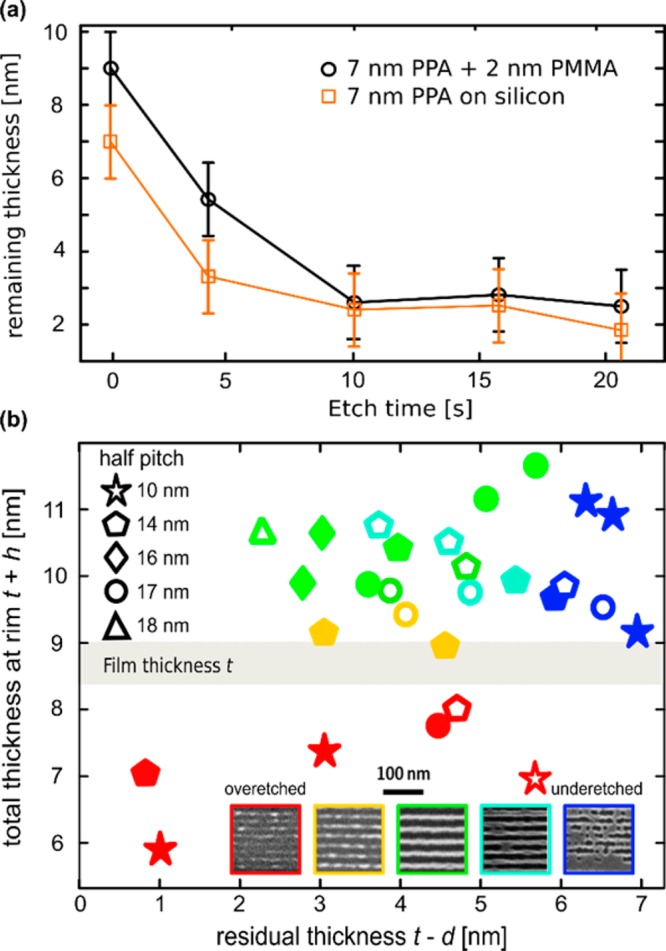
Etch characterization. (a) Remaining polymer thickness of an initially 9 nm thick PMMA (2 nm) and PPA (7 nm) layer on the pattern transfer stack and a 7 nm thick PPA layer on silicon as a function of the etch time in the O₂/N₂ plasma. The errors involved in the atomic force microscopy (AFM) measurements of the film thickness are estimated to be 1 nm. (b) Quality of transferred patterns as a function of PPA pattern geometry for 10 nm (stars), 14 nm (pentagons), 16 nm (diamonds), 17 nm (circles), and 18 nm (triangle) half-pitch lines. The colors indicate whether the transferred patterns (insets) were overetched (red), slightly overetched (yellow), defect free (green), slightly underetched (cyan), or underetched (blue). Etch times of 4 s (open symbols) and 6 s (filled symbols) were used. Each data point was calculated from average d and h values and the film thickness t, measured by AFM. The area shaded in gray indicates the measured range of film thicknesses t = 8.7 ± 0.3 nm of the spin-coated PPA and PMMA layers.

For six patterned and processed samples, we precisely measured d, h, and t and correlated the data to the fidelity of the patterns after transfer into silicon. The results are shown in Figure 2b. The final patterns of the silicon nanowires (SiNWs; see insets) were rated in five steps from being underetched (trenches not fully transferred) to overetched (walls exhibiting gaps). Each of these samples had been used to pattern several arrays of lines with half-pitches of 10, 14, 16, 17, and 18 nm. Each point of the graph corresponds to the average value of the atomic force microscopy (AFM) cross section over an array of t-SPL lines. We converted the measured film thickness t, the average heights h between consecutive lines, and the average pattern depths d into a residual film thickness in the trench, t – d, and a total thickness of the film at the rim position, t + h. Four of the samples were etched for 6 s (filled symbols) and two for 4 s (open symbols).

We find that for all our samples etched for 6 s, the transfer resulted in defect free patterns (green) for sufficiently deep patterns (t – d ≤ 5.5 nm) and for a, compared with the film thickness, elevated rim t + h ≥ 9.5 nm. For 4 s etch time, more underetched samples were found, consistent with Figure 2a, indicating that 1–2 nm less material was removed. The data indicate that the etch process is controlled with a precision better than 0.5 nm. Furthermore, a reliable transfer process is achieved using 6 s etch time if the written patterns fulfill the two criteria h > 0.5 nm and d > 3 nm. Note that for all samples the surface outside the patterned areas was not overetched. We attribute the beneficial effect of a positive rim height to a better stabilization of the patterned walls during the etch process. We note that the formation of the rim was previously observed in plowing nanolithography²² and exploited for pattern transfer.²³

Using these requirements as a benchmark for the patterns, we now investigate the pattern formation as a function of the applied force and temperature. Despite using reproducibly sharp tips, there still are variations in the patterning behavior, which are likely caused by a varying thermal resistance of the nanometer scale tips. Therefore, the optimal temperature and force conditions to pattern arrays of lines at a given half-pitch must be determined. For this, we screen the patterning behavior by patterning small arrays of dense lines in a temperature and force grid. Figure 3a shows an AFM topographic image of the patterns using 14 nm half-pitch. The heater temperature varies along the vertical axis from T_H = 525 to 800 °C in increments of 25 °C. The applied force varies from 0 to 30 nN along the horizontal axis. The range of the force decreases with the temperature because at higher temperature less force is needed to reach the same depth.

Figure 3.

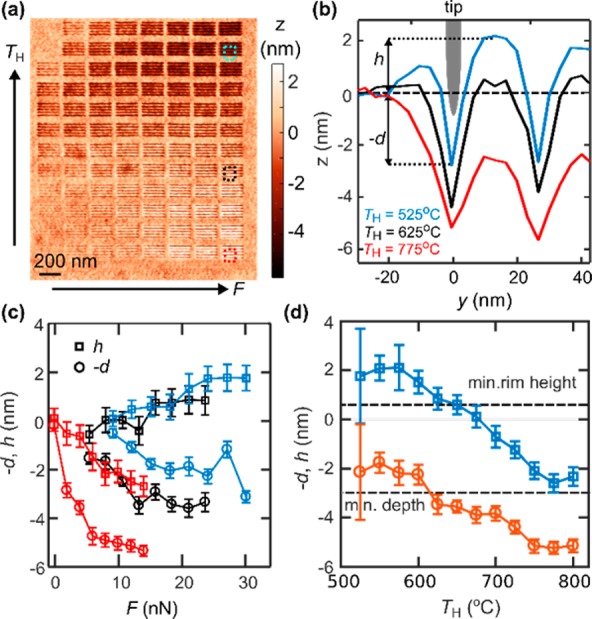
Force–temperature screening of high-resolution t-SPL lines. (a) Topography image of arrays of 14 nm half-pitch lines patterned by t-SPL. Each array consists of five individual lines and is patterned under different force and temperature conditions. The temperatures range from 525 to 800 °C and the forces from 0 to 30 nN. (b) Average cross sections for T_H = 525 °C (blue), 625 °C (black), and 775 °C (red) of consecutive patterned lines indicated by the dotted boxes in (a). The maximum elevation between the lines is h and the pattern depth d. The tip is sketched at scale for comparison. (c) Line depth d (circles) and rim height h (squares) as a function of the applied force for the three temperatures mentioned in (b). (d) Average h and d for the two highest forces as a function of heater temperature T_H. For successful pattern transfer and sufficient protection of the unpatterned surface, a minimum rim height of 0.5 nm and a minimum depth of 3 nm are required, respectively. The best pattern transfer performance is expected for a temperature of 625 °C.

Cross section profiles for hot (T_H = 775 °C), cold (T_H = 525 °C), and intermediate (T_H = 625 °C) patterning conditions are shown in Figure 3b. The height h of the rim and the line depth d are measured from the surface level (see Figure 3b). For cold patterning (T_H = 525 °C and F = 30 nN), the profile consists of a groove and a rim adjacent to the groove. The rim (h > 0) is a sign of plastic deformation,²⁴⁻²⁶ in which material from the center of the line is pushed to the outside. For hot patterning, the rim is absent, and the maximum height between two neighboring lines remains below the surface level, h < 0. Note also that the width of the patterned lines increases from cold to hot patterning.

Figure 3c displays the line depth d and the rim height h as a function of the applied force. For cold patterning, a threshold force is required to initiate the patterning. We attribute this fact to the existence of a finite yield stress for mechanical deformation that must be overcome. Similarly, the elastic modulus of the polymer is still substantial, and high forces are required to reach significant patterning depths. Moreover, a rim is formed adjacent to the lines due to plastic deformation of the material. For intermediate temperatures, the yield stress reduces to zero, indicating that the material approaches the glass transition at approximately 650 °C heater temperature (see Supporting Information). At the same time, the rim vanishes and is absent for higher temperatures. For hot patterning, the initial slope of the patterning depth is on the order of 1 nm/nN. Such a sensitive patterning behavior has also been observed on thicker films and is ideal for grayscale patterning.²⁷ However, for the high-resolution patterning discussed here, the hot conditions lead to a widening of the observed line profiles, a reduction of h, and thus to a loss of achievable resolution. Owing to the finite PPA film thickness of 6–7 nm, the patterning depth levels off at 5 nm. Both the absence of the rim and the small residual PPA thickness of ∼1 nm indicate that PPA is efficiently decomposed and removed from the surface using hot conditions.

For pattern transfer, minimum values for d and h need to be fulfilled (see Figure 2b). Their maximum values within the force range used here are shown in Figure 3d as a function of temperature. Although d is highest for hot patterning, h is negative, which would necessitate a thicker PPA layer for a successful transfer. For intermediate and cold patterning, h becomes positive, but d decreases. Using the two limiting values determined above, we expect an optimal pattern transfer using T_H = 625 °C, for which we obtain h = 0.9 ± 0.4 nm and d = 3.5 ± 0.4 nm. In total, we studied 25 samples using new, randomly selected tips for each sample and generally found similar results. For all tips and samples, resolutions at or below 16 nm could be achieved, providing sufficient d and h values for an etch transfer. The optimal force and temperature values for the best patterning were found to be 25 ± 6 nN and 550–700 °C, respectively. Despite this tip-dependent variability of the optimal conditions, the patterning regimes discussed above and their corresponding line profiles are common to all the samples and independent of the tip. The capability to find and maintain the optimal patterning parameters in situ is a key strength of t-SPL for achieving reliable high-resolution patterning and pattern transfer.

Next, we study the geometry of the patterned lines as a function of the half-pitch of the dense line patterns for optimized patterning conditions. For this, we patterned several arrays of dense lines with increasing half-pitch. Figure 4a shows the AFM topography of the line arrays with half-pitches of 10, 14, 17, 21, and 30 nm, patterned with the same tip at 600 °C and 24 nN. Averaged cross sections of two consecutive lines are shown for the lowest four half-pitch values in Figure 4b. We again analyze the height of the rim h and the line depth d and plot the results as a function of dense line half-pitch values (see Figure 4c).

Figure 4.

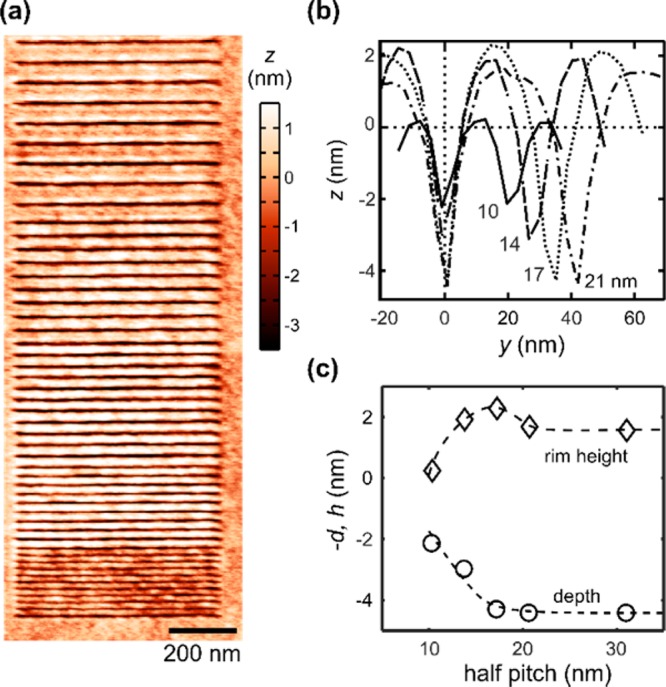
Interference of consecutively patterned lines as a function of the pattern half-pitch. (a) Topography image of line arrays patterned with half-pitches of 10, 14, 17, 21, and 30 nm at 600 °C and 24 nN. (b) Average cross sections of two consecutively patterned lines from (a) for the four lowest half-pitch values. The horizontal dashed black line marks the unpatterned PPA surface level. (c) Average line depths (circles) and rim heights (diamonds) as a function of the half-pitch. Dashed lines are guides for the eye.

At 30 nm half-pitch, the line patterned last does not interfere with the previous line (cross section not shown). At this pitch, d ∼ 4.2 nm and h ∼ 1.5 nm are sufficient conditions for a stable pattern transfer. At 21 nm half-pitch, the rims merge to a wider elevation with similar h and d values. At 17 nm half-pitch, h increases and d is still unaffected. Below 17 nm half-pitch, d reduces sharply, to 70 and 50% of the initial value at 14 and 10 nm half-pitch, respectively. At the same time, h decreases to 0 at 10 nm half-pitch. Clearly, for 14 nm half-pitch, a pattern transfer is still possible, but the 10 nm half-pitch pattern is too shallow for a successful transfer.

Figure 5 shows the results of the high-resolution SiNWs fabricated after applying optimal t-SPL pattering conditions for a successful pattern transfer through the transfer stack to the ultrathin silicon-on-insulator (SOI). In Figure 5a, a SEM in-lens image of two arrays of 10 SiNWs at 14 and 16 nm half-pitch is shown. The PPA layer thickness was 6.8 nm. The patterning conditions were 550 °C and 30 nN. The PPA thinning etch time was 6 s. Using the edge analysis method described in previous works,^16,21,27 we calculated the 3σ line edge roughness (LER). We obtained an LER of 2.6 ± 0.4 nm for the 14 nm half-pitch pattern and 2.4 ± 0.3 nm for the 16 nm half-pitch pattern. The values obtained are slightly better than the 2.9 ± 0.5 nm reported previously.¹⁶

Figure 5.

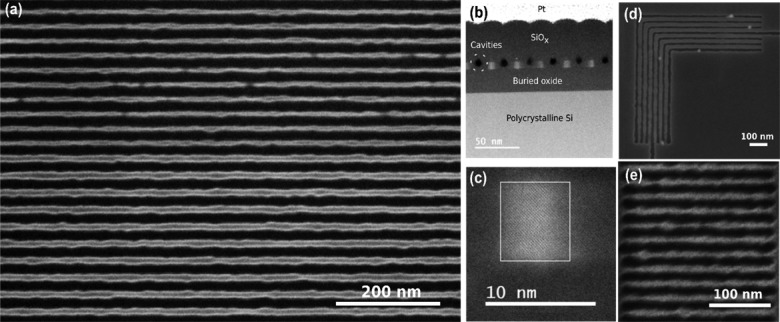
(a) SEM image of SiNW patterns with half-pitches of 14 nm (top) and 16 nm (bottom). For the 14 and 16 nm half-pitch SiNWs, a LER (3σ) of 2.6 ± 0.4 nm and 2.4 ± 0.3 nm was measured, respectively. To perform the LER analysis, the whole area of the image for each half-pitch was taken. The error values given denote standard deviations of the LER measured for at least 20 edges. (b,c) STEM cross sections of a 14 nm half-pitch SiNW array. A lamellae was prepared by focused ion beam milling after deposition of 45 nm SiO_x by plasma-enhanced chemical vapor deposition and a thick layer of Pt. The black holes (marked by the white dashed circle) are cavities formed during the deposition of SiO_x. The STEM image in (c) resolves the crystalline silicon lattice of the sub-10 nm wide nanowires. The box is a guide for the eye. (d) 14 nm half-pitch L-shaped SiNWs; (e) 11 nm half-pitch dense lines transferred into the 20 nm HM8006 transfer mask.

The resolution of our SEM is not sufficient to determine the line and trench dimensions of the dense lines reliably. To assess these dimensions, we therefore performed STEM high-resolution imaging of focused ion beam (FIB) prepared cross sections of a 14 nm half-pitch SiNW pattern (Figure 5b) transferred into a nominally 12 nm thick silicon layer of a SOI substrate (see Figure 1a). In Figure 5b, the Pt and SiO_x capping layers, the SiNWs, and the 25 nm buried oxide are shown. We attribute the black features to air cavities formed in the SiO_x plasma-enhanced chemical vapor deposition step. One of the SiNWs imaged at atomic resolution is shown in Figure 5c. This image shows that the SiNW is crystalline and is approximately 7 nm wide. The faded outline of the crystalline structure is due to the LER discussed above. Given the 14 nm half-pitch of these structures, the 7 nm wide silicon lines reveal that the trench width after pattern transfer was ∼21 nm. This is consistent with previous observations of higher trench dimensions in the transferred pattern compared with those in the patterned dimensions.²¹ This effect is caused by the finite tip size and the imperfectly anisotropic character of the etch transfer.

Figure 5d shows that also dense L-lines can be transferred at 14 nm half-pitch. The PPA layer was 6 nm thick, and the PPA thinning etch time was 5 s. The SiNWs in both directions are continuous, but the SiNWs along the vertical (slow scan) direction exhibit a higher LER. Figure 5e shows an example of a successful transfer of 11 nm half-pitch lines to a 20 nm HM8006 layer. The PPA layer thickness in this case was reduced to 5 nm to decrease the residual thickness and avoid underetching. The rim height of the patterns was h = 1.5 nm, the pattern depth was d = 2.5 nm. The PPA thinning etch time was 5 s.

Discussion

Our experiments reveal that, for highest resolution patterning of substrates by t-SPL, the details of the etch transfer process including the thickness of the polymeric layers on the SiO₂ hard mask and the line shape of the patterned lines have to be considered jointly to achieve a successful sub-15 nm half-pitch pattern transfer. Moreover, our analysis of the line shape provides insight into the physical processes that govern the line formation at these highest resolutions and thereby limit the resolution of t-SPL patterning on the patterning stack.

We show in Figure 3b that, with increasing temperature, d increased but that the sidewall slope decreased. We can understand this effect by considering the mechanical indentation and the temperature distribution in our system (see Figure 6a).

Figure 6.

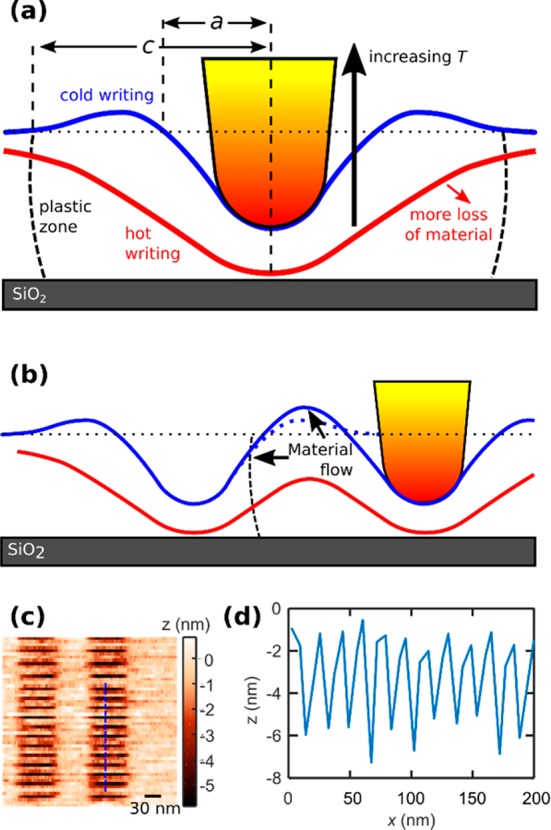
(a) Schematics of the patterning process. Blue and red lines indicate estimated profiles for cold and hot (above the decomposition temperature) patterning, respectively. The profiles patterned at cold conditions are less deep because of enhanced elastic recovery. In addition, we expect that material is pushed backward along the line, partially refilling the previously patterned pixel. For hotter patterning, the yield stress is reduced and material is partially or fully removed. This leads to deeper lines at lower force. However, the temperature gradient in the tip and the stack reduces the steepness of the profile. (b) For cold patterned lines (blue line), the material flow in the plastic zone first increases the rim height (the dotted line indicates the undisturbed profile) and at closer pitch reduces the line depth. As long as plastic deformation is present, the plastic zone will have a similar extent, limiting the proximity of the neighboring lines. For hot patterning (red line), plastic deformation can be absent, but the widening of the profile restricts resolution. (c) Topography image of a 9 nm half-pitch pattern in a 5 nm thick PPA layer on 20 nm polymethylglutarimide. (d) Cross section along the blue line in (c), indicating 4 nm pattern amplitude.

At low temperatures, we observe a finite yield stress indicating that the PPA film is in the glassy state (see Supporting Information). We also observe the formation of a rim, a clear indicator of plastic deformation, as the polymer is below the glass transition temperature. In the glassy state, the elastic modulus is high, on the order of a few GPa, and high forces are required to form a permanent indent. Moreover, the subsequent indent causes plastic flow, pushing some material into the site of the preceding indent. All these effects limit the achievable patterning depth at low temperatures. The high forces also lead to an elastic deformation of the surrounding patterning stack and the material below the tip. Upon removal of the load, this elastic deformation recovers, which leads to the observed widening of the indent (a > R) compared with the shape of the tip.

For higher temperature, we find that the finite force required to nucleate a pattern and thus the yield stress of the material vanishes and the rim disappears (see Supporting Information). The vanishing yield stress is a sign for the glass transition of the material. The vanishing rim indicates that the decomposition process is triggered in the same temperature range (see Supporting Information). Indeed, in differential scanning calorimetry measurements, we found that the decomposition process is linked to the glass transition temperature.²⁸ Accordingly, the elastic modulus drops, the yield stress approaches zero, and less force is required to form deep indents. Therefore, elastic recovery should be reduced, which should lead to narrower indentations for a given indent depth, and this was indeed observed previously for highly cross-linked materials.²⁹ However, in our current experiments, we instead observe a widening of the profiles with increasing temperature. We attribute this widening to a partial decomposition of the material and a higher loss of material at the side of the indent than at the bottom of the indent. This enhanced loss of material is consistent with the temperature gradient in the system and the less confined state of the material close to the film surface (see Figure 6a).

In Figure 4, we found that at a critical pitch the depth of the lines starts to decrease rapidly. As shown in Figure 6b and observed previously,^18,29 this can be understood by considering plastic deformation. For a spherical indenter, the boundary to the fully plastic regime³⁰ is given by E*a/YR ≈ 40, where Y is the yield stress, E* is the elastic modulus, and a is the contact radius of the tip. In our system, we form indents that are deeper than the tip radius R and therefore may approximate a ∼ R. Moreover, because, for amorphous polymers, the yield stress Y is typically more than 40 times smaller than the effective elastic modulus E*, we are in the fully plastic regime. According to the spherical cavity model,³⁰ a fully plastic indentation is characterized by a “plastic zone”, that is, a spherical shell around the indenter in which the material is plastically deformed. The shell is marked at the surface by a rim with an outer radius c (see Figure 6a). Within this plastic zone, the material flows to form a volume of constant stress.³⁰ As soon as this plastic zone approaches a previously formed indent, material will flow into that space. Consistent with Figure 4b, this first leads to an increase of the rim height and, at even closer proximity, a reduction of the line depth. In previous work on highly cross-linked materials,¹⁸ we have observed that the depth of indents reduces to half of the value for widely spaced indents at a pitch of 0.75c. According to Figure 4c, this suggests c ∼ 20 nm, which is consistent with the shape of the cross sections in Figure 4b.

For patterning at higher temperatures that sill involve mechanical deformation, we do not expect the geometry of the plastic deformation to change significantly. Because the ratio c/a is a pure function of the indenter geometry in the fully plastic regime. In addition, the observed widening of the lines at higher temperature prevents the formation of more closely spaced lines with high amplitudes. Thus, our finding here is that the resolution is limited by this plastically deformed region. However, here we observe a value of c ∼ 20 nm for an indenter radius of 3 nm. In indentation theory, the extent of the plastic zone may be roughly estimated from the spherical cavity model³⁰ to be c/a ∼ 2.3. For an ideal indent, we set a = R, which would yield c ∼ 7 nm. However, also for highly cross-linked polymers at 4 nm indent, depth c was observed to be 22 nm for the best tips.¹⁸ Moreover, extrapolating to zero tip radius and zero indent depth, a limiting value c₀ = 12 nm was found. We attributed²⁹ this finding to the finite size (∼3 nm) of cooperative rearranging regions (CRR).³¹ A minimum strain is required across the CRR to trigger the fundamental motion of the polymer backbone for a permanent deformation. Therefore, the size of the CRR limits the achievable size of permanent deformations. Our results for the size of the plastic radius in non-cross-linked PPA polymer are remarkably similar, indicating that on our hard mask stack the size of the CRR was similar to that of the cross-linked system. However, it is not clear whether the thin film geometry and the confinement provided by the hard SiO₂ interface will influence the achievable resolution in the system. It is known that a hard substrate enhances the apparent hardness and yield stress of a thin soft film top layer.³² It is not clear, however, whether in nanoscale thin film experiments also the CRR is affected, which could compromise the achievable resolution in the system. Indeed, we found that for a mechanically less confined system of a 5 nm thick PPA layer on a 20 nm polymethylglutarimide (Omnicoat, MicroChem) membrane the achievable pattern amplitude at low pitch is much higher. Figure 6c,d shows the topography and the cross section of a 9 nm half-pitch pattern with an amplitude of 4 nm, indicating that for such a system it is possible to reach sufficiently deep patterns for a pattern transfer. Of course, a transfer mechanism has yet to be developed for this soft system.

Conclusion

In conclusion, we found that the resolution in t-SPL is limited by the extent of the plastic zone in thermo-mechanical indentation on the pattern transfer stack because, at temperatures approaching the resist’s decomposition temperature, the line shape widens, reducing the achievable resolution. For a successful transfer into a substrate, the properties of our pattern transfer stack and etching process determine the required minimum film thickness of the topmost imaging layer, the minimum patterning depth of 3 nm, and a favorable existence of an elevated topography between neighboring trenches. Under these geometrical constraints, we achieved reliable transfer of patterned dense lines down to 14 nm half-pitch and in the best case 11 nm half-pitch. Furthermore, there is evidence that an enhanced resolution below 10 nm half-pitch might be possible on a mechanically different transfer stack.

At 14 and 16 nm half-pitch, we find a line edge roughness of 2.4 and 2.6 nm, slightly better than in previous investigations¹⁶ and consistent with the steeper side walls observed at the colder patterning conditions. Furthermore, we succeeded in fabricating 7 nm wide features in a SOI substrate. Clearly our patterning process and the transfer characteristics currently applied²¹ favor wider trenches and narrower walls. In combination with a reliable sub-5 nm overlay accuracy,¹³ the potential to fabricate sub-10 nm features without proximity corrections in a controlled and reproducible manner creates exciting possibilities for nanoscale device fabrication.

Methods

The t-SPL resist material is polyphthalaldehyde (linear PPA, average molecular weight = 5000–8000 g/mol, Sigma-Aldrich). PPA is a self-amplified depolymerization polymer with an unzip temperature of approximately 120–150 °C, which decomposes upon contact with the hot tip, with contact times on the order of a few microseconds per pixel.²⁷ The films with 6.7 ± 0.3 nm thickness used in this work were prepared by spin-coating 0.5 wt % PPA in anisole solution at 3000–4000 rpm. Thicknesses were determined by applying a mechanical scratch which was inspected using atomic force microscopy.

The 6.7 ± 0.3 nm PPA layer is the top layer of the slightly modified pattern transfer stack,¹⁶ followed by a 2 nm PMMA (950 kg/mol, Allresist AR-P 672.02, diluted by 1:19 in anisole) tip protection layer, a 2.5 nm SiO₂ hard mask layer, and a 20 nm HM8006 (JSR Corporation) transfer layer on the substrate. As substrates, we used ultrathin silicon on insulator (SunEdison Semiconductor, USA) with a nominally 12 nm thick silicon layer and 25 nm buried oxide (see Figure 1a). The pattern transfer process by RIE is described in a previous work.¹⁶ For reference, the relevant details are summarized in Table 1.

The silicon cantilevers used in the experiments comprise an integrated thermal read sensor, a tip heater for patterning, and an electrostatic platform for efficient actuation as described in detail elsewhere.¹⁵ The tip heater is n-doped at 1.25 × 10¹⁸ cm^–3 by phosphor implantation, resulting in an intrinsic temperature of approximately 700 °C used for the temperature calibration of the tip heater.³³

The forces are calibrated by measuring the voltage required to bring the (heated) tip into contact with the surface from a defined distance as described in detail elsewhere.¹⁴ Briefly, we fit the calibration data with a capacitor spring model which then provides the forces as a function of the initial tip–surface distance, applied voltage, and tip heater temperature. We note that this procedure corresponds to the calibration of the static force and does not provide information on dynamic lever effects. Furthermore, a force constant of 0.3 N/m obtained from finite element simulations of the cantilever structure³³ was used to convert the measured distances to forces. To minimize calibration uncertainties, we determine the force when a hot tip first starts to produce a permanent feature as the zero force.

The t-SPL step for patterning the high-resolution lines was performed in the home-built scanning probe system described in previous works.^15,27 During patterning, the tip raster scans the substrate at a fixed distance of ∼250 nm. For each pixel, two voltages, V_F and V_H, are applied to create the patterns (see Figure 1a). V_H is applied to resistively heat the tip. A thermal bimorph effect in the cantilever simultaneously reduces the tip distance to ∼50 nm.¹⁴V_F is applied to the substrate to pull the tip into contact with the surface by electrostatic actuation. V_F also controls the applied force that is used to regulate the mechanical indentation part of the patterning mechanism. The hot tip is responsible for the removal of the resist by polymer evaporation. The results presented in this study were obtained from an investigation of 25 samples with identical transfer stack and materials. The samples were used for determining the optimal thicknesses and etch conditions, preparing the lamellae to be inspected by STEM, and for obtaining the results shown in the figures in the main text. The applied forces were in the range of 0–30 nN. The applied temperature T_H was in the range of 525–850 °C. However, the effective temperature T_eff reached at the PPA surface in contact with the tip is a factor of 0.4–0.6 times T_H because of the thermal resistance of the tip, the substrate, and their interface.³⁴ The patterning pixel pitch used in the etch study was 6.9 or 5.7 nm, with a force pulse duration of 5 μs and a linear scan speed of 0.15–0.20 mm/s.

For the STEM analysis of the silicon nanowires, 45 nm thick SiO_x and platinum were deposited by plasma enhanced chemical vapor deposition and thermal evaporation, respectively. A lamellae with a thickness in the range of 50–100 nm was then cut by FIB (Helios 450 S, FEI). The lamellae were inspected using a JEOL ARM200F STEM at 200 kV.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b06307.

• Detailed line geometry vs force plots and thermogravimetric analysis/differential scanning calorimetry measurements (PDF)

The work was supported by the European Commission FP7-ICT-2011 No. 318804 and by the European Research Council StG No. 307079.

The authors declare no competing financial interest.