Long-Range Organization of Membrane-Curving Proteins

Abstract

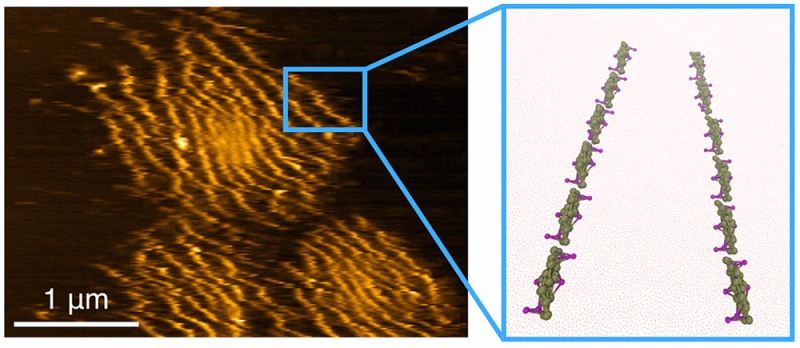
Biological membranes have a central role in mediating the organization of membrane-curving proteins, a dynamic process that has proven to be challenging to probe experimentally. Using atomic force microscopy, we capture the hierarchically organized assemblies of Bin/amphiphysin/Rvs (BAR) proteins on supported lipid membranes. Their structure reveals distinct long linear aggregates of proteins, regularly spaced by up to 300 nm. Employing accurate free-energy calculations from large-scale coarse-grained computer simulations, we found that the membrane mediates the interaction among protein filaments as a combination of short- and long-ranged interactions. The long-ranged component acts at strikingly long distances, giving rise to a variety of micron-sized ordered patterns. This mechanism may contribute to the long-ranged spatiotemporal control of membrane remodeling by proteins in the cell.

Short abstract

High-resolution imaging and free-energy simulations reveal unexpected long-ranged interactions between filaments of membrane-curving proteins.

Introduction

Lipid bilayers have a remarkable range of material properties that allow them to serve as an elastic interface between the cell and its environment. In response to cues given by proteins, membranes undergo shape changes affecting the architecture of a cell from nanometer to micrometer scales.¹ The reshaping of the membrane facilitates trafficking, communication, cell migration, infection, immune response, and other important cellular processes. However, it has become apparent that membranes can mediate the interactions among proteins,²⁻⁴ and in this way potentially initiate cellular pathways upstream of protein cues. Theory predicts that membrane fluctuations or local membrane curvature can generate effective interactions between proteins, whose sign, strength, and maximum range of interactions depends on the shape of the proteins and the way they interact with the membrane.^3,5−7 However, accounting for all of the interactions is nearly impossible in analytical modeling given the complexity of the components involved in cellular phenomena. At the same time, the highly dynamic and inherently multiscale nature of such events makes them very challenging to capture experimentally. Thus, a key question in membrane biology remains unresolved: how do proteins assemble correctly and in the right place to initiate the membrane-remodeling phenomena?

Proteins that contain one of many Bin/amphiphysin/Rvs (BAR) domains are among the most notable membrane remodelers in the cell. They have been found in a number of cellular phenomena, such as endocytosis, intracellular trafficking, cytokinesis, the formation of T-tubules, and the shaping of the endoplasmic reticulum.^8,9 Depending on their concentration and the mechanical properties of the membrane, BAR proteins couple with membrane curvature in different ways: they can detect curvature, induce large-scale membrane remodeling, and even induce membrane scission.^10,11

When bound at a sufficiently high density on the membrane, BAR proteins induce the formation of tubules whose sign and magnitude of curvature varies among BAR proteins (e.g., refs (12−18)). Tubules can emerge from the surface upon a continuous increase in local protein concentration, as shown by computer simulations^19,20 or form by breaking the bilayer topology upon a rapid high density binding of proteins, demonstrated by simulations and electron microscopy.²¹ Furthermore, the way BAR proteins pack on the membrane in this very high-density regime and the way their amphipathic helices make lateral contacts greatly impacts the stability^22,23 and the radius²⁴ of tubules.

At the onset of endocytosis, however, the surface density of BAR proteins is much lower than required to generate tubules. According to our recent coarse-grained (CG) simulations, N-BAR domains (BARs with N-terminal amphipathic helices) undergo spontaneous linear aggregation on a flat membrane, a large liposome, and even a membrane nanotube at 4–30% protein surface densities, forming filamentous oligomers and meshes.²⁵⁻²⁷ This behavior is similar to that predicted for anisotropic inclusions or spherical particles,^28,29 but the crescent shape and the amphipathic helices of the N-BARs can make linear aggregation more prominent. Moreover, owing to their anisotropy, the strength of membrane-mediated protein–protein attractions, the geometry of their assembly, and the onset of tubulation are modulated by lateral membrane tension.^13,26 Subsequent computational studies employing different models have confirmed the formation of linear aggregates and meshes by various anisotropic inclusions.^19,30 Remarkably, recent electron microscopy revealed filaments or “strings” of F-BAR proteins on membrane vesicles, a structure that hypothetically forms at the interface of a dividing cell just prior to cytokinesis.^31,32

In light of continuously emerging information on the varied roles of BAR proteins in the cell, it is key to better understand the origins of the interactions that drive their complex assembly on the membrane. Here, we studied the assembly of the N-BAR domain of endophilin, a protein whose isoforms are involved in synaptic and clathrin-mediated endocytosis, apoptosis, autophagy, mitochondrial network dynamics, and, as recently discovered, a protein that drives a fast endocytosis of some signaling receptors and bacterial toxins.^8,9,33,34 In our previous computational work, we investigated the initial assembly of individual N-BAR proteins and their effect on membrane curvature. Here, we focus on the mesoscopic scale, explicitly measuring the free energy profiles that lead to a hierarchical assembly of multiple protein filaments on the membrane. Moreover, we directly compare our simulations to high-resolution imaging at similar scales. Namely, we have used atomic force microscopy (AFM) to capture the hierarchical structure of self-assembled proteins on a supported lipid membrane, revealing regularly spaced patterns of protein filaments, separated by a distance 10-fold the size of one protein. By employing free energy calculations from coarse-grained (CG) molecular dynamics (MD) simulations of N-BAR proteins on near-micron sized bilayers, we have revealed large length-scale interactions between protein filaments mediated by the membrane. Distinct from previous theoretical work that is largely focused on interactions between two membrane-bound nanoobjects (e.g., ref (35)), our calculations demonstrate the long ranged interactions between structures containing multiple proteins. Understanding such complex interactions is key to understanding the intermediate structure of protein assemblies formed prior to large-scale membrane remodeling.

Results and Discussion

N-BAR Domains Form a Hierarchically Organized Structure on Supported Lipid Membranes

We used AFM imaging to capture the assembly of N-BAR proteins on supported lipid bilayers. We tested two different membrane compositions: DOPC/DOPS (7:3, molar ratio) and DOPC/DOPS/PIP₂ (85:10:5, molar ratio). Note that BAR proteins require charged lipids to bind to the membrane.¹² When creating supported bilayers, we deposited an excess of small vesicles to ensure a contiguous membrane on the surface. It also ensures as little tension as possible, although presumably still nonzero.

Prior to adding the protein, we confirmed that the bilayer is contiguous and smooth. Namely, by scratching away a square piece of the membrane, we measured a thickness of ∼4 nm, as expected for dioleoyl lipid bilayers (Figure 1A). Next, we injected the N-BAR domain of endophilin at a bulk concentration of 75 nM (N-BAR dimer concentration) over the supported bilayer. Several minutes later, we observed roughly circular clusters 1–3 μm in diameter (Figure 1B). Within the clusters, we reproducibly resolved self-assembled filamentous protein aggregates that organized parallel to one another (Figure 1C). Such formations occurred in all our experiments: four experiments on a 30% DOPS bilayer and three experiments on a 5% PIP₂ bilayer. We did not see a significant difference in the structure or size of protein filaments between the two lipid compositions.

Figure 1.

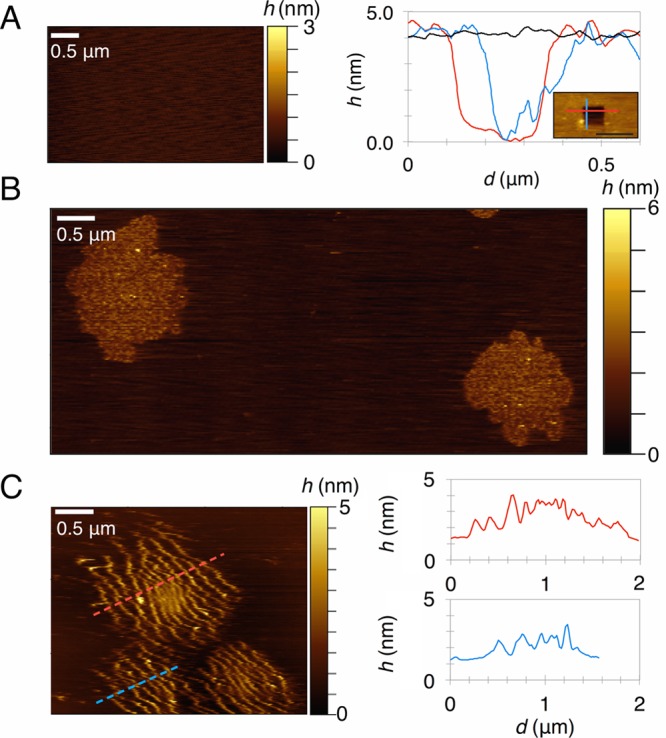
AFM micrographs of N-BAR domain assembly on the 30% DOPS membrane. (A) Left: bilayer prior to adding the protein. Right: surface profile of a scratched out rectangular region of the membrane along the blue and red lines shown in the micrograph (inset), compared to the flat region along the black line. (B) Clusters of N-BAR proteins minutes after injection. (C) Left: Another example of an aggregate, taken with at less aggressive scanning parameters than in B and on a smaller imaging surface, clearly resolving linear aggregates; right: surface profile along the dotted lines shown in the micrograph. Note the small adjacent clusters in the micrograph could be part of a larger cluster.

One must be aware that N-BARs form and coat membrane tubules with a diameter of ∼20 nm when adhered at sufficient densities on the membrane surface.^12,14,22,27 However, based on the maximum height in our micrographs (<10 nm) (Figure 1C), we conclude that the structures are not collapsed membrane protrusions. Besides, the formation of tubules is expected at much higher protein concentrations.^14,27 Importantly, the crystal structures of the N-BAR domain of endophilin show that the protein is ∼3 nm in height,⁸ which is in excellent agreement with our imaging (Figure 1C).

We also considered that the structures could be a result of a scanning artifact. Generally, imaging biological samples with AFM is challenging due to the softness of such systems. When using aggressive scanning parameters, the cantilever tip can drag the material with it, typically manifested as structureless streaks parallel to the direction of the scan. In our micrographs, the observed filaments are sharp, and, as shown in Figure 1C, they can be aligned perpendicular to the scan (in all images, the AFM tip scanned in the left–right direction). When we imaged at very high contact forces with the sample, the tip would clearly perturb the surface, dragging the material in the direction of the scan, as expected (data not shown). Therefore, it is unlikely that the filamentous structures are a result of a scanning artifact. There is still a possibility, however, that AFM imaging could affect the orientation of the clusters, due to the softness and the fluidity of the system.

It is to be noted that a previous AFM study of endophilin on supported bilayers revealed a disruption of the membrane surface, a similar effect we also observed but only at a higher protein bulk concentration (>500 nM per dimer, data not shown).³⁶ Curiously, the reported measurement of the bilayer thickness in that work was half the expected value, indicating potentially aggressive scanning parameters that precluded capturing protein assemblies at high resolution in that study.

Next, we studied the quantitative aspects of filament assembly. The surface profile of the micrograph in Figure 1C shows that the distance between adjacent protein lines ranges from 40 to 300 nm. The lower limit is in a good agreement with the mesh size of an N-BAR network observed in previous computational studies.^25,26 However, the unusually high spatial correlation between proteins seen here and a large separation (>150 nm) between lines cannot be accounted for by the previous predictions. We elucidate the nature of these interactions next.

N-BARs Form Long Parallel Filaments Due to Very Long-Ranged Membrane-Mediated Repulsions

To elucidate the physical forces underlying the apparent long-range interactions and large-scale ordering of the N-BARs, we carried out CG MD simulations of two parallel lines of N-BARs, each in an end-to-end formation (Figure 2A). For the membrane, we used a three-site hybrid CG lipid model, where the CG forces were derived from the underlying atomic interactions and supplemented with analytical functions in regions poorly sampled by atomic simulations.³⁷ Such a hybrid bottom-up analytical approach allows very efficient but thermodynamically accurate simulations. We have previously validated that the CG membrane reproduces the key molecular and macroscopic features of lipid membrane behavior, such as the structural parameters, thermal fluctuations, and bending modulus.³⁷ It is to be noted that at this high level of coarseness, which is essential to access experimentally relevant length and time scales, the chemical identity of lipids at the atomic level is lost. Therefore, we do not test the effect of lipid composition in our simulations. However, based on our experiments discussed in the previous section, the phenomenon appears composition independent, at least for the two tested setups and, of course, as long as the protein binds strongly enough to the membrane. The N-BAR domain was modeled as a 26-site elastic network model, with CG interactions cast in the form of a Lennard-Jones potential (see Methods). The protein–protein and protein–membrane interactions were parametrized in our previous work and include weak nonspecific attractions between protein sites and strong attractions between proteins and lipids.^21,25,26 In the simulations, two N-BAR filaments of varying size were placed parallel to each other on a very large planar bilayer, 150–300 nm in length and width (Figure 2A). The bilayer laterally interacted with its periodic images; however, it was large enough to ensure that the protein filaments are far enough from their periodic images. We used umbrella sampling calculations³⁸ to estimate the potential of mean force (PMF, F) as a function of the separation distance between the centers of mass of the two N-BAR filaments. In this way, we calculate the free energy that arises from interactions between large-scale protein assemblies.

Figure 2.

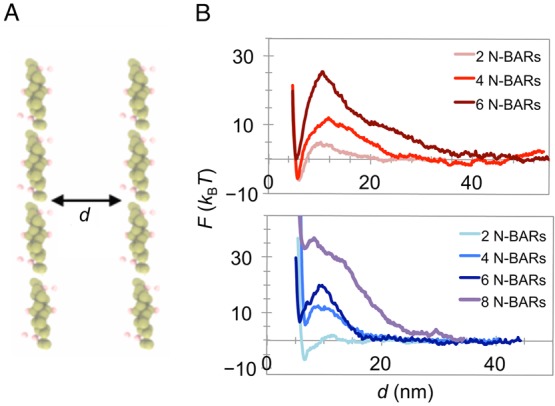
Free energy of interactions between N-BAR protein filaments. (A) A representative CG MD configuration from which the free energy was calculated. Shown are two parallel filaments, each comprising four N-BARs, separated by a distance d (the lipid bilayer underneath is not shown). (B) Potential of mean force (PMF), F, as a function of d calculated from CG MD simulations on a planar bilayer using umbrella sampling. The number of proteins indicated is the number of N-BARs per filament. Membrane tension: vanishing (top panel) and 1.1 mN m^–1 (bottom panel). Maximum error per PMF calculation (in k_BT) for, respectively, 2 N-BARs, 4 N-BARs, and 6 N-BARs is ±0.32, ±1.1, and ±2.6 in the top plot and ±0.47, ±0.75, and ±5.60 in the bottom plot. Here, k_B is the Boltzmann constant and T is the thermodynamic temperature.

At vanishing tension, it is seen that lines of proteins experience a combination of attractions at a short-range (<5 nm) and strong repulsions at a longer range. The magnitude of repulsion is stronger with the increased filament length (Figure 2B). This repulsion could likely be responsible for the observed highly parallel ordering of N-BAR domains in AFM. Moreover, it seems that two lines start interacting at strikingly long distances, which also increases with the line length. In particular, for two filaments each comprising six N-BARs, the interaction range is ∼50 nm, about 2 orders of magnitude larger than the Debye length. Considering that on supported bilayers we often detect chains hundreds of nanometers in length (Figure 1C), i.e., 10–20 N-BARs, the observed separations of >100 nm in AFM images is hence in excellent agreement with the calculations.

It is important to note that one potential caveat to our study lies in comparing the assembly of proteins on a supported bilayer in experiments with a freestanding bilayer in simulations. The precise molecular details of how the membrane interacts with the solid support, and how the support affects the membrane’s out-of-plane behavior, are unclear. It is known that the bilayer is separated from its underlying support by a hydration layer,³⁹⁻⁴¹ arguably helping it exhibit a degree of softness. One way to test the influence of a support is to simulate the membrane under nonzero lateral stress, modeling the effective tension imposed by the support. It is to be noted however that the effective surface tension of supported bilayers is hard to predict, so we repeated the measurements at relatively high membrane tension of 1.1 mN m^–1. Interestingly, under these conditions the free energy of filament interactions from simulations showed a nearly identical shape, with the free energy barrier decreasing by ∼5 k_BT for a chain of six N-BARs and negligibly decreasing for a chain of four N-BARs. The interaction range, on the other hand, decreased by 30 nm in the case of six N-BARs per line (Figure 2B). Clearly, even at very high tension, the long-range repulsive interactions are still present, albeit acting at shorter ranges for the same chain length. Interestingly, high tension reduces the short-range attractions, indicating a dominant contribution of the local curvature in determining these interactions.

Complex Interactions between Multiple N-BAR Filaments Give Rise to a Striped Pattern

Previous efforts have been made to formulate an analytical description of membrane-mediated interactions between two lines or rods adsorbed on a membrane.⁴²⁻⁴⁸ It has been found that two membrane-bending cylinders adsorbing on the same side of a planar membrane experience an effective repulsive interaction.^43,44 Also, it has been found that the membrane can mediate repulsions between conical inclusions which induce deformations of the same sign.⁴⁹ Our PMF calculations for the case of the interaction between two filaments agree well with these predictions of the long-ranged repulsion driven by membrane bending effects, acting over a distance of several cylinder diameters. However, when considering the case of multiple proteins, and an even more difficult case of multiple protein oligomers, such as those that we observe with AFM, the situation is far more complicated. The multibody effect can change the qualitative behavior provided by the pair-picture, and an analytical treatment of these interactions becomes challenging.³⁵ Moreover, we cannot exclude the possibility that our AFM imaging also contains N-BAR oligomers that interact side-by-side.²⁶ Therefore, it is valuable to compute how the presence of multiple lines affects the free energy of interfilament interactions.

To obtain a quantitative understanding of how more complicated geometries would affect the interfilament spacing, we extended the PMF calculations presented in the previous section to explore two scenarios of multiline interactions. In the first, we simulated a filament moving between two parallel filaments that were kept at a large fixed distance of 100 nm (Figure 3, blue plot). At such a large distance, the two outer filaments do not feel each other’s presence (as demonstrated in Figure 2B). All three filaments contained six N-BAR domains and were parallel to one another. The simulations were run at a nonvanishing tension of 0.15 mN m^–1 to prevent significant membrane deformations due to multibody interactions, often seen in configurations with three lines. Also, as argued, applying tension more faithfully models a supported bilayer. Our umbrella sampling calculations resulted in a free energy profile that almost perfectly aligned with the control case of only two interacting filaments at the same tension (Figure 3, compare blue and black plots). It appears that bringing a third linear aggregate at a large distance does not affect the interaction strength and length scale of two noninteracting lines. Therefore, each protein filament has a range of movement between two surrounding filaments, allowing it to form an ordered pattern albeit with a wider distribution of interfilament distances, as observed in our AFM imaging (Figure 1C). This range is expected to narrow down with decreased membrane tension as the repulsion is experienced at longer distances (Figure 2B).

Figure 3.

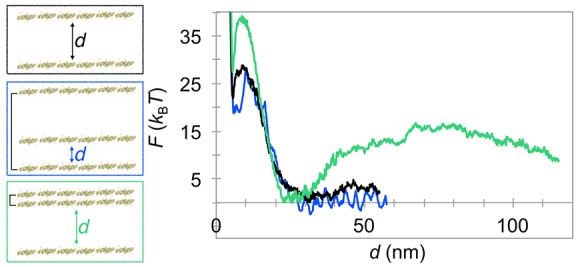
Interactions among multiple N-BAR filaments. Left are shown protein configurations from CG MD simulations used to calculate the potential of mean force, F, as a function of distance between two filaments of interest, d, as displayed in the plot on the right. In the center and bottom configurations, the black line connects two filaments whose distance was kept constant throughout the simulation. The colors in the plot match the colors in the protein configurations. The black plot serves as a control of only two filaments. All filaments contain six N-BARs. CG MD simulations were carried out at ∼0.15 mN m^–1. Maximum error per PMF calculation (in k_BT) for, respectively, black, green, and blue plots is ±1.6, ± 1.1, and ±1.1. The Boltzmann constant is k_B, and T is the thermodynamic temperature.

Another scenario of multiple filaments comes from a possibility that two lines may join side by side, due to the favorable interaction at short distances, as also sometimes observed in CG MD simulations.^25,26 To test how such an assembly may influence the interfilament separation range, we created a configuration where adjoined filaments interacted with a third (Figure 3, green). Again, we see the familiar short-ranged attraction, followed by the repulsion at intermediate distances, with the same minimum as the control albeit with a higher energy barrier (Figure 3, compare green and black plots). The increase in the free energy barrier can be attributed to the larger membrane deformation imposed by two filaments compared to a single one. More interestingly, a distinct secondary minimum beyond 100 nm appears, which can further support the appearance of the striped protein AFM pattern. Obviously, the two deformations largely differ in their range and amplitude in this case, yielding complex interactions even in this simplest case of multiple filaments, where the reasoning drawn from considering only two-body interactions⁷ cannot be applied.

Mechanism of Forming Protein Filamentous Stripes and Networks

As mentioned earlier, physical arguments that consider the membrane deformation profile explain well the observed interactions.^43,44 At short distances, weak explicit interprotein interactions likely contribute to the attractions, and protein filaments share the same deformation. At intermediate separation (i.e., 10–50 nm), on the other hand, for the case of two filaments the two protein lines seem to considerably deform the membrane. To gain a better quantitative understanding of this observation, we measured the global membrane deformation for individual snapshots in a simulation of two six-N-BAR-long filaments and compared them with the filament separation. We calculated the membrane deformation as the z-separation between two most distant CG lipids of a single layer in a single snapshot, z_max–z_min. For a planar membrane, this measure is a good indicator of global curvature. We indeed found that z_max–z_min grows with decreasing interfilament distance and is highest for filament separations that correspond to the maximum in the free-energy profiles (Figure 4A). The maximum deformation measure cannot however tell us where the deformation in the membrane is located; therefore we show top-views of two snapshots corresponding to filament separations with high (Figure 4B, the case of d ≈ 25 nm) and low (the case of d ≈ 45 nm) global deformation, color-coded based on their height profiles. It is seen that a significant deformation adjacent to the filaments is induced. As the interline distance increases, the repulsion vanishes and the global membrane deformation is decreased. In the case of three lines, the deformation created by the two adjoining lines forms a barrier for the third line (Figure 4C), which we speculate is a plausible source of the secondary repulsion seen in the free-energy profile in Figure 3. This observation implies that if multiple proteins are found in the same region, they quickly assemble into filaments; the filaments locally deform the membrane and create a repulsive barrier in between them, ultimately giving rise to the striped pattern.

Figure 4.

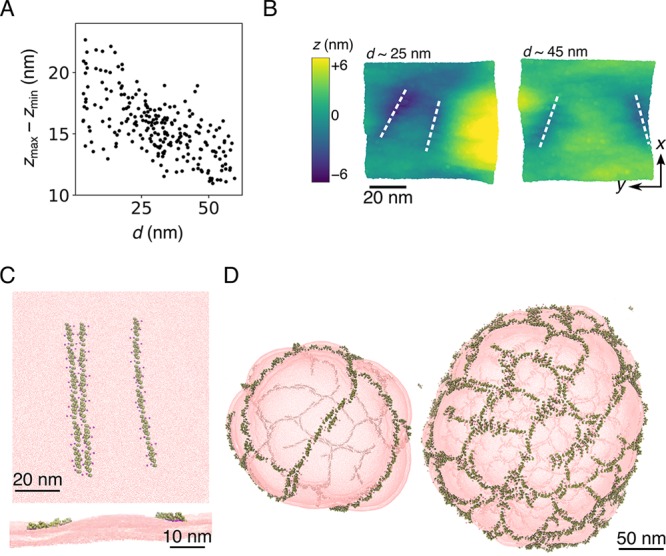
N-BARs forming striped patterns and meshes. (A) Maximum membrane deformation, z_max–z_min, vs the interfilament distance, d, for the CG MD simulation of six N-BARs per filament at vanishing tension. It was calculated for individual snapshot considering only the top CG lipid site of the protein-bound layer, and it is measured for the whole simulated membrane. (B) Top-view of example snapshots at different filament separations, d, and color-coded based on the height, z. Zero on the scale denotes the mean position of the single layer. White dashed lines denote locations of N-BAR protein filaments. Shown is a patch of the membrane near the proteins. (C) Top view (top panel) and side views (bottom panel) of the membrane deformation caused by approaching filaments for the case of a line approaching two adjoined lines at nonvanishing tension. The example of strongest repulsion observed is shown, demonstrating a deformation in between filaments. The snapshot is taken from the CG MD simulations presented in Figure 3. (D) Final snapshots of a CG MD simulation of N-BARs on liposomes at 20% (left) and 30% (right) protein surface coverage. Protein filaments have a strong propensity to spontaneously form a parallel arrangement (left). As the protein density increases, the filaments cross-link into meshes (right). The configurations were rendered from data generated in our previous work.²⁵ In the depiction, the membrane is semitransparent, and the fainter lines are N-BAR filaments on the opposite side of the vesicle.

Our free energy calculations, therefore, provide a quantitative description of the complex multibody interactions that govern hierarchical aggregation of membrane-bound proteins. We note that although the thermal Casimir effect could also give rise to attraction between filaments,^4,7,50 according to the estimates from the literature, this effect should be smaller than the attractive potential in our calculations.

One might speculate that a solid support of a bilayer would suppress membrane undulations and therefore the effective protein–protein interactions. Clearly, however, in our experiments protein filaments form large-scale assemblies despite the presence of the substrate. Furthermore, as mentioned previously, we observe the same qualitative effect even in CG MD simulations where we applied moderate tension. In those simulations, membrane deformations between two filaments are on the order of ∼3–4 nm (Figure 4C), similar to the size of the hydration layer underneath the bilayer.³⁹ Therefore, we assert that the interaction between two filaments is not significantly altered by the presence of the substrate and that even a relatively small deformation can cause significant interfilament repulsions.

How will then filaments assemble on vesicles? To gain insight into this question, we revisited data generated in our previous study.²⁵ There, we simulated CG N-BAR domains on liposomes 200–300 nm in diameter at varying protein surface densities. In a simulation at 20% surface coverage, proteins spontaneously formed very long filaments in a clear parallel arrangement with a ∼100 nm spacing (Figure 4D, left), which is in good agreement with AFM micrographs and free energy calculations. As the protein density increased, the spatial confinement caused the filaments to form double lines and cross-link into a mesh (Figure 4D, right), with a ∼70 nm separation size, in striking similarity with the secondary repulsion maximum from free-energy calculations (Figure 3). Hence we conclude that protein meshing is a result of membrane-mediated filament repulsion.

Conclusions

The findings reported here reveal a significant complexity in membrane-mediated protein–protein interactions, which can give rise to ordered striped patterns of membrane-curving proteins in AFM imaging. Our results thus highlight the importance of membranes in creating complex supramolecular assemblies. Although pairwise interactions between rod-like particles included or adsorbed on membranes have been theoretically explored,^42−46,49 their transferability to protein systems, and in particular to membrane curving proteins, in terms of their sign, magnitude, and range, is largely unknown. These interactions further compete with other membrane-mediated interactions, such as those due to the perturbation in lipid bilayer structure, or membrane fluctuations, in a manner that depends on their relative amplitudes and is tied to the exact physical parameters of the system. Crucially, and as shown in this paper, the multibody effects can clearly change the pair-interaction picture, resulting in a rich and complex behavior that may need to be addressed on a case-to-case basis.

The present work leads to a number of questions and new directions from both the physicochemical and the biological points of view. The crucial new direction is to investigate the detailed origin of the effective membrane mediated forces between protein assemblies, which must account for interactions between deformations of different and variable magnitudes, as they apparently give rise to more complex interaction potentials (Figures 3 and 4). It would thus be of great value to employ quantitative microscopy techniques to directly measure the forces driving large-scale protein assemblies. As our study focused on N-BAR proteins, which by nature impart positive curvature, it would be interesting to see how proteins that induce negative curvature, such as I-BAR proteins, would affect the observed phenomenon.

In a recent study, a membrane associated protein from the influenza C virus, the M1 protein, was found to form a filamentous network on giant vesicles, forming a highly ordered striped pattern, similar to our experimental observations, albeit with larger filament separation at ∼1 μm (ref (51)). This work not only provides additional support for the mechanism we describe here, but also shows the generality of long-ranged membrane-mediated repulsions and their potential broad importance. It potentially represents a crucial mechanism of modulating membrane remodeling and other functional processes in the cell. We also hope our work will motivate further efforts in quantitative characterization of the role of the membranes in mediating the hierarchical organization of proteins in vitro and in vivo.

Methods

Reagents

All reagents to make buffers were purchased from Sigma. 1,2-Dioleoyl-sn-glycero-3-phosphatidylcholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphatidylserine (DOPS), and l-α-phosphatidylinositol-4,5-bisphosphate (840046P) (PIP₂) were purchased from Avanti Polar Lipids. The purified N-BAR domain of endophilin A1 was a generous gift of Carsten Mim and Vinzenz Unger (Northwestern University).

Preparation of Supported Bilayers

First, a lipid mix (at 1 g L^–1, see main text for compositions) was completely dried under nitrogen gas in a glass vial by rapidly rotating the vial to evenly spread the lipids on the bottom and the walls. The mixture was dried in a vacuum overnight to remove all solvent molecules. The total mass of dried lipids was ∼1 mg. The mix was hydrated in 1 mL of 200 mM sucrose and then shaken for an hour at 37 °C. The hydrated lipids (in a reinforced glass vial) were subjected to five rounds of flash freezing in a cold bath (dry ice in ethanol) and then rethawing. The thawed lipids were extruded through a 100 nm polycarbonate filter 21 times. This procedure creates large unilamellar vesicles that were kept in the fridge (4 °C) for no more than a week. Small unilamellar vesicles were prepared by ultrasonication of the above-prepared solution of large vesicles until a clear solution was obtained.

Just prior to an AFM experiment, we cleaved a mica surface (Hi-grade V2 mica, Ted Pella, Redding, CA) and placed it on the piezoelectric actuator stage. Next, we mounted the chamber holding the cantilever atop the mica surface, cushioned by a silicon ring protecting the chamber from leaking. We filled the chamber with a ∼1 g L^–1 solution of the above-prepared small vesicles, then incubated for 10 min, during which time the vesicles burst on the mica surface forming a bilayer. Next, we carefully rinsed the chamber with 10 mM MgCl₂ and then again with the filtered experimental buffer (100 mM NaCl, 10 mM HEPES buffered at pH = 7.4). As mentioned in the main text, a large concentration of vesicles ensured a contiguous coverage of the surface.

AFM Imaging

We imaged the samples in contact mode at ambient temperature using a Multimode Nanoscope IIIA scanning probe microscope (Bruker, Santa Barbara, CA) with a Type J scanner. We used a probe composed of the Si-nitride lever (200 μm long, 0.05 N/m spring constant) with a sharpened Si tip (HYDRA-All, AppNano), which gave the best resolution for our sample. The tips were decontaminated by ultraviolet-generated ozone before sampling (PSD-UV Surface Decontamination System, Novascan, Ames, IA). An amplitude set point of 0 V was used during imaging to minimize the contact forces and hence film damage. Micrographs were obtained at a scan rate of 1.0 Hz at a resolution of 512 pixels per line.

To image the proteins, we displaced the content of the chamber with the protein solution (dissolved in the experimental buffer at 75 nM per N-BAR dimer). We started imaging immediately thereafter and continued imaging for ∼30 min.

Computational Models

We used a previously developed solvent-free three-site CG lipid model that has been validated to reproduce the structural and mechanical behavior of experimental membranes. The bending rigidity of our simulated membrane is 6.6 × 10^–20 J, comparing well to the experimentally determined 5.5 × 10^–20 J for a DLPC membrane⁵² on which the modeling was based.³⁷ To simulate the protein, we used the 26-site CG model of the N-BAR domain of endophilin A1, as described previously.^21,25,26,53 The intraprotein interactions were modeled as harmonic bonds by using the elastic network model, whereas protein–protein and protein–lipid interactions were modeled with a Lennard-Jones potential.⁵³ The same as in our recent applications, the Lennard-Jones parameters were 1.8 kcal mol^–1 well depth at 1.5 nm between sites representing amphipathic helices and lipid head groups, 0.2 kcal mol^–1 at 1.5 nm for other protein sites and the lipid headgroup, and 0.24 kcal mol^–1 at 2 nm for all protein–protein interactions.^21,25,26

Free Energy Simulations

We created a lipid bilayer patch of dimensions 200 nm by 170 nm for simulations with two N-BAR lines or 300 nm by 170 nm for simulations of three N-BAR lines. Lipid bilayer interacted with its mirror images in the x and y directions, while the very large size of the simulation box ensured that the lines of N-BARs do not interact across periodic boundaries.

Two or three lines of N-BAR proteins—each comprising 2–8 N-BARs—were manually placed parallel to one another on a membrane surface. In simulations, a quadratic potential was placed on the distance between the centers of mass of two lines with a force constant of 1–2 kcal Å^–2 mol^–1, with umbrella sampling³⁸ windows spaced at 2 Å, each run 100 000 time steps. The chains were kept linear (a) by applying a weak constraint between adjacent N-BARs at 25 Å and an angle of 180°, (b) by constraining the y-positions of the two terminal N-BARs (to prevent the chains from sliding), and (c) by keeping a 90° angle between three terminal CG sites of two lines, in all cases using a force constant of 0.05 kcal Å^–2 mol^–1. Note, as PMF is by virtue of the calculation a relative measure, and since all the simulations were done under the same constraints, these additional constraints are subtracted when constructing the PMF. Each simulation was run in two replicas.

The simulations were carried out under constant Np_xyT ensemble, using Nosé–Hoover equations of motion within the MD suite LAMMPS.⁵⁴ The size of the box in x and y dimensions was allowed to change by using a barostat with a coupling constant of 600 τ (τ = 48.89 fs, being the time constant), either applying no external pressure (for vanishing tension simulations) or applying a negative pressure from zero to −4 atm as previously described.²⁶ Surface tension, σ, was calculated as σ = ⟨l_z × (p_zz – 0.5(p_xx + p_yy))⟩, where l_z is the thickness of the bilayer, p_xx and p_yy are the tangential components and p_zz is the normal component of the pressure tensor. The box in the z-direction remained constant. The thermostat was set to T = 300 K, with a coupling constant of 6 τ. Initial simulation system for each configuration was equilibrated by slowly increasing the time step and the temperature in 1.2 million time steps. Production runs were carried at a time step of 0.5 τ. We calculated the PMF using the weighted histogram analysis method and the error in PMF calculation by bootstrapping.⁵⁵

Author Present Address

^# Center for Studies in Physics and Biology, The Rockefeller University, 1230 York Avenue, New York, NY 10065, USA.

The National Institute of General Medical Sciences of the National Institutes of Health (Award Number R01GM063796), the National Science Foundation (Grant MCB-1413613), and the NSF-supported MRSEC program at the University of Chicago (Grant DMR-1420709).

The authors declare no competing financial interest.