Abstract

The development of experimental techniques capable of probing the viscoelasticity of soft materials over a broad range of time scales is essential to uncovering the physics that governs their behavior. In this work, we develop a microrheology technique that requires only 12 μL of sample and is capable of resolving dynamic behavior ranging in time scales from 10–6 to 10 s. Our approach, based on dynamic light scattering in the single-scattering limit, enables the study of polymer gels and other soft materials over a vastly larger hierarchy of time scales than macrorheology measurements. Our technique captures the viscoelastic modulus of polymer hydrogels with a broad range of stiffnesses from 10 to 104 Pa. We harness these capabilities to capture hierarchical molecular relaxations in DNA and to study the rheology of precious biological materials that are impractical for macrorheology measurements, including decellularized extracellular matrices and intestinal mucus. The use of a commercially available benchtop setup that is already available to a variety of soft matter researchers renders microrheology measurements accessible to a broader range of users than existing techniques, with the potential to reveal the physics that underlies complex polymer hydrogels and biological materials.
Short abstract
A broadly accessible microrheology technique is developed that reveals viscoelasticity across broad time scales for a variety of soft and biological materials.
Introduction
Soft materials exhibit a rich range of rheological behaviors that play a central role in determining their processing behavior and practical functions. Examples include the engineered materials for biomedical applications,1 self-healing materials for synthetic skin and flexible electronics,2 self-assembling copolymers for nanopatterning,3 and the active cytoskeleton of living cells.4 The rheology of soft materials is governed by physical processes that occur over a vast range of time scales,5 which presents a formidable challenge for unlocking the molecular underpinnings of viscoelastic behavior. Thus, the development of rheological measurement techniques that interrogate the viscoelasticity of soft materials across disparate time scales offers the opportunity to gain deep insights into the molecular physics of soft matter with broad applications across scientific, engineering, and medical disciplines. Despite significant progress that has been forged in developing microrheology techniques that surpass the capabilities of conventional rheology and are amenable to the small sample quantities often encountered for biological materials,6−8 the requirements for specialized expertise, time-consuming data acquisition and analysis, or a limited range of detectable material properties pose substantial barriers to establishing these techniques as accessible characterization tools across a broader community of materials chemistry and biomaterials researchers.
Conventional rheological techniques (macrorheology), which measure the material response to macroscopic external perturbations, typically provide access to a very limited range of time scales. In particular, oscillatory rheology provides access to frequencies ω of only up to about 102 s–1. Although broader ranges of time scales can be accessed by combining oscillatory shear rheology with squeeze-flow and torsional resonance techniques, this requires the combined use of three separate measurements to access the frequency range of interest.9,10 Furthermore, such macrorheology experiments typically require large volumes of material, which prohibits measurements on certain precious biological samples, where only microliter-scale volumes can be obtained and procurement is often time-consuming and costly.
To surmount these challenges, a variety of microrheology techniques have emerged that probe the viscoelasticity of soft matter at time scales and sample volumes beyond the reach of conventional macrorheology.6,7,11,12 Microrheology techniques typically employ micrometer-scale probe particles that sense their local viscoelastic environment in response to thermal (passive) or external (active) forces. Among these techniques, video particle tracking (VPT)7,13,14 and quadrant detection8,12,15−17 microrheology have enjoyed extensive implementation for probing spatially localized viscoelasticity in heterogeneous samples and living cells and require very low sample volumes (<1 μL). Spatially localized information from these techniques is achieved either by explicitly tracking particle trajectories by optical microscopy (VPT) or by focusing a laser onto individual probe particles and monitoring laser deflections onto a quadrant photodiode detector (quadrant detection). For bulk-averaged viscoelasticity across broad time scales, dynamic light scattering in the multiple-scattering limit, i.e., diffusing wave spectroscopy (DWS), has also been widely leveraged.11,15,18 However, each of these techniques suffers from distinct requirements that limit their widespread adoption by users beyond microrheology specialists, such as applicability to only soft materials (G < 100 Pa for VPT19), technically challenging implementation (quadrant detection and VPT), low statistical power (quadrant detection), or large sample volume requirements (at least 150 μL for DWS6,20−27). Thus, there exists a critical need for a technique that is readily available to researchers with a broad range of expertise and that measures precious soft and biological materials across a breadth of viscoelastic properties and time scales.
Here, we develop a technique that is broadly accessible to users with a range of expertise and that interrogates viscoelasticity of small-volume samples over a vast spectrum of material properties and time scales. Our experimental methodology is based on dynamic light scattering (DLS) in the single-scattering limit and hence requires only dilute probe concentrations (<0.5%). This DLS microrheology (DLSμR) technique extracts the frequency-dependent shear moduli of materials with a broad range of stiffnesses up to 104 Pa and over a vastly broader range of time scales (10–1 to 106 s–1) than oscillatory macrorheology (<102 s–1). This is achieved using a commercial benchtop instrument that is already available to a variety of materials chemists, involves minimal user intervention, and requires sample volumes as low as 12 μL. We leverage this technique to measure the hierarchy of molecular relaxations that occur in DNA solutions and to capture the viscoelastic behavior of precious biological materials, including extracellular matrices and mucus, where conventional macrorheology is impractical (Figure 1). This technique is accessible to a wide range of users and opens opportunities for studying a range of complex biological and soft materials.
Figure 1.
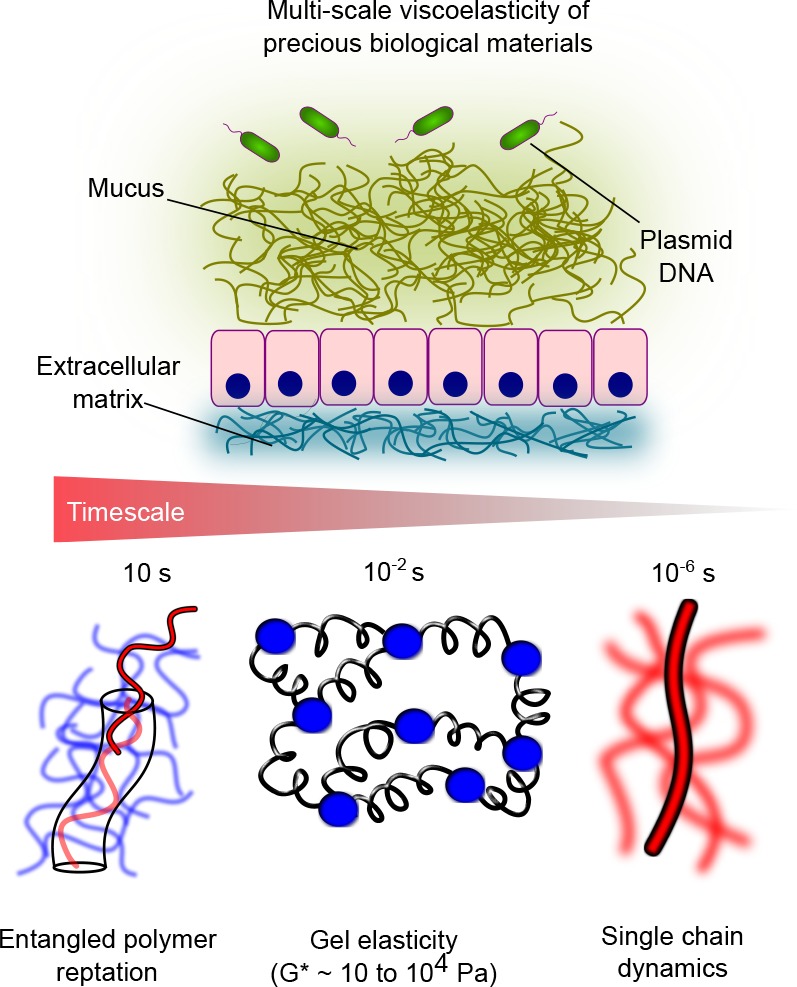
DLSμR captures the multiscale viscoelasticity of soft matter, including polymeric gels and precious biological materials, such as DNA solutions, intestinal mucus, and extracellular matrices. DLSμR reveals signatures of molecular relaxations that occur over 7 decades in time, ranging from 10 s down to 10–6 s, which spans the time scales associated with reptation of polymers in entangled networks, entropic elasticity of cross-linked or entangled gels, and internal relaxations of individual polymer chains.
The ranges of frequency and viscoelasticity that we explore in this work have typically been viewed to be inaccessible to DLS in the single-scattering limit.18,28−31 However, as we demonstrate, this perceived limitation reflects misconceptions related to the statistics of photon correlation in single-scattering detection. We harness the highest spatial resolution accessible to single-scattering DLS by operating in noninvasive backscatter detection mode, and prove that commercial photon correlation instruments are capable of capturing probe fluctuations at nanometer-scale resolution. This reveals access to time scales and material stiffness previously viewed to be accessible by microrheology only through DWS and quadrant detection.
Results
DLSμR Offers an Accessible Technique for Rheological Measurements of Soft Matter over a Wide Spectrum of Time Scales and Material Properties
Figure 2 illustrates our workflow for extracting the frequency-dependent shear modulus G*(ω) of soft materials using a commercially available DLS instrument. In contrast to DWS, by operating in the single-scattering limit, our methodology involves dilute concentrations of probe particles (<0.5% w/v) that serve as light scatterers.
Figure 2.
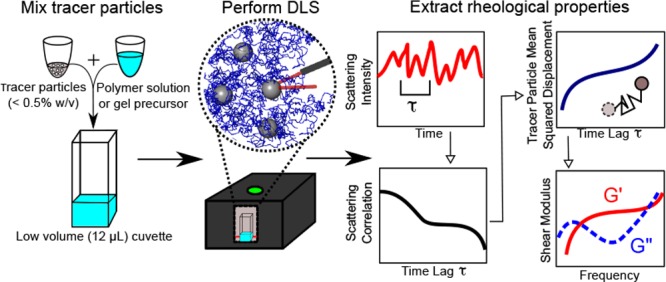
DLSμR workflow. The polymer solution or gel precursor is mixed with a dilute concentration of tracer particles (<0.5% w/v). DLS is performed in a backscattering configuration using a commercial benchtop instrument. Brownian motion of the tracer particles produces fluctuations in scattering intensity that give rise to a characteristic scattering intensity autocorrelation. The autocorrelation is analyzed by our custom software to extract the mean-squared displacement of particles, which is used to determine the frequency-dependent linear viscoelastic shear modulus G*(ω).
The commercial benchtop instrument we leverage here illuminates the sample with a 50 μm diameter laser beam, and scattered light is focused onto a photodiode detector using a translating lens to collect photons from a specified scattering volume within the sample of about 1.4 nL. In practice, we use a total sample volume of 12 μL. This strikingly contrasts with the volume requirements of DWS, where at least 150 μL of sample is typically required.6,20−27We perform DLS in backscatter detection mode, which offers the smallest length scale of resolution accessible to the wavelength of the laser, thereby capturing time scales that are inaccessible to oscillatory shear rheology and VPT. In contrast to DWS, the low probe concentrations typically required for performing single-scattering DLS can present a challenge for separating the scattering by probe particles from background scattering by the material.32 Another key advantage of the backscattering optics utilized here is that much higher probe concentrations can be used without exiting the single-scattering regime due to the shorter photon path length in the backscattering configuration and the ability to tune the photon path length using the translating lens system.33 Leveraging these capabilities enables us to use probe concentrations (0.1% to 0.25%) that are 1–2 orders of magnitude greater than those typically implemented for single-scattering DLS,18,31,32 thereby ensuring dominance of scattering from probe particles.
Thermal fluctuations of the tracer particles give rise to scattering intensity fluctuations, which are described by a time lag τ dependent scattering intensity autocorrelation g(2)(τ). Scattering photon autocorrelations are collected using a digital correlator with delay times ranging from 0.5 μs to 70 s, and the experimentally accessible frequency range within this window is dictated by the time scales over which particle displacements are detectable. The intensity autocorrelation encodes the average mean-squared displacement of tracer particles within the scattering volume ⟨Δr2(τ)⟩ over the time lag τ. The mean-squared displacement of particles with radius a in turn can be used to extract the frequency-dependent shear modulus according to the generalized Stokes–Einstein relation, G*(ω) = kBT/[πa i ω⟨Δr2(ω)⟩]. Our custom software package analyzes raw scattering intensity autocorrelations to extract G*(ω) of the material.
To investigate the capability of our technique to capture the viscoelastic behavior of polymer gels, we study chemically cross-linked polyacrylamide networks over a broad range of stiffnesses (shear moduli G* from 10 to 104 Pa) and compare our DLSμR measurements to those obtained from conventional oscillatory macrorheology. Over this full range of stiffnesses, our DLSμR measurements exhibit excellent agreement with macrorheology in the frequency range in which the two techniques overlap (Figure 3). This viscoelasticity spectrum accessible to DLSμR spans the stiffnesses of a diverse range of biological tissues, ranging from mucus to skeletal muscle.34 This range of biologically relevant stiffnesses is inaccessible to VPT, which would be limited to materials with |G*| < 102 Pa using the 100 nm diameter probe particles used in our experiments.19 We note that although generally good agreement is found between our DLSμR measurements and macrorheology, the modulus in our DLSμR experiments underestimates the modulus by about a factor of 2 for the stiffer (5% and 10%) gels. This may be due to inhomogeneities formed during the free-radical polymerization, which are likely to be more prevalent in the more rapidly forming gels.35 Such inhomogeneities may force the probe particles into more compliant regions of the network. A similar effect of inhomogeneities in gel microrheology has been previously described,7 and particle tracking microrheology experiments have demonstrated the existence of mechanical heterogeneity in polyacrylamide gels.31
Figure 3.
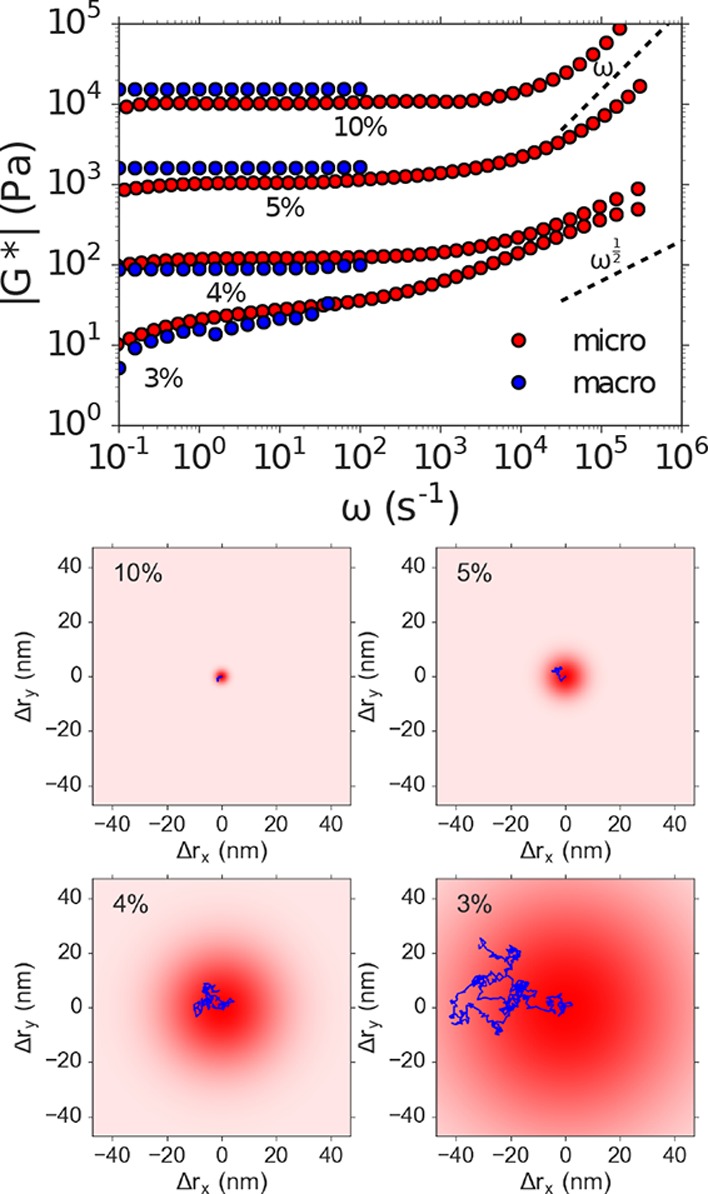
DLSμR recapitulates macrorheology in cross-linked polyacrylamide gels with shear moduli G* spanning 101 to 104 Pa. Top: Comparison of the frequency ω dependence of the magnitude of the shear modulus |G*| obtained by DLSμR and macrorheology of polyacrylamide gels with varying polacrylamide concentrations (% w/v). The dashed lines represent the high-frequency scaling of a Rouse polymer G* ∼ ω1/2 and space-filling branched polymer fractals with nondraining hydrodynamics G* ∼ ω. Bottom: Illustration of typical particle trajectories occurring over a time interval corresponding to the angular frequency ω = 101 s for a 100 nm diameter tracer particle embedded in gels with the indicated polyacrylamide composition.
Moreover, DLSμR captures a vastly broader range of time scales than conventional oscillatory macrorheology and VPT, ranging from frequencies ω of 10–1 to 106 s–1. Although similar frequency ranges have been captured in macrorheology measurements that combine oscillatory rheology, squeeze-flow, and torsional resonance, this is achieved only with the combined use of 3 separate measurements, in total requiring hundreds of microliters of material.9,10 Our technique enables us to probe a hierarchy of viscoelastic processes in the material in a single measurement with only 12 μL of sample. Our measurements demonstrate that, at intermediate to long time scales, the gels behave as elastic solids in which G* is approximately constant with respect to frequency. At short time scales, the tracer particles probe faster relaxation modes in the gel due to effective elastic chains that give rise to a power-law scaling with G* ∼ ωα. Consistent with the decreasing molecular weight of effective elastic chains with increasing cross-linking density, we find that the time scale at which these relaxation modes emerge decreases by 2 orders of magnitude as the gel stiffness increases across the range spanned in our measurements (Supporting Information and Supporting Figure 1).
For the most compliant gels, α ≈ 1/2, consistent with freely draining Rouse dynamics of flexible partial chains between cross-links.36 This suggests that, at low polymer concentrations, the gel network is formed from loosely cross-linked high molecular weight polymers in which each effective elastic chain experiences overlap with surrounding chains that screen hydrodynamic interactions. For the more densely cross-linked gels, the high-frequency scaling behavior approaches α ≈ 1, which coincides with the critical scaling predicted by percolation theory at the gel point for nondraining percolating clusters37 as well as the expected scaling behavior for nondraining Zimm relaxation of self-similar branched chains with a fractal dimension Df = 3.38 This relaxation can be interpreted in terms of a network that consists of effective elastic chains that possess an internal fractal branched structure that is space-filling at all length scales below the gel correlation length and retains high-frequency signatures of the fractal structure and dynamics present at the percolation point (see Supporting Information for derivation). This is consistent with time–temperature superposition experiments in which fully formed gels often exhibit scaling of G″ that mirrors the fractal dynamics at the gel point.39
The transition in the high-frequency relaxation from Rouse to critically overlapped Zimm dynamics suggests that the greater cross-linking efficiency in the higher concentration gels produces more tightly cross-linked networks consisting of branched effective elastic chains that do not overlap with surrounding chains, and therefore do not experience screening of hydrodynamic interactions. This is consistent with time-cure superposition experiments just above the gel point, which show larger critical relaxation scaling exponents with greater cross-linking efficiency (compare ref (40) and ref (41)) or lower molecular weight polymer precursors.42 Similarly, atomic force microscopy microrheology experiments on polyacrylamide gels at frequencies up to ω ≈ 103 rad/s have demonstrated a high-frequency scaling exponent that increases with polyacrylamide content, approaching α ≈ 1 for 10 kPa gels.43 Our technique thus offers a substantial advantage over oscillatory shear rheology in terms of elucidating the hierarchy of physical processes that govern the behavior of polymer gels.
Unlike VPT and quadrant detection microrheology, which involve explicit tracking of particle trajectories, DLSμR yields measurements of tracer particle fluctuations that are directly averaged over the 1.4 nL scattering volume. Hence, VPT and quadrant detection extract spatially heterogeneous viscoelasticity that is concealed by averaging inherent to DLSμR. However, our technique offers a more streamlined and accessible work flow for diverse users than VPT and quadrant detection microrheology. In contrast to VPT, in which each time point requires a full microscopy image of tracer particle positions to be acquired, stored, and processed, DLSμR measurements directly provide the statistically averaged particle fluctuations in the form of the scattering intensity autocorrelation function, thereby reducing the data footprint associated with each measurement by several orders of magnitude. Unlike VPT, quadrant detection can access the range of viscoelasticity and time scales that are encompassed by DLSμR, but quadrant detection requires tracking individual trajectories at a time by optically trapping single probe particles. This comes at the expense of vastly decreased statistical power, even compared to VPT, in which approximately 100 particles are typically present in the field of view. Moreover, quadrant detection microrheology requires expertise with optical traps that is not commonly found in many soft materials laboratories. Together, these limitations render quadrant detection a far less accessible and more technically challenging approach. By comparison, DLSμR is readily implemented on a benchtop commercial instrument that is already available to many materials chemistry and biomaterials researchers and can rapidly capture viscoelasticity with high statistical power while requiring minimal user intervention.
Historically, DLSμR in the single-scattering limit has found limited use in comparison to VPT, quadrant detection, and DWS, and it is conventionally considered to be inadequate for viscoelastic properties in the stiffness and time-scale ranges probed in our measurements.18,28−31 By comparison to quadrant detection and DWS, previous studies in single-scattering detection have typically explored a much more limited range of stiffnesses (G* < 100 Pa) and frequencies ω < 104 s–1.18,31,32,44−46 The range of stiffnesses and time scales accessible is fundamentally limited by the length scale of tracer particle fluctuations to which the light-scattering configuration is sensitive (visualized in Figure 3). This can be understood on the basis of the generalized Stokes–Einstein relation, wherein the mean-squared displacements of tracer particles in an elastic gel are inversely proportional to the shear modulus.11 Thus, the sensitivity is dictated by the smallest length scale of probe fluctuations that produce detectable decreases in the scattering intensity autocorrelation g(2)(τ).
We find that the backscattering optics utilized here are capable of resolving decreases in the scattering intensity autocorrelation that correspond to mean-squared displacements of about 1 nm2, which are 2 orders of magnitude smaller than the mean-squared displacements detectable by VPT,19 as well as those previously accessed using single-scattering DLS for microrheology of soft polyacrylamide gels.31 In accordance with the generalized Stokes–Einstein relation, the minimum detectable displacement, together with the probe particle size, dictates the maximum measurable stiffness. The 1 nm resolution achieved here renders measurements on gels as stiff as 104 Pa possible using 100 nm beads, and the maximum accessible stiffness scales inversely with the size of the probe that is required to satisfy the continuum assumption of the Stokes–Einstein relation. In our experiments, the 100 nm beads are much larger than the mesh size of the polyacrylamide network, which will be about 10 nm or less in the range of concentrations we probe,47 and are therefore sufficiently large to ensure that the continuum limit is reached.
It is noteworthy that the length scale of fluctuations to which we are sensitive is much smaller than the length scale that would be estimated based on the scattering wave vector q. For the backscattering angle θ (173°), the wavelength λ of the laser (633 nm), and a refractive index n equal to that of water, the scattering wave vector in our experiments q = 4πn sin(θ/2)/λ corresponds to a length scale q–1 = 38 nm.48 For this reason, DLSμR in single-scattering detection has often been viewed as unsuitable for measurements in the stiffness and frequency ranges that require the spatial resolution captured in our experiments.18,28 In addition to improved spatial resolution through the use of backscattering optics compared to some previous studies using forward or orthogonal scattering,18,31 higher spatial resolution is also achieved by accurate estimation of the correlation function zero-time intercept using the methods described in the Supporting Information. Accurate estimation of the zero-time correlation intercept has been previously reported to represent a limitation for DLS microrheology.18 Our results emphasize the importance of considering the sensitivity of photon correlation detection and the reliability of correlation intercept estimation in evaluating the limits of the DLSμR technique.
Polymer gels exhibit broken ergodicity due to frozen-in density fluctuations formed during the gelation process, which must be accounted for in interpretation of DLS autocorrelation data.49 In principle, broken ergodicity can be corrected for by obtaining ensemble-averaged scattering intensity autocorrelation functions by collecting the time-averaged autocorrelation across an ensemble of spatial positions in the sample, which is time-consuming and tedious. The broken-ergodicity correction we implement here (described in the Supporting Information) enables extraction of the contribution to the scattering intensity due to dynamic fluctuations within the scattering volume of interest, while obviating the need for full ensemble averaging of the correlation function. However, we note that the acquisition times we use here to collect high-quality photon statistics are not amenable to rapidly evolving materials, such as during the gelation process.
DLSμR Elucidates Hierarchical Molecular Relaxations in DNA
The broad spectrum of time scales probed by DLS offers the opportunity to gain insights into the physics of macromolecules that exhibit distinct relaxation behaviors at different time scales. Semiflexible polymers constitute an important class of macromolecules that exhibit distinct physics at different length scales and time scales. The physical behavior of such polymers is governed by bending elasticity on the scale of their persistence length lp, but they can exhibit flexible Gaussian chain behavior at lengths much longer than their persistence length. DNA represents an excellent model system for exploring this relaxation hierarchy, since its persistence length (lp ≈ 50 nm)50 is sufficiently short to produce flexible Gaussian chain statistics at experimentally accessible molecular weights, but provides sufficient bending stiffness to yield semiflexible polymer behavior at experimentally accessible length scales and time scales.
DLSμR measurements were performed on semidilute, unentangled solutions of linear DNA (1.0 mg/mL of 5.8 kilobase chains, i.e., contour length L ≈ 1.9 μm). Our results elucidate a hierarchy of regimes of physical behavior (Figure 4, designated as A, B, and C). We relate the transition between these regimes to two theoretically predicted time scales (τ ∼ ω–1): the bending relaxation time of semiflexible subsections of the DNA chain τbend and the Rouse time associated with total relaxation of all internal polymer elastic modes τR. These time scales approximately define three regimes that correspond at the shortest times (τ < τbend < τR) to bending fluctuations in the semiflexible DNA double helix, at intermediate times (τbend < τ < τR) to relaxations of internal segments of the chain that behave like flexible segments, and at the longest times (τbend < τR < τ) to total chain diffusion. Our DLSμR measurements agree quantitatively with theoretical predictions (dotted and solid curves in Figure 4) for a wormlike chain (WLC), which we obtain by combining the high-frequency scaling limit of a WLC with the full analytical solution of a Rouse polymer, as described in the Supporting Information and Supporting Figure 5.
Figure 4.
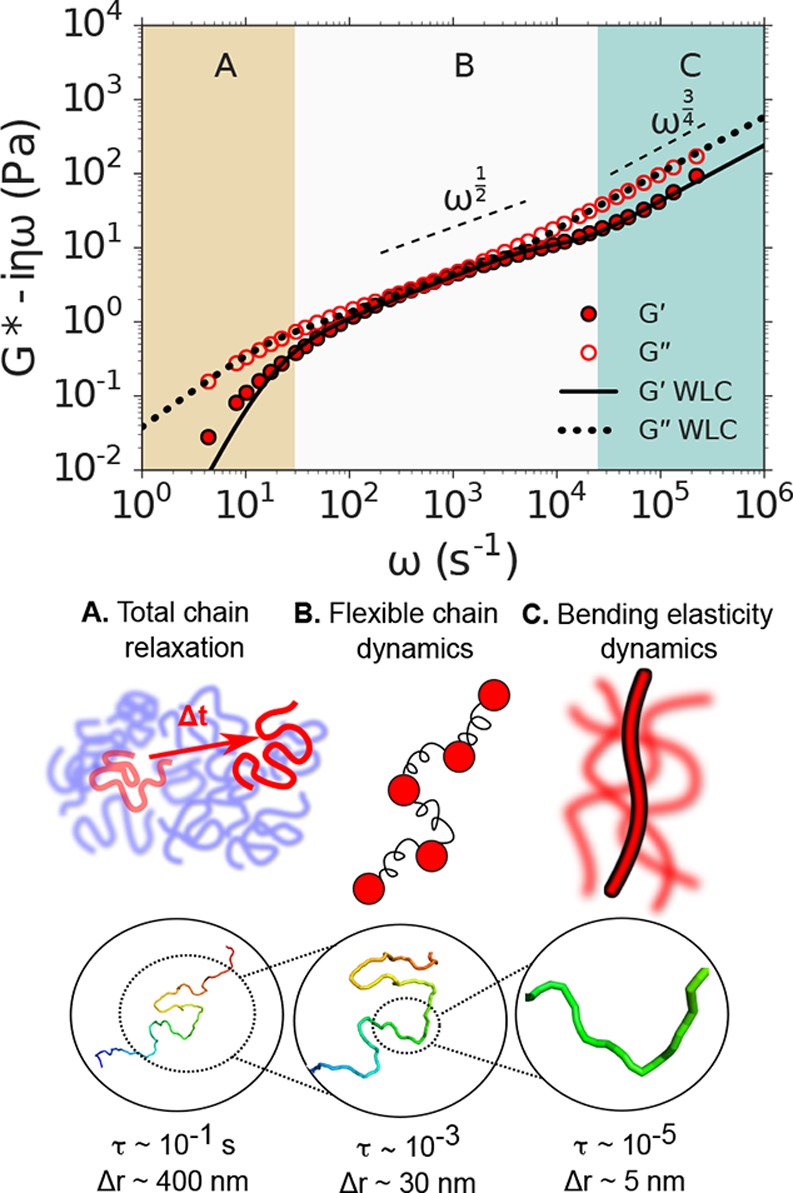
DLSμR of DNA solutions reveals a hierarchy of molecular relaxations. Top: Shear modulus G* as a function of angular frequency ω of semidilute DNA solutions. Regions A, B, and C represent approximate regimes in which the viscoelastic response is expected to probe the total chain relaxation, internal flexible chain relaxation, and bend relaxation, respectively. Dashed lines indicate the expected scaling laws for a Rouse polymer (G* ∼ ω1/2) and a freely draining semiflexible chain (G* ∼ ω3/4) . The dotted and solid lines indicate the theoretical predictions for G′ and G″, respectively, of a semiflexible polymer modeled as a WLC. Middle: Illustrations of the physical behavior probed at the time-scale regimes annotated A, B, and C in the top plot. Bottom: Representative snapshot of a 5.8 kilobase DNA molecule modeled as a WLC obtained by Monte Carlo simulation. Magnifications represent the approximate contour length of the DNA molecule whose relaxations dominate the viscoelastic response that is probed at time scales τ (which reside within regimes A, B, and C) by tracer particles undergoing approximate displacements Δr.
At the shortest times (largest ω, region
C), we identify
a rheological response which reflects thermal bending fluctuations
in the DNA double helix due to its finite bending stiffness. In this
regime, the scaling behavior in our DLSμR measurements approaches
the theoretical predictions for the high-frequency response of a WLC,
in which the polymer contribution to the shear
modulus is 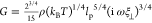 ,51,52 where ρ is the
polymer contour length per unit volume, kBT is thermal energy, lp is the persistence length, and ξ⊥ is the
transverse friction coefficient per unit length (which we estimate
to be 4 × 10–2 Pa × s by fitting
theoretical predictions for a WLC to our data using ξ⊥ as a fitting parameter). We theoretically estimate the time scale
where these bending fluctuations will manifest to be τbend = ξ⊥(2lp)4/[(3π/2)4lpkBT] ≈ 40 μs.53 This theoretically predicted time scale (indicated
by the boundary between regions B and C in Figure 4) corresponds approximately to the frequency
ω = τbend–1 near which the rheological behavior from DLSμR
transitions to the high-frequency scaling limit.
,51,52 where ρ is the
polymer contour length per unit volume, kBT is thermal energy, lp is the persistence length, and ξ⊥ is the
transverse friction coefficient per unit length (which we estimate
to be 4 × 10–2 Pa × s by fitting
theoretical predictions for a WLC to our data using ξ⊥ as a fitting parameter). We theoretically estimate the time scale
where these bending fluctuations will manifest to be τbend = ξ⊥(2lp)4/[(3π/2)4lpkBT] ≈ 40 μs.53 This theoretically predicted time scale (indicated
by the boundary between regions B and C in Figure 4) corresponds approximately to the frequency
ω = τbend–1 near which the rheological behavior from DLSμR
transitions to the high-frequency scaling limit.
At intermediate time scales (region B), which are long in comparison to the relaxation time of bending modes but shorter than the time required for relaxation of all internal polymer elastic modes, the shear modulus reflects the viscoelastic relaxation of flexible subchains that behave like entropic springs. For a Rouse-like polymer, in which hydrodynamic interactions can be neglected, this is theoretically predicted to produce a shear modulus in which the storage and loss moduli scale as G′ = G″ ∼ ω1/2.5 Our measurements show that the relaxation behavior of the DNA chains approaches this scaling behavior over a limited range of frequencies (102 < ω < 103) before transitioning to total chain diffusion at longer time scales and bend fluctuation dynamics at shorter time scales.
At the longest time scales (smallest ω, region A), all internal modes of the polymer chain have fully relaxed, and the shear modulus captures the viscoelastic response due to translational diffusion of the polymer chains. For semidilute unentangled solutions, this response is anticipated at times longer than the Rouse relaxation time of the entire polymer contour length L: τR = 2lpξRL2/(3π2kBT) ≈ 3 × 10–2 s.5 At frequencies ω < τR–1, our measurements exhibit a transition to viscous dynamics, with G″ > G′, which is consistent with relaxation of the internal entropic elastic modes of the polymers and a transition toward total chain diffusion. This transition is in excellent agreement with theoretical predictions for a WLC that exhibits flexible chain behavior at these time scales, which we obtain using a Rouse monomer friction coefficient per unit length of ξR = 1.0 × 10–2 Pa × s based on the fitting procedure described in Supporting Information. The value of ξR we obtain is about 4 times smaller than the transverse friction coefficient ξ⊥.
In order to evaluate the consistency of our fitted friction coefficients, we compare the value of ξR obtained from our DLSμR data to existing diffusivity measurements and relate our observation that ξ⊥ ≈ 4ξR to polymer physics theory. In the semidilute regime, the effective Rouse friction coefficient ξR is dependent on the polymer concentration, which defines the length scale for hydrodynamic screening by overlapping polymers. At length scales larger than the hydrodynamic screening length, each polymer in the semidilute network can be viewed as consisting of coarse-grained polymer “blobs” that diffuse like effective Rouse monomers36 and exhibit internal hydrodynamic interactions at smaller length and time scales. Measurements of the diffusivity D of fluorescently labeled 5.9 kb DNA have confirmed this concentration dependence and at a concentration of 1.0 mg/mL provide a Rouse friction coefficient ξR = kBT/(DL) = 0.6 × 10–2 Pa × s.54,55 This is somewhat lower than our value ξR = 1.0 × 10–2 Pa × s, and further investigation is required to elucidate the origin of this discrepancy.
Below the hydrodynamic screening length, and within each effective Rouse monomer, DNA may be expected to behave according to slender body hydrodynamics.56 In this regime, the hydrodynamics are described by two friction coefficients, ξ⊥ and ξ∥, which represent the transverse and longitudinal friction, respectively, and ξ⊥ = 2ξ∥. If the friction coefficient of each Rouse monomer corresponds to the total friction of each subsection that obeys slender body dynamics, then slender body theory implies that ξR = 3(2/ξ⊥ + 1/ξ∥)−1 = 3ξ⊥/4. However, our fit to the DLSμR data instead yields ξR ≈ ξ⊥/4. The origin of this disagreement is unclear, and may reflect additional many-body effects due to the semidilute solution not considered by slender body theory.
Importantly, our results are only slightly dependent on probe particle size for probe diameters of at least 500 nm (the probe size used in Figure 4), indicating that the probes sense the continuum viscoelasticity of the fluid (Supporting Figure 2). This is consistent with previous microrheology studies of linear DNA solutions, which show that, at the concentration used in our work, and with DNA molecular weights where entanglements are weak or nonexistent, noncontinuum effects such as polymer depletion are not substantial, provided the probes are larger than the radius of gyration of the polymers.57,58 Unlike the polyacrylamide gels, 100 nm probes do not satisfy the continuum assumption of the Stokes–Einstein relation, since the radius of gyration of a 5.8 kilobase Gaussian DNA chain is about 180 nm, and the system resides close to the critical overlap concentration.
The transition to an ω3/4 scaling behavior at high frequencies has been previously demonstrated using quadrant detection and DWS microrheology of other semiflexible polymers, such as F-actin, wormlike micelles, and polysaccharides.8,59−62 However, despite the extensive history of DNA as a model polymer in the polymer physics community, previous microrheology studies on DNA solutions were conducted at much lower frequencies than the maximum frequency accessed here.6,63,64 Our measurements not only capture the expected high-frequency scaling behavior that has been confirmed in experiments on other semiflexible polymers but also exhibit quantitative agreement with polymer physics theory across the full range of molecular relaxations.
DLSμR Accesses Multiscale Relaxation in Extracellular Matrices Where Time–Temperature Superposition Fails
Time–temperature superposition is a widely implemented technique for broadening the frequency range that is accessed in a conventional macrorheology experiment. In brief, this technique involves collecting the frequency-dependent shear modulus at a range of temperatures and horizontally shifting the isotherms to construct a single “master curve” that encompasses a substantially broader range of frequencies than those accessed at any particular temperature.65 However, this construction is valid only for materials in which the relaxation rates and physical processes that govern the viscoelastic behavior can be described by a single temperature dependence.
Biological systems provide a variety of instances in which the assumptions underlying time–temperature superposition fail. In fact, in general, time–temperature superposition does not substantially broaden the frequency range for aqueous polymer systems, since the available temperature variations do not lead to substantial frequency shift factors. In particular, extracellular matrices represent an important class of biological materials that exhibit nontrivial thermal responsiveness that violates time–temperature superposition. Furthermore, the rheological behavior of extracellular matrices exhibits a profound impact on directing cellular behavior.66,67
To illustrate the utility of the DLSμR for these materials, we conducted measurements on Matrigel across temperatures spanning its sol–gel transition. Matrigel consists of a complex mixture of extracellular matrix proteins and is widely used in mammalian tissue culture.68 We find that DLSμR provides excellent agreement with macrorheology at fixed temperature (Supporting Figure 3), but reveals a temperature-dependent viscoelastic spectrum that clearly violates time–temperature superposition (Figure 5). Below the sol–gel transition, Matrigel exhibits viscoelastic power-law behavior with G″ > G′ over the full range of accessible frequencies. Above the sol–gel transition, the shear modulus displays two distinct regimes consistent with a polymer hydrogel. At low to intermediate frequencies, a plateau modulus with a weak frequency dependence emerges with G′ > G″, reflecting behavior reminiscent of an elastic solid. At high frequencies (ω > 104 s–1), the shear modulus increases with frequency and approaches a power-law behavior that reflects coupling to the underlying internal relaxation modes. These results demonstrate that DLSμR enables measurements of the broad frequency viscoelasticity of biological materials where conventional oscillatory rheology with time–temperature superposition is not an option.
Figure 5.
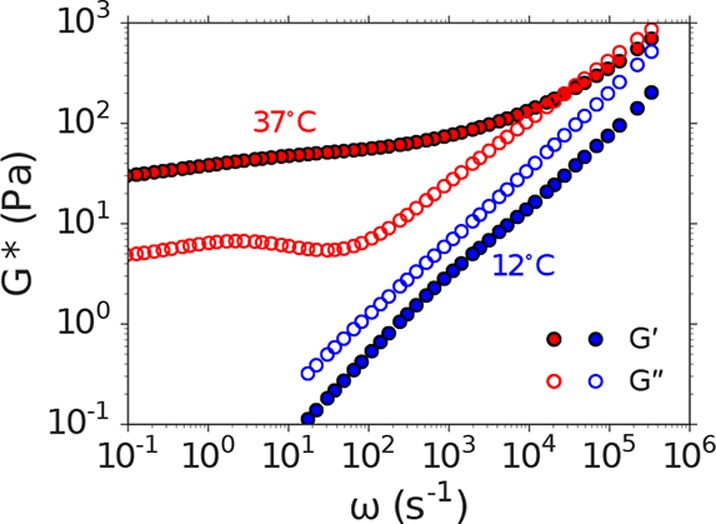
DLSμR captures the viscoelastic response of Matrigel across a broad range of time scales where time–temperature superposition fails. Closed and open symbols represent frequency dependence ω of the storage and loss shear moduli (G′ and G″, respectively) at temperatures below (12°, blue) and above (37°, red) the sol–gel transition of Matrigel.
DLSμR Reveals Broad Frequency Entanglement Dynamics in Intestinal Mucus for Which Macrorheology Is Impractical
Intestinal mucus lines the luminal surface of the intestinal epithelium and serves as an essential barrier whose functions include acting as a physical barrier against microbial invasion and providing nutritional support to the host microbiome.69−71 Disruptions to the mucosal layer are implicated in a variety of diseases, which suggests that the ability to quantify the physical properties of the mucosal layer may provide biophysical insights into the role of mucus in such pathologies. Intestinal mucus is available in only small quantities from small animal models and human patients, as only a small amount can be recovered from a single animal in a mouse model, and in human patients, mucus must be obtained from biopsies. Thus, intestinal mucus represents an excellent example of a biological material in which acquiring macrorheology measurements is challenging, costly, and impractical.
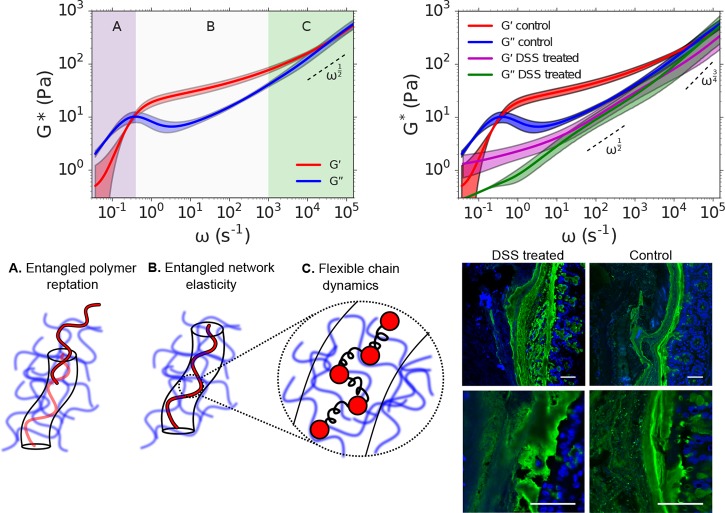
Our DLSμR measurements on intestinal mucus isolated from healthy mice (Figure 6) reveal a viscoelastic spectrum that spans 6 decades in time and exhibits signatures of a hydrogel formed by a network of physical entanglements among macromolecules. The frequency-dependent shear modulus reflects three distinct regimes of physical behavior that are predicted by the Doi and Edwards tube theory for entangled polymers. In this model, polymers within an entangled network are envisioned to be confined by the surrounding network within an effective tube that restricts their motion within the tube diameter (see illustrations in Figure 6). At short times (large ω, region C), the viscoelastic spectrum is dominated by the internal relaxation of flexible subsections of the polymers that are smaller than the effective tube diameter and have yet to “discover” that they are confined by entanglements within the surrounding network. In this regime, G*(ω) possesses a frequency scaling behavior that reflects single chain dynamics that are intermediate between a Rouse polymer and a WLC. At intermediate times (region B), polymer relaxations are governed by entanglement constraints with the surrounding polymer matrix, which produces an extended elastic plateau modulus in which G′ > G″ and G′ exhibits a weak frequency dependence. At sufficiently long times (small ω, region A), the polymers are able to escape their local entanglements by reptation, which enables the material to flow, yielding a viscous response with G″ > G′.
Figure 6.
DLSμR captures the entangled dynamics of intestinal mucus of healthy and colitic mice. Top left: Dependence of the shear modulus G* on angular frequency ω of intestinal mucus isolated from healthy mice. The shear modulus exhibits three regimes, A, B, and C, which we identify as corresponding to reptation of polymers within an entangled network, elastic behavior due to entanglement constraints, and Rouse-like flexible chain dynamics at length scales below the entanglement confinement length, respectively. Solid curves represent the mean among 3 independent biological reproductions. Shading represents 90% confidence intervals of the mean generated by bootstrap resampling spectra from independent biological reproductions. The dashed line represents the high-frequency scaling behavior of a Rouse polymer G* ∼ ω1/2, which is provided to guide the eye. Bottom left: Illustration of the physical behavior probed in time-scale regimes annotated A, B, and C, as they are interpreted in terms of the Doi and Edwards tube model of entangled polymer dynamics. Top right: Comparison of the frequency-dependent shear modulus G* of intestinal mucus isolated from healthy (control) mice and mice treated with dextran sulfate sodium (DSS) to induce colitis. The high frequency scaling behaviors of a Rouse polymer and a WLC (G* ∼ ω1/2 and G* ∼ ω3/4, respectively) are indicated with dashed lines for reference. Bottom right: Confocal imaging of DSS treated and control mouse colons recapitulates physical disruption of mucus. The intestinal sections were stained to highlight the mucus (UEA-1, green) and the DNA (DAPI, blue). In DSS treated mice the distal colon mucus loses much of the usual striated organization. Scale bars are 50 μm.
The rheological properties of intestinal mucus may play a pivotal role in gut barrier function as well as the growth of microbes embedded within the matrix.71,72 To demonstrate the capability of DLSμR to capture changes in mucus rheology associated with loss of barrier function, we investigate intestinal mucus in a mouse colitis model. Incorporation of dextran sulfate sodium (DSS) into the drinking water of mice disrupts barrier function of intestinal mucus and induces inflammation of the underlying epithelium.73Figure 6 illustrates the change in mucus rheology between healthy and DSS treated (colitic) mice measured by DLSμR. Our results exhibit a striking change in mucus rheology in the colitis model in which the mucus is substantially softened by DSS treatment, suggestive of a substantial reduction in the overall cross-linking density of the matrix (Figure 6). This perturbation to mucus viscoelasticity coincides with physical disruption of mucus morphology within the colon, as visualized by confocal microscopy (Figure 6). Furthermore, although we cannot obtain mucus from mice in sufficient quantities for macrorheology, to validate our DLSμR measurements on mucus samples, we performed DLSμR on reconstituted porcine gastric mucus and found quantitative agreement with macrorheology (Supporting Figure 4). These findings suggest that DLSμR may serve as a valuable tool for investigating biophysical connections between intestinal mucus viscoelasticity and gut barrier status.
Conclusions
In this work, we present a microrheology technique based on DLS in the single-scattering limit that provides access to the frequency-dependent viscoelasticity of soft materials across up to 7 decades in time scale. This technique requires only 12 μL of sample, which renders it amenable to precious materials where sample volume requirements for macrorheology and broad-frequency DWS are impractical. Moreover, we demonstrate that, contrary to common belief, DLSμR in single-scattering detection mode is capable of probing the viscoelasticity of polymer hydrogels with a broad range of material properties, with shear moduli spanning 10 to 104 Pa, which encompasses stiffnesses across a variety of biological tissues. Importantly, this technique is implemented with a commercial benchtop instrument and is therefore accessible to users with a broad range of expertise.
DLSμR represents a valuable contribution to a suite of rheological tools that are available to researchers, and extends the domain of microrheology to a broader base of users. For applications where rapid characterization of ensemble-averaged viscoelasticity of precious materials is desired, DLSμR provides a powerful and accessible alternative to existing techniques. Although VPT and quadrant detection microrheology extract spatially heterogeneous viscoelasticity that is lost by ensemble averaging in DLSμR, our technique overcomes crucial challenges in these established approaches that present barriers to their widespread implementation in the materials chemistry and biomaterials communities. By comparison to VPT, DLSμR reveals viscoelasticity in materials 2 orders of magnitude stiffer and across a range of time scales that is 4 orders of magnitude greater than those accessible to VPT, while obviating the need for the large data footprint and cumbersome data analysis that is required of optical microscopy. In contrast to quadrant detection and related optical trap techniques, which present a substantial technical challenge for many users and provide low statistical power, DLSμR is readily implemented on a commercial benchtop platform and delivers statistically averaged quantities with minimal user “hands-on” time.
We exploit these capabilities to interrogate the hierarchical molecular relaxations that occur in polymeric gels and precious biological materials, including DNA, extracellular matrix, and intestinal mucus. Our measurements capture physical processes ranging from the rapid bending fluctuations of individual polymers to the long-time-scale relaxations in entangled macromolecular networks, and are rationalized in terms of existing polymer physics theories. Together, these findings demonstrate that DLSμR is a powerful tool for exploring the rheological behavior of a variety of precious soft and biological materials that can be readily adopted by an expansive scope of researchers.
Methods
Detailed experimental methods are provided in the Supporting Information.
Acknowledgments
The authors acknowledge financial support from the Stanford BioX Graduate Fellowship program (B.A.K), the James S. McDonnell Studying Complex Systems Postdoctoral Fellowship (C.T.), the National Science Foundation DMR 1508006 (S.C.H), and the National Science Foundation DMR 1707751 (A.J.S.). We thank Sebastian Doniach, Nicholas Melosh, and Gerald Fuller for useful discussions.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.7b00449.
Figures, detailed experimental methods and analysis, a derivation for the predicted high-frequency scaling behavior of polyacrylamide gels, theoretical analysis of wormlike chains, comparison between microrheology and macrorheology for Matrigel, and DLSμR experiments (PDF)
Author Contributions
B.A.K. designed research, conducted research, contributed new analytical tools, and wrote the paper. C.T. designed and conducted research and wrote the paper. P.D. and A.Z. conducted research. J.L.S designed research. S.C.H. and A.J.S designed research and wrote the paper.
The authors declare no competing financial interest.
Supplementary Material
References
- Kim M.; Tang S.; Olsen B. D. Physics of engineered protein hydrogels. J. Polym. Sci., Part B: Polym. Phys. 2013, 51, 587–601. 10.1002/polb.23270. [DOI] [Google Scholar]
- Benight S. J.; Wang C.; Tok J. B. H.; Bao Z. Stretchable and self-healing polymers and devices for electronic skin. Prog. Polym. Sci. 2013, 38, 1961–1977. 10.1016/j.progpolymsci.2013.08.001. [DOI] [Google Scholar]
- Olsen B. D.; Teclemariam N. P.; Muller S. J.; Segalman R. A. Rheological properties and the mechanical signatures of phase transitions in weakly-segregated rod-coil block copolymers. Soft Matter 2009, 5, 2453–2462. 10.1039/b817680a. [DOI] [Google Scholar]
- Wirtz D. Particle-tracking microrheology of living cells: principles and applications. Annu. Rev. Biophys. 2009, 38, 301–326. 10.1146/annurev.biophys.050708.133724. [DOI] [PubMed] [Google Scholar]
- Doi M.; Edwards S.. The Theory of Polymer Dynamics; Clarendon Press: Oxford, 1988. [Google Scholar]
- Mason T. G.; Ganesan K.; van Zanten J.; Wirtz D.; Kuo S. Particle Tracking Microrheology of Complex Fluids. Phys. Rev. Lett. 1997, 79, 3282–3285. 10.1103/PhysRevLett.79.3282. [DOI] [Google Scholar]
- Crocker J. C.; Valentine M. T.; Weeks E. R.; Gisler T.; Kaplan P. D.; Yodh A. G.; Weitz D. A. Two-point microrheology of inhomogeneous soft materials. Phys. Rev. Lett. 2000, 85, 888–891. 10.1103/PhysRevLett.85.888. [DOI] [PubMed] [Google Scholar]
- Gittes F.; Schnurr B.; Olmsted P. D.; Mackintosh F. C.; Schmidt C. F. Microscopic Viscoelasticity: Shear Moduli of Soft Materials Determined from Thermal Fluctuations. Phys. Rev. Lett. 1997, 79, 3286–3289. 10.1103/PhysRevLett.79.3286. [DOI] [Google Scholar]
- Willenbacher N.; Oelschlaeger C. Dynamics and structure of complex fluids from high frequency mechanical and optical rheometry. Curr. Opin. Colloid Interface Sci. 2007, 12, 43–49. 10.1016/j.cocis.2007.03.004. [DOI] [Google Scholar]
- Kowalczyk A.; Hochstein B.; Stähle P.; Willenbacher N. Characterization of complex fluids at very low frequency: Experimental verification of the strain rate-frequency superposition (SRFS) method. Appl. Rheol. 2010, 20, 1–12. [Google Scholar]
- Mason T. G.; Weitz D. A. Optical measurements of frequency-dependent linear viscoelastic moduli of complex fluids. Phys. Rev. Lett. 1995, 74, 1250–1253. 10.1103/PhysRevLett.74.1250. [DOI] [PubMed] [Google Scholar]
- Mizuno D.; Head D. A.; Mackintosh F. C.; Schmidt C. F. Active and Passive Microrheology in Equilibrium and Nonequilibrium Systems. Macromolecules 2008, 41, 7194–7202. 10.1021/ma801218z. [DOI] [Google Scholar]
- Tseng Y. Micro-organization and visco-elasticity of the interphase nucleus revealed by particle nanotracking. J. Cell Sci. 2004, 117, 2159–2167. 10.1242/jcs.01073. [DOI] [PubMed] [Google Scholar]
- Panorchan P.; Lee J. S. H.; Kole T. P.; Tseng Y.; Wirtz D. Microrheology and ROCK signaling of human endothelial cells embedded in a 3D matrix. Biophys. J. 2006, 91, 3499–3507. 10.1529/biophysj.106.084988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mason T. G.; Gang H.; Weitz D. A. Diffusing-wave-spectroscopy measurements of viscoelasticity of complex fluids. J. Opt. Soc. Am. A 1997, 14, 139. 10.1364/JOSAA.14.000139. [DOI] [Google Scholar]
- Yamada S.; Wirtz D.; Kuo S. C. Mechanics of Living Cells Measured by Laser Tracking Microrheology. Biophys. J. 2000, 78, 1736–1747. 10.1016/S0006-3495(00)76725-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atakhorrami M.; Sulkowska J. I.; Addas K. M.; Koenderink G. H.; Tang J. X.; Levine A. J.; Mackintosh F. C.; Schmidt C. F. Correlated fluctuations of microparticles in viscoelastic solutions: Quantitative measurement of material properties by microrheology in the presence of optical traps. Phys. Rev. E 2006, 73, 061501. 10.1103/PhysRevE.73.061501. [DOI] [PubMed] [Google Scholar]
- Dasgupta B. R.; Tee S. Y.; Crocker J. C.; Frisken B. J.; Weitz D. A. Microrheology of polyethylene oxide using diffusing wave spectroscopy and single scattering. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2002, 65, 051505. 10.1103/PhysRevE.65.051505. [DOI] [PubMed] [Google Scholar]
- Schultz K. M.; Furst E. M. Microrheology of biomaterial hydrogelators. Soft Matter 2012, 8, 6198–6205. 10.1039/c2sm25187f. [DOI] [Google Scholar]
- Waigh T. A. Advances in the microrheology of complex fluids. Rep. Prog. Phys. 2016, 79, 074601. 10.1088/0034-4885/79/7/074601. [DOI] [PubMed] [Google Scholar]
- Pawelzyk P.; Mücke N.; Herrmann H.; Willenbacher N. Attractive interactions among intermediate filaments determine network mechanics in vitro. PLoS One 2014, 9, e93194. 10.1371/journal.pone.0093194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy-Smith K.; Beltramo P. J.; Moore E.; Tycko R.; Furst E. M.; Schneider J. P. Molecular, Local, and Network-Level Basis for the Enhanced Stiffness of Hydrogel Networks Formed from Coassembled Racemic Peptides: Predictions from Pauling and Corey. ACS Cent. Sci. 2017, 3, 586–597. 10.1021/acscentsci.7b00115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alam M. M.; Mezzenga R. Particle tracking microrheology of lyotropic liquid crystals. Langmuir 2011, 27, 6171–6178. 10.1021/la200116e. [DOI] [PubMed] [Google Scholar]
- Dominguez-Garcia P.; Cardinaux F.; Bertseva E.; Forro L.; Scheffold F.; Jeney S. Accounting for inertia effects to access the high-frequency microrheology of viscoelastic fluids. Phys. Rev. E 2014, 90, 060301. 10.1103/PhysRevE.90.060301. [DOI] [PubMed] [Google Scholar]
- Liu J.; Boyko V.; Yi Z.; Men Y. Temperature-dependent gelation process in colloidal dispersions by diffusing wave spectroscopy. Langmuir 2013, 29, 14044–14049. 10.1021/la402996v. [DOI] [PubMed] [Google Scholar]
- Narita T.; Mayumi K.; Ducouret G.; Hébraud P. Viscoelastic properties of poly(vinyl alcohol) hydrogels having permanent and transient cross-links studied by microrheology, classical rheometry, and dynamic light scattering. Macromolecules 2013, 46, 4174–4183. 10.1021/ma400600f. [DOI] [Google Scholar]
- Martiel I.; Sagalowicz L.; Mezzenga R. Viscoelasticity and interface bending properties of lecithin reverse wormlike micelles studied by diffusive wave spectroscopy in hydrophobic environment. Langmuir 2014, 30, 10751–10759. 10.1021/la502748e. [DOI] [PubMed] [Google Scholar]
- Gardel M. L.; Valentine M. T.; Weitz D. A. Microrheology. Microscale Diagnostic Techniques 2005, 1–49. 10.1007/3-540-26449-3_1. [DOI] [Google Scholar]
- Abdala A. A.; Amin S.; Van Zanten J. H.; Khan S. A. Tracer microrheology study of a hydrophobically modified comblike associative polymer. Langmuir 2015, 31, 3944–3951. 10.1021/la504904n. [DOI] [PubMed] [Google Scholar]
- Larobina D.; Cipelletti L. Hierarchical cross-linking in physical alginate gels: a rheological and dynamic light scattering investigation. Soft Matter 2013, 9, 10005. 10.1039/c3sm52006d. [DOI] [Google Scholar]
- Dasgupta B. R.; Weitz D. A. Microrheology of cross-linked polyacrylamide networks. Phys. Rev. E 2005, 71, 021504. 10.1103/PhysRevE.71.021504. [DOI] [PubMed] [Google Scholar]
- He F.; Becker G. W.; Litowski J. R.; Narhi L. O.; Brems D. N.; Razinkov V. I. High-throughput dynamic light scattering method for measuring viscosity of concentrated protein solutions. Anal. Biochem. 2010, 399, 141–143. 10.1016/j.ab.2009.12.003. [DOI] [PubMed] [Google Scholar]
- Kaszuba M.; Connah M. T.; McNeil-Watson F. K.; Nobbmann U. Resolving concentrated particle size mixtures using dynamic light scattering. Particle and Particle Systems Characterization 2007, 24, 159–162. 10.1002/ppsc.200601035. [DOI] [Google Scholar]
- Butcher D. T.; Alliston T.; Weaver V. M. A tense situation: forcing tumour progression. Nat. Rev. Cancer 2009, 9, 108–22. 10.1038/nrc2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basu A.; Wen Q.; Mao X.; Lubensky T. C.; Janmey P. A.; Yodh A. G. Nonaffine displacements in flexible polymer networks. Macromolecules 2011, 44, 1671–1679. 10.1021/ma1026803. [DOI] [Google Scholar]
- Rubinstein M.; Colby R.. Polymer Physics; Oxford University Press: New York, 2003. [Google Scholar]
- Martin J. E.; Adolf D.; Wilcoxon J. P. Viscoelasticity of near-critical gels. Phys. Rev. Lett. 1988, 61, 2620–2623. 10.1103/PhysRevLett.61.2620. [DOI] [PubMed] [Google Scholar]
- Cates M. E. Brownian dynamics of self-similar macromolecules. J. Phys. (Paris) 1985, 46, 1059–1077. 10.1051/jphys:019850046070105900. [DOI] [Google Scholar]
- Adolf D.; Martin J. E. Ultraslow Relaxations in Networks: Evidence for Remnant Fractal Structures. Macromolecules 1991, 24, 6721–6724. 10.1021/ma00025a025. [DOI] [Google Scholar]
- Larsen T. H.; Furst E. M. Microrheology of the liquid-solid transition during gelation. Phys. Rev. Lett. 2008, 100, 146001. 10.1103/PhysRevLett.100.146001. [DOI] [PubMed] [Google Scholar]
- Adibnia V.; Hill R. J. Universal aspects of hydrogel gelation kinetics, percolation and viscoelasticity from PA-hydrogel rheology. J. Rheol. 2016, 60, 541–548. 10.1122/1.4948428. [DOI] [Google Scholar]
- Schultz K. M.; Baldwin A. D.; Kiick K. L.; Furst E. M. Gelation of covalently cross-linked PEG-heparin hydrogels. Macromolecules 2009, 42, 5310–5315. 10.1021/ma900766u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abidine Y.; Laurent V. M.; Michel R.; Duperray A.; Palade L. I.; Verdier C. Physical properties of polyacrylamide gels probed by AFM and rheology. EPL 2015, 109, 38003. 10.1209/0295-5075/109/38003. [DOI] [Google Scholar]
- Amin S.; Rega C. A.; Jankevics H. Detection of viscoelasticity in aggregating dilute protein solutions through dynamic light scattering-based optical microrheology. Rheol. Acta 2012, 51, 329–342. 10.1007/s00397-011-0606-6. [DOI] [Google Scholar]
- Amin S.; Blake S.; Kenyon S. M.; Kennel R. C.; Lewis E. N. A novel combination of DLS-optical microrheology and low frequency Raman spectroscopy to reveal underlying biopolymer self-assembly and gelation mechanisms. J. Chem. Phys. 2014, 141, 234201. 10.1063/1.4903785. [DOI] [PubMed] [Google Scholar]
- Parmar A. S.; Hill S.; Vidyasagar A.; Bello C.; Toomey R.; Muschol M. Frequency and temperature dependence of poly(N-isopropylacrylamide) gel rheology. J. Appl. Polym. Sci. 2013, 127, 1527–1537. 10.1002/app.37561. [DOI] [Google Scholar]
- Urueña J. M.; Pitenis A. A.; Nixon R. M.; Schulze K. D.; Angelini T. E.; Gregory Sawyer W. Mesh Size Control of Polymer Fluctuation Lubrication in Gemini Hydrogels. Biotribology 2015, 1–2, 24–29. 10.1016/j.biotri.2015.03.001. [DOI] [Google Scholar]
- Berne B. J.; Pecora R.. Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics; Wiley: New York, 2003. [Google Scholar]
- Pusey P. N.; Van Megen W. Dynamic light scattering by non-ergodic media. Phys. A 1989, 157, 705–741. 10.1016/0378-4371(89)90063-0. [DOI] [Google Scholar]
- Marko J. F.; Siggia E. D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. 10.1021/ma00130a008. [DOI] [Google Scholar]
- Morse D. C. Viscoelasticity of tightly entangled solutions of semiflexible polymers. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1998, 58, R1237–R1240. 10.1103/PhysRevE.58.R1237. [DOI] [Google Scholar]
- Gittes F.; MacKintosh F. C. Dynamic shear modulus of a semiflexible polymer network. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 1998, 58, R1241–R1244. 10.1103/PhysRevE.58.R1241. [DOI] [Google Scholar]
- Morse D. C. Viscoelasticity of Concentrated Isotropic Solutions of Semiflexible Polymers. 1. Model and Stress Tensor. Macromolecules 1998, 31, 7030–7043. 10.1021/ma9803032. [DOI] [Google Scholar]
- Robertson R. M.; Smith D. E. Self-diffusion of entangled linear and circular DNA molecules: Dependence on length and concentration. Macromolecules 2007, 40, 3373–3377. 10.1021/ma070051h. [DOI] [Google Scholar]
- Robertson R. M.; Smith D. E. Strong effects of molecular topology on diffusion of entangled DNA molecules. Proc. Natl. Acad. Sci. U. S. A. 2007, 104, 4824. 10.1073/pnas.0700137104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eimer W.; Pecora R. Rotational and translational diffusion of short rodlike molecules in solution: Oligonucleotides. J. Chem. Phys. 1991, 94, 2324–2329. 10.1063/1.459904. [DOI] [Google Scholar]
- Zhu X.; Kundukad B.; Van Der Maarel J. R. Viscoelasticity of entangled λ -phage DNA solutions. J. Chem. Phys. 2008, 129, 185103. 10.1063/1.3009249. [DOI] [PubMed] [Google Scholar]
- Chapman C. D.; Lee K.; Henze D.; Smith D. E.; Robertson-Anderson R. M. Onset of non-continuum effects in microrheology of entangled polymer solutions. Macromolecules 2014, 47, 1181–1186. 10.1021/ma401615m. [DOI] [Google Scholar]
- Gisler T.; Weitz D. Scaling of the Microrheology of Semidilute F-Actin Solutions. Phys. Rev. Lett. 1999, 82, 1606–1609. 10.1103/PhysRevLett.82.1606. [DOI] [Google Scholar]
- Oelschlaeger C.; Cota Pinto Coelho M.; Willenbacher N. Chain Flexibility and Dynamics of Polysaccharide Hyaluronan in Entangled Solutions: A High Frequency Rheology and Diffusing Wave Spectroscopy Study. Biomacromolecules 2013, 14, 3689–3696. 10.1021/bm4010436. [DOI] [PubMed] [Google Scholar]
- Willenbacher N.; Oelschlaeger C.; Schopferer M.; Fischer P.; Cardinaux F.; Scheffold F. Broad bandwidth optical and mechanical rheometry of wormlike micelle solutions. Phys. Rev. Lett. 2007, 99, 068302. 10.1103/PhysRevLett.99.068302. [DOI] [PubMed] [Google Scholar]
- Le Goff L.; Amblard F.; Furst E. M. Motor-Driven Dynamics in Actin-Myosin Networks. Phys. Rev. Lett. 2001, 88, 018101. 10.1103/PhysRevLett.88.018101. [DOI] [PubMed] [Google Scholar]
- Mason T. G.; Dhople a.; Wirtz D. Linear Viscoelastic Moduli of Concentrated DNA Solutions. Macromolecules 1998, 31, 3600–3603. 10.1021/ma970564w. [DOI] [Google Scholar]
- Goodman A.; Tseng Y.; Wirtz D. Effect of length, topology, and concentration on the microviscosity and microheterogeneity of DNA solutions. J. Mol. Biol. 2002, 323, 199–215. 10.1016/S0022-2836(02)00893-8. [DOI] [PubMed] [Google Scholar]
- Ferry J. D.Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, 1980. [Google Scholar]
- Paszek M. J.; Zahir N.; Johnson K. R.; Lakins J. N.; Rozenberg G. I.; Gefen A.; Reinhart-King C. A.; Margulies S. S.; Dembo M.; Boettiger D.; Hammer D. A.; Weaver V. M. Tensional homeostasis and the malignant phenotype. Cancer Cell 2005, 8, 241–254. 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- Engler A. J.; Sen S.; Sweeney H. L.; Discher D. E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell 2006, 126, 677–689. 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- Hughes C. S.; Postovit L. M.; Lajoie G. A. Matrigel: a complex protein mixture required for optimal growth of cell culture. Proteomics 2010, 10, 1886–1890. 10.1002/pmic.200900758. [DOI] [PubMed] [Google Scholar]
- McGuckin M. A.; Lindén S. K.; Sutton P.; Florin T. H. Mucin dynamics and enteric pathogens. Nat. Rev. Microbiol. 2011, 9, 265–278. 10.1038/nrmicro2538. [DOI] [PubMed] [Google Scholar]
- Tropini C.; Earle K. A.; Huang K. C.; Sonnenburg J. L. The Gut Microbiome: Connecting Spatial Organization to Function. Cell Host Microbe 2017, 21, 433–442. 10.1016/j.chom.2017.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson M. E. V.; Hansson G. C. Immunological aspects of intestinal mucus and mucins. Nat. Rev. Immunol. 2016, 16, 639–649. 10.1038/nri.2016.88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuson H. H.; Auer G. K.; Renner L. D.; Hasebe M.; Tropini C.; Salick M.; Crone W. C.; Gopinathan A.; Huang K. C.; Weibel D. B. Measuring the stiffness of bacterial cells from growth rates in hydrogels of tunable elasticity. Mol. Microbiol. 2012, 84, 874–891. 10.1111/j.1365-2958.2012.08063.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson M. E. V.; Gustafsson J. K.; Sjöberg K. E.; Petersson J.; Holm L.; Sjövall H.; Hansson G. C. Bacteria penetrate the inner mucus layer before inflammation in the dextran sulfate colitis model. PLoS One 2010, 5, e12238. 10.1371/journal.pone.0012238. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.