Extended beta distributions open the access to fast gating in bilayer experiments—assigning the voltage‐dependent gating to the selectivity filter

Abstract

Lipid bilayers provide many benefits for ion channel recordings, such as control of membrane composition and transport molecules. However, they suffer from high membrane capacitance limiting the bandwidth and impeding analysis of fast gating. This can be overcome by fitting the deviations of the open‐channel noise from the baseline noise by extended beta distributions. We demonstrate this analysis step‐by‐step by applying it to the example of viral K⁺ channels (Kcv), from the choice of the gating model through the fitting process, validation of the results, and what kinds of results can be obtained. These voltage sensor‐less channels show profoundly voltage‐dependent gating with dwell times in the closed state of about 50 μs. Mutations assign it to the selectivity filter.

Abbreviations

CMOS, complementary metal‐oxide semiconductor

NLPs, complementary metal‐oxide semiconductor , nanolipoproteins

VSD, complementary metal‐oxide semiconductor , voltage‐sensing domains

Using artificial bilayers to record single‐channel currents 1 provides a number of benefits. The composition of the membrane is known and can be chosen as desired. Also, there is no interference from endogenous transport molecules. Solutions can easily be exchanged at either side of the membrane up to several molar. Long‐term studies on one channel for several days are possible. Mutants of channels can easily be created and reconstituted using site‐directed mutagenesis and in vitro expression based on nanodiscs 2, 3.

However, the bilayer technique has a drawback when it comes to the recording of fast gating events. The capacitance of the membrane determines the baseline current noise 4. In most bilayer systems, we measured a capacitance of around 70 pF as compared to less than 10 pF in the case of pipettes used for patch‐clamp studies. As a result, bilayer currents must generally be low‐pass filtered at 1–5 kHz bandwidth or lower to achieve reasonable signal‐to‐noise ratios 5. In contrast, optimized patch‐clamp recordings allow up to 20 or 50 kHz 6. A significant reduction of capacitance (to less than 5 pF) can be achieved by fabricating a microcavity for bilayer formation directly on top of the measuring electronics fully integrated in complementary metal‐oxide semiconductor (CMOS) technology 7, 8.

Even though temporal resolution for the detection of open‐closed transitions can be increased by improved jump detection 9, 10, deconvoluting the filter response 11, or missed events correction 12, 13, 14, the gain in resolution is moderate. Using a direct fit of the time series 15, 16 gives similar improvements.

Fitting of amplitude histograms by extended beta distributions 17 leads to much higher resolution 18. No jump detector is involved, instead, time is converted to amplitude. The low‐pass filter converts every jump between levels to a smooth filter response, leading to characteristic mostly non‐Gaussian curve shapes of the amplitude histograms. Analysis of these histograms yields the rate constants of the involved hidden fast gating processes and the “true” single‐channel current 17. The latter is a problem often ignored, namely that averaging over undetected fast gating delivers an apparent single‐channel current, I _app, which is smaller than the “true” single‐channel current, I _true, which would be measured with a fictional amplifier of 100 MHz bandwidth.

The usage of beta distributions for ion channel analysis was introduced in 1983 19 and enabled the analysis of hitherto unresolved fast gating 20, 21. However, these studies employed an analytical expression for the beta distributions. This holds only for first‐order filters and two‐state Markov models of gating. There is no analytical solution if these conditions are not fulfilled. Instead, a set of differential equations has to be solved by an iterative numerical process for multistate Markov models 22 and also for higher order low‐pass filters.

The extended beta distributions used here are not based on the solution of the differential equations, but on the simulation of a time series 17, 18, 23, 24, 25. This way, all experimental parameters can be included without any simplifying assumptions, such as higher order filters, multistate Markov models, multichannel recordings, or the amplitude histogram of (even non‐Gaussian) set‐up noise.

Here, we illustrate the details of the procedure step by step for the analysis of a phenomenon, which otherwise could not be quantified. The choice of this example is not only useful to make the procedure more intelligible but also provides a scientific fringe benefit. At negative membrane voltages, the single‐channel current–voltage relationships (IV curves) of the viral Kcv K⁺ channels show a negative slope 26, 27, 28. Extended beta distribution analysis reveals that this is caused by normally hidden fast gating with dwell times in the closed state of about 50 μs. We show how the extended beta distribution analysis enables determination of the voltage dependence of the rate constants. In combination with mutations we can also identify the selectivity filter as the locus of this gating.

The choice of these minimal size K⁺ channels as an example is motivated by the fact that they are typical candidates for bilayer experiments. Different behavior of individual members of the family is related to just a few different residues. This yields a plethora of guide lines for mutations, calling for a rapid functional test as provided by in vitro expression and reconstitution 3, 28.

Materials and Methods

In vitro protein expression and purification

The viruses encoding for Kcv_NTS and Kcv_NH were isolated from lakes in Nebraska 29 and New Hampshire, respectively. The proteins were expressed in vitro and purified as described previously 28. Briefly, the respective genes were cloned into a pEXP5‐CT/TOPO^®‐vector (Invitrogen, Carlsbad, CA, USA) with a stop codon directly upstream of the coding sequence of a 6xHis‐tag. Mutations were introduced by site‐directed mutagenesis, following the QuickChange method 30. All mutants were sequenced.

Expression of the proteins was performed with the MembraneMax™ HN Protein Expression Kit (Invitrogen, Carlsbad, CA). The resulting complexes, containing native channel proteins and His‐tagged nanolipoproteins (NLPs, “nanodiscs”) 2 were purified on a 0.2 mL HisPur™ Ni‐nitrilotriacetic acid spin column (ThermoFisher Scientific, Waltham, MA, USA). Elution was done in three fractions (200 μL each) with 250 mm imidazole.

Lipid bilayer experiments

Vertical lipid bilayer experiments 1 were performed at 20–25 °C with a conventional bilayer set‐up (IonoVation, Osnabrück, Germany). The recording chambers were prepared as described previously 3, and 1,2‐diphytanoyl‐sn‐glycero‐3‐phosphocholine (DPhPC, from Avanti Polar Lipids, Alabaster, AL, USA) bilayers were formed by the pseudopainting/air bubble technique 31. For reconstitution of the channels, a small amount (1–3 μL) of the purified NLP/Kcv_NTS conjugates diluted in 250 mm imidazole solution was added directly below the bilayer in the trans compartment.

After incorporation of a single channel into the bilayer, constant voltages as indicated in the figures were applied for 1–5 min. Both compartments of the bilayer chamber were connected with Ag/AgCl electrodes to the headstage of a patch‐clamp amplifier (L/M‐EPC‐7, List‐Medical, Darmstadt, Germany). Membrane voltages were applied to the cis compartment, the trans compartment was grounded. K⁺ concentration was changed by replacing an appropriate amount of the solution by 3 m KCl stock solution and thorough mixing. All solutions and stock solutions contained 10 mm HEPES, pH was adjusted to 7.0 with KOH. The orientation of the protein in the bilayer was identified by the negative slope at negative voltages 32 found in the apparent current, I _app (Fig. 1D, below). Positive currents correspond to outward currents in the in vivo situation. Currents were filtered with a 1‐kHz 4‐pole Bessel filter and sampled at 5 kHz by a 16‐bit A/D‐converter (LIH 1600, HEKA Elektronik, Lambrecht, Germany).

Figure 1.

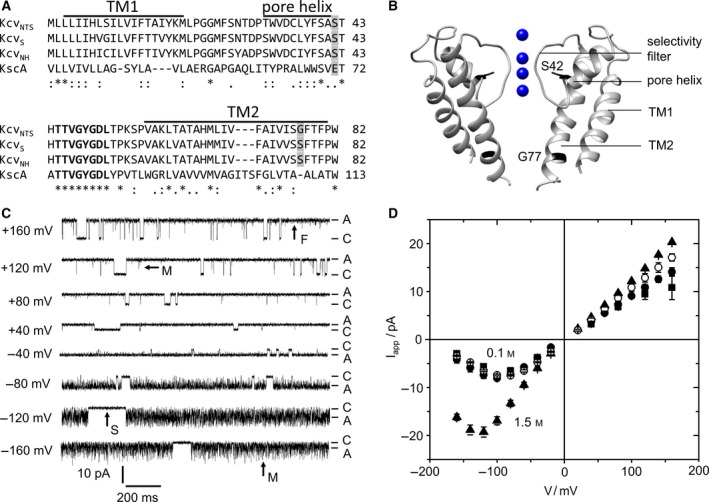
Characteristics of viral K⁺ channels (Kcv). (A) Alignment of 3 Kcv isoforms with KcsA. The conserved selectivity filter sequence is printed in bold, bars mark the predicted transmembrane helices (TM1, TM2), and pore helix of Kcv_NTS 28. Positions mutated in this study are shaded in gray. (B) Structural model of Kcv_NTS with those positions highlighted that were mutated in this study. The homology model was built with Swissmodel 51 after KirBac1.1 (PDB 1P7B 52 ). (C) Current traces of a single in vitro expressed Kcv_NTS channel in a DPhPC bilayer in symmetrical 0.1 m KCl, pH 7. Membrane voltage is indicated at each trace. C and A label the closed state (baseline) and apparent open current I_app, respectively. Examples of slow (S), medium (M), and fast (F) gating are indicated by arrows. (D) Apparent single‐channel IV curves of Kcv_NTS (filled circles), Kcv_NH (squares), and Kcv_NH S77G (open circles) for symmetrical 0.1 m and of Kcv_NTS in 1.5 m (triangles) KCl. Mean of 3 experiments, 6 for Kcv_NTS at 0.1 m. The standard deviation is mostly smaller than the symbols.

Additionally, an alternative set‐up was used to perform experiments at higher bandwidth of 10 kHz, as described in the Appendix S1.

Extended beta distribution analysis

The generation of simulated time series starts from a Markov model of gating with suggested rate constants and value of the “true” single‐channel current, I _true. A list of jumps in continuous time is generated. Each jump induces a step response of current identical to that of the employed low‐pass filter. All responses are added (as long as their contributions exceed one bit) to furnish the filtered time series of current. It is sampled with the same rate as used in the experiment, and the amplitude histogram is created. Noise is added by a convolution of this histogram with that of the baseline noise.

This simulated amplitude histogram is compared with the measured one by calculating the weighted squared error sum ${\mathit{\chi }}^2={\sum }_i{\left(n_{exp,i}-n_{sim,i}\right)}^2/n_{sim,i}$, with n being the frequency. The current has been binned at 50 fA intervals. The model parameters are optimized by a simplex search algorithm 33 in repetitive runs. The rate constants and I _true of the best fit are taken as the best parameters for the investigated system.

More details on the method can be found in Appendix S2. The program bownhill.exe can be downloaded from http://www.bio.tu-darmstadt.de/ag/professuren/indraschroeder/software.en.jsp.

Definitions

Gating: Here, the term gating is also used for spontaneous opening and closing of the conductive pathway including flickering.

I _app: The apparent current, obtained directly from the current record without gating analysis, that is, from averaging over sojourns in the apparent open state (A in Fig. 1C) or from the open peak of the amplitude histogram.

I _true: The true open‐channel current, which would be measured by an (hypothetical) amplifier with infinite bandwidth.

I _OF: Obtained from averaging over the very fast gating (O‐F gating, below).

Results and Discussion

Kcv channels used as an example for the application of extended beta distributions

The viral proteins Kcv_NTS and Kcv_NH form homotetramers with merely 82 amino acids per monomer. The predicted structure of Kcv_NTS (Fig. 1B) matches the canonical K⁺ channel pore with two transmembrane helices and a pore loop containing the selectivity filter and a short pore helix 3, 28, 34, 35. The consensus selectivity filter sequence 36 is perfectly conserved (Fig. 1A). The channel lacks any cytosolic domains and has only a very short extracellular loop. Despite their minimal structure, Kcv channels are selective 32, show a complex spontaneous gating behavior (Fig. 1C) 27, 28, and can be blocked by typical K⁺ channel blockers such as Ba²⁺ 32. Thus, they represent the minimal consensus for structure and function of a K⁺ channel 37.

The gating behavior of Kcv channels in planar lipid bilayers is illustrated for Kcv_NTS in Fig. 1C. Kcv_NTS gates spontaneously with a high open probability of >80% (Fig. 1C) 3, 28. Some long, clearly detectable closed events (arrow “S” = “slow” in Fig. 1C) are accessible to dwell time analysis 28. Faster gating processes are attenuated by the limited recording bandwidth of the 1‐kHz filter. This results in incomplete closures (“spikes”) and “excess” open‐channel noise. For instance, at positive membrane voltages, there are a few spikes, which do not quite reach the baseline (arrow “M” = “medium” at +120 mV in Fig. 1C). We call this phenomenon the medium gating process or submillisecond gating. The noise of the open state is slightly broader than that of the closed state, resulting from an even faster gating process (arrow “F” = “fast” in Fig. 1C), which becomes more obvious in the amplitude histograms shown in Fig. 2B,C, below. At negative voltages, the medium gating process becomes dominant, appearing as strong flickering (arrow “M” at ‐160 mV in Fig. 1C). The “apparent” current, I _app (Fig. 1D), has been obtained from amplitude histograms created from smoothed time series with 10 adjacent data points being averaged. The fast gating processes M and F are the reason why Kcv channels are used as examples to illustrate the analysis by means of extended beta distributions.

Figure 2.

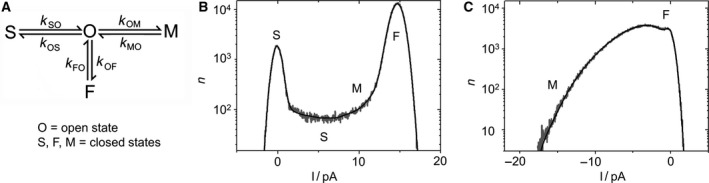
Fitting extended beta distributions to measured amplitude histograms. (A) Four‐state Markov model used for the generation of the theoretical amplitude histograms (extended beta distributions) by simulated current traces. (B,C) Representative current amplitude histograms of Kcv_NTS in 0.1 m KCl, pH 7 (gray) and the best fit with the model in (A) (black). Regions dominated by one of the closed states F, M, or S are indicated. At +160 mV (B), both the closed (at 0 pA) and open peak (at 14.6 pA) are well defined. At ‐160 mV (C), the open peak is extremely broadened and skewed, corresponding to the large, asymmetric open‐channel noise in the current trace (Fig. 1C).

Determination of gating rate constants and open‐channel current by extended beta distributions

Selection of the gating model as illustrated for Kcv_NTS

The first step of a model‐based gating analysis is to select a Markov model with the appropriate number of states and an appropriate topology. For Kcv_NTS, the minimum number of states is one open state (O) and three closed states (S, F, M) as shown in the model in Fig. 2A. The three gating processes, O‐S, O‐M, and O‐F, are found in the current traces (Fig. 1C), as described above. They can be identified even more clearly in the amplitude histograms (Figs. 2B,C). The fast O‐F gating determines the shape of the open peak (width and asymmetry). The medium O‐M gating process forms the slope at the foot of the open peak (steepness and height). All slow gating processes reach the full apparent levels after each jump and yield identical contributions to the amplitude histogram. Thus, they cannot be distinguished by the analysis and are merged into one process. This slow (O‐S) process determines the ratio of the heights of the closed peak and the open peak, and contributes to the height of the valley between the two peaks. The relationship between the rate constants and the shape of the histograms is sufficiently unique so that good guesses for starting values for the fit can be made.

The second part of choosing the model, the arrangement of the states (Fig. 2A) is based on the following considerations: The three closed states, S, M, and F have very different dwell times. The longest closed state S must not be positioned between the open state O and any one of the two other closed states, because this would hide M and F from experimental observation. By the same argument, the shortest closed state F must be directly coupled to O. Since the O‐S gating has to be investigated separately by dwell time analysis 28, we constrain the consideration to the submodel consisting of O, F, and M.

Here, we can either choose O‐F‐M, F‐O‐M (Fig. 2A), or a cyclic model. The “star‐shaped” model in Fig. 2A is the most efficient one for fitting. If future data will show that a different model topology is needed, one 3‐state model can be transformed into another one 38. Under the numerical conditions here, the conversion is quite simple, and the voltage dependence of the rate constants of state M would remain unchanged (Appendix S4, Eqns S2 and S3). Similar principles can be used to choose appropriate gating models for different channels. In a simple fast blocking process for example, a two‐state model might be sufficient 39.

Extracting open‐channel current and gating rate constants by extended beta distributions

After the model has been chosen, the simulated amplitude histograms are fitted to the measured ones as described above. Figure 2B and C show typical results of the analysis for the Kcv_NTS example: The theoretical curve (black) fits the measured histogram (gray). The analysis yields the rate constants of the three involved gating processes (Fig. 3A,B) and the true open‐channel current I _true presented by a linear IV curve in Fig. 3C. Because of the tight relation of rate constants and the shape of the histograms (as described above, see also Appendix S3, Fig. S1), the scatter is appreciably low.

Figure 3.

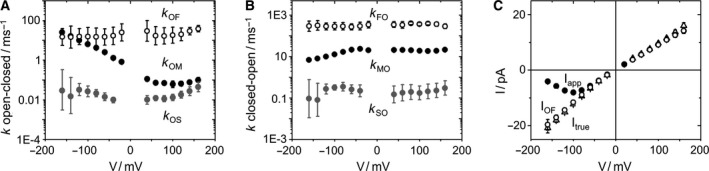
Fit results for Kcv_NTS in 0.1 m KCl. (A,B) The rate constants of the model in Fig. 2A as obtained from fitting amplitude histograms like those in Fig. 2B,C by means of extended beta distributions. (C) The three different currents defined in the M&M section: I_true (triangles) obtained from the fitting routine, I_OF (open circles) obtained from averaging over the O‐F gating [Eqn (1)] and I_app (closed circles) directly obtained from the time series. Mean of six experiments. The standard deviation is mostly smaller than the symbols.

Test of the reliability of the fits

An experimental demonstration of the reliability of the analysis is shown in Fig. 4A. As defined in the Materials and Methods section, there are different currents: I _true would be measured with an amplifier of infinite bandwidth. I _OF would be measured with an amplifier that can resolve the O‐M gating, but not the O‐F gating. Thus, it results from averaging over the O‐F gating as follows

$$I_{\mathit{OF}}=I_{\mathit{true}}\frac{k_{\mathit{FO}}}{k_{\mathit{FO}}+k_{\mathit{OF}}}$$ (1)

Figure 4.

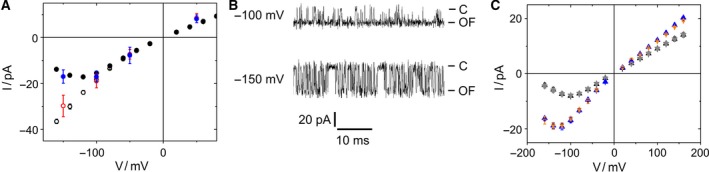
Reliability of the extended beta distribution fit. (A) I _app of Kcv_NTS at 1 m KCl as obtained with the 1‐kHz filter (black circles) or from filtering the 10‐kHz data from Meca‐4 chips to ca. 1 kHz by a moving average filter (blue circles). I _OF as determined by the extended beta distribution fit with 1‐kHz filter [Eqn (1)], open black circles, n = 3) and I _OF directly measured with the 10‐kHz filter (open red circles n = 4). (B) Representative current traces of Kcv_NTS in 1 m KCl filtered at 10 kHz. Closed channel and I _OF are labeled as C and OF, respectively. (C) Current I _app measured at 1 kHz for Kcv_NTS at 0.1 m (black) and 1.5 m KCl (blue) compared with I _app (gray and orange) as calculated from averaging over O‐M and O‐F gating [Eqn (2)]. Mean and standard deviation of 6 and 3 experiments at 0.1 and 1.5 m, respectively.

I _app is directly obtained from the peaks of the smoothed amplitude histograms, and should be identical to I _app obtained from averaging over O‐M and O‐F gating

$$I_{\mathit{app}}=I_{\mathit{true}}\frac{k_{\mathit{FO}}}{k_{\mathit{FO}}+k_{\mathit{OF}}}·\frac{k_{\mathit{MO}}}{k_{\mathit{MO}}+k_{\mathit{OM}}}=I_{\mathit{OF}}\frac{k_{\mathit{MO}}}{k_{\mathit{MO}}+k_{\mathit{OM}}}$$ (2)

Using a low‐noise high‐bandwidth amplifier in combination with a membrane with a diameter of 50 μm allowed us to decrease the system's noise and test the model predictions. In 1 m KCl, the signal‐to‐noise ratio became good enough to use a 10‐kHz filter, which largely avoided averaging over the O‐M gating. The fast O‐F gating still remains hidden. Under these conditions, it became possible to determine I _OF directly from the measured time series (Fig. 4B). Now, the time series look similar to those measured with a 1‐kHz filter at positive potentials (Fig. 1C) where the narrow noisy sojourns indicate that I _OF has been reached and I _app and I _OF coincide (Fig. 3C).

I _OF obtained at 1 m KCl with the 10‐kHz filter provides a comparison with the I _OF value determined by Eqn (1) using the parameters obtained from the analysis of the 1‐kHz recordings. Figure 4A shows that I _OF obtained from the analysis (black open circles) coincides with that one directly obtained from 10‐kHz recordings (red open circles). The inverse procedure also works (Fig. 4A). A 1000‐point moving average filter reduces the bandwidth of the 10‐kHz data, which were sampled at 1 MHz, to approximately 1 kHz. This leads to the same I _app (blue circles) as measured with the 1‐kHz filter (black circles). However, the direct determination of I _OF only works at high KCl concentrations, and even then the related rate constants cannot be revealed reliably by dwell time analysis, because the noise level is still too high and the O‐M gating is not perfectly resolved (Fig. 4B).

However, with high current amplitudes, as, for example, delivered by the Ryanodine receptor RyR1, the combination of a low‐capacitance amplifier/bilayer system, and extended beta distribution analysis is able to push the temporal resolution down to 30 ns 8.

Another approach to check the reliability of the fits is demonstrated in Appendix S5. Plotting the dependence of the error sum on the fit parameters (Fig. S2) gives an estimate of the uniqueness of the fit solution. In the Kcv_NTS example, we only show the dependence on one of the 8 rate constant, k _OM, since it is the most interesting one because of its strong voltage dependence (Fig. 3A), and on the open‐channel current I _true.

Examples of what extended beta distribution analysis can reveal

Identifying O‐M gating as the origin of the apparent negative slope

In the case of the Kcv_NTS example, the difference between the apparent current I _app and the true open‐channel current I _true (Fig. 3C) demonstrates that the negative slope of I _app is an artifact arising from the voltage‐dependent O‐M gating (Fig. 3A,B). The measured apparent IV curve coincides with the theoretical I _app [Eqn (2)] calculated from averaging over the O‐M and O‐F gating (Fig. 4C). I _OF is the current resulting from averaging over O‐F gating [Eqn (1)]. Since I _OF /I _true is not very voltage‐dependent (Fig. 3), it is obvious that the voltage‐dependent reduction of I _app (and thus the negative slope) originates from the term k _MO/(k _OM+k _MO), that is, from O‐M gating.

Phenomenological description of the voltage dependence of the O‐M gating

As a first step in the interpretation of the results of the gating analysis, we search for a phenomenological description of the rate constants. For the Kcv_NTS example, the rate constant of channel closing k _OM (Fig. 3A) can be fitted with the phenomenological equation

$$k_{\mathit{OM}}=q_{\mathit{OM}}+b_{\mathit{OM}}exp(-V/V_{\mathit{OM}})$$ (3)

with q _OM , b _OM being scaling factors, V _OM the characteristic voltage (Fig. 5A). The steepness of the curves is a shared parameter with V _OM = 36 mV for both 0.1 and 1.5 m KCl. The sum of two terms in Eqn (3) suggests that the O‐M gating processes at positive and negative voltages belong to different mechanisms. The constant q _OM roughly describes the almost voltage‐independent behavior at positive voltages.

Figure 5.

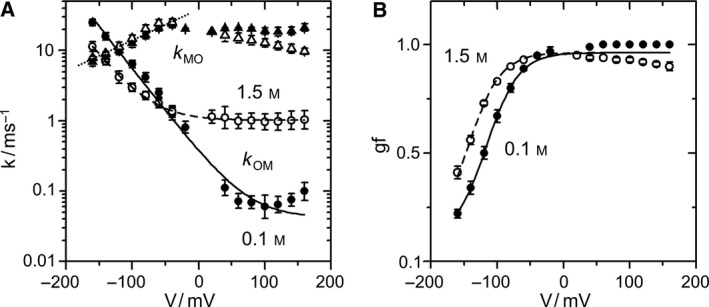
Phenomenological fits of the voltage dependence of O‐M gating (A) Voltage dependencies of k _OM (filled and open circles for 0.1 and 1.5 m KCl, respectively). The lines show the fit with the parameters of Eqn (3): V _OM = 36 mV, q _OM = 0.042 and 1.013 ms⁻¹, b _OM = 0.340 and 0.123 ms⁻¹ for 0.1 m KCl (solid line) and 1.5 m KCl (dashed line), respectively. k _MO (filled and open triangles for 0.1 and 1.5 m KCl, respectively) was fitted with Eqn (4) (dotted line) with V _MO = 99 mV, k _MO,0 = 38 ms⁻¹ for both concentrations. (B) Gating factor gf [Eqn (5)] obtained in symmetrical KCl solutions at 0.1 m (filled circles) or 1.5 m (open circles). The shared parameters of fits of gf are gf _min = 0.1, gf _max = 0.96, V _gf = 24.3 mV. V _1/2 = −116 mV and −144 mV for 0.1 m (solid line) and 1.5 m KCl (dashed line), respectively.

Fitting the rate constant of channel opening k _MO (Fig. 3B) at negative voltages by

$$k_{\mathit{MO}}=k_{MO,0}exp(V/V_{\mathit{MO}})$$ (4)

reveals a lower voltage sensitivity for k _MO with a characteristic voltage of V _MO = 99 mV (Fig. 5A). The scaling factor k _MO,0 is quite independent of [K⁺] (see legend of Fig. 5).

The “open probability” of the O‐M process (gating factor gf) determines the negative slope of the IV curves (Fig. 3C). Conventionally, open probability is described by a Boltzmann equation

$$gf=\frac{k_{\mathit{MO}}}{k_{\mathit{OM}}+k_{\mathit{MO}}}=g{f}_{\mathit{min}}+\frac{g{f}_{\mathit{max}}-g{f}_{\mathit{min}}}{1+exp\left(-\frac{V-V_{1/2}}{V_{\mathit{gf}}}\right)}$$ (5)

In Appendix S6, Eqns (3), (4) are used to calculate gf. The result (Eqns S4 and S5) resembles Eqn (5). The characteristic voltage calculated from V _OM and V _MO in Eqn (S5) is 26.4 mV, equivalent to V _gf = 24.3 mV (legend of Fig. 5B). Eqns (S5) and 5 differ with respect to gf _min, which is not included in Eqn (S5). gf _min occurs at negative voltages outside the investigated range. Indeed, there are some rare indications that k _MO deviates at high negative voltages from the exponential form of Eqn (4). However, this has not been evaluated as the membranes did not resist the high voltages required for a detailed analysis of this effect.

The characteristic voltage V _gf = 24.3 mV corresponds to the movement of one charge through the entire electrical field. Kv channels with dedicated voltage‐sensing domains (VSD) have gating charges from 1 in BK 40 to 12 in Shaker 41.

Identification of two different O‐M gating processes at negative and positive voltages

The phenomenological description of k _OM (Fig. 5A) requires a sum of an exponential voltage dependence with a (roughly) voltage‐independent component [Eqn (3)], suggesting that two different processes are involved. Furthermore, the K⁺ dependence is opposite and very different at positive and negative voltages (Fig. 5A). The hypothesis is confirmed by mutational studies, which assign the O‐M gating at positive and negative voltages to different parts of the channel protein.

The O‐M gating at positive voltages is located in the inner gate

Kcv_S has a lower open probability of the slow gating than Kcv_NTS 28. The reason is a newly detected type of inner gate, which moves F78 into the pathway of ions. This movement is controlled by the interaction of S77 in Kcv_S with the backbone of TM2 28. Kcv_NTS and Kcv_S differ at position 77 (Fig. 1A). G77 in Kcv_NTS corresponds to S77 in Kcv_S. In addition to the difference in slow gating, this results in different values of k _OM at positive voltages (Fig. 6A), whereas there is no significant difference at negative voltages. Exchanging S and G in Kcv_NTS and Kcv_S shows that they are the major determinants of this behavior. Kcv_NTS G77S has increased values of k _OM at positive voltages similar to those of Kcv_S wt. The glycine in Kcv_NTS wt and Kcv_S S77G leads to identical behavior. In either case, there is a negligible influence on k _OM at negative voltages.

Figure 6.

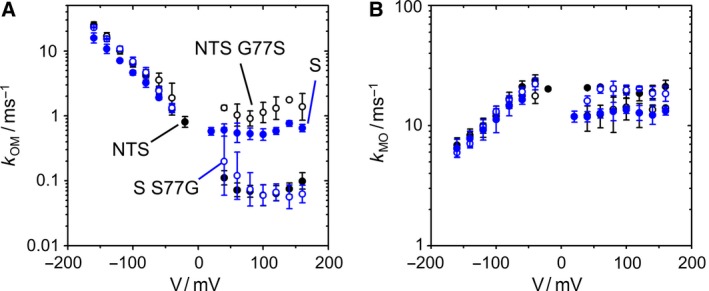
Two different mechanisms of O‐M gating at negative and positive voltages. (A) The two channels with Ser at position 77 at the cytosolic gate (Kcv_S, filled blue circles, and Kcv_NTS G77S, open black circles) have higher values for k _OM (channel closing) at positive voltages than those channels with Gly at position 77 (Kcv_S S77G, open blue circles and Kcv_NTS, filled black circles). The voltage dependence at negative voltages is not affected by the mutations, neither is the rate constant of channel opening, k _MO (B). N = 3 for Kcv_S, Kcv_S S77G, and Kcv_NTS G77S, n = 6 for Kcv_NTS wt.

The selectivity filter is the locus of voltage‐dependent O‐M gating

The voltage‐dependent O‐M gating at negative voltages is not located in the cytosolic gate (Fig. 6). To test whether it is located in the selectivity filter, we mutated a position that is known to be crucial for selectivity filter stability. Mutating E71 at the C‐terminal end of the pore helix of KcsA has a huge impact on inactivation of the selectivity filter 42, 43. The analogous position in Kcv channels is S42 (Fig. 1A).

As a background, we chose Kcv_NH S77G. The selectivity filter of Kcv_NH is identical to those of Kcv_NTS and Kcv_S, and their voltage dependence at negative voltages is the same (Fig. 7C,D). In Kcv_NH S77G, the inner gate is identical to that of Kcv_NTS, and indeed, k _OM at positive voltages matches that of Kcv_NTS and Kcv_S S77G (Figs. 6A and 7C).

Figure 7.

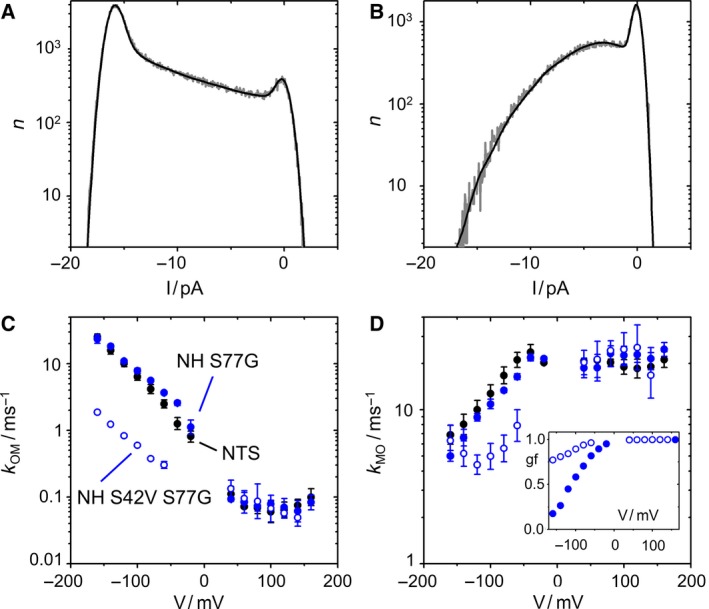
Influence of mutating Ser42 in the pore helix anchoring the selectivity filter (Fig. 1B) on O‐M gating at negative voltages. (A,B) Comparison of the amplitude histogram at −140 mV of Kcv_NH S42V S77G (A) with that of Kcv_NH S77G (B). Representative histograms in 0.1 m KCl, pH 7 (gray) and the best fit with the model in Fig. 2A (black). (C,D) Comparison of the voltage dependence of k _OM (C) and k _MO (D) of Kcv_NH S42V S77G (blue open circles) with that of Kcv_NH S77G (blue filled circles) and Kcv_NTS (black circles). Inset in D: Gating factor gf [Eqn (5)] for Kcv_NH S77G and Kcv_NH S42V S77G, symbols are the same as in (C) and (D). Recordings in symmetrical 0.1 m KCl from three different bilayers for each Kcv_NH mutant and six for Kcv_NTS, respectively.

The S42V mutation has a dramatic effect on the area between the closed and the open peak, which is dominated by the O‐M gating (Fig. 7A,B). k _OM is strongly left‐shifted (Fig. 7C), while k _MO is right‐shifted (Fig. 7D). Consequently, the gating factor in Eqn (5), that is, the open probability of the O‐M gating process is much higher in the double mutant (inset in Fig. 7D).

In summary, the mutational studies show that mutations in the inner gate (residue 77) influence the O‐M gating at positive voltages (Fig. 6). In contrast, a mutation in the pore helix anchoring the selectivity filter (residue 42) strongly influences O‐M gating at negative voltages (Fig. 7). This assigns the voltage‐dependent O‐M gating to the selectivity filter. These results are in line with the identification of voltage‐dependent gating with the selectivity filter in pore‐only channels without dedicated voltage sensor domain 44, 45, 46, 47, 48, 49. Further details for the assignment of fast gating to the selectivity filter have been summarized elsewhere 50. In our study, the combination of analyzing single‐channel gating with high resolution and mutations in a minimal size channel provides a basis for a future understanding of the structure/function correlates of a distinct gate in the selectivity filter.

Conclusion

The analysis based on extended beta distributions reaches resolution in the microsecond range. It can be further extended for channels with high currents, an increased signal‐to‐noise ratio or with better amplifiers. This will open the possibility to provide experimental parameters of gating to check predictions from MD simulations. The present application of the method to the gating in Kcv channels serves as an example of its power. It could reveal details of submillisecond gating from classical bilayer recordings in quantitative terms. In the case of the Kcv channel, the O‐M gating could be identified as the origin of the negative slope of the IV curve at negative voltages. The voltage dependence of the rate constants could be quantified, and the equivalent charge determined. Without this analytical tool, one of the most fascinating processes in Kcv, the strong voltage dependence of O‐M gating would remain hidden.

Author contributions

OR performed experiments; UPH designed research, did the curve fitting, and wrote the manuscript; SM performed experiments on the Kcv_NH mutants; AH and KS provided the measured data for I _OF in Fig. 4A, GT designed research; IS designed research, did the curve fitting and wrote the manuscript.

Supporting information

Fig. S1. Mutual independence of the influence of individual gating processes on an amplitude histogram (black) obtained from a current trace of Kcv_NTS measured in 1.5 m symmetrical KCl at ‐80 mV.

Fig. S2. Test of the reliability of the determination of current (A, C, E, G) and of the rate constant k _OM (B, D, F, H).

Appendix S1 High‐resolution experiments with a new type of bilayer array and amplifier.

Appendix S2 The improvements of the extended beta distribution fit over the classical beta distribution fit.Appendix S3 Relationship between individual gating processes and characteristics of the amplitude histogram.

Appendix S4 Simplified equations for converting the topology of the Markov model from the branched one in Fig. 2A to the linear model S‐O‐F‐M.

Appendix S5 Tests of the reliability of extended beta distribution fits.

Appendix S6 The relationship between the rate constant k _OM and k _MO and the gating factor gf.