Abstract
Studies in epigenetics have shown that DNA methylation is a key factor in regulating gene expression. Aberrant DNA methylation is often associated with DNA instability, which could lead to development of diseases such as cancer. DNA methylation typically occurs in CpG context. When located in a gene promoter, DNA methylation often acts to repress transcription and gene expression. The most commonly used technology of studying DNA methylation is bisulfite sequencing (BS-seq), which can be used to measure genomewide methylation levels on the single-nucleotide scale. Notably, BS-seq can also be combined with enrichment strategies, such as reduced representation bisulfite sequencing (RRBS), to target CpG-rich regions in order to save per-sample costs. A typical DNA methylation analysis involves identifying differentially methylated regions (DMRs) between different experimental conditions. Many statistical methods have been developed for finding DMRs in BS-seq data. In this workflow, we propose a novel approach of detecting DMRs using edgeR. By providing a complete analysis of RRBS profiles of epithelial populations in the mouse mammary gland, we will demonstrate that differential methylation analyses can be fit into the existing pipelines specifically designed for RNA-seq differential expression studies.
In addition, the edgeR generalized linear model framework offers great flexibilities for complex experimental design, while still accounting for the biological variability. The analysis approach illustrated in this article can be applied to any BS-seq data that includes some replication, but it is especially appropriate for RRBS data with small numbers of biological replicates.
Keywords: Methylation, BS-seq, differential methylation analysis, Bioconductor
Introduction
Studies in the past have shown that DNA methylation, as an important epigenetic factor, plays a vital role in genomic imprinting, X-chromosome inactivation and regulation of gene expression 1. Aberrant DNA methylation is often correlated with DNA instability, which leads to development of diseases including imprinting disorders and cancer 2, 3.
In mammals, DNA methylation almost exclusively occurs at CpG sites, i.e. regions of DNA where a cytosine (C) is linked by a phosphate (p) and bond to a guanine (G) in the nucleotide sequence from 5’ to 3’. It has been found that 70% ∼ 80% of CpG cytosines are methylated in mammals, regardless of the cell type 4. Unmethylated CpGs usually group together in clusters of regions known as CpG islands 5, which cover about 2% of the entire genome. Around 40% of mammalian genes and 70% of human genes have CpG islands enriched in their promoter regions 6– 8. CpG methylation in gene promoters is generally associated with repression of transcription, and hence silencing of gene expression 5. When occurring at the promoters of tumor suppressor gene, DNA methylation could repress the tumour suppressors, leading to oncogenesis 3. In contrast, high levels of methylation have been observed in the gene body of highly expressed genes 9, which implies positive correlation between gene body methylation and gene expression.
Among numerous existing technologies, the most widely used method to investigate DNA methylation is bisulfite sequencing (BS-seq), which produces data on the single-nucleotide scale 10. Unmethylated cytosines (C) are converted to Uracils (U) by sodium bisulfite and then deaminated to thymines (T) during PCR amplification. Methylated Cs, on the other hand, remain intact after bisulfite treatment. The BS-seq technique can be used to measure genome-wide single-cytosine methylation levels by sequencing the entire genome. This strategy produces whole genome bisulfite sequencing (WGBS) data. However, the WGBS approach could be cost-prohibitive for species, such as human, with large genome. In addition, the fact that CpG islands reside in only 2% of the entire genome makes the WGBS approach inefficient when comparing a large number of samples.
To improve the efficiency and bring down the scale and cost of WGBS, enrichment strategies have been developed and combined with BS-seq to target a specific fraction of the genome. A common targeted approach is reduced representation bisulfite sequencing (RRBS) that targets CpG-rich regions 11. Under the RRBS strategy, small fragments that compose only 1% of the genome are generated using MspI digestion, which means fewer reads are required to obtain accurate sequencing. The RRBS approach can capture approximately 70% of gene promoters and 85% of CpG islands, while requiring only small quantities of input sample 12. In general, RRBS has great advantages in cost and efficiency when dealing with large scale data, whereas WGBS is more suitable for studies where all CpG islands or promoters across the entire genome are of interest.
The first step of analyzing BS-seq data is to align short reads to genome. The number of C-to-T conversions are then counted for all the mapped reads. A number of software tools have been developed for the purposes of read mapping and methylation calling of BS-seq data. Popular ones include Bismark 13, MethylCoder 14, BRAT 15, BS-Seeker 16 and BSMAP 17. Most of the software tools rely on existing short read aligners, such as Bowtie 18.
Typical downstream DNA methylation studies often involve finding differentially methylated regions (DMRs) between different experimental conditions. A number of statistical methods and software packages have been developed for detecting DMRs using the BS-seq technology. methylkit 19 and RnBeads 20 implement Fisher’s Exact Test, which is a popular choice for two-group comparisons with no replicates. In the case of complex experimental designs, regression methods are widely used to model methylation levels or read counts. RnBeads offers a linear regression approach based on the moderated t-test and empirical Bayes method implemented in limma 21. BSmooth 22 is another analysis pipeline that uses linear regression and empirical Bayes together with a local likelihood smoother. methylkit also has an option to apply logistic regression with overdispersion correction 19. Some other methods have been developed based on beta-binomial distribution to achieve better variance modelling. For example, DSS fits a Bayesian hierarchical beta-binomial model to BS-seq data and uses Wald tests to detect DMRs 23. Other software using beta-binomial model include BiSeq 24, MOABS 25 and RADMeth 26.
In this workflow, we demonstrate an edgeR approach of differential methylation analysis. edgeR is one of the most popular Bioconductor packages for assessing differential expression in RNA-seq data 27. It is based on the negative binomial (NB) distribution and it models the variation between biological replicates through the NB dispersion parameter. Unlike other approaches to methylation sequencing data, the analysis explained in this workflow keeps the counts for methylated and unmethylated reads as separate observations. edgeR linear models are used to fit the total read count (methylated plus unmethylated) at each genomic locus, in such a way that the proportion of methylated reads at each locus is modelled indirectly as an over-dispersed binomial distribution. This approach has a number of advantages. First, it allows the differential methylation analysis to be undertaken using existing edgeR pipelines developed originally for RNA-seq differential expression analyses. The edgeR generalized linear model (GLM) framework offers great flexibility for analysing complex experimental designs while still accounting for the biological variability. Second, keeping methylated and unmethylated read count as separate data observations allows the inherent variability of the data to be modeled more directly and perhaps more realistically. Differential methylation is assessed by likelihood ratio tests so we do not need to assume that the log-fold-changes or other coefficient estimators are normally distributed.
This article presents an analysis of an RRBS data set generated by the authors containing replicated RRBS profiles of basal and luminal cell populations from the mouse mammary epithelium. As with other articles in the Bioconductor Gateway series, our aim is to provide an example analysis with complete start to finish code. As with other Bioconductor workflow articles, we illustrate one analysis strategy in detail rather than comparing different pipelines. The analysis approach illustrated in this article can be applied to any BS-seq data that includes some replication, but is especially appropriate for RRBS data with small numbers of biological replicates. The results shown in this article were generated using Bioconductor Release 3.6.
The NB linear modeling approach to BS-seq data
A small example
To introduce the edgeR linear modeling approach to BS-seq data, consider a genomic locus that has m A methylated and u A unmethylated reads in condition A and m B methylated and u B unmethylated reads in condition B. Our approach is to model all four counts as NB distributed with the same dispersion but different means. Suppose the data is as given in Table 1. If this were a complete dataset, then it could be analyzed in edgeR as follows.
> counts <- matrix(c(2,12,11,0),1,4)
> dimnames(counts) <- list("Locus", c("A_Me","A_Un","B_Me","B_Un")))
> counts
A_Me A_Un B_Me B_Un
Locus 2 12 11 0
> design <- cbind(Sample1 = c(1,1,0,0),
Sample2 = c(0,0,1,1),
A_MvsU = c(1,0,1,0),
BvsA_MvsU = c(0,0,1,0))
> fit <- glmFit(counts, design, lib.size=c(100,100,100,100), dispersion=0.0247)
> lrt <- glmLRT(fit, coef="BvsA_MvsU")
> topTags(lrt)
Coefficient: BvsA_MvsU
logFC logCPM LR PValue FDR
Locus 8.99 16.3 20.7 5.27e-06 5.27e-06
Table 1. A small example data set.
| Sample | Condition | Methylated Count | Unmethylated Count |
|---|---|---|---|
| 1 | 1 | 2 | 12 |
| 2 | 2 | 11 | 0 |
In this analysis, the first two coefficients are used to model the total number of reads (methylated or unmethylated) for samples 1 and 2, respectively. Coefficient 3 ( A_MvsU) estimates the log ratio of methylated to unmethylated reads for sample 1, a quantity that can also be viewed as the logit proportion of methylated reads in sample 1. Coefficient 4 ( BvsA_MvsU) estimates the difference in logit proportions of mythylated reads between conditions B and A. The difference in logits is estimated here as 8.99 on the log2 scale. The P-value for differential methylation (B vs A) is P = 5.27 × 10 -6.
The dispersion parameter controls the degree of biological variability 28. If we had set dispersion=0 in the above code, then the above analysis would be exactly equivalent to a logistic binomial regression, with the methylated counts as responses and the total counts as sizes, and with a likelihood ratio test for a difference in proportions between conditions A and B. Positive values for the dispersion produce over-dispersion relative to the binomial distribution. We have set the dispersion here equal to the value that is estimated below for the mammary epithelial data.
In the above code, the two library sizes for each sample should be equal. Otherwise, the library size values are arbitrary and any settings would have lead to the same P-value.
Relationship to beta-binomial modeling
It is interesting to compare this approach with beta-binomial modeling. It is well known that if m and u are independent Poisson random variables with means µ m and µ u, then the conditional distribution of m given m + u is binomial with success probability p = µ m /( µ m + µ u). If the Poisson means µ m and µ u themselves follow gamma distributions, then the marginal distributions of m and u are NB instead of Poisson. If the two NB distributions have different dispersions, and have expected values in inverse proportion to the dispersions, then the conditional distribution of m given m + u follows a beta-binomial distribution. The approach taken in this article is closely related to the beta-binomial approach but makes different and seemingly more natural assumptions about the NB distributions. We instead assume the two NB distributions to have the same dispersion but different means. The NB linear modeling approach allows the means and dispersions of the two NB distributions to be estimated separately, in concordance with the data instead of being artificially linked.
Description of the biological experiment
Aim of the study
The epithelium of the mammary gland exists in a highly dynamic state, undergoing dramatic morphogenetic changes during puberty, pregnancy, lactation, and regression 29. Characterization of the lineage hierarchy of cells in the mammary epithelium is an important step toward understanding which cells are predisposed to oncogenesis. In this study, we profiled the methylation status of the two major functionally distinct epithelial compartments: basal and luminal cells. The basal cells were further divided into those showing high or low expression of the surface marker Itga5 as part of our investigation of heterogeneity within the basal compartment. We carried out global RRBS DNA methylation assays on two biological replicates of each of the three cell populations to determine whether the epigenetic machinery played a potential role in (i) differentiation of luminal cells from basal and (ii) any compartmentalization of the basal cells associated with Itga5.
Sample preparation
Inguinal mammary glands (minus lymph node) were harvested from FVB/N mice. All animal experiments were conducted using mice bred at and maintained in our animal facility, according to the Walter and Eliza Hall Institute of Medical Research Animal Ethics Committee guidelines. Epithelial cells were suspended and fluorescence-activated cell sorting (FACS) was used to isolate basal and luminal cell populations 30. Genomic DNA (gDNA) was extracted from freshly sorted cells using the Qiagen DNeasy kit. Around 25ng gDNA input was subjected to DNA methylation analysis by BS-seq using the Ovation RRBS Methyl-seq kit from NuGEN. The process includes MspI digestion of gDNA, sequencing adapter ligation, end repair, bisulfite conversion, and PCR amplification to produce the final sequencing library. The Qiagen EpiTect Bisulfite kit was used for bisulfite-mediated conversion of unmethylated cytosines.
Experimental design
There are three groups of samples: luminal population, Itga5- basal population and Itga5+ basal population. Two biological replicates were collected for each group. This experimental design is summarized in the table below.
> targets
<- read.delim
(
"targets.txt"
,
stringsAsFactors
=
FALSE
)
> targets
Sample Population Description
1 P6_1 P6 Luminal
2 P6_4 P6 Luminal
3 P7_2 P7 Basal_Itga5_neg
4 P7_5 P7 Basal_Itga5_neg
5 P8_3 P8 Basal_Itga5_pos
6 P8_6 P8 Basal_Itga5_pos
The experiment has a simple one-way layout with three groups. A single grouping factor is made as follows:
> Group
<- factor
(targets
$
Population)
> Group
[1] P6 P6 P7 P7 P8 P8
Levels: P6 P7 P8
The sequencing was carried out on the Illumina NextSeq 500 platform. About 30 million 75bp paired-end reads were generated for each sample.
Differential methylation analysis at CpG loci
Processing bisulfite sequencing FASTQ files
The first step of the analysis is to map the sequencing reads from the FASTQ files to the mouse genome and then perform methylation calls. Though many options are available, we use Bismark for read alignment and methylation calling. Bismark is one of the most popular software tools to perform alignments of bisulfite-treated sequencing reads to a genome of interest and perform methylation calls. It maps sequencing reads using the short read aligner Bowtie 1 18 or alternatively Bowtie 2 31.
To increase alignment rates and reduce false methylation calls, it is recommended to trim poor quality reads on sequence ends and remove adapters that can be potentially sequenced prior to the alignment. This is done using trim_galore ( https://www.bioinformatics.babraham.ac.uk/projects/trim_galore/). After that, Bismark version v0.13.0 is used to align the reads to the mouse genome mm10. The final methylation calls are made using bismark_methylation_extractor.
Downloading the data
The Bismark outputs include one coverage bed file of the methylation in CpG context for each sample. The coverage outputs from Bismark are available at http://bioinf.wehi.edu.au/edgeR/F1000Research2017/. Readers wishing to reproduce the analysis presented in this article can download the zipped coverage bed files produced by Bismark from the above link.
Bed files can be read into R using read.delim as for txt files. Each of the bed files has the following format:
> P6_1 <- read.delim("P6_1.bismark.cov.gz", header=FALSE)
> head(P6_1)
V1 V2 V3 V4 V5 V6
1 chr6 3052156 3052156 87.9 51 7
2 chr6 3052157 3052157 85.7 6 1
3 chr6 3052246 3052246 0.0 0 1
4 chr6 3052415 3052415 100.0 57 0
5 chr6 3052416 3052416 100.0 7 0
6 chr6 3052434 3052434 94.7 54 3
The columns in the bed file represent: V1: chromosome number; V2: start position of the CpG site; V3: end position of the CpG site; V4: methylation proportion; V5: number of methylated Cs; V6: number of unmethylated Cs.
Reading in the data
Since the start and end positions in the coverage outputs are identical for each CpG site, only one of them is needed for marking the location of each. We also ignore the methylation proportion as it can be directly calculated from the number of methylated and unmethylated Cs. The data can then be read into a list in R:
> Sample
<-
targets
$
Sample
> fn
<- paste0
(Sample,
".bismark.cov.gz"
)
> data
<- list
()
>
for
(i
in
1
:
length
(Sample)) {
+ data[[i]]
<- read.delim
(
file
=fn[i],
header
=
FALSE
)[,-(
3
:
4
)]
+
names
(data[[i]])
<- c
(
"Chr"
,
"Position"
,
"Meth"
,
"Un"
)
+ }
The data object is a list containing six data frames, each of which represents one sample. The first and second columns of each data frame are the chromosome numbers and positions of all the CpG loci observed in that sample. The last two columns contain the numbers of methylated and unmethylated Cs detected at those loci. Since the number of reported CpG loci varies across different samples, care is required to combine the information from all the samples. We first obtain all unique CpG loci observed in at least one of the six samples. This is done by combining the chromosome number and position of each CpG site. Then we extract read counts of methylated and unmethylated Cs at these locations across all the samples and combine them into a count matrix.
> position
<- sapply
(data,
function
(
x
)
paste
(x[,
1
],
x[,
2
],
sep
=
"-"
) )
> position_all
<- unique
(
unlist
(position))
> counts
<- matrix
(
0L,
nrow
=
length
(position_all),
ncol
=
2
*
length
(Sample))
>
for
(i
in
1
:
length
(Sample)) {
+ m
<- match
(position[[i]], position_all)
+ counts[m,
c(
2
*
i-
1
,
2
*
i)]
<- as.matrix
(data[[i]][,
3
:
4
])
+ }
The counts object is a matrix of integer counts with 12 columns, two for each sample. The odd number of columns contain the numbers of methylated Cs, whereas the even number of columns contain the numbers of unmethylated Cs. The genomic positions are used as the row names of the count matrix.
>
rownames
(counts)
<-
position_all
> Sample2
<- rep
(Sample,
each
=
2
)
> Sample2
<- factor
(Sample2)
> Meth
<- rep
(
c
(
"Me"
,
"Un"
),
length
(Sample))
> Meth
<- factor
(Meth,
levels
=
c(
"Un"
,
"Me"
))
>
colnames
(counts)
<- paste
(Sample2, Meth,
sep
=
"-"
)
>
head
(counts)
P6_1-Me P6_1-Un P6_4-Me P6_4-Un P7_2-Me P7_2-Un P7_5-Me P7_5-Un
chr6-3052156 51 7 62 13 48 3 31 8
chr6-3052157 6 1 5 0 0 0 3 1
chr6-3052246 0 1 0 0 0 0 2 0
chr6-3052415 57 0 75 1 50 1 36 1
chr6-3052416 7 0 5 0 0 0 4 0
chr6-3052434 54 3 72 4 48 3 36 1
P8_3-Me P8_3-Un P8_6-Me P8_6-Un
chr6-3052156 40 9 28 10
chr6-3052157 0 0 2 0
chr6-3052246 1 1 2 0
chr6-3052415 46 1 36 0
chr6-3052416 0 0 2 0
chr6-3052434 47 0 36 0
We then proceed to the edgeR analysis of the methylation data. The edgeR package stores data in a simple list-based data object called a DGEList. We first create a DGEList object using the count matrix generated before. The information of CpG sites is converted into a data frame and stored in the genes component of the DGEList object.
>
library
(edgeR)
>
options
(
digits
=
3
)
> Chr
<- gsub
(
"-.*$"
,
""
, position_all)
> Position
<- gsub
(
"^.*-"
,
""
, position_all)
> Genes
<- data.frame
(
Chr
=Chr,
Position
=Position)
> y
<- DGEList
(counts,
genes
=Genes,
group
=
rep
(Group,
each
=
2
))
Filtering to remove low counts
We first sum up the read counts of both methylated and unmethylated Cs at each CpG site within each sample.
> counts_total
<- t
(
rowsum
(
t
(counts), Sample2))
>
head
(counts_total)
P6_1 P6_4 P7_2 P7_5 P8_3 P8_6
chr6-3052156 58 75 51 39 49 38
chr6-3052157 7 5 0 4 0 2
chr6-3052246 1 0 0 2 2 2
chr6-3052415 57 76 51 37 47 36
chr6-3052416 7 5 0 4 0 2
chr6-3052434 57 76 51 37 47 36
CpG loci that have very low counts across all the samples shall be removed prior to downstream analysis as they provide little information for assessing methylation levels. As a rule of thumb, we require a CpG site to have a total count (both methylated and unmethylated) of at least 10 across all the samples before it is considered in the study.
> keep
<- rowSums
(counts_total
>=
10
)
==
6
>
table
(keep)
keep
FALSE TRUE
3139160 398926
The DGEList object is subsetted to retain only the non-filtered loci:
> y
<-
y
[
keep,,
keep.lib.sizes
=
FALSE
]
The option keep.lib.sizes=FALSE causes the library sizes to be recomputed after the filtering. This is generally recommended, although the effect on the downstream analysis is usually small.
Normalization
A key difference between BS-seq and other sequencing data is that the pair of libraries holding the methylated and unmethylated reads for a particular sample are treated as a unit. To ensure that the methylated and unmethylated reads for the same sample are treated on the same scale, we need to set the library sizes to be equal for each pair of libraries. We set the library sizes for each sample to be the average of the total read counts for the methylated and unmethylated libraries:
> TotalReadCount
<- colMeans
(
matrix
(y
$
samples
$
lib.size,
nrow
=
2
,
ncol
=
6
))
> y
$
samples$
lib.size
<- rep
(TotalReadCount,
each
=
2
)
> y
$
samples
group lib.size norm.factors
P6_1-Me P6 12620834 1
P6_1-Un P6 12620834 1
P6_4-Me P6 19410820 1
P6_4-Un P6 19410820 1
P7_2-Me P7 10272918 1
P7_2-Un P7 10272918 1
P7_5-Me P7 12055355 1
P7_5-Un P7 12055355 1
P8_3-Me P8 9055759 1
P8_3-Un P8 9055759 1
P8_6-Me P8 7475953 1
P8_6-Un P8 7475953 1
Other normalization methods developed for RNA-seq data, such as TMM 32, are not required for BS-seq data.
Exploring differences between samples
In DNA methylation studies, methylation levels are of most interest. For Illumina methylation assay, two common measurements of methylation levels are β-values and M-values, which are defined as β = M /( M+ U) and M-value= log 2( M / U) where M and U denote the methylated and unmethylated intensity 33. Here we adopt the same idea and extend the two measurements to BS-seq data. That is, denote the methylated and unmethylated Cs by M and U respectively, and define the β-values and M-values in the same way as above.
In practice, for a particular CpG site in one sample, the M-value can be computed by subtracting the log2 count-per-million (CPM) of the unmethylated Cs from that of the methylated Cs. This is equivalent to the calculation of the defined M-values as the library sizes are set to be the same for each pair of methylated and unmethylated columns and they cancel each other out in the subtraction. A prior count of 2 is added to the calculation of log2-CPM to avoid undefined values and to reduce the variability of M-values for CpG sites with low counts. The calculation of β-value is straight-forward though a small offset may also be added to the calculation.
> Beta
<-
y
$
counts[, Meth
==
"Me"
] /
counts_total[keep, ]
> logCPM
<- cpm
(y,
log
=
TRUE
,
prior.count
=
2
)
> M
<-
logCPM[, Meth
==
"Me"
]
-
logCPM[, Meth
==
"Un"
]
>
colnames
(Beta)
<- colnames
(M)
<-
Sample
The outputs Beta and M are numeric matrices with six columns, each of which contains the β-values or M-values calculated at each CpG site in one sample. Then we can generate multi-dimensional scaling (MDS) plots to explore the overall differences between the methylation levels of the different samples. Here we decorate the MDS plots to indicate the cell groups:
>
par
(
mfrow
=
c
(
1
,
2
))
>
plotMDS
(Beta,
col
=
rep
(
1
:
3
,
each
=
2
),
main
=
"Beta-values"
)
>
plotMDS
(M,
col
=
rep
(
1
:
3
,
each
=
2
),
main
=
"M-values"
)
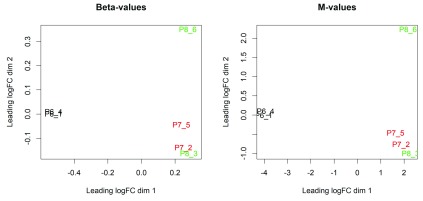
Figure 1 shows the resulting plots. In these plots, the distance between each pair of samples represents the average log-fold change between the samples for the top most differentially methylated CpG loci between that pair of samples. (We call this average the leading log-fold change.) The two replicate samples from the luminal population (P6) are seen to be well separated from the four basal samples (populations P7 and P8).
Figure 1. The MDS plots of the methylation levels of the data set.
Methylation levels are measured in beta values (left) and M-values (right). Samples are separated by the cell population in the first dimension in both MDS plots.
Design matrix
One aim of this study is to identify differentially methylated regions (DMRs) between different groups. In edgeR, this can be done by fitting linear models under a specified design matrix and testing for corresponding coefficients or contrasts. Here, a design matrix is constructed as follows:
> design
<- model.matrix
(
~
Sample2
+
Meth)
>
colnames
(design)
<- gsub
(
"Sample2"
,
""
,
colnames
(design))
>
colnames
(design)
<- gsub
(
"Meth"
,
""
,
colnames
(design))
>
colnames
(design)[
1
]
<-
"Int"
> design
<- cbind
(design,
+
Me2
=
c
(
0
,
0
,
0
,
0
,
1
,
0
,
1
,
0
,
0
,
0
,
0
,
0
),
+
Me3
=
c
(
0
,
0
,
0
,
0
,
0
,
0
,
0
,
0
,
1
,
0
,
1
,
0
))
> design
Int P6_4 P7_2 P7_5 P8_3 P8_6 Me Me2 Me3
1 1 0 0 0 0 0 1 0 0
2 1 0 0 0 0 0 0 0 0
3 1 1 0 0 0 0 1 0 0
4 1 1 0 0 0 0 0 0 0
5 1 0 1 0 0 0 1 1 0
6 1 0 1 0 0 0 0 0 0
7 1 0 0 1 0 0 1 1 0
8 1 0 0 1 0 0 0 0 0
9 1 0 0 0 1 0 1 0 1
10 1 0 0 0 1 0 0 0 0
11 1 0 0 0 0 1 1 0 1
12 1 0 0 0 0 1 0 0 0
The first six columns represent the sample effect. It accounts for the fact that each pair of columns of the count matrix are from one of the six samples. The 7th column “Me" represents the methylation level (in M-value) in the P6 group. The 8th column “Me2" represents the difference in methylation level between the P7 and P6 groups. Finally, the last column “Me3" represents the difference in methylation level between the P8 and P6 groups.
Dispersion estimation
With the design matrix specified, we can now proceed to the standard edgeR pipeline and analyze the data in the same way as for RNA-seq data. Similar to the RNA-seq data, the variability between biological replicates has also been observed in bisulfite sequencing data. This variability can be captured by the NB dispersion parameter under the generalized linear model (GLM) framework in edgeR.
The mean-dispersion relationship of BS-seq data has been studied in the past and no apparent mean-dispersion trend was observed 23. This is also verified through our own practice. Therefore, we would not consider a mean-dependent dispersion trend as we normally would for RNA-seq data. A common dispersion estimate for all the loci, as well as an empirical Bayes moderated dispersion for each individual locus, can be obtained from the estimateDisp function in edgeR:
> y
<- estimateDisp
(y,
design
=design,
trend
=
"none"
)
> y
$
common.dispersion
[1] 0.0247
>
summary
(y
$
prior.df)
Min. 1st Qu. Median Mean 3rd Qu. Max.
Inf Inf Inf Inf Inf Inf
This returns a DGEList object with additional components ( common.dispersion and tagwise.dispersion) added to hold the estimated dispersions. Here the estimation of trended dispersion has been turned off by setting trend="none". For this data, the estimated prior degrees of freedom (df) are infinite for all the loci, which implies all the CpG-wise dispersions are exactly the same as the common dispersion. A BCV plot is often useful to visualize the dispersion estimates, but it is not informative in this case.
Testing for differentially methylated CpG loci
We first fit NB GLMs for all the CpG loci using the glmFit function in edgeR.
> fit
<- glmFit
(y, design)
Then we can proceed to testing for differentially methylated CpG sites between different populations. One of the most interesting comparisons is between the basal (P7 and P8) and luminal (P6) groups. The contrast corresponding to any specified comparison can be constructed conveniently using the makeContrasts function:
> contr
<- makeContrasts
(
BvsL
=
0.5
*
(Me2
+
Me3),
levels
=design)
The actual testing is performed using likelihood ratio tests (LRT) in edgeR.
> lrt
<- glmLRT
(fit,
contrast
=contr)
The top set of most differentially methylated (DM) CpG sites can be viewed with topTags:
>
topTags
(lrt)
Coefficient: 0.5*Me2 0.5*Me3
Chr Position logFC logCPM LR PValue FDR
chr13-45709467 chr13 45709467 -7.60 3.06 342 2.71e-76 9.62e-71
chr16-76326604 chr16 76326604 8.87 2.60 341 4.82e-76 9.62e-71
chr10-40387375 chr10 40387375 8.13 2.85 333 2.48e-74 3.30e-69
chr11-100144651 chr11 100144651 8.19 2.66 326 8.36e-73 8.34e-68
chr17-46572098 chr17 46572098 -9.10 2.69 320 1.57e-71 1.26e-66
chr13-45709489 chr13 45709489 -7.47 3.05 315 1.52e-70 1.01e-65
chr13-45709480 chr13 45709480 -7.70 3.05 312 8.98e-70 5.12e-65
chr3-54724012 chr3 54724012 8.39 2.39 309 3.36e-69 1.68e-64
chr8-120068504 chr8 120068504 -7.42 2.81 304 4.04e-68 1.79e-63
chr2-69631013 chr2 69631013 7.30 3.11 296 2.15e-66 8.59e-62
Here positive log-fold changes represent CpG sites that have higher methylation level in the basal population compared to the luminal population. The Benjamini-Hochberg multiple testing correction is applied to control the false discovery rate (FDR).
The total number of DM CpG sites identified at an FDR of 5% can be shown with decideTestsDGE. There are in fact more than 50,000 differentially methylated CpGs in this comparison:
>
summary
(
decideTests
(lrt))
0.5*Me2 0.5*Me3
-1 35891
0 344846
1 18189
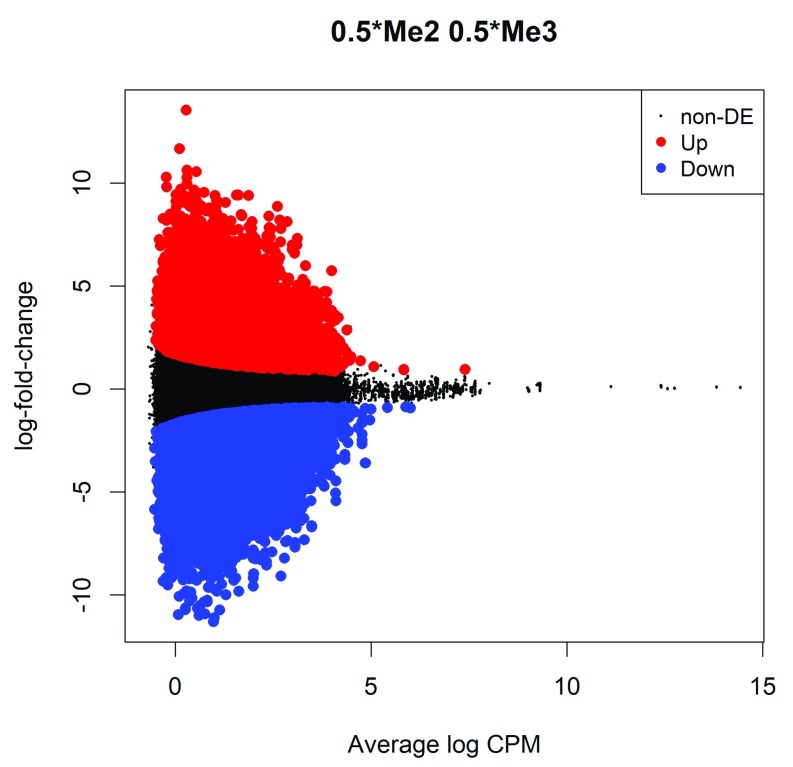
The differential methylation results can be visualized with an MD plot (see Figure 2):
Figure 2. MD plot showing the log-fold change of the methylation level and average abundance of each CpG site.
Significantly up and down methylated CpGs are highlighted in red and blue, respectively.
The logFC of the methylation level for each CpG site is plotted against the average abundance in log2-CPM. Significantly differentially methylated CpGs are highlighted.
>
plotMD
(lrt)
Differential methylation in gene promoters
Pre-defined gene promoters
The majority of CpGs are methylated in mammals. On the other hand, unmethylated CpGs tend to group into clusters of CpG islands, which are often enriched in gene promoters. CpG methylation in promoter regions is often associated with silencing of transcription and gene expression 5. Therefore it is of great biological interest to examine the methylation level within the gene promoter regions.
For simplicity, we define the promoter of a gene as the region from 2kb upstream to 1kb downstream of the transcription start site of that gene. The genomic locations and their associated annotations of the promoters can be obtained using the TxDb.Mmusculus.UCSC.mm10.knownGene package.
>
library
(TxDb.Mmusculus.UCSC.mm10.knownGene)
> genes_Mm
<- genes
(TxDb.Mmusculus.UCSC.mm10.knownGene)
> pr
<- promoters
(genes_Mm,
upstream
=
2000
,
downstream
=
1000
)
> pr
GRanges object with 24044 ranges and 1 metadata column:
seqnames ranges strand | gene_id
<Rle> <IRanges> <Rle> | <character>
100009600 chr9 [ 21074497, 21077496] - | 100009600
100009609 chr7 [ 84963010, 84966009] - | 100009609
100009614 chr10 [ 77709446, 77712445] + | 100009614
100009664 chr11 [ 45806083, 45809082] + | 100009664
100012 chr4 [144161652, 144164651] - | 100012
... ... ... ... . ...
99889 chr3 [ 85886519, 85889518] - | 99889
99890 chr3 [110250000, 110252999] - | 99890
99899 chr3 [151748960, 151751959] - | 99899
99929 chr3 [ 65526447, 65529446] + | 99929
99982 chr4 [136601724, 136604723] - | 99982
-------
seqinfo: 66 sequences (1 circular) from mm10 genome
Here, pr is a GRanges class object that contains the genomic ranges of the promoters of all the known mouse genes in the annotation package.
Summarizing counts in promoter regions
We create another GRanges class object sites, which contains the genomic locations of all the observed CpG sites.
> Position
<- as.numeric
(Position)
> sites
<- GRanges
(
seqnames
=Chr,
ranges
=
IRanges
(
start
=Position,
end
=Position))
Then we find the overlaps between the gene promoter regions and all the CpG sites in the data using findOverlaps.
> olap
<- findOverlaps
(
query
=pr,
subject
=sites)
> olap
Hits object with 1522464 hits and 0 metadata columns:
queryHits subjectHits
<integer> <integer>
[1] 3 2493045
[2] 3 2493046
[3] 3 2493047
[4] 3 2493048
[5] 6 1898041
... ... ...
[1522460] 24044 3077832
[1522461] 24044 3317008
[1522462] 24044 3317009
[1522463] 24044 3317010
[1522464] 24044 3434601
-------
queryLength: 24044 / subjectLength: 3538086
The queryHits component of olap marks the indices of the promoter region as in pr, whereas the subjectHits component contains the indices of the CpG sites as in sites that overlap with the corresponding promoter regions.
The numbers of methylated and unmethylated CpGs overlapping with gene promoters are summed up for each promoter.
> counts2
<-
counts[
subjectHits
(olap), ]
> counts2
<- rowsum
(counts2,
queryHits
(olap))
The integer matrix counts2 contains the total numbers of methylated and unmethylated CpGs observed within the promoter of each gene. Same as before, counts2 has 12 columns, two for each sample. The odd number of columns contain the numbers of methylated Cs, whereas the even number of columns contain the numbers of unmethylated Cs. The only difference is that each row of counts2 now represents a gene promoter instead of an individual CpG site.
The gene symbol information can be added to the annotation using the org.Mm.eg.db package. A DGEList object is created for the downstream edgeR analysis.
> ind
<- as.numeric
(
rownames
(counts2))
>
rownames
(counts2)
<-
pr
$
gene_id[ind]
>
library
(org.Mm.eg.db)
> anno
<- select
(org.Mm.eg.db,
keys
=pr
$
gene_id,
columns
=
"SYMBOL"
,
+
keytype
=
"ENTREZID"
)
> anno
<- data.frame
(
Symbol
=anno
$
SYMBOL[ind])
> y2
<- DGEList
(counts2,
genes
=anno,
group
=
rep
(Group,
each
=
2
))
We sum up the read counts of both methylated and unmethylated Cs at each CpG sites within each sample.
> counts2_total
<- t
(
rowsum
(
t
(counts2), Sample2))
Filtering to remove low counts
Filtering is performed in the same way as before. Since each row represents a 3,000-bp-wide promoter region that contains multiple CpG sites, we would expect less filtering than before.
> keep2
<- rowSums
(counts2_total
>=
10
)
==
6
>
table
(keep2)
keep2
FALSE TRUE
1754 16790
> y2
<-
y2[keep2,,
keep.lib.sizes
=
FALSE
]
Same as before, we do not perform normalization but set the library sizes for each sample to be the average of the total read counts for the methylated and unmethylated libraries.
> TotalReadCount2
<- colMeans
(
matrix
(y2
$
samples
$
lib.size,
nrow
=
2
,
ncol
=
6
))
> y2
$
samples
$
lib.size
<- rep
(TotalReadCount2,
each
=
2
)
> y2
$
samples
group lib.size norm.factors
P6_1-Me P6 12474999 1
P6_1-Un P6 12474999 1
P6_4-Me P6 12579436 1
P6_4-Un P6 12579436 1
P7_2-Me P7 5110397 1
P7_2-Un P7 5110397 1
P7_5-Me P7 11189796 1
P7_5-Un P7 11189796 1
P8_3-Me P8 4123987 1
P8_3-Un P8 4123987 1
P8_6-Me P8 3562239 1
P8_6-Un P8 3562239 1
Exploring differences between samples
Same as before, we measure the methylation levels of gene promoter regions using both β-values and M-values. A prior count of 2 is added to the calculation of log2-CPM to avoid undefined values and to reduce the variability of M-values for gene promoters with low counts. Then MDS plots are produced to examine the overall differences between the methylation levels of the different samples.
> Beta2
<-
y2
$
counts[, Meth
==
"Me"
]
/
counts2_total[keep2, ]
> logCPM2
<- cpm
(y2,
log
=
TRUE
,
prior.count
=
2
)
> M2
<-
logCPM2[, Meth
==
"Me"
]
-
logCPM2[, Meth
==
"Un"
]
>
colnames
(Beta2)
<- colnames
(M2)
<-
Sample
>
par
(
mfrow
=
c
(
1
,
2
))
>
plotMDS
(Beta2,
col
=
rep
(
1
:
3
,
each
=
2
),
main
=
"Beta-values"
)
>
plotMDS
(M2,
col
=
rep
(
1
:
3
,
each
=
2
),
main
=
"M-values"
)
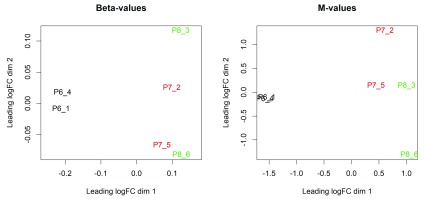
The resulting Figure 3 shows that the two replicate samples from the luminal population (P6) are well separated from the four replicate samples from the basal population (P7 and P8).
Figure 3. The MDS plots of the methylation levels at gene promoters.
Methylation levels are measured in beta values (left) and M-values (right). Samples are separated by the cell population in the first dimension in both MDS plots.
Dispersion estimation
We estimate the NB dispersions using the estimateDisp function in edgeR. For the same reason, we do not consider a mean-dependent dispersion trend as we normally would for RNA-seq data.
> y2
<- estimateDisp
(y2,
design
=design,
trend
=
"none"
,
robust
=
TRUE
)
> y2
$
common.dispersion
[1] 0.0301
>
summary
(y2
$
prior.df)
Min. 1st Qu. Median Mean 3rd Qu. Max.
10.2 10.2 10.3 10.3 10.4 10.4
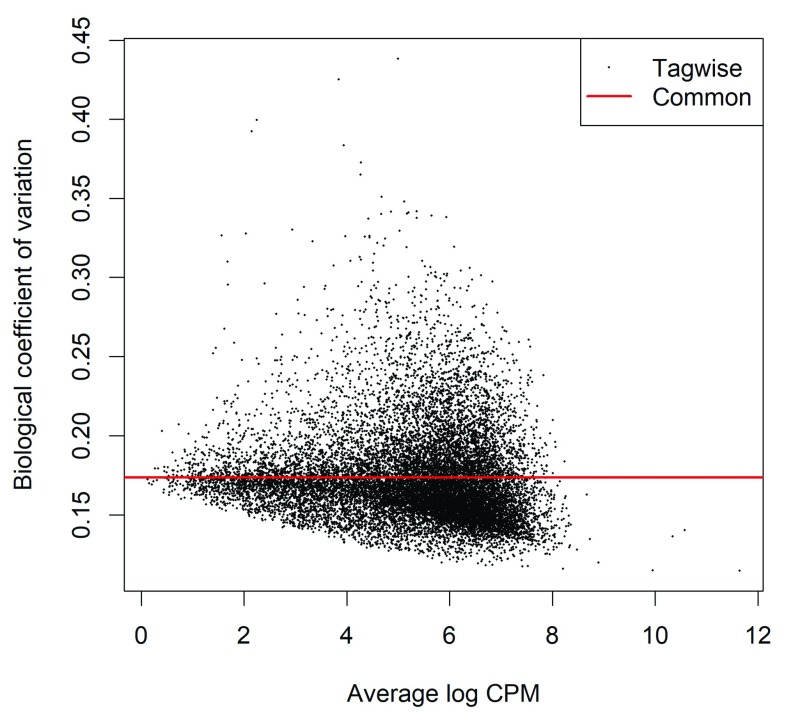
The dispersion estimates can be visualized with a BCV plot (see Figure 4):
Figure 4. Scatterplot of the BCV against the average abundance of CpG sites in each gene promoter.
The plot shows the square-root estimates of the common and tagwise NB dispersions.
>
plotBCV
(y2)
Testing for differential methylation in gene promoters
We first fit NB GLMs for all the gene promoters using glmFit.
> fit2
<- glmFit
(y2, design)
Then we can proceed to testing for differentially methylation in gene promoter regions between different populations. Suppose the comparison of interest is same as before. The same contrast can be used for the testing.
> lrt2
<- glmLRT
(fit2,
contrast
=contr)
The top set of most differentially methylated gene promoters can be viewed with topTags:
>
topTags
(lrt2)
Coefficient: 0.5*Me2 0.5*Me3
Symbol logFC logCPM LR PValue FDR
16924 Lnx1 6.85 5.24 314 2.49e-70 4.18e-66
238161 Akap6 5.26 4.06 249 4.19e-56 3.52e-52
64082 Popdc2 -4.91 5.84 226 4.07e-51 2.28e-47
11601 Angpt2 -5.58 3.30 209 2.23e-47 9.37e-44
12740 Cldn4 5.56 5.16 190 3.81e-43 1.28e-39
387514 Tas2r143 -4.52 4.49 178 1.39e-40 3.88e-37
73644 2210039B01Rik 4.03 5.44 169 1.21e-38 2.91e-35
321019 Gpr183 -5.86 2.82 153 3.44e-35 7.22e-32
76509 Plet1 6.00 2.35 146 1.13e-33 2.03e-30
100043766 Gm14057 -5.40 3.64 146 1.21e-33 2.03e-30
Here positive log-fold changes represent gene promoters that have higher methylation level in the basal population compared to the luminal population. The Benjamini-Hochberg multiple testing correction is applied to control the false discovery rate (FDR).
The total number of DM gene promoters identified at an FDR of 5% can be shown with decideTestsDGE. There are in fact about 1,200 differentially methylated gene promoters in this comparison:
>
summary
(
decideTests
(lrt2))
0.5*Me2 0.5*Me3
-1 817
0 15617
1 356
The differential methylation results can be visualized with an MD plot (see Figure 5):
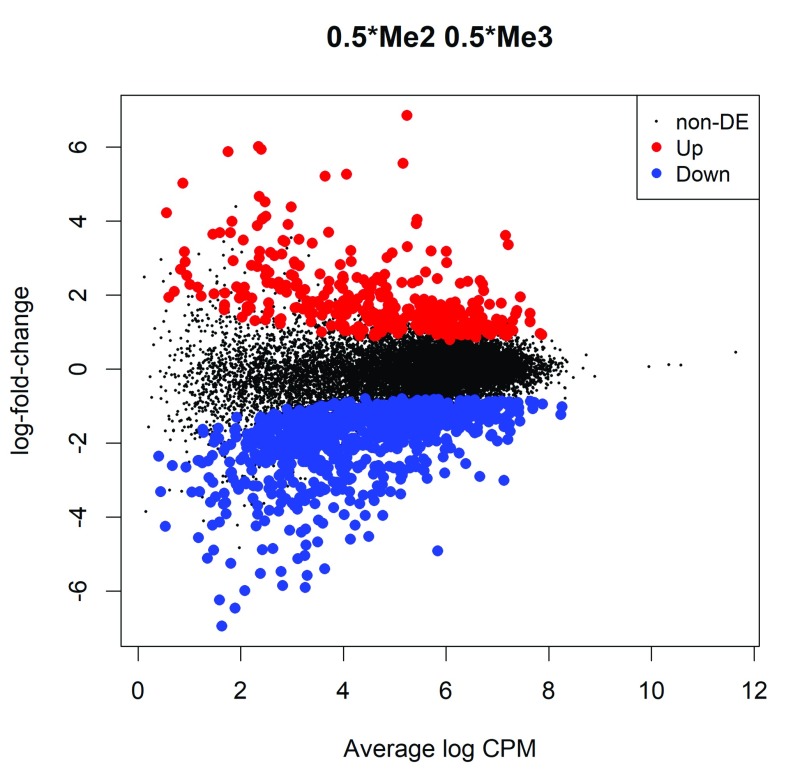
Figure 5. MD plot showing the log-fold change of the methylation level and average abundance of CpG sites in each gene promoter.
Significantly up and down methylated gene promoters are highlighted in red and blue, respectively.
>
plotMD
(lrt2)
Correlate with RNA-seq profiles
RNA-seq profiles of mouse epithelium
To show that DNA methylation (particularly in the promoter regions) represses gene expression, we relate the differential methylation results to the gene expression profiles of the RNA-Seq data. The RNA-seq data used here is from a study of the epithelial cell lineage in the mouse mammary gland 34, in which the expression profiles of basal stem-cell enriched cells and committed luminal cells in the mammary glands of virgin, pregnant and lactating mice were examined. The complete differential expression analysis of the data is described in Chen et al. 35.
The RNA-seq data is stored in the format of a DGEList object y_rna and saved in a RData file rna.RData. The object y_rna contains the count matrix, sample information, gene annotation, design matrix and dispersion estimates of the RNA-seq data. The gene filtering, normalization and dispersion estimation were performed in the same way as described in Chen et al. 35. The DE analysis between the basal and luminal in the virgin mice was performed using glmTreat with a fold-change threshold of 3. The results are saved in the spread sheet BvsL-fc3.csv. Both rna.RData and BvsL-fc3.csv are available for download at http://bioinf. wehi.edu.au/edgeR/F1000Research2017/.
We load the RData file and read in the DE results from the spread sheet.
>
load
(
"rna.RData"
)
> y_rna
An object of class "DGEList"
$counts
MCL1.DG MCL1.DH MCL1.DI MCL1.DJ MCL1.DK MCL1.DL MCL1.LA MCL1.LB MCL1.LC
497097 438 300 65 237 354 287 0 0 0
20671 106 182 82 105 43 82 16 25 18
27395 309 234 337 300 290 270 560 464 489
18777 652 515 948 935 928 791 826 862 668
21399 1604 1495 1721 1317 1159 1066 1334 1258 1068
MCL1.LD MCL1.LE MCL1.LF
497097 0 0 0
20671 8 3 10
27395 328 307 342
18777 646 544 581
21399 926 508 500
15636 more rows ...
$samples
group lib.size norm.factors
MCL1.DG B.virgin 23137472 1.23
MCL1.DH B.virgin 21687755 1.21
MCL1.DI B.pregnant 23974787 1.13
MCL1.DJ B.pregnant 22545375 1.07
MCL1.DK B.lactating 21420532 1.04
7 more rows ...
$genes
Length Symbol
497097 3634 Xkr4
20671 3130 Sox17
27395 4203 Mrpl15
18777 2433 Lypla1
21399 2847 Tcea1
15636 more rows ...
$design
B.lactating B.pregnant B.virgin L.lactating L.pregnant L.virgin
1 0 0 1 0 0 0
2 0 0 1 0 0 0
3 0 1 0 0 0 0
4 0 1 0 0 0 0
5 1 0 0 0 0 0
7 more rows ...
$common.dispersion
[1] 0.0134
$trended.dispersion
[1] 0.02086 0.03012 0.01303 0.01007 0.00957
15636 more elements ...
$tagwise.dispersion
[1] 0.13795 0.08336 0.01387 0.00678 0.00631
15636 more elements ...
$AveLogCPM
[1] 2.58 1.32 4.00 5.06 5.64
15636 more elements ...
$trend.method
[1] "locfit"
$prior.df
[1] 4.68 6.08 6.77 6.77 6.77
15636 more elements ...
$prior.n
[1] 0.78 1.01 1.13 1.13 1.13
15636 more elements ...
$span
[1] 0.292
> rna_DE
<- read.csv
(
"BvsL-fc3.csv"
,
row.names
=
"GeneID"
)
>
head
(rna_DE)
Length Symbol logFC unshrunk.logFC logCPM PValue FDR
24117 2242 Wif1 9.15 9.18 6.77 1.79e-15 1.67e-11
69538 5264 Antxr1 7.35 7.36 7.66 2.67e-15 1.67e-11
55987 3506 Cpxm2 8.15 8.18 6.01 3.20e-15 1.67e-11
12293 7493 Cacna2d1 8.30 8.31 6.81 7.01e-15 2.74e-11
12560 3995 Cdh3 6.98 6.98 7.54 1.14e-14 3.51e-11
110308 2190 Krt5 8.94 8.94 10.27 1.35e-14 3.51e-11
Correlation between the two datasets
We select the genes of which the promoters are significantly DM (FDR < 0.05) and examine their expression level in the RNA-Seq data. A data frame object lfc is created to store the gene information, log-fold change of methylation level and log-fold change of gene expression of the selected genes.
> tp
<- topTags
(lrt2,
n
=
Inf
,
p
=
0.05
)
$
table
> m
<- match
(
row.names
(tp),
row.names
(rna_DE))
> lfc
<-
tp[,
c
(
"Symbol"
,
"logFC"
)]
>
names
(lfc)[
2
]
<-
"ME"
> lfc
$
RNA
<-
rna_DE
$
logFC[m]
> lfc
<-
lfc[
!
is.na
(lfc
$
RNA), ]
>
head
(lfc)
Symbol ME RNA
16924 Lnx1 6.85 -2.27
238161 Akap6 5.26 3.23
64082 Popdc2 -4.91 7.67
11601 Angpt2 -5.58 2.10
12740 Cldn4 5.56 -5.10
387514 Tas2r143 -4.52 3.10
The Pearson correlation coefficient between the two log-fold changes of the selected genes is estimated. The result shows high negative correlation between gene expression and methylation in gene promoters.
>
cor
(lfc
$
ME, lfc
$
RNA)
[1] -0.47
The log-fold changes of the selected genes from the two datasets are plotted against each other for visualization (see Figure 6):
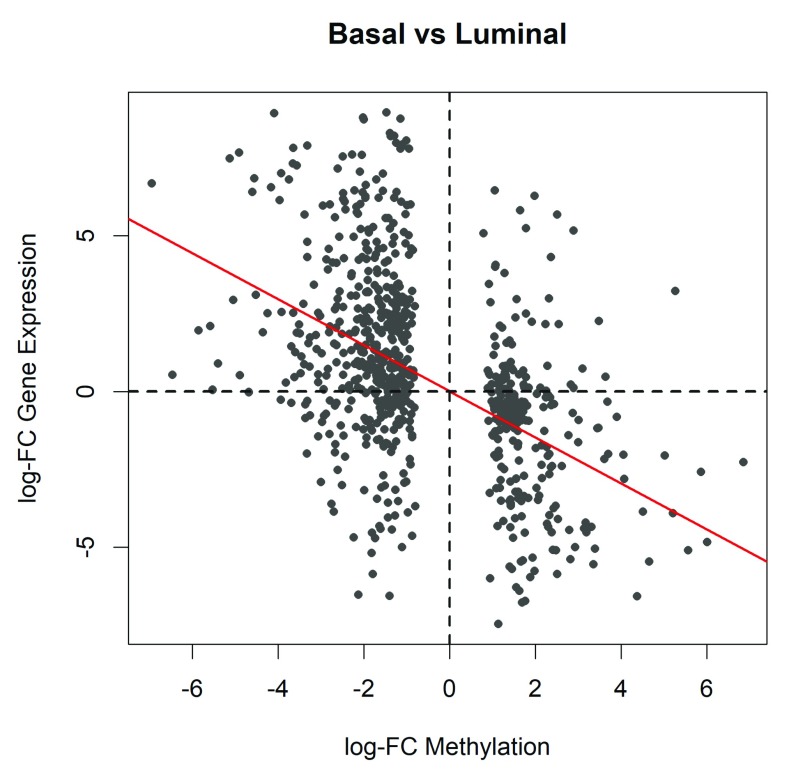
Figure 6. Scatter plot of the log-fold changes of methylation levels in gene promoters (x-axis) vs the log fold-changes of gene expression (y-axis).
The plot shows results for the genes of which the promoters are significantly differentially methylated between basal and luminal. The red line shows the least squares line with zero intercept. A strong negative correlation is observed.
>
plot
(lfc
$
ME, lfc
$
RNA,
main
=
"Basal vs Luminal"
,
xlab
=
"log-FC Methylation"
,
+
ylab
=
"log-FC Gene Expression"
,
pch
=
16
,
cex
=
0.8
,
col
=
"gray30"
)
>
abline
(
h
=
0
,
v
=
0
,
col
=
"gray10"
,
lty
=
2
,
lwd
=
2
)
The horizontal axis of the scatterplot shows the log-fold change in methylation level for each gene while the vertical axis shows the log-fold change in expression. To assess the correlation, we fit a least squares regression line through the origin and compute the p-value:
> u
<- lm
(lfc
$
RNA
~
0
+
lfc
$
ME)
>
coef
(
summary
(u))
Estimate Std. Error t value Pr(>|t|)
lfc$ME -0.739 0.0473 -15.6 1.08e-47
>
abline
(u,
col
=
"red"
,
lwd
=
2
)
The negative association is highly significant ( P = 10 –47). The last line of code adds the regression line to the plot ( Figure 6).
Gene set testing
A rotation gene set test can be performed to further examine the relationship between gene expression and methylation in gene promoters. This is to test whether the set of genes (i.e., genes of which the promoters are differentially methylated) are differentially expressed (DE) and in which direction they are DE.
The indices are made by matching the Entrez Gene Ids between the two datasets. The log-fold changes of methylation level in gene promoters are used as weights for those genes. The test is conducted using the fry function in edgeR. The contrast is set to compare basal with luminal in virgin mice.
> ME
<- data.frame
(
GeneID
=
row.names
(lfc),
weights
=lfc
$
ME)
>
fry
(y_rna,
index
=ME,
design
=y_rna
$
design,
contrast
=
c
(
0
,
0
,
1
,
0
,
0
,
-
1
))
NGenes Direction PValue PValue.Mixed
set1 731 Down 1.51e-09 7.17e-11
The small PValue indicates the significant testing result. The result Down in the Direction column indicates negative correlation between the methylation and gene expression.
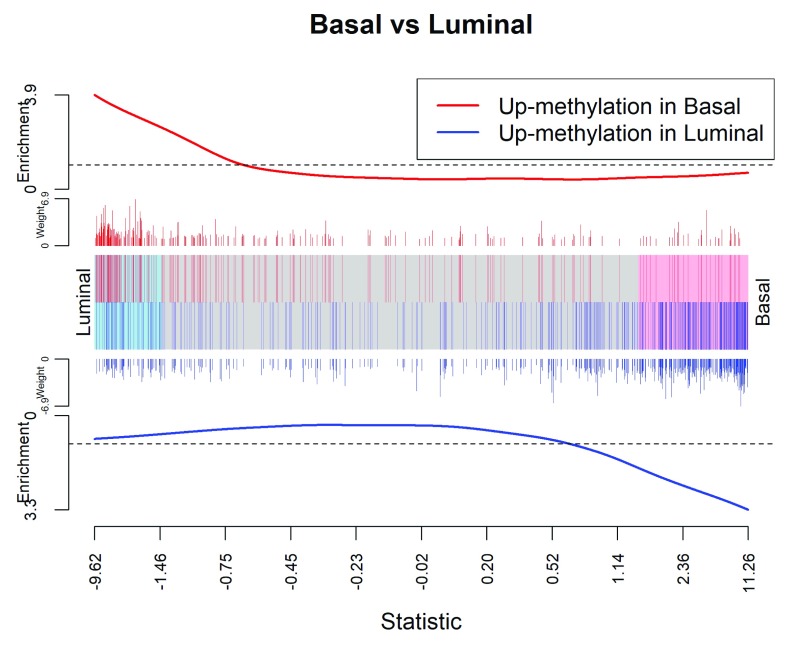
We can visualize the gene set results with a barcode plot (see Figure 7):
Figure 7. Barcode plot showing strong negative correlation between gene expression and DNA methy lation in gene promoters.
> m
<- match
(
row.names
(rna_DE),
row.names
(tp))
> gw
<-
tp
$
logFC[m]
> gw[
is.na
(gw)]
<-
0
>
barcodeplot
(rna_DE
$
logFC,
gene.weights
=gw,
labels
=
c
(
"Luminal"
,
"Basal"
),
+
main
=
"Basal vs Luminal"
)
>
legend
(
"topright"
,
col
=
c
(
"red"
,
"blue"
),
lty
=
1
,
lwd
=
2
,
+
legend
=
c
(
"Up-methylation in Basal"
,
"Up-methylation in Luminal"
) )
In the barcode plot, genes are sorted left to right according to expression changes. Genes up-regulated in luminal are on the left and genes up-regulated in basal are on the right. The x-axis shows the expression log2-fold change between basal and luminal. The vertical red bars indicate genes up-methylated in basal and vertical blue bars indicate genes down-methylated in basal. The variable-height vertical bars represent the methylation log-fold changes. The red and blue worms measure relative enrichment, showing that increased methylation is associated with decreased regulation and down-methylation is associated with up-regulation. In other words, there is a negative association between methylation of promotor regions and expression of the corresponding gene.
Packages used
This workflow depends on various packages from version 3.6 of the Bioconductor project, running on R version
3.4.0 or higher. Most of the workflow also works with Bioconductor 3.5, but the code in the last section (Correlate with RNA-seq samples) requires some minor changes for use with Bioconductor 3.5 because the earlier version of topTags did not preserve row names in the output table. A complete list of the packages used for this workflow is shown below:
>
sessionInfo
()
R version 3.4.2 (2017-09-28)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 15063)
Matrix products: default
locale:
[1] LC_COLLATE=English_Australia.1252 LC_CTYPE=English_Australia.1252
[3] LC_MONETARY=English_Australia.1252 LC_NUMERIC=C
[5] LC_TIME=English_Australia.1252
attached base packages:
[1] stats4 parallel stats graphics grDevices utils datasets methods
[9] base
other attached packages:
[1] org.Mm.eg.db_3.4.2
[2] TxDb.Mmusculus.UCSC.mm10.knownGene_3.4.0
[3] GenomicFeatures_1.30.0
[4] AnnotationDbi_1.40.0
[5] Biobase_2.38.0
[6] GenomicRanges_1.30.0
[7] GenomeInfoDb_1.14.0
[8] IRanges_2.12.0
[9] S4Vectors_0.16.0
[10] BiocGenerics_0.24.0
[11] edgeR_3.20.1
[12] limma_3.34.0
[13] knitr_1.17
loaded via a namespace (and not attached):
[1] Rcpp_0.12.13 compiler_3.4.2
[3] highr_0.6 XVector_0.18.0
[5] prettyunits_1.0.2 bitops_1.0-6
[7] tools_3.4.2 zlibbioc_1.24.0
[9] progress_1.1.2 statmod_1.4.30
[11] biomaRt_2.34.0 digest_0.6.12
[13] bit_1.1-12 RSQLite_2.0
[15] evaluate_0.10.1 memoise_1.1.0
[17] tibble_1.3.4 lattice_0.20-35
[19] pkgconfig_2.0.1 rlang_0.1.4
[21] Matrix_1.2-11 DelayedArray_0.4.1
[23] DBI_0.7 GenomeInfoDbData_0.99.1
[25] rtracklayer_1.38.0 stringr_1.2.0
[27] Biostrings_2.46.0 locfit_1.5-9.1
[29] bit64_0.9-7 grid_3.4.2
[31] R6_2.2.2 BiocParallel_1.12.0
[33] XML_3.98-1.9 RMySQL_0.10.13
[35] blob_1.1.0 magrittr_1.5
[37] matrixStats_0.52.2 GenomicAlignments_1.14.0
[39] Rsamtools_1.30.0 SummarizedExperiment_1.8.0
[41] assertthat_0.2.0 stringi_1.1.5
[43] RCurl_1.95-4.8
Data and software availability
All data and supporting files used in this workflow are available from: http://bioinf.wehi.edu.au/edgeR/F1000Research2017
Archived code/data as at time of publication: http://doi.org/10.5281/zenodo.1052871 36
All software used is publicly available as part of Bioconductor 3.6.
Acknowledgments
The authors thank Andrew Keniry for help on Bismark.
Funding Statement
This work was supported by the National Health and Medical Research Council (Fellowship 1058892 and Program 1054618 to G.K.S, Independent Research Institutes Infrastructure Support to the Walter and Eliza Hall Institute) and by a Victorian State Government Operational Infrastructure Support Grant.
The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
[version 1; referees: 2 approved
References
- 1. Bird A: Perceptions of epigenetics. Nature. 2007;447(7143):396–8. 10.1038/nature05913 [DOI] [PubMed] [Google Scholar]
- 2. Jones PA, Laird PW: Cancer epigenetics comes of age. Nat Genet. 1999;21(2):163–7. 10.1038/5947 [DOI] [PubMed] [Google Scholar]
- 3. Jones PA, Baylin SB: The fundamental role of epigenetic events in cancer. Nat Rev Genet. 2002;3(6):415–28. 10.1038/nrg816 [DOI] [PubMed] [Google Scholar]
- 4. Jabbari K, Bernardi G: Cytosine methylation and CpG, TpG (CpA) and TpA frequencies. Gene. 2004;333:143–149. 10.1016/j.gene.2004.02.043 [DOI] [PubMed] [Google Scholar]
- 5. Bird AP: CpG-rich islands and the function of DNA methylation. Nature. 1986;321(6067):209–213. 10.1038/321209a0 [DOI] [PubMed] [Google Scholar]
- 6. Fatemi M, Pao MM, Jeong S, et al. : Footprinting of mammalian promoters: use of a CpG DNA methyltransferase revealing nucleosome positions at a single molecule level. Nucleic Acids Res. 2005;33(20):e176. 10.1093/nar/gni180 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Deaton AM, Bird A: CpG islands and the regulation of transcription. Genes Dev. 2011;25(10):1010–1022. 10.1101/gad.2037511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Saxonov S, Berg P, Brutlag DL: A genome-wide analysis of CpG dinucleotides in the human genome distinguishes two distinct classes of promoters. Proc Natl Acad Sci U S A. 2006;103(5):1412–1417. 10.1073/pnas.0510310103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Lister R, Pelizzola M, Dowen RH, et al. : Human DNA methylomes at base resolution show widespread epigenomic differences. Nature. 2009;462(7271):315–22. 10.1038/nature08514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Frommer M, McDonald LE, Millar DS, et al. : A genomic sequencing protocol that yields a positive display of 5-methylcytosine residues in individual DNA strands. Proc Natl Acad Sci U S A. 1992;89(5):1827–1831. 10.1073/pnas.89.5.1827 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Meissner A, Gnirke A, Bell GW, et al. : Reduced representation bisulfite sequencing for comparative high-resolution DNA methylation analysis. Nucleic Acids Res. 2005;33(18):5868–5877. 10.1093/nar/gki901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Gu H, Smith ZD, Bock C, et al. : Preparation of reduced representation bisulfite sequencing libraries for genome-scale DNA methylation profiling. Nat Protoc. 2011;6(4):468–81. 10.1038/nprot.2010.190 [DOI] [PubMed] [Google Scholar]
- 13. Krueger F, Andrews SR: Bismark: a flexible aligner and methylation caller for Bisulfite-Seq applications. Bioinformatics. 2011;27(11):1571–1572. 10.1093/bioinformatics/btr167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Pedersen B, Hsieh TF, Ibarra C, et al. : MethylCoder: software pipeline for bisulfite-treated sequences. Bioinformatics. 2011;27(17):2435–2436. 10.1093/bioinformatics/btr394 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Harris EY, Ponts N, Levchuk A, et al. : BRAT: bisulfite-treated reads analysis tool. Bioinformatics. 2010;26(4):572–573. 10.1093/bioinformatics/btp706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Chen PY, Cokus SJ, Pellegrini M: BS Seeker: precise mapping for bisulfite sequencing. BMC Bioinformatics. 2010;11(1):203. 10.1186/1471-2105-11-203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Xi Y, Li W: BSMAP: whole genome bisulfite sequence MAPping program. BMC Bioinformatics. 2009;10(1):232. 10.1186/1471-2105-10-232 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Langmead B, Trapnell C, Pop M, et al. : Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009;10(3):R25. 10.1186/gb-2009-10-3-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Akalin A, Kormaksson M, Li S, et al. : methylKit: a comprehensive R package for the analysis of genome-wide DNA methylation profiles. Genome Biol. 2012;13(10):R87. 10.1186/gb-2012-13-10-r87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Assenov Y, Müller F, Lutsik P, et al. : Comprehensive analysis of DNA methylation data with rnbeads. Nat Methods. 2014;11(11):1138–1140. 10.1038/nmeth.3115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Ritchie ME, Phipson B, Wu D, et al. : limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015;43(7):e47. 10.1093/nar/gkv007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Hansen KD, Langmead B, Irizarry RA: BSmooth: from whole genome bisulfite sequencing reads to differentially methylated regions. Genome Biol. 2012;13(10):R83. 10.1186/gb-2012-13-10-r83 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Feng H, Conneely KN, Wu H: A Bayesian hierarchical model to detect differentially methylated loci from single nucleotide resolution sequencing data. Nucleic Acids Res. 2014;42(8):e69. 10.1093/nar/gku154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Hebestreit K, Dugas M, Klein HU: Detection of significantly differentially methylated regions in targeted bisulfite sequencing data. Bioinformatics. 2013;29(13):1647–1653. 10.1093/bioinformatics/btt263 [DOI] [PubMed] [Google Scholar]
- 25. Sun D, Xi Y, Rodriguez B, et al. : MOABS: model based analysis of bisulfite sequencing data. Genome Biol. 2014;15(2):R38. 10.1186/gb-2014-15-2-r38 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Dolzhenko E, Smith AD: Using beta-binomial regression for high-precision differential methylation analysis in multifactor whole-genome bisulfite sequencing experiments. BMC Bioinformatics. 2014;15(1):215. 10.1186/1471-2105-15-215 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Robinson MD, McCarthy DJ, Smyth GK: edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26(1):139–140. 10.1093/bioinformatics/btp616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. McCarthy DJ, Chen Y, Smyth GK: Differential expression analysis of multifactor RNA-Seq experiments with respect to biological variation. Nucleic Acids Res. 2012;40(10):4288–4297. 10.1093/nar/gks042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Visvader JE: Keeping abreast of the mammary epithelial hierarchy and breast tumorigenesis. Genes Dev. 2009;23(22):2563–2577. 10.1101/gad.1849509 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Shackleton M, Vaillant F, Simpson KJ, et al. : Generation of a functional mammary gland from a single stem cell. Nature. 2006;439(7072):84–8. 10.1038/nature04372 [DOI] [PubMed] [Google Scholar]
- 31. Langmead B, Salzberg SL: Fast gapped-read alignment with Bowtie 2. Nat Methods. 2012;9(4):357–359. 10.1038/nmeth.1923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Robinson MD, Oshlack A: A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010;11(3):R25. 10.1186/gb-2010-11-3-r25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Du P, Zhang X, Huang CC, et al. : Comparison of Beta-value and M-value methods for quantifying methylation levels by microarray analysis. BMC Bioinformatics. 2010;11(1):587. 10.1186/1471-2105-11-587 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Fu NY, Rios AC, Pal B, et al. : EGF-mediated induction of Mcl-1 at the switch to lactation is essential for alveolar cell survival. Nat Cell Biol. 2015;17(4):365–75. 10.1038/ncb3117 [DOI] [PubMed] [Google Scholar]
- 35. Chen Y, Lun AT, Smyth GK: From reads to genes to pathways: differential expression analysis of RNA-Seq experiments using Rsubread and the edgeR quasi-likelihood pipeline [version 2; referees: 5 approved]. F1000Res. 2016;5:1438. 10.12688/f1000research.8987.2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Chen Y, Pal B, Visvader JE, et al. : Data and code for “Differential methylation analysis of reduced representation bisulfite sequencing experiments using edgeR” [Dataset].. Zenodo. 2017. Data Source [DOI] [PMC free article] [PubMed] [Google Scholar]