Network diffusion model of progression predicts longitudinal patterns of atrophy and metabolism in Alzheimer’s Disease

Summary

Alzheimer’s Disease pathology (AD) originates in the hippocampus and subsequently spreads to temporal, parietal and prefrontal association cortices in a relatively stereotyped progression. Current evidence attributes this orderly progression to trans-neuronal transmission of misfolded proteins along the projection pathways of affected neurons. A network diffusion model was recently proposed to mathematically predict disease topography resulting from trans-neuronal transmission on the brain’s connectivity network. Here we use this model to predict future patterns of regional atrophy and metabolism from baseline regional patterns of 418 patients. The model accurately predicts end of study regional atrophy and metabolism starting from baseline data, with significantly higher correlation strength than given by the baseline statistics directly. The model’s rate parameter encapsulates overall atrophy progression rate; group analysis revealed this rate to depend on diagnosis as well as baseline CSF biomarker levels. This work helps validate the model as a prognostic tool for Alzheimer’s disease assessment.

Introduction

Alzheimer’s Disease (AD) is an amyloid facilitated tauopathy (Braak et al., 2000) whose origin and subsequent advance within the brain is well characterized: the disease begins in the mesial temporal lobe, an event accompanied by the accumulation of misfolded beta amyloid and tau proteins, and thence progresses along fiber pathways. Histopathological evidence of this highly stereotyped progression has come to be known as the Braak model (Braak and Braak, 1996): neurofibrillary tau tangles are first found in entorhinal cortex and hippocampus (stages I–II), then spread into the amygdala and basolateral temporal lobe (stages III–IV), followed by isocortical association areas (stages V–VI). Morphological changes accompanying this pathological progression are clearly visible on MRI, especially from cross-sectional and longitudinal morphometric mapping (Fischl et al., 2002; Klauschen et al., 2009; Smith et al., 2004; Wu et al., 2007). Longitudinal studies (Apostolova and Thompson, 2008; Apostolova et al., 2007; Thompson et al., 2003; Whitwell et al., 2007) confirm that progression follows vulnerable fiber pathways rather than spatial proximity (Englund et al., 1988; Kuczynski et al., 2010; Villain et al., 2008), closely mirroring Braak pathological stages (Whitwell et al., 2007).

Until recently, the causative mechanisms for this networked spread were thought to be passive, including secondary Wallerian degeneration, disconnection, loss of signaling, axonal reaction and post-synaptic dendrite retraction (Seeley et al., 2009a). Latest evidence however favors a transneuronal “prion-like” mechanism (Frost and Diamond, 2010; Jucker and Walker, 2013), whereby implicated proteins misfold, trigger misfolding of adjacent same-species proteins, and thereupon cascade along neuronal pathways via transsynaptic or transneuronal spread (Clavaguera et al., 2009; Frost et al., 2009; Jucker and Walker, 2011, 2013; Palop and Mucke, 2010). Exogenous seeding of pathogenic proteins in the hippocampus caused remote pathology in connected regions (Clavaguera et al., 2009; Jucker and Walker, 2013). Seeded templating of misfolded protein species can therefore be thought of as the causative “propagating” event, and other observed phenotypes - hypometabolism, atrophy and cognitive dysfunction – result from the pathology.

Recently trans-neuronal transmission was mathematically modeled in our laboratory (Raj et al., 2012) by a diffusive mechanism mediated by and restricted to the brain’s connectivity network, and the resulting topography of the disease was mathematically deduced. The network was obtained using diffusion MRI-derived healthy “connectomes” (Lo et al., 2010). Intriguingly, the macroscopic consequences of diffusive prion-like propagation (the “network diffusion or ND model”) on healthy networks recapitulated patterns of atrophy in various dementias. Specifically, the model predicted spatially distinct “eigen-modes,” which mirrored disjoint brain regions known to be selectively targeted by different dementias (Buckner et al., 2005; Seeley et al., 2009b). This mathematical reformulation of descriptive neuropathological observations into a deterministic encapsulation of neurodegenerative progression opens the possibility of dementia prognostication.

The goal of this study is to develop the theoretical model of (Raj et al., 2012) into a clinically useful computational biomarker with the ability to predict future patterns of atrophy in susceptible individuals. Implicit in this work is that baseline atrophy is sufficient to give future predictions. Although motivated by stereotyped Braak-type progression, individual subjects’ model predictions do not rely on a priori monolithic Braak staging assumptions. We are aware of no other existing tool that can predict future topography of AD atrophy and metabolism in individuals. There are clear applications of our biomarker in prognosis and as a monitoring tool in clinical trials.

To assess our biomarker’s relative utility, we compare it against quantitative models representing the alternative hypothesis that growth of degeneration in different regions are independent processes which are not transmitted via white matter connections. We chose two established hypotheses: a) a sigmoid model of disease progression (Jack Jr et al., 2010), which was verified using CSF amyloid scans (Jack et al., 2013), whereby every brain region undergoes a separate but temporally well defined degeneration characterized by slow initial growth rate, peak intermediate growth, and a declining eventual growth rate reflecting saturation effects; and b) an exponential model, where highly affected regions undergo faster degeneration, separately and independently from other regions. The exponential model also describes activity-dependent degeneration, whereby lifetime neuronal activity, rather than network transmission, is thought to govern degeneration and rapidity (Buckner et al., 2005; Greicius et al., 2004).

Results

The study cohort consists of all ADNI subjects who had 2–4 longitudinal MRI and FDG-PET scans; their demographics are summarized in Table 1. Where appropriate, results are stratified by diagnosis-mild cognitive impaired (MCI) converters, MCI non-converters, AD. The outcome of the analysis pipeline on this data procedure was a regional atrophy/metabolism number for each subject, evaluated at 90 regions covering the entire cerebral gray matter, with no gaps, taken from a neuro-anatomically accurate parcellated brain atlas.

Table 1.

Demographic characteristics of the study cohorts

Gender	Young control (age)	ADNI control (age)	ADNI AD (age)	ADNI MCI (age)
Female	29 (23.0 ± 5.8)	37 (75.8 ± 5.8)	39 (74.8 ± 6.9)	49 (74.9 ± 8.2)
Male	44 (23.2 ± 4.3)	58 (73.6 ± 5.4)	60 (76.5 ± 7.2)	102 (75.5 ± 6.7)

Testing the regionally varying relationship between baseline and rate of change

Scatter plots of the empirical relationship between baseline atrophy/metabolism and their rate of change are shown in Supplemental Figure 1. Each dot represents a parcellated GM structure of each subject, where x-axis represents baseline value and y-axis the slope. There is no simple relationship between baseline atrophy/hypometabolism and its slope that fits all regions and subjects. Neither the straight line (exponential, green) nor parabola (sigmoid, cyan) captures this relationship fully, although both capture portions of the data. The ND model prediction (red, middle panel) appears to successfully cover the atrophy-slope plane. A topographic rendering of this relationship is shown in Supplemental Figure 2, top: regional baseline t-statistic of all patients’ FDG-derived regional hypometabolism (left), its rate of change (middle), and the network diffusion model-predicted rate of change (right). The slope in hypometabolism is not simply proportional to baseline: there is general agreement in temporoparietal regions, but not in frontal and occipital regions. Black arrows point to specific structures that are discordant. Conversely, in mesial temporal structures the rate of change is less than would be predicted by linearly extrapolating the baseline map. In these discordant structures, the network diffusion model appears to be a better predictor of slope than the baseline map.

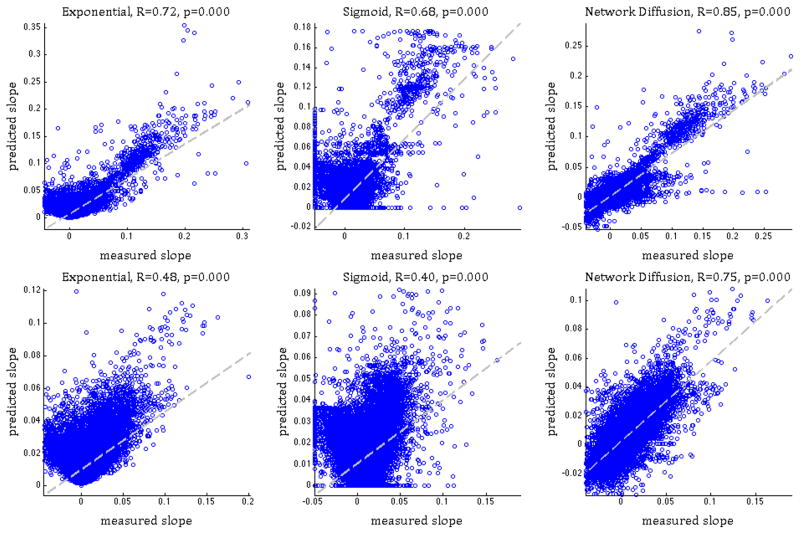
Next we assess the accuracy of each model in predicting the regional rate of change from baseline in both MRI atrophy and FDG-PET-derived hypometabolism (Figure 1). The correlation between the measured and predicted slope of the entire MCI+AD cohort gave the following values. Atrophy: R=0.72 (exponential model), R=0.68 (sigmoid), R=0.85 (Network diffusion); FDG hypometabolism: R=0.48 (exponential), R=0.40 (sigmoid), R=0.75 (Network diffusion). While all 3 models considered here capture to some extent the slope of atrophy/hypometabolism, the ND model achieves the highest correlation. Fisher’s R-to-z transform gave a significant difference in the reported R achieved by the proposed model and both competing models (p < 10⁻²).

Figure 1. Correlation between measured and predicted atrophy/metabolism slope.

exponential model (linear relationship, left panel), sigmoid model (middle) and Network Diffusion model (right). Pearson’s R and p are shown alongside. Top panel shows MRI atrophy and the bottom FDG-PET hypometabolism data. In both cases, the network diffusion model gives stronger correlations than the other two models. See also Supplemental Figure 1.

Predicting future patterns of atrophy and hypometabolism

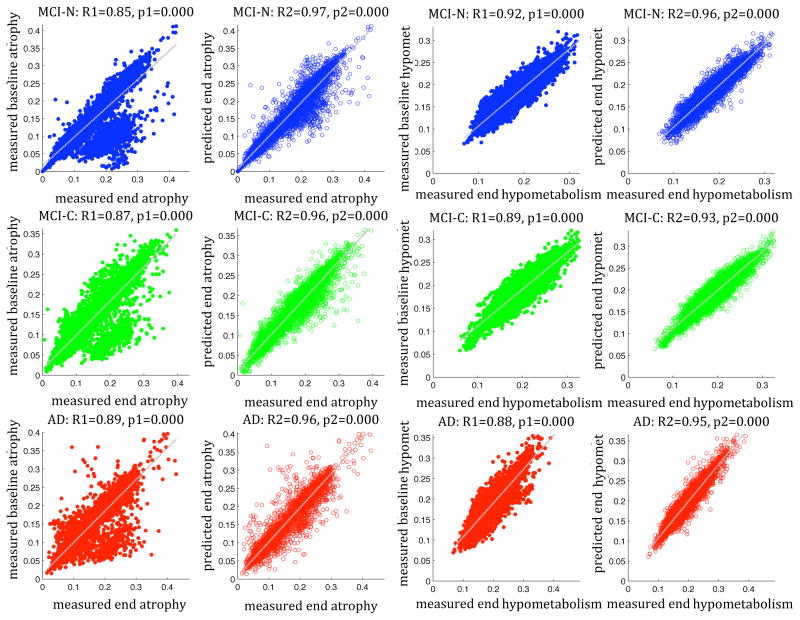
Validation of the predictive ability of our model is contained in scatter plots in Figure 2. Each point corresponds to a single region in a single subject. Both MRI-derived atrophy and FDG-PET-derived hypometabolism are shown. Measured regional baseline statistics already exhibit a strong and significant relationship to atrophy/metabolism at end of study (1^st and 3^rd columns), expectedly, since drastic progression within 2–4 years is unlikely. Correlation strength is generally higher for hypometabolism than for atrophy, probably due to lower noise and fewer artifact-inducing processing steps in FDG-PET images. Interestingly, a significant subset of regional atrophy data appears to stray from the diagonal (1^st column), implying that localized relationships are not sufficient to capture disease dynamics. A closer investigation of these discordant regions (see Supplementary Experimental Procedures, Supplemental Figure 2, bottom) revealed them to occur mostly in the frontal and occipital cortex in MCI converters. These regions are typically involved in late but not early stages, distal but connected to vulnerable temporoparietal areas, hence “next-in-line” for future progression.

Figure 2. Validation of the predictive power of the network diffusion model.

Columns 1,2 pertain to MRI-derived atrophy data and columns 3,4 to FDG-PET-derived hypometabolism data. The ADNI cohort is stratified by diagnosis: MCI-nonconverters (top row), MCI-converters (middle) and AD (bottom). The relationship between baseline regional atrophy and atrophy at end of study is strong and significant in all cases, including measured data (1^st and 3^rd columns) and model predictions (2^nd and 4^th columns). However, the correlation strength is greatly and significantly improved in all diagnosis types by the network diffusion model. See also Supplemental Figure 2 and Supplementary Experimental Procedures.

The correlation strength R (Table 2) is significantly improved in all diagnoses by adding the ND model, and the above discordant “off-diagonal” regions were brought back onto the diagonal. Fisher’s R to z transform indicates these improvements to be highly significant, implying that the model is adding strong predictive power that cannot be explained by the baseline data alone. The model greatly reduces unexplained variance (1-R²), for instance in MCI-converters, where it goes from 0.24 using baseline alone, to 0.08 using the ND model, constituting a net improvement of 300%. Note that these data are group-level summaries of individual subjects’ predictions, using each individual’s baseline scan. Hence, while these numbers amply characterize the capability of the prognostic biomarker, they do not indicate prediction performance for a given individual.

Table 2.

Summary of correlation statistics between baseline and end of study regional statistics – atrophy from MRI and hypometabolism from FDG-PET.

Dataset	Stats (measured)	Stats (model)	95% CI of model stats	Unexplained variance (measured)	Unexplained variance (model)	Significance of Fisher’s R-z
MCI-N atrophy	0.85	0.97	[0.951, 0.98]	0.28	0.059	p < 10−4
MCI-C atrophy	0.87	0.96	[0.94, 0.974]	0.24	0.078	p < 10−4
AD atrophy	0.89	0.96	[0.933, 0.975]	0.21	0.078	p < 10−4
MCI-N FDG	0.92	0.96	[0.95, 0.968]	0.15	0.078	p < 10−2
MCI-C FDG	0.89	0.93	[0.926, 0.951]	0.21	0.14	p < 10−2
AD FDG	0.88	0.95	[0.944, 0.964]	0.23	0.10	p < 10−4

Robustness Analysis

To characterize the robustness of our putative biomarker against noise and inter-subject variability, increasing amounts of independent Gaussian noise was added to the reference connectomes and the confidence interval of the R statistic in Table 2 was estimated using Monte Carlo simulations with 100 trials (Supplemental Figure 6-A). Predicted R appears tolerant to moderate levels of connectome noise. Second, the effect of inter-subject variability in the R statistic was explored via bootstrap analysis by repeatedly resampling 1000 times from the ADNI cohort (see Supplementary Procedures and Supplemental Figure 6-B). The 95% confidence interval of predicted R statistic is listed in Table 2. Clearly our results have almost zero bias, are highly robust to inter-subject variability and well within the range expected from sampling errors. Interestingly, connectome noise-induced variability in R is actually less than that due to variability in patients.

Example future predictions of atrophy and hypometabolism

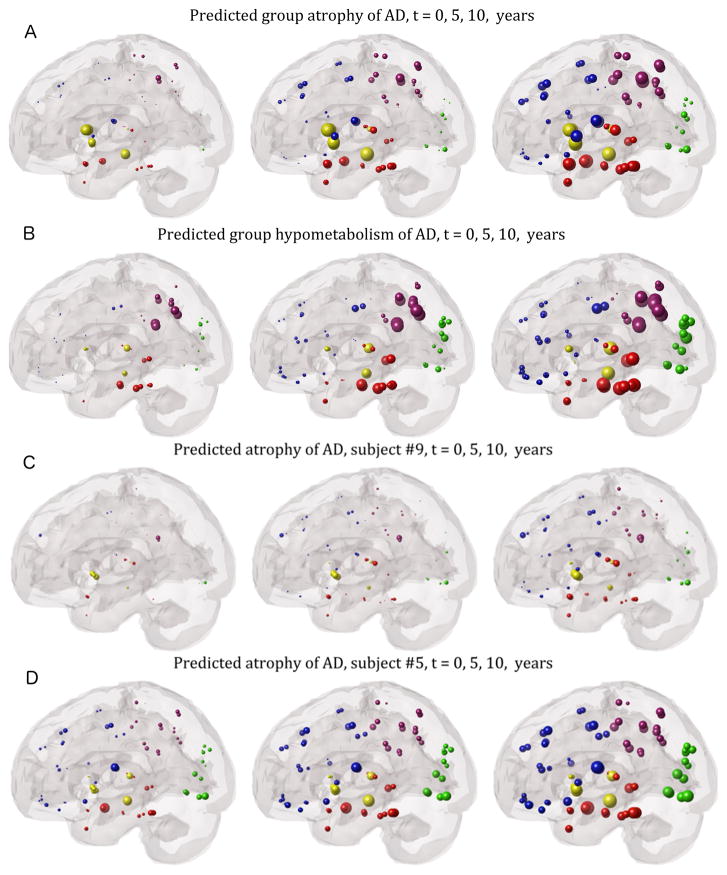
Some visually illustrated anecdotal examples of future progression are presented, going beyond the 2–4 year time window of ADNI data. Figure 3 verifies that the group statistics of AD subjects, the best characterized and stereotyped group, follows expected progression. The spheres are proportional to the t-statistic of MRI atrophy after logistic transform, and color-coded by lobe – frontal=blue, parietal=purple, occipital=green, temporal=red, subcortical=yellow. The ND model correctly recapitulates the classic Alzheimer progression from mesial temporal structures to parietal and finally frontal areas. The rate of progression parameter was estimated by empirical fitting to individual subject data as described earlier, but in order to minimize risk of over-fitting, the time-since-onset parameter was fitted to each diagnostic group rather than to individuals. FDG hypometabolism results (Figure 3B) are similar. Next we show 6 examples drawn from individual subjects from all 3 diagnosis categories, selected via visual inspection as typifying the most common modes of behavior we observed in each disease group. Figures 3(C,D) show two representative AD examples, whose classic temporal-dominant atrophy pattern remains steady over extrapolated timescales as it progressively grows more severe.

Figure 3. “Glass brain” illustrations of regional statistics of AD subjects from the ADNI cohort.

The spheres are proportional to effect size, and color-coded by lobe: frontal=blue, parietal=purple, occipital=green, temporal=red, subcortical=yellow. Group regional atrophy (A) and metabolism (B) statistics of all AD subjects are shown. Left: regional t-statistic at baseline with respect to ADNI healthy controls, after logistic transform. Network diffusion model prediction based on baseline atrophy, extrapolated to 5 years out (middle) and 10 years out (right). Our extrapolations recapitulate the classic pattern of AD progression, from mesial temporal to parietal and finally frontal structures. Panels C and D show two illustrative AD examples. In both cases the classic AD-pattern of atrophy is seen at baseline as well as at predicted future time points, albeit with increasing severity.

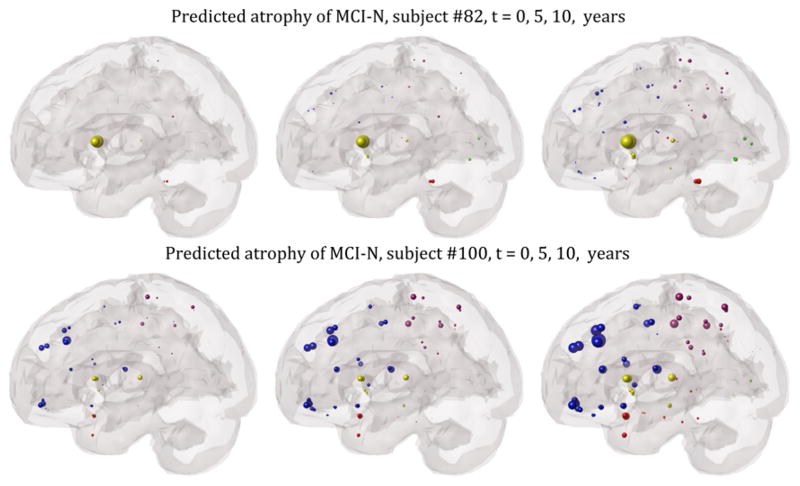
Figure 4 shows two example MCI non-converters; the left panel depicts regional MRI-derived atrophy at baseline with respect to ADNI healthy controls, after logistic transform to convert z-scores to positive atrophy values between 0 and 1. The next two panels show the network diffusion model prediction from baseline atrophy, extrapolated to 5 years and ten years out. The top case exhibits classic MCI topography with hippocampal involvement, but model extrapolation does not indicate subsequent extra-hippocampal spread or temporal involvement, consistent with MCI-nonconverter status. The bottom case is an interesting variant of the non-converter case, with prominent widespread atrophy at baseline in the frontal cortex. However, extrapolated atrophy patterns stay within the frontal areas, and subsequently spread to parietal, but not temporal, regions – in consonance with MCI-nonconverter diagnosis.

Figure 4. “Glass brain” illustrations of two example MCI non-converters from the ADNI cohort.

The spheres are proportional to effect size, and color-coded by lobe: frontal=blue, parietal=purple, occipital=green, temporal=red, subcortical=yellow. Left: regional z-score of MRI-derived atrophy at baseline with respect to ADNI healthy controls, after logistic transform. Network diffusion model prediction based on baseline atrophy, extrapolated to 5 years out (middle) and 10 years out (right). Neither case progresses into prominent temporal involvement.

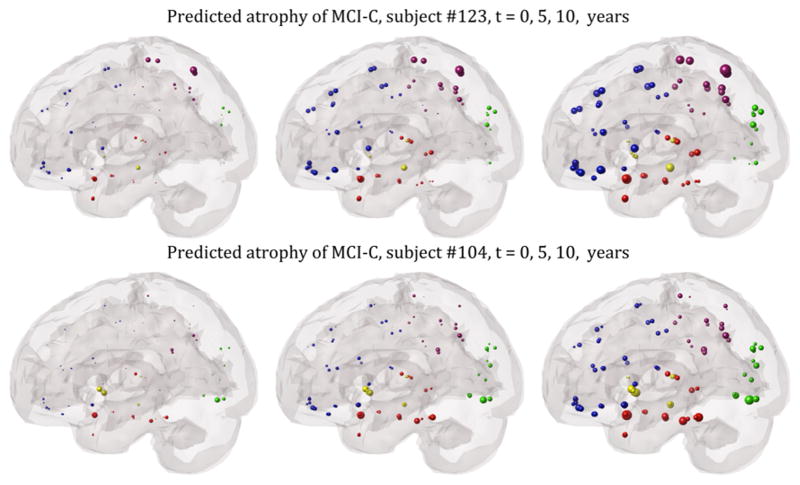
Figure 5 shows two examples of MCI-converters, one of which (bottom row) exhibits the classic AD pattern of progression within and outwards from the temporal lobe. Baseline atrophy is overall mild, but the extrapolated patterns show the classic progression from MCI to AD. Specifically, the recruitment of temporal and subcortical regions, which are associated with memory-related cognitive dysfunction, increases prominently. The top case also exhibits prominent and early temporal involvement, but longitudinal predictions are more prominent in frontal and parietal regions. This case is consistent with current diagnosis of MCI-converter, but worsening frontoparietal atrophy may be expected.

Figure 5.

Glass brain illustration of the predictive ability of the model on two example MCI converters, with mild but early temporal involvement, progressing to the classic AD-type topography with prominent temporal involvement.

Results of subject-wise fitting of model parameters

The fitted model parameters - time between onset and baseline scan t_post−onset and the rate constant of network diffusion β- are quite variable across subjects. The distribution of β, shown in Supplemental Figure 3, categorized by diagnosis, appears to follow an exponential distribution, whose parameters we fit using MATLAB’s expfit() function, and display in Table 3. Since the 95% confidence intervals (CI) pertaining to the 3 groups do not overlap, it may be concluded that the rate parameters of the 3 groups are statistically significant and come from different distributions. Notably, a clear order emerges, such that β(MCI − N) ≈ β(MCI − C) < β(AD), with the mean rate parameter of AD group almost twice as large as the MCI groups, whether it is fitted to MRI atrophy or FDG hypometabolism data, an intuitive and expected result. Supplemental Figure 3 shows that post-onset time is widely distributed, without a discernible difference between groups.

Table 3.

Exponential distribution parameter λ of subject-wise β in each diagnostic, CSF amyloid or APOE grouping. Significance of MCI versus AD group, and low-versus high-CSF amyloid and APOE carrier versus non-carriers groups, are denoted by * when their 95% confidence intervals do not overlap. See also Supplemental Figure 3–5.

Group	λ from atrophy	95% CI	λ from FDG	95% CI
MCI-N	0.025 *	[0.022, 0.030]	0.022 *	[0.019, 0.026]
MCI-C	0.020 *	[0.016, 0.025]	0.024 *	[0.020, 0.029]
AD	0.037	[0.030, 0.045]	0.046	[0.038, 0.056]
Aβ – 42 > 192 pg/ml	0.012 *	[0.009, 0.016]	0.022 *	[0.017, 0.029]
Aβ – 42 < 192 pg/ml	0.027 *	[0.023, 0.032]	0.036 *	[0.031, 0.043]
APOE-ε4 non-carriers	0.030	[0.026, 0.035]	0.029 *	[0.025, 0.035]
APOE-ε4 carriers	0.030	[0.026, 0.035]	0.045 *	[0.039, 0.053]

Given that baseline CSF biomarkers of amyloid deposition (Aβ − 42), tau (tau and p-tau) and their ratio ( $\frac{A\beta -42}{\mathit{tau}}$) are known to be correlated with diagnosis (Da et al., 2013; Dickerson and Wolk, 2013; Roe et al., 2011; Shaw et al., 2011), we next investigated whether these biomarkers impart a similar influence on the rate constant and post-onset time. Scatter plots depicting these potential influences are shown in Supplementary Information (Supplemental Figure 4), along with Pearson correlation statistics. These results suggest little independent role for CSF biomarkers, after accounting for the information contained in the baseline image, in determining the rate of progression or time since onset. Given that CSF biomarkers are known to have a threshold effect, whereby their effect is imparted only at pathological levels (Fjell et al., 2010), we next dichotomize the ADNI subjects into two groups: pathological baseline CSF Aβ − 42 (< 192 pg/ml) and non-pathological (> 192 pg/ml, bottom). The histogram of β in Supplemental Figure 5 and distribution statistics in Table 3 demonstrate that β, our marker of the rate of progression, is significantly higher in the pathological versus non-pathological group. We repeated this analysis for genotypic dichotomization into APOE-ε4 allele non-carriers and carriers (Supplemental Figure 5, right). There was no difference between the two groups when fitting β to MRI atrophy, but a significant difference was observed when fitting to FDG-PET, where exponential parameter λ was 0.29 for the former group and 0.45 for the latter group.

Discussion

Summary of results

The proposed predictive model captures diffusive inter-neuronal propagation enacted on the brain’s connectivity network, an approach that was previously shown to recapitulate classic topographic patterns of common dementias (Raj et al., 2012). Although the concepts on which this model is based are known, our main contribution is that we were able to formalize and mathematically encode existing understanding and employ them towards the goal of predicting future progression in individual subjects. By turning different competing descriptive hypotheses into testable predictions, we were able to statistically compare them. We found strong statistical evidence in favor of the network diffusion model.

The major findings of this study were: First, using baseline MRI volumetrics and PET-based glucose hypometabolism, the model predicted future atrophy/metabolism patterns of AD and MCI subjects drawn from the ADNI database. Second, the model captured the regionally varying baseline/slope relationship accurately and to a larger extent than alternate localized growth models, viz sigmoid and exponential growth. Third, an investigation of the fitted rate of progression in individuals showed group differences between MCI and AD. The role of CSF biomarkers in determining the rate of progression is revealed only after dichotomizing the CSF data. Evidence for the role of APOE allele status is mixed. Since the proposed predictive model works on individual subjects it is a computational prognostic biomarker. Group-level summary statistics are presented here to characterize this biomarker, but the underlying data come from individual subjects’ predictions. A thorough robustness analysis via Monte Carlo simulations and bootstrap analysis demonstrated the predictor performance to be insensitive to connectome noise and inter-subject variability. Each result is discussed below in the context of current literature.

Capturing the relationship between regional atrophy and its rate of change

The regional baseline/slope relationship provides an effective way of testing the validity of progression models, since in the 2–4 year window of observation the progression in the ADNI cohort may be considered roughly linear. It is known from morphometric AD studies that the baseline/rate relationship is complex (Jack et al., 2009); atrophied regions appeared to evolve differently depending on disease stage (Whitwell et al., 2007), and atrophy rate was reported to have a regionally varying relationship with Aβ deposition (Tosun et al., 2011). Our result (Supplemental Figures 1,2) also suggests a regionally varying baseline/slope relationship. Baseline and change values are in good agreement in classically vulnerable temporoparietal regions, but not in frontal and occipital regions, which give the “off-diagonal” effect seen in Figure 2. However, these regions are strongly connected to already-affected regions, hence “next-in-line” for future changes according to the trans-neuronal transmission hypothesis. Thus, without considering network connectivity, these regions would arguably be prone to under-estimation as sites of future change. Examining the correlation strength between measured atrophy slope and model prediction (Figure 1), the network model is strongly predictive of slope (R=0.85 for atrophy slope, R=0.75 for hypometabolism slope). Non-networked model of localized spread, whether exponential (predicting a linear relationship) or sigmoid (parabolic relationship) also predict the slope, but not as well.

Comments on alternative localized growth models

The localized growth models were obtained by mathematically encoding existing hypotheses. We allowed different regions and subjects to be placed at different points along the sigmoid/exponential curves, since they may be at different stages of degeneration. In (Jack et al., 2013), a similar strategy of placing different subjects (although not regions) at different points along the sigmoid curve demonstrated that long non-linear sigmoid or exponential dynamics over the duration of the disease can be fit to narrow time windows exhibiting only linear trends. The choice of these simple local growth models in favor of non-local statistical models, e.g. projections to “AD-signature” regions (Da et al., 2013), was motivated by our goal of assessing the specific role of the network in determining the dynamics of AD.

Agreement with prior longitudinal imaging studies

MRI atrophy is strongly correlated with cognitive impairment and its topographic distribution correlates well with Braak staging at autopsy (Jack Jr et al., 2010; Whitwell et al., 2009). FDG-PET is correlated with impaired synaptic function (Rocher et al., 2003), cognitive impairment and post-mortem AD diagnosis (Hoffman et al., 2000). Apostolova et al elegantly described the patterns of AD progression from longitudinal MRI, showing stereotyped spread of atrophy from temporal to parietal and frontal regions (Apostolova and Thompson, 2008; Apostolova et al., 2007). Morphological changes in MCI patients measured using voxel based morphometry (VBM) followed a classic Braak pattern of progression, starting from anterior medial temporal regions at 3 years prior to conversion, spreading to nearby temporal and parietal cortices and at AD diagnosis encompassing the classic temporoparietofrontal AD pattern (Whitwell et al., 2007). The ND model’s predictions (Eq 5) are in good agreement with these longitudinal observations. The MCI-converter examples (Figure 4) recapitulate almost perfectly the progression described in (Whitwell et al., 2007). Similarly, the AD cases (Figure 3) are in good agreement with the topographic evolution shown in (Apostolova and Thompson, 2008; Whitwell et al., 2007). Of note, the ND model gives more accurate prediction than linear local growth reflected by baseline correlations.

The role of focal origin, syndromic, pathological and genotypic characteristics

We do not explicitly rely on any kind of selective vulnerability or origination site, e.g. entorhinal cortex and hippocampus (Braak and Braak, 1992; Braak and Del Tredici, 2012; Braak et al., 2000), this being implicit in the baseline scan. Origination site might be dictated by selective vulnerability due to various stressors (Braak et al., 2000; Palop et al., 2006; Saxena and Caroni, 2011; Seeley et al., 2009a) or innate gene expression in origination sites (Goel et al., 2014). Presented data suggests that even if origination sites are anatomically or architectonically determined, subsequent spread and eventual topographic fate of AD pathology are likely determined by network topology.

The puzzling dissociation between imaging based neurodegenerative patterns and the distribution of AD-causing pathology (tau and Aβ) is well known (Jack Jr et al., 2010). MRI MRI atrophy and FDG-PET binding are closely associated with cognitive deficits and tangles, but not with Aβ deposition (Jack Jr et al., 2010; Landau et al., 2012; Murray et al., 2011; Robinson et al., 2011). Three distinct topographical patterns were reported in AD – classical (75%), limbic predominant (14%) and hippocampus sparing (11%), reflecting heterogeneous origination and spread sites (Murray et al., 2011). Approximately 20–40% of cognitively normal elderly people have significant Aβ plaque deposition (Jack Jr et al., 2010). Given these dissociations, the utility of a single spread model in describing AD topography might be doubted. However, the model’s function is not to capture a specific pathologic agent like amyloid or tau, but to model progression starting at baseline markers of degeneration, howsoever they may have arisen.

Interestingly, we found a strong dependence of the subject-wise fitted rate of progression parameter β on subjects’ diagnostic status, but no correlation between baseline CSF biomarkers and rate of progression. A strong group difference was however seen when the subjects are dichotomized into high or low biomarker regimes (Table 3). Numerous prior reports show a definite association between CSF biomarker levels and risk of AD. It could be that our fitting procedure or CSF biomarker levels or both are noisy. Since the subject’s morphometric information is already built into the estimate of β via Eq (6), our result might simply imply that CSF biomarkers lack incremental power to predict rate of progression, beyond what is explained by imaging. This is in line with converging understanding based on the early deposition and subsequent plateauing of amyloid (Villemagne et al., 2013), that while CSF biomarkers are good predictors of conversion risk, neurodegenerative markers like MRI are more sensitive predictors of current disease state and its rate of decline (Da et al., 2013; Dickerson and Wolk, 2013; Fjell and Walhovd, 2011; Jack et al., 2009; Vemuri et al., 2009). Our dichotomized CSF results support this interpretation, such that CSF biomarker levels appear to exert an effect on rate of progression only beyond the pathologic threshold (Fjell et al., 2010; Mattsson et al., 2014; Schott et al., 2010). The effect of APOE status on rate of decline β was mixed: non-significant for MRI atrophy but significant for FDG-PET; potentially this could be due to the generally higher SNR observed in FDG data.

Clinical and diagnostic implications

These results provide support to the network diffusion model as a prognostic aid to the clinician, allowing them to predict what the patient’s neuroanatomic state will be at any given point in the future. Knowledge of what the future holds can empower patients and allow informed choices regarding lifestyle, therapeutic and non-therapeutic interventions. The ND model could potentially be used to enhance cohort stratification and monitoring accuracy in large-scale clinical trials, and thus improve statistical power at a lower cost. By allowing extrapolation of baseline state regardless of syndromic classification these data could present an opportunity to disentangle and disambiguate AD subtypes in a clinical setting. Future neuroradiologists might plausibly eschew uncertain syndromic categorization in favor of quantitative models of topographical patterning of future disease states as early markers of disease. Cases of mixed dementia could also benefit, where classical region-based atrophy descriptors might prove unsatisfactory.

Limitations

This is a first order, linear, parsimonious model of diffusive spread that assumes static networks, even though both atrophy and the network must dynamically evolve. However these non-linear effects are difficult to capture analytically, and can only be accessed via numerical finite difference computations – a topic of future work. The model only considers the long-range transmission of proteopathic carriers, and not their local “leaking” via synapses and dendrites, because local circuitry is neither observable by non-invasive tractography nor necessary for modeling large-scale macroscopic patterns. Technical limitations of the volumetric and tractography processing pipelines include HARDI spatial and angular resolution, co-registration errors, low test-retest reliability of volumetric data and the distance bias inherent in tractography. These issues are even more problematic in longitudinal analysis, but we believe this high-powered study is able to withstand these challenges. Although the model enables long-term projections, its validation was limited to public (ADNI) datasets of rather narrow time span (2–4 years), precluding long-term longitudinal follow up. One of the most attractive aspects of our model, its ability to capture non-linear trajectories of disease, is poorly tested by these data. We hope that future work will address this gap. Finally, healthy reference rather than individual patients’ connectomes were used for individual prediction, to avoid individual variability and noise and because ADNI database did not contain diffusion MRI scans. However, variability in connectomes appears to exert only minor influence on our model (see Supplemental Figure 6, Fig S5 of (Raj et al., 2012)); hence our conclusions should remain valid and withstand the scrutiny of future investigations.

Experimental Procedures

Data Description

Healthy cohort

Axial T1 weighted FSPGR scans (TE = 1.5 ms, TR = 6.3 ms, TI = 400 ms, 15° flip angle, 230 × 230 × 156 isotropic 1 mm voxels) and High Angular Resolution Diffusion Imaging (HARDI) data (55 directions, b = 1000 s/mm², 72 1.8-mm thick interleaved slices, 0.8594 × 0.8594 mm planar resolution) were acquired on a 3 Tesla GE Signa EXCITE scanner from 73 fully consented young healthy volunteers under a previous IRB-approved study (Kuceyeski 2014).

Age-matched normal, AD, and MCI cohorts

Data used in this article were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (www.adni.loni.usc.edu). Launched in 2003 as a $60 million, 5-year public-private partnership, ADNI aims to test whether serial MRI, PET, other biological markers and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. More details of ADNI methodology are in Supplemental Experimental Procedure 4. Diagnosis is established by ADNI at each longitudinal time point based on natural history and cognitive assessment. We further classified MCI subjects as MCI-converter or MCI-nonconverter, depending on whether their baseline diagnosis changed to AD at follow up. Volumetric 3D MPRAGE or equivalent T1-weighted 1.5 Tesla images are available at ADNI, with 1.25×1.25×1.2 mm resolution; acquisition parameters are reported elsewhere (Mueller et al., 2005). FDG-PET scans: Subjects were injected with 5 mCI F18-FDG 30 minutes prior to FDG-PET scanning, and six 5-minute frames were acquired by the ADNI consortium.

Image Processing

In our laboratory ADNI PET frames were co-registered to eliminate the effects of motion, an average image was generated and then intensity normalized such that the average of voxels within the subject’s mask is exactly one. The average image was nonlinearly warped into MNI152 space using SPM5 software toolbox, with 2mm isotropic voxels and 79×95×69 (in x y z) matrix size. Regional FDG uptake was normalized by the subject’s cerebellar reference uptake. GM brain regions were parcellated from all subjects’ T1-MRI scans using an atlas-based parcellation scheme (SPM(Klauschen et al., 2009), IBASPM(Alemán-Gómez et al. 2005)) to extract 116 regions of interest (ROIs). The T1 image tissue segmentations in 1-mm isotropic MNI space were used to create a normalized atlas, and the FDG PET images were resliced to matching resolution in SPM. The MNI atlas was then applied to the resliced FDG to calculate signal mean for each of the 116 regions. Twenty-six cerebellar regions were removed, giving regional statistics on 90 regions covering the cerebrum with no gaps. Connectomes from healthy HARDI scans were extracted using previously described methodology (Kuceyeski et al., 2013), which included Q-ball reconstruction followed by probabilistic tractography seeded at the gray-white interface voxels of the parcellated ROIs, with 1000 streamlines drawn per seed voxel. Each streamline is assigned a probability score (Iturria-Medina et al. 2008) and connection strength is estimated by summing the probabilities of the streamlines terminating in the two regions. A combined connectivity matrix C is then obtained by averaging across healthy subjects.

Model validation against ADNI data

Normalized atrophy of each ADNI subject was computed in terms of regional z-score of volume with respect to age-matched ADNI normal, such that for subject k and brain region i,

$$z_k(i)=\frac{t_k(i)-{\mu }_h(i)}{{\sigma }_h(i)}$$

where μ_n(i), σ_n(i) are the ADNI healthy controls’ mean and standard deviation of volume of region i. Since only the highest positive values denote atrophy, the z-scores were converted into a positive atrophy measure in [0,1) via the well-known logistic transform

$${\psi }_k(i)=\frac{1}{e^{-z_k(i)/\sigma }+e^{z_k(i)/\sigma }}$$

where the parameter σ controls the steepness of the logistic function. Analogous formulas govern regional hypometabolism statistics obtained from FDG-PET maps. These statistics are vectorized over all regions, to give measured atrophy vectors ψ_k for all subjects k. All regional statistics, whether measured or predicted, were mapped within the brain using a “glass brain” rendering using in house open source MATLAB Brainography toolkit (LoCastro et al., 2013).

Development of a Predictive Network Diffusion Model of Dementia

The connectivity matrices above define a network or graph 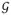= { 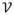, 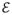} whose nodes v_i ∈ 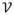represent grey matter structures, and edges e_i,j ∈ 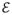represent fiber connectivity. The burden of disease-causing proteinopathic agent is represented by the vector x(t) = {x(v, t), v ∈ 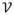} at time t at each node. It was proposed in (Raj et al., 2012) that dementia progression into this network in a diffusive manner is captured by a so-called “network heat equation”(Lafferty Kondor, 2002)

$$\frac{d\mathbf{x}(t)}{dt}=-\beta \mathrm{H}\mathbf{x}(t)$$ (1)

where H is the graph Laplacian matrix whose entries are given, for all node labels i, j, j′, by

$$H_{i,j}=\{\begin{array}{c}-c_{i,j}\mathit{for}i\ne j\mathit{and}{c}_{i,j}\ne 0\\ {\sum }_{i,j^{\prime }:e_{i,j^{\prime }}\in \mathcal{E}}{c}_{i,j^{\prime }}\mathit{for}i=j\\ 0\mathit{otherwise}\end{array}$$

This is the graph-equivalent of the Laplacian diffusion operator Δx ≜ ∇²x. Since all brain regions are not the same size, each row and column of the Laplacian is normalized by their sums. This diffusion model captures trans-neuronal propagation as a connectivity-rather than distance-based process, enacted via active axonal transport followed by membrane- or exocytotic-processes into extracellular space. Fiber length does not enter this model since there is no evidence that axonal transport efficiency is dependent on fiber length.

From matrix algebra, eq. (1) is satisfied by

$$\mathbf{x}(t)=e^{-\beta Ht}{\mathbf{x}}_0$$ (2)

where x₀ is the initial pattern of the disease process, on which the term e^−βHt acts essentially as a spatial and temporal blurring operator. We therefore call e^−βHt the diffusion kernel, and Eq (2) is interpreted as the impulse response function of the network. Since the above requires matrix exponentiation, it is solved via the eigen-decomposition of the network Laplacian H into a number of “eigenmodes” into which the diffusive process becomes trapped, and disease evolution will be governed by these eigenmodes:

$$\mathbf{x}(t)=U{e}^{-\mathrm{\Lambda }\mathrm{\beta }t}{U}^{†}{\mathbf{x}}_0={\sum }_{i=1}^N(e^{-\beta {\lambda }_{i}t}{\mathbf{u}}_i^{†}{\mathbf{x}}_0){\mathbf{u}}_i$$ (3)

The eigenvalues λ_i of the Laplacian H are in the interval [0,1], with a single 0 eigenvalue and a small number of near-zero eignevalues. Most eigen-modes u_i correspond to large eigenvalues that quickly decay due to exponentiation, leaving only the small eigen-modes that remain operative.

Relationship to atrophy/metabolism

The measurable phenotype (regional atrophy in MRI, hypometabolism in FDG-PET) in region k is assumed to be the consequence of the accumulation of pathology, hence it is modeled as the integral

$${\varphi }_k(t)={\int }_0^t{x}_k(\tau )d\tau$$ (4)

On the whole brain this gives $\mathbf{\Phi }(t)={\int }_0^t\mathbf{x}(\tau )d\tau$. These results are summarized from (Raj et al., 2012), and below we derive new results capturing the temporal dynamics of the model.

Prediction of future atrophy/metabolism

Expanding Eqs (3,4) via eigen-decomposition H = UΛU^†,

$$\mathbf{\Phi }(t)={\int }_0^t{e}^{-H\beta t}{\mathbf{x}}_{0}dt=U\frac{1}{\beta }{\mathrm{\Lambda }}^{-1}(I-e^{-\mathrm{\Lambda }\beta t})U^{†}{\mathbf{x}}_{\mathbf{0}}=U\mathit{diag}\left(\left\{\begin{array}{c}t,i=1\\ \frac{1-e^{-{\lambda }_{\mathrm{i}}\beta t}}{\beta {\lambda }_i},i>1\end{array}\right\}\right)U^{†}{\mathbf{x}}_{\mathbf{0}}$$

The last expression is necessitated by the fact that λ₁ = 0, which gives ${lim}_{{\lambda }_1\to 0}\frac{1-e^{-{\lambda }_1\beta t}}{{\lambda }_1\beta }=t$. Note also that early in the disease, ${lim}_{t\to 0}U\frac{1}{\beta }{\mathrm{\Lambda }}^{-1}(I-e^{-\mathrm{\Lambda }\beta t})U^{†}{\mathbf{x}}_{\mathbf{0}}=t{\mathbf{x}}_{\mathbf{0}}$. For tractability we assume that this relationship hold in all subjects, such that Φ(t_post−onset) ≈ t_post−onsetx₀, where t_post−onset is the time elapsed between disease onset and baseline scan. Then, for any time t > t_post−onset,

$$\mathbf{\Phi }(t)=\frac{1}{\beta t_{\mathit{post}-\mathit{onset}}}U\mathit{diag}\left(\left\{\begin{array}{c}\beta t,i=1\\ \frac{1-e^{-{\lambda }_{\mathrm{i}}\beta t}}{{\lambda }_i},i>1\end{array}\right\}\right)U^{†}{\mathbf{\Phi }}_{\mathit{baseline}}$$ (5)

We perform prediction of future atrophy and hypometabolism in patients using Eq (5).

Relationship between atrophy and its rate of change

From the above, we have

$${\mathbf{x}}_{\mathbf{0}}=\beta U\mathit{diag}\left(\left\{\begin{array}{c}1/\beta t,i=1\\ \frac{{\lambda }_i}{1-e^{-{\lambda }_{\mathrm{i}}\beta t}},i>1\end{array}\right\}\right)U^{†}\mathbf{\Phi }(t)$$

Thus,

$$\frac{d\mathbf{\Phi }(t)}{dt}=e^{-H\beta t}{\mathbf{x}}_0=\beta U\mathit{diag}\left(\left\{\begin{array}{c}\frac{1}{\beta t},i=1\\ \frac{{\lambda }_i{e}^{-{\lambda }_{\mathrm{i}}\beta t}}{1-e^{-{\lambda }_{\mathrm{i}}\beta t}},i>1\end{array}\right\}\right)U^{†}\mathbf{\Phi }(t)\triangleq \beta \stackrel{\sim }{H}(\beta t)\mathbf{\Phi }(t)$$ (6)

Thus, the network diffusion model deterministically predicts that the atrophy or hypometabolism at any time point and their rate of change are related via the matrix H̃(βt).

Non-networked models – sigmoid and exponential

The exponential growth model is mathematically given by $\mathbf{\Phi }(t)\propto exp\left(\frac{t}{a}\right){\mathbf{\Phi }}_0$, and the sigmoid by $\mathbf{\Phi }(t)\propto \frac{1}{exp\left(\frac{t}{a}\right)+exp\left(-\frac{t}{a}\right)}{\mathbf{\Phi }}_0$. However, it is known that different brain regions and different subjects experience atrophy, hypometabolism and pathology at different time points, hence we allow different subjects and brain regions to be placed at different points along the above curves, such that for region j of subject k, we hypothesize

$$\begin{array}{c}{\mathit{\Phi }}_{j,k}(t)\propto exp\left(\frac{t-t_{j,k}}{a}\right){\mathit{\Phi }}_{j,k}^0(\text{exponential})\\ {\mathit{\Phi }}_{j,k}(t)\propto \frac{1}{exp\left(\frac{t-t_{j,k}}{a}\right)+exp\left(-\frac{t-t_{j,k}}{a}\right)}{\mathit{\Phi }}_{j,k}^0(\mathit{sigmoid})\end{array}$$

where t_j,k is the time since disease onset of region j in subject k. Thus all subjects and regions are hypothesized to fall on the same growth curve with a single scale parameter a, albeit different temporal location t_j,k. Note that neither non-networked model formula involves connectivity, since they assume localized progression.

The corresponding relationship predicted by the exponential model is, by definition, $\frac{d{\mathit{\Phi }}_{j,k}(t)}{dt}\propto {\mathit{\Phi }}_{j,k}(t)$. It can be shown that the sigmoid model would predict that $\frac{d{\mathit{\Phi }}_{j,k}(t)}{dt}\propto {\mathit{\Phi }}_{j,k}(t)(max({\mathit{\Phi }}_{j,k})-{\mathit{\Phi }}_{j,k}(t))$ - an analytic result that appears to have been reproduced statistically in an earlier thorough investigation of longitudinal behavior of amyloid PET data (Jack et al., 2013). In that paper a B-spline fitting procedure revealed that an “inverted U” shaped curve best described the relationship between amyloid burden at baseline and its rate of change. The quadratic expression above would predict exactly this curve shape.

Estimating unknown model parameters

For prediction of individual subjects, two unknown parameters must be estimated for each subject: the time between onset and baseline scan t_post−onset and the rate constant of network diffusion β. We do this by fitting these parameters to measured regional slope data, using the baseline-slope relationship given by Eq (6). Denoting y(βt) ≜ H̃(βt)ψ_baseline, we estimate:

$$\widehat{\beta t}={\mathit{argmax}}_{\beta t}\{\mathit{corr}(\mathbf{y}(\beta t),\frac{\mathit{\Delta }\mathbf{\psi }}{\mathit{\Delta }t})\}$$

where corr(·, ·) refers to the Pearson correlation coefficient between two vectors, ψ is the measured atrophy or hypometabolism of the given subject and $\frac{\mathit{\Delta }\mathbf{\psi }}{\mathit{\Delta }t}$ is the measured slope. Then the rate constant β is given by the best estimate of the scaling required for the fit:

$$\widehat{\beta }=\frac{\mathbf{y}{(\widehat{\beta t})}^T}{\mathbf{y}{(\widehat{\beta t})}^T\mathbf{y}(\widehat{\beta t})}\frac{\mathit{\Delta }\mathbf{\psi }}{\mathit{\Delta }t}$$

Finally,

$$t_{\mathit{post}-\mathit{onset}}=\frac{\widehat{\beta t}}{\widehat{\beta }}$$

CSF biomarkers analysis

CSF biomarker levels of amyloid, tau and p-tau were obtained from the ADNI database, and subsequently their prediction ability of ND model parameters was investigated using Pearson correlation. The statistics of CSF biomarkers was also investigated within dichotomized groups (based on diagnosis, APOE status and baseline CSF biomarker level), as described in Results. Histograms were fitted to exponential distributions using MATLAB’s expfit() function, and its mean parameter obtained, as enumerated in Supplemental Figures 3–5.