Rigid-body motion correction of the liver in image reconstruction for golden-angle stack-of-stars DCE MRI

Abstract

Purpose

Respiratory motion can affect pharmacokinetic perfusion parameters quantified from liver DCE-MRI. Image registration can be used to align dynamic images post-reconstruction. However, intra-image motion blur remains after alignment and can alter the shape of contrast-agent uptake curves. We introduce a method to correct for inter- and intra-image motion during image reconstruction.

Methods

16 liver DCE-MRI examinations of 9 subjects were performed using a golden-angle stack-of-stars sequence. For each examination, an image time series with high temporal resolution but severe streak artifacts was reconstructed. Images were aligned using region-limited rigid image registration within a region of interest covering the liver. The transforms resulting from alignment were used to correct raw data for motion by modulating and rotating acquired lines in k-space. The corrected data was then reconstructed using view-sharing.

Results

Portal-venous input functions extracted from motion-corrected images had significantly greater peak signal enhancements (mean increase: 16%, t-test, p ≪ 0.001) than those from images aligned using image registration after reconstruction. Also, portal-venous perfusion maps estimated from motion-corrected images showed fewer artifacts close to the edge of the liver.

Conclusion

Motion-corrected image reconstruction restores uptake curves distorted by motion. Motion correction also reduces motion artifacts in estimated perfusion parameter maps.

Introduction

The liver is supplied by blood from the hepatic artery and the portal vein. Arterial and portal-venous perfusion can provide different pieces of information about the state of the liver. Increases in the size of intrahepatic tumor subvolumes that demonstrate elevated arterial perfusion have been shown to predict tumor progression during radiotherapy (1) whereas portal-venous perfusion of normal liver parenchyma has been correlated with local and global liver function used to help assess the risk of radiation-induced liver disease (RILD) (2–5).

Liver perfusion can be quantified using dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) (6). However, tissue motion during dynamic imaging, due to processes including breathing, peristalsis and heartbeat, can result in a given voxel not covering the same piece of tissue throughout an examination. This may lead to corruption of the contrast-agent (CA) uptake curves for imaged voxels, potentially confounding the analysis and mapping of perfusion parameters calculated from abdominal DCE images. In addition to spatial mismatch, motion can cause image blurring, signal loss, and other artifacts, such as streaks. The resulting uptake curves may then exhibit oscillations and spurious peaks that are not related to the CA dynamics, or they may have their amplitudes and shapes systematically altered by motion-induced partial volume effects.

To counteract the effects of motion, liver DCE-MRI has been acquired during repeated breath holding (5). However, some subjects may fail to hold their breath for a sufficient amount of time to sample the arterial and portal-venous input functions. Also, deep inhales taken in between breath holds introduce gaps in the CA uptake curves and such gaps may conceal important uptake-curve features. If a subject is instead asked to breathe freely during a DCE examination, large bulk motion as well as severe motion blur will often be observed. Consequently, it is necessary to compensate for motion as a part of image reconstruction or post-processing.

Region-limited rigid image registration has previously been used to align moving organs in images from DCE-MRI (7). However, motion-induced image blur still remains after image alignment if temporal resolution is insufficient. A high temporal resolution is also needed to faithfully capture the CA uptake dynamics. Therefore, extensive efforts have gone into developing imaging methods that can acquire images faster without sacrificing spatial resolution. Many of these imaging methods use stack-of-stars or stack-of-spirals sampling schemes combined with view sharing, parallel imaging or compressed sensing to push the boundary of spatiotemporal resolution (8–11) or to produce more benign artefacts, such as blurring, rather than streaks and ghosts (12–15). Yet, even at the high temporal resolutions seen to date, some intra-image motion blur can persist. To compensate for such motion-induced artifacts within an image, respiratory self-gated k-space data has been corrected for translation by minimizing the regional image entropy (16,17).

In this work we introduce a method to correct for inter- and intra-image motion as a part of the image-reconstruction process. We first propose a motion signal generated from rigidly aligning images reconstructed from severely undersampled data. In this context, undersampling supports image creation with a temporal resolution sufficient to resolve the breathing cycle. Secondly, the motion signal, consisting of a time series of rigid transforms (translation and rotation), is used to correct k-space data for rigid motion. Finally, the corrected data is reconstructed into DCE-MRI time series using temporal view sharing. The method is evaluated by comparing portal-venous input functions and portal-venous perfusion maps derived from images reconstructed from motion-corrected k-space data to those derived from images aligned using image registration after reconstruction.

Theory

In MRI acquisition, the raw samples collected in k-space by an imaging sequence can be interpreted as samples of the Fourier transform, s(k) = ℱS(k), of a sought image, S(r), where k = (k_x, k_y, k_z)^T is a position in k-space and r = (x, y, z)^T a position in image space. If motion occurs during acquisition, the image S(r, t) and its Fourier transform s(k, t) will depend on time. Affine motion can be thought of as a dynamic spatial transformation of a motionless image S̃(r) such that

$$\stackrel{\sim }{S}(\mathbf{r})=S(A(t)\mathbf{r}+\mathbf{b}(t),t)$$ (1)

where A(t) is a time-dependent 3×3 transformation matrix and b(t) is a time-dependent translation vector. For the case of rigid-body motion, A(t) is a rotation matrix. In k-space, the effect of the transformation in (1) is a combination of a linear transformation of k and a signal modulation. Dropping the t for notational simplicity, the Fourier transform s̃(k) = ℱS̃(k) can be written (16–18) as

$$ℱ(\mathbf{r}\mapsto S(A\mathbf{r}+\mathbf{b}))(\mathbf{k})=\text{exp}(2\pi i\mathbf{b}·A^{-\mathrm{T}}\mathbf{k})\times \frac{1}{|\text{det }A|}s(A^{-\mathrm{T}}\mathbf{k}).$$ (2)

Therefore, a motion-corrupted sample s_i = s(k_i) collected at position k_i can be transformed into a motion-corrected sample s̃_i with apparent sample position k̃_i using the following relations.

$${\stackrel{\sim }{s}}_i=\text{exp}(2\pi i\mathbf{b}·{\mathbf{k}}_i)s_i$$ (3)

$${\stackrel{\sim }{\mathbf{k}}}_i=A^{\mathrm{T}}{\mathbf{k}}_i$$ (4)

Equations (3) and (4) provide means to correct motion-corrupted k-space data before reconstruction if A(t) and b(t) are known.

Methods

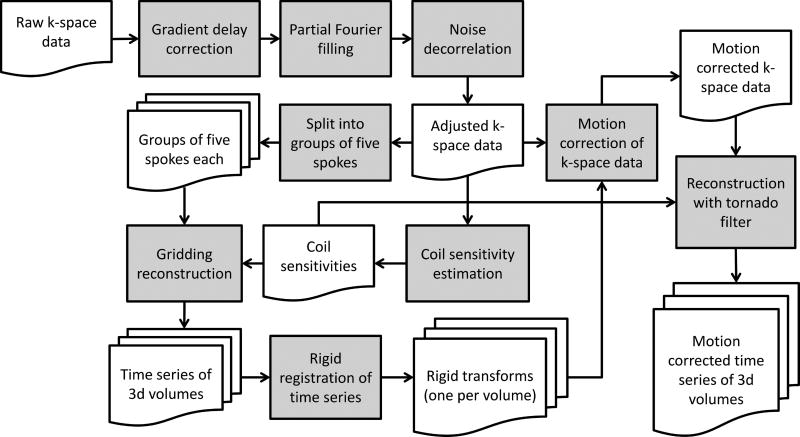
A framework to perform motion-corrected reconstruction of a DCE-MRI time series from k-space data acquired by a gradient-echo stack-of-stars sequence with golden-angle sampling is illustrated by the flowchart in Fig. 1. The framework consists of five major processing steps: 1) pre-processing of raw k-space data, 2) reconstruction of dynamic images with high temporal resolution, 3) creation of a motion signal (A(t), b(t)) through image registration of the high temporal resolution images, 4) motion correction of k-space data, and 5) final reconstruction of the 3D time series with a tornado filter (19). The different components of the processing pipeline are described in the following subsections.

FIG. 1.

Motion-corrected image reconstruction pipeline. The raw k-space data from the MRI scanner (upper left corner) is reconstructed into a motion-corrected DCE-MRI time series (lower right corner).

Imaging

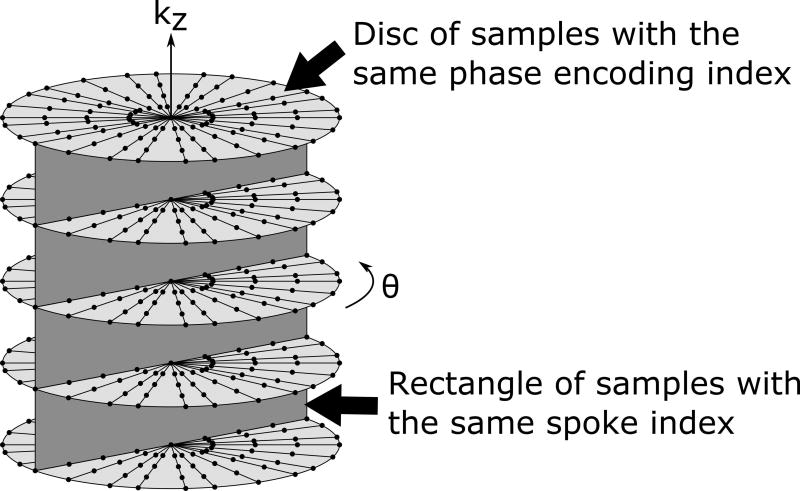
A prototype gradient-echo stack-of-stars sequence with golden-angle sampling (Radial VIBE, Siemens Healthineers, Erlangen, Germany) was used for scanning (20,21). This sequence was provided as a work-in-progress package by the vendor for evaluation. As the sampling pattern illustrated in Fig. 2 shows, radial readout lines are acquired in the x-y plane with a golden angle scheme while Cartesian phase encoding is performed in the k_z direction. Also, readout lines at each angle are acquired for all k_z values before progressing to the next angle, as illustrated by the dark gray rectangle in Fig. 2. The lines in this rectangle are collectively referred to as a spoke. The sampling pattern was oriented such that radial sampling was parallel to the transverse plane and Cartesian sampling was along the superior-inferior direction in k-space.

FIG. 2.

Golden-angle stack-of-stars k-space sampling pattern used by the Radial VIBE sequence. Straight black radial lines represent readout lines in k-space. The top light gray disc touches all lines belonging to one particular k_z phase encoding index and the vertical dark gray rectangle touches all lines with a particular spoke index.

Reconstruction with high temporal resolution

Raw data was collected from the scanner and partitioned into successive groups of 5 spokes. A three-dimensional volume was reconstructed using gridding (22,23) for each group of spokes. Prior to gridding reconstruction, a number of adjustments were made to the raw data. Small gradient delays have little effect on Cartesian imaging but can lead to artifacts for radial sampling schemes if not corrected for (24). Therefore the gradient delay was estimated by fitting a straight line to the phase difference of radial readout lines acquired in almost opposite direction. The slope of this line is proportional to the size of the gradient delay. As an approximation, this delay was assumed to be independent of the readout direction. Readout lines were corrected by shifting them along the readout direction such that the slope of the phase difference became zero. Missing k-space lines were synthesized using an iterative partial-Fourier reconstruction method (25). The noise covariance for the receiver coils was estimated using samples collected at the edge of k-space. The resulting covariance matrix was then used to perform a whitening transform of the collected data. The result of this noise decorrelation was to produce a set of synthetic coil signals with independent noise (26). These synthetic coil signals were then used in place of the original signals. A seven-grid-sample-wide cubic Kaiser-Bessel kernel was used for gridding. The k-space grid was oversampled by 37.5 percent compared to the inverse of the nominal field of view (22). Coil images were combined for optimal signal-to-noise ratio using estimated coil sensitivity profiles (27). These profiles were estimated by dividing coil images reconstructed from 500 spokes at the latter half of the examination with the root-sum-of-squares image. Each reconstructed volume was assigned a timestamp equal to the timestamp of the acquisition line passing through the center of k-space for the third spoke in its five spoke group.

Image registration

The reconstructed time series was aligned using region-limited rigid registration with a mutual information metric defining the optimization cost function for alignment. Because of the severe aliasing caused by using only five spokes, simple registration to one reference 3d image was not sufficient. Instead each image was registered to twenty other randomly selected images within the high-temporal-resolution time series to form an overdetermined system of transform equations. This system was then solved in the L_1/2 sense using iteratively reweighted least squares (IRLS) (28) to reject outlier transforms caused by bad alignments (29). The registration metric was only evaluated within an ROI drawn to cover the liver as it appeared in a reference volume previously selected by a physician to use for radiation therapy treatment planning guidance due to its lesion contrast. The registration produced a set of rigid transforms describing the relative position and orientation of the liver in each volume with respect to the reference volume.

Raw data motion correction

The transform time series produced by registration was interpolated using the matrix logarithm (30) to form one rigid transform for each spoke. The matrix logarithm was used to produce a smooth rigid body motion in 3d space. The acquired k-space data was then corrected for motion using equations (3) and (4). Data from each coil was corrected separately and no correction for the shift of the coil sensitivity profiles with respect to anatomy was applied.

Reconstruction with tornado filter

The radial sampling schemes used leads to a denser sampling of the center of k-space than the outer parts. After motion correction the raw data was reconstructed into a time series using a tornado filter (19) that included temporally neighboring samples to ensure that the sampling density met the Nyquist criterion for a majority of k-space. The tornado filter therefore compensates for the difference in sampling densities between the center and outer parts of k-space by sharing samples from neighboring temporal views thereby reducing aliasing at the cost of reduced temporal resolution for higher spatial frequencies. The number of spokes needed for k-space to be fully sampled was determined by the single spoke density compensation weights, ν(k), which equals the k-space volume of a semicylindrical shell with central radius |k| and with height and shell width equal to the sample spacing in the longitudinal and radial directions respectively. To reduce ringing, the effective resolution of the image was reduced slightly below the resolution of the nominal voxel size by reducing the weights with a Gaussian k-space window

$$G(\mathbf{k})=e^{-2\pi {\sigma }^2{\Vert \mathbf{k}\Vert }^2}$$ (5)

with σ = 1/3 voxels, such that a new density compensation w₀(k) = ν(k)G(k) is formed. With respect to time the tornado filter was not a rect-function as in (19) but had the shape of a truncated Gaussian

$$T(\mathbf{k},j)=\frac{w_0}{w}\text{exp }(-\pi {\left(\frac{j-j_0}{w}\right)}^2)\text{ rect }\left(\frac{j-j_0}{w_{\mathit{\text{max}}}}\right)$$ (6)

where j is the spoke index and j₀ the index of the centermost spoke of the current volume being reconstructed. The width w of the Gaussian in Eq. 6 was given by

$$w(\mathbf{k})={(\frac{1}{w_0^2+w_{\mathit{\text{min}}}^2}+\frac{1}{w_{\mathit{\text{max}}}^2})}^{-1/2}$$ (7)

such that the width was never below w_min = 21 spokes or above w_max = 144 spokes. Filter weights were calculated based on the golden angle sampling pattern and no corrections of the weights were applied for the shift of apparent sample locations caused by motion correction. Aside from correcting the data for motion and replacing the 5-spoke sliding window filter with a tornado filter, other parts of the reconstruction chain, such as partial Fourier reconstruction and optimal coil combining, were identical to those used for reconstruction of images with high temporal resolution.

Evaluation

Under institutional review board approval, 16 DCE-MRI examinations with raw k-space data from 9 patients were included in this study (women, 2; men, 7; age at examination, 48–76; number of examinations per patient, 1–3). As the study investigates the possibility of individualized adaptive radiotherapy for hepatocellular carcinoma, all subjects had tumors in the liver. Subjects were scanned for about 5 min on a 3 T MRI scanner (Magnetom Skyra, Siemens Healthineers, Erlangen, Germany) while breathing freely. After 30 s of scanning 20 ml (0.5 M) of a Gd-BOPTA-based contrast agent (MultiHance, Bracco Diagnostics Inc., Monroe, NJ) was administered intravenously. Sequence parameters are shown in Table 1. They were allowed to vary slightly among patients to ensure liver coverage and avoid system-reported patient-heating issues.

Table 1.

Sequence parameters used for DCE-MRI imaging with Radial VIBE.

Sequence Parameter	Value
Echo time	1.16 ms–1.22 ms
Repetition time	2.72 ms–4.00 ms
Flip angle	11°–14°
Image matrix size	192×192
Number of slices	64
Number of phase encoding steps	46
Number of radial spokes	2000
Voxel size, in-plane (transversal)	2 mm–2.3 mm
Slice thickness	3 mm–4 mm

Images reconstructed with our motion-corrected reconstruction algorithm were compared to images reconstructed without motion correction but aligned in the image domain after reconstruction using region-limited rigid-body image registration (29). Two sets of images without motion correction were used for this purpose. The first set was reconstructed identically to the motion corrected images but with A(t) = I and b(t) = (0,0,0)^T, i.e. assuming no subject motion. The second set of images was reconstructed by vendor software on the scanner employing KWIC (12) without motion correction.

For each set of images, time series portal-venous input functions were extracted and portal-venous perfusion maps estimated using a dual-input single-compartment perfusion model (6). The portal-venous perfusion maps were compared across the reconstruction algorithms qualitatively. Also, the maximum signal enhancement was determined for each extracted portal-venous input function and used as a quantitative evaluation metric. This metric was chosen because the portal vein is a small structure that appears brighter than surrounding liver tissue before contrast administration and darker than surrounding tissue after administration. Therefore motion-induced blurring will reduced the signal enhancement from pre- to post-contrast images. The arterial input function used for perfusion estimation was measured in the aorta, which moves less than the liver during breathing, and thus was extracted from images that were not motion corrected or registered.

Reconstruction of motion states

Images showing the different states of the breathing cycle can be used to characterize the spatial transformation that organs undergo. In order to reconstruct images representative of the average configuration and position of the liver at various points in the breathing cycle, the range of values for the translational displacement of the liver in the superior-inferior direction was divided into five intervals of equal length. Motion corrected raw data was then sorted according to what interval it belonged to and one motion state was reconstructed from all spokes in each interval. The inhale motion states were aligned to the exhale states with deformable registration using NiftyReg(31). The resulting deformation vector fields then show the residual deformation after rigid alignment. The median as well as the 95 percentile of the magnitude of the residual displacement was determined for each patient.

Results

Image registration

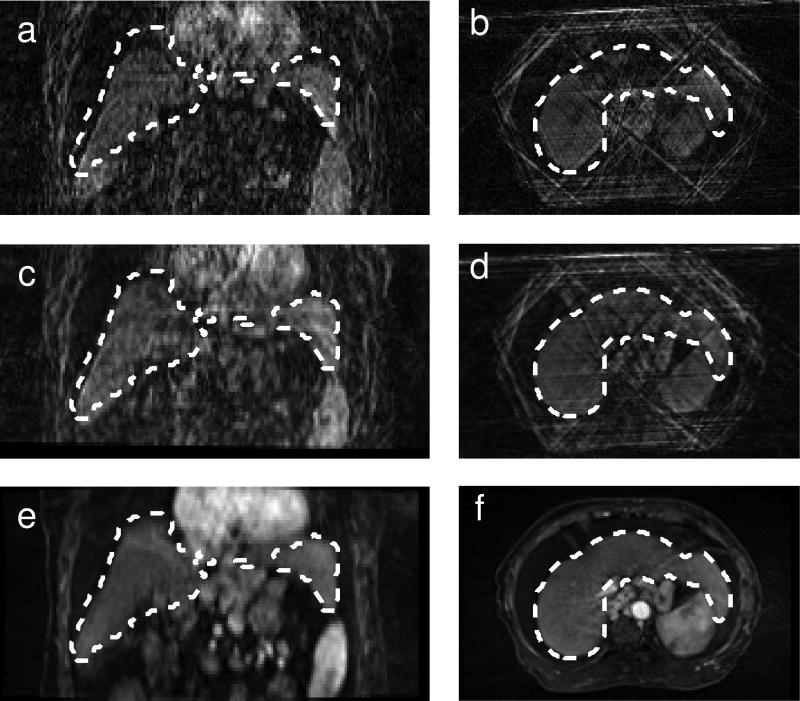
Images reconstructed from five spokes showed streak artifacts due to undersampling. However, the image quality was still sufficient for rigid alignment as seen in Fig. 3.

FIG. 3.

Example of images reconstructed from five spokes before (a, b) and after (c, d) registration. The reference volume on which the liver ROI used for registration was drawn (e, f) is also shown. This reference image was reconstructed without motion correction from a large number of spokes. The dashed white line shows the position of the liver in the reference volume.

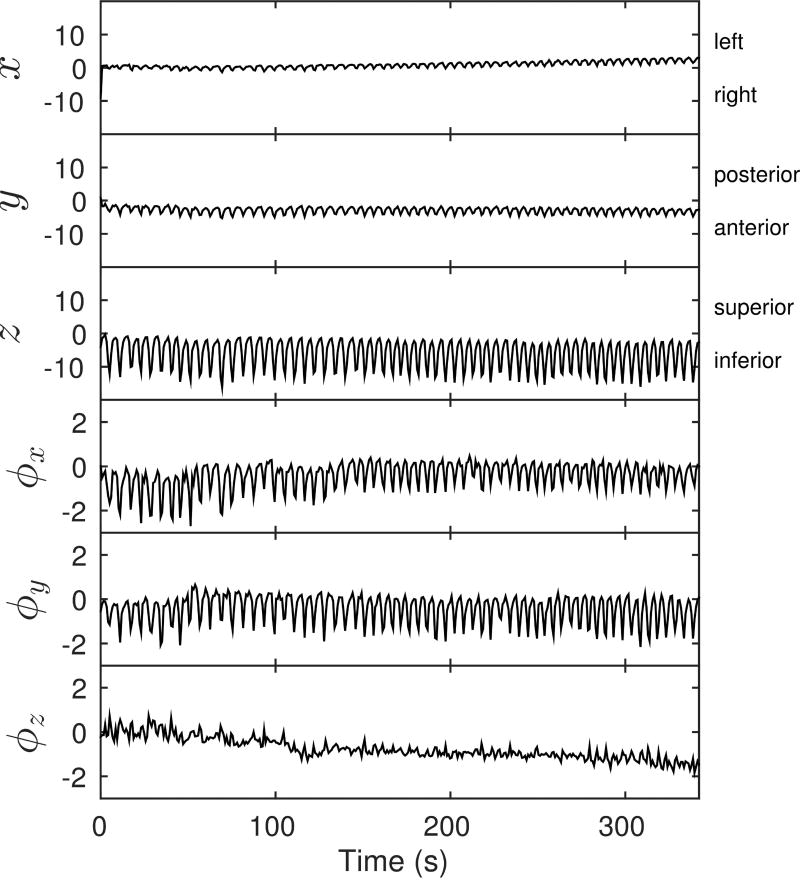
An example of a motion signal measured from a subject is shown in Fig. 4. The largest translational motion is seen along the superior–inferior direction and the largest rotational motions occur about the anterior–posterior and left–right axes. The mean range of motion measured from all studies is listed in Table 2.

FIG. 4.

Rigid-body motion signal components with respect to time. The first three components (x, y and z – left, posterior and superior in mm) describe the 3D translation of the center of the liver. The last three components (ϕ_x, ϕ_y and ϕ_z in degrees) are the elements of an axis-angle representation of the rotation in degrees.

Table 2.

The population means and standard deviations of the within-examination motion ranges for different modes of motion.

Type of motion	Mean range (standard deviation) of motion
Translation, left–right, x	3.6(1.1) mm
Translation, posterior–anterior, y	9.1(4.2) mm
Translation, superior–inferior, z	19.9(9.1) mm
Rotation, sagittal plane, ϕx	4.2(1.8)°
Rotation, coronal plane, ϕy	4.0(2.0)°
Rotation, transverse plane, ϕz	3.3(1.3)°

Reconstruction using the tornado filter

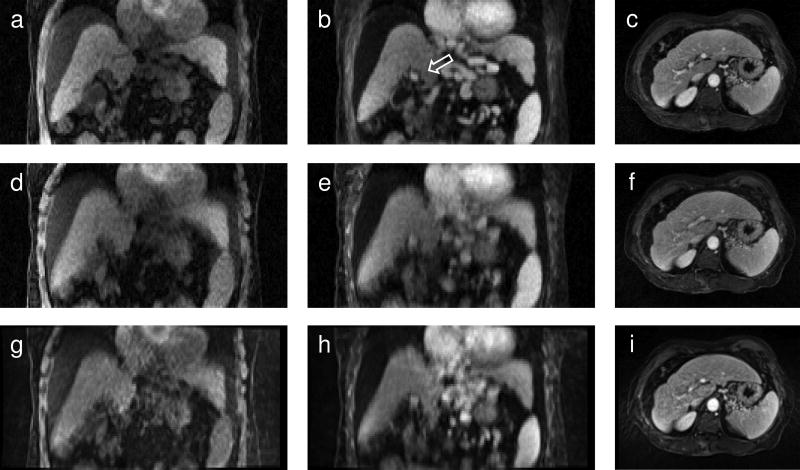
The effect of k-space motion correction on images reconstructed with the tornado filter is seen in Fig. 5a–f. The same images reconstructed by the vendor software on the scanner are also shown (Fig. 5g–i). The k-space motion corrected images exhibit less motion blur, particularly at the dome and inferior tip of the liver, and for small structures, e.g., the portal vein (Fig. 5b). The images reconstructed on the scanner show similar motion artifacts to those from the uncorrected tornado reconstruction.

FIG. 5.

Images reconstructed using the tornado filter with k-space motion correction (a, b, c) and without motion correction (d, e, f).Vendor-reconstructed images are shown in (g) through (i). The left column (a, d, g) shows pre-contrast and the middle column (b, e, h) post-contrast images in the coronal plane for one subject. The arrow in (b) points to the portal vein which appears as a bright spot. The right column (c, f, i) shows how motion artifacts appear in the transverse plane for another subject. Streak and motion artifacts in (i) obscure the portal vein. In (f) streak artifacts are reduced by the tornado filter and in (c) motion correction further enhances the contrast between the portal vein and surrounding tissue.

Impact on measured contrast dynamics and perfusion maps

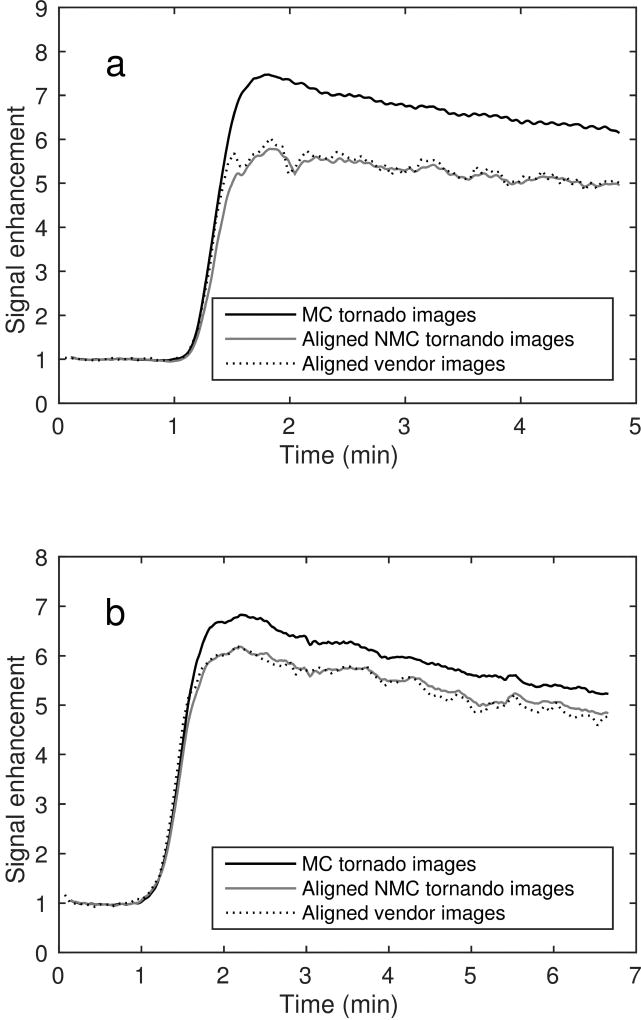
Fig. 6 shows the time–intensity curves of an ROI drawn to determine the portal-venous input function (PVIF) for two subjects. The signal enhancement compared to the baseline is larger for the motion-corrected images than for the uncorrected ones due to reduced motion-induced partial-volume effects. The maximum signal enhancement from the pre-contrast baseline to the peak of the portal-venous input function was determined for each patient with and without motion correction. For all examinations the maximum signal enhancement was higher for the motion corrected input function (mean increase: 16%, range of increase: [5%, 35%], 95% confidence interval of the mean increase: [12%, 20%]). The mean increase of the signal enhancement was significantly higher (significance level: 5%) for motion corrected images (Student’s t-test, p ≪ 0.001). Similar results were found when comparing motion-corrected to vendor-reconstructed images (mean increase: 20%, p ≪ 0.001). No significant difference was found between the mean maximum signal enhancements for the vendor-reconstructed images and the tornado-reconstructed images without motion correction (mean difference: −2%, p = 0.3).

FIG. 6.

Portal-venous input functions from two different patients are shown in (a) and (b). For each patient, input functions derived from motion-corrected (MC) and non-motion-corrected (NMC) images reconstructed with the tornado filter are shown as well as NMC images reconstructed by vendor software on the scanner. NMC images were aligned using rigid image registration before extraction of the input functions. Input function from MC images exhibit larger maximum signal enhancements and are smoother compared to their NMC counterparts. The temporal distance between images is about 1 s for the tornado images and about 3 s for the vendor images. However, the effective temporal resolution for the tornado images is about 7.7 s in the portal vein due to the width of the tornado filter.

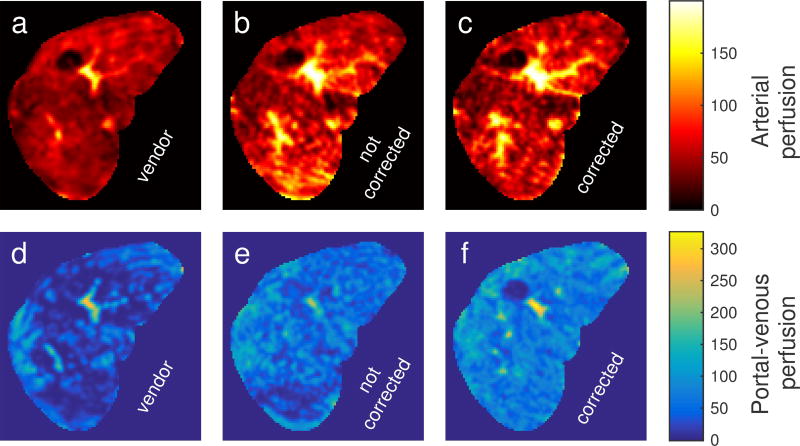
Transverse perfusion parameter maps for a subject are shown in Fig. 7. The motion-corrected PVIF and liver uptake curves produced a portal-venous perfusion parameter map (Fig. 7f) that differed markedly from the parameter maps produced by the uncorrected images (Fig. 7d–e). A prominent artifact in Fig. 7e is the low perfusion in the posterior part of the liver (bottom of image). Here, motion of surrounding tissue into and out of the liver ROI causes an erroneous estimated reduced venous perfusion. Similar perfusion bias artifacts were observed for several of the subjects included in this study.

FIG. 7.

Transverse arterial (a–c) and portal-venous (d–f) perfusion maps calculated from DCE-MRI time series reconstructed by vendor software on the scanner without (first column), by a tornado filter without motion correction (second column) and by a tornado filter with motion correction (third column) for a subject. The portal-venous perfusion map in (e) exhibits severe artifacts caused by motion. Perfusion is given in ml/(100 ml · min).

Motion states

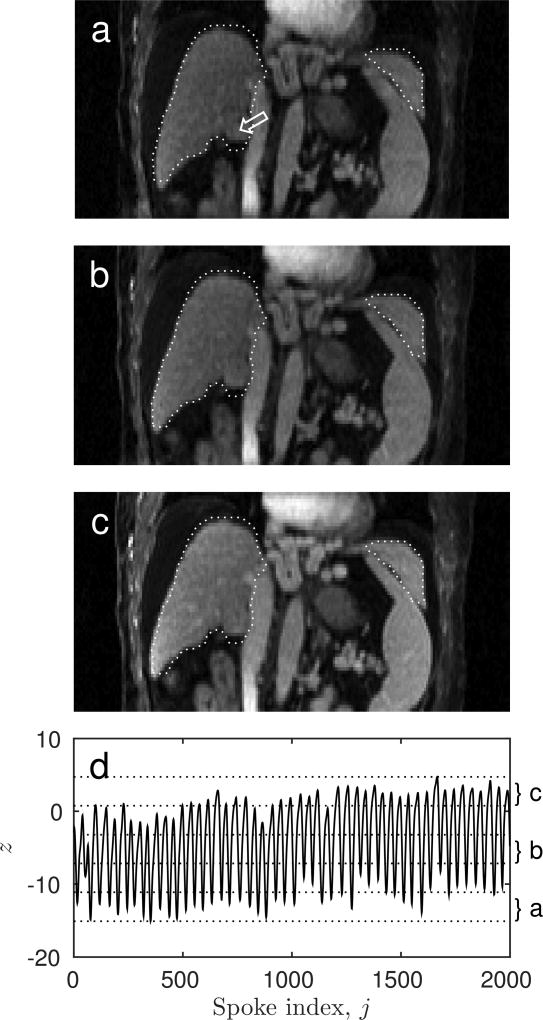
Three of the five reconstructed motion states for one subject are shown in Fig. 8. These motion states show sharp liver edges and internal structures. They also show that residual motion remains for the inferior tip of the liver after rigid-body motion correction. Because translation and rotation have been corrected for, the remaining modes of motion are the deformations that the liver undergoes during the breathing cycle, such as bending or compression. These cannot be corrected for using rigid-body registration, but require deformable image registration instead. The median residual displacement after rigid alignment as determined using deformable alignment was found to vary between 2.2 and 6.9 mm with a mean of 3.0 mm among patients. The 95th percentile of the residual displacement varied between 4.6 mm and 15.7 mm. For two examinations the 95th percentile of the residual displacement was larger than 10 mm. For 10 examinations the 95th percentile was larger than 6 mm or two voxels.

FIG. 8.

Three ((a) first, (b) third and (c) fifth) of five reconstructed motion states from an example subject as well as the superior-inferior motion that was used for sorting k-space data into states (d).The dotted white ROI indicates the liver contour in the reference volume. The white arrow in (a) points to the location of a tumor. Because the motion states were corrected for rigid-body motion the remaining differences are the result of deformations, such as bending.

Discussion

Respiratory motion introduces organ displacements as well as streaking and blurring into images reconstructed from DCE-MRI examinations. Unless corrected for, these effects can distort CA uptake curves and cause error in estimated perfusion parameter maps of the liver. Previous studies have shown that partitioning acquired spokes into smaller sets before reconstruction can help to reduce image blurring. The reduction in set sizes can be achieved by a higher temporal resolution or by introducing an extra motion-state dimension to complement the spatial and temporal dimensions. In both cases the reduction in set sizes must be accompanied by more advanced reconstruction methods such as through-time GRAPPA (10) or compressed sensing (9) to counteract the more severe streak artifacts that would otherwise result. Rather than partitioning acquired data into smaller sets, the presented study builds upon earlier work (16) to perform motion correction in k-space before reconstruction. Motion-corrected DCE-MRI k-space data can then be reconstructed into time series with arbitrary temporal resolution (14) or into dedicated arterial and portal-venous phase images without motion artifacts. In the radiation therapy clinic this versatility could produce an image time-series for perfusion estimation as well as a smaller set of images with less aliasing and noise for tumor delineation.

The robust image registration algorithm used to align the high-temporal-resolution images in this study was able to produce a rigid-body motion signal that reflected the semi-periodic pattern of respiratory motion despite the changing image contrast introduced by the contrast agent dynamics. Because the motion signal was derived from registration of each image in the whole time series it does not enforce periodicity in the breathing pattern. By applying the rigid-body motion correction to the acquired k-space data, time-series images with reduced motion blur were reconstructed. After motion correction, the portal-venous input functions demonstrated larger maximum signal enhancement for all of the DCE-MRI examinations in this study. This can be understood by considering that the portal vein is darker than surrounding liver tissue prior to CA administration. After administration it appears brighter due to its higher CA concentration. Motion-induced partial volume effects will therefore reduce the dynamic range of the signal enhancement in the portal vein. By correcting for motion, the higher signal enhancement of the portal vein is recovered. This ability to recover contrast lost due to blurring is an advantage over other free-breathing imaging techniques that attempt to reduce the severity of motion-induced artifacts by promoting motion blur over streaks and ghosting through temporal regularization (8) or view sharing (13) without motion correction. Since the motion of the portal vein is similar to that of the liver it is reasonable to assume that the signal enhancements of smaller structures, such as blood vessels and lesions, are also smeared due to breathing, leading to a potential loss of lesion contrast.

Only respiratory and slower motions as they affect the liver were characterized and corrected for in this study. Cardiac motion cannot currently be resolved by the presented technique and was therefore not corrected for. No assumption about the pattern of motion, such as periodicity, was assumed and the method was therefore also able to characterize and correct for slow drifts in liver position throughout the 5 min examination. Including other modes of motion such as cardiac and gastrointestinal in our motion model is a focus of future research.

Parameter maps estimated from motion-corrected images showed fewer motion artifacts than those from non-corrected images. Visually, the anatomic structure of the liver was more consistently represented on motion-corrected images. This was particularly true for the dome and lower tip of the liver that move in and out of regions covered by other organs with minimal contrast uptake and thus lower intensity.

Because the temporal width of the tornado filter depends on the distance from the center of k-space, the temporal resolution of different structures in the images will depend on their size and texture. At the center of k-space the temporal resolution will be about 3.2 s whereas the edge of k-space only will have a temporal resolution of about 22 s. Larger structure, like the aorta and homogenous pieces of liver will have a higher temporal resolution, whereas thinner arteries within the liver will have lower temporal resolution. This could affect uptake curves (10), especially for thin arteries but should have little effect for liver parenchyma where the uptake dynamics have already been filtered to a lower temporal frequency content, or for the aorta which is large enough to accurately reflect the more rapid changes in CA concentration. For the portal vein the effective temporal resolution is about 7.7 s. This is lower than what would be needed to represent the AIF from the aorta, but as the portal-venous input function contains less rapid dynamics, the initial rise and the slowly decaying plateau can be accurately represented at this resolution.

The coil sensitivity maps used to combine coil images were estimated using a rather simple method. Because these profiles were only used to combine coil images through voxel-wise weighting the only effect from errors in sensitivity is a small potential reduction in SNR. However if parallel-imaging techniques were to be included in the reconstruction method, more accurate sensitivity maps would be needed (32).

The rigid-body motion correction used in this work cannot compensate for deformations of the liver (such as bending). Nonetheless, it does correct for the majority of the displacement experienced by most parts of the liver and therefore improves the sharpness of reconstructed images. For most patients, the residual deformation as determined by deformable registration between inhale and exhale states was in the order of a voxel. However, for 2 examinations of 16, at least 5% of the liver showed residual motion larger than 10 mm. Residual nonrigid-body motion of this larger magnitude could influence perfusion quantification in the affected area. If needed, the motion corrected motion state images presented in this work could be used as a starting point for deformable registration and iterative model-based reconstruction (33). These motion state images exhibit less motion blur for inhale phases than their non-motion-corrected counterparts and could therefore provide sharper image details to help guide deformable image registration. Ongoing studies are investigating applications of such deformable motion correction. We have found that deformable alignment would be needed for about 13% and 60% of the examinations in this work in order to bring the 95th percentile of the residual displacement below 10 mm and 6 mm, respectively, for all examinations.

Conclusions

A framework for DCE-MRI time series reconstruction with rigid-body motion correction of the liver position and orientation was presented. A robust image-space registration procedure was used to produce a rigid-body motion signal that was insensitive to the CA uptake dynamics. Employed in the presented motion-corrected reconstruction algorithm for acquired k-space data, alignment helped reduce motion blur and large displacements in DCE-MRI time series of the liver. Consequently, partial volume effects were reduced and higher maximum signal enhancements were recovered for the portal-venous input functions for all DCE-MRI examinations in the study. In addition, motion correction reduced artifacts in estimated portal-venous perfusion maps, in particular for regions close to the edge of the liver. For 13% of subjects, at least 5% of the liver showed residual deformation in excess of 10 mm after motion correction. For these cases, the derived motion signal can be used to reconstruct sharpened breathing state images in preparation for image reconstruction with deformable motion correction.

Abbreviations

CA

contrast agent

DCE-MRI

dynamic contrast-enhanced MRI

FOV

field of view

Gd-BOPTA

gadobenate dimeglumine

MR

magnetic resonance

PK

pharmacokinetic

VIBE

volume interpolated breathhold examination