How Acidic Is Carbonic Acid?

Abstract

Carbonic, lactic, and pyruvic acids have been generated in aqueous solution by the transient protonation of their corresponding conjugate bases by a tailor-made photoacid, the 6-hydroxy-1-sulfonate pyrene sodium salt molecule. A particular goal is to establish the pK_a of carbonic acid H₂CO₃. The on-contact proton transfer (PT) reaction rate from the optically excited photoacid to the carboxylic bases was derived, with unprecedented precision, from time-correlated single-photon-counting measurements of the fluorescence lifetime of the photoacid in the presence of the proton acceptors. The time-dependent diffusion-assisted PT rate was analyzed using the Szabo–Collins–Kimball equation with a radiation boundary condition. The on-contact PT rates were found to follow the acidity order of the carboxylic acids: the stronger was the acid, the slower was the PT reaction to its conjugate base. The pK_a of carbonic acid was found to be 3.49 ± 0.05 using both the Marcus and Kiefer–Hynes free energy correlations. This establishes H₂CO₃ as being 0.37 pK_a units stronger and about 1 pK_a unit weaker, respectively, than the physiologically important lactic and pyruvic acids. The considerable acid strength of intact carbonic acid indicates that it is an important protonation agent under physiological conditions.

Graphical abstract

1. INTRODUCTION

In the present work, we describe our study of the relative reactivity of three important small carboxylate bases naturally occurring in the blood plasma: the bicarbonate, lactate, and pyruvate bases. The aqueous bicarbonate buffer comprises bicarbonate (HCO₃⁻), carbonate (CO₃²⁻), CO₂, and carbonic acid (H₂CO₃); it is the most important pH buffer in the blood plasma as well as in the world open seas and oceans. It helps to maintain the normal pH of the blood at about 7.4^1,2 pH units and stabilizes the pH of the surface ocean waters, which are currently at about the 8.0 pH units level.³ With the present study, we establish the relative acid strength of the corresponding carbonic, lactic, and pyruvic acids, and in particular, we establish the pK_a value for carbonic acid.

While lactic and pyruvic acids are stable acids in aqueous solution, carbonic acid decomposes reversibly in aqueous solutions to CO₂ and H₂O with a first-order rate constant corresponding to a lifetime of about 60 ms at room temperature.^4–6 For this reason, little is known about the chemical and biochemical reactivity of intact carbonic acid. In particular, the precise value of the equilibrium constant K_a of aqueous H₂CO₃ has been a subject of debate for many decades and is still under consideration.⁷ The precise value of carbonic acid’s K_a in combination with the pH value of a solution containing a known concentration of bicarbonate will allow determining the exact concentration of intact carbonic acid in this solution regardless of its instability.

Turning to pyruvate, its mean blood concentration in healthy subjects is 0.05 mM.⁸ Pyruvic acid (CH₃COCOOH) is the simplest of the α-keto acids, with a carboxylic acid and a ketone functional group. It supplies energy to living cells through the citric acid cycle (the Krebs cycle) when oxygen is present (aerobic respiration), and alternatively ferments to produce lactate when oxygen is lacking (fermentation).

In humans, lactate exists in the levorotatory isoform. The normal lactate concentration in the plasma is 0.3–1.3 mM.⁹ Such plasma concentrations represent a balance between lactate production and metabolism. Glycolysis in the cytoplasm produces the intermediate metabolite pyruvate. Under aerobic conditions, this pyruvate is converted after decarboxylation and release of CO₂ to acetyl CoA to enter the Krebs cycle, while under anaerobic conditions, it is converted by lactate dehydrogenase (LDH) to lactic acid. In the plasma, lactate is buffered by NaHCO₃ since it is typically at much smaller concentrations than bicarbonate (25 mM).

In order to elucidate the relative reactivities of the carboxylic bases, we have utilized the hydrogen transfer from a novel photoacid to the lactate, peruvate, and bicarbonate anions.

The use of time-resolved fluorescence spectroscopy allows determination of the intrinsic proton transfer (PT) rate from the photoacid 6-hydroxypyrene-1-sulfonate to the three carboxylate bases and thus establishment of the order of their chemical reactivity. The relative order of the K_a values of the three carboxylic acids can then be determined, with the assumption of a free energy relationship between the PT rate and ΔpK_a, the difference in the (negative logarithms of the) equilibrium constants of the photoacid and the various carboxylic acids. Finally, using the well-established K_a values of the photoacid and the lactic and pyruvic acids as anchor values pK_a(lactic) = 3.86 and pK_a(pyruvic) = 2.50,¹⁰ we have precisely determined the pK_a value of carbonic acid, our major goal.

The general outline of the remainder of this contribution is as follows. First, we describe in some detail the acid–base equilibria of carbonic acid and place the importance of its K_a value in perspective. Second, we characterize the photoacidity of a novel photoacid used in our experiments as the protonation agent of the carboxylate bases. We then describe how we have obtained from the time-resolved measurements the intrinsic PT rates within the various reaction complexes; these are the rates needed for the free energy correlation. Finally, we discuss first the general free energy correlation between rate and equilibria that we have found in PT reactions in aqueous solutions and then how we use and implement this correlation for the measured intrinsic PT rates in order to obtain carbonic acid’s pK_a value.

2. ACID–BASE EQILIBRIA OF CARBONIC ACID

2.1. Analytic and Experimental Considerations of the K_a of Carbonic Acid

The protolytic and decomposition reactions of carbonic acid (CA) in neutral and acidic solutions may be compactly written as

$${\mathrm{H}}_2\mathrm{O}+{\text{CO}}_2\rightleftarrows {\mathrm{H}}_2{\text{CO}}_3\rightleftarrows {\mathrm{H}}^{+}+{{\text{HCO}}_3}^{-}$$ (1)

Equation 1 does not depend on the mechanism but is sufficient for the definition of the equilibrium constant. An apparent pK_a value (pK_app) for CA of 6.35 ± 0.02 at 25 °C—which corresponds to the equilibrium constant involving also aqueous CO₂ in equilibrium with H₂CO₃, K_app = [H⁺][HCO₃⁻]/CO₂—has been routinely reported in chemistry textbooks.¹¹ However, the photolytic K_a value of CA which represents the fundamental proton dissociation reaction,

$$K_{\mathrm{a}}=[{\mathrm{H}}^{+}][{{\text{HCO}}_3}^{-}]/[{\mathrm{H}}_2{\text{CO}}_3]$$ (2)

is substantially larger than K_app

$$\begin{gathered} K_{\text{app}}=[{\mathrm{H}}^{+}][{{\text{HCO}}_3}^{-}]/\{[{\mathrm{H}}_2{\text{CO}}_3]K_{\mathrm{D}}\}=K_{\mathrm{a}}/K_{\mathrm{D}}, \\ {K}_{\mathrm{D}}=[{\text{CO}}_2]/[{\mathrm{H}}_2{\text{CO}}_3]\gg 1 \end{gathered}$$ (3)

In order to discuss the impact for the CA K_a value, we use the relation which follows from the definitions in eqs 2 and 3:

$$[{\mathrm{H}}_2{\text{CO}}_3]/[{\mathrm{H}}^{+}]=[{{\text{HCO}}_3}^{-}]/K_{\mathrm{a}}$$ (4)

Equation 4 allows the direct determination of the important value of the concentration ratio of carbonic acid and the proton, regardless of the decomposition of carbonic acid to CO₂ and H₂O. The ratio [H₂CO₃]/[H⁺] is much greater than 1 in the blood buffer and in the oceans. It only depends on the concentration of bicarbonate, which is very accurately known, and on K_a, whose exact value determination is the subject of this study.

From eq 3, we may write pK_a in the form

$$\mathrm{p}{K}_{\mathrm{A}}=\mathrm{p}{K}_{\text{app}}-log(K_{\mathrm{D}})$$ (5)

The value of the equilibrium constant K_D (defined in eq 3) is not known exactly and is the major reason for the difficulties in obtaining the exact value of K_a. It is generally accepted that the value of K_D lies between about 300 and 900.¹² Combination of these limiting values of K_D with the value of K_app¹¹—which may be accurately determined by simple analytic procedures such as pH measurements of aqueous solutions of bicarbonate—sets the limits for the acceptable value of K_a of H₂CO₃ at room temperatures (20 °C < T < 25 °C) at zero ionic strength, as 3.4 < pK_a < 3.9.

It follows from eqs 4 and 5 that for the accurate determination of K_a one should know the fraction of intact CA in the solution when in equilibrium with bicarbonate and dissolved CO₂ under constant gas pressure; this is a challenging task. To circumvent this difficulty, one may instead determine the reactivity of the bicarbonate anion, the conjugate and stable base of carbonic acid. In a recent experiment exploiting this idea, an ultrafast IR pump–probe setup was used for estimating the pK_a of CA, using a reactive series of carboxylate bases¹³ analyzed using a Brønsted-type free energy correlation between rates and equilibria.¹³ In this experiment, CA was transiently generated^14,15 in D₂O solutions by ultrafast deuteration of the bicarbonate base by a transiently excited photoacid;^16–19 the rate and structure of the generated CA were then probed by a femtosecond mid-IR laser pulse which was variably delayed with respect to the first photoacid excitation pulse.^13,24 This experiment, and perspective for it, are now discussed.

2.2. Exact Value of the Acidity Constant K_a of Carbonic Acid

The on-contact deuteron transfer rate from the electronically excited acid 2-naphthol 6,8-disulfonate to bicarbonate base was found from the measured diffusion-controlled (time-dependent) reaction rates between the photoacid and various concentrations of DCO₃^−.13 The time-resolved measurement of the time-dependent rate constant of the deuteron transfer between the photoacid and DCO₃⁻ allowed estimation of the on-contact proton transfer rate, needed for carrying out the free energy correlation. The free energy correlation allowed the estimation of CA’s pK_a value from the measured rate of the on-contact deuteron transfer to DCO₃⁻ and the known pK_a value of the photoacid: This gave the estimation pK_a = 3.45 ± 0.15 for CA, which is in the lower range of the pK_a values found in various other experimental studies.^{4–6,14–21} Finally, a recent work reports a pK_a value of 3.65 based on a stopped-flow setup and the global kinetic analysis of the bicarbonate, CO₂, and carbonate system at equilibrium.²¹ However, this result is outside the pK_a range between 3.30 and 3.60 set by Adamczyk et al.¹³ and demonstrates that the exact value of K_a of aqueous carbonic acid is still a matter of debate, which we wish to resolve here.

Several computational studies support a pK_a value for CA lying toward the lower side of the range of the acceptable experimental values.^37–39 However, these studies have not provided a precise value, due (among other issues) to the multiple configurations of carbonic acid’s two OH groups with respect to the carbonyl oxygen, with each of these configurations having a well-separated pK_a value. In one representative calculation, pK_a values of 3.8, 3.6, and 2.2 were found for the trans–trans, cis–trans, and cis–cis carbonic acid conformers, respectively.²² In a different study, a pK_a value of 3.7 was calculated for the cis–trans configuration using Car–Parrinello molecular dynamics with metadynamics.²³ Obviously, the pK_a of CA in aqueous solution should reflect a weighted average of the individual pK_a’s of all possible stable conformers of the acid. The recently computed set of pK_a values by Galib and Hanna²⁴ is, according to their own assessment, consistent with a pK_a value being in the lowest experimentally acceptable pK_a range; i.e., pK_a = 3.4–3.5.

2.3. Significance of the Exact pK_a Value for Carbonic Acid

It is important to stress that the exact value of CA’s K_a is, in fact, of great importance for many research areas. Perhaps the most immediate benefit from its obtainment would be the knowledge of the exact value of the equilibrium constant K_D = [CO₂]/[H₂CO₃] in fresh water (see eq 3), which would provide the precise concentration of CA in unbuffered fresh water in equilibrium with the atmospheric pressure. A similar advantageous outcome pertains to buffered aqueous solutions; a particularly important such solution is blood plasma, which provides an important arena for carbonic acid as a key protonation agent, as we now argue.

The concentration of bicarbonate in the blood plasma of human adults is about 25 mM. Combination of this concentration with the true pK_a of CA (adjusted for the ionic strength of the plasma and ion activities) would allow the estimation of the equilibrium concentration of CA in the blood plasma. Although this concentration is very small, it is still much larger than the concentration of H⁺ in the plasma: the normal pH of the blood plasma is 7.4, so the concentration of the “free” [H⁺] in the plasma is only 4 × 10⁻⁸ M; this is to be compared—with the assumption of the CA pK_a value of about 3.4 under physiological conditions—to the much larger CA concentration of about 10⁻⁶ M! The key relevance of this is that, given CA’s relatively low pK_a and strong acidity, it should be able to efficiently protonate basic groups such as aliphatic amine groups that naturally occur in the blood plasma. Such a considerable reactivity of CA may be physiologically important, especially if slow protonation rates may set the limits for the efficiency of biological processes. Thus, CA has the potential of being a major protonating agent in the blood, competing with other important protonating agents there such as H₂PO₄⁻ and lactic acid.

CA must also be considered a part of the total buffer capacity provided by the bicarbonate systerm (CO₂/HCO₃⁻/H₂CO₃) in our blood. This system provides about 83% of the total buffer capacity in the blood plasma, with proteins providing about 15% of the capacity. The remaining capacity, about 2%, is provided by inorganic phosphate buffer. In the blood erthrocytes, the main buffer is hemoglobin (about 61%) compared to about 32% of the bicarbonate buffer and the rest, about 7%, is composed of inorganic and organic phosphate.^1,2

3. EXPERIMENTAL SECTION

3.1. Solution Preparation and Materials

The solution concentration of the bicarbonate anion cannot be maintained constant at pH < 7 because it slowly decomposes to H₂O and CO₂ under such conditions. In order to avoid HCO₃⁻ decomposition, one has to work with photoacid solutions at pH > 7. Solutions buffered at pH = 7.6 ± 0.2—which is slightly higher than the physiological pH of 7.4 of the blood plasma—were used in corked cuvettes to minimize the slow HCO₃⁻ decomposition during the time-resolved measurements (see below). In addition, the duration of the entire process of solution preparation and kinetic measurement was kept to below 15 min, in order to avoid any appreciable loss of bicarbonate during the optical measurement.

6-Hydroxypyrene-1-sulfonate (HPMS), a moderately strong photoacid, was synthesized to serve as the transient protonation agent of bicarbonate (Figure 1). HPMS was selected among other possible photoacids because of several favorable properties. It has a relatively low acidity in the ground state (pK_a(S₀) = 8.5), and it has a just strong enough photoacidity (see below) while in the excited state (pK_a(S₁) = 1.7) in H₂O at zero ionic strength as determined by the Förster cycle.²⁵ The low ground-state acidity is needed so that the photoacid would be largely in its protonated form in the buffer used to keep bicarbonate stable in slightly basic conditions. The excited-state HPMS photoacidity is almost optimally tuned for the task of transiently protonating bicarbonate: the photoacid is sufficiently strong compared to CA to allow the PT to bicarbonate to be ultrafast, while at the same time having a relatively slow (about 700 ps⁻¹) rate of proton dissociation to the water solvent. This last PT rate requirement ensures that the direct PT reaction to bicarbonate and even to the weaker pyruvate base would constitute the major deprotonation route for the photoacid even at the lowest 0.05 M base concentration.

Figure 1.

6-Hydroxypyrene-1-sulfonate (HPMS) sodium salt.

Advantages of HPMS become especially evident upon its comparison to the two photoacids previously used for similar purposes.^13,26–33 First, HPMS is considerably less acidic in the ground state (pK_a(S₀) = 8.5) than 8-hydroxypyrene-1,3,6-trisulfonate (HPTS, pyranine) (pK_a(S₀) = 7.3) at 0.1 M ionic strength. Second, in the excited state, HPMS is about 1 order of magnitude less reactive with water than are both HPTS and 2-hydroxynaphthalene-6,8-disulfonate. Finally, HPMS is only singly charged while HPTS and 2-hydroxynaphthalene-6,8-disulfonate are triply and doubly charged, respectively. This charge difference makes the pK_a of HPMS considerably less sensitive to the ionic strength than for the two other photoacids.

The concentrations of sodium lactate and carbonate bases (both from Aldrich) were 0.05, 0.1, and 0.25 M. In order to minimize sample degradation due to chemical instability under either acidic or basic conditions, the solutions were buffered with TRIS (tris(hydroxymethyl)aminomethane saline by Fluka; pH 7.6 ± 0.2 (25 °C)). The solution was prepared within a quartz cell having a volume of about 2.5 cm³ that was filled to about three-fourths of its volume with the solution, leaving about 0.5 cm³ of the cell volume filled with air. A Teflon cork wrapped in sealing material (paraffin paper) was used to seal the cell and to prevent any CO₂ gas evolving to the air from the solution within the solvent free volume of the cell during the spectroscopic measurement. No CO₂ bubbles were observed in the buffered bicarbonate solution, and the pressure rise within the optical cell must have been very small because there was no visible disturbance of the gentle arrangement used for sealing the cell.

All experiments were performed at room temperature (20.5 ± 1 °C). The time duration of the solution preparation and the kinetic measurements was kept to below 15 min to reduce any bicarbonate loss via slow decomposition. We estimate the maximum mass loss of bicarbonate during all stages of the experiment to be below 5%. This was checked by repeating the preparation procedure on an analytic balance and keeping the bicarbonate solution in an open vessel on the analytic weight for 25 min while monitoring over time the mass loss due to CO₂ evolution into the air. Under such conditions, the maximum bicarbonate loss measured for an open system of a 0.1 M solution of sodium bicarbonate under normal atmospheric pressure was about 5% after 15 min at 21.5 ± 0.5 °C and pH = 7.77. We have thus decided to lower the bicarbonate concentrations used in our kinetic analysis by 3%, which reflects an average 3% mass loss during our 15 min measurements. This small correction reflects the average mass loss in the bicarbonate concentration we expect to have occurred during solution preparation and the time of our measurements.

3.2. Time-Resolved Measurements

The transient excitation of the HPMS photoacid employed a 1 ps pulse at 375 nm using the second harmonic of the Ti-Sapphire laser operating at 750 nm. The steady-state absorption and fluorescence spectra have been recorded on a JASCO 570 spectrophotometer and a Cary Eclipse fluorometer from Varian Inc., respectively. Time-correlated single-photon-counting (TCSPC) measurements were carried out using a data acquisition card (SPC130) of Becker & Hickle GmbH. The card’s time resolution was either 12 ps per channel at the 50 ns full scale or 1.2 ps per channel at the 5 ns full scale of the card. The kinetic decay curves were analyzed by convoluting synthetic decay profiles with the measured instrument response function and then searching for a best fit with the measured decay profile using Matlab software version 7.2.

3.3. Synthetic Procedure for 6-Hydroxypyrene-1-sulfonate Sodium Salt

For the synthesis of the HPMS salt, a solution of 1-hydroxypyrene (1.2 g, 0.027 mol) in nitrobenzene at 10 °C was mixed with 0.7 mL of chlorosulfonic acid (99%, Sigma-Aldrich). The mixture was then stirred for 3 h while slowly increasing the temperature to 20 °C. The reaction mixture was vigorously stirred at this temperature for 20 h, and the resulting mixture was vacuum-filtered. The residue was dissolved in water and steam-distilled. The cold distillate was filtered and NaCl (2.6 g) was added to it while the solution was mechanically stirred. The resulting greenish precipitate was filtered off and purified by crystallization from ethanol, yielding 0.5 g of white product (yield, 40%). The NMR spectra of the product verified that its structure was consistent with that of HPMS (¹H NMR (DMSO-d₈): δ 10.8 (s, OH), 8.83 (d, 1H, pyrene), 8.39 (d, 1H, pyrene) 8.29 (d, 1H, pyrene), 8.08 (d, 1H, pyrene), 7.9(dd, 1H, pyrene)).

4. RESULTS

4.1. Kinetic Characterization of the HPMS Photoacid

Photoexcitation abruptly switches the acidity of photoacids, making them much stronger acids. Typically such acids, here denoted by R*OH, are capable of efficiently protonating ground-state bases when these are present in the same solution at the time of the laser pulse excitation of the photoacid. When present alone in solution, R*OH photoacids may undergo a photoprotolytic cycle—the Förster cycle.²⁵ The Förster cycle allows the calculation of the excited-state K*_a of the photoacid using the transition energies between the ground and the excited states of the photoacid and its conjugate base forms. We have carried out this procedure for calculating the pK*_a of HPMS, a novel photoacid having almost the optimal properties in our experiments; see the discussion of the HPMS properties in the Experimental Section. Figure 2 shows the HPMS photoacid’s absorption and fluorescence spectra at two representative pH values.

Figure 2.

Absorption (a) and fluorescence (b) spectrum of the photoacid HPMS in water at two representive pH values at which the proton-dissociated anion (red) or the acid (blue) form of HPMS dominates the absorption spectrum. The steady-state fluorescence spectrum of the excited molecule at 375 nm photoacid consists of fluorescence originating from both the acid and base forms of the photoacid and reflects the excited-state reaction of proton dissociation to the bulk solvent producing the excited base form. Excitation of the ground-state photobase results in fluorescence originating only from the excited base form of the photoacid.

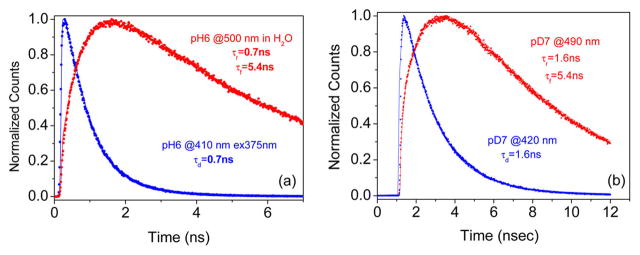
The deprotonation rate of excited HPMS was determined by collecting the time-resolved fluorescence of the protonated and deprotonated forms of the HPMS photoacid at 410 and at 490 nm, respectively. The time-resolved measurements were carried out in both H₂O and D₂O solvents; see Figure 3. The acidic form of HPMS decays with time constants of τ_H2O = 0.7 ns and τ_D2O = 1.6 ns in H₂O and D₂O, respectively. Using the measured fluorescence lifetimes and taking into account the radiative lifetime of the excited state in the absence of PT, we have found for the proton dissociation rate constants k_off = 1.25 × 10⁹ and 0.44 × 10⁹ s⁻¹ in H₂O and D₂O, respectively. The kinetic isotope effect k_off(H₂O)/k_off(D₂O) for the proton dissociation reaction—as judged by the fluorescence lifetime of the acid form of HPMS in water—is about 2.9. Similar PT time constants and kinetic isotope effect were found when analyzing the fluorescence rise time of the deprotonated form of HPMS measured at 490 nm.

Figure 3.

Normalized plots of the fluorescence decay and the fluorescence rise of the protonated and deprotonated forms of HPMS, respectively, following a 1 ps long laser pulse excitation. Points are the experimental data, and the full curves are the best fit exponential decay and rise time constants. λ_ex = 375 nm; λ_em = 490 nm. (a) Measurement taken in water at pH 6.10. (b) Measurement taken in D₂O at pD 7.0. Notice the difference in the time scale for a and b due to the slower deuteron dissociation rate.

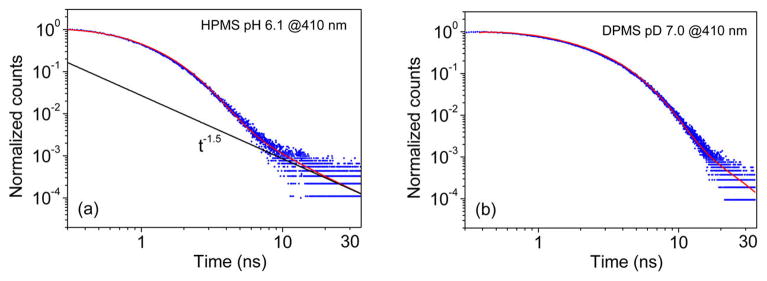
The existence of a non-exponential fluorescence tail (delayed fluorescence) in the decay curves of the acid form which are displayed in Figure 3 is apparent in the log–log plots of the same experimental data (Figure 4). This long-time tail is indicative of a diffusion-assisted reversible germinate-recombination process. The geminate proton recombination reaction of the proton with the photobase occurs with no apparent fluorescence quenching and reversibly re-forms the photoacid in the electronically excited state.^34–37 These observations demonstrate the full reversibility of the PT reaction of the electronically excited photoacid; accordingly, it is indeed justified to assign to the electronic excited state an equilibrium constant exactly as is done for ground-state acids. This gives credibility for the use of HPMS for probing the excited-state PT to the carboxylic bases by assuming a free energy correlation between the PT rate and the difference in the acidities of the excited photoacid and the carboxylic acids. This correlation will be effected in section 5.2.

Figure 4.

log–log plot of normalized fluorescence decay of the acid form of HPMS after it was multiplied by exp(τ_f) (involving the fluorescence decay lifetime of the HPMS anion) to compensate for the population loss of the re-formed photoacid due to the finite lifetime of the kinetic system in the electronic excited state. Points in blue are experimental data at λ_ex= 375 nm and λ_em= 410 nm in water at pH 6.1 (a) and in D₂O at pD 7.0 (b). The red solid curves which fit the experimental data are the numerical solutions of the Debye–Smoluchowski equation^39,40 using the SSDP program³⁸ convoluted with the instrument response function. The full line shown in panel a is the asymptotic slope of the numerical solution of the reversible diffusion geminate-recombination problem which is 1.50.^34–37 For the slower deutron dissociation-recombination reaction in D₂O (panel b), the time range of the measurement is not sufficient for showing the characteristic long-time behavior of the diffusion-reaction problem, which is reached only after about 200 ns.

The numerical fitting of the TCSPC data in H₂O and D₂O (solid lines in Figure 4) was carried out by the Windows version of the spherical symmetric diffusion problem (SSDP) program of Krissinel and Agmon,³⁸ which was developed for numerically solving the time-dependent kinetic model for reversible geminate-recombination reactions introduced by Pines et al.^34–37

$$\mathrm{R}\ast \text{OH}\rightleftarrows {[\mathrm{R}\ast {\mathrm{O}}^{-}\cdots {\mathrm{H}}^{+}]}_a\rightleftarrows \mathrm{R}\ast {\mathrm{O}}^{-}+{\mathrm{H}}^{+}$$ (6)

The following reaction parameters were used in the SSDP program: 5.4 Å for the reaction radius a and a Debye radius³⁹ $R_{\mathrm{D}}^{\text{RO-H}}$ of 14.2 Å which gives a scaled measure of the Coulomb interaction between the doubly negatively charged photoacid base and the proton,

$$R_{\mathrm{D}}=z_1{z}_2{e}^2/\epsilon k_{\mathrm{B}}T$$ (7)

where k_B is Boltzmann’s constant, ε is the dielectric constant of the solution, e is the elementary electron charge, and z₁ = −2 and z₂ = +1 are the charge numbers of the photoacid’s conjugate base and the proton, respectively. The relative diffusion constants of HPMS and the proton were taken as 8.9 × 10⁻⁵ and 6.7 × 10⁻⁵ cm² s⁻¹ in H₂O and D₂O, respectively.²⁷ Using these reaction parameters and best fitting, we have found the following for the proton dissociation (k_off) and recombination (k_on) rates: k_off = 1.25 × 10⁹ s⁻¹ and k_on = 9.5 Å ns⁻¹ in H₂O and k_off = 0.44 × 10⁹ s⁻¹ and k_on = 7.0 Å ns⁻¹ in D₂O, these values exhibiting an isotope effect of 1.4 in k_on and of 2.9 in k_off. This isotope effect for k_off is practically identical with the one calculated for k_off under the assumption of irreversible proton transfer at early times of the photoacid dissociation reaction. With the SSDP fitting procedure, we were able to fit the experimental data at all measurement times down to the signal-to-noise (S/N) limit of the TCSPC system, thus ruling out the possibility of any appreciable fluorescence quenching process associated with the excited-state reversible PT reactions of the photoacid.

The log–log plots of the experimental decay curve of HPMS (Figure 4a) reveal that the curve for reversible proton transfer in H₂O approaches after about 20 ns a t^−3/2 dependence on time, which is the predicted theoretical curve for a fully reversible and diffusion-assisted geminate-recombination reaction. ^34–37

4.2. Fluorescence Decay of the HPMS Photoacid in the Presence of Bicarbonate, Lactate, and Pyruvate Proton Bases

In the presence of a proton base capable of accepting a proton in a bimolecular neutralization reaction, a parallel PT route (eq 8) is open to HPMS in addition to the proton dissociation reaction to the solvent (eq 6):

$$\mathrm{R}\ast \text{OH}+{\mathrm{B}}^{-}\rightleftarrows \mathrm{R}\ast {\mathrm{O}}^{-}+\text{HB}$$ (8)

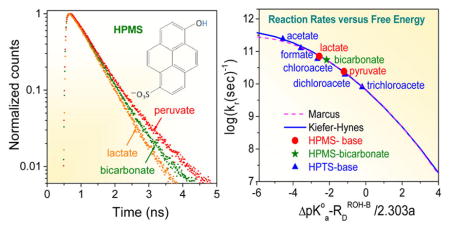
In the presence of a proton base, the dissociation of HPMS becomes more rapid than the dissociation of the photoacid in just bulk water, to a degree dependent on the base’s concentration and strength. Addition of 0.05–0.1 M concentrations of carboxylate bases to the HPMS solutions led to a much faster decay of the fluorescence of HPMS and to a corresponding faster rise in the fluorescence of the deprotonated form of HPMS. These results point to a more rapid PT reaction of the photoacid in the presence of these proton acceptors.

Figure 5 shows the transient fluorescence spectra of HPMS recorded for 0, 0.1, 0.25, 0.5, and 1 M solutions of lactate and bicarbonate anions (the 0.05 M curve has been omitted to avoid graphical congestion). Faster decays of HPMS in the lactate solutions compared to those in the bicarbonate solutions are clearly evident. This proves the lactate anion to be a stronger base than the bicarbonate anion, and concomitantly shows carbonic acid to be a stronger acid than lactic acid with a pK_a(CA) less than the pK_a value of lactic acid, 3.86¹⁰.

Figure 5.

TCSPC decay of the HPMS photoacid measured as a function of base concentration in buffer solution (black dots), and 0.1, 0.25, 0.5, and 1 M of base in H₂O solutions of lactate (blue dots). The bicarbonate data are present for comparison (red solid lines).

Figure 6 shows the fluorescence of the HPMS photoacid measured in H₂O solutions of 0.1 M pyruvate, bicarbonate, and lactate bases. Slower decay of the photoacid in the presence of the pyruvate base compared to decays in the lactate and bicarbonate solutions is clearly evident. This observation demonstrates that the pyruvate base is a significantly weaker base than either lactate or bicarbonate, which is consistent with the fact that it is the conjugate base of a much stronger acid than either lactic or carbonic acids (pK_a of pyruvic acid = 2.50¹⁰). Observations such as those shown in Figure 6 firmly establish the concept of a reaction series where the reactivities of the various members of a series are ordered according to the relative value of their equilibrium constant.

Figure 6.

TCSPC decay of the HPMS photoacid measured in 0.1 M solutions of pyruvate, bicarbonate, and lactate bases.

5. DISCUSSION

5.1. PT between a Photoacid and a Base

The dynamics of PT between a photoacid and a base in aqueous solution is a theoretically challenging problem, not least due to the assorted phenomena that can be involved. This situation requires a certain amount of discussion in order to describe our treatment of the PT reactions of interest here. In addition to direct proton transfer from the photoacid to the base, there is also possible PT through intervening one or two water molecules bridging the acid and base or even through the bulk solvent.²⁸ The pK*_a of the photoacid, the relative basicity of the base, and base concentration play a key role in determing which of the proton transfer routes would be the dominant one.

In our case, the assumption of the acid and base molecules diffusing to some fixed contact separation where they react is justified (see below). Under reactive conditions, reactive pairs having shorter initial separation distances disappear from the distribution faster than pairs having longer initial separation distances. When the PT reaction is initiated in conditions pertaining to a nonreactive ensemble of acid and base molecules suddenly becoming reactive due to a short-pulse excitation of the photoacid, the ensuing PT reaction rate constant is time-dependent. The time dependence of the effective rate constant will persist until steady-state conditions will be achieved. Such a kinetic situation is adequately described by the Collins and Kimball (CK) expression.⁴¹ The main kinetic ingredient in the CK model is the assumption of a finite reaction rate at the reaction contact radius when the acid and base encounter each other following their mutual diffusion in the bulk solution. This is in contrast with the diffusion limit of the reaction used in the Debye–Smoluchowski equation, where the reactants are assumed to react with each other immediately upon their first encounter, i.e., when arriving at the contact radius.^39–41 The CK description has been expanded to charged species interacting in a finite ionic strength environment by Szabo.⁴² The Szabo–Collins–Kimball (SCK) description has been used to describe many aqueous acid–base neutralization reactions.^{26,27,43–45}

Naturally, we need to understand if the SCK description applies to our systems. At above 1 M concentration of proton bases and for strong photoacids (not used in the present study), the sometimes termed “peripatetic” proton⁴⁶ may be transferred via several reaction centers of different sizes which differ by the number of water molecules intervening between the acid and base.^26–30 This was the case for the strong photoacid HPTS reacting with carboxylate bases in molar concentrations.^26–33 However, for the present case with the weaker HPMS acid in the presence of moderate base concentrations—where practically all of the acid and base molecules need to diffuse through the bulk solution before reacting with each other—it is justified to model the reaction by the SCK equation with a unique contact radius. The additional minority reaction of the photoacid dissociating to the bulk water is treated as a homogeneous reaction independent of the base; this reaction determines the reference (exponential) lifetime of the photoacid in the excited state in a manner similar to that for an effective fluorescence lifetime.

We refer to earlier studies^{26,27,43–45,47,48} for additional technical details of the kinetic analysis using the SCK model. We now apply this model description to our systems.

The survival probability, S_R*OH(t), of a photoexcited proton donor R*OH, surrounded by an equilibrium distribution of proton acceptor molecules with the initial condition S_R*OH(0) = 1 is given by

$$S_{\mathrm{R}\ast \text{OH}}(t)=exp\{-k_{\mathrm{w}}t-{\int }_0^t{c}_{0}k(t^{\prime })\mathrm{d}{t}^{\prime }\}$$ (9)

where k_w is the apparent first-order rate constant of the proton donor (acid) for dissociation to the solvent (k_w also includes all other nonradiative and radiative decay routes of the photoacid), c₀ is the bulk (homogeneous) concentration of the proton acceptor, and k(t) is a time-dependent rate constant for the R*OH decay. The dissociation of the photoacid is assumed in eq 9 to be an irreversible process which is an excellent assumption under our experimental conditions where relatively strong bases at high concentrations were used as irreversible proton acceptors. For a screened Coulomb potential (which we will employ; see below), it is not possible to solve the Debye–Smoluchowski diffusion-reaction equation analytically using the SCK boundary condition, but a useful analytic approximation due to Szabo⁴² for the time-dependent rate constant k(t) is

$$k(t)=\frac{k_{\text{SD}}{k}_0{\mathrm{e}}^{-U(a)/k_{\mathrm{B}}T}}{k_{\text{SD}}+k_0{\mathrm{e}}^{-U(a)/k_{\mathrm{B}}T}}\left[1+\frac{k_0{\mathrm{e}}^{-U(a)/k_{\mathrm{B}}T}}{k_{\text{SD}}}exp({{\gamma }^{\prime }}^{2}Dt)\text{erfc}(\sqrt{{{\gamma }^{\prime }}^{2}Dt})\right]$$ (10)

Here k₀ is the bimolecular rate constant of the PT reaction upon contact and γ′ is given by

$${\gamma }^{\prime }={a_{\text{eff}}}^{-1}\left[1+\frac{k_0{\mathrm{e}}^{-U(a)/k_{\mathrm{B}}T}}{k_{\text{SD}}}\right]$$ (11)

in which the screened potential U, here evaluated at the contact radius a, will be defined below, and erfc means complementary error function. Further,

$$k_{\text{SD}}=4\pi {\mathit{DNa}}_{\text{eff}}$$ (12)

is the steady-state diffusion rate constant with the effective radius a_eff defined as

$${a_{\text{eff}}}^{-1}={\int }_0^{\infty }{\mathrm{e}}^{U(a)/k_{\mathrm{B}}T}{r}^{-2}\mathrm{d}r$$ (13)

and D is a relative diffusion coefficient of the HPMS molecule and the base.

In our experiment, the solution ionic strength is sufficiently small for us to approximate the effective potential between the photoacid HPMS and the Brønsted base at separation r by the extended Debye–Hückel (DH) ionic screening law^43,49

$$U(r)/k_{\mathrm{B}}T=\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{r}\frac{{\mathrm{e}}^{-{\kappa }_{\text{DH}}(r-a)}}{1+a{\kappa }_{\text{DH}}}$$ (14)

Here $R_{\mathrm{D}}^{\text{ROH-B}}$ is the Debye radius (eq 7) of the Coulomb interaction between the single negatively charged photoacid ROH (z₁ = −1) and the base (z₂ = −1) where we have indicated the charge numbers of the photoacid and the base, respectively, κ_DH² = 8πe²I/εk_BT, where κ_DH⁻¹ is the Debye–Huckel screening length and I is the ionic strength. Finally, eq 9 requires the integral of the time-dependent rate constant k(t), which has the form

$${\int }_0^{t}k(t^{\prime })\mathrm{d}{t}^{\prime }=\frac{k_{\text{SD}}{k}_0}{k_{\text{SD}}+k_0}\left\{t+\frac{k_0}{k_{\text{SD}}D{({\gamma }^{\prime })}^2}\times [exp({({\gamma }^{\prime })}^{2}Dt)\text{erfc}(\sqrt{{{\gamma }^{\prime })}^2})+2\sqrt{{({\gamma }^{\prime })}^{2}Dt/\pi }-1]\right\}$$ (15)

Data-fitting curves according to the model (eqs 9–15) for several concentrations of proton acceptors are shown as solid lines in Figure 7, with the fitting parameters for 0.1 and 0.25 M solutions given in Table 1. The diffusion coefficients D_B of the carboxylate bases at T = 20 °C were taken from the literature: D_B(lactate) = 1.04 × 10⁻⁹ m²/s, D_B(bicarbonate) = 1.19 × 10⁻⁹ m²/s, and D_B(pyruvate) = 0.84 × 10⁻⁹ m²/s.^50,51

Figure 7.

TCSPC decay of the HPMS photoacid measured in 0.1, 0.25, and 0.5 M aqueous solutions of lactate (a) and of bicarbonate base (b). The fluorescence decay was fitted using eqs 9–15 (the solid lines are practically indistinguishable from the experimental data). The fitting parameters for 0.1 and 0.25 M solutions are summarized in Table 1.

Table 1.

Fitting Parameters Using Equations 9–15 for the PT Reactions between HPMS Photoacid and Lactate or Bicarbonate Bases (0.1 and 0.25 M Solutions) As Shown in Figure 7

c0, M	aeff, Åa	D(lactate),b 10−9 m2 s−1	k0(lactate), 10−10 M−1 s−1	D(bicarbonate),b 10−9 m2 s−1	k0(bicarbonate), 10−10 M−1 s−1
0.1	4.0	1.6	2.81	1.8	2.18
0.25	4.4	1.6	2.81	1.8	2.18

^aIonic strength calculated for c₀ + (0.05 M buffer); contact radius a = 5.4 Å.

^bD = D(HPMS) + D(base) denotes the relative diffusion coefficients of HPMS and the base.

In the above, we have assumed that the physical properties of the solvent do not change significantly when moving from 0.1 to 0.25 M solutions. The experimental error associated with measurements in 0.05 M solutions is considerably higher than that in the more concentrated solutions; in addition, the 0.5 M solutions are too concentrated for the physical properties of the solvent to remain practically constant. Accordingly, we have omitted the 0.05 and 0.5 M measurements in Table 1 (although in fact they yielded qualitatively similar reaction parameters). The reaction parameters listed in Table 1 are typical of those found for many bimolecular PT reactions from photoacids to various bases in aqueous solutions.^52–56

In order to find the unimolecular PT rate constant k_r within the reaction complex, we have used the relation eq 16 between the bimolecular reaction constant k₀ (having the units of M⁻¹ s⁻¹) and k_r (having the units of s⁻¹), whose validity was first established by Shoup and Szabo,⁵⁷

$$k_{\mathrm{r}}=\frac{3}{4\pi a^{3}N}{k}_0$$ (16)

where N is the number of particles present in 1 cm³ of a 1 M solution of particles and is sometimes referred to as the Avogadro’s number per mM. It then follows that k_r is equal to k₀ multiplied by the local concentration of the reactive acid–base pair while at the contact separation a. The unimolecular on-contact reaction rate constant found for lactate is k_r = 7.1 × 10¹⁰ s⁻¹, which is about 25% larger than that found for bicarbonate, k_r = 5.7 × 10¹⁰ s⁻¹. A considerably smaller k_r value was found for pyruvate, 2.6 × 10¹⁰ s⁻¹, in accordance with (a) the fact that pyruvate is a much weaker base than both bicarbonate and lactate in combination with (b) the assumption of a free energy correlation between the basicity of the proton acceptor and its protonation rate by HPMS.

5.2. Free Energy Relationship

In order to compare lactic, pyruvic and carbonic acids by finding the ΔpK_a difference between them, we utilize a free energy relationship between the reaction rate and free energy of the PT reactions. A numerical fit of the experimental PT rate constant k_r versus ΔpK_a data for acid–base pairs with known ΔpK_a values provides a reference free energy relationship. Interpolation of this relationship with the HPMS bicarbonate PT rate constant k_r allows for evaluation of the carbonic acid pK_a by estimating the ΔpK_a for that acid–base pair.

The starting point for the analysis is the transition-state theory rate constant for the PT when the acid and base form a reactive pair,

$$k_{\mathrm{r}}=k_{\mathrm{a}}exp(-\mathrm{\Delta }{G}^{‡}/RT)$$ (17)

where k_a can be regarded as a (purely notional) effective activationless PT rate constant and ΔG^‡ is the activation free energy barrier. With the knowledge of an approximate k_a value, one may calculate the free energy barrier for every measured PT rate constant k_r by manipulating eq 17; i.e.,^62,63

$$\mathrm{\Delta }{G}^{‡}=-\mathit{RT}ln(k_r(\mathrm{\Delta }{G}_{\text{reacn}})/k_{\mathrm{a}})$$ (18)

Thus, the appropriate thermodynamic driving force ΔG_reacn, the free energy change in the contact PT reaction, is implicit in the variation of the activation free energy for the pair ΔG^‡.

We stress that here we have defined ΔG_reacn as the free energy for the reaction converting reactants to products in the contact pair

$$\mathrm{R}\ast \text{OH}\cdots \mathrm{B}\rightleftarrows \mathrm{R}\ast {\mathrm{O}}^{-}\cdots {\mathrm{H}}^{+}\mathrm{B}$$ (19)

but this is not the standard reaction free energy ΔG° associated with both the infinitely separated reactants R*OH and B and products R*O⁻ and H⁺B. It is ΔG° that is more readily available, but we correlate the contact pair rate constant with the thermodynamic driving force ΔG_reacn as per eq 17, so we need to relate ΔG_reacn to ΔG°. We now deal with this issue.

The standard thermodynamic state for acid–base equilibria applies to conditions of infinite dilution when the activity coeficient of all reactants and products is equal to unity.

The ΔG° value for the reaction

$$\mathrm{R}\ast \text{OH}+\mathrm{B}\rightleftarrows \mathrm{R}\ast \text{OH}\cdots \mathrm{B}\rightleftarrows \mathrm{R}\ast {\mathrm{O}}^{-}\cdots {\mathrm{H}}^{+}\mathrm{B}\rightleftarrows \mathrm{R}\ast {\mathrm{O}}^{-}+\text{HB}$$ (20)

differs from our defined ΔG_reacn in that ΔG° includes the work needed to bring the acid and from infinite separation (∞) into contact (c) from the reactant side ΔG_∞c, and the work needed to separate the PT contact (c) product pair to infinite (∞) distance, ΔG_c∞. This gives the relations

$$\mathrm{\Delta }G°=\mathrm{\Delta }{G}_{\infty c}+\mathrm{\Delta }{G}_{\text{reacn}}+\mathrm{\Delta }{G}_{c\infty }$$ (21)

for free energy changes and the corresponding equilibrium constants

$$K{°}_{\mathrm{a}}=K_{\infty c}{K}_{a,\text{reacn}}{K}_{c\infty }$$ (22)

such that the general relation between a free energy change ΔG and its corresponding pK is given by

$$\mathrm{\Delta }G=\frac{RT\mathrm{p}K}{log(e)}$$ (23)

and may be written for each stage of the reaction referred to in eqs 21 and 22.

At this point, we need to recall that, for the present cases, in the reactions in eqs 19 and 20 the reactant acid R*OH is the singly negatively charged HPMS, Figure 1, and the various reactant bases B (bicarbonate and so on) are all singly negatively charged. The products R*O⁻ and H⁺B after PT are then respectively the doubly negatively charged conjugate base of HPMS and the neutral protonated bases. The equilibrium constant K_∞c for infinitely separated charged reactants forming contact ion pair at a contact separation a is usually identified with the electrostatic work done, i.e., the electrostatic free energy change, in this process. The electrostatic work is calculated using the Fuoss–Eigen equation proposed independently by Eigen and Fuoss;^58,59

$$K_{\infty c}=\frac{4\pi a^3{N}^{\prime }}{3}exp\left(\frac{-R_{\mathrm{D}}^{\text{ROH-B}}}{a}\right)$$ (24)

for a reaction where both acid and base molecules are charged and either attract or repel—as in our case—each other electrostatically prior to proton transfer. $R_{\mathrm{D}}^{\text{ROH-B}}$, the Debye radius, with the charges z₁ = −1 (HPMS) and z₂ = −1 (base). For the triply charged HPTS photoacid z₁ = −3.

The separation from contact to infinity equilibrium constant K_c∞, when—as in our case—at least one of the products is uncharged so that the product separation process takes place without charge–charge electrostatic interaction, is given by

$$K_{c\infty }={\left(\frac{4\pi a^3{N}^{\prime }}{3}\right)}^{-1}$$ (25)

We can now employ the preceding equations to relate the contact reactant free energy ΔG_reacn (which is related to pK_a,reacn via the appropriate form of eq 23) and the thermodynamic, infinite separation pK°_a (which is associated with ΔG° via the appropriate version of eq 23). With the assumption of an identical contact radius a for both the reactants and the products within the reaction complex, we first have

$$K{°}_{\mathrm{a}}=K_{\mathrm{a},\text{reacn}}exp\left(\frac{-R_{\mathrm{D}}^{\text{ROH-B}}}{a}\right)$$ (26)

or equivalently

$$K_{\mathrm{a},\text{reacn}}=K{°}_{\mathrm{a}}exp\left(\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{a}\right)$$ (27)

which provides the connection

$$\begin{gathered} \mathrm{p}{K}_{\mathrm{a},\text{reacn}}=\mathrm{p}K{°}_{\mathrm{a}}-log(e)\left(\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{a}\right) \\ =\mathrm{\Delta }\mathrm{p}{K}_{\mathrm{a}}-log(e)\left(\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{a}\right) \end{gathered}$$ (28)

We then substitute the pK°_a of the acid–base reaction in eq 28 by ΔpK_a (which is the pK_a of the acid minus the pK_a of the conjugate acid of the base) for the thermodynamic infinite separation case. We thus finally obtain the desired relation between ΔG_reacn for the contact pair and the accessible infinite separation ΔpK_a

$$\mathrm{\Delta }{G}_{\text{reacn}}=\frac{RT}{log(e)}\left(\mathrm{\Delta }\mathrm{p}{K}_{\mathrm{a}}-\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{a}log(e)\right)$$ (29)

We also note that for the cases of the carbonic, lactic, and pyruvic acid PT to water reactions, there is a different but similar relation since there the reactants are neutral and involve no work function correction, but the charged products do involve such an electrostatic work contribution.

After these preliminaries, we now begin our examination of a plot of ln (k_r) for the contact pair PT rate constant versus the activation free energy ΔG^‡ for that reaction in order to extract a desired relation

$$ln(k_r)=ln(k_{\mathrm{a}})-\mathrm{\Delta }{G}^{‡}(\mathrm{\Delta }{G}_{\text{reacn}})/RT$$ (30)

To this end, we employ a second-order expansion around the thermoneutral contact pair PT reaction ΔG_reacn = 0 for the ΔG^‡ versus ΔG_reacn free energy relationship,

$$\mathrm{\Delta }{G}^{‡}=\mathrm{\Delta }{G}_0^{‡}+{\beta }_o\mathrm{\Delta }{G}_{\text{reacn}}+\frac{1}{2}{\beta }_{\mathrm{o}}^{\prime }\mathrm{\Delta }{G_{\text{reacn}}}^2$$ (31)

Equation 31 can be regarded as just a Brønsted relationship up to second order. The first term in eq 30 is by definition the activation free energy barrier for the thermoneutral case, and the linear coefficient β_o is the Brønsted coefficient, which according to the Leffler–Hammond postulate is related to the transition-state structure (e.g., early or late).^60,61 The final, nonlinear term includes the derivative of a (variable) Brønsted coefficient ${\beta }_o^{\prime }$.

Physical insight into the three coefficients in eq 30 was provided by Kiefer and Hynes (KH),^62–66 who derived a similar free energy relationship for quantum PT reactions in solution (the KH relation involves an expansion in the reaction free energy, not necessarily equal to its standard state value, so that it is in the proper form vis a vis eq 30). The KH relation was derived from the perspective that the reaction coordinate and free energy barrier ΔG^‡ are both intimately related to the activation of solvent molecules surrounding the acid–base pair, including a quantum zero point energy in addition to the solvent environmental (and a hydrogen bond) contribution. The coefficient β_o is related to the transition-state structure for the thermally neutral reaction case, where that structure includes the activated solvation structure as well as the electronic structure of the H-bonded complex pair. For reactions of an acid–base contact pair, the Brønsted coefficient is expected to be 1/2 for the symmetric H-bonded complex situation ΔG_reacn = 0. Finally, the second-order coefficient ${\beta }_o^{\prime }$ in the KH perspectives related to the rate of change of the ΔG^‡ transition-state structure with respect to the PT reaction pair’s reaction free energy asymmetry ΔG_reacn.

For comparison, the relationship derived by Marcus for electron transfer may be also used as an empirical relation for PT reactions^67–73 and has the following form^70,74,75

$$\mathrm{\Delta }{G}^{‡}=\mathrm{\Delta }{G}_0^{‡}+\frac{\mathrm{\Delta }{G}_{\text{reacn}}}{2}+\frac{\mathrm{\Delta }{G_{\text{reacn}}}^2}{16\mathrm{\Delta }{G}_0^{‡}}$$ (32)

Figure 8 shows the PT on-contact k_r versus the ΔpK_a values adjusted to be those appropriate for the contact pair PT reactions $\mathrm{\Delta }\mathrm{p}{K}_{\mathrm{a}}-\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{2.303a}$, for various PT reactions; these include the present results for HPMS PT to lactate and pyruvate according to the KH eqs 30 and 31. The dashed line in Figure 8 is a Marcus fit (eq 31) solely to just the two HPMS PT points. The free energy correlation curve eq 31 is thus found to well-correlate the present experimental results as well as the previously published kinetic data on the on-contact PT reaction between HPTS, a photoacid with a structure closely similar to HPMS, and the acetate and formate bases.¹³

Figure 8.

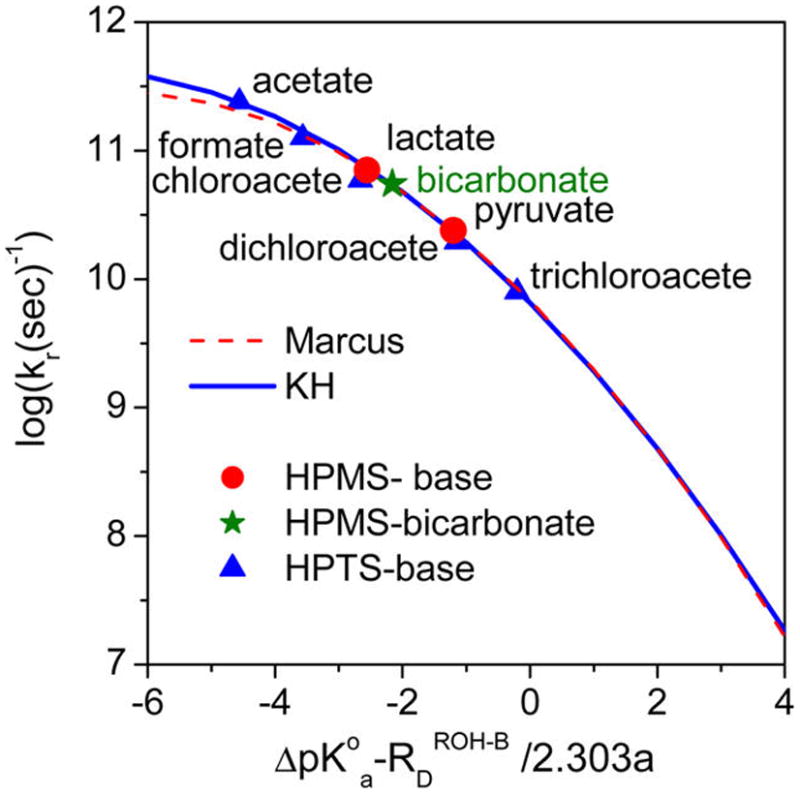
Free energy vs PT rate curves. Red points, the HPMS-lactate and HPMS-pyruvate reaction results; olive star, HPMS-bicarbonate result; blue triangles, HPTS-base results.^13,26–30 The $\mathrm{\Delta }\mathrm{p}{K}_{\mathrm{a}}-\frac{R_{\mathrm{D}}^{\text{ROH-B}}}{2.303a}$ values involve the adjustment of ΔpK_a values to those appropriate for the contact pair PT reactions rather than using the conventional infinite separation values (see the text).The blue curve is the second-order fit for all points including the HPTS data according to the Kiefer–Hynes perspective eq 30^62–66 with correlation parameters summarized in Table 2. The red dashed curve is calculated for only the HPMS-lactate and HPMS-pyruvate reactions using Marcus theory for electron transfer (eq 31).^70,74,75

The fitting procedure now to be described correlates ΔpK_a,reacn (eq 27) rather than absolute pK_a values and has allowed us to correlate the HPTS data on the same correlation line that we have accurately obtained for HPMS. First, HPTS values were obtained in D₂O for D⁺ transfer so they are rescaled in Figure 8 by a factor of 1.45 to approximate H⁺ transfer. Second, we took into account the difference in the on-contact photoacidities of HPTS and HPMS (1.05 pK unit).

The relative basicity of the various bases used in the correlation shown in Figure 8 may be found by shifting the position of the bases in the HPTS series to the right of the x axis by 1.05 pK_a units. It follows the order acetate > lactate ≥ formate > bicarbonate > pyruvate > dichloroacetate > trichloroacetate. The acidities of the conjugate acids follow the opposite order, which means that carbonic acid is measurably stronger than both formic and lactic acids and is appreciably weaker than pyruvic acid.

The key consequence of these considerations is that, since Figure 8 is based on accurately determined pK_a values of stable acids and bases, it allows the accurate determination of the pK_a of carbonic acid from the measured value of the PT rate to bicarbonate. We find by the Figure 8 correlation that carbonic acid is 0.37 pK_a units stronger than lactic acid and is weaker by about a 1.0 pK_a unit than pyruvic acid. This then places the pK_a of carbonic acid to be equal to 3.86 – 0.37 = 3.49 pK_a units, with error bars of ±0.05 pK_a units. The value we find is similar to the one given in ref 13 (3.45 ± 0.15) but has much smaller error bars.

This present result firmly places the pK_a of carbonic acid in the lower part of the accepted range for its pK_a values, i.e., below the 3.6 pK_a mark. It also firmly establishes carbonic acid to be stronger than acetic, lactic, and even formic acids (pK_a = 4.75, 3.86, and 3.75, respectively). Further, it confirms carbonic acid as a plausible important proton donor in blood plasma.

6. CONCLUDING REMARKS

We have established the pK_a value of carbonic acid to be 3.49 ± 0.05 in aqueous solutions. This pK_a value was determined using free energy correlations of the PT rates from the novel photoacid HPMS to the bicarbonate, lactate, and pyruvate bases in aqueous solutions. Both the Marcus and the Kiefer–Hynes equations give a pK_a difference of 0.37 pK_a units between lactic and carbonic acids and of about one pK_a unit between carbonic acid and pyruvic acid, with carbonic acid being a stronger acid than lactic acid and a weaker acid than pyruvic acid. We have thus established the acidity of carbonic acid pK_a 3.49 ± 0.05 units with a much narrower range than previously available. This pK_a range for carbonic acid brings the value of the all important fractionation constant between CO₂ and carbonic acid in water under atmospheric pressure and at ambient temperatures K_D, to be 715 ± 35, significantly narrowing the previously reported K_D range.

Our study shows carbonic acid to possess a considerable acid strength. Since it is a part of the CO₂/bicarbonate buffer which is largely responsible for maintaining the pH of the blood plasma and the world oceans, carbonic acid should be regarded as a very common reactive chemical substance. This context and its considerable acidity highlight the possible rule of intact carbonic acid as an important protonating agent in blood plasma and in the earth oceans. This further aspect of the chemistry of carbonic acid merits thorough consideration and is currently under further investigation.

Table 2.

KH Second-Order Free Energy Relationship Equation 31 and Marcus Equation 32 Coefficients

	ka, s−1	$\mathrm{\Delta }{G}_{\mathrm{o}}^{‡}$, kcal/mol	βo	${\beta }_{\mathrm{o}}^{\prime }$, mol/kcal
Kiefer–Hynes	4.1 × 1011	2.40	0.5	0.057
Marcus	4.1 × 1011	2.40