Clinical models of decision making in addiction

Abstract

As research on decision making in addiction accumulates, it is increasingly clear that decision-making processes are dysfunctional in addiction and that this dysfunction may be fundamental to the initiation and maintenance of addictive behavior. How drug-dependent individuals value and choose among drug and nondrug rewards is consistently different from non-dependent individuals. The present review focuses on the assessment of decision-making in addiction. We cover the common behavioral tasks that have shown to be fruitful in decision-making research and highlight analytical and graphical considerations, when available, to facilitate comparisons within and among studies. Delay discounting tasks, drug demand tasks, drug choice tasks, the Iowa Gambling Task, and the Balloon Analogue Risk Task are included.

1. Introduction

As research on decision making in addiction accumulates, it is increasingly clear that decision-making processes are dysfunctional in addiction and that this dysfunction may be fundamental to the initiation and maintenance of addictive behavior. How drug-dependent individuals value and choose among drug and nondrug rewards is consistently different from non-dependent individuals. A number of recent reviews from our laboratory and others have catalogued these differences (Bickel et al., 2014a, 2014b, 2012; MacKillop et al., 2011, 2010a), and we suggest that readers interested in how these measures relate to various aspects of addiction consult these papers. The present review focuses on the assessment of decision-making in addiction. We will cover the common behavioral tasks that have shown to be fruitful in decision-making research and highlight analytical and graphical considerations when available, to facilitate comparisons within and among studies.

2. Delay discounting

2.1. Role of delay discounting in addiction

It is normal to prefer a reward available now to the same reward available after some delay, but excessively discounting the value of delayed rewards can represent an overemphasis on near-term rewards (e.g., drug high) instead of more long-term rewards (e.g., career, good health, interpersonal relationships; Ainslie, 1975). Excessive delay discounting seems to be a reliable marker of short-sighted unhealthy behavior (Bickel and Marsch, 2001) with substance use and addiction being prototypical examples (Bickel et al., 2012; MacKillop et al., 2011; Madden and Bickel, 2010). The evidence supporting a link between excessive delay discounting and addiction now spans most common classes of addictive drugs including alcohol (MacKillop et al., 2010a), tobacco (Bickel et al., 1999; Johnson et al., 2007), stimulants (Coffey et al., 2003; Heil et al., 2006; Hoffman et al., 2006; Washio et al., 2011), opiates (Kirby et al., 1999; Petry et al., 1998), and possibly marijuana (Johnson et al., 2010). This body of research has firmly established a robust relationship across studies and contexts, as was confirmed by a recent meta-analysis (Amlung et al., 2017).

Research also supports an etiological role of excessive discounting in addiction. Excessive discounting predates the initiation of smoking (Audrain-McGovern et al., 2009), and the similar construct of delay of gratification predicts later drug use (Ayduk et al., 2000). Among substance users entering treatment, relatively self-controlled responding on delay discounting tasks predicts treatment success (Dallery and Raiff, 2007; MacKillop and Kahler, 2009; Mueller et al., 2009; Sheffer et al., 2012; Stanger et al., 2012; Yoon et al., 2007), indicating that excessive delay discounting may be behavioral marker of both the onset of drug use and difficulty abstaining after use is established (Bickel et al., 2014b).

2.2. Delay discounting tasks

Delay discounting tasks measure how delaying a reward reduces the value of that reward, typically by arranging a series of discrete choices between some amount of a commodity available at a short delay (or no delay) and a larger amount of that commodity available at a longer delay. A series of questions of this type can be used to infer indifference points, or a series of values that represent the amount of an immediately available commodity that is subjectively equivalent to a greater amount of that commodity available after a delay. For example, if someone were to indicate a preference for $870 right now over $1000 in one month while also indicating a preference for $1000 in one month over $850 right now, we could conclude that $1000 in one month is worth somewhere between $850 and $870 right now. In other words, this individual is indifferent between ~$860 now and $1000 in one month. By assessing a series of indifference points across a range of delays, a discount rate can be calculated.

The first addiction delay discounting studies used a task where indifference points were obtained by asking two series of questions at each of seven delays (Madden et al., 1999, 1997; Rachlin et al., 1991). The first of these series started with a question between a set amount of a commodity available after a delay and the same amount available immediately (e.g., $1000 now versus $1000 in one month), with the expectation that everyone would choose the immediate option. The amount available immediately was then progressively decreased until the participant switched to the delayed amount. An analogous series of questions started with the same delayed amount and none of the commodity available immediately (e.g., $0 now versus $1000 in one month) with the expectation that everyone would then choose the delayed option. The immediate amount was then progressively increased until the participant switched to that option. These two switchover points were then averaged for each delay. This procedure seemed to work well, but was time consuming. Adaptive algorithms were developed by a number of labs, most of which shortened the number of choice trials necessary to obtain an indifference point. Probably the most commonly used today of these is a simple adjusting amount algorithm that was developed by Du et al. (2002). This procedure starts at each delay by asking participants to choose between a set delayed amount and half that amount available immediately. The immediate amount then adjusts up or down depending on the participant's choice in a series of five choice trials to narrow in on the indifference point. These five trials take little participant time while still allowing for 2⁵ or 32 discrete indifference points at each delay.

2.3. Measuring rate of discounting

Indifference points generated from a discounting task are typically fit with a curve to obtain an overall rate of discounting. Although different methods for obtaining discount rates have been proposed (Laibson, 1997; Mazur, 1987; Myerson and Green, 1995; Rachlin, 2006; Samuelson, 1937), the most common method in the psychology literature consists of fitting the indifference points with nonlinear regression to a hyperbolic curve first validated by Mazur (1987):

$$V=\frac{A}{1+\mathit{\text{kD}}}$$ (1)

where V is the discounted value (i.e., indifference point) of the delayed amount A at a given delay, D. The single free parameter, k, represents the rate of discounting. This model has a number of attractive features. First, it requires only a single free parameter to quantify discount rate, making comparisons among individuals or groups relatively straight-forward. Second, this model has been shown to provide a good description of delay discounting data, particularly compared to an exponential decay model that was assumed to describe intertemporal choice for many years (Green and Myerson, 2004; Madden et al., 1999). The discounting rate k has a unit of 1/time or time⁻¹, which is not straightforward to interpret. A more intuitive alternative to reporting k has been proposed in the form of an effective delay 50 (ED50; Yoon and Higgins, 2008), or the delay at which the delayed commodity loses half of its subjective value. This measure can be shown to be the simple reciprocal of k (i.e., is equal to 1/k), and because of this, the transformation does not affect statistical comparisons. An ED50 of 90 days, indicating that a commodity loses half of its value when delayed 90 days, is arguably more intuitive than the equivalent k value of 0.011 days⁻¹. Both k values and ED50 values are typically not normally distributed and must be logarithmically transformed prior to parametric statistical analysis (Mitchell et al., 2015).

While the model above typically describes discounting data well, systematic deviations from the hyperbolic shape described by this function have been noted (Green and Myerson, 1996; Rachlin, 2006). Often, these deviations consist of more pronounced discounting (i.e., steep slope) over relatively brief delays and less pronounced discounting (i.e., shallow slope) at longer delays than what is predicted by Mazur's hyperbola. As a result, multi-parameter, hyperbola-like models have been proposed to better account for these deviations. The most prevalent of these are extensions of Mazur's equation with an additional free parameter. Rachlin (2006) proposed that a free parameter should be inserted as an exponent on D (delay), while Myerson and Green (1995) proposed that the entire denominator of the right side of Eq. (1) be raised to a freely varying exponent. Each of these modifications allow the shape of the discounting curve to better approximate the shape of much discounting data, albeit in slightly different ways and at the cost of an additional free parameter in the model (McKerchar et al., 2009). These additional free parameters typically improve fit, but complicate interpretation of the data. In both cases, we have shown (Franck et al., 2015) that the added exponents are not independent of the k parameter, and therefore k cannot be compared directly across conditions or individuals if the exponents also vary. This is a problem for most experiments where discount rate is the variable of interest. Furthermore, several interpretations of the exponent exist (McKerchar et al., 2010; Myerson et al., 2011), and in the context of delay discounting may be related to nonlinear scaling of time (Green and Myerson, 1996), a psychophysical phenomenon known for some time (Stevens, 1957). We have proposed ED50 as a solution to this problem of collinear parameters (Franck et al., 2015). This measure can be straightforwardly calculated from both single- and multi-parameter discounting models, and importantly, its scale and interpretation is unaffected by the underlying model. If different models are used in different experiments or even different subjects within a single experiment, the ED50 can still be compared across all the data.

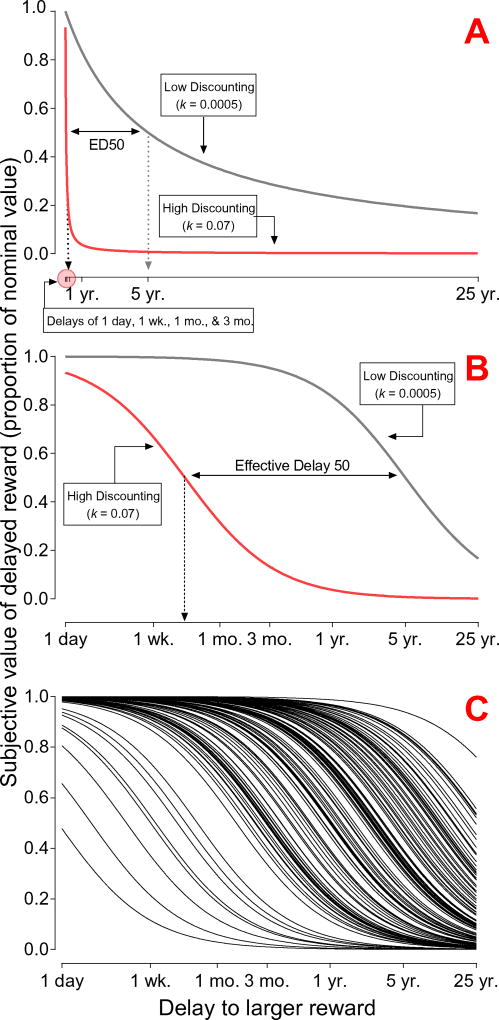
The nonlinear scaling of time that forms the basis of these multi-parameter models may actually be the basis for the human tendency to discount value hyperbolically instead of exponentially (Takahashi et al., 2008). Since from a psychophysical perspective time is perceived nonlinearly, we propose that discount curves ought to be best depicted graphically in log-linear space (see Fig. 1). We propose this for several reasons. First, with a logarithmic x-axis, Mazur's (1987) hyperbolic curve forms an ‘S’ shape (compare A and B of Fig. 1). The ‘S’ curve transitions from asymptotic valuations near a proportion of 1.0 to asymptotic valuations near 0.0 with the midpoint of this transition being the participant's ED50 value. This makes differences in discount rate or ED50 more easily observed and visually discern. Second, using the same equation (the simple hyperbolic in this case), differences in discounting can be seen as a location shift of the curve. The curve itself maintains the same shape; it is its location along the x-axis that shifts. This may suggest that in psychophysical space, the shape of discounting curves do not differ by rate, only the delay range over which the valuation transition takes place differs among people. Third, depicting curves in this way provides rationale for using longer delays, especially in the case of discounting among typical controls or the general population. Panel C of Fig. 1 displays individual-subject data from a dataset we reported previously (Koffarnus and Bickel, 2014) of college participants who completed an adjusting amount discounting task (Du et al., 2002). As can be seen, the transition point of many of the curves and the corresponding ED50 values fall on the right side of graph, centered around the longer delays. In some cases, especially with control or participants unaffected by addiction, excluding longer delays results in only a partial understanding of the participant's decision-making process.

Fig. 1.

Panels A and B show hypothetical discounting curves for relatively high (i.e., steep) and low (i.e., shallow) discount rates. Panel A depicts discounting curves as displayed on a linearly scaled x-axis, where spacing between delay values is arithmetic. Many of the shorter delays are grouped together in an indistinguishable bunch as shown in the circled area of the x-axis. Panel B depicts discounting curves on a logarithmic x-axis, where the progression of values is exponential. Note that effective delay 50 (ED50) is more easily identifiable and differences in discount rates are manifested in a location shift (i.e., left or right) along the x-axis. Panel C depicts real data from Koffarnus and Bickel (2014) for college-aged participants completing an adjusting amount discounting task showing the range of discounting rates seen with control subjects.

An alternative to finding k values with nonlinear regression is calculating area under the curve (AUC), or the area below a series of trapezoids formed by connecting the indifference points with successive straight lines (Myerson et al., 2001). Although this method alleviates complications and interpretations associated with model selection and curve fitting, it is not free from other analytic challenges. Recent analysis has shown that AUC, as it is typically calculated, is heavily influenced by the indifference points associated with the largest delays, while the shorter delays contribute a trivial amount to the AUC measure (Borges et al., 2016; Yoon et al., 2017). This is directly the cause of the linear x-axis that is commonly used with discounting data. The k parameter, however, is influenced by choices across the range of delays. Borges and colleagues suggest alternate methods of calculating AUC that correct this imbalance – either weighting all delays identically in AUC calculations or using a log-transformed delay spacing before drawing the trapezoids forming the AUC. For the reasons discussed above, a log-transformed delay sequence is not only more convenient for measurement and graphical display, it better represents the psychophysical scaling of time perception (Takahashi et al., 2008). If AUC is used to quantify discount rate, these proposed methods may provide measurements that more realistically characterize the choices made by participants.

The distribution of each of these variables used to quantify delay discounting rate should be examined for normality before statistical analysis. Discount rates quantified as a k value, AUC, or ED50 have all been shown to typically be highly skewed (e.g., Mitchell et al., 2015; Yoon et al., 2017). Often, logarithmic transformation normalizes these data, but differences among data collection methods and analytical models result in a need to carefully consider skewness with each new dataset.

2.4. Brief discounting measures

While the majority of delay discounting tasks resolve a discounting rate by generating a series of indifference points and fitting those to a nonlinear curve or calculating AUC, brief discounting measures have been developed to measure discounting rates in situations where there is little time to devote to the task or the subject population has limited attention, making a longer task onerous. The first of these is the monetary choice questionnaire (Kirby et al., 1999), which consists of 27 predetermined questions. This questionnaire can save some time over tasks like the adjusting amount task described above (Du et al., 2002), but at 27 questions, is only slightly shorter than the commonly used 35 question adjusting amount task with seven delays. Use of the monetary choice questionnaire is especially advantageous in situations where computerized administration is not feasible. Most discounting tasks are administered on a computer due to branching logic that adjusts question options dependent on the participant's previous responses. One disadvantage of the monetary choice questionnaire is that the number of discount rates is bounded within a specified range, given the finite number of response combinations of the 27 predetermined questions. Another disadvantage is that its scoring procedure can be complex and time consuming, however we recently developed Excel-based software to help alleviate these burdens (Kaplan et al., 2016). In addition, Wileyto et al. (2004) have proposed the use of logistic regression to estimate k from the monetary choice questionnaire. They found close correspondence in the resulting values when standard scoring was compared to the logistic regression.

To maximize brevity for situations where task administration time is a concern, we recently developed a brief, adjusting delay discounting task that can measure discount rates with only five questions (Koffarnus and Bickel, 2014). This task uses branching logic to assign participants one of 32 discount rates with just five questions, providing more range and resolution than the monetary choice questionnaire with fewer questions. We found that discount rates measured with this task were highly correlated with rates from a longer adjusting amount task and we were able to replicate a number of reliable effects in the literature with the abbreviated task. The advantage of this task is its very brief duration, taking participants around 30 s to complete. The task, however, is unable to discern responding that is internally inconsistent since any series of responses in such a short task are plausible.

2.5. Probability discounting

In addition to discounting of delayed rewards, much research has also been devoted to discounting of probabilistic rewards. Probability discounting assesses how the value of a reward is diminished by the odds against receiving it (Rachlin et al., 1991). When indifference points are plotted as a function of odds against receiving the award, the same hyperbolic and hyperbolic-like functions described above fit the data well. This process seems to be largely distinct from delay discounting (Green and Myerson, 2004; Ohmura et al., 2005), and its relationship to addiction is not entirely clear. Unlike with delay discounting rates, probability discounting rates do not appear to robustly distinguish people diagnosed with a drug addiction from those without a diagnosis (for a review, see Bickel et al., 2014a). In contrast, probability discounting rates do often distinguish problem gamblers from nongamblers (Holt et al., 2003; Madden and Bickel, 2010). In an analogous way to delay discounting differentiating drug addicts, probability discounting provides a measure of how problem gamblers overvalue probabilistic rewards leading to excessive gambling choices. Probability discounting may be better than delay discounting, however, in detecting acute alcohol intoxication (Bidwell et al., 2013).

2.6. Other types of discounting

A discounting framework can be used to assess how many manipulations affect reward value. For example, in addition to delay to receipt and probability of receipt, effort required to obtain a reward (Mitchell, 2004) and closeness of social relationship to the reward recipient (Jones and Rachlin, 2006) have been modeled in a discounting framework. While interesting in other contexts, neither of these measures has received much attention in relation to addiction. A modification of delay discounting to model risky sexual choices is related to addiction, however. Stimulant users are known to have a greater incidence risky sexual behavior and a corresponding increased rate of HIV infection (Joe and Simpson, 1995). The sexual delay discounting task was developed to model the decision-making process in risky sexual choices. Participants are asked to choose between having safer sex now with a condom or other barrier protection and having riskier sex after a delay to get a condom (Johnson and Bruner, 2012). All choices are made regarding hypothetical sexual partners chosen by the participants from an array of images of clothed individuals who vary in appearance. Discounting rates from this task are related to self-reported risky sexual behavior (Johnson and Bruner, 2012), are increased by alcohol intoxication (Johnson et al., 2016), are increased by acute stimulant administration commiserate when those stimulants cause sexual arousal (Johnson et al., 2017), and are greater in stimulant users than controls (Herrmann et al., 2014; Koffarnus et al., 2016).

2.7. Task fidelity and dealing with nonsystematic data

Delay discounting tasks consist of a series of hypothetical self-reported preferences and as such, fidelity of participant responses may be a concern. Not all studies use hypothetical rewards instead of actual rewards that are given to the participant, but most do. Research comparing hypothetical and real rewards has found that similar data are obtained with either, including behavioral choice data (Baker et al., 2003; Johnson et al., 2007; Johnson and Bickel, 2002; Lagorio and Madden, 2005; Madden et al., 2004, 2003) and the neural correlates of those choices (Bickel et al., 2009). These data suggest that in most situations, hypothetical rewards are sufficient for studying intertemporal choice with delay discounting tasks. In addition, hypothetical rewards allow for studying time frames that are unrealistic for real rewards (e.g., 5 years or more) and commodities that are impractical or unethical to arrange in a laboratory setting (e.g., risky sexual encounters; Johnson and Bruner, 2012).

Delay discounting tasks operate on the fundamental assumption that a delayed reward is less valuable than an immediate one. When a participant's choices violate this assumption, it is likely that the participant was not attending to the task, did not understand the task, or was responding dishonestly. When this occurs, researchers may want to isolate that participant's data to apply greater scrutiny and possibly remove it from the main analysis. Johnson and Bickel (2008) have proposed two criteria to judge whether data adhere to the assumption that value is systematically related to delay. These criteria are ‘bounce’ and ‘trend’, where bounce refers to how often value increases instead of decreases from one delay in the series assessed to the next longest delay, and trend refers to whether value is lower at the longest delay than at the shortest. The authors of these rules also suggest that they be used as guidelines and adapted as necessary to the specific experiment. For example, in the sexual delay discounting task described above (Johnson and Bruner, 2012), participants choose between hypothetical activity with or without a condom. One of these qualitatively different options may be preferred exclusively, which would indicate no effect of delay and indicate a violation of the ‘trend’ rule of Johnson and Bickel (2008). However, exclusive responding in this case could be perfectly logical if someone prefers one option enough that delay to the safer sex option has no impact on choice. In this case, only the ‘bounce’ criteria make sense to use.

2.8. Assessing goodness of fit for nonlinear discounting models

When fitting data to a nonlinear regression model like those commonly used to fit indifference points from a delay discounting task, it is good practice to report one or more goodness-of-fit statistics to describe how well the model's predictions map onto the obtained data. Goodness-of-fit statistics report how close the observed data are to a model fit, and therefore tend to focus on the residual sum of squares (SS_residual), or the sum of the squared distance along the y-axis from each point to the regression line. There are at least three general approaches taken to report the SS_residual by goodness-of-fit statistics, which we have summarized in Table 1. R² is probably the most commonly reported, and is the SS_residual expressed as a ratio to the total variability in the dataset (SS_total). Note that there are different ways of calculating R², but we are using the one identified as most conceptually appealing by Kvålseth (1985) and also commonly used in software packages such as GraphPad Prism. As a ratio expressing the proportion of the spread in the data that is reduced by the model, R² is independent of the units the data are in and has the same interpretation across datasets and experiments. However, this statistic has been criticized as a goodness-of-fit measure for nonlinear regression in some contexts. Instead of R², others have promoted the use of either root mean squared error (RMSE; Johnson and Bickel, 2008) or Akaike's information criterion (AIC; Spiess and Neumeyer, 2010). Both of these statistics are closely related to R² and each other, with RMSE simply being a transformation of the SS_residual without expressing it as a ratio to the total sum of squares, and AIC being a transformation of the SS_residual that is penalized by the model complexity (i.e., the number of fitted parameters in the model). Bayesian information criterion and adjusted R² are other goodness-of-fit measures with penalties for model complexity (e.g., Raftery, 1995). As interrelated descriptive statistics, we think each of these three measures has a place. Previous criticisms of R² were made in specific contexts where the authors were right to point out that R² is not appropriate. Johnson and Bickel (2008) correctly pointed out that arbitrary R² cutoffs should not be used to identify datasets for elimination from an experiment, and Spiess and Neumeyer (2010) correctly pointed out that R² should not be used to compare nonlinear regression models of differing complexities. We do not disagree with either of these papers, but we would also warn against overextending these conclusions to other contexts. Each of these statistics has its place, which we have high-lighted in Table 1. For example, we recently used R² to compare a model separately applied to untransformed and logarithmically transformed data, and we specifically chose this statistic because the models were of equal complexity and the different scale of the transformed and untransformed data precluded the use of either RMSE or AIC (Koffarnus et al., 2015).

Table 1.

A comparison of goodness-of-fit statistics for the characterization or comparison of nonlinear regression models. Care should be taken to choose the appropriate statistic(s) for the intended use case.

Statistic	Formulation	What is described	Unit independent	Range of possible values	Direction of better fits	Appropriate use cases
R2	$1.0-\frac{{\mathit{\text{SS}}}_{\mathit{\text{residual}}}}{{\mathit{\text{SS}}}_{\mathit{\text{total}}}}$	The SSresidual expressed as a proportion of SStotal.	Yes	−∞ ↔ 1.0	Closer to 1.0	Describing how much of the variability in a dataset is accounted for by a model
RMSE	$\sqrt{\frac{{\mathit{\text{SS}}}_{\mathit{\text{residual}}}}{n-1}}$	The square root of the mean SSresidual	No	0 ↔ ∞	Closer to 0.0	Describing the fit of the model in the units of the dependent variable without considering total data variability
AIC	$n\times \text{ln}\left(\frac{{\mathit{\text{SS}}}_{\mathit{\text{residual}}}}{n}\right)+2k$	The mean SSresidual with an additional penalty for the complexity of the model	No	−∞ ↔ ∞	Lower values	Determine which of a set of models is the most parsimonious after accounting for model complexity

Note: SS = sum of squares; n = number of data points; k = number of fitted parameters in the regression model.

3. Drug demand

3.1. Role of drug demand in addiction

Standard economic demand analyses quantify the relationship between the cost of a commodity and population-level measures of consumption of that commodity. Behavioral economic demand analyses are analogous to these population-level analyses, but can be used to understand the level of motivation to consume a product on either an individual or small group level, including for cigarettes (Bickel et al., 1991; MacKillop et al., 2008), alcohol (Gray and MacKillop, 2015; MacKillop et al., 2010a; Murphy and MacKillop, 2006), and other drugs (Aston et al., 2015; Bruner and Johnson, 2014; Christensen et al., 2008; Jacobs and Bickel, 1999; Johnson and Johnson, 2014; Reed et al., 2016a). This level of analysis allows for experimental manipulations to be made on variables of interest. By quantifying how consumption decreases as costs to obtain and consume a product increase, important indices of demand are obtained. These indices can be grouped into two main measures of consumption, demand intensity and demand elasticity, which are associated with use level and dependence severity (MacKillop et al., 2010a, 2009, 2008; Murphy et al., 2011). Demand intensity is the amount of the commodity consumed when available at a very low cost approaching free, and demand elasticity quantifies the degree to which the individual is willing to increase monetary or effort-based expenditures to maintain the same level of consumption as costs increase. Elasticity of demand has been shown to be a characteristic of the drug itself and independent of drug dose for many drugs. That is, when consumption is plotted as a function of unit price (responses/mg of drug), the consumption data from each dose converges to a single function (Bickel et al., 1991; Hursh and Roma, 2013; Hursh and Silberberg, 2008; Hursh and Winger, 1995). This makes demand elasticity a convenient measure of drug abuse liability without the complication of selecting a representative dose that could impact conclusions drawn.

3.2. Demand tasks

Fundamentally, demand measures are obtained by measuring consumption of a commodity over a range of prices for that commodity. Price can be conceptualized as either monetary cost per unit of drug or effort required per unit of drug. Procedures to assess consumption across unit price can be grouped into two types. First, there are laboratory self-administration measures modeled after preclinical self-administration procedures (Greenwald and Hursh, 2006; Johnson and Bickel, 2006; Madden et al., 2000; Spiga et al., 2005). Participants make responses on a manipulandum for some drug reward (e.g., a puff from a cigarette; Shahan et al., 2001), and actually consume those drug rewards in the context of the session. The number of responses per unit of drug reward is considered the price, and this is typically varied across or within sessions to obtain consumption across prices.

The second main category of demand tasks consist of drug purchase tasks (for a review of purchase tasks generally, see Reed et al., 2016b). Here, participants are asked to indicate how much of a drug they would purchase for their own consumption at a range of monetary prices. The first drug purchase task study was conducted with units of heroin (Jacobs and Bickel, 1999), but research has since greatly expanded with alcohol (Murphy and MacKillop, 2006) and cigarette purchase tasks (Murphy et al., 2011). In drug purchase tasks, price is conceptualized as monetary cost, with the price typically varied across a wide range (e.g., $0.01 per cigarette to $1000 per cigarette). While hypothetical purchases are often used, similar data are obtained with hypothetical purchases and actual purchases of products in a lab setting (Amlung et al., 2012; Wilson et al., 2016). These tasks have been used in combination with cue-reactivity paradigms (e.g., Acker and MacKillop, 2013; Amlung and MacKillop, 2014; Mackillop et al., 2012; MacKillop et al., 2010b), whereby following cue exposure (e.g., smelling an alcoholic drink, opening a pack of cigarettes) responses on the task typically increase coinciding with increases in self-reported cravings for that drug. Thus, demand tasks may serve as a valid, alternative measure of state-based craving.

A related variant of the drug purchase task is the Brief Assessment of Alcohol Demand (BAAD) developed by Owens et al. (2015). Rather than assessing purchasing at a range of prices, the BAAD contains three questions: (1) “If drinks were free, how many would you have?”, (2) “What is the maximum total amount that you would spend on drinking (approximately)?”, and (3) “What is the maximum you would pay for a single drink?”. These three questions are intended to quickly assess demand intensity, O_max (the maximum expenditure at any price, closely correlated with P_max or the price at which O_max occurs), and breakpoint. Although this task is indeed brief, measures of elasticity are necessarily unable to be determined.

3.3. Assessing product interactions

Single-commodity demand tasks measure how the consumption of a single commodity decreases with increases in price, but do not directly assess choice. Choice is implied, since decreasing consumption at high prices is typically replaced by increased consumption of other commodities, but single-commodity demand tasks do not overtly assess this. Multiple-commodity demand tasks can more straightforwardly assess how decisions are made among the many products available to us every day. Like single-commodity tasks, multiple-commodity tasks still ask about consumption patterns across a range of prices for a specific variable-price commodity (e.g., cigarettes). However, consumption of one or more other constant-price products (e.g., nicotine gum) is measured as a function of the price of the variable-price commodity. By measuring consumption of both products, the researcher can determine how these products interact. Three types of economic interactions are possible, which can be illustrated with the cigarette and nicotine gum example with cigarettes being a variable-price (i.e., primary) product and gum being a constant-price (i.e., alternative) product (Hursh and Roma, 2013). If the consumption of nicotine gum does not vary with the price of cigarettes (and declining consumption of cigarettes), then the two are economic independents. If the consumption of nicotine gum follows that of cigarettes (i.e., both decrease together as cigarette price increases), then they are complements. If nicotine gum consumption increases when cigarette consumption decreases, then gum is a substitute for cigarettes.

Most multiple commodity demand tasks have focused on two to three commodities or drugs available at the same time to model specific questions. For example, Johnson et al. (2004) found that nicotine gum and cigarettes with most of the nicotine removed were both substitutes for conventional cigarettes. Focusing on interactions between a limited number of products simplifies the experimental context, but such focus may not capture the complex economic choices we make every day where seemingly hundreds of product choices are available for purchase in the real-world marketplace. These complex interactions have recently been modeled with studies using the Experimental Tobacco Marketplace (Quisenberry et al., 2016), a modification of procedures used with complex food purchasing choices (Epstein et al., 2010). In this model, multiple products are available simultaneously in a web-based storefront, similar to a real-world marketplace. Participants allocate a budget to whatever mix of products they choose, and the procedure is repeated with the primary product of interest set to a new price. This procedure allows for the measurement of multiple product interactions simultaneously, which can both save time and more closely resemble actual product marketplaces.

3.4. Extracting behavioral economic demand parameters

Consumption for a variable-price commodity decrease as price increases in a characteristic way that is well described by a function first proposed by Hursh and Silberberg (2008):

$${\mathit{\text{log}}}_{10}Q={\mathit{\text{log}}}_{10}{Q}_0+k(e^{-\alpha Q_{0}C}-1)$$ (2)

where Q is consumption of a given commodity at price C, Q₀ is derived consumption as price approaches zero and is a measure of demand intensity, α is demand elasticity, and k is the vertical span of the function in log₁₀ units from unconstrained consumption (free price) to the minimum consumption as price approaches infinity. Span can be set to a constant determined separately from the main analysis by either fitting it as a global shared parameter to all data under consideration or setting it to the actual span from the log-transformed consumption at the lowest price to the log-transformed consumption at the highest price. By fixing span to a constant across analyses, two free parameters representing demand intensity (Q₀) and demand elasticity (α) remain. This equation generally provides very good fits to data from a wide variety of contexts (Amlung et al., 2012; Aston et al., 2015; Madden and Kalman, 2010; Roma et al., 2016). However, the left side of this equation is log₁₀-transformed consumption data. Log transforming consumption data can pose a logistical problem as zero consumption values cannot be log transformed. With a sufficiently wide range of prices assessed, zero consumption values are inevitable. Both removing zeros and replacing them with nonzero values create problems of their own (Koffarnus et al., 2015; Liao et al., 2013; Yu et al., 2014), so to alleviate those issues, we recently proposed a modification of the Hursh and Silberberg (2008) function:

$$Q={Q_0}^{\ast }{10}^{k(e^{-\alpha Q_{0}C}-1)}$$ (3)

where Q, C, Q₀, k, and α function the same as in Eq. (2). The only difference between the two is that we raised each side of the equation to a power of 10 so the untransformed consumption (Q) data can be fit without log transformation. We found that this modification allows for the same interpretation of the fitted parameters and, if anything, improved fits to the data (Koffarnus et al., 2015), as did an independent follow-up evaluation (Strickland et al., 2016).

Similar to discounting parameters, fitted demand parameters are often highly skewed (e.g. Lemley et al., 2016; MacKillop et al., 2010a). If these parameters are to be incorporated in statistical models that assume normally distributed data, transformation should be considered before proceeding with data analysis. Demand parameters can often be normalized with a logarithmic or square-root transformation (e.g., Amlung et al., 2013; Koffarnus et al., 2015), although this may not hold for all datasets. Also note that when selecting a goodness-of-fit statistic, the same considerations discussed in Section 2.8 and summarized in Table 1 apply as with nonlinear regression models applied to discounting data.

3.4.1. Normalization

When demand elasticity is the primary emphasis of a figure, normalization is a procedure that can be used to visually isolate those differences. A fundamental aspect of Eqs. (2) and (3) is that α is standardized based on level of consumption at free price (i.e., Q₀), such that magnitude differences in a commodity reflect the same elasticity, or as termed by Hursh and Silberberg (2008), “essential value.” A full explanation is beyond the scope of this paper, so we direct readers to their 2008 publication; rather, here we aim to distinguish the standardization procedure inherent within the aforementioned equations with the normalization procedure proposed by Hursh and Winger (1995). In Hursh and Winger's normalization procedure,¹ both unit price and consumption data are standardized to a “normalized dose”, which is equal to 100 ÷ Q₀, Using this quantity, normalized consumption (Q_norm) is calculated as: Q_norm = (Q * 100) ÷ Q₀ and normalized price (P_norm) is calculated as: P_norm = (C * Q₀) ÷100. Normalized consumption is then plotted as a function of normalized price. As long as the parameters in Eqs. (2) or (3) are held constant, values of α are identical to that of non-normalized data.

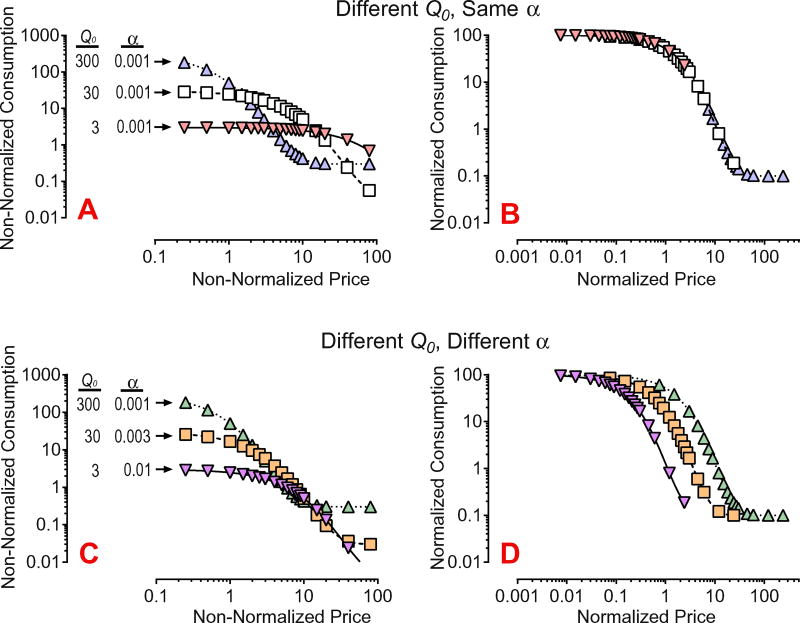
Take Fig. 2 for illustration. We generated a series of curves using known, a priori selected parameters (see figure and caption for specific values) and graphed the normalized and non-normalized data. Panel A in Fig. 2 shows non-normalized data. Notice that although the curves with differing values of Q₀ intersect, the values of α are identical. It may be difficult to judge the equality of α by visual analysis alone, so this is made easier when data are transformed using the normalization procedure just described (i.e., the overlapping curves; Panel B). On normalized coordinates, demand curves with the same elasticity values will always fall on the same curve. Contrast this with the bottom two panels in Fig. 2. Here, we have generated three sets of curves with differing values of α and Q₀. In Panel C, it is still difficult to tell the degrees of differences in elasticity between the curves as compared to Panel A. However, now when normalized transformed data are depicted (and levels of Q₀ are again not of interest as all three curves start at 100; same as Panel B), it is much easier to visualize differences in α, which now show up as roughly parallel curves (Panel D).

Fig. 2.

Typical examples of how differences in demand intensity (Q₀) and elasticity (α) are affected by the normalization procedure proposed by Hursh and Winger (1995). When Q₀ differs (panel A), it can be hard to identify curves with similar elasticities, but normalization of the same data makes this obvious visually because all data with the same elasticity fall on the same curve when normalized (panel B). When both Q₀ and α differ (panel C), distinguishing which curve is most or least elastic is also difficult, but normalization of these data produces parallel curves aligned from highest to lowest elasticity (panel D).

3.4.2. Cross-product interactions

To measure product interactions, Hursh and Roma (2013) proposed a cross-price elasticity equation as a complement to Eq. (2) above:

$${\text{log}}_{10}Q={\text{log}}_{10}{Q}_{\mathit{\text{alone}}}+(I^{\ast }{e}^{-\beta C})$$ (4)

In this equation, Q_alone represents the maximum consumption of the fixed-price commodity when the primary commodity has a price high enough to drive its consumption to zero, β is the sensitivity of fixed-price commodity consumption to the price of the primary commodity, I is an interaction parameter that indicates whether the fixed-price commodity is a substitute (positive I value), complement (negative I value), or independent (I value near zero), and Q and C represent consumption of the fixed-price commodity and cost of the primary commodity, respectively, and are known from data. Like Eq. (2), this equation requires log-transformed data to be fitted, which poses more of a problem than with the Eq. (2) since zero consumption data can be very common in substitution experiments (e.g., Quisenberry et al., 2016). Analogous to how we modified Eq. (3) above to allow for untransformed data to be fit, a logical extension of Eq. (4) would be to raise it to the power of 10 to fit cross price elasticity data including zero consumption values. Future work will determine the utility of this approach.

3.5. Nonsystematic data

Like with discounting data, data are sometimes obtained from demand tasks that are not internally consistent or indicate illogical responding. For example, a participant may indicate they would consume 1000 cigarettes in a 24-hour period, a level of consumption that would not be feasible. Alternatively, a participant may indicate no consumption at $5 per cigarette, but report they would consume 10 cigarettes at $100 per cigarette, a pattern that defies logic. These patterns can make it difficult to compare groups because they often represent outlier data that is not under the control of the experimental manipulations. Data consistency checks analogous to those proposed by Johnson and Bickel (2008) for discounting data have been used (Bruner and Johnson, 2014) and formally proposed (Stein et al., 2015) to identify and potentially censor datasets with illogical response patterns. Three criteria were proposed. The first two are ‘bounce’ and ‘trend’, which are directly analogous to the similarly named criteria for discounting data proposed by Johnson and Bickel (2008). Bounce refers to how often consumption increases as price increases, and trend refers to whether consumption is lower at the highest price than at the lowest price. Additionally, a third category, ‘reversals from zero’ was proposed as a special case of the pattern described in the bounce criterion. This criterion flags nonzero consumption at a price higher than a price where the participant indicated zero consumption, even if the increase was too small to be detected by the bounce criterion.

4. Drug choice

Drug abuse and addiction, fundamentally, can be conceptualized as repeated decisions to take a drug over abstaining. Drug choice procedures have been used to straightforwardly model the tendency to repeatedly take a drug by arranging a series of choices between an active drug and a comparator, typically placebo and/or an alternative drug. Participants are usually allowed to sample the drug or drugs in a blinded fashion, which is followed by a series of choice trials on separate sessions or within a session. Drug choice procedures have been used to study choices to use coffee (Griffiths et al., 1986), alcohol (de Wit and Chutuape, 1993), pentobarbital (Griffiths et al., 1980), diazepam (Griffiths et al., 1980; Johanson and Uhlenhuth, 1980a), and amphetamine (Johanson and Uhlenhuth, 1980b). Although studies of this type are often considered the gold standard of abuse liability assessments, most standard drug choice research where each option chosen is consumed by the subject is conducted in animal models due to the greater flexibility and control that is possible (Bergman and Paronis, 2006).

Another common drug choice procedure presents the opportunity to self-administer a drug against a non-drug reinforcer, which is typically money or a close analogue of money (e.g., vouchers). If the monetary amount is varied across trials, these procedures have the added ability to provide a measure of how much a drug is worth to participants. This type of procedure has been used widely to study self-administration of opiates like heroin, oxycodone, morphine, hydromorphone, and buprenorphine (Comer et al., 2013, 2005a, 2005b, 2002, 2001, 1999; Comer and Collins, 2002; Greenwald and Hursh, 2006; Greenwald and Steinmiller, 2009; Jones et al., 2014; Middleton et al., 2012). Additional drugs from other classes have also been studied like marijuana (Hart et al., 2002).

4.1. Multiple-choice procedure

The multiple-choice procedure was developed in response to the time consuming nature of human drug choice procedures and drug self-administration procedures that were impractical to conduct in many situations (Griffiths et al., 1993). Traditional choice procedures arranged the delivery of each consequence chosen. Since multiple choice trials are typically necessary to determine if a drug has abuse liability or a treatment is effective, these procedures are time-consuming. The multiple-choice procedure typically begins with an exposure period where the participants sample a drug, although this step can be skipped if the drug is not delivered blinded and the participant is familiar with it (e.g., Benson et al., 2009 with alcohol choices). This exposure period is followed by a series of choice trials all completed in a short time frame. Instead of delivering the consequence of each choice trial, participants are told that they will receive the option chosen for one of the choice trials that will be randomly selected. This preserves the fidelity of the data because any given choice in the experiment could be selected as the ‘real’ one, but a great deal of experimental time is saved since many choices can be made in a single session.

Since it was first developed (Griffiths et al., 1993), the multiple-choice procedure has been used in a number of contexts. A frequent use has been to assess abuse liability of a drug. In these experiments, participants are typically exposed to a blinded drug dose and a comparator (often money) on separate sessions. If the participant then chooses the active drug over money on subsequent choice trials, the drug can be said to have some abuse liability. This procedure has the extra benefit of being able to determine not only if the participant would like to self-administer the drug, but how much those administrations are worth. This procedure has been used to assess the abuse liability of a range of drugs including pentobarbital (Griffiths et al., 1993), cigarettes (Griffiths et al., 1996), alcohol (Benson et al., 2009; Correia and Little, 2006), stimulants (Alessi et al., 2003; Jones et al., 1999; Stoops, 2003), MDMA (Tancer and Johanson, 2006), electronic cigarettes (Vansickel et al., 2012), caffeine (Garrett and Griffiths, 1998; Schuh and Griffiths, 1997), marijuana (Greenwald and Stitzer, 2000), opiates (Greenwald et al., 1999), and tobacco/alcohol combinations (Schmitz et al., 2003). This procedure has also been used to evaluate treatment services. Effectiveness of treatment components can be evaluated by their ability to reduce or abolish choices for drug over alternatives in the multiple-choice procedure (e.g., Lile et al., 2004), and patient preference for different treatment approaches have also been evaluated (Chutuape et al., 1998; Kidorf et al., 1995).

4.2. Quantifying drug choice

Choice experiments typically present participants with a series of discrete choices with the chosen drug or drug alternative given to the participant for at least one of the choices. The quantification of drug choice is then simply the number of times it was chosen compared to an alternative. However, some researchers have begun to apply behavioral economic demand analyses to serial money vs. choice data collected from these experiments (e.g., Greenwald and Hursh, 2006). The combination of choice and demand methodologies may allow for the integration of concepts such as demand intensity and elasticity with discrete-trial choice data.

5. Iowa Gambling Task (IGT)

Initially developed as a task to detect insufficiencies/damage to the ventromedial prefrontal cortex (Bechara et al., 1994) in individuals who otherwise displayed normal performance on other decision-making tasks, applications of the IGT have been expanded to assess a wide range of decision-making and cognitive deficits (Bechara, 2007), including addiction and pathological gambling.

The original implementation of the IGT (also known simply as the gambling task) used physical decks of cards and although it is now often administered electronically (e.g., via computer), core aspects of the task remain. Importantly, research suggests performance is comparable between both versions (Bechara et al., 2000; Bowman et al., 2005). However, it appears that the instruction set is likely to affect performance (Fernie and Tunney, 2006). In addition, performance on versions using real or facsimile money (Bowman and Turnbull, 2003; Carter and Pasqualini, 2004) is comparable. In the IGT, participants are endowed with $2000 of “play money” and they are told to choose cards from four decks of cards, identical in appearance, to maximize the amount of money earned. Typically ended after 100 trials, participants are not told how many choices they will have to make.

In the long run, two of the four decks, decks A and B, are considered disadvantageous, whereas the other two decks, decks C and D, are considered advantageous. Each card choice in decks A and B results in a $100 gain and each card choice in decks C and D results in a $50 gain. In this respect, it would be advantageous to choose cards from the first two decks. However, each deck is also associated with a punishment contingency. For each card chosen from any deck, there is a chance that a participant will lose money (in addition to what is gained). Associated with each of block of 10 trials, decks A and B result in a net loss of $250, whereas decks C and D results in a net gain of $250. Further broken down within each block of 10 trials, decks A and C are associated with more frequent, yet smaller money losses and decks B and D with one large money loss. More choices of the advantageous decks indicate more optimal performance. Bechara et al. (1994) found that compared to healthy controls, participants with damage to parts of their ventromedial prefrontal cortex chose more cards from the disadvantageous decks and that selections from these decks persisted. Control participants, on the other hand, sampled from all decks initially, but allocated more choices towards the advantageous decks as trials progressed.

5.1. Role of IGT in addiction

Similar to choice trials in the delay discounting paradigm, the IGT incorporates outcomes where decisions can result in relatively immediate, large gains, but that are also associated with greater long-term losses. Additionally, optimal responding requires an accurate accounting of probabilistic rewards, which relates to probability discounting as well. Poor performance on the IGT may be reflective of greater sensitivity to immediate rewards or low sensitivity to probabilistic losses. An individual who is insensitive to smaller, more frequent losses and to long term payouts (i.e., outcomes) would be more likely to persist in choosing from deck A. A similar individual who is also insensitive to the delayed outcomes, but is sensitive to the more frequent punishments may be more likely to persist on deck B. Recall, however, that both of these decks are disadvantageous in the long run.

5.2. Distinguishing addiction from typical performance

Several studies have evaluated performance on the IGT among a variety of clinical populations including alcohol, nicotine, cocaine, opiate, and marijuana users. Overall, results from these studies indicate suboptimal performance (i.e., persistence in card selections from the disadvantageous decks) by substance abusers compared to controls, however caution must be exercised given the different methods by which performance on the IGT can be measured. For example, alcohol-dependent participants had lower scores compared to healthy controls during the latter blocks of the IGT (Kim et al., 2011). Alcohol-dependent participants scored lower on all blocks of trials compared to controls (Goudriaan et al., 2005). Fein et al. (2004) showed that long-term abstinent (≥6 mo) alcoholics performed more poorly on the task (less difference between advantageous and disadvantageous decks) compared to controls. However, not all of the research clearly points to decreased performance (Bowden-Jones et al., 2005) and differences exist between initial trials and later trials (Ernst et al., 2003).

Similar decrements in performance were noted in other substance using populations compared to controls, including opiate users (Mintzer and Stitzer, 2002; Petry et al., 1998) and cocaine users (Verdejo-Garcia et al., 2007; Stout et al., 2004).

In addition to distinguishing drug users from controls, IGT performance is also related to drug use severity or frequency. Higher reported amounts of cocaine use was related to poorer performance (Monterosso et al., 2001) among cocaine-dependent participants and longer-term heavy marijuana use was also associated with decreased performance (Whitlow et al., 2004).

Finally, IGT performance has also been shown to be associated with initiation and maintenance of abstinence among substance users. Bartzokis et al. (2000) found recently abstinent cocaine-dependent males performed statistically significantly better than current cocaine-dependent males. Nejtek et al. (2013) conducted a longitudinal study with two groups of participants: individuals with comorbid mood disorder and cocaine/methamphetamine use and cocaine-dependent individuals with no mood disorders. Although they found no group differences in IGT performance, baseline performance (i.e., selections from the disadvantageous decks) of the comorbid group statistically significantly predicted the number of negative urine tests throughout the 20-week study. In contrast, Schmitz et al. (2009) found that IGT score was not predictive of retention in a treatment program for cocaine-dependent participants, yet they did find that participants who successfully achieved abstinence scored better on the task. Bolla et al. (2005) examined performance among recently abstinent (~25 days) marijuana users and found they performed more poorly compared to controls.

5.3. Measuring the IGT

Outcome measures from the IGT include total amount of money earned and choice allocation among the two sets of decks. Most often, choice allocation, or a net score, is defined as the difference between card selections from the advantageous deck and from the disadvantageous deck. Choice allocation may also be broken down by subsets of trials, typically five blocks of 20 trials each. More rarely, however, cutoff scores may be used (Bechara et al., 2001; Verdejo-Garcia et al., 2006). In these cases, a cutoff score of 10 or less, calculated by taking the sum of advantageous decks minus the sum of disadvantageous decks, has been used.

6. Balloon Analogue Risk Task (BART)

The BART is a behavioral task used to measure risky behavior (Lejuez et al., 2002). The task is administered electronically (i.e., on a computer). Participants view what looks to be a balloon, which is the same size at the beginning of each trial. At any time during the task, participants have two options: they can click the balloon or click a button to redeem the money earned thus far from pumping up the balloon. Choosing the latter ends the current trial, money is earned, and a new trial begins. Each time the participant clicks on the balloon, it gets larger (e.g., 0.125 in increase) and the participant is awarded (e.g., 5 cents). However, associated with each pump is a probability that the balloon explodes, a “popping” sound is emitted, and the participant loses any money that had been accrued during that trial. Three different balloon colors (i.e., blue, yellow, orange) are presented during 90 trials and each balloon color is associated with a different probability of exploding, resulting in an expected 64, 16, and 4 pumps before popping, respectively. Variants of the task use fewer trials or colors (Lejuez et al., 2003).

6.1. Role of BART in addiction

The BART attempts to approximate risky choice in everyday behavior, such that at some point there are diminished returns for continuing to engage in a given behavior (e.g., drinking alcohol). With everyday behavior, one simply stops engaging in that behavior and with the BART, the individual can “cash out”. The BART may be conceived in a loose sense as having similar features to both the IGT. The IGT consists of risky choices that also pay out, very much similar to the BART.

In their seminal article, Lejuez et al. (2002) demonstrated performance on the BART was statistically significantly correlated with self-report measures of impulsivity, including the Barratt Impulsiveness total score (Barratt, 1985), Eysenck Impulsivity subscale score (Eysenck et al., 1984), Multidimensional Personality Questionnaire Behavioral Constraint subfactor score (Tellegen and Waller, 2008), and Sensation Seeking total score (Zuckerman and Eysenck, 1978). The researchers also found performance was correlated with self-report measures of everyday risk behavior, for example, scores on the Alcohol Use Disorders Identification Task, number of cigarettes smoked per day, and gambling behavior. Lejuez et al. also demonstrated the BART had incremental validity over and above demographic and impulsivity self-report measures when predicting delinquency risk behaviors and substance use and sexual risk behaviors.

More pumps may be thought of as indicative of greater impulsivity and risk taking because each additional pump increases the chances of the balloon popping and, thus, losing all money earned during that trial. However, many of the studies examining the BART reveal that participants (designated as a clinical sample or not) do not pump past the “optimal” number, for example 64 pumps on the blue balloon and so, although risky, more pumps ultimately earn more money.

6.2. Distinguishing addiction from typical performance

Lejuez et al. (2005, 2003) found smokers displayed greater adjusted scores (average number of pumps for all non-exploded balloons) and higher earnings compared to control participants. However, Dean et al. (2011) were unable to replicate these results in smokers. Crowley et al. (2006) found that adolescents with substance use and conduct disorder engaged in more pumps compared to the control participants. Performance on the BART was also correlated with number of alcoholic drinks consumed per week, AUDIT score, and binge drinking questionnaire score among college students (Fernie et al., 2010). The BART is sensitive to individuals' histories of alcohol use disorders. In a comparison of three groups that included participants diagnosed with bipolar disorder with a history of alcohol use disorder, bipolar with no history of alcohol use disorder, and healthy controls, the group with a history of alcohol use disorder displayed statistically significantly greater number of pumps than the comparison groups (Holmes et al., 2009). Healthy controls and those with no history of an alcohol use disorder did not differ. Hopko et al. (2006) found differences in BART scores between college-aged participants who had never used MDMA (i.e., ecstasy), had used MDMA once, and had used MDMA more than once. Never users scored the lowest, whereas multiple-time users scored the highest.

6.3. Measuring the BART

Measures calculated from performance on the BART include monetary earnings, number of pumps, and number of explosions. Number of pumps can be adjusted (as a relative measure) by taking the average of only the pumps when balloons did not explode as this measure is “… preferable because the number of pumps was necessarily constrained on balloons that exploded, thereby limiting between-subjects variability in the absolute averages” (Lejuez et al., 2002; p. 78).

7. Conclusions

Delay discounting tasks, demand tasks, choice tasks, the IGT, and the BART are all commonly used to study dysfunctional decision making in addiction. As researchers continue to investigate how decision making is integral to addiction processes, the wealth of methodological detail reviewed here should assist them in their efforts.