Brain state expression and transitions are related to complex executive cognition in normative neurodevelopment

Abstract

Adolescence is marked by rapid development of executive function. Mounting evidence suggests that executive function in adults may be driven by dynamic control of neurophysiological processes. Yet, how these dynamics evolve over adolescence and contribute to cognitive development is unknown. In a sample of 780 youth aged 8–22 yr (42.7% male) from the Philadelphia Neurodevelopment Cohort, we use a dynamic graph approach to extract activation states in BOLD fMRI data from 264 brain regions. We construct a graph in which each observation in time is a node and the similarity in brain states at two different times is an edge. Using this graphical approach, we identify two primary brain states reminiscent of intrinsic and task-evoked systems. We show that time spent in these two states is higher in older adolescents, as is the flexibility with which the brain switches between them. Increasing time spent in primary states and flexibility among states relates to increases in a complex executive accuracy factor score over adolescence. Flexibility is more positively associated with accuracy toward early adulthood. These findings suggest that brain state dynamics are associated with complex executive function across a critical period of adolescence.

Introduction

Executive functions include our ability to organize and execute behavior, and are frequently measured by tests that assess planning, complex reasoning, set shifting, and inhibition. These abilities are involved in virtually all complex activities that humans engage in, and are ubiquitously affected in neurodevelopmental (Arnsten and Rubia, 2012) and neuropsychiatric (Millan et al., 2012) conditions. Indeed, failures in executive function fundamentally contribute to neurodevelopmental syndromes ranging from autism (O’Hearn et al., 2008) to learning disabilities (Swanson and Sachse-Lee, 2001). Executive functions develop markedly over adolescence (Gur et al., 2012), but little is known regarding how the complex dynamics of the human brain develop to support effective cognitive and executive abilities.

Recently, studies in network science have begun to reframe our understanding of the brain, complementing an earlier emphasis on the contributions of individual brain regions with an understanding of inter-regional interactions. Tools for dynamic network analysis are particularly appropriate for addressing questions in developmental cognitive neuroscience where spatiotemporal changes in the patterns of functional connectivity can be probed both within a single scanning session and over the early lifespan (Hutchison and Morton, 2016). Indeed, as the human brain matures, the structural and functional relationships among brain areas reorganize (Hutchison and Morton, 2016; Supekar et al., 2010). Functional within-community interactions increase in the context of increasing segregation and differentiation of network communities (Satterthwaite et al., 2013c; Gu et al., 2015). Such reconfiguration is critical for forming the increasingly interactive circuits (Cao et al., 2015; Betzel et al., 2014) thought to drive adaptive executive functions in adulthood (Heinzle et al., 2012; Ekman et al., 2012; Hutchison and Morton, 2016). Yet, how these changes relate to evolving executive accuracy in an adolescent (Anderson, 2002) is unknown. Emerging evidence in adults highlights the flexibility of local (frontal) systems as a correlate of individual differences in executive ability (Braun et al., 2015), as well as the flexibility of global (whole-brain) networks associated with individual differences in adaptive behaviors (Bassett et al., 2015).

However, theoretical tensions have hampered an integrated understanding of developing executive capabilities. In a single brain region, neural processes and neurophysiological noise produce increased signal complexity during development (Hutchison and Morton, 2015, 2016), potentially enabling brain regions to express a larger repertoire of microstates – transient patterns of activity in the brain (Khanna et al., 2015). Conversely, the whole brain displays increased integration between widely distributed neuronal populations, potentially enabling the brain to express a more focal repertoire of microstates (Khanna et al., 2015). Resolving these conflicting predictions requires a framework that examines the stable global features of brain dynamics while remaining sensitive to local variation (Turk-Browne, 2013). Recent investigations have used sliding window approaches to quantify developmental changes in integrated processing among systems in the brain at rest and during the performance of cognitive control tasks (Hutchison and Morton, 2015, 2016). What has been relatively unexplored, however, is the role of trait-like moment-to-moment state organization and transitions in executive functions across development. Moment-to-moment states are the foundation of connectivity analyses, and examining brain state structure and flexibility at this relatively fine temporal scale may provide a context within which to understand behavioral phenotypes that may be observed over longer time scales.

To this end, we treat the brain as a dynamical system with both local and global contributions to executive function that evolve during neurodevelopment to enable individual differences in cognition. Whereas the majority of research concerning complex cognition involving executive functions has emphasized the role of the frontal cortex, these abilities may also depend on flexible interactions across other distributed circuits (Cole et al., 2013). To assess this broader view, we study framewise transitions in BOLD fMRI time series that may represent transient brain-wide processes that support executive function. Specifically, we posit that two dynamic properties are associated with executive function: (i) traversal of several distinct brain states (which we define below), and (ii) a preference for a few brain states (Khanna et al., 2015). These features support both flexible transitions between cognitive processes (Khanna et al., 2015; Shanahan, 2010) and stable task performance. We hypothesize that improvements in executive accuracy in development will rely on the brain’s ability to transition between states and the ability to return to common states. Finally, we predict that inter-individual variability in brain-wide dynamics underlies individual differences in executive function.

To address these hypotheses, we use a dynamic graph approach to examine brain states and flexible transitions between states in 780 youth from the ages of 8–22. Graph theoretic approaches to neuroimaging data have now been widely applied to investigate the organization of the human brain and the basis of cognitive function (Medaglia et al., 2015). Recently, they have been applied to robustly identify “fingerprints” of individual functional connectivity profiles (Finn et al., 2015). These approaches generally have in common a mapping from brain regions to network nodes, and from associations between brain regions (e.g., gray matter volume measurements, white matter tracts, functional connections represented by correlations, coherence, or mutual information) to network edges. Here, we instead map a unit of time to a network node, and we map similarities in brain states at two different times to a network edge. In this time-by-time network, we can define common states independent of their temporal order using network-based clustering algorithms. This method gives us access to information about which brain state (activity profile) is present at any particular time, and how the brain transitions between states over time; importantly, such information is hidden in traditional functional or structural brain networks. Because BOLD state activity profiles and their dynamics underlie the network organization captured in graph statistics, the study of brain state spaces and their transition dynamics can complement graph theoretical approaches by characterizing the temporal organization of the brain and processes that support cognition (Liu et al., 2013; Deco and Corbettta, 2011). State-level transitions may also underlie observed patterns of dynamic connectivity (Bassett et al., 2011, 2012b, 2013c), including the recruitment of and integration between network communities or cognitive systems that enable behavior (Bassett et al., 2015; Mattar et al., 2015a).

Specifically, we examine brain state organization and flexibility in resting BOLD fMRI time series in a large sample (N = 780) of youth from the Philadelphia Neurodevelopmental Cohort (Gur et al., 2012). We define the momentary (single TR) pattern of fMRI BOLD activity across N = 264 functionally-defined areas (Power et al., 2011a) as a brain state. Next, we map a single state (time point) to a network node, and we map similarities in brain states at two different time points to a network edge. To this time-by-time network, we apply a clustering algorithm in individual subjects to define common brain states independent of their temporal order. We cluster over these states to find common states in each portion of the sample in ten evenly spaced age bins (see Fig. 1 for a schematic overview of the methods and Figure A.3 in the Appendix for the state distributions for the ten age bins. See also Figure A.4 in the Appendix for a replication in the Human Connectome Project Neurodevelopmental Cohort). We then quantify the type of states observed in neurodevelopment, how these states evolve throughout adolescence, and how dominant states and flexible state transitions relate to a factor score representing a complex pattern of cognitive and executive accuracy (henceforth “complex executive accuracy”), which provides a statistically reliable representative measurement of overall executive abilities in this sample (Moore et al., 2015). Finally, we examine the specificity of brain dynamics to specific measures of complex executive accuracy over adolescence. We hypothesized that the time spent in dominant states —corresponding especially to connectivity profiles representing the brain’s default mode and task control systems — would be more prominently observed in later development. Moreover, we expected state flexibility to associate with complex executive accuracy (Braun et al., 2015). Finally, we explored the possibility that relationships between both dynamic measures and complex executive accuracy change with age (Hutchison and Morton, 2015).

Fig. 1. Schematic of Methods.

(A) In each subject, we define 264 cortical and subcortical regions of interest (ROIs) (Power et al., 2011a). (B) We extract mean resting BOLD time series from each ROI. (C) We define the momentary (one volume at time resolution; TR) pattern of BOLD magnitude across ROIs as a brain state, which we represent as an N × 1 dimensional vector. (D) We then compute the Euclidean distance between every pair of state vectors. We summarize pairwise distances between states in a T × T adjacency matrix, where T = 120 TRs. (E) Each colored box at the top of the hierarchy represents one TR: a single 264 × 1 vector of signals in the 264 nodes from the Power parcellation. For each subject, we distill approximately 4 common states by applying a network-based clustering technique to the adjacency matrix. We then map correspondence between subject-level states by performing a group-level clustering procedure to derive sample level states. (F) We study the frequency distributions of states and observe the presence of two common states as well as a heavy tail of less common states. After defining these states, we estimate the time spent in a state and the flexible shifting between states (G). As illustrated in (G), the analysis applied to the parcellated data uncovers distinct states that exist in the original images. See Appendix for details.

Methods

Subjects

The Philadelphia Neurodevelopmental Cohort (PNC) is a collaboration between the Center for Applied Genomics at Children’s Hospital of Philadelphia (CHOP) and the Brain Behavior Laboratory at the University of Pennsylvania (Penn). Study procedures were approved by the Institutional Review Boards of both Penn and CHOP. The target population-based sample is 10,000 human youths who presented to the CHOP network for a pediatric visit and volunteered to participate in genomic studies of complex pediatric disorders with informed consent (Gur et al., 2012). A subsample of 1445 participants – stratified by age and sex –were randomly selected for neuroimaging (Satterthwaite et al., 2014). Of these, 1275 participated in a neuroimaging study in which resting state fMRI data was acquired. Participants were excluded due to missing cognitive data, poor imaging data quality, or a history that suggested potential abnormalities of brain development. Data regarding medical history was gathered from both self-report at the time of study entry as well as from electronic medical records available from CHOP. Specifically, 234 participants were excluded due to a history of medical problems that might affect brain function, a history of inpatient psychiatric hospitalization, or current use of psychotropic medication. Additionally, 323 participants met exclusion criteria due to poor resting state image quality (Satterthwaite et al., 2013a, c; 2012), including (i) mean relative displacement exceeding 0.2 mm, (ii) greater than 20 vol with relative displacement greater than 0.25 mm, and (iii) gross between-run motion resulting in incomplete brain coverage. Many participants were excluded due to multiple criteria. These exclusion criteria resulted in a final eligible pool of 780 participants aged 8–21 years (mean age 15.63, standard deviation 3.28; 333 males) that were included in the current study. Given that previous analyses of executive cognition and alternate measures of flexibility show small to modest effect sizes (Braun et al., 2015), our inclusion of a sample size of greater than twice that included in previous work was considered adequate to detect the effects of interest. The data for the Philadelphia Neurodevelopmental Cohort are publicly available via the National Center for Biotechnology Information’s database of Genotypes and Phenotypes (http://www.ncbi.nlm.nih.gov/gap).

Behavioral battery

Cognition was measured outside of the scanner using the Penn Computerized Neurocognitive Battery (CNB) (Gur et al., 2010, 2012). Briefly, the 1 h CNB was administered to all participants, and consisted of 14 tests that evaluated a broad range of cognitive functions. While motor tests only measured speed, all non-motor tests measured both accuracy and speed. For this adolescent sample, instructions and vocabulary for verbal stimuli were simplified from the adult CNB (Gur et al., 2010). Cognitive assessment was completed during a session that was separate from the neuroimaging session (mean number of months between sessions was 3.4, with a standard deviation of 5.4). The assessment session was scheduled at home (68.8% of participants) or in the laboratory (31.2%), according to family and subject preferences (Gur et al., 2012). During task administration, potential interference was minimized, standard instructions were read aloud in addition to appearing on the screen, and a professional testing environment was maintained. Tests were administered in a fixed order; breaks were offered approximately every 15 min. Accuracy for each test was z-transformed. Overall cognitive performance was summarized as the average z-transformed accuracy scores across all tests administered within age bins. Factor scores used in the current study are described in (Moore et al., 2015); specifically, the factor score for complex executive accuracy in a best-fitting confirmatory three factor solution comprised tests from executive (mental flexibility, attention, working memory) and complex reasoning (language reasoning, nonverbal reasoning, spatial ability) domains, in addition to a weaker cross-loading contribution from memory (spatial memory). The tests contributing to the complex executive accuracy score include the Penn Conditional Exclusion Test, the Penn Continuous Performance Test, the Letter N-Back task, the Penn Matrix Reasoning Test, the Penn Verbal Reasoning Test, and the Penn Line Orientation Test (Moore et al., 2015). Thus, the complex executive accuracy score applied here involves contributions from basic executive abilities in addition to tasks that require the coordination of several executive abilities to achieve task goals, which we refer to as “complex executive accuracy.” All complex executive accuracy factor scores were age-normed prior to use in statistical analyses by computing the z-score compared to the mean of each age bin over two-year intervals. These scores were used to examine the relationship between brain dynamics and cognition in subsequent analyses above and beyond the primary effects of age.

Neuroimaging data acquisition and preprocessing

A full description of the imaging methodology for this study can be found in Ref (Satterthwaite et al., 2014). Briefly, all subject data were acquired on the same scanner (Siemens Tim Trio 3 T, Erlangen, Germany; 32 channel head coil) using the same imaging sequences. Blood oxygen level dependent (BOLD) fMRI was acquired using a whole-brain, single-shot, multi-slice, gradient-echo (GE) echoplanar (EPI) sequence of 124 vol with the following parameters: TR/TE = 3000/32 ms, flip = 90°, FOV = 192 × 192 mm, matrix = 64 × 64, slice thickness/gap = 3 mm/0 mm. The resulting nominal voxel size was 3.0 × 3.0 × 3.0 mm. A fixation cross was displayed as images were acquired. Subjects were instructed to stay awake, keep their eyes open, fixate on the displayed crosshair, and remain still.

Functional imaging used tools from FSL (FMRIB’s Software Library (www.fmrib.ox.ac.uk/fsl)), and AFNI with a preprocessing scheme described elsewhere (Satterthwaite et al., 2013a). Briefly, time series were processed with a confound regression technique optimized to reduce the influence of subject motion. Specifically, the first 4 volumes were removed for initial signal stabilization, resulting in 120 volumes remaining for subsequent analysis. A study-specific template was generated from a sample of 120 PNC subjects balanced across sex, race, and age bins using the buildTemplateParallel procedure in ANTs (Avants et al., 2011a). Study-specific tissue priors were created using a multi-atlas segmentation procedure (Wang et al., 2014). Next, each subject’s high-resolution structural image was processed using the ANTs Cortical Thickness Pipeline (Tustison et al., 2014). Following bias field correction (Tustison et al., 2010), each structural image was diffeomorphically registered to the study-specific PNC template using the top-performing SyN deformation (Klein et al., 2009). Study-specific tissue priors were used to guide brain extraction and segmentation of the subject’s structural image (Avants et al., 2011b).

fMRI time series were band-pass filtered to retain frequencies between 0.01 and 0.08 Hz. Functional images were re-aligned using MCFLIRT. BET was used to remove non-brain areas from structural images via skull-stripping (Smith, 2002). All functional timeseries were slice-time corrected, motion corrected to the median image using a tri-linear interpolation with 6 degrees of freedom (Jenkinson et al., 2002), and spatially smoothed (6 mm FWHM, isotropic). Confound regression was performed with a 36-parameter model (Yan et al., 2013) including 6 motion parameters from realignment plus global signal, white matter, cerebrospinal fluid, and the temporal derivative, quadratic term, and temporal derivative of each of these nine variables (Satterthwaite et al., 2013a, c). Before confound regression, the confound parameters were band-pass filtered identically to the time series to prevent mismatch in the frequency domain and permit confound parameters to best fit retained signal frequencies. Because spike regression and scrubbing have been found to bias graph properties, they were not applied (Yan et al., 2013). Processed subject-level BOLD images were coregistered to the subject’s T1 image with boundary-based registration with integrated distortion correction from FSL 5 (Greve and Fischl, 2009). Each subject’s registration was inspected manually and evaluated for accuracy using spatial correlations. Regions of interest later to represent network nodes were registered to subject space for time series extraction by concatenating the coregistration, distortion correction, and normalization transformations such that only one interpolation was performed in the entire process.

Temporal network construction and state identification: person-level

We extracted regional mean BOLD time series from 264 functionally defined regions of interest covering cortical and subcortical areas (Power et al., 2011b). We defined the momentary (single TR) pattern of fMRI BOLD activity across these areas as a brain state (Lehmann et al., 1987). We treated each TR as a network node and we treated similarities in brain states at two different TRs as a network edge. We summarized this network in a temporal adjacency matrix A whose element A_ij gave the similarity in BOLD magnitude across regions between time i and time j. We used an inverse distance as the measure of similarity, where $A_{ij}=\frac{1}{D_{ij}}$, and D_ij indicates the Euclidean distance between the state vector of regional activity magnitudes at time i and the state vector of regional activity magnitudes at time j. This temporal adjacency matrix bears a crucial distinction from matrices that represent brain regions as nodes and anatomical or functional connections as edges in regional adjacency matrices. Indeed, tools from graph theory can be generalized to adjacency matrices with different content. Henceforth, we use a clustering algorithm applied to the temporal adjacency matrix rather than a regional adjacency matrix. We use the inverse Euclidean distance computed across regions’ BOLD values to define the adjacency of two states. This procedure allows us to find BOLD states by applying the community detection algorithm to the time-by-time adjacency matrix.

Specifically, to reduce the dimensionality of the data, we assigned state vectors to network communities (henceforth referred to as “states”) using a clustering algorithm developed for networked data (Porter et al., 2009). Specifically, we maximize a common modularity quality function (Newman, 2006), defined as:

$$Q=\sum _{ij}\left[A_{ij}-\gamma P_{ij}\right]\delta \left(g_i,g_j\right),$$ (1)

where time i is assigned to community g_i, time j is assigned to community g_j, the Kronecker delta δ(g_i, g_j) = 1 if g_i = g_j and it equals 0 otherwise, γ is a resolution parameter, and P_ij is the expected weight of the edge connecting time i to time j under a specified null model. The most common null model used in this modularity quality function is the Newman-Girvan (NG) null model (Newman and Girvan, 2004), for which $P_{ij}^{\text{NG}}=\frac{k_i{k}_j}{2m}$, where $k_i={\displaystyle \sum _j}{A}_{ij}$ is the strength (weighted degree) of time point i’s BOLD similarity to all other time points (i.e., the sum of weighted inverse Euclidean distance from all other time points). The term $k_j={\displaystyle \sum _i}{A}_{ij}$ is the strength of time point j. These definitions of k_i and k_j are analogous to the typical approach to computing strength in neuroimaging network analysis, where k_i and k_j are often the strength (i.e., weighted degree) of the connectivity between a single brain region and all other regions in the network. The term $m=\frac{1}{2}{\displaystyle \sum _{ij}}{A}_{ij}$ represents the total edge weight in the network. We note that, intuitively, the NG null model which we use here is specified in terms of edge weight deviations from a network chosen randomly from the set of all graphs with the same expected strength distribution as the actual network.

We use a Louvain-like locally greedy algorithm to maximize this modularity quality function (Blondel et al., 2008; Jutla et al., 2014). In the initialization of the algorithm, there are N communities (where N is the number of nodes in the network), resulting in a modularity value of Q = 0. The algorithm proceeds by iteratively assigning nodes to communities until no appreciable increases in Q are observed. Consistent with the current state of the art, we perform the maximization 100 times per temporal adjacency matrix to address the near degeneracy of the modularity landscape (Good et al., 2010). The modularity quality function contains a resolution parameter, γ, that can be used to tune the relative number of communities identified: high values of γ produce many small communities, and small values of γ produce a few large communities (see section entitled “Robustness of Dynamics”, below). The choice of the structural resolution parameter (γ) is a very important one as it directly tunes the temporal resolution at which we are sensitive to brain states and their dynamics. In current accepted practice, one often considers a small range of γ to examine the robustness of results or to assess the potential existence of hierarchical community structure in the adjacency matrix (Bassett et al., 2013a). Intuitively, as γ increases, the number of identified communities will increase until it reaches the number of nodes in the network, which in this case is the number of TRs in the time series. Similarly, as γ decreases, the number of identified communities will decrease until it reaches 1. The specific values of γ that produce a single community versus the maximum possible number of communities are unknown, and depend nontrivially on the average weight of edges in the network, the variance of edge weights in the network, and the number of nodes in the network. Because community structure can change drastically across a range of γ values, one typically examines robustness of results over a small range of γ values, to determine whether a particularly unusual γ value was inadvertently chosen leading to a result that is not observed at any other γ value. One hopes that results are not robust over a large range of γ values, as this would indicate that the results are in fact not being driven by community structure at all, which changes appreciably across γ.

Because we do not know a priori what value of γ is most appropriate for a given data set, we maximized the modularity quality function using a range of γ values from 1.00 to 1.99 in increments of 0.01. We observed that over this range, the number of average communities increases monotonically toward the total number of nodes in the temporal network. A γ value of 1.02 produced an average of 4.13 states per person (median = 4, mode = 4, range = 3 to 6). We selected this γ value for the current analysis based on its correspondence with the range of states examined in previous studies (Allen et al., 2012; Britz et al., 2010; Khanna et al., 2015). It is important to note that in purely exploratory analyses, we can search for a γ value that achieves a high quality relative to a null model, producing a set of partitions with high similarity across iterations (Bassett et al., 2013a). We can also identify an independent criterion (e.g., a desired central tendency in the number of states) and examine whether the selection was reasonably stable post hoc. We chose the latter strategy here to establish an external basis for state identification. At the individual level, our parameter selection at γ = 1.02 allows us to achieve an average of around 4 states per person, whereas selecting γ = 1.0 results in only 2–3 states per person. Importantly, the presence of only two states per person would suggest that their data exhibits only bistable dynamics, which the brain in general does not (Tognoli and Kelso, 2014). Moreover, using a gamma value that only produces a few states would preclude useful measures like the time spent in primary states or state flexibility: at γ = 1.0 the former would approach 1 for all subjects, and the latter would exhibit a ceiling effect with too few states. Thus, there is practical utility in searching for (i) reasonably high-quality state partitions that (ii) exhibit more than 2–3 states, and (iii) produces a number of states that is consistent with that reported in prior studies. By using this approach, we were able to identify states with similar activity independent of whether they occurred in nearby times or distant times according to an external criterion for use in associating with age and cognitive function.

In addition to analytic considerations, it is also important to note that BOLD states are presumably produced by underlying neurophysiological activity with incompletely understood sources (Singh, 2012). Future studies could attempt to link direct neural recordings to observed BOLD states in animal models or electrocorticographic studies to search for a neural ground truth for the number of BOLD states and their signal characteristics.

Identification of primary states at the group level

While on average 4 states were defined per subject, there is no guarantee from the method that every subject displayed the exact same states. That is to say, there is no necessary correspondence between the activation patterns comprising a state identified in different subjects. To assess individual variability directly, and to identify states that corresponded with one another over individuals, we performed a second-level clustering over the subject-level states. Specifically, for each subject-level state identified at the individual level (i.e., 3 to 6 per person), we computed a representative state. To do so, the BOLD signal for each TR was standardized as the z-score for each region over all 120 original TRs. Then, the mean state vector was computed as the mean of these z-scored vectors for each state identified within each subject. Next, we separated the 780-subject sample into ten bins. We defined age bins a priori by dividing subjects along ten evenly spaced age intervals. The bin sizes are reported above each bin’s state frequency distribution in Appendix Figure A.3. We divided subjects into bins for two reasons. The first is computational: as the size of the graph increases, the time and memory required to obtain the assignment of nodes (BOLD TRs) to communities (states) increases exponentially, and is challenging for many computing systems. Using bins allows us to distill states despite computational limitations. Second, the use of age bins allows us to independently define community assignments in each subgroup, and to check the correspondence of states across age bins. In our supplemental analyses, we demonstrated that the BOLD signal intensity for primary states was highly consistent across bins. This observation motivated an examination of the increase in frequency of state expression over the age bins. Our bins were selected to represent equal age intervals independently from any specific milestone, allowing us to examine state differences over age.

We calculated the mean state vectors from all subjects in a given age bin, and we constructed a group-level state adjacency matrix A_g that represented the distances between these mean state vectors. Finally, we maximized the modularity quality function of this temporal adjacency matrix using the Louvain-like locally greedy algorithm. Consistent with the approach at the single-subject level, we performed the optimization 100 times. We began by using a structural resolution parameter value of γ = 1.00 and then we increased γ incrementally in intervals of 0.01. The two primary states described here were present throughout this range. Beginning at γ = 1.10, the quality of partitions became increasingly variable, and we thus choose γ = 1.09 as a parameter with relatively high quality and low variance (see Figure A.2 in the Appendix); at this parameter value, we identified two primary states followed by a heavy-tailed distribution of less frequent secondary states in each age bin. We also calculated the proportion of time spent in the two primary states and the state flexibility (See Appendix Figure A.3 for the observed state distributions for each age bin).

Assessing the significance of states

We performed two permutation tests to examine the significance of (1) our community (state) organization and (2) the significance of activity in the primary states. First, we performed a permutation test at the state adjacency matrix level for each bin where the upper triangle of the symmetric state adjacency matrix was permuted uniformly at random and transposed to rebuild a symmetric null matrix. This permutation strategy tests against the null hypothesis that the observed state clusters are observed by chance associations among states. We compare the observed quality index Q for each community to the null distribution observed over 10,000 permutations. A community is judged to be significant if it has a greater Q value than 95% of observed communities from the null matrices. Following permutation of the state temporal adjacency matrices within each individual, we find that the two primary clusters (states) were significant at p <0.05 in 100% of participants, and that 96.8% of remaining states were significant at the individual level. At the group level, 100% of primary states and 92% of remaining states were significant at p <0.05.

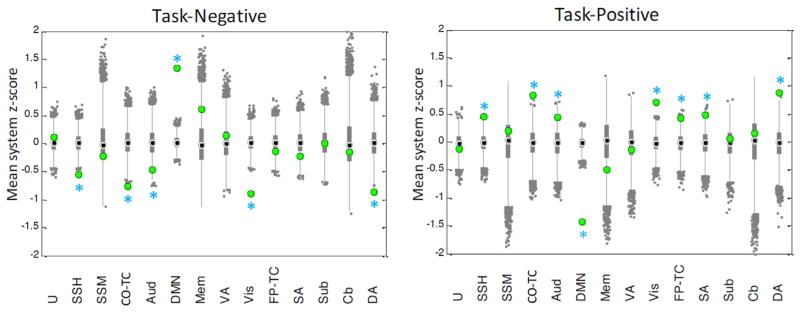
Next, to test the significance of activity in observed states, we performed a permutation test at the level of individual states where the signal intensities (z-scored BOLD signal intensities) in all TRs contributing to the two observed primary state vectors were permuted uniformly at random across the spatial (region) dimension. This procedure allowed us to test whether the observed signal intensities were significantly concentrated in the cognitive systems relative to the results based on shuffled intensities. The null distribution across 10,000 permutations consisted of the mean z-score of BOLD intensities of the regions within each system. A system was considered to demonstrate statistically significant activity if the observed mean z-score of BOLD intensities in the system was greater or lesser than 97.5% of values in the null distribution (the equivalent of a two-tailed test with α = 0.05). The results from this analysis demonstrate that the state activity in the task-negative systems is significantly increased in the task-negative state relative to the null, and that the state activity in the task-positive systems is significantly increased in the task-positive state relative to the null (see Fig. 2).

Fig. 2. Significance of system intensities in primary states.

The results of the intensity permutation test demonstrate that activity in task positive systems and task negative systems is significantly activated or elevated relative to the null distribution. Box and whisker plots represent the observed mean and 95% confidence intervals of z-scored BOLD signal over 10,000 permutations. Gray points represent outliers. Green circles represent the true values of mean system BOLD signal calculated directly from the empirical data. Blue asterisks indicate systems whose intensity is significantly higher/lower than permuted values at p <0.05. U = regions unassigned to a network, SSH = somatosensory hand network, SSM = somatosensory mouth network, CO-TC = cingulo-opercular task control network, Aud = auditory network, DMN = default mode network, Mem = memory network, VA = ventral attention network, Vis = visual network, FP-TC = fronto-parietal task control network, SA = salience network, Cb = cerebellum, DA = dorsal attention network.

Together, these two null model analyses and their respective results indicate that the extracted states reliably represent statistically significant state clusters consistent with task-negative and task-positive systems as defined by previous literature (Power et al., 2011a). Moreover, they suggest that the activity patterns observed in the two states are not anticipated in non-parametric null models constructed from permuting activity levels across brain regions.

The hierarchical approach applied here increases confidence in the states used to compute the dynamic measures. In particular, for a state at the individual level to be considered a primary state, it must be classified as such at the group level clustering solution. While we find that 100% of the states representing task-positive and task-negative systems are significant relative to a permutation-based null model, it is important to test whether the group-level states are also reliable relative to a similar null model. We therefore repeated the permutation test of the adjacency matrix of the group level states (comparing the observed community Q values to the Q values of a null distribution of 10,000 permutations where the states are permuted uniformly at random). This procedure can be used to establish whether the quality of the recovered state assignment is better than chance at the group level. We find that 100% of the primary states (two per age bin) are also significant within the group-level clustering solution. This permutation test demonstrates that the effects we

State flexibility

We define the state flexibility (F) of a subject to be the number of state transitions (T) that occur relative to the number of states (S) observed (F = T/S) inclusive of all primary and secondary states. The use of the number of states as a denominator provides a standardized value for each subject prior to use in behavioral analyses. In the current study, the numerator T is positively correlated with age over subjects (Pearson’s correlation coefficient r = 0.109, p = 0.002), whereas the denominator S does not change with age over subjects (Pearson’s correlation coefficient r = −0.007, p = 0.844). Thus, subsequent analyses examining flexibility over age are driven by changes in the number of transitions. The mean state duration was 2.59 TRs (SD = 0.46) or 7.77 s. Motion was not related to switches within subjects (mean R = 0.03, mean p = 0.74), suggesting that state flexibility is not driven by instantaneous motion.

Regression models

We used general linear models implemented in R (R Core Team., 2015) to examine the relationships between age, motion, sex, age-normed complex executive accuracy factor scores, and the dynamic measures. Factor scores were age-normed consistent with a previous approach (Moore et al., 2015) by z-scoring the complex executive factor scores for individuals relative to the mean in bins corresponding to two year intervals from the age of 8 to the age of 22 years. This procedure allowed us to examine the relationship between brain dynamics and complex executive accuracy. Specifically, we first specified models with main effects without interactions. Then, we examined models with main effects and theoretically relevant interactions and investigated the significance of these parameters and incremental changes in variance explained. This process allowed us to consider the main effects of interest while controlling for variables of non-interest (age, sex, and mean relative displacement) while examining brain dynamics and its relationship to complex executive accuracy.

We found that the two sexes demonstrated similar variance in time spent in the two primary states (males = 0.10, females = 0.09) and state flexibility (males = 3.66, females = 3.37). The dependent variables used across the models (age, sex, mean relative displacement, time in two primary states, and state flexibility) exhibited low multicollinearity: condition indices under the Belsley test (Belsley, 1991) were less than 12 for all independent variables. An additional parameter, variance inflation factor (VIF), can be used to examine multicollinearity, where a VIF > 10 can be considered to be too high (Obrien, 2007). The variation inflation factors for the three covariates and two dynamic parameters were all well below this range (mean relative displacement = 1.013; sex = 1.005; age = 1.037; time in primary states = 1.041, and state flexibility = 1.029), demonstrating that collinearity does not preclude the application of linear regression with these variables. The model residuals exhibited constant error variance (homoscedasticity) under the Breusch-Pagan test (Breusch and Pagan, 1979), and linear fits on visual inspection of component and residual plots. All test statistics used two-sided hypotheses.

For each main effects analysis we considered the effects of several independent variables on one of two types of dependent variables: either brain dynamics or complex executive accuracy. To examine the effects of age, motion, and sex on the summary statistics of brain state dynamics, the independent variables included age, motion, and sex, and the dependent variable was either (1) time in two primary states or (2) state flexibility. Then, to examine the effect of brain state dynamics on complex executive accuracy, we used similar main effects models where the dependent variable was complex executive accuracy, and independent variables included age, motion, sex, and either (1) time in two primary states or (2) state flexibility. To examine the combined effects of state flexibility and time spent in common states on complex executive accuracy, we applied a single main effects model where the independent variables included age, motion, sex, time in two primary states, and state flexibility.

Following the application of main effects models, we examined the effect of the inclusion of interactions between independent variables (age and each of the dynamic measures) on the dependent variable (complex executive accuracy). We were specifically interested in determining whether the relationship between brain dynamics and complex executive accuracy was stable over age. We applied models including the main effects of age, motion, and sex, and either (1) time in two primary states or (2) state flexibility, as well as the interaction between age and the dynamic measure (either time in two primary states or state flexibility).

Code availability

Code used to compute dynamic measures in temporal networks such as those investigated here are available in the Network Community Toolbox at http://commdetect.weebly.com.

Results

Dominant states over neurodevelopment

In the youngest age bin, we observe two states that frequently occur across all subjects in the sample. We refer to these states as primary states, and we note that the first primary state displays high activity in brain regions traditionally observed to be active at rest (hereafter “task-negative”), and the second primary state displays high activity in regions traditionally observed to be active during cognitive tasks (“task-positive”) (Fox et al., 2005) (see Fig. 3 and Fig. 4. See also Figure A.5 in the Appendix for the results of a replication analysis in the Human Connectome Project Neurodevelopmental Cohort). To examine whether the patterns of BOLD magnitude in the two primary states that we observed in the youngest age bin were robustly observed in all other age bins, we computed the Pearson’s correlation coefficient between the mean system-level values of BOLD magnitude for the primary states in pairs of age bins. That is, for each of the most frequently identified task-positive or task-negative states in each pair of bins, we computed the Pearson’s correlation coefficient between the mean BOLD values for each system for each state pair. We found that the correlation in BOLD among average task-negative states extracted from each age group was r = 0.90 (SD = 0.08, df = 12, average p = 2.77 × 10⁻⁵ across bin pairs) and among task-positive states was r = 0.92 (SD = 0.05, df = 12, average p = 8.45 × 10⁻⁶ across bin pairs). These high correlation values with low standard deviations suggest that the two primary states computed independently in each of the ten bins were present throughout the sample.

Fig. 3. Two primary states.

Two states were consistently observed over age. One state exhibited high activity in the default mode network, and the other exhibited high activity in so-called task-positive regions from the dorsal attention, cingulo-opercular, and visual systems. The states depicted represent the average for each state across all states assigned as primary (most frequent) states in the sample. The state images were created by computing the average BOLD signal at each voxel in the spatially normalized images corresponding to the BOLD TRs assigned to each state in our hierarchical clustering strategy.

Fig. 4. Activity in main states.

Two highly robust states were observed over age. One state was characterized by high activity in default mode and memory regions, while the other state was characterized by high activity across several task-positive regions from the dorsal attention, cingulo-opercular, and visual systems. Error bars indicate standard deviation of the state means over age bins. U = Uncertain, SSH = Somatosensory/Hand, SSM = Somatosensory/Mouth, CO/TC = Cingulo-Opercular/Task Control, Aud = Auditory, DMN = Default Mode Network, Mem = Memory, VA = Ventral Attention, Vis = Visual, FP-TC = Fronto-Parietal Task Control, SA = Salience, Cb = Cerebellum, DA = Dorsal Attention.

The presence of these two primary states complements an extensive literature describing the default mode and task-positive systems as large-scale opponent processes driven by spontaneous local neuronal dynamics (Deco and Corbetta, 2011) and related to general cognitive function involving working memory, semantic and episodic memory, and reasoning (Keller et al., 2015; Kim et al., 2010). Yet, interestingly, these two primary states comprise only approximately 42% (SD = 26.8) of all TRs. The remaining 58% of TRs includes states that each occur relatively infrequently, and we refer to these states as secondary states. The presence of both primary and secondary states demonstrates that youth tend to predominantly transition between task-positive and task-negative states interspersed with a rich landscape of other states.

State dynamics over neurodevelopment

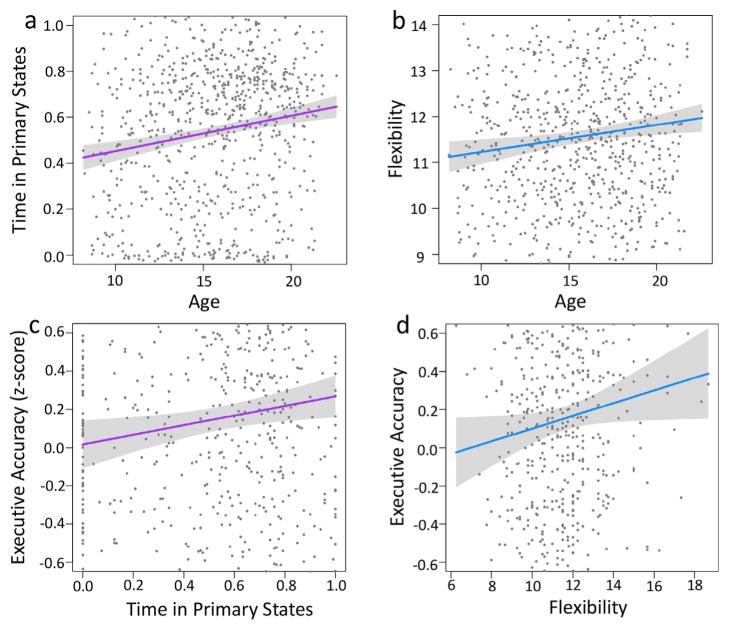
To examine the extent to which brain states vary across adolescence, we define two summary statistics: the time spent in primary states and the flexibility between states. We estimate the time spent in the two primary states as the number of volumes (TRs) assigned to those states. In linear regression models, we observe that the time spent in the two primary states increases with age (controlling for motion and sex in this model and henceforth; the model is significant at F(3, 776) = 14.15, p = 5.464 × 10⁻⁹, specific effect of age: t(776) = 4.64, p = 4.04 × 10⁻⁶) (see Fig. 5). Children around 8 years of age spend approximately 40% of TRs in the primary states, while young adults around 21 years of age spend approximately 60% of TRs in primary states. This result indicates that these two robust states exist early in development and display an increasing presence over adolescence. To understand how the brain transitions between states (both primary and secondary), we define the state flexibility (F) of a subject to be the number of state transitions (T) that occur relative to the number of states (S) observed (F = T/S). State flexibility increases over age (F(3, 776) = 7.78, p = 4.059 × 10⁻⁵, specific effect of age: t(776) = 2.86, p = 0.004). Collectively, these results suggest that in the developing brain, older individuals spend more time in primary states, while – somewhat surprisingly – also becoming increasingly flexible: the partial correlation between the two variables is r = 0.16 (p = 3.5 × 10⁻⁶) corrected for age, motion, and sex. See also Table A.1 in the Appendix for additional tests demonstrating no quadratic effects of age.

Fig. 5. Dynamic development and complex executive accuracy.

For the 780 participants: (a,b) Linear regression reveals that time in the two primary states (F(3, 776) = 14.15, p <0.001) and state flexibility (F(3, 776) = 7.78, p <0.001) both increase with age. Adolescents were noted to shift an average of 11.5 times relative to number of observed states. (c,d) In addition, time in two primary states (F(3, 776) = 6.13, p <0.001) and state flexibility (F(3, 776) = 5.24, p <0.001) are positively related to complex executive accuracy beyond the primary effect of age. Both trends are robust to motion and sex. In (c), the x-axis represents the proportion of time in primary states. In (d), the x-axis represents state flexibility, defined as the number of state transitions divided by the number of states observed in the subject. Gray envelopes represent 95% confidence interval for the line of best fit. Effects of covariates not visualized; see Tables A.1 and A.2 in the Appendix for model reports.

State dynamics and executive function

Next, we ask whether variation in state occupancy across individuals is associated with complex executive accuracy. We considered the dynamic measures in two separate models, then together in a single model to examine their potentially unique contributions to complex executive accuracy. We observe that individual differences in the time spent in the two primary states (t(776) = 2.78, p = 0.005) and state flexibility (t(776) = 2.06, p = 0.039) is positively associated with complex executive accuracy while controlling for age, sex, and motion (see Fig. 5). Critically, these results support the notion that the greater complex executive accuracy in adulthood is supported by increasing refinement of brain state dynamics, which in turn is characterized by greater time spent in primary states (suggesting stable brain state maintenance (Braun et al., 2015; Bassett et al., 2015)), as well as greater flexibility of state transitions (suggesting cognitive flexibility (Cole et al., 2013)).

The previous findings do not address the question of whether brain state dynamics differentially drive cognitive variation in younger children versus older children. Differential effects in young versus old children have previously been observed in the relationship between cortical thinning and age: a negative correlation between intelligence and cortical thickness in early childhood has been observed that changes to a positive correlation in late childhood and beyond (Shaw et al., 2006). In addition, connection strength variability changes over age in rest compared to cognitive control over the transition to adulthood (Hutchison and Morton, 2015). To determine if such an inversion is observed between brain state dynamics and executive function, we examine the previous models with the addition of interactions between age and brain state dynamics on complex executive accuracy. The relationship between complex executive accuracy and the time spent in primary states shows no significant interaction with age (t(776) = 1.61, p = 0.109). In contrast, the relationship between complex executive accuracy and state flexibility does show a significant interaction with age (t(776) = 2.38, p = 0.021): greater state flexibility was related to poorer complex executive accuracy in children, and better complex executive accuracy in young adults (Fig. 6). We speculate that the brain’s exploration of many cognitive states in childhood is disadvantageous for cognitive control, but advantageous for learning specifically and behavioral adaptation more generally (Munakata et al., 2015). Over development, this mode of cognitive exploration turns to a mode of exploitation, where a streamlined set of cognitive modes are under tight complex executive control (Cohen et al., 2007). See Table A.2 in the Appendix for model reports.

Fig. 6. Interaction between state flexibility and age.

Linear regression reveals that the relationship between state flexibility and complex executive accuracy changes with age (t(776) = 2.06, p = 0.039). Early in development, increased state flexibility is negatively associated with complex executive accuracy. In middle adolescence, state flexibility is not related to complex executive accuracy. By early adulthood, increased state flexibility is positively associated with complex executive accuracy in the context of increased time spent in primary states, demonstrating that as the brain’s state organization consolidates and transitions accelerate, complex executive function is supported by increasing state flexibility. Shaded envelopes represent 95% confidence intervals for the lines of best fit.

Specificity of dynamic effects on complex executive accuracy

While state flexibility and time spent in two primary states both positively relate to complex executive accuracy, it is possible that the contributions of these dynamics to complex executive accuracy may be related to one another. Thus, to examine if these parameters explain unique variance relative to one another, we examined them in a single model with complex executive accuracy as the dependent variable. When considered in a single model as main effects with no interactions, the specific effect of time in primary states remained significant (t(776) = 2.41, p = 0.016) but the effect of state flexibility did not (t(776) = 1.63, p = 0.20). In addition, we also examined potential interactions between these two dynamic measures and found that it was not significant (t(773) = 0.608, p = 0.54). From this set of models, we can conclude that the two summary statistics of brain state dynamics share appreciable variance. The variability in complex executive accuracy performance explained by the main effect of time spent in the two primary states remains consistent when state flexibility is considered simultaneously, indicating that the time spent in primary states accounts for unique variability in complex executive accuracy. See Table A.2 in the Appendix for the final models associating dynamics to complex executive accuracy.

Specificity of dynamic effects on complex executive cognition measures

It is important to consider whether the dynamic associations with complex executive accuracy are represented by the latent structure for complex executive accuracy, or by individual executive domains. To address this question, we implemented additional post-hoc regression models using dynamic measures as independent variables, specific executive accuracy measures as dependent variables, and mean relative displacement, age, and sex as covariates. In these analyses, we observe a double dissociation: a measure of complex reasoning was positively associated with time in primary states (Penn Verbal Reasoning Test, t(773) = 2.412, p = 0.016), whereas mental flexibility was positively associated with state flexibility (Penn Conditional Exclusion Test, t(773) = 2.412, p = 0.016). These results suggest that the ability to integrate across multiple domains involving the manipulation of symbolic information in complex decision making depends on the contribution of well-consolidated states and the increasing activation and suppression of task-positive systems. In addition, mental flexibility in a task requiring the adaptive shift between principles is intuitively linked to the observed flexibility of the resting brain, which may predispose the individual to be better prepared for flexible thinking in tasks that specifically demand it. The interaction between age and state flexibility was not significant for any measure, suggesting that the observed relationship between this interaction and the general factor scores is representative of developing global executive function. See Table A.3 in the Appendix for models examining the relationship between the dynamic measures and specific executive performance measure.

Specificity of dynamic effects to the complex executive cognition domain

In addition to functions in the executive domain, we conducted a post-hoc exploratory analysis examining the uniqueness of the association between the brain dynamics measures and complex executive accuracy. To do so, we used regression models with measures of brain dynamics as dependent variables, the complex executive factor score and either (1) the general accuracy factor score, (2) the social cognitive accuracy score, or (3) the memory factor score as independent variables, and with age, sex, and motion as covariates. We found that the relationship between complex executive accuracy and time in primary states remained significant with no additional contribution in the models including general accuracy and social cognitive accuracy. The contribution of complex executive accuracy was insignificant only when memory accuracy was included. We additionally found that the relationship between complex executive accuracy and flexibility remained significant when the general accuracy factor score was included, but not the memory accuracy factor score. The relationship between state flexibility and complex executive accuracy dropped to near-significant when considered with social cognition. Taken together, these results suggest that increasing time in dual task-positive and task-negative states contributes to shared processes associated with memory and executive function. State flexibility is associated with shared variance between complex executive and memory function, and relatively weaker shared variance between complex executive and social cognitive function. Flexible transitions in brain states may be recruited in the context of complex executive demands especially where the memory domain requires mental flexibility. Notably, the complex executive factor score and memory score covary strongly in the current sample (Pearson’s r = 0.73, p = 7.16 × 10⁻¹³⁵). We speak further to the link between memory and complex executive accuracy and these brain dynamics in the Discussion. See Appendix Table 4 for a full report of these models.

Sex differences in dynamics and cognition

An important question is whether biological sex plays a role in the summary statistics of brain state dynamics. To address this question, we used a general linear model that treated motion, age, and sex as independent variables, and treated one of the summary statistics as a dependent variable. We observed a significant effect of sex on the time spent in the two primary states (t(776) = −2.38), indicating that females spent more time in the two primary states than males. We did not observe a significant effect of sex on state flexibility (t(776) = −0.20), indicating that male and female state transitions are similarly flexible overall.

A second important question is whether sex plays a role in the observed relationship between complex executive accuracy and the summary statistics of brain state dynamics. To address this question, we used a second set of general linear models that included the time spent in the two primary states, age, motion, and sex as independent variables, complex executive accuracy as the dependent variable, and an interaction term between the time spent in the two primary states and sex. We did not observe a significant interaction effect (t(775) = 0.07, p = 0.95). This suggests that the relationship between this dynamic statistic and complex executive accuracy is consistent across the sexes across age. The time spent in the two primary states was positively associated with complex executive accuracy across both sexes.

Brief summary of dynamic-behavior relationships

Concisely, the preceding results describe several main conclusions. First, a pair of opponent states that heavily involve either “task-negative” default mode and memory systems or “task-positive” task control, visual, and attention systems exist prominently across neurodevelopment, and more so in young adults. In addition, flexible transitions among all observed states increase with age, and are initially negatively and later positively related to complex executive function, consistently across both sexes. A double dissociation is observed, where time in primary states is related to a task of verbal reasoning and state flexibility is related to adaptive mental shifting. Finally, increasing time in the two primary states that involve memory and executive systems is related to both complex executive and memory functioning.

Discussion

We investigated the developing state space of the adolescent brain in the Philadelphia Neurodevelopmental cohort at rest. Specifically, we examined the dominant brain states over neurodevelopment, flexibility in state transitions, and associations between these dynamic measures and complex executive accuracy as assessed by a neuropsychological task battery. Collectively, our results indicate that common states – which prominently involve (i) the default mode network and (ii) task control and attention systems – exist at all ages examined, and the time spent in these two primary states increases in frequency with age. This characteristic of brain state dynamics contextualizes several major developmental studies of functional brain connectivity (Hwang et al., 2013; Fair et al., 2009; Cao et al., 2015; Betzel et al., 2014; Gu et al., 2015; Hutchison and Morton, 2015).

Our findings place a spotlight on the critical need to understand the relationship between brain activity and brain connectivity as the two approaches continue to offer differential insights into cognitive function (Bassett et al., 2012a, 2015; Medaglia et al., 2015) but are physically interdependent and only partially accounted for by structural network architecture (Hansen et al., 2015). The current results complement and provide context for a similar approach applied to the 1000 Connectomes data, where numerous distinct states in adult fMRI data were quantified (Liu et al., 2013) including DMN and task control networks, among others. Our data suggest that the brain’s adolescent state space has an emerging dynamic core in adolescence within which robust primary states and interindividually variable tendencies for state transitions may be observed. In particular, neurodevelopmental changes in functional network topology (Hutchison and Morton, 2015) observed in resting BOLD time series may represent dynamic combinations of a finite set of brain states, the most common of which already comprise approximately one third of brain states by age 8 and two thirds of brain states by early adulthood. The dynamic brain expresses a core of two robust states with an increasing degree of flexibility. Conceptually, these findings suggest that the brain may exhibit a counterintuitive codevelopment of two seemingly competitive processes: the consolidation of the brain’s dynamic repertoire toward adulthood (Khanna et al., 2015) and the growth of flexible dynamics potentially enabling functional diversity (Mattar et al., 2015a; Hutchison and Morton, 2015). Previous work has indicated that working memory performance over neurodevelopment is strongly related to reciprocal activation of the executive system and deactivation of the default mode network (Satterthwaite et al., 2013b). Here, our findings suggest that a balance of state dominance and flexibility contributes to variation in complex executive accuracy that contributes to multiple tasks with executive demands. The organization of states over the timescales of moments and years relate to the capacity for individuals to express variable degrees of executive function.

In this vein, previous literature from research applying EEG additionally suggests that much of the topological activity observed across the brain can be reduced to a finite set of “microstates” (Khanna et al., 2015). Microstate analyses have revealed scale-free dynamics in EEG data that, when convolved with the hemodynamic response function, correlate significantly with fMRI resting-state networks (Musso et al., 2010). The scale-free nature of these states exhibit a dynamic profile from 256 ms up to 16 s, putatively supporting cognition and network adaptation (Van de Ville et al., 2010) Thus, the dynamics present in fMRI data can be examined as a collection of transient states, which in turn may be reducible to microstates observable with EEG (Khanna et al., 2015). It is an open question how microstates examined with EEG may develop over adolescence and relate to the dynamics reported here. Crucially, fast timescale analysis of microstates in EEG at rest and during tasks may provide further insight into the state space dynamics underlying the development of diverse executive functions. In addition, there is an emerging body of research indicating that resting-state network variation can result from noise-driven transitions between multistable states that are facilitated by interactions between fast local dynamics in the γ-range (approximately 40 Hz) and ultraslow oscillations (approximately 0.1 Hz) at the global level of brain organization (Deco et al., 2011). Studies could attempt to link changes in inter-frequency interactions across the brain to establish models predicting developmental change. Such an effort would potentially allows us to identify the scales of mechanisms responsible for the major states that we observe within fMRI data.

Specificity of dynamics and cognition

When we analyzed the associations between specific executive functioning measures and dynamic measures of brain function, we observed a double dissociation. Specifically, time in primary states related to measures of complex reasoning in the verbal and visual domains, whereas state flexibility related to mental flexibility. This observation establishes an intuitive link between two properties of the dynamic brain and distinct executive abilities. Here, the verbal analogical reasoning test and matrix test require the ability to detect abstract associations in symbolic information to solve problems. Here, our task-positive states load heavily onto the frontoparietal, cingulo-opercular task control, and dorsal attention networks, which are flexibly and ubiquitously recruited across tasks demanding executive function (Cole et al., 2013; Hutchison and Morton, 2015). The increasing presence of this state in the context of its opponent task-negative state may represent the brain’s underlying ability to co-recruit systems involved in switching, updating, and sustained attention to perform complex executive tasks (Power and Petersen, 2013) across multiple modalities. Conversely, brain state flexibility confers an advantage to a mental flexibility requiring sensitivity to shifting task demands. Notably, the task used to measure state flexibility is similar to clinical tests that measure perseveration – the inability to flexibly respond to changes in rules – often observed in neurological disorders and brain injury (Robinson et al., 1980). Thus, examining the brain’s tendency to transition fluidly may prove to be a biologically sensitive marker of adaptability to structured environmental demands and underlying neurobiological dysfunction.

More broadly, our findings indicate that in complex executive domains, at least some of performance depends not only on the contributions of the frontal lobes, but also the contribution of brain-wide states and flexibility among them. Here, our findings imply that state flexibility is only advantageous in a broader context: transitions that include a disproportionate traversal of non-primary states may represent transitions that are not supportive of strong executive function. In older adolescents in whom the time spent in task-positive and task-negative states is higher, flexibility is positively associated with complex executive accuracy. This observation has potential links to recent interest in the (potentially opponent) relationship between executive functions and creativity (Thompson-Schill et al., 2009). Future measures could explore brain flexibility in young individuals to examine whether they show greater levels of creativity under some conditions at a period when complex executive functions are still developing (Kleibeuker et al., 2013; Stevenson et al., 2014).

We additionally examined the specificity of dynamic measures of brain function with complex executive accuracy by including memory and social cognitive accuracy in our regression models. In these analyses, we observed that the association between complex executive accuracy and brain dynamics is lessened when considering the contributions of memory accuracy. Executive function and memory covary across individuals (Duff et al., 2005), and the executive and memory accuracy factor scores used here are highly related in this sample (Moore et al., 2015). Our results suggest that part of the relationship between executive and memory function is correlated with the task-positive and task-negative states as well as flexible state transitions. Whereas the task-positive state represents systems commonly recruited in executive tasks, the default mode network is recruited in the task-negative state as task control and dorsal attention systems are suppressed. However, the frontoparietal network rests around its baseline in task-negative states. This finding may represent the fact that part of the transition between task-negative and task-positive states may be mediated through the spontaneous engagement of the frontoparietal system as attention fluctuates (Hellyer et al., 2014). Whereas attentional variability can be a hallmark of cognitive syndromes such as ADHD, it is intuitively possible that a resting propensity toward attentional flexibility can prepare the healthy brain for effective on-task engagement. Notably, previous studies indicate that interactions involving dynamics in task-positive and task-negative networks support memory function (Ward et al., 2014) and its failure in dementia (Franzmeier et al., 2015). In addition, complex executive function has been shown to mediate the relationship between age and memory decline in healthy aging (Troyer et al., 1994), and has been most consistently linked to brain dynamics in studies to date (Cocchi et al., 2013; Cole et al., 2013; Braun et al., 2015). Thus, future analysis could examine the specificity of the frontoparietal network’s driving role in task-positive to task-negative state transitions in development and disease.

Sex differences

Interestingly, we observed that females spent more time in the two primary states than males. Previous work in time-invariant functional connectivity has shown that females have more network segregation characterized by increased within-community connectivity relative to males (Satterthwaite and Baker, 2015). This topological pattern may be in part accounted for by increased time spent in the two primary states detected here, which could manifest as increased within-community connectivity in traditional timeseries analysis in graph theoretical studies. It is interesting to speculate about the origin of sex differences in state space dynamics. Differences in general dynamic tendencies may be partly attributable to underlying sex differences in white matter organization. In particular, females display more prominant interhemispheric connectivity relative to males (Ingalhalikar et al., 2014) in addition to numerous voxel and tract level differences (Herting et al., 2012; Kanaan et al., 2012; Kumar et al., 2012) that are expressed differently over age (Bava et al., 2011; Lebel et al., 2010).

Importantly, underlying structure in brain networks is associated with and constrains overlying functional topology measured by fMRI (Hermundstad et al., 2013). However, how the underlying connectomics of the brain constrain state evolution is unknown, and their specific contributions to complex executive functions remain similarly obscure. Differences in inter- and intra-hemispheric connectivity may mediate differences in functional state formation. In the current study, the state evolution of the dynamic brain could represent the crucial variable between structure and behavior, and future work could examine simulated approaches (Ritter et al., 2013) to recovering sex differences in functional state formation and transitions as a function of underlying structure (Khanna et al., 2015). Together, these features may explain variability in cognition in specific domains including complex executive accuracy.

Relationship to other approaches to studying dynamics in neuroimaging data

A number of other approaches to studying dynamics in neuroimaging data are available and rapidly proliferating. Notable alternative approaches include dynamic independent components analysis (ICA (Calhoun et al., 2014)) and selective averaging of individual fMRI time frames using clustering (Liu et al., 2013). In comparison to ICA, our approach does not enforce an assumption of independence on community structure, and can identify communities that are highly overlapping. In addition, group level ICA, commonly applied in the literature, loses sensitivity to individual differences in state structure that may exist across individuals. Here, different individuals may have both different types and numbers of clusters. Moreover, our hierarchical clustering over individual level states allows for the identification of common states across individuals, facilitating an examination of the correspondence between communities in different people while still maintaining their inherent differences. Some temporal dynamics can be examined using both information defined solely on the individual level (e.g., state flexibility) and information from the hierarchical approach (e.g., time spent in two primary group-level states).

In addition, principal components analysis (PCA), which enforces the identification of orthogonal components, is a transformation that can be applied to BOLD fMRI time series. In comparison to PCA, the current approach does not enforce orthogonality, and instead can recover ”fuzzy” (non-independent) clusters in data. To compare to the current approach, we applied an exploratory PCA to the same data reported here. The results of the PCA indicate that the first component explains an average of 19.8% of variance in the data. We observed a significant correlation between the first component score loadings and the Task-Negative state across regions (Pearson’s correlation coefficient r = −0.69), as well as between the second component loadings and the Task-Positive state across the regions (Pearson’s correlation coefficient r = 0.66). Intuitively, these values indicate that the first principal component explains only 43%–47% of variance in the two primary states. These data support our conclusion that the community detection algorithm extracts states whose features are not well-represented by orthogonal components.

In comparison to previous approaches to time-frame analysis using k-means clustering (Liu et al., 2013), our approach is distinct in its use of hierarchical clustering. In addition, the generalized Louvain algorithm (Blondel et al., 2008) does not require an a priori specification of the number of desired communities, and instead optimizes the modularity quality function for a given γ value by iteratively testing the community structure for robustness to small perturbations. Thus, k-means optimizes toward a specific number of clusters with secondary emphasis on modularity quality, whereas the generalized Louvain algorithm optimizes modularity at a given resolution of the network, which does not require enforcement of an a priori assumption on the number of communities present (Bassett et al., 2013b); rather, γ is a free parameter and its impact on resulting community structure can be explored.

More generally, by clustering BOLD TRs into robust states based on their spatial patterns, transitions from state to state, time spent in states, and dwell time can be observed. These features cannot be directly quantified using component-based and other window-based dynamic connectivity approaches. State-level dynamic analysis can provide an important complement to other approaches by connecting BOLD signal analysis to physical systems approaches that quantify the metastability and multistability of neural systems Deco et al. (2011). It remains to be seen whether the signal organization and dynamics observed in state level analyses can provide novel insight into cognitive neurodevelopment in specific task-related and pathological contexts. Future BOLD fMRI analysis can be applied to examine how state level and functional connectivity level BOLD organization develop to support cognitive function.

Methodological limitations

Some limitations apply to the current work. While we investigate dynamic parameters and their relationship to cognition in a large sample of youth, the cross-sectional nature of our study limits generalization and inferences about causal or time-varying relationships (Kraemer et al., 2000). Future studies should follow youths from a young age range to replicate the analyses reported here in a within-subjects design. In addition, individuals in the current sample exhibited higher complex executive cognition performance than the sample including all individuals assessed in the Philadelphia Neurodevelopmental Cohort; while these individuals were excluded to prevent spurious effects of motion on our analyses, it is possible that findings would not generalize through the lowest ranges of executive abilities. Finally, we use a robust, statistically-derived measure from a large factor analysis of performance on a neurocognitive battery (Moore et al., 2015). This factor score represents complex executive accuracy with contributions from many traditional neuropsychological tests. Other studies have focused on the factor structure of different batteries of traditional “cognitive control” tests (Miyake et al., 2000) and the representation of executive cognition in frontal cortex (Nee and D’Esposito, 2016) and distributed functional networks (Reineberg et al., 2015). An integrated account will inevitably involve further construct refinement in the early lifespan (Moore et al., 2015) compared to adulthood and further multimodal approaches (Banich, 2009).

With respect to dynamic analyses, we applied a network-based clustering technique to obtain an average of 4 states per individual. While this resolution provides a number of states consistent with several prior studies (Allen et al., 2012; Britz et al., 2010), it may also be of interest to use these techniques to study brain state dynamics at a higher temporal resolution (Calhoun et al., 2014), especially in data with higher sampling frequency. Indeed, exploring a wide spectrum of temporal resolutions –from a few longer states to many shorter states – may reveal novel transitory dynamics that are relevant to individual differences in cognition. While our neuroimaging sequences were consistently acquired with a standardized time resolution over several years within the Philadelphia Neurodevelopmental Cohort, modern neuroimaging sequences using fast multiband protocols are now available, which could improve sensitivity to dynamic properties in BOLD timeseries. A higher time-resolution and the opportunity to collect many more observations per subject may allow us to robustly quantify the presence of states beyond the two most prominent states described here. In addition, future studies in task-related conditions could examine whether the presence of task-positive and task-negative states and flexible transitions between them might account for in-scanner performance. Alternate measures in similar analyses could include the dwell times for each state, average and variability of state dispersions over time, and quantification of the walks through individual state spaces. It is also worth pointing out that our parcellation also limits our ability to observe some brain systems. In the current study, we used an independently defined parcellation (Power et al., 2011b) to study brain networks of interest. While this parcellation allowed us to robustly recover states representing the default mode and frontoparietal control systems, it may undersample smaller or more specific networks. In future studies, alternate parcellations or systems of interest defined a priori could form the basis for state-level analyses linking brain dynamics to cognitive measures. Finally, no ground truth is available in the current data investigating BOLD fMRI dynamics, and future studies using techniques such as electrocorticography and magnetoencephalography could be used to examine system microstates and possible development in metastable, multistable, and critical dynamics in adolescent development. The use of techniques such as electrocorticography could examine the ground truth of brain state spatiotemporal organization.

In a similar vein, while we term the present states “task-positive” and “task-negative” based on the observed activation of previously defined systems in the two main states that conforms to cognitive systems (Power et al., 2011b; Cole et al., 2014; Mattar et al., 2015b), the exact interpretation of networks observed at rest is incompletely developed in “resting state” paradigms (Cole et al., 2010). Future large-scale studies could aim to extract robust states in samples with multiple cognitive tasks to detect whether task-specific states are recruited or form to support task performance. In addition, the specific state BOLD signal distributions identified here do not concentrate specifically in any single network, but instead represent composites of activity across several previously defined systems. Prior studies have demonstrated that longer timescale dynamics express different patterns of distributed connectivity that maintain much of the organization observed in resting state connectivity, but change with cognitive demands (Cole et al., 2014; Mattar et al., 2015b) as a result of moment-to-moment activity “flow” Cole et al. (2016). Examining the moment-to-moment modulation and flow of states may provide insight into the relative contributions of systems expressed in the primary states observed here. Notably, the states recovered here bear resemblance to the task-active and baseline states uncovered during attention (Shine et al., 2016a,b) and n-back performance in a different parcellation, suggesting that they may be more generally observed to oppose one another during tasks demanding executive function. In addition, physiological nuisance artifacts may contribute to some BOLD signal characteristics. While the BOLD data examined here were bandpass filtered to a range presumed to be robust to physiological nuisance parameters (Birn, 2012), it is possible that heart rate and respiration effects that vary with age may introduce spurious frequency components or power differences into BOLD time courses via aliasing. Future state-level studies could attempt to relate physiological effects to BOLD signals over neurodevelopment.

Conclusion

In closing, we illustrate the utility of network approaches beyond traditional functional and structural connectivity by exploring time-by-time networks, identifying brain states, and quantifying the dynamics of their transitions in neurodevelopment. Two frequently observed brain states exist early in development and are more prominent in young adulthood. These primary states are complemented by a rich set of less frequent states that differ across individuals. Flexible transitions between these states are related to executive function across adolescence. These findings motivate future work to determine whether brain state dynamics provide a basis for understanding the development of the functional connectome, the emergence of cognition, and alteration of these biomarkers in psychopathology.

Appendix A. Supplementary data

Supplementary data related to this article can be found at https://doi.org/10.1016/j.neuroimage.2017.10.048.