Critical dynamics in population vaccinating behavior

Significance

Complex adaptive systems exhibit characteristic dynamics near tipping points such as critical slowing down (declining resilience to perturbations). We studied Twitter and Google search data about measles from California and the United States before and after the 2014–2015 Disneyland, California measles outbreak. We find critical slowing down starting a few years before the outbreak. However, population response to the outbreak causes resilience to increase afterward. A mathematical model of measles transmission and population vaccine sentiment predicts the same patterns. Crucially, critical slowing down begins long before a system actually reaches a tipping point. Thus, it may be possible to develop analytical tools to detect populations at heightened risk of a future episode of widespread vaccine refusal.

Abstract

Vaccine refusal can lead to renewed outbreaks of previously eliminated diseases and even delay global eradication. Vaccinating decisions exemplify a complex, coupled system where vaccinating behavior and disease dynamics influence one another. Such systems often exhibit critical phenomena—special dynamics close to a tipping point leading to a new dynamical regime. For instance, critical slowing down (declining rate of recovery from small perturbations) may emerge as a tipping point is approached. Here, we collected and geocoded tweets about measles–mumps–rubella vaccine and classified their sentiment using machine-learning algorithms. We also extracted data on measles-related Google searches. We find critical slowing down in the data at the level of California and the United States in the years before and after the 2014–2015 Disneyland, California measles outbreak. Critical slowing down starts growing appreciably several years before the Disneyland outbreak as vaccine uptake declines and the population approaches the tipping point. However, due to the adaptive nature of coupled behavior–disease systems, the population responds to the outbreak by moving away from the tipping point, causing “critical speeding up” whereby resilience to perturbations increases. A mathematical model of measles transmission and vaccine sentiment predicts the same qualitative patterns in the neighborhood of a tipping point to greatly reduced vaccine uptake and large epidemics. These results support the hypothesis that population vaccinating behavior near the disease elimination threshold is a critical phenomenon. Developing new analytical tools to detect these patterns in digital social data might help us identify populations at heightened risk of widespread vaccine refusal.

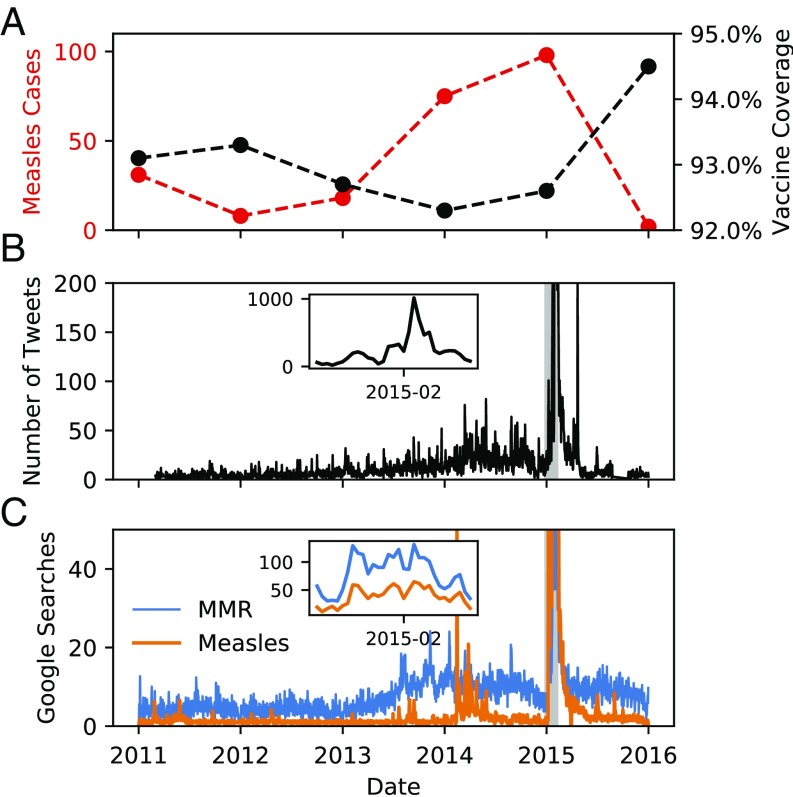
In recent decades, vaccine refusal has contributed to the resurgence of measles and pertussis and significantly delayed the global eradication of polio (1, 2). For instance, the 2014–2015 measles outbreak in Disneyland, California was preceded by declining kindergarten measles–mumps–rubella (MMR) vaccine coverage in California between 2010 and 2014 (3) (Fig. 1A). Vaccine compliance at school entry fell to 70–90% in many cases and sometimes even lower in some Los Angeles schools (3). Inadequate vaccine compliance appears to have played a role in the outbreak (4), contributing to a significant peak in California measles case notifications in late 2014 and early 2015 (5) (Fig. 1A). The outbreak garnered significant public interest, causing a large spike in both US-geocoded tweets regarding measles (Fig. 1B) and Google Internet searches in California for “MMR” and “measles” (Fig. 1C) as reports of cases began to flow in. Amid the resulting public outcry, the California legislature began taking steps to disallow nonmedical exemptions (6–8), although statewide MMR vaccine uptake began to recover before these policy changes went into effect (3) (Fig. 1A).

Fig. 1.

Interactions between disease spread, vaccine uptake, and online activity before, during, and after the 2014–2015 Disneyland, California measles outbreak. (A) Kindergarten MMR vaccine uptake (black; note vertical scale) and measles case notifications in California (red): year in horizontal axis for vaccine uptake corresponds to the ending calendar year of the corresponding academic year (e.g., 2016 means 2015–2016 academic year). Case notifications in 2016 go only to November 18. Most 2014 cases occurred at the end of the year. (B) Number of US geocoded tweets for measles-relevant search terms, 2011–2016, with a sharp spike in early 2015 corresponding to Disneyland measles outbreak. (C) GT Internet search index for MMR (blue) or measles (orange) in California, 2011–2016, with a sharp spike in early 2015 corresponding to the Disneyland measles outbreak. Shaded region in B and C indicates outbreak time period. See SI Appendix, sections S1 and S2 for details on search terms, data sources, and data extraction.

The changes in vaccinating behavior before and after the Disneyland measles outbreak are consistent with a coupled behavior–disease dynamic in which vaccinating decisions and disease dynamics influence one another in a nonlinear feedback loop. The mathematical modeling of coupled behavior–disease dynamics is growing rapidly (9–12), although relatively little attention has been devoted to critical phenomena in such systems. The theory of critical transitions (tipping points) and their early warning signals may help public health officials anticipate when and where resistance to vaccination might develop and intensify. A critical transition occurs when a complex system shifts abruptly to a strongly contrasting state as an external driver moves the system past a bifurcation point (13, 14). These shifts may exhibit characteristic early warning signals as a consequence of critical slowing down (CSD), in which a declining rate of recovery from small perturbations causes dynamics to become more variable. CSD can be detected by changes in indicators such the variance, lag-1 autocorrelation (AC), and coefficient of variation in high-resolution time series of state variables (13, 14).

Social norms tend to reinforce currently accepted behavior and thus promote status quo practices in populations (15–17). However, individuals also make vaccinating decisions based on the perceived risks of the vaccine and the diseases they prevent (15). Here, we hypothesize that coupled behavior–disease systems exhibit a tipping point arising from interactions between social norms, perceived vaccine risk, and perceived disease risks. Specifically, we investigate the effects of risk perception in terms of the ratio of the magnitude of perceived vaccine risk to the magnitude of perceived risk of disease complications (we will call this “relative vaccine risk” for short). Rising public concern about potential vaccine complications can cause the relative vaccine risk to grow to a tipping point where social norms in support of a status quo of high vaccine acceptance can no longer prevent a drop in provaccine sentiment. If the population moves beyond this tipping point, a decline in provaccine sentiment causes fewer people to seek vaccination and herd immunity breaks down, enabling outbreaks of various sizes. However, before the tipping point is reached, CSD causes the variance, lag-1 AC, and coefficient of variation of time series of population sentiment toward the vaccine to increase. Importantly, the increase in these three indicators should be noticeable long before any significant change is obvious in the raw time series of population sentiment toward the vaccine. In other words, they provide an early warning signal of a potential tipping point.

However, coupled behavior–disease systems are complex adaptive systems, which introduces an important twist to our hypothesis. The relative vaccine risk is not simply an external driver pushing the system past a tipping point. It also responds to changes in infection prevalence. When an outbreak occurs, the relative vaccine risk drops. Hence, a critical transition can be avoided if the population responds to the small outbreaks that begin to occur near a tipping point (18). We hypothesize that these dynamics could lead to CSD before the outbreak followed by “critical speeding up” (improving resilience to perturbations) after the outbreak as the population recedes from the tipping point. Although CSD in a time series of population vaccine sentiment will not necessarily predict whether the population will pull back from the critical transition or go through the transition, it can at least tell us that the population is getting dangerously close to a tipping point.

In this article, we report evidence for CSD in sentiment-classified tweets and in Google searches about measles before the Disneyland measles outbreak, followed by critical speeding up afterward. These empirical digital signals show patterns that match those exhibited by a mathematical model of the coupled dynamics of measles transmission and vaccine sentiment that has been previously tested against case notification and vaccine uptake data for measles and pertussis (19–21). Hence, these digital signals could be used as an early warning signal of tipping points in coupled behavior–disease systems.

Results

Model.

The mathematical model captures the interplay between disease dynamics, social learning, social norms, and perceived risk:

$$\frac{dS}{dt}=\mu \left(1-x\right)-\mu S-\beta SI,$$ [1]

$$\frac{dI}{dt}=-\mu I+\beta SI-\gamma I,$$ [2]

$$\frac{dx}{dt}=\kappa x\left(1-x\right)\left(-\omega \left(t\right)+I\left(t\right)+\delta \left(2x-1\right)\right),$$ [3]

where S is the proportion of susceptible individuals; I is the proportion of infected individuals, x is the proportion of individuals with provaccine sentiment; μ is the per capita birth and death rate, β is the transmission rate, γ is the rate of recovery from infection, κ is the social learning rate, δ is the strength of social norms, and ω(t) is the relative vaccine risk. We note that Eq. 3 has been rescaled and that the proportion of recovered individuals R is simply 1 − S − I. From Eq. 1, vaccine uptake is given by x, and thus all provaccine individuals choose vaccination, while the remainder 1 − x of antivaccinators avoid it. Provaccine sentiment becomes more widespread when infection prevalence I(t) is higher or when vaccine risk ω(t) is lower. Social norms reinforce whichever sentiment—provaccine or antivaccine—is more common.

We chose a simple model because CSD only requires that the eigenvalue go to zero at the bifurcation point. This is universal to many types of local bifurcations in both simple and complex models (14). Hence, a broad class of more complicated models should predict the same patterns. (For instance, it is possible to show that including a third category of individuals with neutral sentiment also exhibits CSD.) Additional details about model derivation, parameterization, and simulation appear in SI Appendix, section S3.

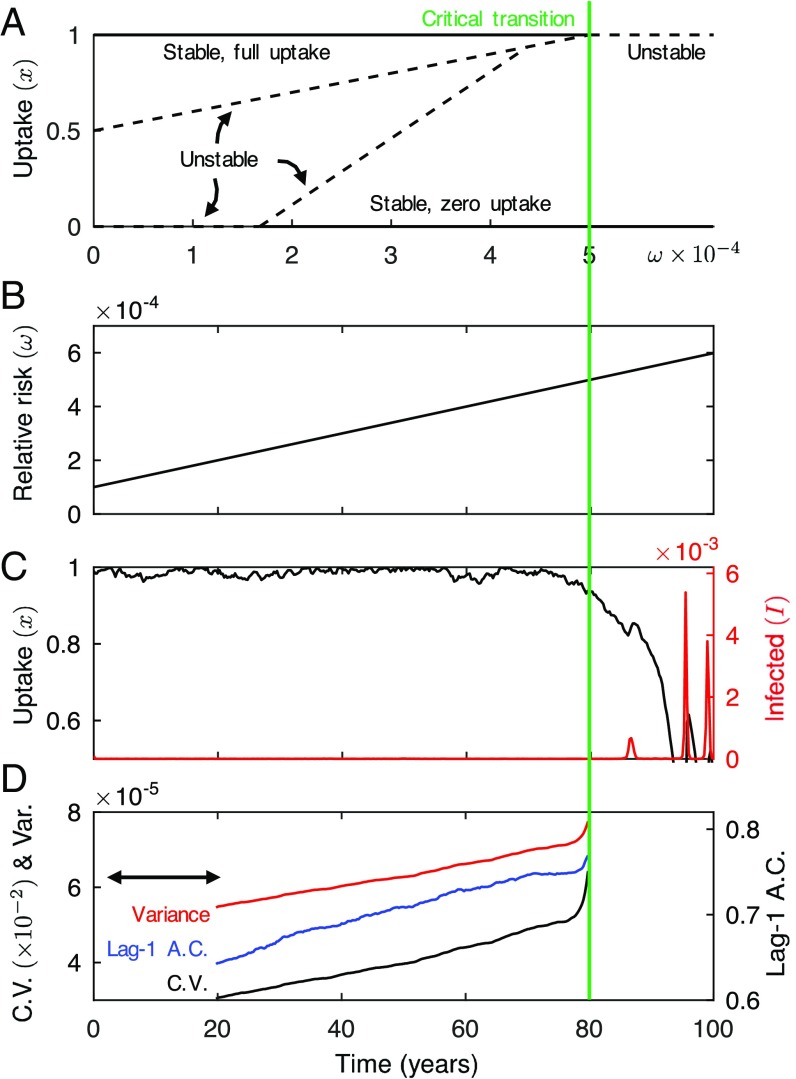
In the case of fixed vaccine risk, ω(t) = ω, the model has multiple stable equilibria (19). The equilibrium (S, I, x) = (0, 0, 1) is of particular interest because it corresponds to a disease-free state with full vaccine uptake that is stable when relative vaccine risk is less than the strength of social norms (ω < δ). However, as ω increases past δ, the equilibrium is destabilized through a critical transition at ω = δ and the population converges to a state of endemic infection and no vaccine uptake (Fig. 2A). At other parameter values, a drop to endemic infection and intermediate vaccine coverage is also possible.

Fig. 2.

Coupled behavior–disease model shows early warning signals as perceived risk increases toward a critical transition. Green line indicates location/time of critical transition in all panels. (A) Bifurcation diagram of vaccine uptake showing a critical transition from full to zero vaccine uptake when perceived relative risk (ω) exceeds social norm strength (δ) (solid lines are stable branches; dashed are unstable). (B) ω (solid line) increasing linearly past critical transition at ω = δ. (C) Vaccine uptake (black) and infection prevalence (red) as ω increases as in B. (D) Variance (red), lag-1 AC (blue), and coefficient of variation (black) for the time series in C (mean values at each time point across 500 realizations). Methodological details appear in Methods and SI Appendix, sections S3 and S4.

To study CSD, the model was converted to a stochastic model by including an additive Wiener process (SI Appendix, section S3). When ω(t) increases linearly until it crosses the tipping point (Fig. 2B), vaccine uptake collapses and an epidemic occurs (Fig. 2C). However, before this happens, the variance, lag-1 AC, and coefficient of variation of the time series of provaccine sentiment (x) increase as the critical transition is approached (Fig. 2D). The increase begins long before any significant change is obvious in the raw x time series, and hence they provide an early warning signal of the critical transition. We will show later in Results that the proportion of individuals with antivaccine sentiment (1 − x) also exhibits CSD.

Approach.

In the next subsection, we compare the temporal evolution of the three indicators in digital social data before and after the Disneyland measles outbreak to the model predictions when the relative vaccine risk ω(t) increases linearly to the tipping point at ω = δ and then decreases linearly back to a baseline level (SI Appendix, section S3)—this is intended as a first approximation to how CSD might occur before the outbreak, followed by critical speeding up after.

We treated CSD in the time series of number of tweets with provaccine (respectively, antivaccine) sentiment as a proxy for CSD in the time series of the proportion of individuals with provaccine (respectively, antivaccine) sentiment in the general population (x and 1 − x; note that x is also vaccine uptake in the model). This is supported by research showing a correlation between sentiment of tweets on influenza vaccine and actual influenza vaccine uptake (22), and between discussion of individuals’ health status in social media and their actual health status (23). We also show that CSD in total tweets of a given sentiment is a good proxy for CSD in population vaccine sentiment and uptake in a broad class of expanded models in which a critical transition in abundance of individuals with provaccine or antivaccine sentiment drives an observable change in the number of provaccine or antivaccine tweets in online social media (SI Appendix, section S6).

We analyzed three empirical datasets. The US GPS dataset included measles-related tweets with latitude and longitude coordinates in the United States. The much larger California and US Location Field datasets included measles-related tweets from users indicating a California or US location in their user location field. We used a machine-learning algorithm to classify tweet sentiment in the Location Field datasets into provaccine, vaccine, or other. The US GPS dataset sentiment was classified using Amazon Mechanical Turk (Methods).

Provaccine Tweets.

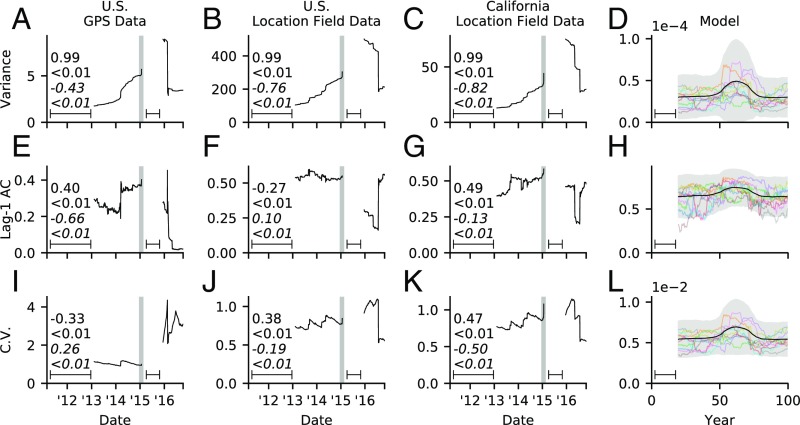
The time series of provaccine tweets shows evidence for CSD in the years before the Disneyland outbreak (Fig. 3). In the California Location Field dataset, we observe that the variance (Fig. 3C), lag-1 AC (Fig. 3G), and coefficient of variation (Fig. 3K) all increase significantly before the outbreak. The increase in these indicators begins well before the rolling window used for local temporal averaging reaches the time of the outbreak. Hence, the analysis reveals a long-term trend in indicators beginning several years before the outbreak. We interpret this trend as the system’s growing variability as the population approaches a critical transition to widespread reductions in vaccine uptake (Fig. 2).

Fig. 3.

CSD provaccine tweets before and after Disneyland measles outbreak. (A–D) Variance, (E–H) lag-1 AC, and (I–L) coefficient of variation for (A, E, and I) US GPS, (B, F, and J) US Location Field, (C, G, and K) California Location Field data, and (D, H, and l) model. The residual time series was used for variance and lag-1 AC. Kendall tau rank correlation coefficients are displayed before (regular font) and after (italic) the Disneyland peak with P values denoted by <. Window width used to compute rolling averages is indicated by line interval. Shaded region indicates outbreak time period. Model panels show indicators averaged across 500 stochastic model realizations (black), 2 SDs (shaded), and 10 example realizations (colored lines). See Methods and SI Appendix, sections S3–S5 for details.

After the outbreak, however, California responds by receding from the critical transition, rather than being pushed past it to a new dynamical regime of endemic infection and significantly reduced vaccine uptake [as occurred for whole-cell pertussis vaccination in the United Kingdom, for instance (21)]. This is indicated by a decline in all three indicators after the outbreak (Fig. 3 C, G, and K), as well as by a reversal of the declining trend in vaccine coverage (Fig. 1C). The system’s resilience to perturbations improves as the population recedes from the tipping point.

The decrease in the indicators after the outbreak is also a useful test of whether underlying changes in the total number of Twitter users over the study time window could be driving the observed increase in the indicators before the outbreak. If this were the case, we would not expect to see a decline in the indicators or the number of raw tweets after the outbreak.

The patterns are similar but not as consistent for the datasets from the much larger US population, as expected. Variance increases for both US GPS and US Location Field datasets (Fig. 3 A and B), but lag-1 AC increases only for the US GPS dataset (Fig. 3E), and the coefficient of variance increases only for the US Location Field dataset (Fig. 3J). After the outbreak, the same indicators in the same datasets decline (Fig. 3 A, B, E, and J), while the indicator increases in two of the subpanels (Fig. 3 I and F).

The mathematical model shows the same general trends, including a stronger signal for variance than for lag-1 AC or coefficient of variation. The three indicators grow and then decline on average in a pattern similar to that observed in the data, as the perceived relative risk ω(t) approaches and then recedes from the tipping point (Fig. 3 D, H, and I). The relative magnitude of change in the indicators is also similar in model and data: changes in variance are largest, followed by coefficient of variation, followed in turn by lag-1 AC. In the model, only 66%, 63%, and 67% of stochastic realizations exhibit an increase followed by a decrease in the Kendall tau coefficient for variance, lag-1 AC, and coefficient of variation, respectively.

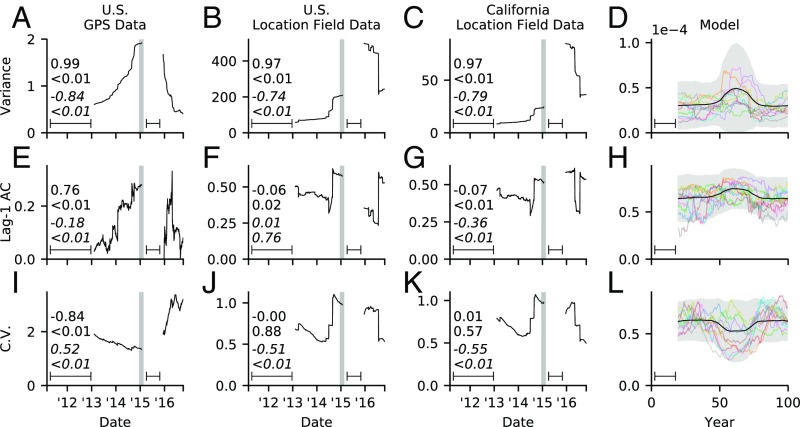
Antivaccine Tweets.

Similar trends are observed for antivaccine tweets (Fig. 4), with a surprising exception. As before, the increasing and then decreasing trend in variance is strongest in both model and the three datasets (Fig. 4 A–D). However, using Kendall tau values as the criterion, lag-1 AC increases before the outbreak in only one of the three datasets (the US GPS dataset; Fig. 4E) and decreases after the outbreak in only two of the datasets (Fig. 4 E and G). Trends in lag-1 AC in the model are correspondingly weak, with many stochastic realizations failing to exhibit the increase and decrease (Fig. 4H).

Fig. 4.

CSD in antivaccine tweets before and after Disneyland measles outbreak. (A–D) Variance, (E–H) lag-1 AC, and (I–L) coefficient of variation for (A, E, and I) US GPS, (B, F, and J) US Location Field, (C, G, and K) California Location Field data, and (D, H, and I) model. The residual time series was used for variance and lag-1 AC. Kendall tau rank correlation coefficients are displayed before (regular font) and after (italic) the Disneyland peak with P values denoted by <. Window width used to compute rolling averages is indicated by line interval. Shaded region indicates outbreak time period. Model panels show indicators averaged across 500 stochastic model realizations (black), 2 SDs (shaded), and 10 example realizations (colored lines). See Methods and SI Appendix, sections S3–S5 for details.

Surprisingly, the coefficient of variation decreases consistently over most of the preoutbreak time period in all three datasets (Fig. 4 I–K). The model also exhibits this inversion (Fig. 4L), with a decrease in the indicator as the tipping point is approached and an increase as the population recedes from it, on average and in 59% of the stochastic realizations (Fig. 4L). Hence the datasets show a postoutbreak decrease as well, and not all preoutbreak Kendall tau values are negative at the 5% significance level if the time just before the Disneyland outbreak is included. The decline in the coefficient of variation before the tipping point for antivaccine but not provaccine sentiment occurs because the statistic divides the SD by the mean. The mean number of nonvaccinators increases from a small value as the tipping point is approached, while the mean number of vaccinators decreases.

Google Trends.

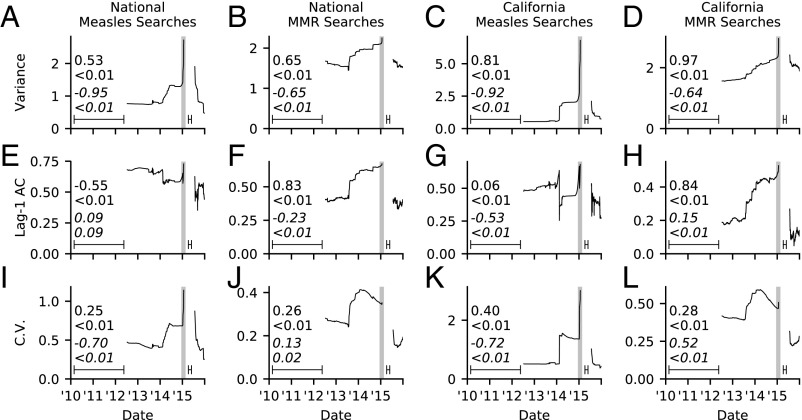
Google Trends (GT) is increasingly used in social science and behavioral research (24) and the study of infectious diseases (25, 26). Our search terms did not permit an analysis of sentiment, but previous research indicates that salient and controversial issues generate higher search volumes (27–29), including a study finding a significant inverse correlation between MMR vaccination coverage and Internet search activity, tweets, and Facebook posts (28). If we assume salient and controversial issues are ones on which population opinion is more divided, we can study CSD in the GT Internet search index concerning measles-related searches. These data are also consistent with critical dynamics near a tipping point. The GT data at the national and state levels generally show the same pattern as the Twitter data, with a rise in indicators before the outbreak and a decline afterward (Fig. 5). Trends are stronger at state than national levels, and for MMR rather than measles searches, which may reflect the greater volume of GT data on MMR than measles (Fig. 1B).

Fig. 5.

CSD in GT search index before and after Disneyland measles outbreak. (A–D) Variance, (E–H) lag-1 AC, and (I–L) coefficient of variation for (A, E, and I) US searches for measles, (B, F, and J) US searches for MMR, (C, G, and K) California searches for measles, and (D, H, and L) California searches for MMR. The residual time series was used for variance and lag-1 AC. Kendall tau rank correlation coefficients are displayed before (regular font) and after (italic) the Disneyland peak with P values denoted by <. Window width used to compute rolling averages is indicated by line interval. Shaded region indicates outbreak time period. See Methods and SI Appendix, section S4 for details.

Sensitivity Analyses.

We generated Figs. 3 and 4 using weekly instead of daily bins. For provaccine tweets (SI Appendix, Fig. S1), the variance always increases and then decreases, similar to the daily data. Lag-1 AC shows no trend or tends to decline before the tipping point. However, lag-1 AC measures changes in memory, and this is to be expected in a system where memory is short-lived: the life span of a typical online social media news item is less than 24 h (30), suggesting daily or subdaily granularity may be required to detect changes in lag-1 AC. The coefficient of variation exhibits a statistically significant increase and decrease before and after the outbreak. Most of these patterns are repeated in the analysis of antivaccine tweets using weekly bins (SI Appendix, Fig. S2). Results were also qualitatively unchanged when changing the rolling window width used for temporal averaging (SI Appendix, Figs. S3–S11).

We analyzed an extended model that includes seasonal variation in the transmission rate and an Erlang-distributed infectious period, both of which are known to influence disease dynamics (31, 32). We found that the indicator trends were unaffected (SI Appendix, Fig. S12). Through a probabilistic sensitivity analysis, we found that results are qualitatively unchanged across a broad range of parameter values (SI Appendix, Fig. S13). To study when happens when the relative vaccine risk responds to infection incidence, we simulated a variant model where ω(t) = a + bI(t). This variant exhibited growth and decline in the indicators before and after outbreaks, similar to Figs. 3–5 (SI Appendix, Figs. S14–S16). To rule out that the observed increase and decrease in the indicators can also happen around ordinary (noncritical) outbreaks, we simulated the model at a fixed value of ω far from the critical point. We found that all indicators were flat both before and after noncritical outbreaks (SI Appendix, Fig. S17).

Discussion

This article presents evidence that coupled behavior–disease dynamics near the disease elimination threshold is a critical phenomenon. We analyzed tweets and Google searches and showed how the patterns in the empirical data matched those exhibited by a mathematical model of coupled dynamics of measles transmission and vaccine sentiment and uptake. The three indicators—variance, lag-1 AC, and coefficient of variance—tended to increase before the Disneyland outbreak due to CSD, and then decrease after the outbreak due to critical speeding up (with the unexpected exception of the coefficient of variation in antivaccinators where the trend was inverted). Our model predicts the same trends in a population that approaches but then recedes from a tipping point.

The variance indicator showed the most robust trends. However, the coefficient of variation has the advantage that it inherently adjusts for changes in the mean number of tweets, and therefore does not require further processing of the data through computing a residual time series, as required for variance and lag-1 AC. The lag-1 AC tests for changes in system memory (13). This indicator often—but not always—showed the expected trends in our data, and trends were not as strong under weekly binning. We speculate this is either because memory is too short-lived in online social media for changes to be detected in data with daily or weekly granularity, or due to the presence of higher-order autoregressive processes that cannot be detected by lag-1 AC (33, 34).

The Disneyland outbreak was small and the response in population vaccine uptake rapid compared with other episodes of vaccine refusal where populations appear to have crossed a threshold into a regime of endemic infection and significantly reduced population-wide vaccine coverage. This latter scenario occurred for MMR vaccine in England and Wales in the 1990s and 2000s (80% minimum coverage) (21); whole-cell pertussis vaccine in England and Wales in the 1970s (30% minimum coverage) (21); and oral polio vaccine in northern Nigeria in 2003–2004 (1). In recent years, measles outbreaks larger than the Disneyland outbreak have occurred in many undervaccinated European populations (35). The social media response to the Disneyland outbreak was enormous considering the relatively small size of the outbreak. We speculate this was because the outbreak was the largest in California in many years and it started in a major tourist destination.

A limitation of our model is that it does not account for spatial clustering. This is a key aspect given the presence of clusters of nonvaccinators during the Disneyland measles outbreak (3), and it presents an opportunity for further research given the importance of networks in both infection transmission and strategic interactions (36, 37). The growth of clusters of nonvaccinators is not necessarily a competing hypothesis but rather could represent the spatial manifestation of critical dynamics. Spatially explicit models of behavioral dynamics in related systems develop clusters of individuals with homogeneous opinions as the population starts to “bubble” near a critical phase transition (38). CSD near a phase transition can manifest in similar ways in both spatial and temporal indicators because the underlying process is similar. Hence, the growing clusters of unvaccinated individuals observed before the Disneyland measles outbreak may signify bubbling near a critical phase transition. This hypothesis could be tested through further research on critical transitions in social networks of Twitter users. We also note that spatiotemporal analysis may take advantage of different and potentially better indicators than purely temporal analysis (39). More research is needed to better understand the informational content of the indicators in spatially structured populations and thereby distinguish qualitatively different outcomes, such as a quick and effective population response versus a protracted period of reduced vaccine coverage and endemic infection. Such analysis could incorporate vaccine uptake data if it has good spatial and temporal resolution (3).

A second limitation is our use of CSD in the number of sentiment-classified tweets as a proxy for CSD in vaccine sentiment and uptake in the general population. This assumption could be relaxed by using more detailed models that include a submodel for online social media activity that accounts for how different users generate differing numbers of tweets and how online social media activity interacts with social processes in the general population.

Our empirical results are largely consistent with our model predictions but cannot definitively establish causality. Future research could evaluate out-of-sample model predictions and consider the relationship between contemporaneous indicators of vaccine sentiment, such as tweets and search data, and observed vaccine uptake. It would also be valuable to consider other events that might affect sentiment dynamics near tipping points and to evaluate whether the significant population response to the Disneyland outbreak depended on its extensive media coverage.

Still, these results suggest that population vaccinating behavior near the elimination threshold can be characterized as a critical phenomenon near a tipping point in a coupled behavior–disease system. Our findings highlight the value of using digital social data to identify early warning signals of critical dynamics in adaptive behavior–disease systems and socioecological systems more generally (18). They also demonstrate the value of using dynamical systems theory in data science. The theory of critical phenomena in complex systems may shed light on other study systems represented in very large social media datasets.

Methods

Twitter Data.

For the US GPS dataset, we obtained 27,906 measles-related tweets from March 2, 2011, to October 9, 2016, with GPS coordinates in the United States. We used Amazon Mechanical Turk to classify the sentiment of these tweets into 10,926 “provaccine,” 2,136 “antivaccine,” and 14,844 “other” categories. A tweet was defined as provaccine (respectively, anti-vaccine) if the tweet content suggested the tweeter had a positive (respectively, negative) sentiment toward vaccines. This included any information about their feelings or opinions toward vaccines or the diseases they prevent. A tweet was placed in other if it was neither provaccine nor antivaccine, for instance, because it was irrelevant, ambiguous, or if the sentiment of the tweeter could not be clearly ascertained. Baseline analysis used daily bins. Additional details appear in SI Appendix, sections S2 and S5. Over the same time period, 11,685,264 tweets had information in the user location field. To generate the Location Field datasets, these tweets were geotagged using a modified version of the Geodict library and classified into pro-vaccine, anti-vaccine, and other using a linear support vector machine. The classifier obtained precision scores of 80%, 90%, and 79%, and recall scores of 83%, 82%, and 82% for antivaccine, other, and provaccine tweets, respectively (F1 scores: 81%, 86%, and 80%). The process identified 660,477 antivaccine, 883,570 provaccine, and 483,636 other tweets in the US dataset, and 101,683 antivaccine, 112,741 provaccine, and 59,030 other tweets in the California dataset. Baseline analysis used daily bins. Additional details including references appear in SI Appendix, sections S2 and S5. Data are available in Datasets S1–S3.

GT Data Extraction.

We analyzed GT search data for January 2011 to December 2015 using the gtrendsR (40) package. Unfortunately, the longest range of day-level query data Google provides is 3 months, which generates results in the arbitrary units of GT data that are not comparable between searches. (GT returns an estimate of the relative prevalence of searches matching the query for the time period and geography in question when the prevalence of the search term or terms exceeds some unspecified threshold.) As a result, we ran multiple day-level queries for each search (e.g., US measles, US MMR, California measles, California MMR) to cover the entire time period and then stacked the resulting data. We then ran a single corresponding week-level query for each search and used this to calculate an adjustment factor (specifically, we multiply each day-level value by the week-level query result divided by the week-level average from the daily data). This adjustment accounts for differences in the relative prevalence of searches over time in the stacked day-level data (41, 42).

CSD Indicators.

To adjust for long-term changes in the mean number of tweets, we used the residual time series of sentiment-classified tweets for lag-1 AC and variance, generated by subtracting the raw time series from a detrended time series. This is not necessary for the coefficient of variation since it already adjusts for long-term changes in number of tweets. We also removed the Disneyland social media peak (taken as running from January 22 to February 14 based on the US GPS dataset) to avoid issues with nonstationarity caused by the Disneyland outlier, and also because our focus is on CSD in the time before and after the outbreak. The methodology of computing indicators for the model was otherwise identical to that for the tweets and GT data. We used the Kendall tau rank correlation to quantify indicator trends (13), although we note that this statistic does not account for the size of increases or decreases over previous time points. Additional details appear in SI Appendix, section S4.