Ultrafast rotation in an amphidynamic crystalline metal organic framework

Significance

The control of matter at the molecular scale is a key requirement for the development of smart materials and artificial molecular machines. A challenging but promising platform in this emergent field of science is the development of crystalline materials with components that experience motion in a structurally predetermined manner, such that changes in their state of motion and the collective orientation of suitably functionalized molecules may lead to useful thermal, dielectric, and optical properties in response to external physical or chemical influences. Here, we describe a metal organic framework with elements that have no steric hindrance or electronic barriers, such that they can rotate in the solid as fast as they would it if they were in the gas phase.

Abstract

Amphidynamic crystals are an emergent class of condensed phase matter designed with a combination of lattice-forming elements linked to components that display engineered dynamics in the solid state. Here, we address the design of a crystalline array of molecular rotors with inertial diffusional rotation at the nanoscale, characterized by the absence of steric or electronic barriers. We solved this challenge with 1,4-bicyclo[2.2.2]octane dicarboxylic acid (BODCA)-MOF, a metal-organic framework (MOF) built with a high-symmetry bicyclo[2.2.2]octane dicarboxylate linker in a Zn₄O cubic lattice. Using spin-lattice relaxation ¹H solid-state NMR at 29.49 and 13.87 MHz in the temperature range of 2.3–80 K, we showed that internal rotation occurs in a potential with energy barriers of 0.185 kcal mol⁻¹. These results were confirmed with ²H solid-state NMR line-shape analysis and spin-lattice relaxation at 76.78 MHz obtained between 6 and 298 K, which, combined with molecular dynamics simulations, indicate that inertial diffusional rotation is characterized by a broad range of angular displacements with no residence time at any given site. The ambient temperature rotation of the bicyclo[2.2.2]octane (BCO) group in BODCA-MOF constitutes an example where engineered rotational dynamics in the solid state are as fast as they would be in a high-density gas or in a low-density liquid phase.

Crystalline arrays of barrierless molecular rotors present unique opportunities to explore emergent phenomena while offering opportunities for the development of novel paradigms in materials science and engineering (1). While the juxtaposition of high kinetic energy and long-range molecular order is uncommon, order in motion provides the required anisotropy for the control of thermal, optical, and dielectric properties, as well as for the design of dipolar arrays (2) and the development of artificial molecular machines (3). While some progress has been made in the study of experimental 2D rotary systems by taking advantage of molecules bound to surfaces (4, 5), barrierless molecular rotors in 3D crystals have not been available up to now. The first step to meet this challenge is to identify molecular components with intrinsic (gas-phase) rotational barriers that are smaller than thermal energy (i.e., E_a ≤ 0.596 kcal mol⁻¹ at 300 K), and crystal structures that pose no hindrance to the rotating units. The four key architectural elements to consider are (i) the size and shape of the rotator, which determine its surface area and moment of inertia, (ii) the availability of free volume with a cross-section that is greater than the volume of revolution of the rotator, (iii) the chemical nature and intrinsic torsional barrier of the bond or axle that links the rotator to the stator, and (iv) the axial symmetries of the rotator and the stator.

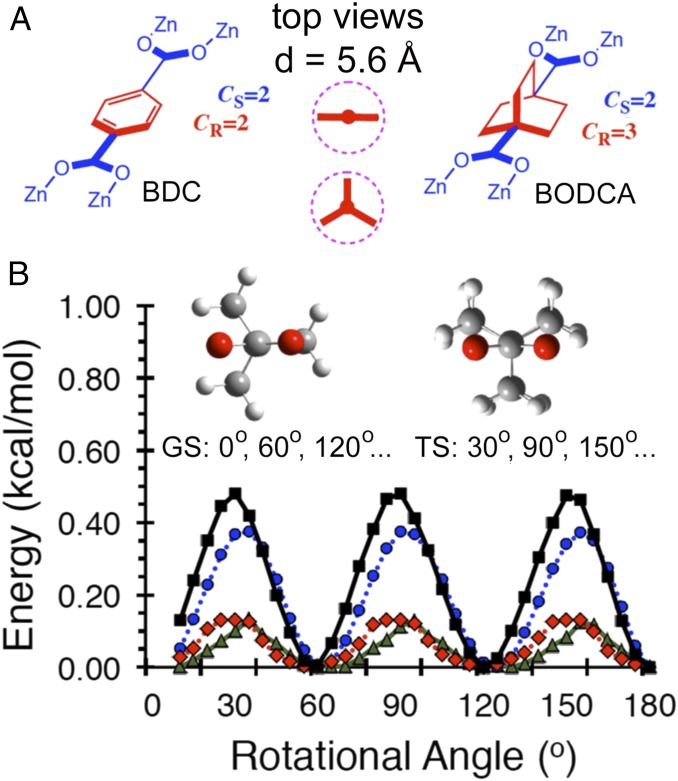
Based on recent observations (6–8), we selected bicyclo[2.2.2]octane (BCO) as a promising rotator for the construction of a crystalline molecular rotor with a barrier that is smaller than thermal energy at 300 K (Fig. 1, Right). In agreement with its relatively small size, globular shape, and small moment of inertia, molecular (7, 8) and supramolecular (9) crystals built with BCO rotators have very low activation energies (E_a ∼ 1.15–2.7 kcal mol⁻¹), and their preexponential factors (attempt frequencies) approach the frequency of the torsional mode that turns into rotations (∼10¹² s⁻¹) (6–8). For the selection of a crystal lattice that can generate an empty volume that is greater than the volume of revolution of the BCO rotator (∼5.6-Å diameter), we decided to explore the use of metal-organic frameworks (MOFs) (9, 10) because of their ability to maintain relatively large and permanent pores in highly robust architectures (11, 12).

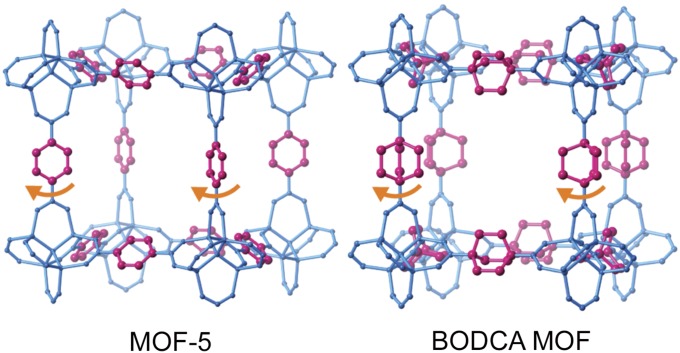
Fig. 1.

Isostructural networks of MOF-5 and BODCA-MOF with the corresponding BDC and BODCA rotators shown in red and the static carboxylate and Zn₄O clusters shown in blue (hydrogen atoms omitted for clarity).

Low-Barrier, High-Symmetry Rotator

Recognizing the similar dimensions of BCO and benzene (Fig. 2A), it seemed reasonable that one should be able to prepare an MOF-like structure based on octahedral Zn₄O nodes. Instead of using 1,4-benzene dicarboxylate (BDC) as the network linker giving rise to the well-known MOF-5, crystals could be built with 1,4-bicyclo[2.2.2]octane dicarboxylic acid (BODCA). While it is known that the rotation of the 1,4-phenylene in MOF-5 has a relatively large energy barrier of ∼11.3 ± 2 kcal mol⁻¹ as a result of loss of conjugation between the benzene ring and the two carboxylates, which renders the transition state a second-order saddle point (9), the absence of π-conjugation between the saturated BCO framework and the carboxylate group generates a low barrier to rotation in the case of BODCA-MOF. Furthermore, the threefold axial symmetry order of the BCO rotator (C_R = 3) combines with the twofold symmetry order of the static carboxylate (C_S = 2) to generate a sixfold degenerate potential (Fig. 2B). Quantum-mechanical calculations indicate that energy minima have an eclipsing interaction between the plane of the carboxylate group and one of the BCO blades, such that degenerate structures are obtained by rotation of the corresponding dihedral every 60°. Energy scans carried out with different methods and basis sets indicated very low-energy barriers. For example, calculations using the hybrid functionals M062X/6–311+G(d) or ωB97XD/6–311+G(d) indicated that the energy barrier is only 0.1 kcal mol⁻¹. By comparison, rotational barriers calculated with MP2/6–31G(d) or B3LYP/6–31G(d) are 0.4 and 0.5 kcal mol⁻¹, respectively. Based on the large empty space of the MOF framework, the relatively small angular steps between adjacent minima (60°), and the cylindrical shape of the BCO rotator, it seems reasonable to expect that rotational barriers should be similar in the solid state.

Fig. 2.

(A) Line structures of BDC, BODCA, and a representation of the cross-section of their volumes of revolution viewed down the main molecular axes. The diameters of the two rotors (d) are 5.6 Å. (B) Results from energy scans illustrating half a period (180°) of the sixfold degenerate energy potential of BODCA-MOF with the ground-state (GS) and transition-state (TS) structures viewed down the BCO-carboxylate linkage [black squares B3LYP/6–31G(d); blue circles MP2/6–31G(d); red rhombs ωB97xd/6–311+G(d); green triangles, M062X/6–311+G(d)]. The rotational angle is defined by the dihedral formed between the pane of the carboxylate and the plane of the BCO blade. GS geometries have dihedral angles of 0, 60, 120, etc.; the TS have dihedral angles of 30, 90, 150, etc. High-temperature measurements with RT > E_a are expected to reflect diffusional rotation, and low-temperature measurements with RT < E_a are expected to occur by a site-exchange mechanism.

Synthesis and Characterization of BODCA-MOF and BODCA-d-MOF

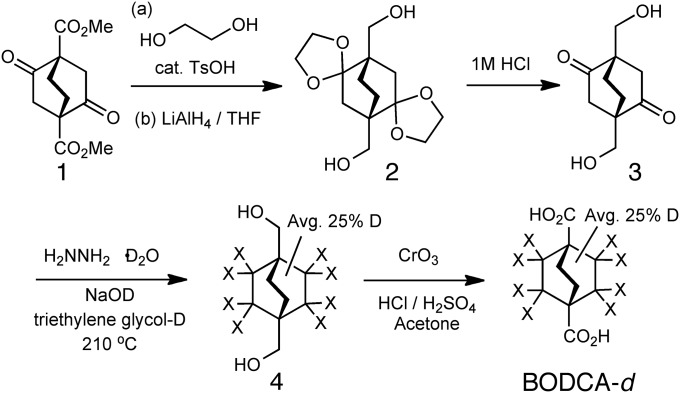
To test our hypothesis, we prepared samples of BODCA as reported in the literature (11). The synthesis of deuteron-enriched BODCA-d ligand for dynamic measurements using quadrupolar echo ²H NMR measurements was accomplished as shown in Fig. 3 by taking advantage of a base-catalyzed H/D exchange during the Huang–Minlon modified Wolff–Kishner reduction (13) of dione 3 by the introduction of triethylene glycol-d₂ and NaOD. This procedure resulted in a statistical d-labeling distribution established through a combination of liquid field desorption ionization mass spectrometry and the integration of the ¹H solution NMR spectrum of deuterated diol 4. On average, three out of the eight exchangeable protons were replaced with deuterons, resulting in a typical D content of 3 out of the 12 total hydrogen positions (four positions are not exchangeable), or 25%, on the bicyclic rotator. As expected, the ¹H and ¹³C solution NMR spectra of diol 4-d and diacid BODCA-d display chemical shifts and coupling with isotope effects due to the various substitution patterns of the deuterons with respect to the NMR-active ¹H and ¹³C nuclei (for NMR and FT-IR spectra, see SI Appendix).

Fig. 3.

Synthesis of the BODCA ligand with modifications to install deuterons on the bicyclic core, X represents H or D atoms.

Crystals of BODCA-MOF and BODCA-d-MOF were obtained via a room-temperature synthesis. Separate solutions of zinc acetate dihydrate and the BODCA ligand (either natural abundance for ¹H NMR studies, or deuteron enriched for ²H NMR studies) in N,N-dimethyl formamide (DMF) were mixed together in a vigorously stirring solution. Upon initial mixing, a white precipitate was immediately observed, suggesting the formation of zinc oxide-carboxylate clusters leading to MOF assembly. Aging of the sample in the mother liquor followed by successive washings (DMF and chloroform) and removal of solvent by heating under vacuum to create empty cores resulted in the desired compound as a white microcrystalline powder. Thermogravimetric analysis of the heat-treated solid confirmed the lack of included solvent and the structural integrity of the desolvated sample. The dinitrogen adsorption isotherm (77 K) of BODCA-MOF displays a sharp uptake with a single adsorption step at p/p_o > 0.01 followed by saturation, indicating a microporous material (SI Appendix, Fig. S27). It can also be described as a type II isotherm under the International Union of Pure and Applied Chemistry (IUPAC) classification system (SI Appendix). Application of the Brunauer–Emmett–Teller (BET) model over 0.005 > p/p_o > 0.05, according to the recommendation by Walton and Snurr (14), resulted in a BET surface area of S_BET = 2,150 m² g⁻¹ (SI Appendix, Fig. S28). The total pore volume was determined from the Dubinin–Raduschevich (DR) model over the 0.13 > p/p_o > 0.35 range, obtaining a V_p,DR = 0.8630 cm³ g⁻¹ (SI Appendix, Fig. S29).

Analysis by ¹³C cross-polarization and magic angle spinning (CP/MAS) solid-state NMR suggested a very high-symmetry structure, as indicated by the presence of only three narrow signals at 188.3, 40.4, and 28.2 ppm, which are assigned to the carboxylate, bridgehead, and methylene carbons of the BODCA linkers (SI Appendix, Fig. S24). Whereas the described synthesis protocol was unable to produce large crystals suitable for single-crystal X-ray diffraction, the microcrystalline powder was studied using powder X-ray diffraction (PXRD) crystallography. BODCA-MOF displays a PXRD pattern that exhibits sharp Bragg peaks (SI Appendix, Fig. S25) between 7° and 80° (2-theta, CuKα radiation) evidencing a high degree of crystallinity with a resolution up to 0.80 Å. Indexing of the diffraction pattern via the TREOR algorithm resulted in a cubic crystal system with cell parameter a_TREOR = 12.678(29) Å [figures of merit M(13) = 17, F₁₃ = 11 (0.021722, 59)], a value very close to MOF-5 in its primitive setting (15). Extraction of the observed integrated intensities through the Pawley method using the cell parameter (a′ = 2a_TREOR) and space groups P23 and P1, for a cubic supercell similar to MOF-5 (SI Appendix), allowed the calculation of low-resolution electron density reconstructions. Electron density maps were obtained using the charge-flipping algorithm integrated in the program SUPERFLIP. The reconstructed maps display regions of electron density that resemble the zinc-oxide clusters of MOF-5 (SI Appendix, Fig. S26), suggesting the isoreticular nature of BODCA-MOF (sharing the same topology as MOF-5). Crystal modeling using the supercell parameter in Materials Studio Modeling Suite (Biovia v8.0) allowed the generation of a plausible crystal model (space group Pm-3) for the crystal solution using the Rietveld method in the general structure analysis system (GSAS) software (16). Rietveld refinement of the experimental diffraction pattern using the modeled crystal allowed the solution of the MOF in the Fm-3m space group (to allow for the high degree of positional disorder, see SI Appendix for refinement residuals and details). The refined structure exhibits a considerable amount of positional disorder at the organic BCO moiety, suggesting a high dynamic behavior of the average structure, in agreement with the proposed cubic space group containing an axially substituted rotator undergoing fast rotation. This result is analogous to that observed with plastic crystals formed by globular molecules where an apparent increase in symmetry is observed as a result of whole-body rotation.

Temperature-Dependent Dynamic Mechanisms for Solid-State ¹H NMR Spin-Lattice Relaxation

As in previous studies (7–9), the rotational dynamics of the BCO rotator in the BODCA-MOF lattice were analyzed by temperature-dependent solid-state ¹H NMR spin-lattice relaxation (T₁). The method relies on the fact that nuclear spin relaxation occurs via stimulated transitions arising from the modulation of dipolar magnetic interactions near the Larmor frequency (ω₀ = 2πν₀) of the observed nucleus, which are caused by dynamic processes with correlation times (τ_c) assumed to follow a temperature-dependent Arrhenius behavior with an activation energy E_a and an attempt frequency (or preexponential factor) τ₀⁻¹ (Eq. 1) (17). The relation between the observed macroscopic spin-lattice relaxation T₁⁻¹ and the molecular correlation times τ_c is given by the Kubo–Tomita equation (Eq. 2) (18, 19), which indicates that relaxation becomes more efficient when the condition τ_c⁻¹ = ω₀ is met by the system. The definition of the constant C is given in Eq. 3. It represents the strength of the dipolar interactions involved in the relaxation process, which is a function of the number of nuclei responsible for the relaxation (n) to the total number of nuclei that need to be relaxed (N), where μ₀ is the permeability of free space, γ is the gyromagnetic ratio, ħ is the reduced Plank constant, and r is the internuclei distance.

$${\tau }_{\mathrm{c}}^{\mathrm{-1}}={\tau }_0^{-1}\exp \left({\mathit{E}}_{\mathit{a}}/\text{RT}\right),$$ [1]

$${\text{T}}_1^{-1}=\text{C}\left[{\tau }_{\text{c}}{\left(1+{\omega }_0^2{\tau }_{\text{c}}^2\right)}^{-1}+4{\tau }_{\text{c}}{\left(1+4{\omega }_0^2{\tau }_{\text{c}}^2\right)}^{-1}\right],$$ [2]

$$\text{C}=\left(n/N\right)\left(9/40\right){\left({\mu }_0/4\mathrm{\pi }\right)}^2{\gamma }^4{\hslash }^2/r^6.$$ [3]

In the case of BODCA-MOF, all ¹H atoms are able to contribute to the ¹H T₁ relaxation process. The distance between ¹H atoms in adjacent rotators is, however, relatively large (r ≥ 4 Å) and gives rise to weak dipolar fields (B_nuc = [γhμ₀/(4πr³)] ≤ 0.44 Gauss), such that relaxation should occur primarily by intrarotor interactions (r ≥ 2.2 Å) giving rise to much greater dipolar fields (B_nuc ∼ 2.5 G). Consequently, the two most important intramolecular degrees of freedom are a low-energy conformational twisting process and the rotation of interest about the BCO 1,4-axis (Fig. 4A). As shown in Fig. 2B, the rotational energy profile about the BCO-dicarboxylate linkage is very shallow with activation energies on the order of ∼0.1–0.5 kcal mol⁻¹, such that that rotation can contribute to the nuclear spin relaxation at sufficiently low temperatures, when it slows down into the megahertz regime.

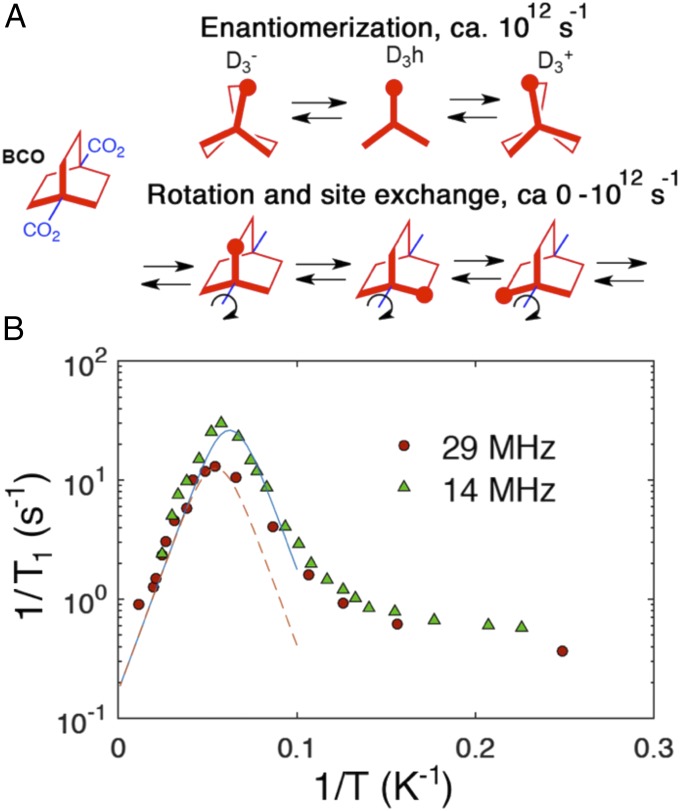
Fig. 4.

(A) Dynamic processes of the 1,4-BCO rotators that may contribute to the spin-lattice relaxation of the ¹H nuclei. Conformational twisting has the characteristics of a normal mode with frequencies that are too high (∼10¹² s⁻¹) to contribute to ¹H spin-lattice relaxation in the megahertz (10⁶–10⁸ s⁻¹) regime. By contrast, inertial rotation and rotation by a site-exchange mechanism has a small barrier and may be slowed down to megahertz regime and constitute an efficient spin-lattice relaxation mechanism. (B) ¹H T₁ relaxation data of the natural abundance BODCA-MOF from T = 2.3–80 K, plotted with a semilog scale for T₁⁻¹ vs. 1/T. The red circles correspond to data collected at a Larmor frequency ν_L= 29.49 MHz and the green triangles correspond to ν_L = 13.87 MHz. The high-temperature data from both high- and low-field experiments can be fit well to the Kubo–Tomita fit (dotted lines), both revealing an activation energy, E_a = 0.185 kcal mol⁻¹, and a preexponential factor, τ₀⁻¹ = 4.7 × 10¹⁰ s⁻¹.

With respect to the conformational twisting mode of the BCO rotator, force-field calculations reported by Dunitz suggested a D_3h transition state that is only ∼0.1 kcal mol⁻¹ higher than two enantiomeric D₃ structures, but likely to have a higher zero-point energy level that explains the mirror-symmetric D_3h structure inferred by single-crystal X-ray diffraction (20). When this was explored with modern computational tools, we found that the detailed results depend on the method, but lead to the same key conclusions within the context of our study. While the MP2/6–31G* method and the B3LYP/6–31G(d) hybrid functional suggest that the D_3h conformation is a minimum with oscillations that explore the twisted D₃+ and D₃− structures (Fig. 4A), the more advanced M062X/6–311+G(d) and ωB97xd/6–311+G(d) hybrid functionals find the D_3h structure to be 0.2–0.35 kcal mol⁻¹ higher than the twisted D₃+ or D₃− enantiomers (SI Appendix, Fig. S40). It should be noted that these small values fall within the limits of current computational methods and should be considered qualitative. Furthermore, they are comparable with the zero-point energy of the corresponding oscillation (0.3 kcal mol⁻¹, or 113 cm⁻¹), suggesting that the enantiomerization process is more a twisting mode than an equilibrium process between two discrete energy minima. With respect to the effect of BODCA MOF dynamics, it should be noted that the magnetic modulation caused by normal-mode frequencies of ∼10¹² s⁻¹ is too far from the Larmor frequency of ¹H NMR in most spectrometers (10⁷–10⁹ s⁻¹), and is not sufficiently temperature dependent, such that this structural twisting cannot contribute to the spin-lattice relaxation. By contrast, rotational motion depends on temperature-dependent, large-amplitude angular displacements about the BCO 1,4-axis expected to occur with a very short correlation time τ_c, which can be slowed down to the regime where the frequency 1/τ_c approaches the Larmor frequency of the ¹H or ²H nuclei.

The solid-state ¹H NMR T₁ measurements were carried out in the range of 2.3–80 K using a homemade cryoprobe with the sample sealed in a capillary tube under ultrahigh-purity helium. Experiments were carried out at spectrometer frequencies of 13.87 and 29.49 MHz. As indicated in Fig. 4B with semilogarithmic plots of the relaxation rate (1/T₁) versus inverse temperature (1/T), there is a well-defined dynamic process with components near the Larmor frequency of ¹H that occurs in the neighborhood of 20 K at both spectrometer fields. There is a small and relatively constant relaxation rate at the lowest temperatures consistent with lattice modes with a very low spectral density in the megahertz regime. As the temperature increases above ∼6 K (1/T = 0.16) the spin-lattice relaxation rate increases, suggesting the activation of dynamic processes that are approaching the spectrometer frequency. A maximum is observed at ∼16.0 K (1/T = 0.0625) when the Larmor frequency is 13.87 MHz (Fig. 4B, green triangles), and another one at 18.2 K (1/T = 0.0549) when the Larmor frequency increases to 29.49 MHz (Fig. 4B, red circles). Increasing the temperature to 80 K in both cases causes a linear decrease in the relaxation rate as the dynamics of the rotor exceed the Larmor frequency. Application of Eq. 2 (16) to the data acquired at 13.87 MHz for T ≥ 16 K reveals an activation energy of 0.185 kcal mol⁻¹. A similar analysis of the data acquired at 29.49 MHz for T ≥ 18.2 K discloses the same activation energy. The preexponential factor required by the two fits is given by the rotational correlation time (τ₀) that would be observed in the absence of a barrier, which corresponds to a frequency factor (or attempt frequency), τ₀⁻¹ = 4.7 × 10¹⁰ s⁻¹. This value is an order of magnitude smaller than the gas-phase inertial rotation estimated from the moment of inertia of the BCO group along its 1,4-axis (21), τ₀⁻¹ = 3.9 × 10¹¹ s⁻¹, or it can be associated with a low-frequency torsional mode (ν_T) of 1.5 cm⁻¹ that is smaller than the value ν_T = 113 cm⁻¹ obtained by density-functional theory calculations with bicyclo[2.2.2]octane dicarboxylate.

Temperature-Dependent Rotational Dynamics and ²H Line-Shape Analysis

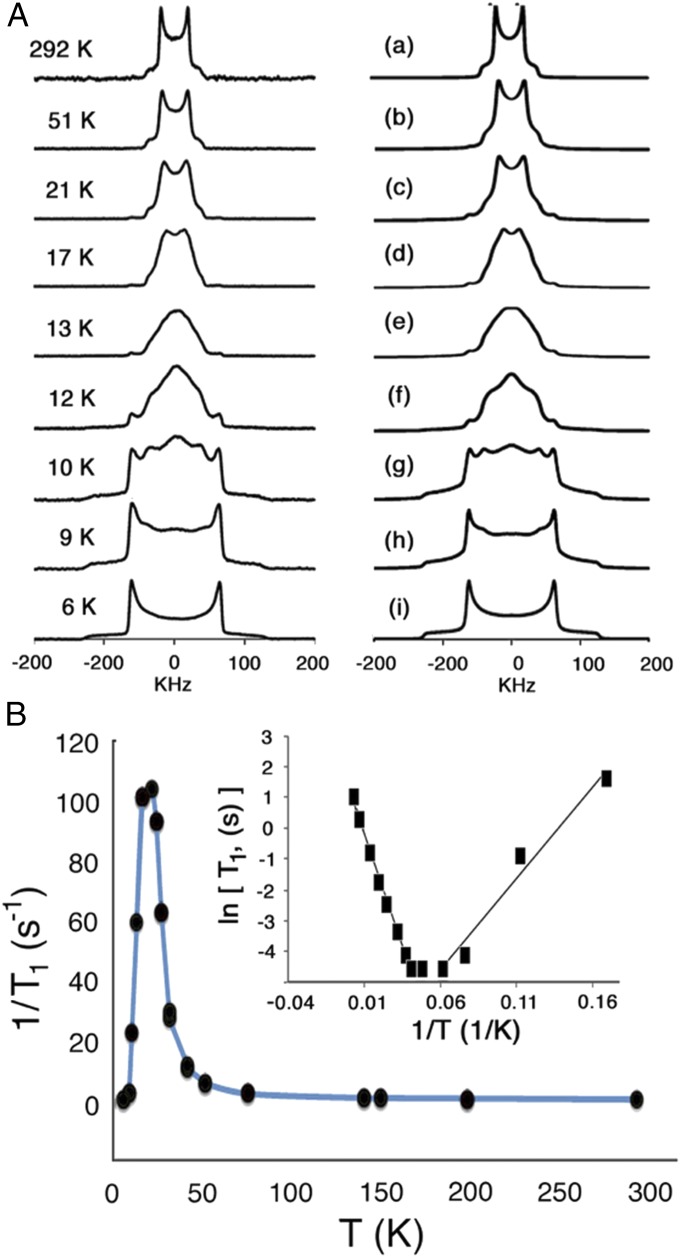
To confirm that the spin-lattice relaxation shown in Fig. 4B occurs primarily by a rotational mechanism, we carried out variable-temperature quadrupolar echo solid-state ²H NMR measurements with deuterium-labeled samples of BODCA-d-MOF in the range of 292 to 6 K (Fig. 5A). The method relies on spectral changes that occur as a result of the dynamic modulation of the quadrupolar interaction between the nuclear spin and the electric field gradient at the nucleus, which depends strongly on the orientation of the C–D bond vector with respect to the direction of the external magnetic field (22–24). Powdered samples with hydrocarbon deuterons that are either static, or undergoing site exchange processes slower than ∼10³ s⁻¹, are characterized by a broad symmetric spectrum known as a Pake pattern that consists of two singularities and two outer shoulders with a separation that depends on the magnitude of the quadrupolar coupling constant (QCC). In the case of BODCA-d, a quadrupolar coupling constant of 168 KHz, consistent with those determined for other rigid saturated hydrocarbons, was determined from the distance between the two peaks (Δν = 3/4 QCC) (25) in the spectrum measured in the lowest-temperature (6 K) spectrum (see below). It is well known that the spectrum of solid samples with groups that experience axial rotation changes as a function of (i) the cone angle formed between the C–D bond vector and the rotational axis, (ii) the number of sites determined by their axial symmetry order, (iii) their corresponding angular displacements, and (iv) their rotational frequencies. In the case of the BCO group, one can observe spectra determined by C–D bonds that explore six- and threefold rotational trajectories with a cone angle of ∼70° determined by an average D_3h symmetry resulting from rapid enantiomerization. Importantly, this method has the potential to distinguish between well-defined discrete jumps among adjacent energy minima in the range of 10⁴ to 10⁸ Hz, and diffusional motion with less-defined angular displacements, which is expected when activation barriers are very low (26).

Fig. 5.

(A) ²H NMR experimental (Left) and simulated spectra (Right) of crystalline BODCA-d-MOF obtained between 292 K and T ≥ 50 K. Spectra can be simulated with a model that considers either threefold or sixfold rotational motion in the fast exchange or diffusional limit. The data recorded between 50 and 21 K can be simulated (A, b and A, c, respectively) by considering motion in the fast exchange in a threefold potential with a Gaussian distribution of jump angles. The same model, but with decreasing exchange frequencies, accounts for data between 17 and 9 K (simulations A, d–A, h). The spectrum obtained at 6 K is characteristic of the slow-exchange regime with rotation lower than ∼10³ s⁻¹ (simulation A, i). (B) Zeeman spin-lattice relaxation for the ²H nuclei in BODCA-d-MOF at 76.78 MHz illustrating a single temperature-dependent dynamic process with an optimal relaxation at 21 K. (Inset) Arrhenius plots of the data in the range of 6 to 100 K indicate activation energies of 0.12 and 0.29 kcal mol⁻¹, respectively, for the low- and high-temperature regions.

To determine and analyze the solid-state ²H NMR spectra, we were guided by the results available from the ¹H T1 data. The corresponding activation parameters (E_a = 0.185 kcal mol⁻¹ and A = 4.7 × 10¹⁰ s⁻¹) indicate a modulation of magnetic interactions that will be sensitive to the ²H NMR line-shape analysis method only within a relatively narrow range of temperatures from ∼6 to 14 K, as the site exchange frequency within that window should vary between ∼1 kHz and 10 MHz. One may predict that spectra will not change too much above this temperature range. This expectation was confirmed with measurements carried out with microcrystalline samples of BODCA-d-MOF sealed under an ultrahigh-purity helium atmosphere in a 5-mm-diameter glass NMR tube. The spectra in Fig. 5A were acquired using a quadrupolar spin-echo pulse sequence at temperatures ranging from 6 to 292 K at 76.78 MHz using a home-built cryogenic 5-mm ²H solid-state NMR probe at Pacific Northwest National Laboratory Environmental Molecular Science’s High Field Magnetic Resonance Facility (further experimental details may be found in SI Appendix). Spectra acquired between 292 and ∼50 K are very narrow and consistent with the averaging expected from unrestricted diffusional motion. As expected from the structural model, the distance between the two central peaks is simulated well by a cone angle of 70° between the C–D bond vector and the BODCA rotational axis. The spectra measured in the range of 50 K > T > 12 K remained very narrow, but lowering the temperatures resulted in the broadening of the two central peaks followed by their coalescence at 13 K. The low-temperature spectra were also characterized by the appearance of a small but growing contribution of a static component, suggesting that the sample is heterogeneous with sites that have slower dynamics. The line-shape changes observed down to 17 K can be simulated with a model that involves motion in the fast exchange regime (>10⁷ s⁻¹) using mean angular displacements of 60° with a Gaussian distribution of ±15°, which are indicative of a smooth transition between diffusional motion and a site exchange process. Simulations of the spectra measured between 13 and 9 K required a reduction of rotational symmetry from sixfold to threefold as the exchange frequency enters the intermediate exchange regime, and with an increasing contribution of the static component. Also in agreement with the ¹H T₁ data, it is not until the temperature reaches 6 K that the spectrum displays the characteristic pattern of the slow exchange regime.

Temperature-Dependent Solid-State ²H NMR Spin-Lattice Relaxation

Finally, to demonstrate that the dynamic behavior of the ²H-labeled sample is essentially identical to that of the natural abundance BODCA-MOF, we carried out a set of solid-state ²H T₁ measurements. Although the rules that govern the spin lattice relaxation of quadrupolar nuclei are slightly different, an optimal relaxation at ∼21 K also indicates a component of the rotational motion that averages the Zeeman interaction at frequency of 2π × 76 MHz. A simple analysis of the high- and low-temperature regions of the Zeeman ²H T₁ data shown in Fig. 5B (Inset) corresponds to activation energies of ∼0.12 and 0.29 kcal mol⁻¹, respectively, which is in good agreement with the value 0.181 derived from the solid-state ¹H T₁ data in Fig. 4B.

Molecular Dynamics Simulations

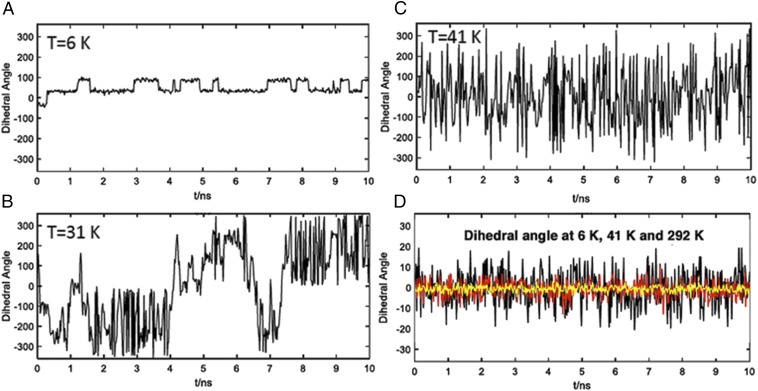
Searching for additional insights into the rotational dynamics of BODCA-MOF, we carried out molecular dynamics (MD) simulations using a model that consists of a BODCA molecule with the terminal carboxyl group fixed. As a starting point, classical MD simulations were carried out at 6, 41, and 292 K with single point charges computed with HF/6–31G(d) theory. All quantum-mechanical (QM) calculations were performed using G09 and the antechamber module in Amber12 to process atomic partial charges from the QM computations. Atomic partial charges were assigned with the RESP model, and the generalized Amber force field was used for further classical MD simulations. The BODCA structures were first optimized in the gas phase, heated to 6, 31, 41, or 292 K, and allowed to equilibrate for 5 ns before the corresponding MD trajectories were generated and collected for 10 ns each. Illustrated in Fig. 6 A–C are the positions of the BODCA rotor defined by the dihedral angle of O–C₁–C₂–C₃ from 360° to −360° as a function of time at 6, 31, and 41 K, respectively. An MD run at 298 K was virtually indistinguishable from the one at 41 K. Fig. 6D shows changes in the enantiomerization angle showing oscillations around the symmetric D_3h structure that take place at all temperatures in the picosecond time scale, although the amplitude of the displacements varies from ∼±5° at 6 K, to ±10° at 40 K, to ±20° at 298 K. One can see in Fig. 6A that discrete Brownian jumps of ±60° occur only at the lowest temperature while inertial or diffusional motion takes place at 31 and 41 K. While discrete jumps are characterized by a distribution of residence times ranging from a few picoseconds to ∼1 ns, diffusional motion in Fig. 6 B and C is characterized by jumps with a wide variation in angular displacement with the rotator spending no time at any given site. It should be noted that the dynamics simulations in Fig. 6 are based on a potential that effectively underestimates the energy barrier, which results in 6-K Brownian jumps with a frequency on the order of 2 ns⁻¹, compared with ∼200 μs⁻¹ that would be consistent with the experimental data. It is clear, however, that while these discrepancies lead to substantial differences at cryogenic temperatures, they are much smaller at 41 K and above. Furthermore, the qualitative consistency among the experimental and computational results helps establish with great confidence that ambient temperature rotation of the BCO group in BODCA MOF occurs in the diffusional regime and constitutes an example where engineered rotational dynamics in the solid state are as fast as they would be in a high-density gas or in a low-density liquid phase.

Fig. 6.

Dynamic simulations for rotation of crystalline BODCA carried out for 10-ns windows at (A) 6 K, (B) 31 K, and (C) 41 K. The amplitudes of the enantiomerization process for runs at 6 K (yellow), 41 K (red), and 292 K (black) are shown in D.

Materials and Methods

Rotator Synthesis.

All of the chemicals and solvents used in this work and their sources and purities are described in detail in SI Appendix. Also included are the full synthetic procedure for the bicyclo[2.2.2]octane dicarboxylic acid in its natural abundance, and deuterated forms as well as their detailed spectroscopic and mass spectrometric characterization are described in detail in SI Appendix.

BODCA-MOF Synthesis and Characterization.

Microcrystalline samples of BODCA-MOF were obtained in DMF at room temperature by mixing solutions of BODCA and zinc acetate dehydrate and letting the mixture stand for 15 h. Crystals were separated by centrifugation and DMF was exchanged by CH₂Cl₂, which was subsequently removed under reduced pressure over night at room temperature followed by heating at 40 °C for 2 h. As described in the text and in detail in SI Appendix, solid samples were characterized by PXRD, solid-state ¹³C CPMAS NMR, thermal analysis, and gas sorption measurements. White microcrystalline powders prepared for ¹H T₁ and ²H spin-echo wide-line solid-state NMR experiments were back-filled with He(g). Detailed procedures are included in SI Appendix.

Solid-State NMR Spectroscopy and Dynamics.

¹H NMR spin-lattice relaxation (T₁) measurements in the solid state were carried out at University of California, Los Angeles at two different ¹H Larmor frequencies of 29.49 and 13.87 MHz and over a wide range of temperatures. Wide-line ¹H spectra from 2.3 to 80 K were measured in a microcrystalline BODCA-MOF sample sealed in a capillary under an ultrahigh-purity helium atmosphere. ²H solid-state NMR wide-line spectra and Zeeman spin-lattice relaxation times were acquired at Pacific Northwest National Laboratory’s (PNNL) Environmental and Molecular Sciences High Field Magnetic Resonance Facility at a Larmor frequency of 76.78 MHz in the temperature range of 6 to 298 K. A detailed description of the experimental parameters and original data are included in SI Appendix.

Also included in SI Appendix are synthesis and spectral characterization of natural abundance and deuterated BODCA ligands; synthesis, diffraction, and adsorption isotherm of BODCA-MOF plus solid-state NMR characterization including ¹³C CP/MAS, variable-temperature ¹H and ²H spin-lattice relaxation, and broad-line ²H NMR spectra, and computational details.