Significance
The recent discovery of nanoscale-confined phonon polaritons in polar dielectric materials has generated vigorous interest because it provides a path to low-loss nanoscale photonics at technologically important mid-IR and terahertz frequencies. In this work, we show that these polar dielectrics can be used to develop a bright and efficient spontaneous emitter of photon pairs. The two-photon emission can completely dominate the total emission for realistic electronic systems, even when competing single-photon emission channels exist. We believe this work acts as a starting point for the development of sources of entangled nano-confined photons at frequency ranges where photon sources are generally considered lacking. Additionally, we believe that these results add a dimension to the great promise of phonon polaritonics.
Keywords: two-photon processes, phonon polaritons, light–matter interactions, Purcell effect, nanophotonics
Abstract
Phonon polaritons are guided hybrid modes of photons and optical phonons that can propagate on the surface of a polar dielectric. In this work, we show that the precise combination of confinement and bandwidth offered by phonon polaritons allows for the ability to create highly efficient sources of polariton pairs in the mid-IR/terahertz frequency ranges. Specifically, these polar dielectrics can cause emitters to preferentially decay by the emission of pairs of phonon polaritons, instead of the previously dominant single-photon emission. We show that such two-photon emission processes can occur on nanosecond time scales and can be nearly 2 orders of magnitude faster than competing single-photon transitions, as opposed to being as much as 8–10 orders of magnitude slower in free space. These results are robust to the choice of polar dielectric, allowing potentially versatile implementation in a host of materials such as hexagonal boron nitride, silicon carbide, and others. Our results suggest a design strategy for quantum light sources in the mid-IR/terahertz: ones that prefer to emit a relatively broad spectrum of photon pairs, potentially allowing for new sources of both single and multiple photons.
Afundamental rule in light–matter interaction is that when an excited electron in an atom has a choice between emitting one photon and emitting two photons simultaneously, it will nearly always decay via the emission of a single photon (1–3). The reason for this is impedance mismatch, or equivalently, the mismatch in size between an emitter and its emitted radiation. Applying this idea to two-photon emission processes, one realizes that two-photon emission suffers much more from impedance mismatch than one-photon emission, leading to its relative suppression.
More quantitatively, the radiation resistance or impedance of a dipole radiator is proportional to , which up to other fundamental constants is proportional to (4). It turns out that the radiation rate of an atomic dipole is precisely proportional to , where is the atomic size, is the wavelength of the emitted light, and is the fine-structure constant. In contrast, the rate of a two-photon process scales as (5–7) and suffers much more than the one-photon process when impedance is mismatched. In atomic systems, , and thus, two-photon emission in atoms is consistently slower than one-photon emission by more than eight orders of magnitude. It is because of this simple scaling argument that two-photon processes are considered insignificant and can thus almost always be ignored for the purposes of analyzing the dynamics of excited emitters. It is also because of this simple scaling argument that, while conventional (one-photon) spontaneous emission engineering is a paradigm in quantum nanophotonics (8–12), similar engineering has not been nearly as actively pursued for two-photon spontaneous emission processes (13–18).
Nevertheless, two-photon spontaneous emission processes have several distinctive features which make them very desirable to access. For example, the photons emitted in such a process are entangled due to energy and angular momentum conservation. For this reason, sources of entangled photons (such as spontaneous parametric down-conversion sources) have become a staple in quantum information protocols. From a more fundamental perspective, the frequency spectrum of two-photon spontaneous emission can be broad, with a spectral width of the order of the transition frequency itself. This is in sharp contrast to one-photon emission, which is spectrally very sharp in the absence of external broadening mechanisms. That implies that if two-photon processes were sufficiently fast, an emitter with discrete energy levels could be a source of light at continuous frequencies, which is in contrast to one of the first things that one learns about quantum mechanics.
In this work, we propose a design strategy for fast production of polariton pairs with quantum efficiencies potentially >90. In other words, we propose a scheme in which an excited emitter prefers to decay via the simultaneous emission of two quanta, despite the possibility of allowed single-photon decay pathways. As a special case, we show how phonon polaritons (PhPs) in boron nitride and silicon carbide (SiC) may allow for the design of a kind of quantum optics source which emits polariton pairs at rates over an order of magnitude faster than any competing one-photon transitions, corresponding to lifetimes approaching 1 ns in atomic-scale two-photon emitters. Our results not only elucidate a technique for efficient sources of potentially entangled polariton pairs but also reveal a class of materials by which to realize extreme regimes of light–matter interactions in which conventionally unobservable high-order emissions become dominant light–matter interactions.
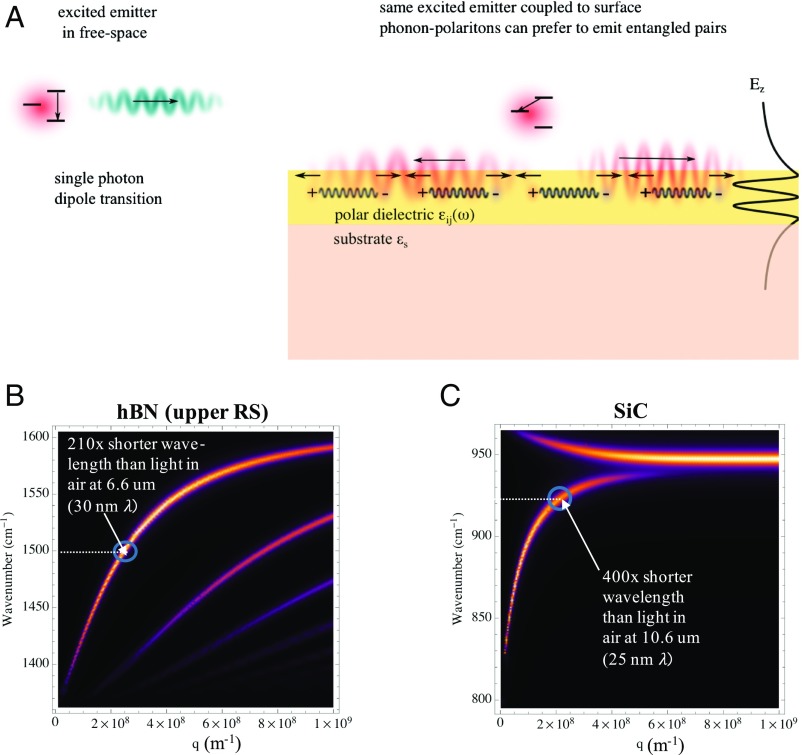
The general scheme for accessing high-efficiency second-order transitions is illustrated in Fig. 1. In free space (and near most nanophotonic structures), an emitter given a choice between different transition pathways will generally take a single-photon dipole (E1) transition over other choices. However, if we have highly confined modes (to impedance match) over a sufficiently narrow frequency band, then we can create a situation in which the single-photon E1 transition is negligibly enhanced, while the two-photon transition is highly enhanced (>10 orders of magnitude relative to the enhancement of the competing E1 transition), so much so that the two-photon transition is strongly preferred. As we will now demonstrate, one of the recent material advances that may admit the construction of such an emitter is the discovery of highly confined PhPs in polar dielectrics.
Fig. 1.
General scheme for accessing two-photon transitions at high efficiency. (A, Left) Typical situation for an emitter: An emitter may have many choices for a transition, but the relatively high-frequency single-photon dipole transition is chosen. (A, Right) When coupling that same excited electron to PhPs in a polar dielectric, the electron can be made to prefer a two-polariton spontaneous emission. (B) Color plot of the imaginary part of the p-polarized reflectivity of 5-nm-thick hBN evaluated at the upper RS band. The center of the sharp peaks signify the dispersion relation. (C) Same for SiC in its sole RS band.
Polar dielectrics like hexagonal boron nitride (hBN) and SiC have been the subject of significant attention over the past few years due to their ability to confine electromagnetic energy in small volumes (length scales <5 nm have been theoretically suggested) (19–32). Moreover, the transversely guided PhPs of these materials have extremely strong spatial confinement only over a narrow spectral band of a few terahertz. Combined with the fact that these PhPs can have substantially lower losses than other surface excitations like plasmons (33) (albeit with lower velocities and similar propagation lengths), they may provide a potentially exciting platform for nanoscale optics in the technologically interesting IR/terahertz regime. Going beyond hBN and SiC, it should also be possible to exploit PhPs at mid-IR/far-IR frequencies in materials like cubic boron nitride (cBN), gallium phosphide, and many others (32). Much effort has been devoted to demonstrating the coupling and propagation of these modes. In this work, we focus on the potential of using the extreme local density of states (LDOS) in the vicinity of polar dielectrics to efficiently access a wide range of light–matter interactions. Before moving on to a quantitative description of the two PhP emission process considered here, we note that throughout the text, we use the terms “two-polariton emission” and “two-photon emission” interchangeably. This is because the PhP modes are described fully in terms of propagating modes of Maxwell’s equations. The primary difference between them and free-space photons is that they are highly confined and cannot escape to spatial infinity in the direction transverse to the polar dielectric slab.
To translate our intuition to a quantitative theory, we develop a formalism to compute the rates of two-photon transitions for emitters placed near films supporting PhP modes(Supporting Information). Our main assumption is that these PhP supporting materials are well-described by a local Lorentz oscillator model (although we allow for the permittivity to be complex and anisotropic). Our permittivity data are taken from ref. 32. Agreement with a local model has been seen in hBN films as thin as 1 nm, although only the long-wavelength part of the dispersion was measured (20). Nevertheless, we will see that the results we arrive at should be achievable for thicknesses between 5 and 10 nm, and for polariton wavelengths of a few tens of nanometers, where a local model should certainly suffice.
Extreme LDOS Near Polar Dielectrics
The main operating principle behind our results is that the LDOS of the electromagnetic field in the vicinity of PhP supporting materials is extremely high. This LDOS can be so high that the emission rate of a dipole within nanometer distances from the surface of the material can be 6 or 7 orders of magnitude faster than in free space (i.e., the Purcell factor can be of order to ). Because the rate of emission of a pair of polaritons depends on two factors of the LDOS, the emission of pairs naively can be maximally enhanced by 12 or 13 orders of magnitude. Our detailed theory of two-photon emission into PhPs corroborates this intuition.
Although Purcell factors for one-photon emission have been predicted in ref. 31 in the context of SiC, and in ref. 9 in the context of hBN, we clarify the basic physics of why the LDOS is so high in the first place with transparent physical formulae, and show that Purcell factors > are to be expected. As is well known, the spontaneous emission rate of an emitter in free space at frequency (wavelength ) goes like:
| [1] |
where is the fine-structure constant, , and is the emitter size. The dimensionless factor is of order for typical atoms and molecules and is indicative of the weak coupling between light and matter in free space. On the other hand, when the emitter is placed at a distance from a polar dielectric supporting PhP modes with polariton wavelength and group velocity , the emission rate will scale like
| [2] |
where , , and we have omitted dimensionless factors that are .* The exponential arises from the evanescent tails of these PhP modes, and the sharpness of those tails requires the emitter to be within 10 nm from the surface of the polar dielectric. Assuming that indeed the emitter is in close enough proximity, the Purcell enhancement is governed by the factor , which is an impedance matching factor, and the factor which is a “slow-light” or density-of-states-enhancement factor. Since both of these properties can be easily gleaned from the dispersion relation of the PhPs, we now estimate the possible LDOS enhancements using the dispersion relations of SiC and hBN plotted in Fig. 1 B and C. As can be seen from the dispersion relations, the wavelength of the polariton can be >100 times shorter than the wavelength of light in free space. When the confinement factor is 100, the group velocity is well over 100 times slower than the velocity of light (due to the highly dispersive nature of these materials), and the corresponding Purcell factors for a sufficiently close emitter tend toward . We emphasize that, although our result in Eq. 2 is just an estimate, we have calculated the Purcell factors using three approaches: a mode quantization approach assuming lossless polar dielectrics; a macroscopic quantum electrodynamics approach using dyadic Green’s functions, taking into account medium losses; and numerically in a finite-difference frequency-domain approach by placing a dipole emitter near polar dielectric surfaces. All three approaches are in agreement and corroborate the estimates provided here, lending support to all of the subsequent results.
To conclude this section, we briefly comment on the experimental state of the art. For substantially thicker films (of order 100-nm thickness), confinement factors >80 have already been observed in hBN associated with third-order modes, corresponding to polariton wavelengths of 80 nm (34). Even larger wavelength confinements (up to 200) have been claimed in nanometric-scale SiC nanoresonators (31). In these SiC nanoresonators, the authors predicted on the basis of the measured quality factor and simulated mode volume a Purcell enhancement of about . The theory we provide here is fully consistent with these findings and predicts a potentially even greater degree of confinement for thinner slabs. That this effect is more visible for thinner films of polar dielectrics is because making the slab thinner pushes the dispersion toward higher wavevectors. A semiinfinite slab of such materials would have very weak confinement, as pointed out, for example, in ref. 25. All this said, an impediment toward experimentally observing even higher confinements comes from the limited resolution of scattering-scanning near-field optical microscopy techniques. Perhaps complementary approaches can make these extremely confined modes more visible.
Two-Photon Emission Enhancement Theory
Moving to two-photon emission, while there is no closed-form expression for the two-photon emission rate of a general emitter (because it depends on the detailed level diagram of the emitter), the emission rate in the absence of radiative cascades will generically scale as:
| [3] |
where is the bandwidth of the two-photon emission spectrum. Note that in free space, it is generally of the order of half the transition frequency, but in the situations we consider, it is typically much less, leading to some suppression relative to what one might expect. The emission is into a continuum of frequency pairs satisfying energy conservation. Such a result is corroborated by more detailed second-order perturbation theory calculations.
In the presence of a surface supporting PhPs, the rate of two-photon/two-polariton emission per unit frequency goes as (ignoring for now evanescent tails):
| [4] |
which, according to the estimates from the previous section would lead to enhancement of the emission spectrum of ∼1012 for an emitter sufficiently close to the surface. By virtue of Eq. 4, it follows that for PhPs with a bandwidth of ∼1/10 of the transition frequency, the total rate enhancement is ∼1011. Going into a more rigorous level of detail, we show in Supporting Information that for an s s transition, the spectral enhancement factor, defined as the ratio of the PhP emission spectrum, , to the free-space emission spectrum is given by:
| [5] |
where is the Purcell factor for a dipole perpendicular to the surface. As is well known, the expression for the Purcell factor for a z-polarized dipole in the geometry of Fig. 1A is simply:
| [6] |
is the -polarized reflectivity of the air-slab-substrate system (plotted in Fig. 1 B and C), and is the free-space photon wavevector (9, 35). We note that the two-photon spectrum is always symmetric with respect to reflection about half of the transition energy. This is because emission at is indistinguishable from emission at .Before turning to a discussion of our results, we discuss the validity of perturbation theory, which we use to arrive at the results above. The main result of this work is that two-phonon-polariton emission beats one-photon emission. Were it also the case that third- and higher-order emission processes were more important than second-order processes, it would be the case that our calculations based on second-order perturbation theory would not be representative of the full dynamics of the electron. We claim that this is not the case in our work and that two-photon emission dominates the perturbation series. An explicit estimate is provided in the final section of Supporting Information. To summarize those estimates, the only reason that two-polariton emission is important is that first-order emission is only negligibly enhanced by polaritons for the transitions we consider. If first-order emission were enhanced, we would find that it would completely dominate two-polariton emission by >3 orders of magnitude. Following this logic, even if third-order emission is enhanced by polaritons, it will be much weaker than second-order emission (by 3 orders of magnitude) since the second-order process is already greatly enhanced by polaritons. That said, it would be very interesting to use the idea proposed in this work to make three- or higher-order emission dominant.
Extreme Enhancement of Polariton-Pair Emission Rates
Having provided the general theory of two-photon emission enhancements and estimates for the degree of the enhancements, we now show by direct calculation that not only is the enhancement of two-photon emission very high, but it can be made higher than the rate of competing one-photon processes as a result of the narrow spectral window in which the LDOS of the material is so high.
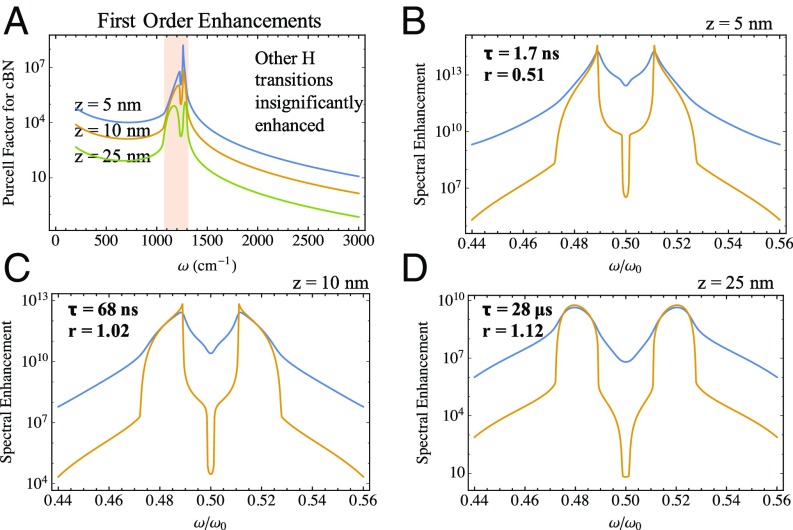
Fig. 2 presents a system where the two-photon emission is made dominant over all other emission pathways. We consider (for concreteness) the example of a hydrogen atom above a cBN slab and present the two-photon spectral enhancement. We choose cBN, a material different from the ones discussed thus far, because in cBN, the Reststrahlen (RS) band coincides with a potential two-photon process in the hydrogen atom. Nevertheless, the basic physical arguments presented in the previous section still apply—just at a different frequency range. cBN, in contrast to hBN, is not hyperbolic, and thus its dispersion is more similar to that of SiC. The hydrogen transition we consider is the 5s to 4s two-photon transition at a transition energy of 2,468 cm−1 (4.05 μm), so that the energies of the emitted polaritons (∼8 μm) fit in the RS band where the Purcell factor is very high (Fig. 2A). In Fig. 2A, we compute the -polarized Purcell spectrum for a first-order dipole transition for atom-surface separations of 5, 10, and 25 nm to get an order of magnitude estimate for the rates of these competing dipole transitions. At 5 nm, the fastest competing transition occurs with a lifetime of order 100 ns. At 10 and 25 nm, the order of magnitude rates of the competing E1 transitions are 1 per s. Interestingly, one also sees that just outside the RS band, there can be strong off-resonant enhancement due to the tail of the resonance lineshape of the Purcell spectrum. Although we do not make use of this fact in the paper, one may also consider using these high Purcell factors to realize the results of this work.
Fig. 2.
Making two-photon emission dominant. (A) Purcell spectra for a z-polarized dipole above 10-nm-thick cBN at atom-surface separations of 5, 10, and 25 nm. (B–D) Two-photon Purcell spectra for an s s transition as a function of photon frequency for the same set of atom-surface separations. Blue denotes the Purcell spectra with losses accounted for, and orange denotes the Purcell spectra for cBN with 100× weaker losses. In B–D, we note both the overall two-photon transition rate between the 5s and 4s states of hydrogen and the corresponding radiative ratio (). The permittivity of the substrate is taken to be 2, and the damping constant for cBN is taken to be 5 cm−1 (∼1012 s−1).
In Fig. 2 B–D, we compute the enhancement of the spectrum of two-photon emission (relative to free-space) from 5s to 4s (due to cBN PhPs), the lifetime of the two-photon transition, and the -values, the last of which we define as the ratio of the decay rate computed assuming no losses () to the decay rate computed with losses taken into account (). The lossless decay rates are computed in Supporting Information based on a mode expansion formalism and are fully consistent with our calculation taking losses into account in the limit of vanishing losses. The -value introduced here is a measure of the extent to which quenching dominates the decay dynamics insofar as a low r value suggests loss-dominated decay. An value of nearly 1 suggests that losses have little impact on the decay rate. (That said, the -value can be >1 because losses can affect the density of states of polariton modes, as is known from the Purcell effect in resonant cavities.) In Fig. 2 B–D, we see that the lifetimes of two-photon spontaneous emission for an emitter 5, 10, and 25 nm away from the surface of 10 nm thick cBN are 1.7 ns, 68 ns, and 28 s, respectively. Their -values are 0.51, 1.02, and 1.12, respectively. Thus, two-photon spontaneous emission into PhPs can be over an order of magnitude faster than single-photon dipole transitions, computed by taking the one-photon free space rates and applying the one-photon Purcell factor. In a system where there is only one competing dipole transition (at a rate of 1 per s), the branching ratio/probability of second-order decay at 10 nm would be . This is in sharp contrast to the situation in free space, where two-photon spontaneous emission is 8–10 orders of magnitude slower. We thus conclude that, by using PhPs, it is possible to create a source of a pair of polaritons pairs with very high efficiency. We now move on to describing the spectral properties of this quantum light source, both in frequency and angle.
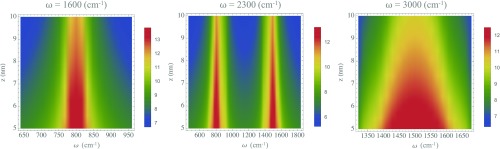
In Fig. 3, we consider the second-order spectral enhancement of Eq. 5 (plotted on log10 scale) for an emitter now near hBN as a function of the transition frequency of the emitter ( cm−1), the emission frequencies (ω), and the emitter-surface separation ( nm). We chose a different material than that of Fig. 2 to show explicitly that two-photon spectral enhancements similar to those in thin cBN are achievable in other materials (the spectral enhancement is of the same order of magnitude as that in cBN (∼1012) and also to show a large number of frequency bands where a two-photon emitter can be designed. What we found is that hBN offers very high spectral enhancement in three different frequency bands, as opposed to one in isotropic polar dielectrics, allowing for compatibility with many more atomic, molecular, or quantum well systems. The reason for this is intercombination: A two-photon emission through near-field polaritons can occur via two photons in the lower RS band, two photons in the upper RS band, or one in the upper RS band and one in the lower RS band. A hypothetical material having three separate RS bands would offer six frequency ranges for two-photon emission enhancement. We also found that increasing the emitter separation causes the emission spectrum not only to be weaker, but also narrower. This allows one to tune not only the emission rate, but also the emission spectrum with atom-surface separation for emitters whose location can potentially be precisely controlled. Before moving on to a discussion of the angular properties of the emitted PhP pairs, we quickly comment on the fact that hyperbolic hBN and its nonhyperbolic relative cBN give similar degrees of enhancement. This is interesting because the character of PhP modes in hBN is very different from in cBN: In hBN, optical rays can propagate in the slab, giving a mode that looks like a slab-waveguide mode in a dielectric waveguide. Meanwhile, in cBN, the mode is more like a plasmonic mode in shape. Nevertheless, they both give similar amounts of emission enhancement because, at the end of the day, the degree of enhancement depends on the modal volume of the PhPs, whose order of magnitude is set by the polariton in-plane wavelength.
Fig. 3.
Hyperbolicity and two photon emitters in multiple bands. Two-polariton spectral enhancement defined as in Eq. 6 for a spherical emitter as a function of transition frequency [1,600 (Left), 2,300 (Center), and 3,000 (Right) cm−1], plotted on log10 scale. The spectral enhancement is plotted with respect to emission frequency and atom-surface separation between 5 and 10 nm. Hyperbolicity allows for enhancement over a large range of frequencies compared with isotropic systems. Moreover, distance can be used to tune the width of the spectrum.
Finally, we consider the angular spectrum of emitted photons. In Supporting Information, we derive the general result that the angle and frequency spectrum of two-photon emission, , is proportional to:
| [7] |
where
| [8] |
in which denotes a dipole matrix element between states and , denotes an intermediate atomic state, denotes the ground state, denotes the excited state, and is the energy of the th state. The are the PhP polarizations in the vicinity of the emitter, given by in the high-confinement limit.
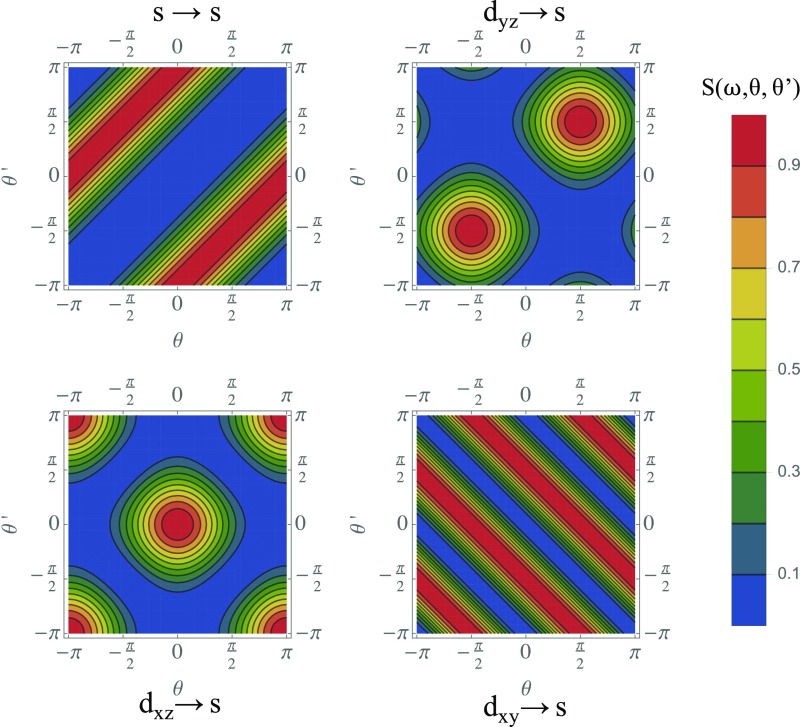
The angular dependence of the spectrum in Eq. 2 will lead to very different angular spectra for different transitions. In Table 1, we show the angular spectrum as a function of different transitions (at ). Strictly speaking, the angular spectrum is frequency-dependent. However, due to the narrowness of the RS band(s), this can be neglected, and thus we only consider the spectrum at half the transition frequency. Remarkably, just by changing the initial state of the system, one can change whether the polariton pairs are preferentially emitted in the same direction (as in Fig. 4, Upper Right and Lower Left) or in opposite directions (as in Fig. 4, Upper Left). There are a number of ways to preferentially populate a particular initial state. One is by exciting the atoms with light of a fixed polarization. Another, appropriate in systems with less extreme degeneracy than hydrogen, is to simply excite the atoms with the appropriate frequency.
Table 1.
A summary of the dependence of the angular spectrum of two-photon radiation as a function of initial and final electronic states for a few selected initial electronic states
| Transition | Angular spectrum |
Fig. 4.
Using the shape of the wavefunction to control the angle spectrum of emitted polariton pairs. Plots of the angular spectrum of two-photon emission as a function of the initial state of the electron for initial states .
Discussion
Although we have considered the hydrogen atom in our calculations, this was just for concreteness, and the physical mechanism for efficient two-photon emitters can readily be extended to many atomic and molecular systems. Here, we propose some emitter platforms for testing the predictions of our theory. For atoms, there are many which have a level structure conducive to the situation described throughout this paper. For example, in the lithium atom there is a transition at 1,611 cm−1, which can potentially occur via emission of a pair of PhPs. All other competing transitions fall well outside of the RS bands of hBN, just as in the example we discussed in Fig. 2. More generally, as all atoms have electronic transitions in the mid-IR, our results should apply to a large portion of the periodic table. It may also be possible that vibrational transitions may be used to observe these effects, although one obstacle toward realizing these effects with molecular vibrations is the generally low multipole moments associated with vibrational transitions. Another exciting possibility is using emitters whose level structure is designable, such as quantum dots or wells. There, one can envision designing a two-photon transition to fall in the RS bands while designing all other one-photon transitions to fall out of the band. Yet another advantage of these artificial atomic systems is their relatively large sizes, allowing for impedance matching to be realized which much less requisite polariton confinement.
In this work, we focused our attention on quantum optics at mid-IR/terahertz frequencies, a relatively undeveloped field, but nonetheless one which would be rather exciting to develop. Moving beyond the mid-IR to the near-IR and eventually visible, it may be possible to realize the effects we describe here using “shaped polaritonic media” (such as nanoresonators of graphene or plasmonic crystals of graphene and other 2D plasmonic materials) supporting (respectively) narrow spectral response or photonic bandgaps. We note that in all of these examples, the emitted quanta are confined modes and do not escape into the far-field unless outcoupled. Outcoupling efficiencies of a few percent were demonstrated in highly confined graphene plasmons, and even higher efficiencies should be demonstrable through optimization. We believe that the results presented in this work may have direct implications for spectroscopy (to infer electronic transitions which cannot be determined with conventional photons), sensors based on forbidden transitions, quantum radiation sources (on-demand generation of single photons and potentially entangled pairs of photons), new platforms for quantum nonlinear optics, the possibility of realizing nonlinearities at the single-photon level, the ability to turn narrow-band emitters into broadband emitters, the ability to turn narrow-band absorbers into broadband absorbers, and, most generally, the ability to completely reshape the ostensibly fixed optical properties of materials.
Supplementary Material
Acknowledgments
The authors thank Prof. E. Ippen, J. J. Lopez, and Prof. B. Zhen for fruitful discussions. Research was supported as part of the Army Research Office through the Institute for Soldier Nanotechnologies under Contract W911NF-13-D-0001 [photon management for developing nuclear-TPV (thermophotovoltaics) and fuel-TPV mm-scale systems]. Research was also supported as part of the S3TEC, an Energy Frontier Research Center funded by the US Department of Energy under Grant DE-SC0001299 [for fundamental photon transport related to solar TPVs and solar TEs (thermoelectrics)]. I.K. was supported in part by Marie Curie Grant 328853-MC-BSiCS. N.R. was supported by Department of Energy Fellowship DE-FG02-97ER25308. G.R. was supported by a fellowship of The Belgian American Educational Foundation and Wallonie-Bruxelles International.
Footnotes
The authors declare no conflict of interest.
*In ref. 33, it was suggested that perhaps the dimensionless factor could be much less than 1 as a result of the strong phononic character of the excitations, thus limiting the degree of enhancement. Being quantitative, one finds that this is not the case. Although most of the electromagnetic energy (incorporating the mechanical energy of vibrations) resides in the polariton sustaining slab, it is not much different from what happens in plasmonics, where most of the energy is inside the metal. Additionally, because of the dispersiveness of the polar dielectric, the group velocity becomes much less than the phase velocity, leading to a larger density of states enhancement than one would get in a comparable plasmonic system. This compensates for the strong phononic component of the excitations.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1713538114/-/DCSupplemental.
References
- 1.Craig DP, Thirunamachandran T. Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions. Academic; London: 1984. [Google Scholar]
- 2.Berestetskii VB, Lifshitz EM, Pitaevskii LP. Quantum Electrodynamics. Vol 4 Butterworth-Heinemann; Oxford: 1982. [Google Scholar]
- 3.Cohen-Tannoudji C, Dupont-Roc J, Grynberg G, Thickstun P. Atom-Photon Interactions: Basic Processes and Applications. Wiley Online Library; New York: 1992. [Google Scholar]
- 4.Eggleston MS, Messer K, Zhang L, Yablonovitch E, Wu MC. Optical antenna enhanced spontaneous emission. Proc Natl Acad Sci USA. 2015;112:1704–1709. doi: 10.1073/pnas.1423294112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Breit G, Teller E. Metastability of hydrogen and helium levels. Astrophys J. 1940;91:215–238. [Google Scholar]
- 6.Shapiro J, Breit G. Metastability of 2 s states of hydrogenic atoms. Phys Rev. 1959;113:179–181. [Google Scholar]
- 7.Göppert M. Über die wahrscheinlichkeit des zusammenwirkens zweier lichtquanten in einem elementarakt. Naturwissenschaften. 1929;17:932–932. [Google Scholar]
- 8.Tame M, et al. Quantum plasmonics. Nat Phys. 2013;9:329–340. [Google Scholar]
- 9.Kumar A, Low T, Fung KH, Avouris P, Fang NX. Tunable light–matter interaction and the role of hyperbolicity in graphene–hBN system. Nano Lett. 2015;15:3172–3180. doi: 10.1021/acs.nanolett.5b01191. [DOI] [PubMed] [Google Scholar]
- 10.Hoang TB, et al. Ultrafast spontaneous emission source using plasmonic nanoantennas. Nat Commun. 2015;6:7788. doi: 10.1038/ncomms8788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Andersen ML, Stobbe S, Sørensen AS, Lodahl P. Strongly modified plasmon-matter interaction with mesoscopic quantum emitters. Nat Phys. 2011;7:215–218. [Google Scholar]
- 12.Tielrooij K, et al. Electrical control of optical emitter relaxation pathways enabled by graphene. Nat Phys. 2015;11:281–287. [Google Scholar]
- 13.Hayat A, Ginzburg P, Orenstein M. Observation of two-photon emission from semiconductors. Nat Photon. 2008;2:238–241. [Google Scholar]
- 14.Nevet A, et al. Plasmonic nanoantennas for broad-band enhancement of two-photon emission from semiconductors. Nano Lett. 2010;10:1848–1852. doi: 10.1021/nl1005806. [DOI] [PubMed] [Google Scholar]
- 15.Hayat A, Nevet A, Ginzburg P, Orenstein M. Applications of two-photon processes in semiconductor photonic devices: Invited review. Semicond Sci Technol. 2011;26:083001. [Google Scholar]
- 16.Ota Y, Iwamoto S, Kumagai N, Arakawa Y. Spontaneous two-photon emission from a single quantum dot. Phys Rev Lett. 2011;107:233602. doi: 10.1103/PhysRevLett.107.233602. [DOI] [PubMed] [Google Scholar]
- 17.Muñoz CS, et al. Emitters of n-photon bundles. Nat Photon. 2014;8:550–555. doi: 10.1038/nphoton.2014.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rivera N, Kaminer I, Zhen B, Joannopoulos JD, Soljačić M. Shrinking light to allow forbidden transitions on the atomic scale. Science. 2016;353:263–269. doi: 10.1126/science.aaf6308. [DOI] [PubMed] [Google Scholar]
- 19.Hillenbrand R, Taubner T, Keilmann F. Phonon-enhanced light–matter interaction at the nanometre scale. Nature. 2002;418:159–162. doi: 10.1038/nature00899. [DOI] [PubMed] [Google Scholar]
- 20.Dai S, et al. Tunable phonon polaritons in atomically thin van der Waals crystals of boron nitride. Science. 2014;343:1125–1129. doi: 10.1126/science.1246833. [DOI] [PubMed] [Google Scholar]
- 21.Xu XG, et al. Mid-infrared polaritonic coupling between boron nitride nanotubes and graphene. ACS Nano. 2014;8:11305–11312. doi: 10.1021/nn504093g. [DOI] [PubMed] [Google Scholar]
- 22.Dai S, et al. Graphene on hexagonal boron nitride as a tunable hyperbolic metamaterial. Nat Nanotechnol. 2015;10:682–686. doi: 10.1038/nnano.2015.131. [DOI] [PubMed] [Google Scholar]
- 23.Dai S, et al. Subdiffractional focusing and guiding of polaritonic rays in a natural hyperbolic material. Nat Commun. 2015;6:6963. doi: 10.1038/ncomms7963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li P, et al. Hyperbolic phonon-polaritons in boron nitride for near-field optical imaging and focusing. Nat Commun. 2015;6:7507. doi: 10.1038/ncomms8507. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Li P, et al. Reversible optical switching of highly confined phonon-polaritons with an ultrathin phase-change material. Nat Mater. 2016;15:870–875. doi: 10.1038/nmat4649. [DOI] [PubMed] [Google Scholar]
- 26.Feng K, et al. Localized surface phonon polariton resonances in polar gallium nitride. Appl Phys Lett. 2015;107:081108. [Google Scholar]
- 27.Tomadin A, Principi A, Song JC, Levitov LS, Polini M. Accessing phonon polaritons in hyperbolic crystals by angle-resolved photoemission spectroscopy. Phys Rev Lett. 2015;115:087401. doi: 10.1103/PhysRevLett.115.087401. [DOI] [PubMed] [Google Scholar]
- 28.Yoxall E, et al. Direct observation of ultraslow hyperbolic polariton propagation with negative phase velocity. Nat Photonics. 2015;9:674–678. [Google Scholar]
- 29.Caldwell JD, Novoselov KS. Van der Waals heterostructures: Mid-infrared nanophotonics. Nat Mater. 2015;14:364–366. doi: 10.1038/nmat4252. [DOI] [PubMed] [Google Scholar]
- 30.Caldwell JD, et al. Sub-diffractional volume-confined polaritons in the natural hyperbolic material hexagonal boron nitride. Nat Commun. 2014;5:5221. doi: 10.1038/ncomms6221. [DOI] [PubMed] [Google Scholar]
- 31.Caldwell JD, et al. Low-loss, extreme subdiffraction photon confinement via silicon carbide localized surface phonon polariton resonators. Nano Lett. 2013;13:3690–3697. doi: 10.1021/nl401590g. [DOI] [PubMed] [Google Scholar]
- 32.Caldwell JD, et al. 2015 Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons. Nanophotonics, https://doi.org/10.1515/nanoph-2014-0003.
- 33.Khurgin JB. How to deal with the loss in plasmonics and metamaterials. Nat Nanotechnol. 2015;10:2–6. doi: 10.1038/nnano.2014.310. [DOI] [PubMed] [Google Scholar]
- 34.Giles AJ, et al. 2017. Ultra-low-loss polaritons in isotopically pure materials: A new approach. arXiv:1705.05971.
- 35.Koppens FH, Chang DE, Garcia de Abajo FJ. Graphene plasmonics: A platform for strong light–matter interactions. Nano Lett. 2011;11:3370–3377. doi: 10.1021/nl201771h. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.