Significance
The discovery of MXenes opens an opportunity on flexible energy storage. We explored systematically several factors including metal species, layer thicknesses, functional group, strain, and Li concentration on the mechanical and electrochemical properties of 2D transition metal carbides (TMCs). Taking the electrode polarization into account, we found several critical factors that govern the ionic mobility on the surface of 2D TMCs. Under multiaxial loadings, the electrical conductivity, high ionic mobility, low equilibrium voltage with good stability, excellent flexibility, and high theoretical capacity offered bare 2D TMCs the potential to be ideal flexible anode materials, whereas the surface functionalization degraded the transport mobility and increased the equilibrium voltage. General rules are proposed to identify the optimal candidate based on a combined analysis of these critical parameters.
Keywords: MXene, 2D material, strain modification, lithium storage, DFT
Abstract
Efficient flexible energy storage systems have received tremendous attention due to their enormous potential applications in self-powering portable electronic devices, including roll-up displays, electronic paper, and “smart” garments outfitted with piezoelectric patches to harvest energy from body movement. Unfortunately, the further development of these technologies faces great challenges due to a lack of ideal electrode materials with the right electrochemical behavior and mechanical properties. MXenes, which exhibit outstanding mechanical properties, hydrophilic surfaces, and high conductivities, have been identified as promising electrode material candidates. In this work, taking 2D transition metal carbides (TMCs) as representatives, we systematically explored several influencing factors, including transition metal species, layer thickness, functional group, and strain on their mechanical properties (e.g., stiffness, flexibility, and strength) and their electrochemical properties (e.g., ionic mobility, equilibrium voltage, and theoretical capacity). Considering potential charge-transfer polarization, we employed a charged electrode model to simulate ionic mobility and found that ionic mobility has a unique dependence on the surface atomic configuration influenced by bond length, valence electron number, functional groups, and strain. Under multiaxial loadings, electrical conductivity, high ionic mobility, low equilibrium voltage with good stability, excellent flexibility, and high theoretical capacity indicate that the bare 2D TMCs have potential to be ideal flexible anode materials, whereas the surface functionalization degrades the transport mobility and increases the equilibrium voltage due to bonding between the nonmetals and Li. These results provide valuable insights for experimental explorations of flexible anode candidates based on 2D TMCs.
Novel electrode materials that provide high-performance energy storage coupled with fabrication flexibility provide access to a wide range of technological applications (1). With the rapid development of flexible devices, flexible energy storage and conversion systems, including lithium-ion batteries (LIBs), have deserved many promising applications (2–4). However, selecting desirable electrode materials with excellent electrochemical properties (e.g., ionic mobility, open-circuit voltage, volumetric capacitance, and cycling performance) and superior mechanical properties, such as elastic stiffness, flexibility, and strength, faces great challenges (5, 6). For LIBs, graphite is the most widely used commercial anode material due to its high columbic efficiency, sufficiently good cycle performance, and low cost. Unfortunately, graphite anodes possess a low power density and moderate theoretical Li capacity (372 mAh⋅g−1) (7). Transition metal oxides (8), such as Si, Sn, and Ge compounds (9–11), also suffer from some critical issues, such as drastic volume changes, large irreversible capacities, high working potentials, poor electrical conductivities, and low power densities, which curtail their extensive applications in LIBs (12). The power capabilities of LIBs critically rely on the rate of Li+ and electron migration through the electrolyte and electrode, and therefore a promising strategy to create high-power LIBs is to develop a new electrode material with high electrical conductivity, large surface area, and excellent ionic diffusion ability (13). However, most electrode materials that can provide intercalation or surface redox capacitances are poor electronic conductors [e.g., graphene oxide or TiO2 (14)] or are hydrophobic [e.g., graphene (15)].
Recently, 2D transition metal carbides (TMCs), carbonitrides, and/or nitrides (MXenes) have been considered as flexible electrode materials for high-performance LIBs due to their high energy densities, high ionic mobilities, excellent mechanical flexibilities, superior strengths, and hydrophilic surfaces. In terms of their electrochemical properties, Barsoum and coworkers (16) reported that MXenes have large and stable volumetric capacitances (>900 F⋅cm−3 in H2SO4 over 10,000 cycles). Upon Li-ion intercalation into Ti3C2Tx, a steady-state capacity of ∼410 mAh⋅g−1 at 1 C is obtained for an additive-free flexible electrode (17). Theoretical calculations further demonstrated that both O-terminated and bare MXenes could be promising anode materials with high capacities, low anode voltages, and good rate capabilities (18–20). Considering mechanical properties, Kurtoglu et al. found that the out-of-plane Young’s modulus of a Ti3C2 monolayer exceeded that of graphene, and its in-plane elasticity have been predicted to approach as high as 0.5 TPa (21, 22). More recently, Guo et al. (23) indicated that the surface-functionalized MXenes may possess excellent mechanical flexibilities with enhanced strengths, which stimulates further interest to determine whether the strain can modify the electrochemical properties of MXenes.
Regarding the ability of strain to tune the electrochemical and other functional properties, progress has recently been achieved and attracted much attention. Wang et al. (24) reported a method to modify the catalytic activity by directly and continuously controlling the lattice strain of a platinum catalyst. Furthermore, a profound effect of strain on the functional properties, such as electronic structure, electronic conductivity, and magnetism, of MXenes has also been demonstrated by several research efforts (25–27). Unfortunately, a theoretical investigation on the strain modification of electrochemical properties is still lacking. MXenes play multiple roles in LIBs: acting as a matrix to provide ion-exchange sites, a buffer layer to effectively accommodate volume expansion/shrinkage during the electrochemical reactions, and a highly conductive matrix to endow LIBs with excellent rate performances (28). Moreover, the lattice confinement and mismatch may provide additional strain on MXenes, particularly in MXene composites with other materials. Although an external load is generally believed to be critical for the service safety of flexible device electrodes, the ability for certain strain conditions to affect the performances of MXenes as anode materials is uncertain. Therefore, exploring the responses of the electrochemical performances of MXenes to applied strains and the fundamental mechanisms behind these responses is critical.
In general, the stability, ionic mobility, voltage, and theoretical capacity are four key parameters that quantify the properties of LIBs (29, 30). Nevertheless, several critical issues related to the stabilities and electrochemical properties of MXenes are still unsolved; solving these issues is important for the realization of future flexible device. (i) The effects of multiaxial loadings (biaxial/uniaxial, tension/compression) on the ionic mobility and equilibrium voltage are unclear. (ii) A charge-transfer polarization might exist during the charging and discharging processes upon passing the electrical current through an electrolytic cell (31), which will generally be accompanied by an external charge (32), electric field (33), vacancies (34), and impurities (35), thus disturbing the charge distribution on the anode surface. In such a case, an investigation of the diffusion processes on the surfaces of charged MXenes has not occurred. (iii) Although the calculated average voltage may correlate to the average effect of the charge/discharge processes, a desirable voltage profile that demonstrates high stability has been nearly unexplored thus far. (iv) The development of general guidelines based on a combined analysis of critical parameters, including stability, ionic mobility, equilibrium voltage, and theoretical capacity, is still necessary to identify an optimal anode candidate.
In this paper, taking 2D TMCs as representative MXenes, we first explored the energetic stabilities, mechanical flexibilities, and strengths of various 2D TMCs. Second, we performed a systematic investigation on the ionic mobilities on the surfaces of 2D TMCs based on the charged model systems and evaluated several critical influence factors, including the transition metal species, layer thickness, functional groups, strain, and Li concentration. Third, a comprehensive analysis of the bonding topology and electronic structure are further performed to underline the origins of changes in the energy barriers of Li+ transport. We showed that the electron capture is one of the most important mechanisms to hinder Li+ transport. Afterward, the voltage profiles are explored by gradually introducing Li on the surfaces of 2D TMCs to simulate the Li+ intercalation/deintercalation processes, and, accordingly, the voltage stabilities of the 2D TMCs are determined. Finally, the guidelines to design promising 2D TMCs with improved electrochemical and mechanical properties are suggested.
Results and Discussion
Models and Regulations of MXenes.
MXenes are prepared by selectively etching the layers of “A” element atoms from their layered MAX precursor phases, which are a large family of ternary carbides and nitrides with more than 70 experimentally reported examples thus far (36). The general formula of MAX is Mn+1AXn, where M represents an early transition metal, A is an A-group element (mostly groups IIIA and IVA), X is carbon and/or nitrogen, and n = 1, 2, or 3 (i.e., M2AX, M3AX2, or M4AX3). In MXenes, n + 1 M layers cover n layers of X in an [MX]nM arrangement (37), such as Ti2CTx (38), Ti3C2Tx (39), and Nb4C3Tx (40), where Tx stands for the surface terminations (hydroxyl, oxygen, or fluorine) (41). Therefore, taking 2D TMCs as representative, we illustrate the four modification schemes in Fig. 1 by changing the transition metal species, layer thickness, surface functional group and mechanical strain. A structural optimization is performed for each 2D TMC (M2C, M3C2, M4C3, and M2CT2), and the calculated equilibrium M–C bond lengths and lattice constants are listed in Table 1, which show good agreement with those in previous publications (23, 25, 41–45).
Fig. 1.
Four methods to modify 2D TMCs, namely, changing the transition metal species (A), strain (B), layer thickness (C), and surface functional group (D). Red circles marked in E and F show two different adsorption sites (i and ii) of surface functional groups in vertical views.
Table 1.
Valance electron numbers of transition metals (Ne), the calculated bond lengths (dM-C), and the optimized lattice constants (a)
| a, Å | |||||
| TMCs | Ne | dM-C, Å | 1 | 2 | 3 |
| M2C | |||||
| Ti2C | 4 | 2.102 | 3.083 | 3.082* | 3.078† |
| Zr2C | 4 | 2.278 | 3.310 | 3.293† | 3.238‡ |
| Hf2C | 4 | 2.238 | 3.211 | 3.212† | 3.239‡ |
| V2C | 5 | 1.993 | 2.896 | 2.897† | 2.869‡ |
| Nb2C | 5 | 2.166 | 3.132 | 3.135† | — |
| Ta2C | 5 | 2.154 | 3.081 | 3.087† | 3.138‡ |
| Cr2C | 6 | 1.935 | 2.828 | 2.787‡ | — |
| Mo2C | 6 | 2.089 | 3.001 | 2.995§ | 2.990¶ |
| W2C | 6 | 2.123 | 2.866 | — | — |
| M3C2 | |||||
| Ti3C2 | 4 | 2.217 | 3.102 | 3.100* | 3.071‡ |
| M4C3 | |||||
| Ti4C3 | 4 | 2.255 | 3.101 | 3.066‡ | — |
| M2CT2 | |||||
| Ti2CO2 | 4 | 2.186 | 3.033 | 3.032* | 3.035§ |
| Ti2CF2 | 4 | 2.103 | 3.057 | 3.060§ | 3.050* |
| Zr2CO2 | 4 | 2.374 | 3.318 | 3.319# | 3.310‖ |
| Zr2CF2 | 4 | 2.277 | 3.309 | 3.312# | 3.300‖ |
Mechanical Stability.
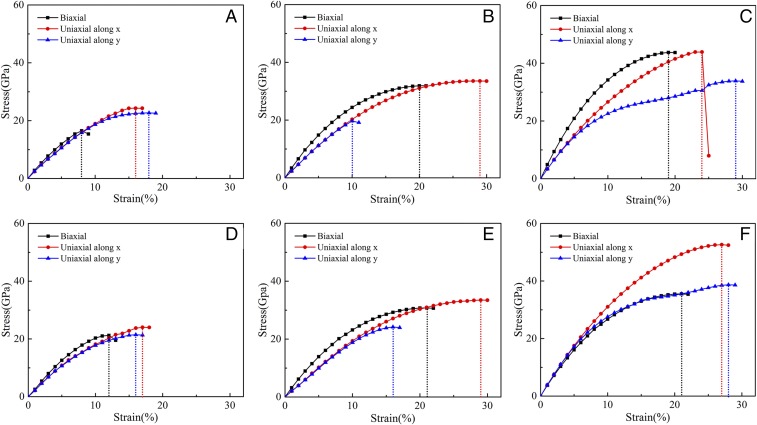
To predict the performances of 2D TMCs as flexible devices, investigating the mechanical properties, such as elastic stiffness, flexibility, and ideal strength, under various deformations is essential. In studying the intrinsic mechanical responses of 2D TMCs to tensile strain we considered three loading conditions (Fig. 1B): biaxial tension, uniaxial tension along x direction (the zigzag direction), and uniaxial tension along y direction (the armchair direction). Fig. 2 A and D present the calculated stress-strain curves for Ti2C and Zr2C under both biaxial and uniaxial load conditions. It is observed that Ti2C (Zr2C) can sustain large strains of 8 (12)%, 16 (16)%, and 18 (17)% under biaxial and uniaxial tensions along the x and y directions, respectively. Fig. S3 presents the stress-strain relationships for Ti2C, Ti3C2, and Ti4C3, and an increase of layer thickness is shown to improve the critical strain. As reported in previous X-ray photoelectron spectroscopy and energy-dispersive X-ray spectroscopy analyses, MXenes are generally terminated with various functional groups, such as O, OH, and F (16, 17, 46), and consequently their electronic structures and electrochemical performances are strongly influenced by these functional groups (42, 47). Thus, an in-depth understanding of the effect of functional groups is critical to pursue an excellent performance. Experimentally, a high temperature induces the conversion from -OH to -O termination based on the reaction -OH + -OH → -O + H2O (47). Therefore, here, we only focus on -F and -O terminations. As shown in Fig. 2C, Ti2CO2 can sustain large strains of 19%, 24%, and 29% under biaxial and uniaxial tensions along x and y direction, respectively, which are obviously larger than the corresponding strains of Ti2C (8%, 16%, and 18%) and graphene (15%, 20%, and 24%) (48). Compared with Ti2C (biaxial 8%), Ti2CF2 can sustain a larger biaxial strain of 20% (Fig. 2B). Similar to Ti2CO2 and Ti2CF2, the surface groups can also increase the critical strain of Zr2C (Fig. 2 D–F). Surface groups (O and F) considerably slow down the collapse of the transition metal layers induced by strain and provide more mechanical flexibility to the 2D TMCs (23). In addition to pure tensile strain, we performed a global exploration of in-plane strains, including both tension and compression. Interestingly, as shown in Fig. S4, a compression strain induces a lattice instability at smaller critical strain in graphene, whereas Ti2C and Ti2CO2 can tolerate higher compression strains up to 8%, suggesting that 2D TMCs may be more promising as flexible materials compared with graphene.
Fig. 2.
Strain-stress relationships for (A) Ti2C, (B) Ti2CF2, (C) Ti2CO2, (D) Zr2C, (E) Zr2CF2, and (F) Zr2CO2 under both biaxial and uniaxial load conditions.
Ionic Mobility.
The rate capability is a crucial factor in the design of promising electrode materials. For example, in cell phones or electric vehicles the full charge time is critical for device usability, while the discharge rate dominates the amount of power that can be delivered in the battery. The rate capabilities of LIBs critically depend on the Li+ and electron diffusion rates. According to the reported transition state, Li hopping is regarded as the microscopic mechanism for Li diffusion. Each individual hopping pathway must overcome the Gibbs free energy of activation during diffusion. The diffusion rate at which the hopping process occurs can be expressed as (49)
| [1] |
where is the temperature-dependent effective attempt frequency, is the Boltzmann constant, and is the temperature. Neglecting the entropy change during diffusion, can be approximated by the activation energy , where and are the energies of the transition and initial state, respectively. Typical values for the prefactor in Eq. 1 are 1011 to 1013 s−1 (50). When the hopping distance is known, the ionic diffusivity can be approximately obtained from (51). Since quantitative data and mechanistic information are hard to obtain in experiments, the theoretical calculations are powerful tools to provide elaborate information on Li diffusion (30). The climbing image nudged elastic band (CI-NEB) method (52) provides an efficient algorithm to compute transition state energies in a quantitative manner.
During the charging/discharging process, the electrode polarization inevitably occurs in LIBs and accordingly an exploration of the influence of polarization on the Li+ diffusion is much demanded. Therefore, we considered two cases: (i) the unpolarization state (i.e., if there is negligible electrical current, the electrode potential keeps a constant; it should be noted that the adsorbed Li atoms become partially ionized because of the sufficient charge transfer between Li and the anode when an Li atom intercalates into the anode) and (ii) the charge-transfer polarization state (i.e., if the electrical current passes through LIBs, the electrode potential deviates from the equilibrium value, and this phenomenon is called the electrode polarization) (31). When the polarization is generated by the charge transfer reaction it is termed charge transfer polarization. In addition, external charge, electric field, vacancy, and impurities generally disturb the charge distribution at the surface of an electrode (32–35).
As a proof of concept, an evaluation of the diffusion barrier, charge, and adsorption height on graphene was first performed under both cases and a similar trend was observed (Fig. S6). In our calculations of the adsorption energy, equilibrium voltage, and theoretical capacity, the unpolarization state is adopted to focus on the equilibrium state involving the surface-adsorbed Li with no electrical current passing through. In our calculations of the ionic mobility, the charge-transfer polarization state is assumed to simulate the dynamic process of Li+ diffusion while passing electrical current. Afterward, the Li+ diffusion barriers on the charged 2D materials are systematically investigated, and the corresponding energy profiles as a function of the diffusion coordinate are presented in Fig. 3 A–E and Fig. S5.
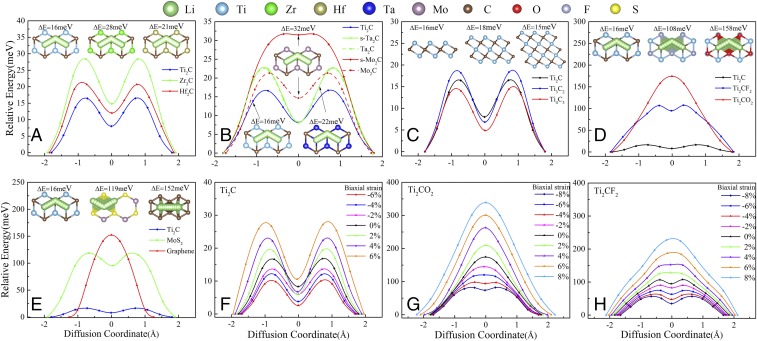
Fig. 3.
Potential-energy profiles of Li+ diffusion on the charged surfaces of (A) pristine Ti2C, Zr2C, and Hf2C; (B) pristine Ti2C, Ta2C, Mo2C, s-Ta2C, and s-Mo2C; (C) pristine Ti2C, Ti3C2, and Ti4C3; (D) pristine Ti2C, Ti2CF2, and Ti2CO2; and (E) pristine Ti2C, MoS2, and graphene. Potential-energy profiles of Li+ diffusion on the charged surfaces of (F) Ti2C, (G) Ti2CF2, and (H) Ti2CO2 under biaxial strain. Schematic representations of the diffusion paths are shown in the Insets. ΔE represents the corresponding diffusion barrier.
Influence of transition metal and thickness.
For bare 2D TMCs the minimum energy pathway (MEP) occurs from the site on top of the metal atom to the site on top of the C atom and then to another site on top of the metal atom. The calculated lattice constants vary distinctly among Ti2C, Zr2C, and Hf2C, which allows a comparative study on the effect of lattice constants by neglecting the influence of the valence electron numbers (VENs). The barriers for Ti2C, Zr2C, and Hf2C are calculated to be ∼16 meV, 29 meV, and 20 meV, respectively (Fig. 3A), and therefore, the Li+ diffuses exceptionally quickly on them. Notably, the M–C bond lengths in Ti2C, Zr2C, and Hf2C are 2.102 Å, 2.278 Å, and 2.238 Å, respectively, which follows interestingly the order of the calculated diffusion barriers. A similar trend between the bond lengths and diffusion barriers is also found for pristine Mo2C and W2C, which possess the same VEN but different lattice constants (Fig. S5A), providing a general rule that a smaller M–C bond length corresponds to a lower Li+ diffusion barrier on the surface of the charged 2D TMCs. However, the energy barriers of W2C and Mo2C are larger than that of Ti2C; simultaneously, the M–C bond lengths of these two species are smaller than that of Ti2C. To explore the influence of VEN on the energy barrier, we forced the lattice constants of Ta2C and Mo2C to be equal to that of Ti2C by applying strain to eliminate the influence of the bond length. As shown in Fig. 3B, the barriers of Ti2C, Ta2C under strain (s-Ta2C), and Mo2C under strain (s-Mo2C) are calculated to be ∼16 meV, 22 meV, and 32 meV, respectively, indicating that a smaller VEN corresponds to a lower Li+ diffusion barrier on the surface of the charged TMCs. Interestingly, the energy barrier increases remarkably by 40% at a 3% strain for Mo2C, indicating that the strain may greatly influence the energy barrier, as will be discussed in the next section. Although large differences exist in the layer thicknesses between pristine Ti2C (4.828 Å), Ti3C2 (7.269 Å), and Ti4C3 (9.794 Å), their diffusion barriers are nearly identical [i.e., 16 meV (Ti2C), 18 meV (Ti3C2), and 15 meV (Ti4C3), respectively], suggesting that the layer thickness has a negligible influence on the Li+ mobility on the charged 2D TMCs.
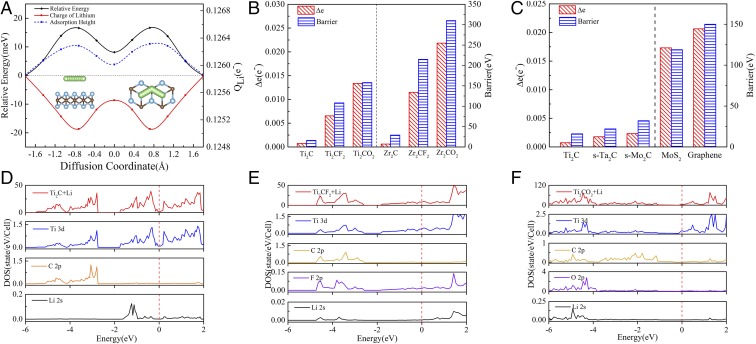
Before continuing our further investigation, the transport properties of 2D TMCs should be compared with those of graphene, a widely studied system for electrode materials. Clearly, the calculated energy barriers of Li+ diffusion for all of the bare 2D TMCs are one order lower than that of graphene (152 meV), supporting bare 2D TMCs as promising anode candidates for LIBs (53). To determine the physical origin for the energy barrier changes we further investigated the electronic interactions between the Li+ and 2D TMCs. Bader charge analysis is used to quantify the charge transfer between Li+ and the substrate. First, the Li+ charges at all points along the diffusion path on Ti2C are calculated (Fig. 4A). The increasing energy barrier follows the same trend as the electron charge reduction, concluding that the charge difference (∆e = eS − eT) between the stable site (eS) and transition site (eT) can also be used to determine the Li+ transport barrier height. Second, to verify this conclusion, the Li+ charges at all of the points along the diffusion path on graphene are calculated, and a similar trend is observed (Fig. S6 A and B).
Fig. 4.
(A) Relative energy, charge, and adsorption height of Li+ diffusion on the charged Ti2C. Charge differences of Li Δe and barriers of (B) Ti2C, Ti2CF2, Ti2CO2, Zr2C, Zr2CF2, and Zr2CO2 and (C) Ti2C, s-Ta2C, s-Mo2C, MoS2, and graphene. TDOS and PDOS of Li on (D) Ti2C, (E) Ti2CF2, and (F) Ti2CO2. The Fermi levels are set to zero and indicated by the dashed lines.
Surface modification effect.
Next, we studied the effect of the surface functional group on the ionic mobility. The MEPs on Ti2CO2 and Ti2CF2 occur from the site on top of the C atom to the site on top of the Ti atom and then stop at the neighboring site on top of the C atom. In both the bare and functionalized 2D TMCs the MEP is purely associated with the atoms on the three surface layers (Fig. S10). The H1 site is on top of FCC hollow, while the H2 site is on top of HCP hollow. The MEP occurs from H1 to H2 then to H1. As shown in Fig. 3D (also in Fig. S5B), the Li+ diffusion barrier follows the order Ti2C (16 meV) < Ti2CF2 (108 meV) < Ti2CO2 (158 meV) [Zr2C (29 meV) < Zr2CF2 (215 meV) < Zr2CO2 (310 meV)], indicating that the bare 2D TMCs have the best high-rate performance. The higher Li+ diffusion barriers for M2CF2 and M2CO2 can be ascribed to the steric hindrance induced by the surface F and O groups. Fig. 4 D–F and Fig. S7 A–C and F depict the computed total density of states (TDOS) and projected DOS (PDOS) for Li adsorption on Ti2C, Ti2CF2, Ti2CO2, Zr2C, Zr2CF2, Zr2CO2, and Hf2CO2. Considerable overlaps are clearly observed between the O 2p, F 2p, and Li 2s orbitals from −6 to −3 eV under the Fermi level, indicating the strong s-p hybridization. Chemical bonding hinders Li+ diffusion, as shown by the increased DOS of the O 2p orbital compared with that of the F 2p orbital. Therefore, the bond between O and Li is stronger than that between F and Li, and the ionic mobility on M2CO2 is slower than that on M2CF2. In addition, the barriers on graphene and MoS2 are ∼152 meV and 119 meV, respectively (Fig. 3E), being close to those of Ti2CO2 and Ti2CF2. The calculated TDOS and PDOS for Li adsorption on graphene and MoS2 suggests that an obvious overlap between the C 2p, S 2p, and the Li 2s orbitals appears from −5 to −3 eV under the Fermi level, indicating that C and S form bonds to Li (Fig. S7 D and E). In brief, the ionic mobility has a strong dependence on the atomic configuration of the first three surface layers. The outermost atoms have the greatest effect on the energy barriers, and the materials with nonmetallic surface atoms have larger barriers than those with metallic surface atoms due to bonding between Li and the nonmetallic atoms, providing an explanation to the much more rapid Li diffusion on the bare 2D TMCs compared with other 2D materials. The Li charge differences Δe and barriers of Ti2C, Ti2CF2, Ti2CO2, Zr2C, Zr2CF2, and Zr2CO2 are shown in Fig. 4B. The Δe follows the same order as the barrier (Ti2C < Ti2CF2 < Ti2CO2, Zr2C < Zr2CF2 < Zr2CO2), and Fig. 4C exhibits the same trend when comparing the barriers of Ti2C, s-Ta2C, s-Mo2C, and those of MoS2 and graphene. Therefore, as ∆e increases, the barrier increases, indicating that electron accumulation is an important physical mechanism that hinders Li+ transport, which is consistent with a previous study (54).
Biaxial strain effect.
Strain is generally regarded as an efficient approach to tune the electrochemical or other functional properties of 2D materials, which has received considerable interest from both experiments and theoretical investigations (55–58). We took Ti2C, Ti2CF2, and Ti2CO2 as representative to explore the biaxial strain effect on the diffusion behavior of Li+. Fig. 3 F–H show the Li+ diffusion barriers on Ti2C, Ti2CF2, and Ti2CO2 under biaxial strain. With an increasing biaxial strain the diffusion barrier also increases. To gain a deeper insight into the effect of the Ti–C bond length, we analyzed the electronic structures of Ti2C during different biaxial strains by calculating the DOS (Fig. S8). Two distinct features are identified. (i) With an increasing strain, a gap appears at −3 eV below the Fermi level, and the peak above −3 eV begins to increase in energy to the Fermi level. (ii) The peak at approximately −6 eV begins to increase in energy. Both effects lead to the appearance of the peaks located from −6 to −3 eV and −3 to 2 eV, suggesting that the Ti and C interaction weakens with an increase of the Ti–C bond length. To obtain insight into the relationship between the diffusion barrier, Ti–C bond length, and Li+ adsorption height, Fig. S9 presents their variations with strain. An increasing strain leads to an increase of the Ti–C bond length and a reduction of the adsorption height, which eventually leads to increases in the charge difference and diffusion barrier, respectively. Therefore, the biaxial compression clearly leads to a reduction in the energy barrier, while the biaxial tension increases the energy barrier; these relationship are likely valid for other MXenes because of their similar topological structures. To verify whether these relationships apply to other 2D materials we calculated the potential-energy curves of Li+ diffusion on the uncharged and charged graphene under biaxial strain and the variations of charge differences Δe and barriers as a function of biaxial strain, as shown in Fig. S6 C–F. Graphene shows the same relationships as 2D TMCs. However, the barrier for 2D TMCs increases more dramatically with an increasing biaxial strain compared with that for graphene, which may be mostly attributed to the changes in bond angle and layer thickness under applied strain for 2D TMCs.
Uniaxial stress effect.
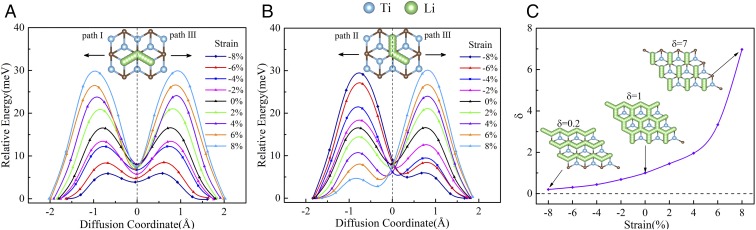
To explore the uniaxial loading effect we applied a uniaxial stress scheme by dynamically adjusting the in-plane strain components that are orthogonal to the stress component. Under a uniaxial stress state, tension/compression stress (not strain) exists in a certain direction, and, accordingly, the effects of uniaxial stress along the x axis and y axis are opposite (i.e., the effect of the x-axis in-plane tension is similar to that of the y-axis compression). Therefore, we took Ti2C under x-axis stress as a representative to explore the uniaxial stress effect on the diffusion behavior of Li+. Fig. 5A shows the energy barriers along the two transport pathways (path I and path III) during tensile and compression loading along the x-axis direction, while Fig. 5B shows the energy barriers along path II and path III. Since path I is completely symmetrical with path III, path I is studied. Both the Ti–C bond length and energy barrier of path I (III) simultaneously increase (decreases) as the x-axis strain increases (Fig. S11), again demonstrating that the energy barrier increases with an increasing Ti–C bond length. To better clarify the energy barrier difference along the different paths, a relative factor is defined as , where and are the energy barriers along path I and path II, respectively. As shown in Fig. 5C, the value increases as the strain increases. At equilibrium, indicates that the energy barrier along path I is equal to that along path II. These results reveal that the Li+ prefers to diffuse between all of the hollow sites. When a compressive strain is applied (i.e., ), the Li+ is more likely to transport along path I and path III. A higher compressive stress results in a smaller and a greater tendency for transportation along path I and path III. When tensile stress is applied, , which favors Li+ transport along path II. Therefore, the uniaxial stress can efficiently modify the Li+ diffusion path. Nevertheless, the energy barrier along the preferred transport pathway will be reduced by either uniaxial tensile or compressive stress. Among all of the studied 2D TMCs, Ti2C possesses the lowest energy barrier under either uniaxial or biaxial loading and therefore is an excellent candidate as a promising flexible LIB anode.
Fig. 5.
Potential-energy profiles of Li+ diffusion on the charged surface of Ti2C under uniaxial strains along (A) path I and path III and along (B) path I and path II. Schematic representations of the diffusion paths are shown in the Insets. (C) Relationship between δ and the uniaxial strain. Path I and path III are along the zigzag path, and path II is along armchair path.
Effect of Li concentration.
Fig. S12 shows the energy barriers at both low Li coverage (i.e., Ti2CO2Li1/9) and high Li coverage (i.e., Ti2CO2Li17/9). In both Li coverages cases the energy barrier increases (decreases) as the biaxial tension (compression) strain increases, and a higher Li coverage greatly increases the energy barriers compared with lower Li coverage. This result suggests that the interactions between Li+ under higher Li coverage impede Li+ diffusion. In comparison with the influence of bond length on the energy barrier, the effect of the Li+ interactions is more critical under high Li coverage. To quantify such an effect under different stress/strain states, we define a relative factor , where and are the energy barriers at high and low Li coverages, respectively. A larger indicates a more profound effect of the Li+ interactions on the energy barrier. As shown in Fig. S12D, increases monotonously as the strain changes from +8% to −8%, providing a general guideline to alter the electrochemical properties by tuning the strain.
Therefore, we can conclude that the Li coverage is another crucial factor that influences the ionic mobility. During the charging process on the anode the charging rate is initially exceptionally fast but slows as the amount of embedded Li increases. Although a compression strain leads to considerable Li+ interactions, an appropriate compression strain increases the ionic mobility at either high or low Li coverage.
Equilibrium Voltage and Theoretical Capacity.
The energy density is another crucial factor in designing promising battery materials. Increasing the cell voltage without exceeding the electrolyte stability window is a promising strategy to enhance the energy densities of LIBs. The equilibrium Li intercalation voltage can be expressed as (30)
| [2] |
where and represent the Li chemical potentials of the cathode and anode, respectively, is the transferred charge, and is the Faraday constant. The average voltage as a function of the free energy change of the combined anode/cathode reaction is calculated using the following equation (30):
| [3] |
At 0 K, the reaction free energy can be approximated by the internal energy, that is, . Therefore, the charging/discharging processes of 2D TMCs follow the common half-cell reaction:
| [4] |
Considering the above reaction, the average voltage of Mn+1CnLix in the concentration range of is obtained by
| [5] |
where and represent the internal energies of and body-centered cubic Li, respectively. The equilibrium voltage between the intermediate phases can be calculated using Eq. 5 after all structures of intermediate phases are determined. Courtney et al. (59) calculated the 0-K voltage profile of the Li-Sn alloy, demonstrating excellent agreement with the experimental voltage curves. However, the intermediate phases cannot always be experimentally obtained, yet first-principles computations provide a suitable pathway for the prediction of stable phases (60). Since the formation energy with respect to stable reference materials quantifies the relative stability of different phases, the following equation is thus used to calculate the formation energy of with an intermediate Li content:
| [6] |
where and are the internal energies of the fully lithiated and delithiated , respectively (61, 62).
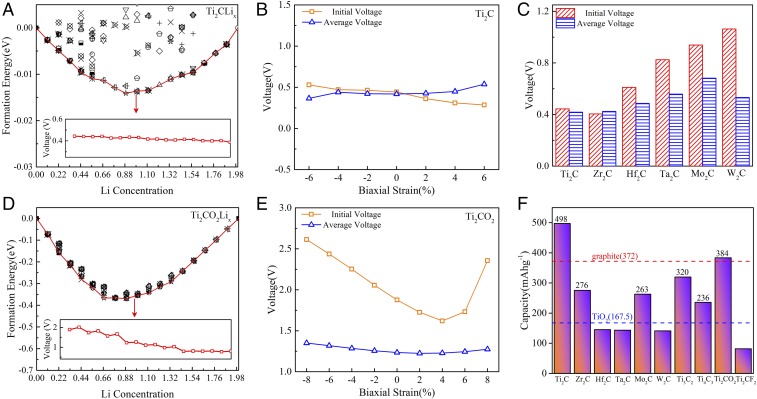
Fig. 6A shows the calculated formation energies and the resulting 0-K voltage profiles for Li adsorption on Ti2C. The formation energy of Ti2C reaches the lowest value at the Li concentration of 0.88, and the subsequent 0-K voltage profile simulates the first charging/discharging process of the corresponding LIB. As the Li concentration increases the voltage of Ti2C remains at ∼0.4 V, whereas for Ti2CO2 the voltage gradually declines from 2 to 0.8 V and remains stable at 0.8 V (Fig. 6D). To determine the stability of the voltage variation in the charging/discharging process, the voltage of the first Li adsorption is defined as the initial voltage, and a smaller difference between the initial and average voltage indicates a more stable voltage in the charging/discharging process. The initial and average voltages of other bare 2D TMCs (M2C, M = Ti, Zr, Hf, Ta, Mo, and W) are also calculated and compared in Fig. 6C. It is found that the voltage is primarily dominated by the VEN, that is, the initial and average voltages increase as the VEN increases, except for W2C. Fig. S13C shows that the initial and average voltages of Ti2C, Ti3C2, and Ti4C3 are nearly identical, indicating that the layer thickness has a negligible effect on the voltage. A desirable potential ranges from 0.1 to 1 V for anode materials, suggesting that all of the bare 2D TMCs are good candidates for low-voltage battery applications. Moreover, the strain effect on the voltage is also considered. Under biaxial strain, the initial and average voltages of Ti2C are maintained at ∼0.4 V, while the initial voltage of Ti2CO2 dramatically changes (Fig. 6 B and E). Therefore, compared with Ti2CO2, Ti2C is more suitable as an anode because of its lower and more stable equilibrium voltage, which is more immune to strain. In addition, for Ti2CF2, a critical composition is observed at x = 0.22, above which the voltage becomes negative (Fig. S13A). Note that the maximum number of Li+ in a 3 × 3 supercell of Ti2CF2 is four, corresponding to a chemical stoichiometry of Ti2CF2Li0.444. The lower Li capacity in Ti2CF2 is mainly attributed to the steric effect of F, which impedes the spatial occupancy of more Li; otherwise, the surface F groups would be repulsed, leading to the formation of LiF by-products.
Fig. 6.
Calculated formation energies and resulting voltage profiles of (A) Ti2C and (D) Ti2CO2 obtained along the energy structures. Initial voltages and average voltages of Ti2C (B) and Ti2CO2 (E) under biaxial strains. (C) Initial voltages and average voltages of M2C. (F) Theoretical gravimetric capacities of the studied 2D TMCs.
The theoretical capacity, a key parameter in evaluating the electrode performance for LIBs, can be estimated from the following equation (18):
| [7] |
where is the number of adsorbed metal adatoms, is the valence state of the metal adatoms, F is the Faraday constant (26,801 mAh⋅mol−1), is the molecular weight of the MXene nanosheet, and is the molecular weight of the metal adatoms. The weight of the adsorbed metal atom is not considered in most calculated capacities presented in the literature. Fig. 6F shows the calculated theoretical capacities of the studied 2D TMCs. The theoretical capacities of many 2D TMCs are much higher than that of a commercial TiO2 anode material (167.5 mAh⋅g−1). In general, Ti2C has the greatest theoretical capacity among all of the bare 2D TMCs, while Ti2CO2 is the best among all of the O-terminated 2D TMCs.
Overall, several key factors, including the bond length, VEN, strain, surface functional group, and layer thickness, can influence the properties of 2D TMCs as anode materials in LIBs. The ionic mobility has a strong dependence on the atomic configuration of the three surface layers. First, the outermost atoms have a dominant effect on the energy barriers, and materials with nonmetallic surface atoms have larger barriers than those with metallic surface atoms due to bonding between Li and the nonmetal, explaining the much more rapid Li diffusion on bare 2D TMCs compared with that on other 2D materials. Second, the energy barrier increases as the bond length and VEN increase. Third, the strain plays a critical role in determining the energy barrier. In general, on one hand the energy barrier increases as the biaxial strain increases within the critical strain. Compared with graphene, the barriers of 2D TMCs increase more dramatically as the biaxial strain increases, which can be primarily attributed to the changes of the bond angle and layer thickness when the 2D TMCs are under applied strain. On the other hand, the uniaxial loading increases the ionic mobility, efficiently modifying the corresponding Li+ diffusion pathway. Moreover, the Li concentration is another crucial factor that influences the ionic mobility owing to the interactions between Li+ at higher Li coverage, impeding the Li+ diffusion. Therefore, increasing the bond length, VEN, biaxial strain, and Li concentration and introducing surface functional group negatively affect the ionic mobility. Similarly, increasing the VEN and introducing surface functional group decrease the cell voltage and capacity. In contrast, introducing surface functional group and increasing the layer thickness have positive effects on the stiffness, mechanical flexibility, and strength.
Suggestions for Fabricating a Promising Anode.
Several critical factors may influence the properties of 2D TMCs as anode materials in LIBs and accordingly can provide strategies for optimizing the performance of 2D TMCs for application in LIBs. For instance,
-
i)
Due to the negative effect of the bond length and VEN on the ionic mobility, Ti2C can be utilized to ensure the highest ionic mobility.
-
ii)
Increasing the layer thickness may improve mechanical flexibility; this, however, slightly reduces the ionic mobility and voltage. As a result, M3C2 and M4C3 are better candidates for applications under relatively large strains.
-
iii)
Strain is a key parameter that affects the energy barrier for Li+ diffusion, while uniaxial stress can efficiently modify the Li+ diffusion path. Interestingly, an appropriate control over the compression strain may increase the ionic mobility by decreasing the energy barrier. Therefore, the diffusion performance on 2D TMCs can be efficiently tuned by strain.
-
iv)
Introducing surface functional groups decreases the ionic mobility, cell voltage, and theoretical capacity. Therefore, the electrochemical properties can be improved by removing surface functional groups. Since the bare 2D TMCs have not been prepared thus far, we propose Ti2CO2 as the best anode material among all of the presented functionalized 2D TMCs for the following reasons. First, first-principles calculations suggest that Ti2CO2 possesses thermodynamic, mechanical, and dynamic stability, indicating that Ti2CO2 can be experimentally realized (44, 63). Second, several experiments provide strong evidence for the possible synthesis of optimal Ti2CO2 (38, 47, 64). Third, compared with TiO2 anode materials, Ti2CO2 possesses enhanced electronic conductivity, faster Li transport, higher charging/discharging rates, decreased equilibrium voltage, and improved Li storage capacity. Compared with graphene, the better mechanical properties and increased theoretical capacity make Ti2CO2 more suitable for flexible anode materials in high-performance LIBs.
Conclusions
In summary, we systematically investigated several key parameters of highly flexible 2D TMCs to determine their battery-related properties (i.e., stability, ionic mobility, equilibrium voltage, and theoretical capacity). Using multiaxial loading schemes (biaxial/uniaxial, tension/compression), the ionic mobilities on 2D TMCs under various strain states are systematically explored. Our theoretical calculations indicated that the bond length dM-C, VEN, and surface functional groups had key influences on the ionic mobility on the charged 2D TMCs, mainly attributed to electronic interactions or redistribution. Electron capture is found to be responsible for the different energy barrier that may be further modified by the strain. As the biaxial tension strain increased the ionic mobility monotonically decreased, while an appropriate control of compression strains effectively increased the ionic mobility. A combination of several extraordinary properties, including excellent electrical conductivity, high ionic mobility, low equilibrium voltage with good stability, and high theoretical Li capacity, indicated that bare 2D TMCs have the potential to be good alternative anode materials to TiO2 in LIBs. Among all 2D TMCs, Ti2C is found to be undoubtedly the most promising anode material. In addition, a low energy barrier for Ti2C under multiaxial loading can be maintained, providing further promise for Ti2C as a potential flexible anode material for high-performance LIBs. However, for the fluorinated and oxidized derivatives of 2D TMCs the surface functional groups form chemical bonds with Li, which consequently degrades Li diffusion and increases the equilibrium voltage. Compared with TiO2 anode materials, Ti2CO2 possesses an enhanced electronic conductivity, faster Li transport, higher charge/discharge rates, decreased equilibrium voltage, and improved Li storage capacity. Therefore, further experimental investigations on Ti2CO2 are highly desirable to shed light on its prospects as a flexible anode material for high-performance LIBs.
Computational Methods
Structure Optimization.
The spin-polarized density functional theory computations are performed based on the generalized gradient approximation (65) designed by Perdew et al. (66) with a plane wave kinetic energy cutoff of 600 eV, as implemented in the Vienna ab initio simulation package (VASP) (67). Core electrons are treated using projector augmented wave pseudopotentials (68). Lattice constants and atomic coordinates are optimized with an energy convergence of 10−6 eV per cell. The criterion for force convergence during the relaxation is 10−3 eV/Å. A k-mesh grid of 8 × 8 × 1 is adopted to sample the first Brillouin zone in the relaxation process. To guarantee that the supercell size of surface model is sufficiently large to avoid the effect of Li+ between their mirror images the calculations are performed with a 3 × 3 × 1 supercell for the 2D TMCs and MoS2 and a 4 × 4 × 1 supercell for graphene. A vacuum of 25 Å is used along the direction perpendicular to the layer to avoid slab interaction with its periodic images.
Ionic Mobility.
The CI-NEB method requires the initial and final states of diffusion as inputs and generates a number of intermediate states by linear interpolation. Then, the MEP between the initial and final state is determined by minimizing the atomic forces in all images simultaneously subject to a harmonic coupling between neighboring images (69). To validate our CI-NEB calculations the diffusion barrier for a Li atom on a graphene surface is evaluated. As shown in Fig. S6A, our calculated diffusion barrier is consistent with a previous study (70). To simulate the charge-transfer polarization state the Li adsorption model is first charged by removing an electron from the system, and then, the compensating background charge is homogeneously distributed over the model to maintain charge neutrality, in a manner similar to that in the previous studies (71).
Mechanical Properties.
The elastic stiffness of 2D layered materials can be evaluated by the critical strain (the strain reached at ideal strength). Equivalent tensile strains are simultaneously applied in the zigzag and armchair directions to investigate the critical biaxial strain. The ideal strength provides the upper limit of a real material and can also be experimentally approached for many materials, especially 2D materials (72). The applied strain is defined as , where and are the lattice constants of the strained and unstrained stable materials, respectively. Considering the 2D character of the simulated 2D materials, the value of the stress should be rescaled by ( is the cell length along the vacuum direction, and is the effective thickness of the slab) (73) to avoid the stress’ being artificially averaged over the entire simulation cell including the vacuum. In general, to obtain a precise layer thickness dL, the layer spacing should be considered, as adopted in previous works on graphene and molybdenum disulfide (74). We optimized the bilayer model of 2D TMCs and calculated the layer thickness as the distance between two carbon layers in the corresponding 2D TMCs with three configurations presented in Fig. S2. Since the van der Waals (vdW) correction is significant for layer interactions, full relaxations are performed to optimize the atomic coordinates by means of the optB88-vdW functional (75) with an energy convergence of 10−6 eV per cell and with a force convergence of 10−3 eV/Å. To study the strain effect on diffusion we applied uniaxial and biaxial tension on the 2D TMCs. To ensure that the 2D TMCs are under uniaxial stress a specific relaxation is performed for both the lattice basis vectors and the atomic coordinates by keeping the applied in-plane strain component fixed and relaxing the other in-plane strain component until their conjugate stress components (i.e., Hellmann–Feynman stresses) reached less than 0.1 GPa. For a 2D material the dimensional length normal to the 2D layer is kept constant during the relaxation to keep a sufficient vacuum thickness. Such a relaxation scheme is accomplished by slightly modifying the VASP code with specific constraints of the strain components. To ensure that the strain path is continuous the starting position at each strain step must be taken from the relaxed coordinates of the previous step. Because the crystal symmetry may change and the Brillouin zone could considerably deform at large strain, we adopted a high energy cutoff of 600 eV and verified the convergence of the tensile calculations with different k-point grids. A similar scheme for the stress-strain calculations of 3D crystals has been described and thoroughly evaluated in our previous papers (76, 77).
Supplementary Material
Acknowledgments
We thank Prof. G. Kresse for valuable advice on the application of VASP and Prof. Qiang Zhu for valuable advice. This work is supported by National Key Research and Development Program of China Grant 2017YFB0702100, National Natural Science Foundation of China Grants 51471018 and 51672015, 111 Project Grant B17002, National Thousand Young Talents Program of China, and Fundamental Research Funds for the Central Universities. D.L. is supported by the European Regional Development Fund in the IT4Innovations national supercomputing center - path to exascale project CZ.02.1.01/0.0/0.0/16_013/0001791 within the Operational Programme Research, Development and Education and Grant 17-27790S from the Czech Science Foundations and the National Programme of Sustainability (NPU II) project IT4Innovations excellence in science—LQ1602.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1717219115/-/DCSupplemental.
References
- 1.Miller JR. Applied physics. Valuing reversible energy storage. Science. 2012;335:1312–1313. doi: 10.1126/science.1219134. [DOI] [PubMed] [Google Scholar]
- 2.Armand M, Tarascon JM. Building better batteries. Nature. 2008;451:652–657. doi: 10.1038/451652a. [DOI] [PubMed] [Google Scholar]
- 3.Dunn B, Kamath H, Tarascon JM. Electrical energy storage for the grid: A battery of choices. Science. 2011;334:928–935. doi: 10.1126/science.1212741. [DOI] [PubMed] [Google Scholar]
- 4.El-Kady MF, Strong V, Dubin S, Kaner RB. Laser scribing of high-performance and flexible graphene-based electrochemical capacitors. Science. 2012;335:1326–1330. doi: 10.1126/science.1216744. [DOI] [PubMed] [Google Scholar]
- 5.Chu S, Majumdar A. Opportunities and challenges for a sustainable energy future. Nature. 2012;488:294–303. doi: 10.1038/nature11475. [DOI] [PubMed] [Google Scholar]
- 6.Bruce PG, Freunberger SA, Hardwick LJ, Tarascon J-M. Li-O2 and Li-S batteries with high energy storage. Nat Mater. 2011;11:19–29. doi: 10.1038/nmat3191. [DOI] [PubMed] [Google Scholar]
- 7.Dahn JR, Zheng T, Liu Y, Xue JS. Mechanisms for lithium insertion in carbonaceous materials. Science. 1995;270:590–593. [Google Scholar]
- 8.Reddy MV, et al. α-Fe2O3 nanoflakes as an anode material for li-ion batteries. Adv Funct Mater. 2007;17:2792–2799. [Google Scholar]
- 9.Chan CK, Zhang XF, Cui Y. High capacity Li ion battery anodes using ge nanowires. Nano Lett. 2008;8:307–309. doi: 10.1021/nl0727157. [DOI] [PubMed] [Google Scholar]
- 10.Chan CK, et al. High-performance lithium battery anodes using silicon nanowires. Nat Nanotechnol. 2008;3:31–35. doi: 10.1038/nnano.2007.411. [DOI] [PubMed] [Google Scholar]
- 11.Idota Y, Kubota T, Matsufuji A, Maekawa Y, Miyasaka T. Tin-based amorphous oxide: A high-capacity lithium-ion-storage material. Science. 1997;276:1395–1397. [Google Scholar]
- 12.Reddy MV, Subba Rao GV, Chowdari BVR. Metal oxides and oxysalts as anode materials for Li ion batteries. Chem Rev. 2013;113:5364–5457. doi: 10.1021/cr3001884. [DOI] [PubMed] [Google Scholar]
- 13.Kaskhedikar NA, Maier J. Lithium storage in carbon nanostructures. Adv Mater. 2009;21:2664–2680. doi: 10.1002/adma.200901079. [DOI] [PubMed] [Google Scholar]
- 14.Stankovich S, et al. Graphene-based composite materials. Nature. 2006;442:282–286. doi: 10.1038/nature04969. [DOI] [PubMed] [Google Scholar]
- 15.Li D, Müller MB, Gilje S, Kaner RB, Wallace GG. Processable aqueous dispersions of graphene nanosheets. Nat Nanotechnol. 2008;3:101–105. doi: 10.1038/nnano.2007.451. [DOI] [PubMed] [Google Scholar]
- 16.Ghidiu M, Lukatskaya MR, Zhao M-Q, Gogotsi Y, Barsoum MW. Conductive two-dimensional titanium carbide ‘clay’ with high volumetric capacitance. Nature. 2014;516:78–81. doi: 10.1038/nature13970. [DOI] [PubMed] [Google Scholar]
- 17.Mashtalir O, et al. Intercalation and delamination of layered carbides and carbonitrides. Nat Commun. 2013;4:1716. doi: 10.1038/ncomms2664. [DOI] [PubMed] [Google Scholar]
- 18.Xie Y, et al. Prediction and characterization of MXene nanosheet anodes for non-lithium-ion batteries. ACS Nano. 2014;8:9606–9615. doi: 10.1021/nn503921j. [DOI] [PubMed] [Google Scholar]
- 19.Eames C, Islam MS. Ion intercalation into two-dimensional transition-metal carbides: Global screening for new high-capacity battery materials. J Am Chem Soc. 2014;136:16270–16276. doi: 10.1021/ja508154e. [DOI] [PubMed] [Google Scholar]
- 20.Tang Q, Zhou Z, Shen P. Are MXenes promising anode materials for Li ion batteries? Computational studies on electronic properties and Li storage capability of Ti3C2 and Ti3C2X2 (X = F, OH) monolayer. J Am Chem Soc. 2012;134:16909–16916. doi: 10.1021/ja308463r. [DOI] [PubMed] [Google Scholar]
- 21.Kurtoglu M, Naguib M, Gogotsi Y, Barsoum MW. First principles study of two-dimensional early transition metal carbides. MRS Commun. 2012;2:133–137. [Google Scholar]
- 22.Borysiuk VN, Mochalin VN, Gogotsi Y. Molecular dynamic study of the mechanical properties of two-dimensional titanium carbides Ti(n+1)C(n) (MXenes) Nanotechnology. 2015;26:265705. doi: 10.1088/0957-4484/26/26/265705. [DOI] [PubMed] [Google Scholar]
- 23.Guo Z, Zhou J, Si C, Sun Z. Flexible two-dimensional Tin+1Cn (n = 1, 2 and 3) and their functionalized MXenes predicted by density functional theories. Phys Chem Chem Phys. 2015;17:15348–15354. doi: 10.1039/c5cp00775e. [DOI] [PubMed] [Google Scholar]
- 24.Wang H, et al. Direct and continuous strain control of catalysts with tunable battery electrode materials. Science. 2016;354:1031–1036. doi: 10.1126/science.aaf7680. [DOI] [PubMed] [Google Scholar]
- 25.Zhao S, Kang W, Xue J. Manipulation of electronic and magnetic properties of M2C (M = Hf, Nb, Sc, Ta, Ti, V, Zr) monolayer by applying mechanical strains. Appl Phys Lett. 2014;104:133106. [Google Scholar]
- 26.Gao G, et al. Monolayer MXenes: Promising half-metals and spin gapless semiconductors. Nanoscale. 2016;8:8986–8994. doi: 10.1039/c6nr01333c. [DOI] [PubMed] [Google Scholar]
- 27.Gan L-Y, Zhao Y-J, Huang D, Schwingenschlögl U. First-principles analysis of MoS2/Ti2C and MoS2/Ti2CY2 (Y=F and OH) all-2D semiconductor/metal contacts. Phys Rev B. 2013;87:245307. [Google Scholar]
- 28.Luo J, et al. Sn4+ ion decorated highly conductive Ti3C2 MXene: Promising lithium-ion anodes with enhanced volumetric capacity and cyclic performance. ACS Nano. 2016;10:2491–2499. doi: 10.1021/acsnano.5b07333. [DOI] [PubMed] [Google Scholar]
- 29.Ong SP, et al. Voltage, stability and diffusion barrier differences between sodium-ion and lithium-ion intercalation materials. Energy Environ Sci. 2011;4:3680–3688. [Google Scholar]
- 30.Urban A, Seo D-H, Ceder G. Computational understanding of Li-ion batteries. npj Compu Mater. 2016;2:16002. [Google Scholar]
- 31.Koryta J, Dvorak W, Kavan L. Principles of Electrochemistry. 2nd Ed Wiley; New York: 1987. [Google Scholar]
- 32.Schedin F, et al. Detection of individual gas molecules adsorbed on graphene. Nat Mater. 2007;6:652–655. doi: 10.1038/nmat1967. [DOI] [PubMed] [Google Scholar]
- 33.Lozovoi AY, Alavi A, Kohanoff J, Lyndenbell RM. Ab initio simulation of charged slabs at constant chemical potential. J Chem Phys. 2001;115:1661–1669. [Google Scholar]
- 34.Schultz PA. Charged local defects in extended systems. Phys Rev Lett. 2000;84:1942–1945. doi: 10.1103/PhysRevLett.84.1942. [DOI] [PubMed] [Google Scholar]
- 35.Walle CGVD, Neugebauer J. First-principles calculations for defects and impurities: Applications to III-nitrides. J Appl Phys. 2004;95:3851–3879. [Google Scholar]
- 36.Barsoum MW, Radovic M. Elastic and mechanical properties of the MAX phases. Annu Rev Mater Res. 2011;41:195–227. [Google Scholar]
- 37.Anasori B, Lukatskaya MR, Gogotsi Y. 2D metal carbides and nitrides (MXenes) for energy storage. Nat Rev Mater. 2017;2:16098. [Google Scholar]
- 38.Naguib M, et al. Two-dimensional transition metal carbides. ACS Nano. 2012;6:1322–1331. doi: 10.1021/nn204153h. [DOI] [PubMed] [Google Scholar]
- 39.Naguib M, et al. Two-dimensional nanocrystals: Two-dimensional nanocrystals produced by exfoliation of Ti3AlC2. Adv Mater. 2011;23:4207. doi: 10.1002/adma.201102306. [DOI] [PubMed] [Google Scholar]
- 40.Ghidiu M, et al. Synthesis and characterization of two-dimensional Nb4C3 (MXene) Chem Commun (Camb) 2014;50:9517–9520. doi: 10.1039/c4cc03366c. [DOI] [PubMed] [Google Scholar]
- 41.Naguib M, Mochalin VN, Barsoum MW, Gogotsi Y. 25th anniversary article: MXenes: A new family of two-dimensional materials. Adv Mater. 2014;26:992–1005. doi: 10.1002/adma.201304138. [DOI] [PubMed] [Google Scholar]
- 42.Khazaei M, et al. Novel electronic and magnetic properties of two-dimensional transition metal carbides and nitrides. Adv Funct Mater. 2013;23:2185–2192. [Google Scholar]
- 43.Cakr D, Sevik C, Gulseren O, Peeters FM. Mo2C as a high capacity anode material: A first-principles study. J Mater Chem A Mater Energy Sustain. 2016;4:6029–6035. [Google Scholar]
- 44.Yorulmaz U, Özden A, Perkgöz NK, Ay F, Sevik C. Vibrational and mechanical properties of single layer MXene structures: A first-principles investigation. Nanotechnology. 2016;27:335702. doi: 10.1088/0957-4484/27/33/335702. [DOI] [PubMed] [Google Scholar]
- 45.Hong L, Klie RF, Öğüt S. First-principles study of size- and edge-dependent properties of MXene nanoribbons. Phys Rev B. 2016;93:115412. [Google Scholar]
- 46.Shi C, et al. Structure of nanocrystalline Ti3C2 MXene using atomic pair distribution function. Phys Rev Lett. 2014;112:125501. doi: 10.1103/PhysRevLett.112.125501. [DOI] [PubMed] [Google Scholar]
- 47.Xie Y, et al. Role of surface structure on Li-ion energy storage capacity of two-dimensional transition-metal carbides. J Am Chem Soc. 2014;136:6385–6394. doi: 10.1021/ja501520b. [DOI] [PubMed] [Google Scholar]
- 48.Si C, Duan W, Liu Z, Liu F. Electronic strengthening of graphene by charge doping. Phys Rev Lett. 2012;109:226802. doi: 10.1103/PhysRevLett.109.226802. [DOI] [PubMed] [Google Scholar]
- 49.Vineyard GH. Frequency factors and isotope effects in solid state rate processes. J Phys Chem Solids. 1957;3:121–127. [Google Scholar]
- 50.Van der Ven A, Thomas JC, Xu Q, Swoboda B, Morgan D. Nondilute diffusion from first principles: Li diffusion in LixTiS2. Phys Rev B. 2008;78:104306. [Google Scholar]
- 51.Halim J, et al. X-ray photoelectron spectroscopy of select multi-layered transition metal carbides (MXenes) Appl Surf Sci. 2016;362:406–417. [Google Scholar]
- 52.Jónsson H, Mills G, Jacobsen KW. Classical and Quantum Dynamics in Condensed Phase Simulations: Proceedings of the International School of Physics. World Scientific; Singapore: 1997. Nudged elastic band method for finding minimum energy paths of transition; pp. 385–404. [Google Scholar]
- 53.Lukatskaya MR, et al. Cation intercalation and high volumetric capacitance of two-dimensional titanium carbide. Science. 2013;341:1502–1505. doi: 10.1126/science.1241488. [DOI] [PubMed] [Google Scholar]
- 54.Tian H, et al. Theoretical investigation of 2D layered materials as protective films for lithium and sodium metal anodes. Adv Energy Mater. 2017;7:1602528. [Google Scholar]
- 55.Come J, et al. Nanoscale elastic changes in 2D Ti3C2Tx (MXene) pseudocapacitive electrodes. Adv Energy Mater. 2016;6:1502290. [Google Scholar]
- 56.Ling Z, et al. Flexible and conductive MXene films and nanocomposites with high capacitance. Proc Natl Acad Sci USA. 2014;111:16676–16681. doi: 10.1073/pnas.1414215111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gogotsi Y, Simon P. Materials science. True performance metrics in electrochemical energy storage. Science. 2011;334:917–918. doi: 10.1126/science.1213003. [DOI] [PubMed] [Google Scholar]
- 58.Yang X, Cheng C, Wang Y, Qiu L, Li D. Liquid-mediated dense integration of graphene materials for compact capacitive energy storage. Science. 2013;341:534–537. doi: 10.1126/science.1239089. [DOI] [PubMed] [Google Scholar]
- 59.Courtney IA, Tse JS, Mao O, Hafner J, Dahn JR. Ab Initio calculation of the lithium-tin voltage profile. Phys Rev B. 1998;58:15583–15588. [Google Scholar]
- 60.Ceder G, Van der Ven A. Phase diagrams of lithium transition metal oxides: Investigations from first principles. Electrochim Acta. 1999;45:131–150. [Google Scholar]
- 61.Van der Ven A, Bhattacharya J, Belak AA. Understanding Li diffusion in Li-intercalation compounds. Acc Chem Res. 2013;46:1216–1225. doi: 10.1021/ar200329r. [DOI] [PubMed] [Google Scholar]
- 62.Van der Ven A, Aydinol MK, Ceder G, Kresse G, Hafner J. First-principles investigation of phase stability in LixCoO2. Phys Rev B. 1998;58:2975–2987. [Google Scholar]
- 63.Ashton M, Mathew K, Hennig RG, Sinnott SB. Predicted surface composition and thermodynamic stability of MXenes in solution. J Phys Chem C. 2016;120:3550–3556. [Google Scholar]
- 64.Hope MA, et al. NMR reveals the surface functionalisation of Ti3C2 MXene. Phys Chem Chem Phys. 2016;18:5099–5102. doi: 10.1039/c6cp00330c. [DOI] [PubMed] [Google Scholar]
- 65.Perdew JP, Wang Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B Condens Matter. 1992;45:13244–13249. doi: 10.1103/physrevb.45.13244. [DOI] [PubMed] [Google Scholar]
- 66.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 67.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 68.Blöchl PE. Projector augmented-wave method. Phys Rev B Condens Matter. 1994;50:17953–17979. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
- 69.Henkelman G, Uberuaga BP, Jónsson H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J Chem Phys. 2000;113:9901–9904. [Google Scholar]
- 70.Lian P, et al. Large reversible capacity of high quality graphene sheets as an anode material for lithium-ion batteries. Electrochim Acta. 2010;55:3909–3914. [Google Scholar]
- 71.Wang Y, et al. Design principles for solid-state lithium superionic conductors. Nat Mater. 2015;14:1026–1031. doi: 10.1038/nmat4369. [DOI] [PubMed] [Google Scholar]
- 72.Bertolazzi S, Brivio J, Kis A. Stretching and breaking of ultrathin MoS2. ACS Nano. 2011;5:9703–9709. doi: 10.1021/nn203879f. [DOI] [PubMed] [Google Scholar]
- 73.Wei Q, Peng X. Superior mechanical flexibility of phosphorene and few-layer black phosphorus. Appl Phys Lett. 2014;104:372–398. [Google Scholar]
- 74.Li T. Ideal strength and phonon instability in single-layer MoS2. Phys Rev B. 2012;85:235407. [Google Scholar]
- 75.Rydberg H, et al. Van der Waals density functional for layered structures. Phys Rev Lett. 2003;91:126402. doi: 10.1103/PhysRevLett.91.126402. [DOI] [PubMed] [Google Scholar]
- 76.Zhang RF, et al. Stability and strength of transition-metal tetraborides and triborides. Phys Rev Lett. 2012;108:255502. doi: 10.1103/PhysRevLett.108.255502. [DOI] [PubMed] [Google Scholar]
- 77.Fu ZH, et al. Stabilization and strengthening effects of functional groups in two-dimensional titanium carbide. Phys Rev B. 2016;94:104103. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.