Abstract
In previous work on point registration, the input point sets are often represented using Gaussian mixture models and the registration is then addressed through a probabilistic approach, which aims to exploit global relationships on the point sets. For non-rigid shapes, however, the local structures among neighboring points are also strong and stable and thus helpful in recovering the point correspondence. In this paper, we formulate point registration as the estimation of a mixture of densities, where local features, such as shape context, are used to assign the membership probabilities of the mixture model. This enables us to preserve both global and local structures during matching. The transformation between the two point sets is specified in a reproducing kernel Hilbert space and a sparse approximation is adopted to achieve a fast implementation. Extensive experiments on both synthesized and real data show the robustness of our approach under various types of distortions such as deformation, noise, outliers, rotation and occlusion. It greatly outperforms state-of-the-art methods, especially when the data is badly degraded.
Index Terms: Registration, shape matching, non-rigid, Gaussian mixture model, global/local
I. Introduction
Finding an optimal alignment between two sets of points is a fundamental problem in computer vision, image analysis and pattern recognition [1], [2], [3], [4]. Many tasks in these fields – such as stereo matching, image registration and shape recognition – can be formulated as a point set registration problem, which requires addressing two issues: find point-to-point correspondences and estimate the underlying spatial transformation which best aligns the two sets [5], [6], [7].
The registration problem can be roughly categorized into rigid or non-rigid registration, depending on the application and the form of the data. With a small number of transformation parameters, rigid registration is relatively easy and has been widely studied [1], [2], [8], [9], [10]. By contrast, non-rigid registration is more difficult because the true underlying non-rigid transformations are often unknown and modeling them is a challenging task [3]. But non-rigid registration is very important because it is required for many real world tasks, including shape recognition, deformable motion tracking and medical image registration.
Existing non-rigid registration methods typically consider the alignment of two point sets as a probability density estimation problem and more specifically, they use Gaussian Mixture Models (GMMs) [11], [12]. This makes the reasonable assumption that points from one set are normally distributed around points belonging to the other set. Hence, the point-to-point assignment problem can be recast into that of estimating the parameters of a mixture distribution. In general, these probabilistic methods are able to exploit global relationships in the point sets, since the rough structure of a point set is typically preserved; otherwise, even people cannot find correspondences reliably under arbitrarily large deformations. However, even for non-rigid shapes, the local structures among neighboring points are strong and stable. For example, most neighboring points on a non-rigid shape (e.g., a human face) cannot move independently under deformation due to physical constraints [13], [14]. Furthermore, preserving local neighborhood structures is also very important for people to detect and recognize shapes efficiently and reliably [15]. As a major contribution of this paper, we propose a uniform framework, which exploits both the global and the local structures in the point sets.
More precisely, we formulate point registration as the estimation of a mixture of densities: A GMM is fitted to one point set, such that the centers of the Gaussian densities are constrained to coincide with the other point set. Meanwhile, we use local features such as shape context to assign the membership probabilities of the mixture model, so that both global and local structures can be preserved during the matching process. The non-rigid transformation is modeled in a functional space, called the reproducing kernel Hilbert space (RKHS) [16], in which the transformation function has an explicit kernel representation.
The rest of the paper is organized as follows. Section II describes background material and related work. In Section III, we present the proposed non-rigid registration algorithm which is able to preserve both global and local structures among the point sets. Section IV illustrates our algorithm on some synthetic registration tasks on both 2D and 3D datasets with comparisons to other approaches, and then tests it for feature matching on real images involving non-rigid deformations. Finally, we conclude this paper in Section V.
II. Related Work
The iterated closest point (ICP) algorithm [2] is one of the best known point registration approaches. It uses nearest-neighbor relationships to assign a binary correspondence and then uses the estimated correspondences to refine the transformation. Efficient versions of ICP use sampling processes, either deterministic or based on heuristics [8]. The nearest point strategy of ICP can be replaced by soft assignments within a continuous optimization framework, e.g., the TPS-RPM [17], [3]. In the recent past, the point registration is typically solved by probabilistic methods [18], [19], [11], [12]. The Kernel Correlation Based Method [18] models each one of the two point sets as two probability distributions and measures the dissimilarity between the two distributions. It was later improved in [19], which represents the point sets using GMMs. In [11] and [12], the GMM is used to recast the point-to-point assignment problem into that of estimating the parameters of a mixture. This is done within the framework of maximum likelihood and the Expectation-Maximization (EM) algorithm [20]. In addition, point registration for articulated shapes has also been investigated using similar methods and shows promising results [21], [12], [22]. The methods mentioned above mainly focus on exploiting the global relationships in the point sets.
To preserve local neighborhood structures, Belongie et al. [23] introduced a registration method based on the shape context descriptor, which incorporates the neighborhood structure of the point set, and helps to establish better point correspondences. Using shape context as a lever, Zheng and Doermann [13] proposed a matching method, called the Robust Point Matching-preserving Local Neighborhood Structures (RPM-LNS) algorithm, which was later improved in [24]. Tu and Yuille [25] presented a shape matching method, based on a generative model and informative features. Wasserman et al. used local structure information to achieve point cloud registration for registering medical images [26], [27]. Recently, Ma et al. introduced Robust Point Matching methods based on local features and a robust L2E estimator (RPM-L2E) [28], [29] or Vector Field Consensus [30], [31], which can exploit both global and local structures. However, they find the correspondences and the transformation separately. In this paper, we propose a method which estimates these two variables jointly under the GMM formulation.
III. Method
We start by introducing a general methodology for non-rigid point set registration using Gaussian mixture models. We next present the layout of our model. We then explain the way we search for an optimal solution, followed by a description of our fast implementation. We also state the differences between our algorithm and several related state-of-the-art algorithms in detail. Finally, we provide the implementation details.
A. Point Registration and Gaussian Mixtures
We denote by X = (x1, ⋯, xN) ∈ IRD×N the coordinates of a set of model points and by Y = (y1, ⋯, yM) ∈ IRD×M the coordinates of a set of observed data points, where each point is represented as a D × 1 dimensional column vector. The model points undergo a non-rigid transformation 𝒯 : IRD → IRD, and the goal is to estimate 𝒯, which warps the model points to the observed data points, so that the two point sets become aligned. In this paper, we will formulate the point registration as the estimation of a mixture of densities, where a Gaussian mixture model (GMM) is fitted to the observed data points Y, such that the GMM centroids of the Gaussian densities are constrained to coincide with the transformed model points 𝒯(X) [11], [19], [12].
Let us introduce a set of latent variables 𝒵 = {zm ∈ INN+1 : m ∈ INM}, where each variable zm assigns an observed data point ym to a GMM centroid 𝒯 (xn), if zm = n, 1 ≤ n ≤ N, or to an additional outlier class, if zm = N + 1. The GMM probability density function then can be defined as
| (1) |
Typically, for point registration, we can use equal isotropic covariances σ2I for all GMM components and the outlier distribution is supposed to be uniform . Note that a more general assumption of anisotropic Gaussian noise in the data, which uses the full Gaussian model, has also been investigated in [12]. We denote by θ = {𝒯, σ2, γ} the set of unknown parameters, where γ ∈ [0, 1] is the percentage of outliers. Let πmn be the membership probability of the GMM, such that . The mixture model then takes the form
| (2) |
We want to recover the non-rigid transformation 𝒯. The slow-and-smooth model [32], which has been shown to account for a range of motion phenomena, suggests that the prior of 𝒯 has the form: , where ϕ(𝒯) is a smoothness functional and λ is a positive real number (we will discuss the details of ϕ(𝒯) later). Using Bayes rule, we estimate a MAP solution of θ, i.e., θ* = arg maxθ P(θ|Y) = arg maxθ P(Y|θ)P(𝒯). This is equivalent to minimizing the negative log posterior
| (3) |
where we make the i.i.d. data assumption. The transformation 𝒯 will be obtained from the optimal solution θ*.
B. Registration Using Global and Local Structures
The above method treats the point set as an instance of a GMM distribution, which aims to exploit the global structures in the point sets. For non-rigid point set registration, the local structures among neighboring points are also very strong and stable and can be used to improve the point correspondences. Next, we show how to use the local structures.
Consider the mixture model in Eq. (2), where we need to assign the membership probability πmn that the observed data point ym belongs to the GMM centroid 𝒯 (xn). It is a prior and is typically assumed to be equal for all GMM components [11], [12], i.e., , ∀m ∈ INM, n ∈ INN. In this paper, we initialize πmn by incorporating the local neighborhood structure information. More specifically, we compute a local feature descriptor for each point [23], [33], and then initialize πmn based on the matching of the feature descriptors of the two sets.
We use shape context [23] as the feature descriptor in the 2D case, using the Hungarian method for matching, with the χ2 test statistic as the cost measure. In the 3D case, the Fast Point Feature Histograms (FPFH) [34] can be used as a feature descriptor and the matching is performed by a Sample Consensus Initial Alignment method. After we obtain the correspondences between the two point sets by matching their feature descriptors, we use them to initialize πmn according to the following two rules:
- For a data point ym, we denote by ℐ the set of model points, which it corresponds to1. We let
where parameter τ, 0 ≤ τ ≤ 1, could be considered as the confidence of a feature correspondence, and | · | denotes the cardinality of a set.(4) If a data point ym does not have a corresponding model point, we use equal membership probabilities for all GMM components, i.e. , ∀n ∈ INN.
Note that in our formulation the membership probability πmn is not assigned as a prior, since it depends on the data.
C. The EM Algorithm
There are several ways to estimate the parameters of the mixture model, such as the EM algorithm, gradient descent and variational inference. The EM algorithm [20] is a technique for learning and inference in the context of latent variables. It alternates between two steps: an expectation step (E-step) and a maximization step (M-step).
We follow standard notation [35] and omit some terms that are independent of θ. Considering the negative log posterior function, i.e., Eq. (3), the complete-data log posterior (also referred to as the posterior expectation of the complete-data log likelihood) is then given by
| (5) |
where .
E-step
We use the current parameter values θold to find the posterior distribution of the latent variables. To this end, we first renew the membership probability πmn based on the feature correspondence between the data points Y and the transformed model points 𝒯(X), as described in Section III-B. We denote by P the posterior probability matrix of size M × N, where the (m, n)-th element pmn = P(zm = n|ym, θold) can be computed by applying Bayes rule:
| (6) |
Note that the local structure is used throughout the EM process. The posterior probability pmn is a soft assignment, which indicates to what degree the observed data point ym coincides with the model point xn under the current estimated transformation 𝒯.
M-step
We compute the revised parameters as2: θnew = arg maxθ 𝒬(θ, θold). Taking derivatives of 𝒬(θ) with respect to γ and σ2, and setting them to zero, we obtain
| (7) |
| (8) |
The estimate of the variance σ2 with a large initial value is conceptually similar to deterministic annealing [3], which uses the solution of an easy (e.g., smoothed) problem to recursively provide the initial conditions to increasingly harder problems, but differs in several aspects (e.g., by not requiring any annealing schedule).
Next we consider the terms of 𝒬(θ) that are related to 𝒯. We define the transformation as the initial position plus a displacement function v: 𝒯(X) = X + v(X), and then obtain a regularized risk functional as:
| (9) |
This is a particular form of Tikhonov regularization [36], and the first term can be seen as a weighted empirical error. Thus the maximization of 𝒬 with respect to 𝒯 is equivalent to minimizing the regularized risk functional (9). To proceed, we model v by requiring it to lie within a vector-valued reproducing kernel Hilbert space (RKHS) ℋ defined by a diagonal Gaussian matrix kernel Γ : IRD × IRD → IRD×D [37], where . A brief introduction of the vector-valued RKHS is given in Appendix A. By using the square norm for the smoothness functional ϕ(v), i.e., , we then have the following representer theorem [38], and the proof is given in Appendix B.
Theorem 1
The optimal solution of the regularized risk functional (9) has the form
| (10) |
with the coefficient set {cn : n ∈ INN} determined by the following linear system:
| (11) |
where C = (c1, ⋯, cN) ∈ IRD×N is the coefficient set, Γ ∈ IRN×N is the so-called Gram matrix with the (i, j)-th element , 1 is a column vector of all ones, and d(·) is the diagonal matrix.
Algorithm 1.
The PR-GLS algorithm
| Input: Two point sets X and Y, parameters γ, β, λ | ||
| Output: Optimal transformation 𝒯 | ||
| 1 | Construct the Gram matrix Γ; | |
| 2 | Initialization: C = 0, ; | |
| 3 | Compute feature descriptors for point set Y; | |
| 4 | repeat | |
| 5 |
|
E-step: |
| 6 | Compute feature descriptors for point set 𝒯 (X); | |
| 7 | Establish correspondence between 𝒯 (X) and Y; | |
| 8 | Initialize πmn based on the feature correspondence; | |
| 9 | Update posterior probability P by Eq. (6); | |
| 10 | M-step: | |
| 11 | Update C by solving the linear system (11); | |
| 12 | Update 𝒯 (X) = X + CΓ; | |
| 13 | Update γ and σ2 by Eqs. (7) and (8); | |
| 14 | until 𝒬 converges; | |
| 15 | The transformation 𝒯 is determined as 𝒯 (X) = X + CΓ. | |
Note that the M-step is different from the standard EM algorithm, where the free parameters are the means and the covariances of the Gaussian mixture, and the estimation of these parameters is quite straightforward. Our problem requires multiple conditional maximization steps and thus the algorithm is referred as the Expectation Conditional Maximization (ECM), which was first introduced into the point registration problem by Horaud et al. [12]. Since our non-rigid Point set Registration algorithm exploits both Global and Local Structures, we call it PR-GLS and summarize it in Algorithm 1.
D. Fast Implementation
Solving for the transformation 𝒯 requires solving the linear system (11). But for large values of N, this may pose a serious problem because this has O(N3) computational complexity. Even if this is tractable, we may prefer a suboptimal, but faster method. In this section, we provide a fast implementation based on an idea related to the Subset of Regressors method [39], [37].
Instead of searching for the optimal solution (10), we use a sparse approximation and randomly pick a subset containing K (K ≪ N) model points {x̃k : k ∈ INK}. Only points in this subset are allowed to have nonzero coefficients in the expansion of the solution, as in [39], [37]. Our experiments showed that simply selecting an arbitrary subset of the training inputs at random does not perform any worse than more sophisticated methods. Therefore, we seek a solution of the form:
| (12) |
with the coefficients C̃ = (c1, ⋯, cK) ∈ IRD×K determined by a linear system
| (13) |
where Γ̃ is the Gram matrix Γ̃ ∈ IRK×K, where , and U ∈ IRN×K with the (i, j)-th element . By using this sparse approximation, the time and space complexities for solving the linear system (11) are reduced from O(N3) and O(N2) to O(K2N) and O(KN), respectively.
E. Related Non-Rigid Registration Methods
The most relevant non-rigid point sets registration algorithm to ours is coherent point drift (CPD) [11], as both algorithms use the GMM formulation and Gaussian radial basis functions to parameterize the transformations. However, our PR-GLS has three major advantages compared to CPD. Firstly, CPD ignores the local structure information in the point sets; it simply uses equal membership probabilities in the mixture model, while our PR-GLS tries to preserve local structures by encouraging the matching of points with similar neighborhood structures, e.g., shape features. Secondly, the outlier percentage γ is fixed and set manually in CPD. This may be problematic in many real-world problems, where the amount of outliers is not known in advance. By contrast, our PR-GLS treats γ as an unknown parameter and estimates it for each EM iteration. Thirdly, CPD can not handle large rotations, e.g., rotations with angles larger than 60°. We solve this problem by choosing rotation invariant features in our formulation.
The two other most relevant non-rigid point sets registration algorithms to ours are RPM-LNS [13] and RPM-L2E [28]. More specifically, they also use local structure information. RPM-LNS formulates point matching as a graph matching problem. RPM-L2E establishes point correspondences by first constructing a large putative set of correspondence and then uses a robust L2E estimator to get rid of the outliers. Both of the two algorithms use shape context to initialize the correspondences. One major drawback of RPM-LNS and RPM-L2E is that they find the correspondence and the transformation separately, while our method estimates these two variables jointly using the GMM formulation. Moreover, RPM-LNS is not applicable to the 3D case.
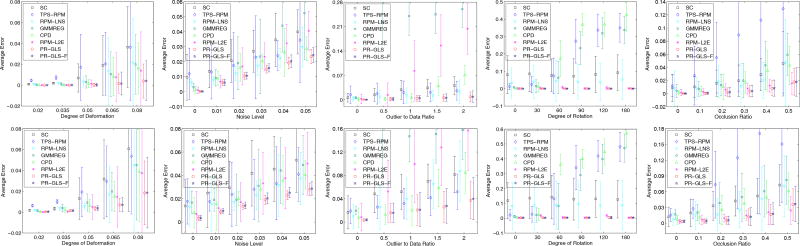
In summary, our main contribution is that we propose an efficient framework for preserving both global and local structures during matching. Compared to other related methods, the efficient use of global and local information in our PR-GLS can lead to big improvements under various degenerations (see Fig. 3).
Fig. 3.
Comparison of PR-GLS and its fast version (PR-GLS-F) with SC [23], TPS-RPM [3], RPM-LNS [13], GMMREG [19], CPD [11] and RPM-L2E [28] on the fish (top) and Chinese character (bottom) [3], [13]. The error bars indicate the registration error means and standard deviations over 100 trials. Note that the variance bar can reach the negative y-axis, where large variance indicates that a method sometimes works well and sometimes totally fails.
F. Implementation Details
The performance of point matching algorithms typically depends on the coordinate system in which the points are expressed. We use data normalization to control this. More specifically, we perform a linear scaling of the coordinates, so that the points in both of the two sets both have zero mean and unit variance.
To assign the membership probability πmn, we need to establish initial correspondences which is usually time consuming. Fortunately, the deformation of the model shape is gradually reduced during the EM iterations and as such, the correspondences between the two shapes will not change too fast. Therefore, to speed-up our algorithm, we update πmn in every 10 iterations rather than in each iteration.
Parameter settings
There are three main parameters in our PR-GLS algorithm: γ, β and λ. Parameter γ reflects our assumption on the amount of outliers in the point sets. Parameters β and λ reflect the amount of the smoothness constraint, where β determines the width of the range of the interaction between samples and λ controls the trade-off between the closeness to the data and the smoothness of the solution. In general, we found that our method was robust to parameter changes. Parameter τ is used to initialize the membership probabilities, which we will discuss in the experiments. Moreover, the uniform distribution parameter a is set to be the volume of the bounding box of the data.
Analysis of convergence
The objective function (3) is not convex, so it is unlikely that any algorithm can find its global minimum. However, a stable local minimum is often enough for many practical applications. To this end, our strategy is to initialize the variance σ2 with a large initial value and then use the EM algorithm. If the value of σ2 is large enough, the objective function becomes convex in a large region which can filter out a lot of unstable shallow local minima. Hence we are likely to find a good minimum for large variance. As σ2 decreases, the objective function tends to change smoothly, which makes it likely that using the old minimum as the initial value could be helpful to converge to a new good minimum. Therefore, as the iterations continue, we have a good chance of reaching a stable local minimum. This is conceptually similar to deterministic annealing [3], which uses the solution of an easy problem to recursively give initial conditions to increasingly harder problems.
IV. Experimental Results
In order to evaluate the performance of our algorithm, we conducted three types of experiments: i) non-rigid point set registration for 2D shapes; ii) non-rigid point set registration for 3D shapes; iii) sparse feature correspondence on real images. The experiments were performed on a laptop with 2.5 GHz Intel® Core™2 Duo CPU, 8 GB memory and Matlab Code.
A. Results on 2D Non-Rigid Shape Matching
We tested our PR-GLS algorithm on the same synthesized data as in [3] and [13]. The data consists of two models with different shapes, where the first model consists of 96 points representing a fish and the second model consists of 108 points, representing a Chinese character. For each model, there are five sets of data designed to measure the robustness of registration algorithms with respect to different degrees of deformation, noise, outliers, rotation and occlusion. In the deformation test, the deformation is generated by using Gaussian radial basis functions with coefficients sampled from a Gaussian distribution with zero mean and a standard deviation ranging from 0.02 to 0.08. In the noise test, Gaussian noise is added with standard deviation ranging from 0 to 0.05. In the outlier test, random outliers are added with the outlier to original data ratio ranging from 0 to 2. In the rotation test, six rotation angles are used: 0, 30, 60, 90, 120, and 180. In the occlusion test, some parts of the data are removed with the removed data to original data ratio ranging from 0 to 0.5. In each test, one of the above distortions is applied to the model set to create an observed data set, and 100 samples are generated for each degradation level. We use shape contexts as the feature descriptor to establish the initial correspondences. It is easy to make the shape context feature descriptors translation and scale invariant and in some applications, rotation invariance is also required. We use the rotation invariant shape context as in [13].
Generally, the parameter τ in Eq. (4) reflects the accuracy of the initial correspondences, which to some extent depends on the degree of the distortion. In these experiments we determine τ adaptively, based on the data. To this end, we first define a registration error ε*, which is independent of the ground truth:
| (14) |
where 𝒮 consists of the min(N, M) matches with the largest posterior matching probabilities, i.e., pmn. For each set of data, we randomly choose 5 of the 100 samples and compute their average registration error with τ = 0.1, 0.3, 0.5, 0.7 and 0.9. Afterwards, we set τ to be the value which achieves the smallest registration error ε*. Typically, τ ≈ 0.9 works well for small distortions and 0.3 for large distortions. For the parameters γ, β and λ, we set them to 0.1, 2 and 3, respectively, throughout the experiments.
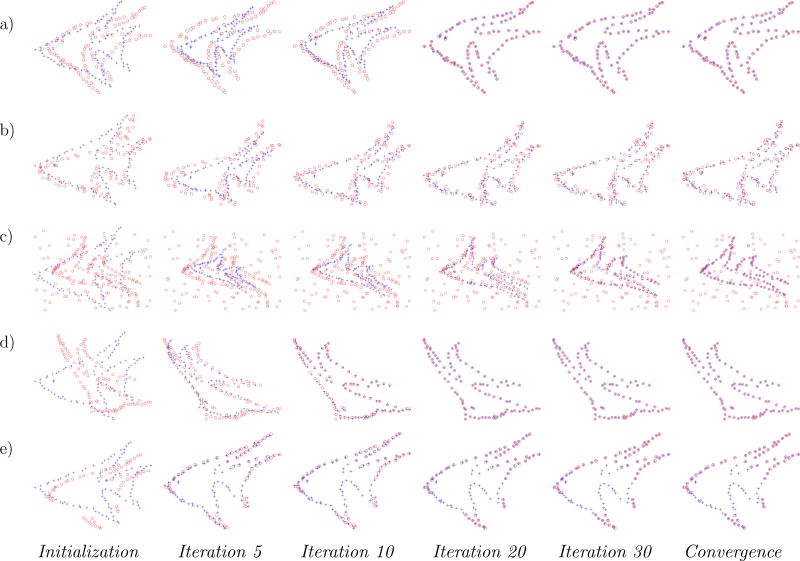
The registration progress on the fish shape is illustrated schematically in Fig. 1. The columns show the iterative progress, and each row provides a different type of distortion. The goal is to align the model point set (blue pluses) onto the observed data point set (red circles). From the results, we see that our RPM-GLS registration is robust and accurate, and it typically converges in about 30 iterations. More qualitative results of our method on the two shape models are presented in Fig. 2. We organize the results in every two rows: the upper row presents the data, while the lower row shows the registration result. For the fish model, the shape is relatively simple and discriminative and as such, both the global and the local structures are preserved well, even under large degradations. Our method in this case produces almost perfect alignments, as shown in the left of Fig. 2. For the Chinese character model, the points are spread out on the shape and the local structure is not preserved as well under large degradations. The matching performance then degrades gradually, but it remains acceptable, even for large degradations. Let us consider the rotation test in (a4, b3) of Fig. 2. It is interesting that our method can handle the fold-back contained in the data shape, which is a desirable property in real-world applications. Moreover, in some extreme cases, such as the deformation test in (a1, b3), as well as the outlier test in (a3, b1), it is hard to establish visual correspondences even by human beings, however, our method can still achieve accurate alignments. The average runtime of our method on 2D shape matching with about 100 points is about 0.4 seconds.
Fig. 1.
Schematic illustration of our method for non-rigid point set registration. The goal is to align the model point set (blue pluses) onto the observed data point set (red circles). The columns show the iterative alignment progress. From top to bottom: results on data degraded by deformation, noise, outliers, rotation and occlusion, respectively. Our RPM-GLS registration is robust and accurate in all experiments.
Fig. 2.
Point set registration results of our method on the fish (left) and Chinese character (right) shapes [3], [13], with deformation, noise, outliers, rotation and occlusion presented in every two rows. The goal is to align the model point set (blue pluses) onto the observed data point set (red circles). For each group, the upper figure is the model and data point sets, and the lower figure is the registration result. From left to right, increasing degree of degradation.
To provide a quantitative comparison, we report the results of six state-of-the-art algorithms, such as shape context (SC) [23], TPS-RPM [3], RPM-LNS [13], GMMREG [19], CPD [11], and RPM-L2E [28] which were implemented using publicly available codes. The registration error of a pair of shapes is quantified as the average Euclidean distance between a point in the warped model shape and the ground truth corresponding point in the observed data shape (note that it is different from ε* defined in Eq. (14)). Then the registration performance of each algorithm is compared by the mean and standard deviation of the registration error of all the 100 samples for each distortion level. The statistical results, error means, and standard deviations for each setting are summarized in Fig. 3.
In the deformation test results, seven algorithms achieve similar performance in both the fish and the Chinese character datasets at low deformation levels. But our PR-GLS outperforms them, especially for large degrees of deformation. In the noise test results, we observe that all algorithms are affected by this type of distortion. Still, our PR-GLS achieves the best registration performance. In the outlier test results, GMMREG is not robust to outliers. RPM-L2E is easily confused and starts to fail once the outlier level becomes relatively high. This is due to that it solves the correspondence and the transformation problems separately. When the outlier level becomes too high, it cannot establish good correspondences in the first step and hence, the final solution will be badly degraded. In contrast, our PR-GLS shows much more robustness, regardless of the outlier level. Note that the original CPD is not robust to changes in the outlier ratios, as it involves a fixed outlier ratio parameter, i.e., parameter γ in Eq. (2). To make a fair comparison, we set it adaptively similar to the setting of parameter τ in our PR-GLS. In the rotation test, TPS-RPM, GMMREG and CPD degenerate rapidly when the rotation angle is larger than 60°, while RPM-L2E and our PR-GLS are not affected, because they are using the rotation invariant shape context. In the occlusion test, the registration error of TPS-RPM is the largest, and our PR-GLS again has the best results in most cases once again. We have also tested the fast version of PR-GLS on this dataset and achieved similar performance, as shown in the last column of each test in Fig. 3.
In our PR-GLS, we assign the membership probability πmn based on shape context feature, so that the local structure information can be used to achieve better performance. To demonstrate the benefits for doing this, we perform experiments on the fish and Chinese character datasets with different degrees of deformations. The results are given in Tables I and II, where CPD assumes equal GMM components (πmn = 1/N), PR-GLS assigns πmn based on local shape features, and GT assigns πmn by using the ground truth correspondences. Clearly, a good initialization of πmn can improve registration performance, especially when the data is badly degraded.
TABLE I.
Average registration error on the fish datasets with different degrees of deformations (DoD) over 100 trials. The last row (GT) uses the ground truth correspondences to initialize πij.
| DoD | 0.02 | 0.035 | 0.05 | 0.065 | 0.08 |
|---|---|---|---|---|---|
| CPD | 2.6×10−5 | 1.3×10−4 | 1.5×10−3 | 8.1×10−3 | 1.6×10−2 |
| PR-GLS | 2.5×10−5 | 7.3×10−5 | 3.6×10−4 | 1.5×10−3 | 4.0×10−3 |
| GT | 2.5×10−5 | 7.3×10−5 | 2.1×10−4 | 5.1×10−4 | 1.0×10−3 |
TABLE II.
Average registration error on the Chinese character datasets with different degrees of deformations (DoD) over 100 trials. The last row (GT) uses the ground truth to initialize πij.
| DoD | 0.02 | 0.035 | 0.05 | 0.065 | 0.08 |
|---|---|---|---|---|---|
| RPM-L2E | 4.3×10−4 | 1.9×10−3 | 5.9×10−3 | 1.5×10−2 | 3.8×10−2 |
| PR-GLS | 4.3×10−4 | 1.4×10−3 | 3.6×10−3 | 7.0×10−3 | 1.8×10−2 |
| GT | 4.3×10−4 | 1.4×10−3 | 3.5×10−3 | 5.9×10−3 | 9.1×10−3 |
In conclusion, our PR-GLS is effective for various non-rigid point set registration problems, regardless of large deformation, noise, outliers, rotation or occlusion.
B. Results on 3D Non-Rigid Shape Matching
We next test our PR-GLS algorithm for 3D shape matching. We adopt the FPFH [34] to determine the initial correspondence. For the dataset, we use two pairs of point sets, representing a wolf in different poses from a surface correspondence benchmark3 [40], as shown in the left two columns of Fig. 4. The ground truth correspondences are supplied by the dataset. Some other challenging benchmark datasets with known ground truth correspondences have also been developed [41], [42]. To assign the membership probability πmn, parameter τ can be determined adaptively according to Eq. (14); here, we fix it to 0.9 for efficiency. Moreover, 3D datasets typically contain thousands of points (e.g., about 5, 000 in the wolf shape), which may pose a serious problem due to heavy computational or memory requirements; here, we use the fast version of our method with K = 50 in Eq. (12).
Fig. 4.
Point set registration results of our method on the 3D wolf shape [40], with deformation, occlusion and outliers presented in every two columns. The goal is to align the model point set (blue dots) onto the observed data point set (red circles). For each group of experiments, the upper figure is the model and data point sets, and the lower figure is the registration result.
Fig. 4 presents the registration results of PR-GLS. In the left two columns, the data contains large rotations and slight pose changes, and our method gives almost perfect alignments. In the middle two and right two columns, we also test our method on occlusion and outliers. In each group, the first set contains a degradation on only one set of points, while the second set contains degradations on both the two point sets. The last column demonstrates a challenging example, where we biased the outliers to the different sides of point sets, and the outliers were generated randomly from a normal distribution rather than a uniform distribution. The results demonstrate that our method is quite robust and is not affected by all these degradations. The average runtime of our method with the fast implementation on 3D shape matching with about 5, 000 points is about 1 minute. Note that in this experiment the FPFH is quite efficient and requires only 1.5 seconds approximately to establish the initial correspondences.
A quantitative comparison of our method with CPD and RPM-L2E is reported in Table III. In addition, we also compare with a recent method using local structure information based on Tensor Fields (TF) [27]. In the case of CPD, we rotate the data, so that the two point sets have roughly similar orientations, since CPD is not robust to large rotations. As shown in Table III, our PR-GLS consistently outperforms the other three algorithms in every case. In conclusion, PR-GLS is effective for non-rigid registration, in both the 2D and the 3D cases.
TABLE III.
Comparison of the registration errors of PR-GLS with respect to CPD [11], RPM-L2E [28] and TF [27] on the 3D wolf shape in Fig. 4. From left to right: deformation (Def1, Def2), occlusion (Occ1, Occ2), and outlier (Out1, Out2).
| Def1 | Def2 | Occ1 | Occ2 | Out1 | Out2 | |
|---|---|---|---|---|---|---|
| CPD | 0.80 | 0.82 | 1.05 | 0.72 | 3.58 | 3.37 |
| RPM-L2E | 1.03 | 1.18 | 1.13 | 0.96 | 1.22 | 1.35 |
| TF | 1.12 | 1.36 | 2.53 | 3.13 | 3.87 | 5.85 |
| PR-GLS | 0.50 | 0.71 | 0.58 | 0.45 | 0.74 | 0.92 |
C. Results on Image Feature Correspondence
In this section, we test our PR-GLS on real image data, focusing on establishing visual correspondences between two images. Here the images contain some deformable objects and consequently, the underlying relationships between the images are non-rigid. We use SIFT [33] for feature detection and description. The goal is to find correspondences/matches between two sets of sparse feature points {xn : n ∈ INN} and {ym : m ∈ INM}, with corresponding feature descriptors. To assign the membership probability πmn, we determine the initial correspondences by searching the nearest neighbors and fix parameter τ to 0.9. Note that since the feature descriptor here is computed based on an image patch rather than the neighboring points, the value of πmn does not need to be recalculated in every iteration.
Fig. 5 contains a T-shirt with different amount of spatial warps, where we aim to establish SIFT matches in each image pair. We consider (xn, ym) to be a correspondence/match if its posterior probability pmn is larger than 0.5. Performance is characterized by the number of correct matches and the matching score (i.e., the ratio between the number of correct matches and the number of total matches). Since the image relations are non-rigid and not known in advance, it is impossible to establish accurate ground truth. We evaluate the matching results by manually checking. Though the judgment of correct match or false match seems arbitrary, we make the benchmark to ensure objectivity.
Fig. 5.
Results of image feature correspondence on image pairs of deformable objects. From left to right, increasing degree of deformation. The lines indicate matching results (blue = correct matches, red = false matches).
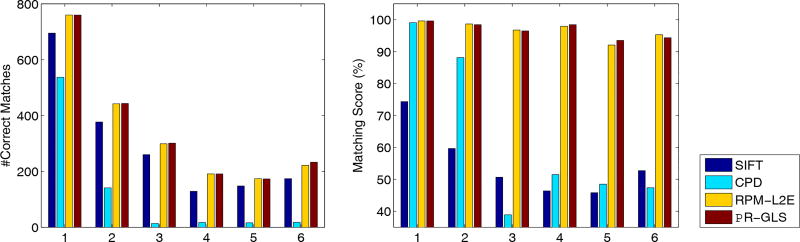
In feature correspondence, the image typically contains hundreds or thousands of feature points, thus, for efficiency, we use the fast version of our method with K = 15 in Eq. (12). The results of our method are presented in Fig. 5. In the left columns, where the deformations are relatively small, our method obtains a lot of correspondences, whereas in the right columns, the deformations are large and the number of correct matches decreases. Still, even in these cases, the matching scores remain quite high, e.g., around 95% or higher. For comparison, we also report three other matching methods as shown in Fig. 6. The SIFT method can be considered as a baseline. To eliminate as many outliers as possible, while preserving the inliers, SIFT compares the distance ratio between the nearest and the second nearest neighbors against a predefined threshold to decide whether they are considered a match or not. From these results, we see that the matching score of SIFT is not good, especially in the case of large deformations. This suggests that using local image features alone is insufficient. CPD is not efficient for such problems, since it ignores the local image features’ information. However, RPM-L2E and PR-GLS consider both global structures and local features and hence, they are able to find more correct matches and achieve high matching scores. The average runtime of our method with the fast implementation on the six image pairs is about 0.5 seconds per pair.
Fig. 6.
Comparison of SIFT [33], CPD [11], RPM-L2E [28] and PR-GLS for feature correspondence. Left: number of correct matches; right: matching score. The horizontal axis corresponds to the six image pair in Fig. 5 (from left to right, top to bottom).
V. Conclusion
In this paper, we presented a new approach for non-rigid registration. A key characteristic of our approach is the preservation of both global and local structures during matching. We also provide an efficient implementation of our method for handling large datasets, which significantly reduces the computational complexity without reducing the quality of the matching significantly. Experiments on public datasets for 2D and 3D non-rigid point registration and on real images for sparse image feature correspondence demonstrate that our approach yields superior results to those of the state-of-the-art methods, when there are significant deformations, noise, outliers, rotations and/or occlusions in the data.
Acknowledgments
This work was supported in part by the China Postdoctoral Science Foundation under Grant 2015M570665, and in part by the NIH under Grant 5R01EY022247-03.
Biographies

Alan L. Yuille received his B.A. in mathematics from the University of Cambridge in 1976, and completed his Ph.D. in theoretical physics at Cambridge in 1980 studying under Stephen Hawking. Following this, he held a postdoc position with the Physics Department, University of Texas at Austin, and the Institute for Theoretical Physics, Santa Barbara. He then joined the Artificial Intelligence Laboratory at MIT (1982–1986), and followed this with a faculty position in the Division of Applied Sciences at Harvard (1986–1995), rising to the position of associate professor. From 1995–2002 Alan worked as a senior scientist at the Smith-Kettlewell Eye Research Institute in San Francisco. In 2002 he accepted a position as full professor in the Department of Statistics at the University of California, Los Angeles. He has over two hundred peer-reviewed publications in vision, neural networks, and physics, and has co-authored two books: Data Fusion for Sensory Information Processing Systems (with J. J. Clark) and Two- and Three- Dimensional Patterns of the Face (with P. W. Hallinan, G. G. Gordon, P. J. Giblin and D. B. Mumford); he also co-edited the book Active Vision (with A. Blake). He has won several academic prizes and is a Fellow of IEEE.

Jiayi Ma received the B.S. degree from the Department of Mathematics, and the Ph.D. Degree from the School of Automation, Huazhong University of Science and Technology, Wuhan, China, in 2008 and 2014, respectively. From 2012 to 2013, he was with the Department of Statistics, University of California at Los Angeles. He is now a postdoctoral research associate with the Electronic Information School, Wuhan University. His current research interests include in the areas of computer vision, machine learning, and pattern recognition.

Ji Zhao received the B.S. degree in automation from Nanjing University of Posts and Telecommunication in 2005. He received the Ph.D. degree in control science and engineering from HUST in 2012. Since 2012, he is a postdoctoral research associate at the Robotics Institute, Carnegie Mellon University. His research interests include image classification, image segmentation and kernel-based learning.
Appendix A
Vector-Valued Reproducing Kernel Hilbert Space
We review the basic theory of vector-valued reproducing kernel Hilbert space, and for further details and references we refer to [38], [43].
Let 𝒳 be a set, for example, 𝒳 ⊆ IRP, 𝒴 a real Hilbert space with inner product (norm) 〈·, ·〉, (‖ · ‖), for example, 𝒴 ⊆ IRD, and ℋ a Hilbert space with inner product (norm) 〈·, ·〉ℋ, (‖ · ‖ℋ), where P = D = 2 or 3 for point matching problem. Note that a norm can be induced by an inner product, for example, . And a Hilbert space is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product. Thus a vector-valued RKHS can be defined as follows.
Definition 1
A Hilbert space ℋ is an RKHS if the evaluation maps eυx : ℋ → 𝒴 (i.e., eυx(f) = f (x)) are bounded, i.e., if ∀x ∈ 𝒳 there exists a positive constant Cx such that
| (15) |
A reproducing kernel Γ: 𝒳 × 𝒳 → ℬ(𝒴) is then defined as: , where ℬ(𝒴) is the Banach space of bounded linear operators (i.e., Γ(x, x′), ∀x, x′ ∈ 𝒳) on 𝒴, for example, ℬ(𝒴) ⊆ IRD×D, and is the adjoint of eυx. We have the following two properties about the RKHS and kernel.
Remark 1
The kernel Γ reproduces the value of a function f ∈ ℋ at a point x ∈ 𝒳. Indeed, ∀x ∈ 𝒳 and y ∈ 𝒴, we have , so that 〈f(x), y〉 = 〈f, Γ(·, x)y〉ℋ.
Remark 2
An RKHS defines a corresponding reproducing kernel. Conversely, a reproducing kernel defines a unique RKHS.
More specifically, for any , and a reproducing kernel Γ, a unique RKHS can be defined by considering the completion of the space
| (16) |
with respect to the norm induced by the inner product
| (17) |
where and .
Appendix B
Proof of Theorem 1
For any given reproducing kernel Γ, we can define a unique RKHS ℋN as in Eq. (16) in Appendix A. Let be a subspace of ℋ,
| (18) |
From the reproducing property, i.e. Remark 1,
| (19) |
Thus is the orthogonal complement of ℋN; then every v ∈ ℋ can be uniquely decomposed into components along and perpendicular to , where vN ∈ ℋN and . Since by orthogonality and by the reproducing property v(xn) = vN(xn), the regularized risk functional then satisfies
| (20) |
Therefore, the optimal solution of the regularized risk functional (9) comes from the space ℋN, and hence has the form (10). To solve the coefficients, we consider the definition of the smoothness functional ϕ(v) and the inner product (17)
| (21) |
where C = (c1, ⋯, cN) ∈ IRD×N is the coefficient set. The regularized risk functional then can be conveniently expressed in the following matrix form:
| (22) |
where Γ ∈ IRN×N is the so-called Gram matrix with the (i, j)-th element , Pm is the m-th row of P, ‖·‖F denotes the Frobenius norm, and d(·) is the diagonal matrix. Taking the derivative of the last equation with respect to C and setting it to zero, we obtain the linear system in Eq. (11). Thus the coefficient set {cn : n ∈ INN} of the optimal solution v is determined by the linear system (11).
Footnotes
Typically, ℐ contains only one point, but multiple correspondences could exist in some cases, for instance, if the matching strategy is not bipartite matching.
Contributor Information
Jiayi Ma, Electronic Information School, Wuhan University, Wuhan, 430072, China.
Ji Zhao, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, 15213, USA.
Alan L. Yuille, Department of Statistics, UCLA, Los Angeles, CA, 90095, USA.
References
- 1.Brown LG. A survey of image registration techniques. ACM Comput. Surv. 1992;24(4):325–376. [Google Scholar]
- 2.Besl PJ, McKay ND. A method for registration of 3-d shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992;14(2):239–256. [Google Scholar]
- 3.Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Comput. Vis. Image Understand. 2003;(89):114–141. [Google Scholar]
- 4.Ma J, Zhou H, Zhao J, Gao Y, Jiang J, Tian J. Robust feature matching for remote sensing image registration via locally linear transforming. IEEE Trans. Geosci. Remote Sens. 2015 doi: 10.1109/TGRS.2015.2441954. [DOI] [Google Scholar]
- 5.Bai X, Yang X, Latecki LJ, Liu W, Tu Z. Learning context-sensitive shape similarity by graph transduction. IEEE Trans. Pattern Anal. Mach. Intell. 2010;32(5):861–874. doi: 10.1109/TPAMI.2009.85. [DOI] [PubMed] [Google Scholar]
- 6.Wang J, Bai X, You X, Liu W, Latecki LJ. Shape matching and classification using height functions. Pattern Recognit. Lett. 2012;33(2):134–143. [Google Scholar]
- 7.Ma J, Zhao J, Ma Y, Tian J. Non-rigid visible and infrared face registration via regularized gaussian fields criterion. Pattern Recognit. 2015;48(3):772–784. [Google Scholar]
- 8.Rusinkiewicz S, Levoy M. Efficient variants of the ICP algorithm. Proc. 3-D Digit. Imag. Model. 2001 May;:145–152. [Google Scholar]
- 9.Fitzgibbon AW. Robust registration of 2d and 3d point sets. Image Vis. Comput. 2003;21(13):1145–1153. [Google Scholar]
- 10.Makadia A, Patterson A, Daniilidis K. Fully automatic registration of 3d point clouds; Proc. IEEE Conf. Comput. Vis. Pattern Recognit; Jun. 2006. pp. 1297–1304. [Google Scholar]
- 11.Myronenko A, Song X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010;32(12):2262–2275. doi: 10.1109/TPAMI.2010.46. [DOI] [PubMed] [Google Scholar]
- 12.Horaud R, Forbes F, Yguel M, Dewaele G, Zhang J. Rigid and articulated point registration with expectation conditional maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33(3):587–602. doi: 10.1109/TPAMI.2010.94. [DOI] [PubMed] [Google Scholar]
- 13.Zheng Y, Doermann D. Robust point matching for nonrigid shapes by preserving local neighborhood structures. IEEE Trans. Pattern Anal. Mach. Intell. 2006;28(4):643–649. doi: 10.1109/TPAMI.2006.81. [DOI] [PubMed] [Google Scholar]
- 14.Bai X, Latecki LJ, Liu W-Y. Skeleton pruning by contour partitioning with discrete curve evolution. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 2007;29(3):449–462. doi: 10.1109/TPAMI.2007.59. [DOI] [PubMed] [Google Scholar]
- 15.Field DJ, Hayes A, Hess RF. Contour integration by the human visual system: Evidence for a local “association field”. Vis. Res. 1993;33(2):173–193. doi: 10.1016/0042-6989(93)90156-q. [DOI] [PubMed] [Google Scholar]
- 16.Aronszajn N. Theory of reproducing kernels. Trans. Amer. Math. Soc. 1950;68(3):337–404. [Google Scholar]
- 17.Rangarajan A, Chui H, Bookstein F. Information Processing in Medical Imaging. New York, NY, USA: Springer; 1997. The softassign procrustes matching algorithm; pp. 29–42. [Google Scholar]
- 18.Tsin Y, Kanade T. A correlation-based approach to robust point set registration; Proc. Eur. Conf. Comput. Vis; May, 2004. pp. 558–569. [Google Scholar]
- 19.Jian B, Vemuri BC. Robust point set registration using gaussian mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33(8):1633–1645. doi: 10.1109/TPAMI.2010.223. [DOI] [PubMed] [Google Scholar]
- 20.Dempster A, Laird N, Rubin DB. Maximum likelihood from incomplete data via the em algorithm. J. R. Statist. Soc. Series B. 1977;39(1):1–38. [Google Scholar]
- 21.Mateus D, Horaud R, Knossow D, Cuzzolin F, Boyer E. Articulated shape matching using laplacian eigenfunctions and unsupervised point registration; Proc. IEEE Conf. Comput. Vis. Pattern Recognit; Jun. 2008. pp. 1–8. [Google Scholar]
- 22.Sharma A, Horaud R, Mateus D. 3D shape registration using spectral graph embedding and probabilistic matching. Image Processing and Analysing with Graphs: Theory and Practice. 2012:441–474. [Google Scholar]
- 23.Belongie S, Malik J, Puzicha J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002;24(24):509–522. [Google Scholar]
- 24.Lee J-H, Won C-H. Topology preserving relaxation labeling for nonrigid point matching. IEEE Trans. Pattern Anal. Mach. Intell. 2011;33(2):427–432. doi: 10.1109/TPAMI.2010.179. [DOI] [PubMed] [Google Scholar]
- 25.Tu Z, Yuille AL. Shape matching and recognition–using generative models and informative features; Proc. Eur. Conf. Comput. Vis; May, 2004. pp. 195–209. [Google Scholar]
- 26.Wassermann D, Ross J, Washko G, Westin C-F, San Jose Estepar R. Diffeomorphic point set registration using non-stationary mixture models; Proc. IEEE Int. Symp. Biomed. Imaging; Apr. 2013. pp. 1042–1045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wassermann D, Ross J, Washko G, Wells WM, Jose-Estepar RS. Deformable registration of feature-endowed point sets based on tensor fields; Proc. IEEE Conf. Comput. Vis. Pattern Recognit; Jun. 2014. pp. 2729–2735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ma J, Zhao J, Tian J, Tu Z, Yuille A. Robust estimation of nonrigid transformation for point set registration; Proc. IEEE Conf. Comput. Vis. Pattern Recognit; Jun. 2013. pp. 2147–2154. [Google Scholar]
- 29.Ma J, Qiu W, Zhao J, Ma Y, Yuille AL, Tu Z. Robust L2E estimation of transformation for non-rigid registration. IEEE Trans. Signal Process. 2015;63(5):1115–1129. [Google Scholar]
- 30.Zhao J, Ma J, Tian J, Ma J, Zhang D. A robust method for vector field learning with application to mismatch removing; Proc. IEEE Conf. Comput. Vis. Pattern Recognit; Jun. 2011. pp. 2977–2984. [Google Scholar]
- 31.Ma J, Zhao J, Tian J, Yuille AL, Tu Z. Robust point matching via vector field consensus. IEEE Trans. Image Process. 2014;23(4):1706–1721. doi: 10.1109/TIP.2014.2307478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yuille AL, Grzywacz NM. A computational theory for the perception of coherent visual motion. Nature. 1988;333(6168):71–74. doi: 10.1038/333071a0. [DOI] [PubMed] [Google Scholar]
- 33.Lowe D. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004;60(2):91–110. [Google Scholar]
- 34.Rusu RB, Blodow N, Beetz M. Fast point feature histograms (FPFH) for 3d registration; Proc. IEEE Int. Conf. Robot. Autom; May, 2009. pp. 3212–3217. [Google Scholar]
- 35.Bishop CM. Pattern Recognition and Machine Learning. New York, NY, USA: Springer-Verlag; 2006. [Google Scholar]
- 36.Tikhonov AN, Arsenin VY. Solutions of Ill-posed Problems. Washington, DC, USA: Winston; 1977. [Google Scholar]
- 37.Ma J, Zhao J, Tian J, Bai X, Tu Z. Regularized vector field learning with sparse approximation for mismatch removal. Pattern Recognit. 2013;46(12):3519–3532. [Google Scholar]
- 38.Micchelli CA, Pontil M. On learning vector-valued functions. Neural Comput. 2005;17(1):177–204. doi: 10.1162/0899766052530802. [DOI] [PubMed] [Google Scholar]
- 39.Rifkin R, Yeo G, Poggio T. Advances in Learning Theory: Methods, Model and Applications. Cambridge, MA, USA: MIT Press; 2003. Regularized least-squares classification. [Google Scholar]
- 40.Kim VG, Lipman Y, Funkhouser T. Blended intrinsic maps. ACM Trans. Graph. 2011;30(4):79. [Google Scholar]
- 41.Bronstein A, et al. SHREC 2010: Robust large-scale shape retrieval benchmark. Proc. Eurographics Workshop 3D Object Retrieval. 2010 May;:71–78. [Google Scholar]
- 42.Lian Z, et al. SHREC’11 track: Shape retrieval on non-rigid 3d watertight meshes. Proc. Eurographics Workshop 3D Object Retrieval. 2011 May;:79–88. [Google Scholar]
- 43.Carmeli C, De Vito E, Toigo A. Vector valued reproducing kernel hilbert spaces of integrable functions and mercer theorem. Anal. Appl. 2006;(4):377–408. [Google Scholar]