Polyamine block of AMPA-type ionotropic glutamate receptors is attenuated by auxiliary proteins stargazin and cornichon-3. Brown et al. show that relief from block is due to enhanced blocker permeation and present a modified model of permeant channel block to account for their experimental findings.
Abstract
Most ligand- and voltage-gated ion channels assemble as signaling complexes consisting of pore-forming and auxiliary subunits. In the mammalian brain, AMPA-type ionotropic glutamate receptors (AMPARs) coassemble with several families of auxiliary subunits that regulate channel gating as well as ion channel block and permeation. Previous work has shown that auxiliary proteins stargazin (or γ2) and cornichon-3 (CNIH-3) attenuate the cytoplasmic polyamine channel block of AMPARs, although the underlying mechanism has yet to be established. Here, we show that γ2 and CNIH-3 relieve channel block by enhancing the rate of blocker permeation. Surprisingly, the relative permeability of the polyamine spermine (Spm) through the pore of the AMPAR-γ2 or -CNIH-3 complexes is considerably more than AMPARs expressed alone. Spm permeability is comparable to that of Na+ for the GluA2-γ2 complex and four times greater than Na+ with GluA2 + CNIH-3. A modified model of permeant channel block fully accounts for both the voltage- and time-dependent nature of Spm block. Estimates of block rate constants reveal that auxiliary subunits do not attenuate block by shifting the location of the block site within the membrane electric field, and they do not affect the blocker’s ability to reach it. Instead, γ2 and CNIH-3 relieve channel block by facilitating the blocker’s exit rates from the open channel. From a physiological perspective, the relief of channel block exerted by γ2 and CNIH-3 ensures that there is unfettered signaling by AMPARs at glutamatergic synapses. Moreover, the pronounced ability of AMPARs to transport polyamines may have an unexpected role in regulating cellular polyamine levels.
Introduction
Voltage-dependent channel block by cytoplasmic polyamines is a regulatory mechanism that affects many families of cation-selective ion channels (Bowie et al., 1999; Baronas and Kurata, 2014). Polyamine block was first described for K+ channels to account for their inward rectification, whereby K+ channels conduct ions more readily in the inward, than outward, direction (Lopatin et al., 1994). Although Mg2+ channel block contributes to the overall mechanism of inward rectification (Horie et al., 1987; Matsuda et al., 1987; Vandenberg, 1987), the discovery of polyamine block explained the steep voltage dependence of inward rectification as well as earlier observations noting that the degree of rectification dissipated in excised patches (because of blocker washout; Matsuda et al., 1987; Vandenberg, 1987). Since then, many cation-selective ion-channel families have been shown to be blocked in a voltage-dependent manner by cytoplasmic polyamines, including AMPA-type (AMPARs) and kainate-type (KARs) ionotropic glutamate receptors (iGluRs; Bowie and Mayer, 1995; Kamboj et al., 1995; Koh et al., 1995), voltage-activated calcium channels (Gomez and Hellstrand, 1995), nicotinic acetylcholine receptors (Haghighi and Cooper, 1998), cyclic nucleotide-gated (CNG) channels (Lu and Ding, 1999; Guo and Lu, 2000), MIC/TRPM7 channels (Kerschbaum et al., 2003), and voltage-gated sodium channels (Fu et al., 2012). A property that has emerged from this work is that some ion channels, particularly nonselective cation channels, are also able to flux polyamines from both the inside and outside of cells as a mechanism to relieve channel block.
AMPARs and KARs are nonselective cation channels that show appreciable block by polyamines at negative and positive membrane potentials near 0 mV but also exhibit relief of block at positive membrane potentials because of blocker permeation. Early studies assumed that the relief of polyamine block of AMPARs and KARs resulted from the permeation of the blocker at extreme positive membrane potentials (Bowie and Mayer, 1995; Bowie et al., 1999). The ability of polyamines to permeate KARs was then formally demonstrated by showing that polyamines carry inward membrane current when acting as the sole charge carrier in the external bathing solution (Bähring et al., 1997). Because relief of block was only evident at extreme positive membrane potentials (>50 mV), it was assumed not to have a role in signaling at glutamatergic synapses (Bowie et al., 1999; Dingledine et al., 1999). Instead, cytoplasmic polyamines were considered to be tonic blockers of AMPARs and KARs at resting negative membrane potentials (Bowie et al., 1999; Dingledine et al., 1999). However, appreciating that auxiliary proteins attenuate channel block in AMPARs and KARs (Jackson and Nicoll, 2011), the potential contribution of blocker permeation to the overall block mechanism has recently been evaluated. For example, a study of homomeric GluK2 KARs revealed that auxiliary proteins Neto1 and Neto2 relieve polyamine channel block by enhancing blocker permeation rates (Brown et al., 2016). A similar mechanism also accounts for the relief of block in GluK2/GluK5 KAR heteromers (Brown et al., 2016), suggesting that multiple structural pathways can affect channel block and permeation. Importantly, under both conditions, blocker permeation occurs at more negative and physiologically relevant membrane potentials (Brown et al., 2016). The AMPAR auxiliary proteins stargazin (γ2) and cornichon-3 (CNIH-3) also attenuate polyamine block (Soto et al., 2007; Coombs et al., 2012), but the underlying mechanism has yet to be determined.
Here, we tested the hypothesis that γ2 and CNIH-3 relieve polyamine channel block by enhancing blocker permeation rates. In agreement with that hypothesis, bi-ionic experiments revealed that the permeability of the polyamine spermine (Spm) relative to Na+ ions is substantially enhanced when AMPARs are coassembled with γ2 or CNIH-3. A modified model of permeant channel block fully accounts for the time-dependent nature of Spm block at all membrane potentials. Fits of the model reveal that the steepness of the onset and relief of block are primarily governed by polyamine exit rates from the channel and not by the rate of blocker binding. As such, cytoplasmic polyamines act on AMPARs through two distinct mechanisms, whereby Spm acts as a channel blocker but also as a permeant ion with a significant contribution to the overall charge transfer.
Materials and methods
Plasmids and molecular biology
All experiments were performed using cDNA of rat GluA2(Q)i and GluA2(Q)i-γ2 (in tandem; Dawe et al., 2016) in pRK5 and human CNIH-3 in pCMV-SPORT6. The sequence encoding for GCaMP6s and a P2A sequence were upstream of GluA2 to identify transfected cells. GluA2-γ2 was cotransfected with a plasmid encoding enhanced green fluorescent protein (eGFP) to identify transfected cells.
Cell culture and transfection
HEK293T/17 cells (ATCC) were maintained in MEM containing GlutaMAX supplemented with 10% fetal bovine serum (Invitrogen). Cells were plated at low density (1.6 × 104 cells/ml) on poly-d-lysine–coated, 35-mm, plastic dishes and were transiently transfected 48 h later using the calcium phosphate technique, as previously described (Brown et al., 2016). A GluA2:CNIH-3 cDNA molar ratio of 1:2 was used, and 30 µM DNQX was included in the medium after transfection to prevent cell death.
Electrophysiological recordings
Experiments were performed 24–48 h after transfection. Agonist solutions were rapidly applied to outside-out patches excised from transfected cells using a piezoelectric stack (Physik Instrumente). Solution exchange (10–90% rise time of 250–350 µs) was determined by measuring the liquid junction current at the end of an experiment. All recordings were performed using an Axopatch 200B (Molecular Devices) with thick-walled, borosilicate glass pipettes (3–6 MΩ) coated with dental wax to reduce electrical noise. Current records were filtered at 10 kHz and digitized at 100 kHz for block rate experiments and were filtered at 5 kHz and digitized at 25 kHz for Spm permeation experiments. Series resistance (3–12 MΩ) was compensated by 95%. Recordings were performed at a range of holding potentials from −100 to 130 mV to study polyamine channel block. Data acquisition was performed using pClamp10 software (Molecular Devices) and was tabulated using Excel (Microsoft Corp.). All experiments were performed at room temperature.
All chemicals were purchased from Sigma-Aldrich, unless otherwise indicated. The external solution contained (in mM) 150 NaCl, 5 HEPES, 0.1 MgCl2, and 0.1 CaCl2, pH 7.3–7.4. Low divalent concentrations were used to avoid substantial divalent channel block but still promote the formation of GΩ patch seals (Wong et al., 2007). The internal solution contained (mM) 115 NaCl, 10 NaF, 5 HEPES, 5 Na4BAPTA (Life Technologies), 1 MgCl2, 0.5 CaCl2, and 10 Na2ATP, pH 7.3–7.4. The osmotic pressure of all solutions was adjusted to 295–300 mOsm with sucrose. In polyamine block experiments, Na2ATP in the internal solution was replaced with 10–100 µM Spm (from a concentrated stock solution), and the osmotic pressure was adjusted to 295–300 mOsm with sucrose. For polyamine permeation experiments, the 150 mM NaCl in the external solution was replaced with 90 mM Spm, pH was adjusted to 7.3–7.4 using the free base of Spm, and the osmotic pressure was adjusted with sucrose. Concentrated (10×) agonist stock solutions were prepared by dissolving l-glutamate in the appropriate external solution and adjusting the pH to 7.3–7.4 and were stored frozen at −20°C. Stocks were thawed on the day of the experiment and used to prepare agonist-containing external solutions.
Data analysis and fitting
Relative Spm permeability (PSpm/PNa) was calculated from the reversal potential (Vrev) measurements in 90 mM Spm external solutions using the following equation from Bähring et al. (1997) (Eq. 1):
| (1) |
where Ix is the current carried by ion X at a membrane potential Vm, Px is the corresponding permeability (PNa = 1), [X]i and [X]o are the internal and external Spm concentrations, z is the valence, F is Faraday’s constant, R is the gas constant, and T is the temperature in Kelvin. Experimentally determined reversal potentials were used for Vm. We obtained PSpm/PNa using the definition that INa + ISpm = 0 at the reversal potential. Reversal potentials were estimated by fitting the I–V relationships with polynomial functions and determining V at I = 0 pA and were corrected for liquid-junction potentials that were determined experimentally.
Agonist-evoked membrane conductance (G) was calculated using Eq. 2:
| (2) |
where I is the current at the V holding potential and Vrev is the reversal potential.
Single permeant blocker model
Conductance–voltage (G–V) relationships were fit using Origin 7 (OriginLab) with the following equation from Bowie et al. (1998) (Eq. 3a):
| (3a) |
where Gmax is the maximal conductance, [Spm] is the internal Spm concentration, and Kd is the dissociation constant.
For fits of the G–V relationships using the Woodhull model, Kd was defined as shown in Eq. 3b:
| (3b) |
where Kd(0) is the dissociation constant at 0 mV, Vm is the membrane potential, z is the valence of the polyamine, θ is the fraction of the membrane electric field measured from the intracellular face of the membrane, and F, R, and T are the same as in Eq. 1.
Kd was defined as shown in Eq. 4a:
| (4a) |
and was then redefined as shown in Eq. 4b:
| (4b) |
where h and k represent the voltage dependence of g (koff/kon) and L (kperm/kon), respectively.
Voltage (V)-dependent binding (kon), unbinding (koff), and permeation (kperm) rates were defined as previously defined in Bowie et al. (1998) and Brown et al. (2016) (Eqs. 5, 6, and 7):
| (5) |
| (6) |
| (7) |
where a, c, and e are the rates of binding, unbinding and permeation, respectively; and b, d, and f are their respective voltage dependence constants.
Auxiliary proteins affect the voltage-dependent conductance of KARs under basal conditions within the range of ±100 mV (Brown et al., 2016). To account for these differences, the intrinsic G–V relationships were fit with Eq. 8 using Origin 7:
| (8) |
where G0 is the minimal conductance, and Vc is a voltage constant.
Current relaxations over time t by polyamine block were fit to function I(t,V) in Eq. 9:
| (9) |
where I0 is the current value before blocker entry, and I∞ is the stable current value after decay by blocker entry. I0 was estimated using an exponential fit. I∞ can be represented as follows (Eq. 10):
| (10) |
To compare the fit block rate constants with those obtained with the G–V relationships, we redefined the constants in Eq. 3a to the following (Eqs. 11, 12, 13, and 14):
| (11) |
| (12) |
| (13) |
| (14) |
Modified permeant blocker model with two conductances (two-conductance model)
G–V relationships were fit using MatLab with Eq. 15:
| (15) |
where Gmax is the maximal conductance, [Spm] is the internal Spm concentration, and kon, koff, kperm, k1, and k1′ are as defined in Eqs. 5, 6, and 7, and Fig. 6 A. GSpm/GNa is the ratio of the Spm conductance over the Na+ conductance and was obtained as follows (Eqs. 16 and 17):
| (16) |
| (17) |
where PSpm/PNa was taken from the permeability experiments as described in Eq. 1.
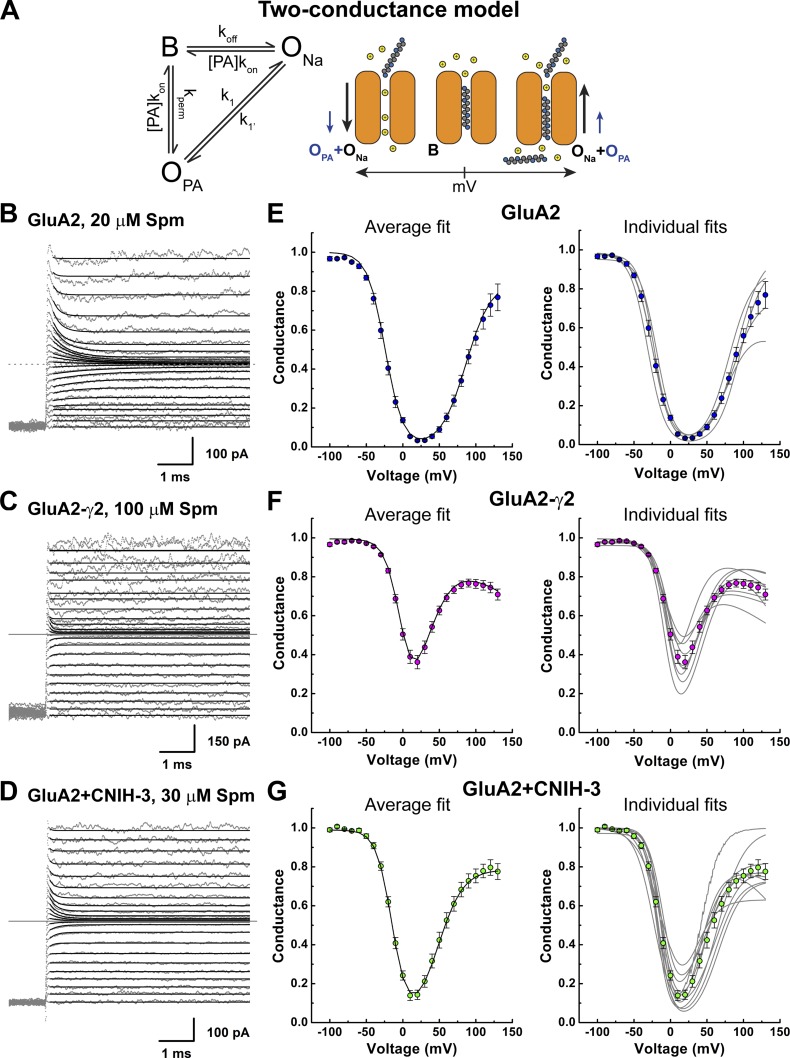
Figure 6.
Polyamine conductance contributes to the overall current. (A) A modified permeant blocker model with two conductance states (two-conductance model). The binding, unbinding, and permeation rates are as shown in Fig. 3; k1 and k1′ are transition rates between ONa and OPA. (Right) A graphical representation of the model. (B–D) Example traces showing fits of the current relaxations with the two-conductance permeant blocker model (Eq. 18) for GluA2 (B; 20 µM Spm(i), patch 151023p3), GluA2-γ2 (C; 100 µM Spm(i), patch 150924p1), and GluA2 + CNIH-3 (D; 30 µM Spm(i), patch 151201p2). (E–G) Means ± SEM (left) and individual (right) fits of the corrected G–V plots with the two-conductance model (Eq. 15) for GluA2 (E), GluA2-γ2 (F), and GluA2 + CNIH-3 (G).
Current relaxations over time t by polyamine block were fit to the function I2(t,V) (Eqs. 18, 19, 20, 21, 22, 23, and 24):
| (18) |
where
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
All the fits were performed using the Levenberg-Marquardt method. A program that performs those tasks was written in MatLab.
Statistics
Statistical analysis was performed using the statistical software SPSS Statistics (IBM Corporation). Data were assumed to be distributed normally. The numbers provided for n refer to the number of individual patches.
All data were illustrated using Origin 7 and Adobe Illustrator.
Online supplemental material
Fig. S1 is an extension of Fig. 5 and includes highlights of the electrophysiological traces and I–V relationships near the reversal potential.
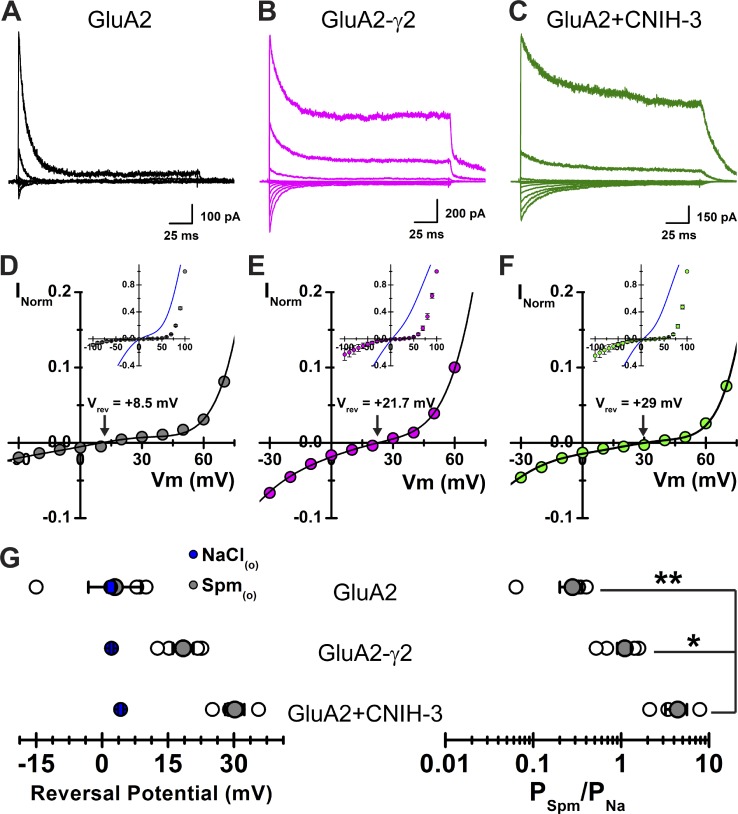
Figure 5.
Spermine permeation through GluA2(Q) is increased by auxiliary proteins. (A–C) Example traces from GluA2 (A; patch 151009p8), GluA2-γ2 (B; patch 151008p5), and GluA2 + CNIH-3 (C; patch 151009p9) at various potentials (range, −100 to 100 mV, 20-mV increments) in the presence of 90 mM Spm(o). (D–F) Corresponding I–V plots, normalized to 100 mV in Spm(o), for the patches shown in A, B, and C (GluA2 [D], GluA2-γ2 [E], GluA2 + CNIH-3 [F]). (Insets) Mean fits of the I–V plots in the presence of NaCl(o) are displayed in blue, and mean I–V plots in the presence of Spm(o) are presented as means ± SEM. (G) Summary of Vrev and relative Spm permeability (PSpm/PNa; Eq. 1) values. Mean Vrev values in the presence of NaCl(o) are displayed in blue. Data are shown as means ± SEM; individual data points are shown as open circles. One-way ANOVA for PSpm/PNa, F2,10 = 10.115. P = 0.004; *, P = 0.016; **, P = 0.005.
Results
AMPAR auxiliary proteins γ2 and CNIH-3 regulate channel gating
Two commonly occurring auxiliary subunits, γ2 and CNIH-3 (Jackson and Nicoll, 2011), were chosen to study how auxiliary proteins regulate the functional behavior of AMPARs. To do that, electrophysiological experiments were performed in outside-out patches excised from HEK293T cells transfected with cDNA encoding a GluA2/TARP tandem construct (i.e., GluA2-γ2) or separate cDNAs for GluA2 and CNIH-3 (i.e., GluA2 + CNIH-3). Cells transfected with cDNA for GluA2 alone were used as controls. Agonist-evoked membrane currents were elicited with a near-saturating concentration of the neurotransmitter l-glutamate (10 mM l-Glu, 200 ms duration) using a rapid concentration clamp perfusion system (Bowie, 2002).
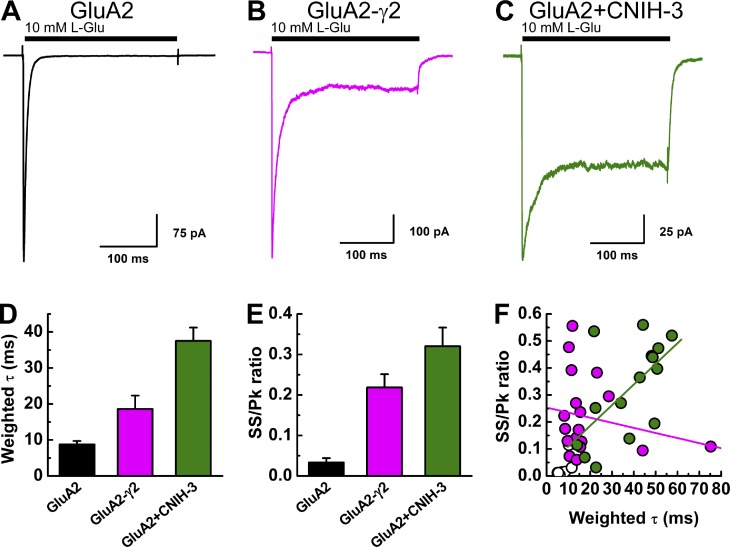
The functional assembly of γ2 or CNIH-3 with GluA2 subunits was confirmed by observing a slowing in the rate of macroscopic desensitization and an increase in equilibrium desensitization (Fig. 1, A–C), as described previously (Tomita et al., 2005; Schwenk et al., 2009; Coombs et al., 2012; Dawe et al., 2016). The weighted τ values for the rate of macroscopic desensitization were 18.6 ± 3.7 ms (n = 19) and 37.5 ± 3.7 ms (n = 15) in patches excised from cells expressing GluA2-γ2 and GluA2 + CNIH-3, respectively, which corresponded to a two- to fourfold slowing of desensitization compared with GluA2 alone (8.6 ± 1.0 ms, n = 15; Fig. 1 D). Likewise, the increase in equilibrium desensitization, as indicated by the change in the steady-state/peak response ratio (ss/pk ratio), was ∼7–10-fold larger with GluA2-γ2 (ss/pk ratio, 0.22 ± 0.03, n = 19) and GluA2 + CNIH-3 (ss/pk ratio, 0.32 ± 0.05, n = 15) compared with GluA2 alone (ss/pk ratio, 0.03 ± 0.01, n = 15; Fig. 1 E). There was a positive correlation between the rate of macroscopic desensitization (i.e., weighted τ) and equilibrium desensitization (i.e., ss/pk ratio) for GluA2 + CNIH-3 (Fig. 1 F, linear regression, n = 15 patches, Pearson’s r = 0.6104, P = 0.01566), which presumably reflects the patch-to-patch variation in the stoichiometric assembly of GluA2 + CNIH-3 complexes. Although that variability would be expected to be absent from patches expressing the GluA2-γ2 tandem construct, the ss/pk ratio remained highly variable (range, 0.06–0.56) between different recordings, although it did not correlate with the rate of desensitization (range, 8.1–75.2 ms). In agreement with this, there was no statistically significant correlation between these two parameters (linear regression, n = 19 patches, Pearson’s r = −0.21297, P = 0.38135; Fig. 1 F).
Figure 1.
Auxiliary proteins regulate the gating properties of AMPARs. (A–C) Example electrophysiological responses from GluA2 (A; patch 150911p1), GluA2-γ2 (B; patch 151126p5), and GluA2 + CNIH-3 (C; patch 151109p4) evoked by 10 mM l-Glu (200 ms, holding potential = −60 mV) in the presence of 150 mM NaCl(o). (D and E) Summary of the decay kinetics (D) and equilibrium currents (ss/pk ratio; E) for GluA2, GluA2-γ2, and GluA2 + CNIH-3. Data are means ± SEM. (F) Scatter plot showing the relationship between the decay kinetics (weighted τ) and the ss/pk ratio for each receptor complex.
AMPAR auxiliary proteins γ2 and CNIH-3 attenuate polyamine channel block
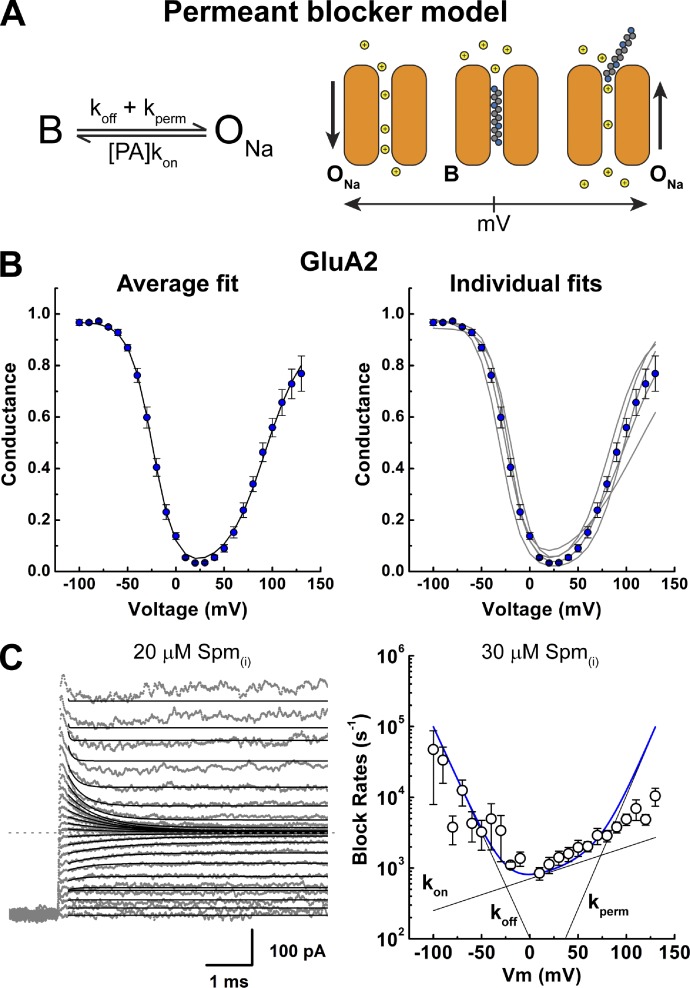
To investigate the channel block mechanism, we designed experiments to observe the time course of polyamine block over a range of membrane potentials. To do this, each outside-out patch was held at a holding potential of −100 mV and then stepped in 10-mV decrements (range, 130 to −100 mV) to observe the onset of block by intracellular spermine (10–30 µM Spm; Fig. 2, see Materials and methods). Agonist-evoked membrane currents were elicited by 10 mM l-Glu in the continued presence of 100 µM cyclothiazide to minimize AMPAR desensitization during the voltage step protocol (Fig. 2 A). Responses were then leak subtracted by repeating the voltage step protocol without agonist present.
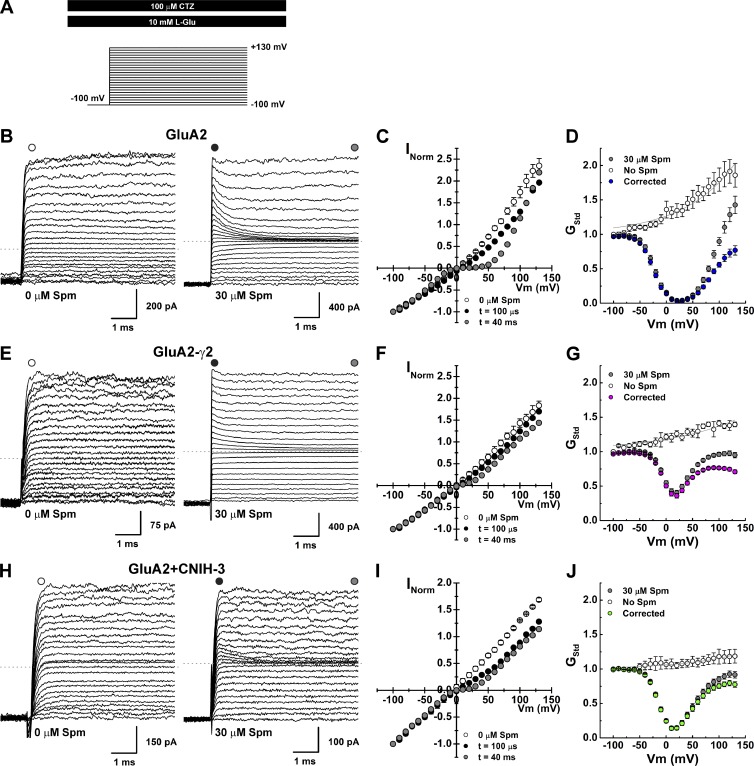
Figure 2.
Channel block of AMPARs in the presence of auxiliary proteins. (A) Schematic of the experimental protocol. (B, E, and H) Raw current traces evoked by 10 mM l-Glu in the presence of 100 µM cyclothiazide, in control or 30 µM Spm(i), after voltage steps (range, −100 to 130 mV; Δ10 mV; GluA2, patches 150724p1 [Ctrl] and 150911p1 [Spm; B], GluA2-γ2, patches 150723p3 [Ctrl} and 151126p5 (Spm; E), GluA2 + CNIH-3, patches 151203p1 [Ctrl] and 151109p4 [Spm; H]). (C, F, and I) I–V plots for each receptor complex. Mean I–V plots in the absence of Spm(i) are shown in open symbols (GluA2, n = 5; GluA2-γ2, n = 4; GluA2 + CNIH-3, n = 3). I–V plots of the peak responses (100–200 µs after the voltage steps) are in black, and equilibrium I–V plots are in gray. (D, G, and J) Mean G–V plots (calculated using Eq. 2) for each receptor complex. G–V plots in the absence of Spm(i) are in white, raw G–V plots with 30 µM Spm(i) are in gray, and corrected G–V plots (see Materials and methods) are colored. Data are means ± SEM.
In the absence of intracellular polyamines, the amplitude of agonist-evoked membrane current was non-decaying at all membrane potentials tested (Fig. 2, B, E, and H, left), suggesting that open-channel probability is unchanged during the duration of the voltage step. However, the equilibrium current-voltage (I–V) relationship for GluA2 AMPARs varied in the degree of outward rectification when expressed with or without auxiliary proteins (open symbols, Fig. 2, C, F, and I). Outward rectification was greater for GluA2 receptors alone, with a rectification ratio (80/−80 mV ratio) of 1.5 ± 0.1 (n = 5), compared with 1.1 ± 0.1 (n = 4) and 1.1 ± 0.1 (n = 3) for cells expressing GluA2-γ2 and GluA2 + CNIH-3, respectively (Fig. 2, D, G, and J). The occurrence of outward rectification has been explained by voltage-dependent differences in the open-channel probability of AMPARs (Prieto and Wollmuth, 2010). Similar differences in the degree of outward rectification have been observed for GluK2 kainate receptors (KARs) expressed with or without the auxiliary proteins Neto1 and Neto2 (Brown et al., 2016), suggesting that the open-channel probability of KARs is similarly voltage dependent and regulated by auxiliary proteins. To more accurately define the degree of outward rectification, conductance-voltage (G–V) plots were fit with Eq. 8 (Fig. 2, D, G, and J, solid line; also see Materials and methods; Bowie et al., 1998; Brown et al., 2016), and the fit parameters were used to correct for the intrinsic outward rectification (see Fig. 2, D, G, and J). A summary of the fit parameters is listed in Table 1.
Table 1. Fit parameters for intrinsic G–V relationships.
| Receptor | G0 | Vc |
|---|---|---|
| GluA2 | 1.2674 | 96.2 |
| GluA2-γ2 | 1.1815 | 140.0 |
| GluA2 + CNIH-3 | 1.0604 | 104.3 |
Unlike control experiments, AMPAR-mediated membrane currents observed with each voltage step exhibited a time-dependent decay when Spm (30 µM, n = 7) was included in the internal pipette solution (Fig. 2, B, E, and H, right). This observation is consistent with an open-channel block mechanism (Bowie et al., 1998). In agreement with this, I–V plots obtained by measuring the current response immediately after the settling of the voltage step (i.e., 100–200 µs) were outwardly rectified, showing little sign of channel block (Fig. 2, C, F, and I), whereas I–V plots of equilibrium current responses measured 40–45 ms after the voltage step were birectifying in nature (Fig. 2, C, F, and I; Bowie and Mayer, 1995). In agreement with previous studies (Soto et al., 2007, 2014; Coombs et al., 2012), the degree of inward rectification observed at positive membrane potentials was greater for GluA2 alone, with a rectification ratio (80/−80 mV) of 0.49 ± 0.04 (n = 5), compared with 0.87 ± 0.02 (n = 9) and 0.73 ± 0.04 (n = 11) for patches expressing GluA2-γ2 and GluA2 + CNIH-3, respectively (Fig. 2, C, F, and I). To estimate the degree of inward rectification observed under equilibrium block conditions, G–V plots were constructed and corrected for intrinsic outward rectification (Fig. 2 D, G, and J), as described previously (Bowie et al., 1998; Brown et al., 2016).
Analysis of polyamine block of AMPARs with a single permeant blocker model
Corrected G–V plots were fit with a single binding site model of channel block (Fig. 3 A) to estimate the dissociation constant for Spm at 0 mV [Kd(0mV)] as well the voltage dependence of block, as described previously for KARs (Bowie et al., 1998; Brown et al., 2016). For GluA2 alone, the birectifying nature of the G–V plot was well fit at all Spm concentrations tested (10–30 µM; not depicted). Fig. 3 B shows the mean G–V plot for GluA2 with 30 µM Spm (left) as well as the data fits from individual patch recordings (right). From those fits, the Kd(0mV) value was estimated to be 2.8 ± 0.4 µM (n = 3), 4.0 ± 1.2 µM (n = 3), and 4.3 ± 0.6 µM (n = 5) for 10, 20, and 30 µM Spm(i), respectively (not depicted). One-way ANOVA determined that these values were not statistically different from one another (F2,8 = 0.955, P = 0.425), and the data were pooled. Similarly, the voltage dependence for the onset and relief of the block were comparable between different Spm concentrations (not depicted). The pooled fit parameters estimated Kd(0mV) to be 3.7 ± 0.4 µM (n = 12) with the voltage dependence for the onset and relief of block to be −11.8 ± 0.4 mV and 24 ± 4 mV, respectively (Table 2).
Figure 3.
Analysis of a polyamine block of GluA2 AMPARs with a single permeant blocker model. (A) The permeant blocker model, in which B denotes a blocked (nonconducting) state, and ONa denotes a Na+-conducting state. The binding, unbinding, and permeation rates are denoted as kon, koff, and kperm, respectively. PA, polyamine. A graphical representation of the model is shown on the right. (B) Mean (left) and individual (right) fits of the corrected G–V plots with the permeant blocker model for GluA2 (Eq. 3a). (C) Example traces showing fits of the GluA2 current relaxation (Eq. 9) induced by 20 µM Spm(i) with the permeant blocker model (left; patch 151023p3). (Right) The estimated rate constants and the sum of those rate constants. Model-independent exponential fits of the data with 30 µM Spm(i) (circles) are well predicted by the model values at most membrane potentials. Data are shown as means ± SEM.
Table 2. Equilibrium spermine block in GluA2 receptors.
| Receptor | Kd(0mV) | h (mV)/δ (1–θ) | k (mV) | n | |||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SEM | Mean | SEM | Mean | SEM | ||||
| Permeant blocker model | h (mV) | ||||||||
| GluA2 | 3.7 | 0.4 | −11.8 | 0.4 | 24 | 4 | 12 | ||
| Woodhull model | δ (1–θ) | ||||||||
| GluA2 | 3.7 | 0.5 | 0.48 | 0.02 | 12 | ||||
| GluA2-γ2 | 41 | 3 | 0.61 | 0.03 | 19 | ||||
| GluA2 + CNIH-3 | 11 | 2 | 0.48 | 0.04 | 12 | ||||
Dissociation constants were obtained by fitting the equilibrium G–V relationships.
In addition to fitting equilibrium channel block data, we also estimated the rate constants for binding (kon), unbinding (koff) and permeation (kperm) of Spm by fitting the current relaxations after each voltage step (Fig. 3 C), as described previously for GluK2 KARs (Bowie et al., 1998). Membrane current relaxations were fit well with the model at almost all membrane potentials except at values >100 mV, where the relief of block dominates (Fig. 3 C, left). Fitting the current relaxations within this range (i.e., −100 to 100 mV) allowed us to estimate the rate constants for Spm binding, unblock, and permeation (Fig. 3 C and Table 3). Based on these fits, the sum of the rate constants predicted well the experimentally observed current relaxations at membrane potentials between −100 and 100 mV (Fig. 3 C, right). The rate of Spm binding to GluA2 was close to the diffusion limit (kon = 29 ± 5 µM−1 s−1) but weakly voltage sensitive, increasing e-fold per 113 ± 13 mV change in the membrane potential (n = 7, Table 3). In contrast, rates of unbinding and permeation were steeply voltage dependent, changing e-fold per −19 ± 1 and 20 ± 3 mV change in membrane potential, respectively (n = 7, Table 3). Consequently, the steepness of the polyamine block of AMPARs, similar to that of KARs (Bowie et al., 1998; Brown et al., 2016), is almost entirely reliant on the voltage dependence of koff and kperm, with a much smaller contribution by kon (Fig. 3 C, right).
Table 3. Spermine block rates in GluA2 receptors.
| Receptor | Permeant blocker model | n | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| kon | koff | kperm | Kd(0mV) | ||||||||
| a (µM−1s−1) | b (mV) | c (s−1) | d (mV) | e (s−1) | f (mV) | (µM) | |||||
| GluA2 | 29 | 113 | 156 | −19 | 32 | 20 | 6 | 7 | |||
| SEM | 5 | 13 | 30 | 1 | 16 | 3 | 1 | ||||
Block rate parameters were obtained by fitting the current relaxation after the voltage steps.
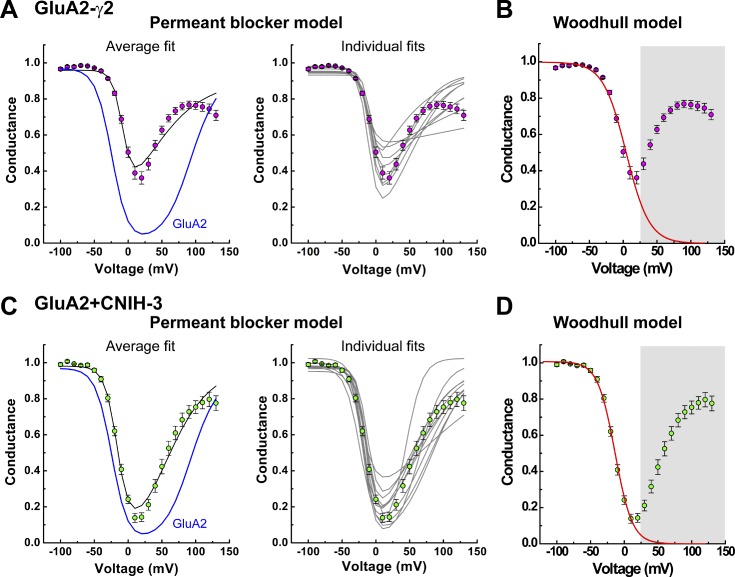
Corrected G–V plots obtained from patches expressing GluA2-γ2 and GluA2 + CNIH-3 channel complexes revealed that both auxiliary proteins attenuate polyamine block of GluA2 AMPARs (Fig. 4). In each case, however, the single permeant blocker model consistently failed to accurately fit the relief of polyamine block at positive membrane potentials, a finding we have previously noted for GluK2 KARs in complex with Neto1 or Neto2 (Brown et al., 2016). Fig. 4 (A and C) show the mean G–V plots for GluA2-γ2 and GluA2 + CNIH-3, respectively, with 30 µM Spm (left) and fits with the single permeant blocker model to data from individual patch recordings (right). Given that the model failed to describe the G–V relationship at positive membrane potentials, we fit each G–V plot with the Woodhull model (Fig. 4, B and D), which is a nonpermeant model of channel block (Woodhull, 1973) that describes the portion of the G–V plot that corresponds to the onset of block at negative membrane potentials. Using this approach, we estimated Kd(0mV) and the voltage dependence of block (zδ) for the data from patches containing GluA2-γ2 and GluA2 + CNIH-3. Estimates of Kd(0mV) and zδ values were similar with different Spm concentrations (not depicted), and the data were, therefore, pooled. Using the Woodhull model, the mean Kd(0mV) was estimated to be 41 ± 3 µM (n = 19) and 11 ± 2 µM (n = 12) for GluA2-γ2 and GluA2 + CNIH-3, respectively, compared with 3.7 ± 0.5 µM (n = 12) for GluA2 alone (Table 2). Assuming that Spm has a valency of 4, the δ values were estimated to be 0.61 ± 0.03 (n = 19) and 0.48 ± 0.04 (n = 12), for GluA2-γ2 and GluA2 + CNIH-3, respectively, compared with 0.48 ± 0.02 (n = 12) for GluA2 alone (Table 2). Interestingly, despite its more significant impact on the decay kinetics and steady-state current (Fig. 1), CNIH-3 was less effective than γ2 at reducing polyamine block of GluA2 (Figs. 2 and 4 and Table 2).
Figure 4.
G–V plots with auxiliary proteins are poorly fit by the permeant blocker model. (A and C) Mean (left) and individual (right) fits of the corrected G–V plots with the permeant blocker model (Eq. 3a) for GluA2-γ2 (A) and GluA2 + CNIH-3 (C). The continuous black lines indicate fits of the data; the continuous blue lines illustrate the fit of the GluA2 data for comparison. (B and D) Mean fits using the Woodhull model (Eq. 3b) for an impermeant blocker for GluA2-γ2 (B) and GluA2 + CNIH-3 (D). Continuous red lines indicate fits of the data (fit range, −100 to 20 mV). Data points between 30 and 130 mV were masked. Data are shown as means ± SEM.
The failure of the single permeant blocker model to fit data at positive membrane potentials suggests one of two possibilities. It could represent the existence of multiple blocked states, as described previously for polyamine block of cGMP-gated channels (Lu and Ding, 1999; Guo and Lu, 2000). In this case, the G–V relationship and its pronounced downturn at extreme positive membrane potentials was explained by Spm acting as both a permeant blocker at negative membrane potentials and a nonpermeant blocker, which dominated at positive potentials. The authors speculated that distinct modes of channel block may reflect different conformations of the Spm molecule in the pore (Lu and Ding, 1999; Guo and Lu, 2000). An alternative possibility is that Spm acts as a permeant channel blocker but that permeation of Spm contributes to the overall AMPAR conductance, particularly at high membrane electric field strengths. This mechanism would account for the complex shape of the G–V relationship, including its pronounced downturn at positive membrane potentials. In keeping with this, we have recently shown that GluK2 KARs in complex with the auxiliary subunits Neto1 or Neto2 exhibit appreciable permeation to Spm (Brown et al., 2016), suggesting that a similar mechanism may occur at GluA2 AMPARs. To test that, we performed experiments to determine whether the association of GluA2 AMPAR with its auxiliary proteins relieved polyamine channel block by enhancing blocker permeation.
γ2 and CNIH-3 relieve channel block by facilitating polyamine permeation
To estimate Spm permeability relative to that of Na+ (PSpm/PNa), we measured the reversal potentials (Vrev) of each receptor complex in solutions in which the main external permeant cation was either Na+ (150 mM) or Spm (90 mM), as described previously (Brown et al., 2016). Fig. 5 (A–C) shows typical membrane currents observed when the main external permeant ion was 90 mM Spm (Fig. S1).
As expected for a cation-selective ion channel, the AMPAR response observed in the presence or absence of auxiliary subunits reversed near 0 mV in symmetrical Na+ solutions (Fig. 5, D–F, insets). The Vrev for GluA2 alone was 2.0 ± 0.1 mV (n = 6), with Vrev values for GluA2-γ2 and GluA2 + CNIH-3 estimated to be 2.1 ± 0.4 mV (n = 7) and 4.2 ± 0.6 mV (n = 9), respectively (Fig. 5 G, left). In contrast, Vrev values were shifted to more positive membrane potentials when external 150 mM Na+ ions were replaced with 90 mM Spm (Fig. 5, D–F). The mean Vrev for GluA2 alone was 2.9 ± 6.0 mV (n = 4), with Vrev values for GluA2-γ2 and GluA2 + CNIH-3 estimated to be 18.4 ± 2.4 mV (n = 5) and 30.2 ± 2.2 mV (n = 4), respectively (Fig. 5 G, left). The permeability of Spm relative to Na+ (i.e., PSpm/PNa) was calculated to be 0.28 ± 0.08 (n = 4) for GluA2 alone (Fig. 5 G, right), demonstrating that Spm is more permeable through AMPARs than GluK2 KARs (Bähring et al., 1997; Brown et al., 2016). The PSpm/PNa ratio was calculated to be 1.1 ± 0.2 (n = 5) and 4.4 ± 1.2 (n = 4) for GluA2-γ2 and GluA2 + CNIH-3, respectively (Fig. 5 G, right), which represented ∼4- and 16-fold increases in Spm permeation compared with GluA2 alone (one-way ANOVA, F2,10 = 10.115, P = 0.004; post hoc Tukey’s honestly significant difference pairwise comparisons, P = 0.005 and 0.014 for the GluA2 + CNIH-3–GluA2 and GluA2 + CNIH-3–GluA2-γ2 comparisons; P = 0.636 for the GluA2–GluA2-γ2 comparison). Taken together, our data demonstrate that the auxiliary proteins, γ2 and CNIH-3, substantially increase Spm permeation through the GluA2 channel pore, an effect that is even greater than the permeation of polyamines through KARs in complexes with Neto2 (Brown et al., 2016). Given this, we concluded that the complex nature of Spm block of GluA2-γ2 and GluA2 + CNIH-3 channels may be explained by an appreciable contribution of Spm permeation to the overall AMPAR conductance.
A modified permeant blocker model accounts for the effects of γ2 and CNIH-3
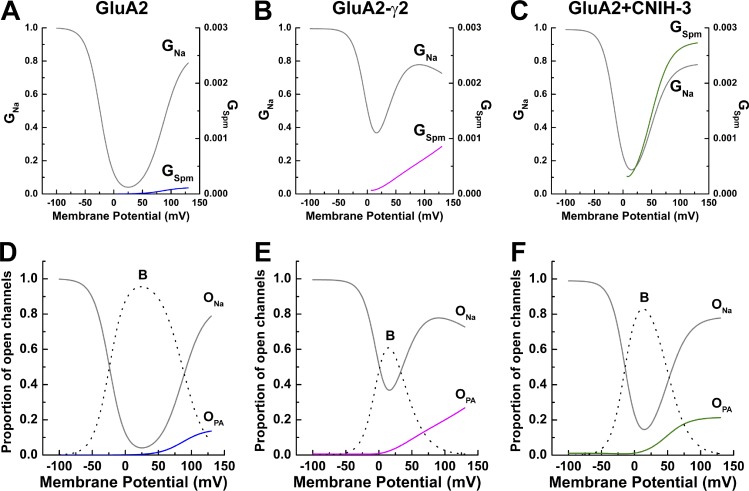
Given the appreciable Spm permeation through GluA2 AMPARs associated with auxiliary proteins, we modified the permeant blocker model to include an additional conductance state, which we termed OPA (Fig. 6 A). With this addition, the modified permeant blocker model contains three states: one of which is a blocked state (B, nonconducting) and two of which are open states (ONa and OPA; Fig. 6 A). Therefore, the two-conductance model accounts for the fractional occupancy of the pore by spermine but now also accounts for the contribution of spermine transport to the overall membrane conductance.
To estimate the voltage dependence of block, we fit the current relaxations observed after each voltage step with the modified permeant blocker model (Fig. 6, B–D). In each case, the experimental traces were well fit by the model at all membrane potentials and conditions tested. As observed with equilibrium G–V plots, fits of current relaxations revealed that Spm block of GluA2 AMPARs was attenuated by coassembly with auxiliary subunits. Kd(0mV) was estimated to be 3.3 ± 0.5 µM (n = 7) for GluA2 alone, compared with 15 ± 4 µM (n = 4) and 4.5 ± 0.9 µM (n = 5) when coassembled with γ2 and CNIH-3, respectively (Table 4). Spm binding (kon) to GluA2 channels alone was also relatively voltage insensitive, changing e-fold per 199 ± 94 mV membrane potential (n = 7, Table 4), which was similar to previous estimates using the single permeant blocker model (compare Fig. 3 C and Table 3). Likewise, the rates of koff and kperm of Spm were steeply voltage dependent, changing e-fold per −20 ± 1 mV (n = 7) and 19 ± 2 mV (n = 7) membrane potential, respectively (Table 4). These findings demonstrate that, although γ2 and CNIH-3 relieve polyamine channel block, the steepness of block is unchanged.
Table 4. Spermine block rates in GluA2 receptors with auxiliary proteins.
| Receptor | Two-conductance permeant blocker model | n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kon | koff | kperm | k1 | k1' | Kd(0mV) | ||||||||
| a (µM−1s−1) | b (mV) | c (s−1) | d (mV) | e (s−1) | f (mV) | (µM) | |||||||
| GluA2 | 31 | 199 | 184 | -20 | 23 | 19 | 4.55E+09 | 2.95E+07 | 3.3 | 7 | |||
| SEM | 6 | 94 | 44 | 1 | 9 | 2 | 1.93E+09 | 2.04E+07 | 0.5 | ||||
| GluA2-γ2 | 24 | 369 | 499 | -13 | 131 | 16 | 1.67E+08 | 4.16E+07 | 15 | 4 | |||
| SEM | 8 | 223 | 147 | 1 | 25 | 2 | 1.64E+08 | 4.12E+07 | 4 | ||||
| GluA2 + CNIH-3 | 44 | 291 | 313 | -19 | 53 | 15 | 2.10E+09 | 1.29E+06 | 4.5 | 5 | |||
| SEM | 16 | 139 | 81 | 3 | 29 | 2 | 1.98E+09 | 1.06E+06 | 0.9 | ||||
Block rate parameters were obtained by fitting the current relaxation after the voltage steps.
Corrected equilibrium G–V plots were then fit with the modified permeant blocker model to estimate the dissociation constant for Spm at 0 mV (Kd(0mV)) as well the voltage dependence of unblock and permeation. The birectifying nature of the G–V plot was well fit at all membrane potentials for all receptor complexes. Fig. 6 (E–G) shows the mean G–V plots for GluA2 in the absence or presence of auxiliary proteins with 30 µM Spm (left), as well as fits of data from individual patch recordings (right). From these fits, the Kd(0mV) value was estimated to be 1.8 ± 0.2 µM (n = 12) for GluA2 alone and 17.9 ± 1.5 µM (n = 19) and 5.1 ± 0.8 µM (n = 12) with γ2 and CNIH-3, respectively (Table 5). As before, the voltage dependence of the Spm unblock was not altered by the presence of auxiliary proteins (Table 5), with values of −13.4 ± 1.0 mV (n = 19) and −11.7 ± 1.1 mV (n = 12) for γ2 and CNIH-3, respectively, compared with −14.1 ± 1.7 mV with GluA2 alone (n = 12; Table 5). Similarly, the voltage dependence of Spm permeation was also unchanged, with values of 15.7 ± 0.5 mV (n = 19) and 16.3 ± 0.7 mV (n = 12) for γ2 and CNIH-3, respectively, compared with 14.5 ± 1.0 mV with GluA2 alone (n = 12; Table 5). These results are consistent with the estimates obtained by fitting the current relaxations, and they further confirm that the steepness of block at AMPAR complexes is unchanged by auxiliary proteins. Consequently, γ2 and CNIH-3 do not attenuate Spm block of AMPARs by shifting the location of the block site within the membrane electric field but, rather, by making the exit of polyamines more energetically favorable.
Table 5. Equilibrium spermine block using the two-conductance model.
| Receptor | Kd(0mV) (µM) | h (mV) | k (mV) | n | |||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | SEM | Mean | SEM | Mean | SEM | ||||
| GluA2 | 1.8 | 0.2 | −14.1 | 1.7 | 14.5 | 1.0 | 12 | ||
| GluA2-γ2 | 17.9 | 1.5 | −13.4 | 1.0 | 15.7 | 0.5 | 19 | ||
| GluA2 + CNIH-3 | 5.1 | 0.8 | −11.7 | 1.1 | 16.3 | 0.7 | 12 | ||
Values were obtained by fitting the equilibrium G–V relationships; h and k were calculated using the mean b value in Table 4.
Fig. 7 summarizes our main findings with the modified permeant blocker model. Fig. 7 (A–C) illustrates the relative contribution of the two open states, ONa and OPA, to the overall AMPAR membrane conductance. As expected, permeation of Spm contributed little to the overall conductance of GluA2 AMPARs alone (Fig. 7 A). However, complex formations with γ2 and CNIH-3 substantially increased the contribution of OPA, particularly at positive membrane potentials (Fig. 7, B and C). This finding is further emphasized by comparing the relative proportion of AMPARs in the three different states (i.e., B, ONa, and OPA) at different membrane potentials (Fig. 7, D–F). These plots also reveal that the blocked state dominates within the physiological membrane potential range (i.e., −50 to 50 mV), underscoring the importance of the polyamine channel block in shaping the signaling properties of AMPARs at glutamatergic synapses.
Figure 7.
Spermine conductance is increased by auxiliary proteins. (A–C) Relative conductance of Na+ (left axis, gray lines) and Spm (right axis, colored lines) for GluA2, GluA2-γ2, and GluA2 + CNIH-3, calculated from G–V fits using the two-conductance model of polyamine block (Eqs. 16 and 17). (D–F) Proportion of open channels that are nonconducting (B; broken lines), conducting either Na+ (ONa, black lines) or Spm (OPA, colored lines), calculated from the two-conductance model of polyamine block (Eqs. 23 and 24).
Discussion
The present study advances our understanding of polyamine channel block of AMPARs in two important ways. First, we show that coassembly of GluA2 AMPARs with auxiliary subunits γ2 and CNIH-3 relieves polyamine channel block by enhancing blocker permeation rates. A similar mechanism also explains the attenuation of polyamine block of GluK2 KARs by Neto1 and Neto2 (Brown et al., 2016), although Spm permeation is almost two orders of magnitude greater for AMPARs. From a physiological perspective, relief of polyamine channel block will ensure unconstrained signaling by AMPARs at glutamatergic synapses expressing γ2 and CNIH-3. Second, we propose that cytoplasmic polyamines act on AMPARs by behaving as both a channel blocker and a permeant ion that contributes appreciably to the overall charge transfer. Whether these different mechanisms can be explained by the blocker molecule adopting two distinct conformations in the pore, as proposed for channel block of cyclic nucleotide-gated channels (Lu and Ding, 1999) or K+ channels (Miller, 1982), awaits future study.
Structural and functional basis of polyamine permeation
The structural mechanism by which AMPAR and KAR auxiliary proteins attenuate polyamine block is still unresolved. Initial studies proposed a charge screening mechanism for relieving polyamine block, whereby positively charged residues in the C-terminal tails of TARP (Soto et al., 2014) and Neto (Fisher and Mott, 2012) auxiliary proteins interact with the cytoplasmic portion of the AMPAR and KAR pore, respectively. This charge screening mechanism would be expected to affect the ability of the blocker to reach its block site. However, given that the rate of channel block (i.e., kon) estimated in this study is unchanged when AMPARs coassemble with γ2 and CNIH-3, an alternative explanation is needed to describe the effects of auxiliary proteins on channel block. Because AMPAR and KAR auxiliary proteins primarily affect blocker exit rates from the open channel (i.e., koff and kperm), it can be concluded that they attenuate block by curtailing the time the blocker molecule resides at its block site. As such, it would be expected that auxiliary subunits alter the properties of the pore, making it unfavorable for channel block, as already proposed for heteromeric KARs (Brown et al., 2016). In agreement with this, several conserved residues along the M3 helix of KARs that are adjacent to the pore are crucial in determining the degree of polyamine block (Wilding et al., 2010; Lopez et al., 2013). Likewise, Neto2 interacts with the M3-S2 linker of KARs (Griffith and Swanson, 2015), which may, in turn, affect the positioning of the pore-lining helices. By interacting with pore-lining or adjacent residues, auxiliary proteins may alter the architecture of the pore, affecting the ability of polyamines to block. More recent work has identified a group of transmembrane residues that are critical for γ2 and CNIH-3 modulation of AMPAR gating, which have yet to be tested for their effect on polyamine channel block (Hawken et al., 2017). Interestingly, auxiliary proteins were also shown to increase the Ca+ permeability through recombinant GluA1 AMPARs (Coombs et al., 2012). Consequently, additional work is still needed to provide a structural understanding of how auxiliary proteins alter the pore properties of AMPARs and KARs.
Does polyamine permeation have a role in regulating cellular polyamine levels?
Polyamines are essential for life and fulfill many roles, such as regulating protein and nucleic acid synthesis and structure, cell proliferation, differentiation, and apoptosis (Miller-Fleming et al., 2015; Pegg, 2016). Not surprisingly, polyamine levels are tightly regulated within cells, and disruption of polyamine metabolism is associated with several disease states from neurodegeneration to metabolic disorders and cancer (Miller-Fleming et al., 2015). Even the relative proportions of different polyamines within cells are critically important. For example, the X-linked intellectual disability disorder, Snyder-Robinson syndrome, is caused by a deficiency in Spm because of the inactivation of the Spm synthase gene (Cason et al., 2003).
Given the importance of polyamines, cells have developed a variety of mechanisms to tightly control their biosynthesis, catabolism, and transport. Although the mechanisms regulating polyamine biosynthesis and catabolism are well understood (Casero and Pegg, 2009; Pegg, 2009), the molecular events that lead to polyamine transport in mammalian cells are less clear (Poulin et al., 2012). It has generally been assumed that mammalian cells must express a currently unidentified polyamine transporter(s) to regulate intracellular polyamine levels (Poulin et al., 2012; though see Sala-Rabanal et al., 2013). As a result, the potential role of ion channels, such as AMPARs, as polyamine transporters has been inadvertently overlooked.
Polyamine transport may be causally linked to AMPARs through their proposed roles in certain cancers. For example, elevated levels of polyamines have long been associated with cell growth and cancer (Gerner and Meyskens, 2004), with more recent work linking AMPARs to cancer. For example, AMPAR expression has been linked to the occurrence of pancreatic (Ripka et al., 2010; Herner et al., 2011) and kidney (Hu et al., 2014; von Roemeling et al., 2014) cancers. Furthermore, AMPAR antagonists attenuate tumor growth in breast and lung carcinoma, colon adenocarcinoma, and neuroblastoma cells (Rzeski et al., 2002; Stepulak et al., 2007). The elevated levels of extracellular polyamine levels, coupled with the prolonged signaling of ionotropic glutamate receptors reported in many cancers (Prickett and Samuels, 2012), would provide the appropriate environment to permit the slow but steady transport of polyamines into cells, even at resting membrane potentials. Consequently, although the mechanism by which AMPARs stimulate tumor growth is still unresolved, the ability of AMPARs to transport polyamines reported in the present study may be an important mechanism to consider in future studies.
Supplementary Material
Acknowledgments
We thank members of the Bowie laboratory for insightful discussions of the manuscript.
This work was supported by an operating grant from the Canadian Institutes of Health Research (grant number: FRN 82804; to D. Bowie). H. McGuire was supported by a postdoctoral fellowship from the Natural Sciences and Engineering Research Council of Canada.
The authors declare no competing financial interests.
Author contributions: P.M.G.E Brown designed and performed experiments, analyzed the data, and wrote the manuscript. H. McGuire designed the experiments and analyzed data. D. Bowie designed the experiments and wrote the manuscript. All authors approved the final version of the manuscript.
Richard W. Aldrich served as editor.
References
- Bähring R., Bowie D., Benveniste M., and Mayer M.L.. 1997. Permeation and block of rat GluR6 glutamate receptor channels by internal and external polyamines. J. Physiol. 502:575–589. 10.1111/j.1469-7793.1997.575bj.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baronas V.A., and Kurata H.T.. 2014. Inward rectifiers and their regulation by endogenous polyamines. Front. Physiol. 5:325 10.3389/fphys.2014.00325 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowie D. 2002. External anions and cations distinguish between AMPA and kainate receptor gating mechanisms. J. Physiol. 539:725–733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowie D., and Mayer M.L.. 1995. Inward rectification of both AMPA and kainate subtype glutamate receptors generated by polyamine-mediated ion channel block. Neuron. 15:453–462. 10.1016/0896-6273(95)90049-7 [DOI] [PubMed] [Google Scholar]
- Bowie D., Lange G.D., and Mayer M.L.. 1998. Activity-dependent modulation of glutamate receptors by polyamines. J Neurosci. 8175–8185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowie D., Bähring R., and Mayer M.L.. 1999. Block of AMPA and kainate receptors by polyamines and arthropod toxins. In Ionotropic Glutamate Receptors in the CNS: Handbook of Experimental Pharmacology. Jonas P., and Monyer H., editors. Springer, Berlin: 251–273. 10.1007/978-3-662-08022-1_7 [DOI] [Google Scholar]
- Brown P.M., Aurousseau M.R., Musgaard M., Biggin P.C., and Bowie D.. 2016. Kainate receptor pore-forming and auxiliary subunits regulate channel block by a novel mechanism. J. Physiol. 594:1821–1840. 10.1113/JP271690 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casero R.A., and Pegg A.E.. 2009. Polyamine catabolism and disease. Biochem. J. 421:323–338. 10.1042/BJ20090598 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cason A.L., Ikeguchi Y., Skinner C., Wood T.C., Holden K.R., Lubs H.A., Martinez F., Simensen R.J., Stevenson R.E., Pegg A.E., and Schwartz C.E.. 2003. X-linked spermine synthase gene (SMS) defect: the first polyamine deficiency syndrome. Eur. J. Hum. Genet. 11:937–944. 10.1038/sj.ejhg.5201072 [DOI] [PubMed] [Google Scholar]
- Coombs I.D., Soto D., Zonouzi M., Renzi M., Shelley C., Farrant M., and Cull-Candy S.G.. 2012. Cornichons modify channel properties of recombinant and glial AMPA receptors. J. Neurosci. 32:9796–9804. 10.1523/JNEUROSCI.0345-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawe G.B., Musgaard M., Aurousseau M.R.P., Nayeem N., Green T., Biggin P.C., and Bowie D.. 2016. Distinct Structural Pathways Coordinate the Activation of AMPA Receptor-Auxiliary Subunit Complexes. Neuron. 89:1264–1276. 10.1016/j.neuron.2016.01.038 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dingledine R., Borges K., Bowie D., and Traynelis S.F.. 1999. The glutamate receptor ion channels. Pharmacol. Rev. 51:7–61. [PubMed] [Google Scholar]
- Fisher J.L., and Mott D.D.. 2012. The auxiliary subunits Neto1 and Neto2 reduce voltage-dependent inhibition of recombinant kainate receptors. J. Neurosci. 32:12928–12933. 10.1523/JNEUROSCI.2211-12.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu L.Y., Cummins T.R., and Moczydlowski E.G.. 2012. Sensitivity of cloned muscle, heart and neuronal voltage-gated sodium channels to block by polyamines: a possible basis for modulation of excitability in vivo. Channels (Austin). 6:41–49. 10.4161/chan.19001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerner E.W., and Meyskens F.L. Jr. 2004. Polyamines and cancer: old molecules, new understanding. Nat. Rev. Cancer. 4:781–792. 10.1038/nrc1454 [DOI] [PubMed] [Google Scholar]
- Gomez M., and Hellstrand P.. 1995. Effects of polyamines on voltage-activated calcium channels in guinea-pig intestinal smooth muscle. Pflugers Arch. 430:501–507. 10.1007/BF00373886 [DOI] [PubMed] [Google Scholar]
- Griffith T.N., and Swanson G.T.. 2015. Identification of critical functional determinants of kainate receptor modulation by auxiliary protein Neto2. J. Physiol. 593:4815–4833. 10.1113/JP271103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo D., and Lu Z.. 2000. Mechanism of cGMP-gated channel block by intracellular polyamines. J. Gen. Physiol. 115:783–798. 10.1085/jgp.115.6.783 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haghighi A.P., and Cooper E.. 1998. Neuronal nicotinic acetylcholine receptors are blocked by intracellular spermine in a voltage-dependent manner. J. Neurosci. 18:4050–4062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hawken N.M., Zaika E.I., and Nakagawa T.. 2017. Engineering defined membrane-embedded elements of AMPA receptor induces opposing gating modulation by cornichon 3 and stargazin. J. Physiol. 595:6517–6539. 10.1113/JP274897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herner A., Sauliunaite D., Michalski C.W., Erkan M., De Oliveira T., Abiatari I., Kong B., Esposito I., Friess H., and Kleeff J.. 2011. Glutamate increases pancreatic cancer cell invasion and migration via AMPA receptor activation and Kras-MAPK signaling. Int. J. Cancer. 129:2349–2359. 10.1002/ijc.25898 [DOI] [PubMed] [Google Scholar]
- Horie M., Irisawa H., and Noma A.. 1987. Voltage-dependent magnesium block of adenosine-triphosphate-sensitive potassium channel in guinea-pig ventricular cells. J. Physiol. 387:251–272. 10.1113/jphysiol.1987.sp016572 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Takano N., Xiang L., Gilkes D.M., Luo W., and Semenza G.L.. 2014. Hypoxia-inducible factors enhance glutamate signaling in cancer cells. Oncotarget. 5:8853–8868. 10.18632/oncotarget.2593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson A.C., and Nicoll R.A.. 2011. The expanding social network of ionotropic glutamate receptors: TARPs and other transmembrane auxiliary subunits. Neuron. 70:178–199. 10.1016/j.neuron.2011.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamboj S.K., Swanson G.T., and Cull-Candy S.G.. 1995. Intracellular spermine confers rectification on rat calcium-permeable AMPA and kainate receptors. J. Physiol. 486:297–303. 10.1113/jphysiol.1995.sp020812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerschbaum H.H., Kozak J.A., and Cahalan M.D.. 2003. Polyvalent cations as permeant probes of MIC and TRPM7 pores. Biophys. J. 84:2293–2305. 10.1016/S0006-3495(03)75035-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koh D.S., Burnashev N., and Jonas P.. 1995. Block of native Ca(2+)-permeable AMPA receptors in rat brain by intracellular polyamines generates double rectification. J. Physiol. 486:305–312. 10.1113/jphysiol.1995.sp020813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopatin A.N., Makhina E.N., and Nichols C.G.. 1994. Potassium channel block by cytoplasmic polyamines as the mechanism of intrinsic rectification. Nature. 372:366–369. 10.1038/372366a0 [DOI] [PubMed] [Google Scholar]
- Lopez M.N., Wilding T.J., and Huettner J.E.. 2013. Q/R site interactions with the M3 helix in GluK2 kainate receptor channels revealed by thermodynamic mutant cycles. J. Gen. Physiol. 142:225–239. 10.1085/jgp.201311000 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z., and Ding L.. 1999. Blockade of a retinal cGMP-gated channel by polyamines. J. Gen. Physiol. 113:35–43. 10.1085/jgp.113.1.35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H., Saigusa A., and Irisawa H.. 1987. Ohmic conductance through the inwardly rectifying K channel and blocking by internal Mg2+. Nature. 325:156–159. 10.1038/325156a0 [DOI] [PubMed] [Google Scholar]
- Miller C. 1982. Bis-quaternary ammonium blockers as structural probes of the sarcoplasmic reticulum K+ channel. J. Gen. Physiol. 79:869–891. 10.1085/jgp.79.5.869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller-Fleming L., Olin-Sandoval V., Campbell K., and Ralser M.. 2015. Remaining Mysteries of Molecular Biology: The Role of Polyamines in the Cell. J. Mol. Biol. 427:3389–3406. 10.1016/j.jmb.2015.06.020 [DOI] [PubMed] [Google Scholar]
- Pegg A.E. 2009. Mammalian polyamine metabolism and function. IUBMB Life. 61:880–894. 10.1002/iub.230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pegg A.E. 2016. Functions of Polyamines in Mammals. J. Biol. Chem. 291:14904–14912. 10.1074/jbc.R116.731661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulin R., Casero R.A., and Soulet D.. 2012. Recent advances in the molecular biology of metazoan polyamine transport. Amino Acids. 42:711–723. 10.1007/s00726-011-0987-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prickett T.D., and Samuels Y.. 2012. Molecular pathways: dysregulated glutamatergic signaling pathways in cancer. Clin. Cancer Res. 18:4240–4246. 10.1158/1078-0432.CCR-11-1217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prieto M.L., and Wollmuth L.P.. 2010. Gating modes in AMPA receptors. J. Neurosci. 30:4449–4459. 10.1523/JNEUROSCI.5613-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ripka S., Riedel J., Neesse A., Griesmann H., Buchholz M., Ellenrieder V., Moeller F., Barth P., Gress T.M., and Michl P.. 2010. Glutamate receptor GRIA3--target of CUX1 and mediator of tumor progression in pancreatic cancer. Neoplasia. 12:659–667. 10.1593/neo.10486 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rzeski W., Ikonomidou C., and Turski L.. 2002. Glutamate antagonists limit tumor growth. Biochem. Pharmacol. 64:1195–1200. 10.1016/S0006-2952(02)01218-2 [DOI] [PubMed] [Google Scholar]
- Sala-Rabanal M., Li D.C., Dake G.R., Kurata H.T., Inyushin M., Skatchkov S.N., and Nichols C.G.. 2013. Polyamine transport by the polyspecific organic cation transporters OCT1, OCT2, and OCT3. Mol. Pharm. 10:1450–1458. 10.1021/mp400024d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwenk J., Harmel N., Zolles G., Bildl W., Kulik A., Heimrich B., Chisaka O., Jonas P., Schulte U., Fakler B., and Klöcker N.. 2009. Functional proteomics identify cornichon proteins as auxiliary subunits of AMPA receptors. Science. 323:1313–1319. 10.1126/science.1167852 [DOI] [PubMed] [Google Scholar]
- Soto D., Coombs I.D., Kelly L., Farrant M., and Cull-Candy S.G.. 2007. Stargazin attenuates intracellular polyamine block of calcium-permeable AMPA receptors. Nat. Neurosci. 10:1260–1267. 10.1038/nn1966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soto D., Coombs I.D., Gratacòs-Batlle E., Farrant M., and Cull-Candy S.G.. 2014. Molecular mechanisms contributing to TARP regulation of channel conductance and polyamine block of calcium-permeable AMPA receptors. J. Neurosci. 34:11673–11683. 10.1523/JNEUROSCI.0383-14.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stepulak A., Sifringer M., Rzeski W., Brocke K., Gratopp A., Pohl E.E., Turski L., and Ikonomidou C.. 2007. AMPA antagonists inhibit the extracellular signal regulated kinase pathway and suppress lung cancer growth. Cancer Biol. Ther. 6:1908–1915. 10.4161/cbt.6.12.4965 [DOI] [PubMed] [Google Scholar]
- Tomita S., Adesnik H., Sekiguchi M., Zhang W., Wada K., Howe J.R., Nicoll R.A., and Bredt D.S.. 2005. Stargazin modulates AMPA receptor gating and trafficking by distinct domains. Nature. 435:1052–1058. 10.1038/nature03624 [DOI] [PubMed] [Google Scholar]
- Vandenberg C.A. 1987. Inward rectification of a potassium channel in cardiac ventricular cells depends on internal magnesium ions. Proc. Natl. Acad. Sci. USA. 84:2560–2564. 10.1073/pnas.84.8.2560 [DOI] [PMC free article] [PubMed] [Google Scholar]
- von Roemeling C.A., Radisky D.C., Marlow L.A., Cooper S.J., Grebe S.K., Anastasiadis P.Z., Tun H.W., and Copland J.A.. 2014. Neuronal pentraxin 2 supports clear cell renal cell carcinoma by activating the AMPA-selective glutamate receptor-4. Cancer Res. 74:4796–4810. 10.1158/0008-5472.CAN-14-0210 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilding T.J., Chen K., and Huettner J.E.. 2010. Fatty acid modulation and polyamine block of GluK2 kainate receptors analyzed by scanning mutagenesis. J. Gen. Physiol. 136:339–352. 10.1085/jgp.201010442 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong A.Y., Maclean D.M., and Bowie D.. 2007. Na+/Cl− dipole couples agonist binding to kainate receptor activation. J. Neurosci. 27:6800–6809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodhull A.M. 1973. Ionic blockage of sodium channels in nerve. J. Gen. Physiol. 61:687–708. 10.1085/jgp.61.6.687 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.