The prokaryotic Na⁺/Ca²⁺ exchanger NCX_Mj transports Na⁺ and Ca²⁺ in a 3:1 stoichiometry

Sodium–calcium exchangers contribute to the generation of intracellular Ca²⁺ signals in numerous physiological processes. Shlosman et al. determine the ion stoichiometry of the only sodium–calcium exchanger of known atomic structure, revealing its functional similarity to mammalian exchangers.

Abstract

Intracellular Ca²⁺ signals control a wide array of cellular processes. These signals require spatial and temporal regulation of the intracellular Ca²⁺ concentration, which is achieved in part by a class of ubiquitous membrane proteins known as sodium–calcium exchangers (NCXs). NCXs are secondary-active antiporters that power the translocation of Ca²⁺ across the cell membrane by coupling it to the flux of Na⁺ in the opposite direction, down an electrochemical gradient. Na⁺ and Ca²⁺ are translocated in separate steps of the antiport cycle, each of which is thought to entail a mechanism whereby ion-binding sites within the protein become alternately exposed to either side of the membrane. The prokaryotic exchanger NCX_Mj, the only member of this family with known structure, has been proposed to be a good functional and structural model of mammalian NCXs; yet our understanding of the functional properties of this protein remains incomplete. Here, we study purified NCX_Mj reconstituted into liposomes under well-controlled experimental conditions and demonstrate that this homologue indeed shares key functional features of the NCX family. Transport assays and reversal-potential measurements enable us to delineate the essential characteristics of this antiporter and establish that its ion-exchange stoichiometry is 3Na⁺:1Ca²⁺. Together with previous studies, this work confirms that NCX_Mj is a valid model system to investigate the mechanism of ion recognition and membrane transport in sodium–calcium exchangers.

Introduction

Ca²⁺ signals control a variety of biological events in excitable and nonexcitable cells, ranging from excitation-contraction coupling in cardiac muscle to immune responses in dendritic cells (Clapham, 2007; Bers, 2008; Shumilina et al., 2011; Brini et al., 2013). Sodium–calcium exchangers (NCXs) are present in nearly every cell type and, alongside ATP-driven Ca²⁺ pumps and Ca²⁺ channels, help to regulate the concentration of intracellular Ca²⁺ (Blaustein and Lederer, 1999; Philipson and Nicoll, 2000; Cai and Lytton, 2004; Khananshvili, 2013). Like other secondary-active transporters, NCXs harness the electrochemical gradient of one substrate to drive the uphill translocation of the other. Under physiological conditions, NCX proteins operate mainly in the “forward” mode, coupling the extrusion of intracellular Ca²⁺ to the downhill uptake of Na⁺, with a stoichiometry of three Na⁺ to one Ca²⁺ (Reeves and Hale, 1984; Rasgado-Flores and Blaustein, 1987; Hinata and Kimura, 2004; Kang and Hilgemann, 2004). However, the direction of Na⁺ and Ca²⁺ fluxes is reversed under some conditions, because it depends solely on the relative concentrations of Na⁺ and Ca²⁺ and the membrane potential. Therefore, changes in these parameters fine-tune the activity of NCXs and thus adjust the concentration of free cytosolic Ca²⁺ in a wide range of biological processes (Blaustein and Lederer, 1999; Török, 2007; Bers, 2008).

To achieve coupled Na⁺/Ca²⁺ antiport, mammalian NCXs use a so-called “ping-pong” mechanism (Khananshvili, 1990; Hilgemann et al., 1991). The linchpin of this mechanism is that only one kind of ion is transported across the membrane at a time (Fig. 1 A). In other words, in contrast to symport, wherein all substrates are transported simultaneously, in NCX antiport, Na⁺ and Ca²⁺ are translocated in separate, mutually exclusive steps of the transport cycle. Each of these ion-translocation steps is thought to entail a series of reversible structural changes in the transmembrane domain of the protein that would expose ion-binding sites to either side of the cellular membrane, but not both concurrently (Liao et al., 2012, 2016; John et al., 2013; Giladi et al., 2017). Crucially, these structural changes should not take place if the antiporter is empty (Fig. 1). This “alternating-access” mechanism would explain the transduction of electrochemical energy between substrates and the well-defined stoichiometry of Na⁺/Ca²⁺ antiport (Jardetzky, 1966; Forrest et al., 2011; Liao et al., 2016). If the ion-binding sites were simultaneously accessible to both sides of the membrane, Na⁺ and Ca²⁺ would flow passively across the membrane, the preexisting electrochemical gradient of Na⁺ would dissipate, and the extruded Ca²⁺ would flow back into the cell.

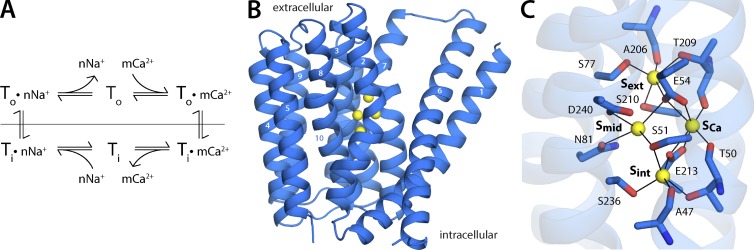
Figure 1.

Antiport cycle and structure of a Na⁺/Ca²⁺ exchanger. (A) The transporter interconverts between two primary conformational states, T_o and T_i, which expose binding sites for Na⁺ and Ca²⁺ to the outside or inside of the cell, respectively; this conformational mechanism is referred to as alternating-access. Na⁺ and Ca²⁺ compete for binding to the transporter and are translocated across the membrane in two different steps of the antiport cycle; this competitive model is referred to as ping-pong. The prototypical stoichiometry of eukaryotic NCXs is n = 3 and m = 1. (B) Crystal structure of NCX_Mj, a Na⁺/Ca²⁺ exchanger from Methanococcus jannaschii, determined by x-ray diffraction in an outward-facing conformation (Liao et al., 2012). The structure comprises 10 transmembrane helices (numbered). Four putative ion-binding sites (yellow spheres) were identified in the electron-density map. (C) Close-up of the ion-binding region. Coordinating residues for each of the four sites, referred to as S_ext, S_mid, S_Ca, and S_int, are indicated.

The recent determination of the atomic structure of an archaeal NCX homologue, denoted NCX_Mj (Fig. 1 B), opened an avenue to begin to establish the relationship between structure and function in this class of transporters (Liao et al., 2012). NCX_Mj lacks the cytosolic regulatory domains found in mammalian NCX, but many of the features of its transmembrane domain suggest that it is a plausible model system of the structural and functional unit that catalyzes Na⁺/Ca²⁺ antiport in this family (Liao et al., 2012, 2016; John et al., 2013). This notion has been substantiated by subsequent biochemical, functional, and computational studies (Almagor et al., 2014; Marinelli et al., 2014; Barthmes et al., 2016; Liao et al., 2016). This progress notwithstanding, the hallmark functional characteristic of mammalian NCX, namely the 3Na⁺:1Ca²⁺ ion-exchange stoichiometry, has not yet been conclusively demonstrated for NCX_Mj.

The initial crystal structure of NCX_Mj, captured in an outward-facing conformation (Fig. 1 B), revealed four putative ion-binding sites deep inside the protein (Fig. 1 C), in a region of high sequence conservation within the NCX family (Liao et al., 2012). Electron density signals in the so-called S_int, S_mid, and S_ext sites were originally assigned to three Na⁺ ions, while one Ca²⁺ was placed in the fourth site, or S_Ca, based on the detection of an anomalous scattering signal (Liao et al., 2012). Although consistent with the expected 3Na⁺:1Ca²⁺ stoichiometry, this assignment was later reevaluated based on subsequent computational and biochemical studies (Marinelli et al., 2014) and additional structural work (Liao et al., 2016). It is now believed that Na⁺ ions bind to S_int, S_ext, and S_Ca; the latter is thus the site for which Ca²⁺ and Na⁺ directly compete. In this view, the remaining site, S_mid, is occupied by a water molecule, not an ion (Marinelli et al., 2014; Liao et al., 2016).

Although this more recent interpretation is again compatible with the antiport stoichiometry of mammalian NCXs, the experimental data obtained to date have been inconclusive. For example, the results of existing crystallographic studies are not unequivocal in that Na⁺ and water are not distinguishable at the resolution of the data. In principle, measurements in which Na⁺ is gradually soaked out from the crystallographic buffer can be useful to conclusively reveal whether this ion is responsible for a given electron-density signal at a specific site. Indeed, for outward-facing NCX_Mj, such experiments showed that S_ext is highly sensitive to Na⁺ depletion, demonstrating that this site binds Na⁺ (Liao et al., 2016). However, the electron-density signals in S_Ca and S_int are fairly insensitive to Na⁺ depletion, as is that for S_mid; these signals change significantly only when Ca²⁺ is introduced, competing out Na⁺. Thus, the hypothesis that Na⁺ does not occupy S_mid is not conclusively ruled out by the crystallographic data, raising the possibility that the stoichiometry of ion exchange in NCX_Mj is 4Na⁺:1Ca²⁺, rather than 3:1.

Indeed, the amino acid composition of the ion-binding sites in NCX_Mj hints at this possibility. Intriguingly, the S_mid site in this exchanger is formed in part by an acidic side-chain, Asp240, which is an asparagine in all mammalian NCXs. An aspartate at this position is one of the distinguishing features of the family of potassium-dependent sodium–calcium exchangers (NCKX), which are also members of the superfamily of Ca²⁺/cation exchangers to which NCXs belong (Altimimi et al., 2013). NCKXs are thought to be structurally very similar to NCXs, but they typically transport four Na⁺ in exchange for one Ca²⁺ and one K⁺ (Szerencsei et al., 2013). Functional studies of NCX_Mj suggest that its activity is not coupled to K⁺ because the Na⁺/Ca²⁺ antiport rate is not influenced by a K⁺ gradient (Liao et al., 2012) and because the Asp240Asn mutant is fully functional (Marinelli et al., 2014). However, these findings do not necessarily rule out that Asp240 facilitates binding of a fourth Na⁺ ion to the S_mid site in the wild-type protein. In NCKX2, asparagine substitution of Asp575 (equivalent to Asp240) renders the transporter K⁺ independent, but its Na⁺/Ca²⁺ antiport activity remains (Kang et al., 2005). It appears, therefore, that the precise specificity of the different families of Ca²⁺/cation exchangers (which also include H⁺/Ca²⁺ antiporters) results from subtle changes in the amino acid composition of the ion-binding region, rather than from large architectural differences (Refaeli et al., 2016). Thus, considerable ambiguity remains regarding the coupling stoichiometry of NCX_Mj antiport, an essential parameter that must be determined to begin to relate the structure and function of this class of proteins.

Here, we probed the specific functional features of NCX_Mj through transport assays, in a reconstituted system, in the presence and absence of different electrochemical gradients and membrane potentials. Using well-controlled experimental conditions, we specifically sought to confirm or refute earlier observations pertaining to the ion specificity, electrogenicity, and mechanism of transport of this exchanger. Importantly, we successfully determined the stoichiometry of Na⁺/Ca²⁺ antiport through a quantitative approach based on reversal-potential measurements.

Materials and methods

Expression and purification

NCX_Mj was expressed and purified essentially as described previously (Liao et al., 2012). Briefly, Top10 Chemically Competent Escherichia coli (Thermo Fisher Scientific) were transformed with pBADhisNCX_Mj, containing NCX_Mj with a C-terminal octa-histidine tag and the mutation L2V. Six 1-liter cultures were grown with 100 µg/ml ampicillin at 37°C to OD₆₀₀ of 0.8–1.0, at which point expression was induced with 0.1% wt/vol l-arabinose. The cultures were incubated for 2–3 h at 37°C with shaking and then harvested and homogenized with 50 mM HEPES, pH 7.4, 50 mM NaCl, 13 mM KCl, and 10 mM CaCl₂ (protease inhibitors and DNases were added to appropriate concentrations immediately before homogenization).

The homogenized cells were lysed using cell disruption, and membrane protein was extracted by incubation with 40 mM n-dodecyl-β-d-maltoside (DDM; Anatrace) for 3–4 h at room temperature. Insoluble cell debris was removed by centrifugation, and the detergent-solubilized fraction was incubated with Talon metal affinity resin (Clontech Laboratories) for 1 h at 4°C. The resin was washed with 20 column volumes of the above buffer supplemented with 4 mM DDM and 15 mM imidazole. Histidine-tagged NCX_Mj was eluted in fractions with 300 mM imidazole-containing buffer. Eluted protein was incubated with thrombin at 10 U/mg of protein concentration for 16–20 h at room temperature to remove the histidine tag. The cleaved protein was collected and concentrated, and buffer was exchanged to 50 mM HEPES, pH 7.4, 150 mM NaCl, 5% glycerol, and 0.1% n-decyl-β-d-maltoside (DM) for further use or storage at −80°C.

Membrane reconstitution and preparation of proteoliposomes

Functional protein reconstitution was performed using a rapid dilution method as described previously (Mulligan et al., 2009). E. coli polar lipids were dried under a flow of nitrogen with swirling, resuspended in 20 mM Mes/Tris, pH 6.3, 120 mM NaCl, and mM KCl, and subjected to three cycles of freeze/thaw. These lipids were then added to the purified and cleaved NCX_Mj in DM-containing buffer to a final concentration of 15–20 µg protein/mg lipid. To achieve incorporation of protein into the E. coli membranes, the solution was rapidly diluted into detergent-free buffer (less than the critical micelle concentration of detergent). Proteoliposomes were then isolated by ultracentrifugation and either used immediately or snap-frozen and stored at −80°C. Before experiments, proteoliposomes were spun down, and buffer was exchanged to the desired buffer using three cycles of freeze/thaw followed by extrusion through a 0.4-µM filter.

Radioactive transport assays

⁴⁵Ca²⁺ transport assays were started by diluting proteoliposomes into the appropriate reaction buffer. The reaction was terminated at various time points by rapid dilution of 0.1–0.25-ml samples into ice-cold quench buffer, consisting of 20 mM Mes/Tris, pH 6.3, and 125 mM choline chloride. The quenched reaction was vacuum-filtered on a nitrocellulose membrane (Merck Millipore) and washed with 3 ml cold quench buffer. Each filter was dissolved in 3 ml scintillation cocktail, and the associated radioactivity was quantified using a scintillation counter (1450 MicroBeta JET; PerkinElmer). Reaction conditions varied depending on the experiment (see figure legends for details), but all assays, unless noted otherwise, were performed at 37°C and at 0 mV set with 5 mM K⁺ and 2 µM valinomycin. Initial rates of ⁴⁵Ca²⁺ uptake represent the change in the intraliposomal radioactivity between the 0- and 20-s time points, hereafter indicated as ΔCPM.

In the pH-dependence experiments, the value of pH was controlled with 50 mM HEPES for pH-7.3 samples; the remaining values (between pH 4.0 and 6.3) were set with 50 mM Mes/Tris. For the voltage dependence experiments, the membrane potential was set and clamped using K⁺ and valinomycin, as described previously (Fitzgerald et al., 2017). The specific buffer compositions used in each of these reversal-potential-shift experiments are given in Table 1.

Table 1. Compositions of the buffers in the reversal-potential experiments used to determine the Na⁺/Ca²⁺ antiport stoichiometry of NCX_Mj.

Figure	NaCl (mM)			45CaCl2 (µM)		KCl (mM)	EK (mV)	ChCl (mM)
	Inside	Outside		Inside	Outside	Outside		Inside	Outside
Figs. 8 A and 9 A	10	15/25		50	25	1/5/10/25/50/100	0/40/60/80/100/120	114	109/105/100/85/60/10
									99/95/90/75/50/0
Figs. 8 B and 9 B	15	25/50		100	30			134	124/120/115/100/75/25
									99/95/90/75/50/0

Probabilistic analysis of reversal-potential measurements based on linear-regression ensembles

Our experimental approach to assess the antiport stoichiometry of NCX_Mj entails tandems of ⁴⁵Ca²⁺ flux assays at different values of the external Na⁺ concentration and under an applied transmembrane potential, with other concentrations unchanged (Table 1). For each value of [Na⁺]_o, the outcome of this assay is a set of measurements of ΔCPM as a function of the applied potential, E_K. In the following, we assumed that the dependence of ΔCPM on the potential is approximately linear in a small range of voltages around the zero-flux condition, i.e., near the “reversal potential.” The rationale of this assumption is that the system is near equilibrium. We therefore used linear-regression analysis to determine the most likely value of the reversal potential associated with each series of ΔCPM measurements and also estimate the uncertainty thereof.

For a given set of n measured ΔCPM values, y_i, and the corresponding set of E_K values, x_i, the best-fit line is obtained by finding the values of two parameters, α and β, that minimize the sum of squared residuals, S, defined as

$$S={\displaystyle \sum }_{i=1}^N{\left(y_i-\alpha x_i-\beta \right)}^2.$$ (1)

The variance of the data are estimated from the best-fit line as

$${\sigma }^2=\frac{S}{N-2}.$$ (2)

If, according to a Bayesian-inference approach, we assume a Gaussian error in the measurements, the probability distribution of parameters α and β in Eq. 1 is given by

$$P\left(\alpha ,\beta \right)\propto \exp \left\{-\frac{{{\displaystyle \sum }}_{i=1}^N{\left(y_i-\alpha x_i-\beta \right)}^2}{2{\sigma }^2}\right\}.$$ (3)

This probability function describes the ensemble of possible linear fits to the experimental data, including the least-squares fit (Fig. 9, A and B). To generate this ensemble, we used a Metropolis Monte-Carlo algorithm in which the line parameters α and β are randomly varied within a plausible range, and Eq. 3 is used to determine whether the resulting fit is added to the sample. From this data, an ensemble of reversal-potential values can be obtained by identifying the x-intercept of each of the fitted lines, that is, the values of E_K for which ΔCPM = 0.

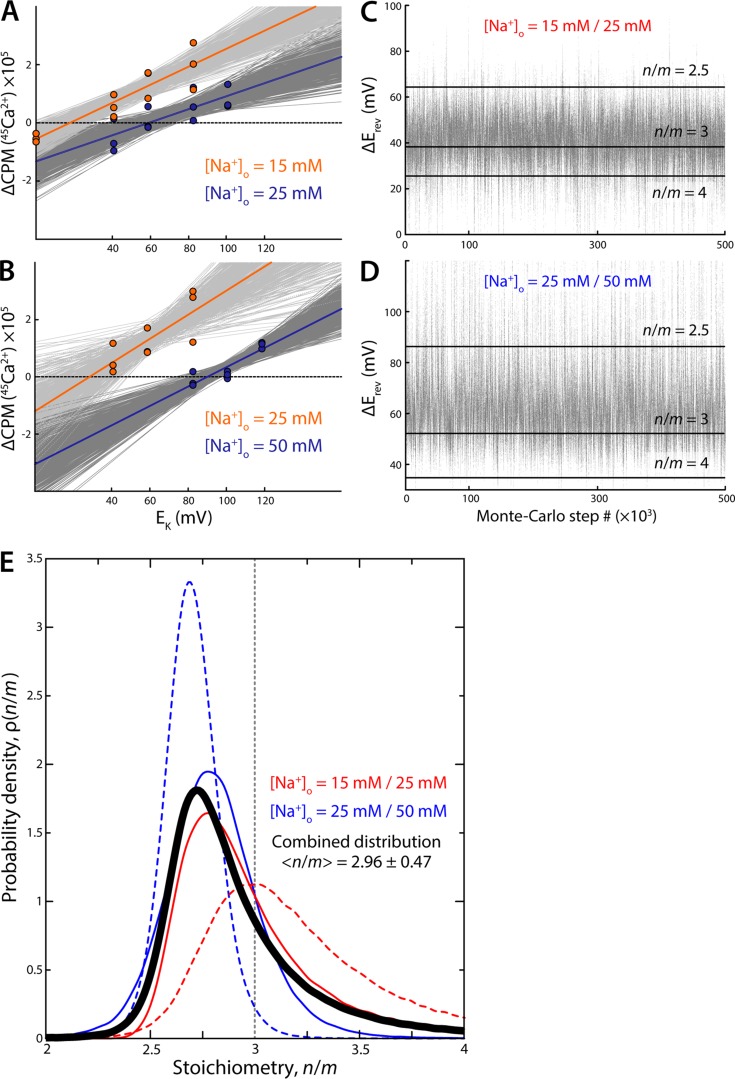
Figure 9.

Statistical derivation of the stoichiometry value from the reversal-potential experiments. (A) Ensemble of linear fits to the experimental data near the zero-flux condition, for two concentrations of external Na⁺. The best-fit line is shown in each case, in orange and blue. Suboptimal fits, characterized by the distribution in Eq. 3 and generated using a Metropolis Monte Carlo algorithm (Materials and methods), are shown in dark and light gray. (B) Same as A for a different set of experimental conditions. (C) Reversal-potential-shift values derived from the ensemble of linear fits in A. Each value in the plot is the difference between the x-intercepts of the two linear fits generated at each step of the Monte Carlo algorithm (one for each value of [Na⁺]_o). Horizontal black lines indicate the expected values of ΔE_rev for stoichiometry n/m = 2.5, n/m = 3, and n/m = 4. (D) Same as C for the experimental condition used in B. (E) Probability distributions of the stoichiometry value deduced from the ensemble of ΔE_rev values in C and D, i.e., from the experimental results in A and B, using Eq. 9 (solid red and blue lines). The distributions obtained using the experimental data shown in Fig. 8 are also shown (dashed lines). The combined probability distribution for these four experiments is shown is black. The expectation value, defined as $⟨x⟩={\int }^{\text{}}x \rho \left(x\right) dx,$ where x = n/m, is indicated.

This approach can be easily extended to analyze the reversal-potential-shift experiments. Specifically, the probability distribution generated by the Monte Carlo approach is now given by

$$P\left({\alpha }_1,{\beta }_1,{\alpha }_2,{\beta }_2\right)= P\left({\alpha }_1,{\beta }_1\right)P\left({\alpha }_2,{\beta }_2\right),$$ (4)

where α₁ and β₁, and α₂ and β₂, are the parameters of the linear regression for each set of measurements, that is, for each value of the external Na⁺ concentration. Note that these two regressions are independent from each other, even though in practice we generate them simultaneously. From this set of tandem fits, it is straightforward to derive the ensemble of values of the shift in reversal potential associated with the two set of ΔCPM measurements, by comparing the respective values of the x-intercepts.

Results

NCX_Mj is a secondary-active Na⁺/Ca²⁺ antiporter

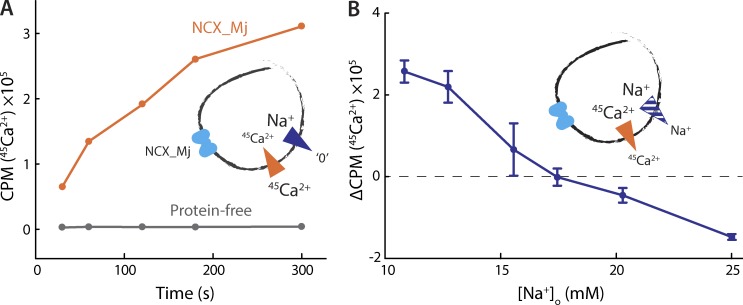
We initially assessed the transport activity of NCX_Mj by reconstituting the protein into liposomes formed from E. coli polar lipids and measuring ⁴⁵Ca²⁺ uptake in the presence of a large, outwardly directed Na⁺ gradient. These experiments reveal robust ⁴⁵Ca²⁺ uptake, presumably coupled to efflux of intraliposomal Na⁺ (Fig. 2 A). Under the same conditions, protein-free liposomes show no change in their radioactivity (Fig. 2 A), implying that the observed ⁴⁵Ca²⁺ uptake results from NCX_Mj-mediated antiport, with both ions moving downhill (internal [⁴⁵Ca²⁺] is clamped near zero with EGTA).

Figure 2.

Functional reconstitution of NCX_Mj. (A) ⁴⁵Ca²⁺ uptake into protein-free (gray) or NCX_Mj-containing (orange) liposomes in the presence of an outwardly directed Na⁺ gradient. The liposomes were preloaded with 100 mM NaCl and 1 µM ⁴⁵Ca²⁺, set with EGTA, and external buffers contained 5 µM ⁴⁵CaCl₂ and were nominally Na⁺-free. The presence of valinomycin and K⁺ dissipated any transmembrane voltage generated by the transport process. Valinomycin and K⁺ were used in all experiments, unless specifically noted otherwise. (B) Initial rates of ⁴⁵Ca²⁺ transport as a function of external Na⁺ concentration. The liposomes were preloaded with buffer containing 25 mM NaCl and 100 µM ⁴⁵CaCl₂. External buffers contained 25 µM ⁴⁵CaCl₂ and varying amounts of NaCl. A triplicate dataset is averaged (error bars represent SEM). This experiment was reproduced on two separate occasions.

We next tested whether NCX_Mj functions as a secondary-active transporter, that is, if a preexisting concentration gradient of either ion drives uphill transport of the other. To this end, we performed a ⁴⁵Ca²⁺ uptake assay with a fixed, outward ⁴⁵Ca²⁺ gradient and a variable, inward Na⁺ gradient, monitoring the resulting direction and magnitude of ⁴⁵Ca²⁺ flow. Initially, in the presence of symmetrical [Na⁺], we observe ⁴⁵Ca²⁺ efflux, driven by its outwardly directed gradient. However, as we gradually increase the outward Na⁺ gradient (by lowering external [Na⁺]), the direction of ⁴⁵Ca²⁺ flux reverses, and uphill ⁴⁵Ca²⁺ uptake occurs instead (Fig. 2 B). These data demonstrate that NCX_Mj can mediate Na⁺-driven active transport of Ca²⁺, and that the direction of ionic flux depends only on the relative concentration gradients of the two ions.

Na⁺ and Ca²⁺ compete for binding to NCX_Mj

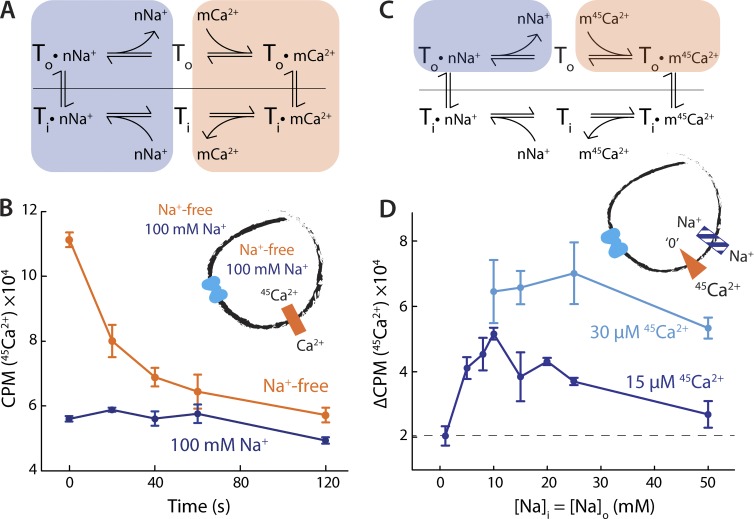
In mammalian NCXs, Na⁺ and Ca²⁺ are translocated in separate steps of the transport cycle (Fig. 3 A), and each ion competes for binding with the other. This so-called ping-pong model implies that in the absence of Na⁺, for example, the antiporter must be able to “exchange” a Ca²⁺ ion from one side of the membrane for another Ca²⁺ ion on the other side (Fig. 3 A, shaded orange portion of the cycle). This process results in no net change in Ca²⁺ concentration because the same chemical species is translocated reversibly back and forth. However, if Ca²⁺ inside the liposome is radioactively labeled, while that outside is not, “hot” and “cold” ions will translocate and rapidly exchange across the membrane, driven by the respective chemical gradients, leading to a detectable efflux of radioactive Ca²⁺.

Figure 3.

Na⁺ and Ca²⁺ compete for binding. (A) Antiport cycle of a prototypical NCX, highlighting the separate Na⁺/Na⁺ and Ca²⁺/Ca²⁺ exchange reactions postulated by the ping-pong model. (B) Ca²⁺/⁴⁵Ca²⁺ exchange in Na⁺-free (orange) or saturating Na⁺ (blue) conditions. The liposomes were preloaded with buffer containing 50 µM ⁴⁵CaCl₂ and either 100 mM NaCl (blue) or 100 mM choline chloride (orange). In the external buffer, ⁴⁵Ca²⁺ was substituted for the same concentration of CaCl₂. Note that buffers for this experiment were valinomycin-free. A triplicate dataset is averaged (error bars represent SEM). This experiment was reproduced on three separate occasions. (C) Antiport cycle of a prototypical NCX, highlighting the process of external competitive binding to the transporter. (D) Initial rates of Na⁺/Ca²⁺ exchange as a function of [Na⁺], as external and internal concentrations were varied simultaneously. The liposomes were preloaded with 100 µM EGTA; either 30 µM (cyan) or 15 µM (blue) ⁴⁵CaCl₂ was applied to the reaction buffer. A triplicate dataset is averaged (error bars represent SEM).

To determine whether NCX_Mj uses a ping-pong mechanism of ion exchange, we therefore tested whether it can exchange Ca²⁺ under nominally Na⁺-free conditions. Indeed, when we loaded NCX_Mj-containing liposomes with radioactively labeled ⁴⁵Ca²⁺ and diluted them into a buffer containing unlabeled Ca²⁺, we observed a time-dependent decrease in luminal radioactivity, indicative of Ca²⁺/⁴⁵Ca²⁺ exchange (Fig. 3 B). The ping-pong model also predicts that an increase in [Na⁺] should result in inhibition of the Ca²⁺/⁴⁵Ca²⁺ exchange reaction, because of the increased population of Na⁺-bound transporters (Fig. 3 A, shaded blue portion). Consistent with this prediction, addition of 100 mM NaCl to internal and external solutions completely abolished Ca²⁺/⁴⁵Ca²⁺ exchange (Fig. 3 B).

If, as we posit, this inhibition is caused by the competition of Na⁺ and Ca²⁺ for binding sites in the transporter, it should be possible to rescue Ca²⁺ binding by either lowering [Na⁺] or increasing [Ca²⁺]. To evaluate whether that is the case, we designed an antiport experiment that specifically probes this hypothetical competition (Fig. 3 C). In this experiment, we applied ⁴⁵Ca²⁺ externally to liposomes preloaded with EGTA (i.e., there is no free Ca²⁺ inside, cold or hot). We also applied varied amounts of Na⁺, with equal concentrations externally and internally. The “infinite” ⁴⁵Ca²⁺ gradient ensures that the initial influx of ⁴⁵Ca²⁺ into the liposomes is effectively irreversible, provided that the internal Na⁺ concentration is high enough to permit the transporter to complete the antiport cycle. However, as the external Na⁺ concentration increases, Na⁺ should begin to compete with ⁴⁵Ca²⁺ for binding to the outward-facing transporters, increasingly hindering ⁴⁵Ca²⁺ uptake.

Consistent with our earlier experiment, we observed minimal ⁴⁵Ca²⁺ uptake at high concentrations of external Na⁺ (Fig. 3 D). Uptake increases with decreasing (symmetric) [Na⁺], peaking at ∼10 mM, and then decreasing again as the internal [Na⁺] becomes insufficient to allow completion of the transport cycle (Fig. 3 D). In a similar way, increasing the concentration of external ⁴⁵Ca²⁺, leaving Na⁺ unchanged, also rescued ⁴⁵Ca²⁺ uptake, again consistent with a model in which the two ions compete for binding (Fig. 3 D). Collectively, these data strongly indicate that Na⁺ and Ca²⁺ are transported separately, that is, that NCX_Mj operates via a ping-pong mechanism, like the mammalian NCXs.

NCX_Mj antiport activity is independent of K⁺

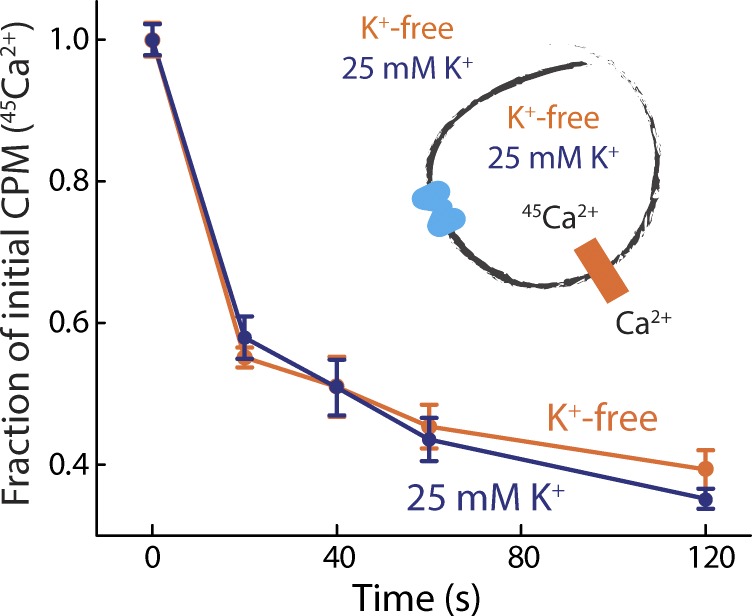
Mammalian Na⁺/Ca²⁺ exchangers are stringently specific for Na⁺ over other monovalent cations and do not cotransport K⁺ (Yasui and Kimura, 1990). However, as previously noted, elements in the ion-binding sites of NCX_Mj resemble those in K⁺-dependent Na⁺/Ca²⁺ exchangers. Earlier ⁴⁵Ca²⁺ flux experiments showed that the rate of antiport of NCX_Mj is not influenced by a K⁺ gradient, contrary to what would be expected for a K⁺-coupled transporter (Liao et al., 2012). Yet these data do not completely rule out the possibility that in NCX_Mj K⁺ is cotranslocated with both Na⁺ and Ca²⁺, or that K⁺ is constitutively bound during the transport cycle. To assess this hypothetical K⁺ dependence, we performed a Ca²⁺/⁴⁵Ca²⁺ exchange assay in the presence or absence of K⁺. Removal of K⁺ from all solutions had no observable effect on the rate of Ca²⁺/⁴⁵Ca²⁺ exchange (Fig. 4), indicating that K⁺ is not required for transport under these conditions. Taken together with earlier ⁴⁵Ca²⁺ flux experiments (Liao et al., 2012), this result also implies that the Na⁺/Ca²⁺ antiport cycle in NCX_Mj is K⁺ independent.

Figure 4.

NCX_Mj activity is independent of K⁺. Ca²⁺/⁴⁵Ca²⁺ exchange in K⁺-free (orange) or 25 mM K⁺ (blue) buffers. Liposomes, preloaded with either choline chloride or KCl buffer with 50 µM ⁴⁵CaCl₂, were diluted into choline chloride or KCl reaction buffer containing 25 µM CaCl₂. Note that buffers for this experiment were valinomycin-free. A triplicate dataset is averaged (error bars represent SEM).

NCX_Mj is inhibited at low pH but does not transport H⁺

The superfamily of Ca²⁺/cation exchangers include not only K⁺-dependent and -independent antiporters, but also Ca²⁺/H⁺ exchangers (Hirschi, 2001; Cai and Lytton, 2004). Na⁺/Ca²⁺ antiport in NCX_Mj is pH dependent (Liao et al., 2012; Marinelli et al., 2014) but it has not been conclusively established whether this dependence is the result of H⁺-driven transport or a different process. Thus, we next set out to determine whether protons are coupled to Ca²⁺ transport in NCX_Mj.

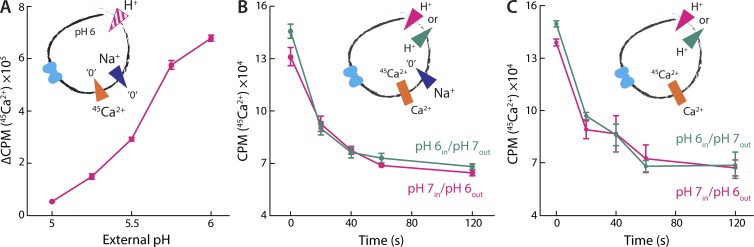
To confirm that Na⁺/Ca²⁺ antiport is pH dependent, we measured Na⁺-driven ⁴⁵Ca²⁺ uptake in the presence of varying external pH. As expected, lowering the external pH from 6 to 5 (at constant internal pH of 6) progressively diminished the rate of ⁴⁵Ca²⁺ uptake; at external pH 5, uptake was negligible (Fig. 5 A). To evaluate the possibility of H⁺/Ca²⁺ antiport, therefore, we considered conditions with pH >6, where NCX_Mj is clearly active. As shown in Fig. 5 B, however, our data demonstrate that opposite pH gradients in this range have no effect on the rate of Na⁺/Ca²⁺ antiport, ruling out the possibility of a proton-driven mechanism. Opposite pH gradients also do not affect Ca²⁺/⁴⁵Ca²⁺ exchange (Fig. 5 C), supporting this conclusion. Thus, the influence of pH on the transport rate likely results from a pH-dependent modulation of the protein activity, through an unknown mechanism. Previous studies have suggested that this modulation might be caused by H⁺ competing out Na⁺ and/or Ca²⁺ binding at sufficiently low pH (Marinelli et al., 2014; Liao et al., 2016). However, other sites in the structure could respond to changes in pH as well. For example, the principal gating element in the alternating-access mechanism of NCX_Mj, thought to comprise helices TM1 and TM6 (Fig. 1 B), features four acidic residues whose protonation state might influence the rate of transport. In future studies, it would be of interest to analyze this mechanism of pH inhibition in greater detail.

Figure 5.

NCX_Mj is inhibited at low pH but does not transport H⁺. (A) Initial rates of Na⁺/⁴⁵Ca²⁺ antiport in the presence of a varying inwardly directed H⁺ gradient. Liposomes were preloaded with MES/Tris pH 6.3 buffer containing 100 mM NaCl and 100 µM EGTA and diluted into Na⁺-free reaction buffers with 50 µM ⁴⁵CaCl₂ and varying pH values. (B) Na⁺/Ca²⁺ antiport with inwardly (pink) and outwardly (green) directed H⁺ gradients. Two sets of liposomes were preloaded with 50 µM ⁴⁵Ca²⁺ and a Na⁺-free buffer with pH set to either 6.3 or 7.3. They were then diluted into their respective reaction buffers containing 100 mM NaCl and 50 µM Ca²⁺ set to pH 7.3 (for pH 6.3 liposomes) and pH 6.3 (for pH 7.3 liposomes). (C) ⁴⁵Ca²⁺/Ca²⁺ exchange under Na⁺-free conditions with inwardly (pink) and outwardly (green) directed H⁺ gradients. Liposomes preloaded with 50 µM ⁴⁵CaCl₂–containing buffer were diluted into a 50 µM CaCl₂–containing buffer. Note that buffers for this experiment were valinomycin-free. A triplicate dataset is averaged (error bars represent SEM).

Na⁺/Ca²⁺ antiport by NCX_Mj is electrogenic and transfers a positive charge

A key physiological feature of mammalian NCXs is that Na⁺/Ca²⁺ antiport is electrogenic, making these transporters sensitive to changes in transmembrane voltage, for example during the generation of cardiac action potentials (Weber et al., 2002). Recent solid supported membrane (SSM)–based electrophysiological recordings have indicated that the Na⁺/Ca²⁺ antiport cycle in NCX_Mj is also electrogenic (Barthmes et al., 2016). We sought to confirm this result by examining the voltage dependence of Na⁺/Ca²⁺ antiport in our experimental conditions.

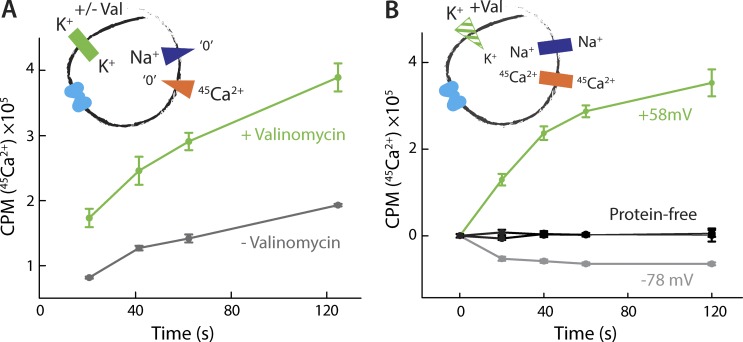
We began by quantifying the rate of Na⁺-driven ⁴⁵Ca²⁺ uptake with or without the K⁺-ionophore valinomycin, under equal K⁺ concentrations on both sides of the membrane. Valinomycin allows K⁺ to permeate the membrane, thereby dissipating voltages generated by an electrogenic transport system. We indeed observed that addition of this ionophore increased the initial rate of ⁴⁵Ca²⁺ uptake dramatically, compared with the valinomycin-free experiment (Fig. 6 A), supporting the notion that the activity of NCX_Mj is electrogenic.

Figure 6.

Electrogenic nature of Na⁺/Ca²⁺ antiport. (A) Na⁺/Ca²⁺ antiport in the presence (green) or absence (gray) of valinomycin. Liposomes were preloaded with 100 mM NaCl buffer and diluted into a reaction buffer containing 50 µM ⁴⁵CaCl₂. This experiment was reproduced on three separate occasions. (B) Na⁺/Ca²⁺ antiport with inside-positive (green) and inside-negative (gray) membrane potentials. Liposomes preloaded with 25 mM NaCl and 50 µM ⁴⁵CaCl₂ were diluted into a reaction buffer containing 25 mM NaCl and 25 µM ⁴⁵CaCl₂. The membrane potential was set with 10 mM KCl internally, and either 100 mM KCl (green) or 0.5 mM (gray) KCl externally. Analogous measurements using protein-free liposomes are also shown (black). A triplicate dataset is averaged (error bars represent SEM).

We further tested whether the direction and magnitude of ionic flux in NCX_Mj are a function of the membrane potential. To do so, we examined antiport in the presence of symmetric concentrations of Na⁺ and ⁴⁵Ca²⁺ and used asymmetrical K⁺ concentrations in the presence of valinomycin to establish an inside-positive or inside-negative transmembrane voltage. These conditions resulted in oppositely directed ⁴⁵Ca²⁺ fluxes, with influx at ∼60 mV and efflux at approximately −80 mV (Fig. 6 B). These data demonstrate that the membrane potential alone is sufficient to drive Na⁺/Ca²⁺ antiport and determine its direction, as is expected for an electrogenic transporter. Moreover, the sign of the voltage dependence demonstrates that the complete antiport cycle results in the net transfer of a positive charge across the membrane, in the same direction as that of Na⁺ flux (i.e., outward in this condition). This result establishes that more than two Na⁺ ions are exchanged for each Ca²⁺ ion in each antiport cycle. However, further experiments are required to reveal the magnitude of this charge, that is, the precise stoichiometry of Na⁺/Ca²⁺ antiport.

Determination of the antiport stoichiometry with reversal-potential measurements

In the antiport cycle of NCX_Mj, m Ca²⁺ ions cross the membrane in stoichiometric exchange with n Na⁺ ions moving in the opposite direction. This process can be represented by the following reaction:

$$n{\mathrm{Na}}_i^{+}+m{\mathrm{Ca}}_o^{2+}\rightleftharpoons n{\mathrm{Na}}_o^{+}+m{\mathrm{Ca}}_i^{2+}.$$

Because Na⁺/Ca²⁺ antiport is electrogenic (Fig. 6), completion of this cycle is accompanied by a net transfer of charge across the membrane. This separation of charge generates a transmembrane voltage that increasingly opposes further accumulation of ions. Ultimately, the system reaches a point where the work that is required to transfer additional charge against the membrane potential matches exactly the free energy gained from moving ions down their concentration gradients, and the net flux becomes zero. At this point of thermodynamic equilibrium, the value of the membrane potential is known as the reversal potential, or E_rev. Specifically, the reversal potential obeys the following relationship:

$$E_{rev}= \frac{-E_{\mathrm{o}}}{\frac{n}{m} - 2}\left(\frac{n}{m}\log \frac{\left[{\mathrm{Na}}_i^{+}\right]}{\left[{\mathrm{Na}}_o^{+}\right]}-\log \frac{\left[{\mathrm{Ca}}_i^{2+}\right]}{\left[{\mathrm{Ca}}_o^{2+}\right]}\right),$$ (5)

where n/m is the stoichiometry of ion antiport; $[X_i^{+}]$ and $[X_o^{+}]$ denote the internal and external concentrations of Na⁺ and Ca²⁺; and E_o = 2.303 k_BT/e ∼59 mV (k_B is the Boltzmann constant, T = 25°C, and e is the elementary charge). Notably, E_rev is a function only of the concentration gradients of the participating ions and the transport stoichiometry. Thus, for a given set of ionic concentrations, the reversal potential is uniquely defined by the stoichiometric ratio n/m. Therefore, if all ion concentrations are precisely known, n/m could be in principle determined by clamping the membrane potential extrinsically (using K⁺ and valinomycin) to a series of values and identifying which voltage results in no net flux (Fitzgerald et al., 2017). That is, only if the applied potential E_K is equal to E_rev will the initial concentrations $[X_i^{+}]$ and $[X_o^{+}]$ remain constant over time.

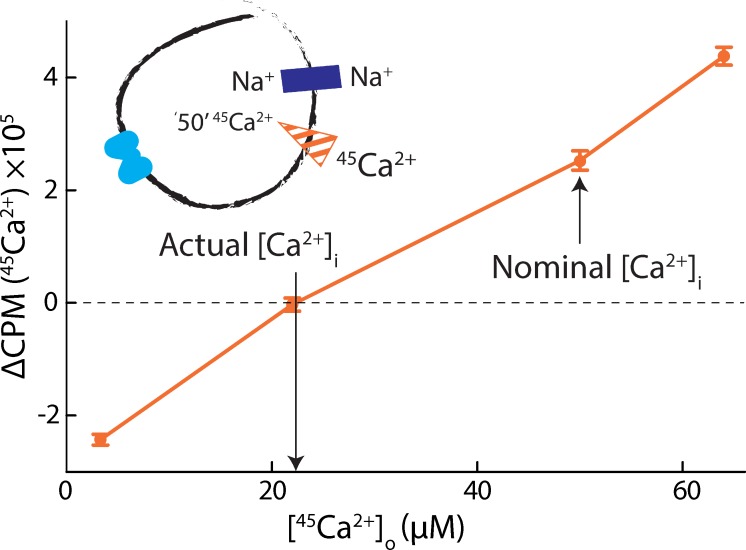
In this study, however, this straightforward approach proved to be practically unfeasible, owing to difficulties in setting and quantifying the concentration of free intraliposomal Ca²⁺ with sufficient precision. The data shown in Fig. 7 illustrate this challenge. In this experiment, the liposomal membrane potential was clamped at E_K = 0 mV with K⁺ and valinomycin, and equal concentrations of Na⁺ were applied internally and externally. In these conditions, Eq. 5 dictates that no net flux of Ca²⁺ should occur when the concentrations of external and luminal Ca²⁺ are identical. That is, if the experiment is designed so that

$$\log \frac{\left[{\mathrm{Na}}_i^{+}\right]}{\left[{\mathrm{Na}}_o^{+}\right]}=0,$$ (6)

then the reversal potential becomes

$$E_{rev}=\frac{59 \mathrm{mV}}{\frac{n}{m}-2}\log \frac{\left[{\mathrm{Ca}}_i^{2+}\right]}{\left[{\mathrm{Ca}}_o^{2+}\right]}.$$ (7)

Because the applied potential E_K is 0 mV, a net flux of Ca²⁺ will be observed unless the initial Ca²⁺ concentrations are such that E_rev is also equal to 0, i.e.,

$$\log \frac{\left[{\mathrm{Ca}}_i^{2+}\right]}{\left[{\mathrm{Ca}}_o^{2+}\right]}=0.$$ (8)

However, in one series of measurements in which we preloaded liposomes with 50 µM ⁴⁵Ca²⁺ and varied the concentration of external ⁴⁵Ca²⁺, we observed the condition of no net flux at external [⁴⁵Ca²⁺] ∼22 µM (Fig. 7). This result implies that the actual concentration of free luminal Ca²⁺ was less than half of its intended value. One possible explanation of these data is that there exists a significant degree of ⁴⁵Ca²⁺ sequestering within the liposomes, owing to the presence of anionic lipids.

Figure 7.

Quantifying intraliposomal Ca²⁺. Initial rates of Na⁺/⁴⁵Ca²⁺ antiport (ΔCPM at 20 s) as a function of external [⁴⁵Ca²⁺]. Liposomes were preloaded with a nominal 50 µM ⁴⁵CaCl₂ and diluted into a buffer with varying ⁴⁵CaCl₂. Internal and external buffers were otherwise symmetric, both with 25 mM NaCl. A triplicate dataset is averaged (error bars represent SEM).

To circumvent this limitation, we reformulated our method so that knowledge of the concentration of intracellular Ca²⁺ is not required. Using an approach commonly used in electrophysiological experiments, we now sought to determine the shift in the reversal potential, ΔE_rev, that would result from the change in only one experimental parameter. Specifically, we varied the external Na⁺ concentration, as it can be controlled accurately, while keeping all other concentrations constant. In such an experiment, and following from Eq. 5, ΔE_rev would fulfill the following relationship:

$$\Delta E_{rev}=E_{rev}-E{\text{'}}_{rev}=\frac{-59\mathrm{ mV}}{\frac{n}{m} - 2}\left(\frac{n}{m}\log \frac{\left[{\mathrm{Na}}_o^{+}\right]}{\left[{\mathrm{Na}}_o^{+}\right]\text{'}}\right).$$ (9)

Note that ΔE_rev is a function only of the stoichiometric ratio n/m and the external Na⁺ concentrations, [Na⁺_o] and [Na⁺_o]′. To determine ΔE_rev, and hence n/m, we performed a series of ⁴⁵Ca²⁺ flux measurements under an applied membrane potential, E_K. We set this potential to values between 0 and 120 mV, using K⁺ and valinomycin (Materials and methods). In each experiment, we repeated flux measurements for two different values of the external Na⁺ concentration, while maintaining all other concentrations constant. (To ensure that the intraliposomal concentrations of ⁴⁵Ca²⁺ and Na⁺ were constant, we used a single preparation of liposome for each series of shift measurements.) Thus, our aim in a given experiment is to identify a pair of zero-flux voltages (for a pair of [Na⁺]): their difference is the reversal-potential shift ΔE_rev in Eq. 9.

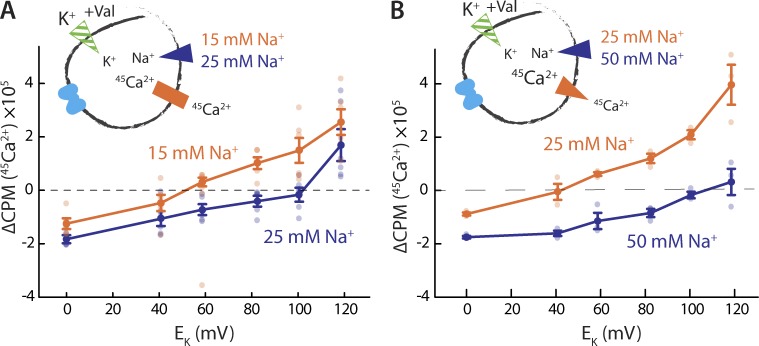
As expected from our specific choice of concentrations, we observed ⁴⁵Ca²⁺ efflux at low E_K values, but as the magnitude of the applied membrane potential increased, the direction of net Ca²⁺ flux eventually reversed, with ⁴⁵Ca²⁺ uptake observed at larger voltages (Fig. 8, A and B). In keeping with Eq. 9, the E_rev shifts to more positive voltage with increasing [Na⁺]_o (Fig. 8, A and B). When [Na⁺]_o is varied from 15 to 25 mM, visual inspection of the results suggest an approximate value of ΔE_rev of 50 mV (Fig. 8 A); in a different experiment, with [Na⁺]_o changing from 25 to 50 mM, ΔE_rev appears to be approximately 65 mV (Fig. 8 B). In the case of 15/25 mM external Na⁺, Eq. 9 predicts a 40-mV shift for n/m = 3 (i.e., 3Na⁺:1Ca²⁺), whereas n/m = 4 would result in a 26-mV shift. With 25/50 mM external Na⁺, the predicted shifts are 53 and 35 mV, respectively. Our results therefore seem to rule out n/m values of 4 or greater, whereas the shifts predicted for a 3:1 ratio are reasonably close, but not identical, to the visual estimates. Given that n/m = 2 can also be ruled out, as it would imply nonelectrogenic antiport, these experimental data suggest an antiport stoichiometry of 3:1 for NCX_Mj.

Figure 8.

Determining stoichiometry with reversal-potential-shift experiments. (A) Initial rates of Na⁺/⁴⁵Ca²⁺ antiport as a function of the membrane potential with either 15 mM (orange) or 25 mM (blue) external NaCl. Liposomes, preloaded with buffer containing 10 mM NaCl, 1 mM KCl, and 50 µM ⁴⁵CaCl₂, were diluted into the reaction buffer with 25 µM ⁴⁵CaCl₂, 25/15 mM NaCl, and varying [KCl]_o. The same liposomes were used for both experiments. Two triplicate datasets are shown (error bars represent SEM). (B) Initial rates of Na⁺/⁴⁵Ca²⁺ antiport as a function of the membrane potential with either 25 mM (orange) or 50 mM (blue) external NaCl. Liposomes, preloaded with buffer containing 15 mM NaCl, 1 mM KCl, and 100 µM ⁴⁵CaCl₂, were diluted into the reaction buffer with 30 µM ⁴⁵CaCl₂, 50/25 mM NaCl, and varying [KCl]_o. One triplicate dataset is shown (error bars represent SEM). In each panel, dark symbols represent averages of results of individual experiments, which are shown as pale symbols of the same color. Both experiments were reproduced on three separate occasions.

Because in each experiment the estimated ΔE_rev value was off from the theoretical value by 10 mV or more, we sought to confirm our visual impressions with a more quantitative approach. Toward this end, we devised a statistical analysis that permits an objective and self-consistent interpretation of all measurements (Materials and methods). Rather than estimate the value of ΔE_rev visually, for each experiment we generated an ensemble of linear fits to each dataset in the vicinity of the no-flux voltage condition using a Monte Carlo method that samples the space of a quality-of-fit parameter according to Eq. 3. The series of linear fits and ΔE_rev values obtained for two of these experiments are shown in Fig. 9 (A and B) and Fig. 9 (C and D), respectively. The varying spacing between horizontal lines indicating various stoichiometries in the latter plots highlights the nonlinearity of the relationship between ΔE_rev and the stoichiometry ratio n/m. As Eq. 9 indicates, ΔE_rev tends to infinity as n/m approaches a value of 2, the case of nonelectrogenic transport. However, stoichiometry ratios >2 are perfectly possible, and in this range the magnitude of ΔE_rev decreases with increasing n/m; the change in ΔE_rev between n/m = 2.5 and 3 is therefore not proportional to that between n/m = 3 and 4 (Fig. 9, C and D).

We then computed probability distributions for the ensemble of ΔE_rev values derived from each experimental set, analyzing a total of four experiments, i.e., the data shown in Fig. 8 and Fig. 9 (A and B). The resulting distributions are shown in Fig. 9 E, alongside the combined normalized distribution that accounts for all measurements. All distributions peak at values between 2.7 and 3.0 and are asymmetric, with tails extending toward higher stoichiometry values because, as mentioned, the experimentally detectable stoichiometry space is itself not uniform. Consistent with the fact that a value of n/m = 2 cannot be detected by reversal-potential measurements, the distributions tail off to zero quite abruptly at n/m < 2.5; however, a value of 4 is possible; hence the distributions extend toward values greater than 3. The expectation value of the combined normalized distribution—that is, the stoichiometry ratio that best reflects all our experimental data—is < n/m > = 2.96 ± 0.47. This quantitative analysis therefore reaffirms the conclusion that the antiport stoichiometry of NCX_Mj is 3Na⁺:1Ca²⁺. (Note that because this distribution is not symmetric, its expectation value is not the peak, as would be expected for a Gaussian distribution, for example.)

Discussion

NCX_Mj is the only member of the sodium–calcium exchanger family for which an atomic structure is available. This prokaryotic homologue has been proposed to represent the basic functional and structural transport unit of the exchangers in this family (Liao et al., 2012, 2016). In this study, we have presented a comprehensive analysis of key mechanistic features of NCX_Mj, which strengthens the case for this protein as a model for mammalian NCXs. We first demonstrated that purified and reconstituted NCX_Mj is capable of driving uphill transport of Ca²⁺ using a preexisting concentration gradient of Na⁺ and thus functions as a secondary-active transporter. This conclusion recapitulates those of earlier functional studies, of both purified NCX_Mj (Liao et al., 2012; Barthmes et al., 2016) and NCX_Mj heterologously overexpressed in E. coli vesicles (Almagor et al., 2014; Marinelli et al., 2014). The observation of Ca²⁺/⁴⁵Ca²⁺ exchange in the latter studies suggests that NCX_Mj functions according to a so-called ping-pong model (Almagor et al., 2014; Marinelli et al., 2014). Here, we corroborate this conclusion on the basis of additional Ca²⁺/⁴⁵Ca²⁺ exchange and Na⁺/Ca²⁺ competition assays in an experimental system in which NCX_Mj is isolated from other native transporters and the composition of internal solutions is well controlled.

We also explored the ion specificity of NCX_Mj-mediated antiport to rule out that this homologue is a K⁺-dependent or H⁺-driven Ca²⁺ transporter. Earlier radioactive flux assays had showed that Na⁺/Ca²⁺ antiport is not affected by the presence of a K⁺ gradient (Liao et al., 2012), suggesting that NCX_Mj does not transport K⁺. We sought to complement these data, in consideration of the sequence similarity in the binding sites of NCX_Mj and K⁺-dependent NCKX proteins. Our data conclusively clarify that NCX_Mj does not require a bound K⁺ ion for antiport. Furthermore, our results rule out the possibility of H⁺-driven Ca²⁺ transport, even though we found that the activity of NCX_Mj is inhibited at low pH, consistent with previous studies (Marinelli et al., 2014; Liao et al., 2016). Finally, we evaluated how the rate of Na⁺-driven Ca²⁺ flux is influenced by a membrane potential, imposed with a K⁺ gradient and valinomycin. This experiment demonstrates that the antiport cycle of NCX_Mj is electrogenic and that it transfers a positive charge in the direction opposite to that of Ca²⁺ flux. Our conclusions concur with those obtained from analysis of transient currents generated by NCX_Mj in SSM-based electrophysiological recordings (Barthmes et al., 2016).

Having verified the expected functional features of NCX_Mj, thereby validating our experimental system, we sought to determine the stoichiometry of the ion-antiport cycle of NCX_Mj and specifically assess whether it matches that of mammalian NCXs, namely 3Na⁺:1Ca²⁺. Our functional analysis demonstrates that NCX_Mj indeed shares this key mechanistic feature of its mammalian homologues and is thus an appropriate model system for the NCX family.

The method that we used to establish the stoichiometry of Na⁺/Ca²⁺ antiport in NCX_Mj is based on the thermodynamic relationship between the transmembrane electrostatic potential and the electrochemical gradients of the various substrates transported by a membrane protein. In electrophysiology, this relationship is the foundation of the so-called reversal-potential experiment, in which a set of voltages is applied across the membrane to determine the value at which the current mediated by a channel or transporter reverses (Accardi and Miller, 2004). Electrical recordings, however, are unfeasible for a wide range of secondary-active electrogenic transporters; particularly, for prokaryotic transporters, which typically do not express readily in eukaryotic cells, and whose turnover rates are in many cases too slow to produce detectable currents. To study NCX_Mj, we expanded on our recent work (Parker et al., 2014; Fitzgerald et al., 2017) translating the basic principles of a reversal-potential electrophysiology experiment into a liposomal system: instead of using a two-electrode voltage clamp, we clamped the membrane potential chemically, i.e., with a K⁺ gradient and the corresponding ionophore, valinomycin; and rather than measuring currents, we detected substrate fluxes (⁴⁵Ca²⁺). The premise of this methodology is that K⁺ does not interact with the protein under study, and that the rate of ionophore-mediated permeation is much faster than the turnover rate of the transporter. In such cases, this approach can be used to set the membrane potential sufficiently accurately in a wide range of voltages (Reeves and Hale, 1984; Fitzgerald et al., 2017).

In practice, quantitative determination of the stoichiometry from the value of the reversal potential requires knowledge of and precise control over the internal and external concentrations of all the species participating in the transport reaction. In some cases, however, this degree of control is not attainable. For instance, we have found that a commonly used method of buffer exchange (freeze/thaw and extrusion) fails to incorporate Ca²⁺ into liposomes at predictable and reproducible concentrations, perhaps because of sequestering of incorporated Ca²⁺ by anionic lipids. We were therefore unable to set the internal concentrations of free Ca²⁺ with the precision required by the aforementioned approach to quantify stoichiometry.

To circumvent this difficulty, we reformulated our approach and deduced the ion transport stoichiometry from the shift in the reversal potential induced by a change in the concentration of one of the substrates, while all others remain unchanged. The rationale of this approach is that the value of the shift depends on one experimental parameter only: the ratio of the concentrations of the substrate that is being varied. Thus, apart from experimental convenience, shift measurements offer an advantage over measurements of the absolute reversal potential in that they are more robust and do not rely on perfect experimental reproducibility of all concentrations; the necessary and sufficient condition is that the concentration of the substrate chosen to induce the potential shift be reproduced and controlled with sufficient precision.

An additional challenge pertains to the resolution with which reversal potentials, or the shifts thereof, can be determined. High precision is likely to be particularly difficult to attain for many prokaryotic transporters, owing to their notoriously slow catalytic rates. For these transporters, measurements around thermodynamic equilibrium, where the rate of flux is slow, are particularly prone to a low signal-to-noise ratio, leading to an ill-defined value of the reversal potential and hence a nontrivial interpretation of experimental data. To overcome this limitation in cases where resolution is insufficient to interpret the experiments by visual inspection, we developed a probabilistic analysis that accounts for the uncertainty associated with the reversal potential measurements and extracts the value that is most consistent with the data. From this analysis, we can then derive a probability distribution for the stoichiometry, that is, assess the likelihood that any given stoichiometry reflects the experimental measurements. This approach is particularly useful in that it discriminates among hypothetical stoichiometry values by comparing their relative likelihoods, while also revealing the uncertainty of the data. Because the transport stoichiometry is set, this tool can also be used to carry out a global analysis of multiple stoichiometric measurements under different experimental conditions.

Our conclusion that NCX_Mj antiports Na⁺ and Ca²⁺ with a 3:1 ratio is consistent with the results of a previous computational study that had considered a diverse set of possible stoichiometries and ion configurations (Marinelli et al., 2014; Liao et al., 2016), as well as with the most recent interpretation of available crystallographic data (Liao et al., 2016). The consensus from these earlier studies is that Ca²⁺ binds to the so-called S_Ca site, or alternatively, that three Na⁺ ions occupy sites S_ext, S_int, and S_Ca. Ion binding to these sites is in part mediated by two highly conserved acidic residues, namely Glu54 or Glu213, which are most likely ionized in the presence of Na⁺ or Ca²⁺. It was also concluded that a fourth site, referred to as S_mid and flanked by Asp240, is not normally occupied by either Na⁺ or Ca²⁺; instead, water molecules are proposed to reside at this site and contribute to coordinate the bound ions, whereas Asp240 is constitutively protonated (Marinelli et al., 2014; Liao et al., 2016). An interesting corollary to this prediction is that the S_mid site may be one of the key evolutionary differentiations between NCXs and K⁺-dependent NCXs because the latter would use S_mid to load a fourth Na⁺ ion, or alternatively, the K⁺ ion that is cotransported with Ca²⁺. This notion is supported by the observation that substitution of Asp240 by asparagine (which is prototypical of eukaryotic NCXs) results in a gain of function in NCX_Mj (Marinelli et al., 2014), and that the same mutation in NCKX2 removes its coupling to K⁺ (Kang et al., 2005). Our data conclusively demonstrate that only three Na⁺ ions are transported by NCX_Mj and that the antiport cycle is independent of K⁺; however, our experiments do not specifically reveal whether S_mid is constitutively occupied by a proton. Thus, further functional assays under well-controlled conditions will be required to continue to dissect the molecular mechanism of ion recognition and translocation of NCXs and related antiporters, and to evaluate and integrate insights attained from structural and computational approaches. The quantitative elucidation of the antiport stoichiometry of NCX_Mj is an important step in that direction.

Finally, it is worth noting that the methodology we use to analyze the experimental data does not assume that the stoichiometry of NCX_Mj must be an integer value, i.e., we do not exclude a priori the possibility of slippage. Our analysis suggests, however, that either slippage does not occur or that it occurs to a degree that is not detectable. From a mechanistic standpoint, the absence of slippage implies that the alternating-access transition between outward- and inward-open states of NCX_Mj is feasible only when three Na⁺ or one Ca²⁺ occupy the transporter. It has been proposed that the reason that this transition is prohibited for other occupancies is that the necessary conformational intermediates that occlude the ion-binding sites to both sides of the membrane are energetically unattainable unless three Na⁺ or one Ca²⁺ are bound (Liao et al., 2016).