GABA Type A Receptor Activation in the Allosteric Coagonist Model Framework: Relationship between EC₅₀ and Basal Activity

Abstract

The concerted transition model for multimeric proteins is a simple formulation for analyzing the behavior of transmitter-gated ion channels. We used the model to examine the relationship between the EC₅₀ for activation of the GABA type A (GABA_A) receptor by the transmitter GABA and basal activity employing concatemeric ternary GABA_A receptors expressed in Xenopus oocytes. Basal activity, reflecting the receptor function in the absence of the transmitter, can be changed either by mutation to increase constitutive activity or by the addition of a second agonist (acting at a different site) to increase background activity. The model predicts that either mechanism for producing a change in basal activity will result in identical effects on the EC₅₀. We examined receptor activation by GABA while changing the level of basal activity with the allosterically acting anesthetics propofol, pentobarbital, or alfaxalone. We found that the relationship between EC₅₀ and basal activity was well described by the concerted transition model. Changes in the basal activity by gain-of-function mutations also resulted in predictable changes in the EC₅₀. Finally, we altered the number of GABA-binding sites by a mutation and again found that the relationship could be well described by the model. Overall, the results support the idea that interactions between the transmitter GABA and the allosteric agonists propofol, pentobarbital, or alfaxalone can be understood as reflecting additive and independent free energy changes, without assuming any specific interactions.

Introduction

The concerted transition model for multimeric proteins introduced by Monod, Wyman, and Changeux (the MWC model; Monod et al., 1965) is an elegantly simple formulation for understanding and analyzing the behavior of transmitter-gated ion channels (Del Castillo and Katz, 1957; Karlin, 1967). The model posits that a protein exists in two interconvertible states: active and inactive. It has one or more sets of drug-binding sites. Each site in a set is equivalent to the other sites in that set, while the properties of the sites differ between the states. The model requires only four parameters to describe the macroscopic activation of a receptor.

On the face of it such a simple model seems unlikely to be able to account for the behavior of transmitter-gated channels. However, the behavior of ion channels in the pentameric transmitter-gated ion channel family is rather well described by this model (Karlin, 1967; Jackson, 1986, 1989; Changeux and Edelstein, 1998; Chang and Weiss, 1999; Auerbach, 2012; Forman, 2012; Ehlert, 2014b; Gupta et al., 2017). For the γ-aminobutyric acid type A (GABA_A) receptor, this area of study was pioneered by Chang and Weiss (1999), who demonstrated that the macroscopic properties of activation of GABA_A receptors by the transmitter could be well described by the MWC model. Further work by Forman and collaborators (Rüsch et al., 2004; Rüsch and Forman, 2005; Ruesch et al., 2012) demonstrated that the actions of several potentiating drugs on the GABA_A receptor could be understood in terms of this model without additional, ad hoc, interactions.

We examined the application of the concerted transition model to the behavior of the GABA_A receptor in terms of the ability of allosteric agents to potentiate activation by GABA. As emphasized by Forman (Ruesch et al., 2012) the ability of a drug to potentiate can be described in terms of its ability to decrease the concentration of agonist required to elicit a half-maximal response (EC₅₀) as well as its ability to increase the response to a given concentration of the agonist. We used examples of three types of intravenous anesthetics as potentiator (propofol, the barbiturate pentobarbital, and the anesthetic steroid alfaxalone) to determine whether the model accurately predicts the shift in EC₅₀ for GABA. We also altered the intrinsic probability of being open for the receptor and the number of binding sites for GABA by mutations. Our results indicate that the model is remarkably successful at accounting for the ability of allosteric agonists or receptor mutations to alter activation by the transmitter.

In particular, the results suggest that the actions of these combinations of agonists do not require any specific interactions between the agents (e.g., changes in affinity) but reflect coupling via additive changes in the free energy as the result of interactions between the receptor and the agonists. In more practical terms, the change in EC₅₀ value for agonist A produced by any concentration of agonist B can be predicted from the direct response to B and the parameters describing activation by A in the absence of other activating agents. Similarly, the effects of mutations that alter constitutive activity of the receptor or the number of sites for an agonist can be predicted.

Materials and Methods

Constructs and Expression.

The experiments were conducted on rat α1β2γ2L GABA_A receptors formed by assembly of two concatemeric constructs comprising β2–α1–γ2L (abbreviated as βαγ) and β2–α1 (βα) subunits. To simplify the presentation, we will refer to “wild-type” βαγ + βα receptors when the concatemers had no mutations present, even though the receptors per se are clearly not wild type. The use of concatemeric receptors enabled the generation of receptors containing controlled numbers and positions of mutations. The generation and functional characterization of these constructs have been reported previously elsewhere (Bracamontes and Steinbach, 2009; Bracamontes et al., 2011).

The functional properties of the wild-type receptors comprising concatemeric constructs and free subunits are quite similar even at the single-channel level (Akk et al., 2009), although most studies have indicated a ∼2-fold right shift in the GABA concentration–response relationships (Baumann et al., 2002; Akk et al., 2009; Bracamontes et al., 2011). The reason for the right-shifted concentration–response relationship is not entirely clear, but a previous single-channel study found that subunit linkage can affect receptor affinity to the transmitter (Akk et al., 2009).

The concatemers are not degraded when expressed in Xenopus oocytes (Bracamontes et al., 2011). Furthermore, receptors activated by 5-μM GABA (approximately EC₇) were potentiated to 308% ± 32% (n = 6) of control in the presence of 1 μM diazepam, indicating that the γ2L subunit was incorporated. Introduction of reporter mutations into the α1 subunit (see Results) indicated that the assembled receptors incorporate both concatemers. Point mutations [α1(L263S), β2(Y205S), β2(Y143W)] were generated using QuikChange (Agilent Technologies, Santa Clara, CA). The cDNAs were subcloned into the pcDNA3 vector in the T7 orientation. The cRNAs were produced using mMessage mMachine (Ambion, Austin, TX) after linearization by digestion with Xba I (NEB Laboratories, Ipswich, MA).

Oocytes from the African clawed frog (Xenopus laevis) were used for expression of the receptors. The frogs were purchased from Xenopus 1 (Dexter, MI), and they were housed and cared for in a Washington University animal care facility under the supervision of the Washington University Division of Comparative Medicine. Harvesting of oocytes was conducted in accordance with the Guide for the Care and Use of Laboratory Animals as adopted and promulgated by the National Institutes of Health. The protocol was approved by the Animal Studies Committee of Washington University in St. Louis (Approval No. 20170071).

Oocytes were injected with a total of 20 ng cRNA in a final volume of 30–70 nl of nuclease-free water (Thermo Fisher Scientific, Waltham, MA) at the ratio of 1:1 (βαγ:βα). After injection, the oocytes were incubated in ND96 buffer (96 mM NaCl, 2 mM KCl, 1.8 mM CaCl₂, 1 mM MgCl₂, 2.5 mM Na pyruvate, 100 U/ml penicillin, 100 μg/ml streptomycin, 50 μg/ml gentamycin, 5 mM HEPES; pH 7.4) at 16°C, and they were used in electrophysiologic recordings within 24 to 72 hours.

Electrophysiology.

The experiments were conducted using standard two-electrode voltage clamp. Voltage and current electrodes were borosilicate glass capillaries (G120F-4, o.d. 1.20 mm, i.d. 0.69 mm; Warner Instruments, Hamden, CT). When filled with 3 M KCl the pipette resistance was less than 1 MΩ. The oocytes were clamped at −60 mV. The chamber (RC-1Z; Warner Instruments) was perfused with bath solution (92.5 mM NaCl, 2.5 mM KCl, 1 mM MgCl₂, 10 mM HEPES; pH 7.4) at approximately 8 ml⋅min⁻¹. Solutions were gravity-applied from 30-ml glass syringes with glass Luer slips via Teflon tubing to reduce adsorption. The application of agonists was typically 20 to 60 seconds long, followed by washout in bath solution (up to 5 minutes) until recovery. The solutions were switched manually. Test applications (e.g., to a saturating concentration of GABA) were performed at the beginning and end of recordings from each cell to verify the overall stability of the responses.

The currents were amplified with an OC-725C (Warner Instruments) or Axoclamp 900A amplifier (Molecular Devices, Sunnyvale, CA) filtered at 40 Hz and digitized with a Digidata 1200 or 1320 series digitizer (Molecular Devices) at 100 Hz, and recorded using pClamp software (Molecular Devices). Current traces were analyzed with Clampfit (Molecular Devices) to determine the peak amplitude of the response measured from the preceding baseline current.

Analysis of Current Responses.

The analysis of electrophysiologic recordings was aimed at determining the concentration–response properties and the level of basal activity for individual receptor-agonist combinations. Two principal types of concentration–response experiments were conducted. In the first type, the oocytes were exposed to a range of concentrations of GABA. The concentration–response curves were fitted for each cell separately with the following equation:

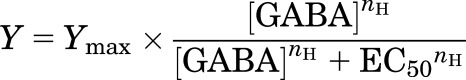(1)

where EC₅₀ is the concentration of GABA producing a half-maximal effect, n_H is the Hill slope, and Y_max is the high-concentration asymptote.

In the second case, oocytes were exposed to a range of concentrations of GABA in the presence of a fixed, low concentration of a secondary activator, termed the “background” drug (propofol, alfaxalone, or pentobarbital). The concentration–response curves were fitted with the following equation:

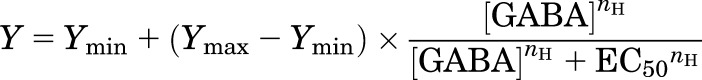(2)

where EC₅₀ is the concentration of GABA producing a half-maximal effect, n_H is the Hill slope, and Y_min and Y_max are the low- and high-concentration asymptotes, respectively. The fitted Y_min was typically indistinguishable from the response to the background activator.

Curve fitting was conducted using the NFIT software (University of Texas Medical Branch at Galveston, Galveston, TX). The results are reported as mean ± S.E.M. (number of cells).

Converting Membrane Current to Probability of Being Open.

We adopted the procedures developed by Forman (Forman, 2012; Forman and Stewart, 2012; Eaton et al., 2016) to establish a scale for converting current responses to an estimated probability of being open [P{open}]. The maximal response possible from a given cell (I_max) was estimated by applying a saturating concentration of GABA plus a potentiator that gave the largest measured response. In the present experiments this was accomplished using 3 mM GABA plus 100 µM pentobarbital. This response was assumed to be equivalent to a P{open} of 1 (Ziemba and Forman, 2016). The probability of being open in the absence of agonist was estimated by blocking any constitutive current using picrotoxin [300 µM for the wild-type concatemeric receptor or 500 µM for receptors containing the α1(L263S) mutation]. The current level in the presence of picrotoxin was assumed to correspond to a P{open} of 0.

The GABA concentration–response relationship in the wild-type βαγ+βα receptor was converted to units of P{open} by normalization to the response to 3 mM GABA in that cell, and scaling by the estimated P{open} for the response to 3 mM GABA:

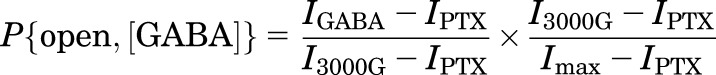(3)

where P{open, [GABA]} is the probability of being open in the presence of a given concentration of GABA, I_GABA is the current response to that concentration of GABA, I_3000G is the current response to 3 mM GABA, and I_PTX is the amplitude of the outward current in the presence of picrotoxin. The term (I_3000G − I_PTX)/(I_max − I_PTX), i.e., the scaling factor providing the estimated P{open} for the response to 3 mM GABA, was determined separately in five cells.

Materials, Drugs, and Solutions.

Most chemicals, including GABA, pentobarbital and the salts used to prepare buffers were purchased from Sigma-Aldrich (St. Louis, MO). Propofol was from MP Biomedicals (Solon, OH), and alphaxalone from Sigma-Aldrich or Tocris (Bio-Techne, Minneapolis, MN).

Stock solutions of GABA (500 mM) and pentobarbital (5 mM) were made in bath solution. Stock solutions of propofol (200 mM) and alphaxalone (10 mM) were made in dimethylsulfoxide (DMSO). Aliquots of GABA stock were kept frozen at −20°C then thawed and diluted as needed on the day of the experiment. Stock solutions of pentobarbital, propofol, and alphaxalone were stored at room temperature.

The maximal DMSO concentration in final working solutions was 0.5%. This concentration of DMSO is without effect on holding current or the peak amplitude of the response to an EC₅₀ concentration of GABA from oocytes expressing α1β3γ2L receptors (Germann et al., 2016).

Results

Description of the Model.

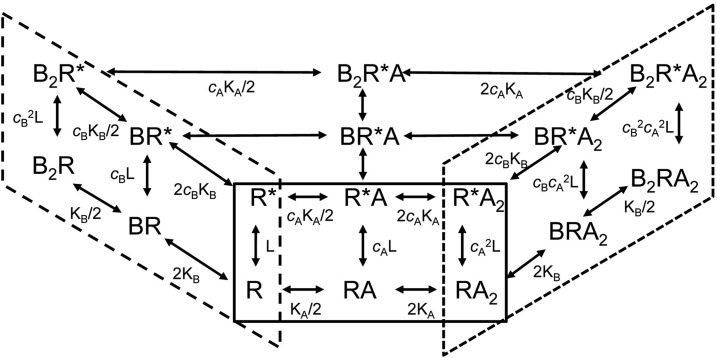
The application of the concerted transition model to the GABA_A receptor was described previously elsewhere (Chang and Weiss, 1999; Forman, 2012). We used this model (Fig. 1) to explore the relationship between the concentration of GABA producing a half-maximal response (EC₅₀), the gating equilibrium constant for unliganded receptors (L), and the number of binding sites for the transmitter (N).

Fig. 1.

Partial state diagram for two drugs (A and B, each with two sites) acting on a receptor following the concerted transition scheme. Closed receptor states (R) occupy the plane at the bottom (note that some states are obscured such as B₂RA) while open states (R*) occupy the plane at the top. The diagram is distorted to show states with only agonist A bound (solid line box at front), only agonist B bound (long dashed line box at left), and some states with both agonists bound (short dash box at right). In the absence of both A and B the receptor activates constitutively with L = R/R*. The value of the parameter L is a property of the receptor, not of any agonist. Agonist A binds to its site with dissociation constant K_A on the closed receptor and K_A* on the open receptor, with c_A = K_A*/K_A. Note that the presence of bound B does not affect binding of A nor vice versa. The equilibrium between R and R* states is determined by the respective values for c, as dictated by detailed mass action in the coupled cycles (e.g., B₂R/B₂R* = c_B²L and B₂RA₂/B₂R*A₂ = c_B²c_A²L).

The state function for the receptor—the probability that a receptor is in the open state or, on a macroscopic level, the fraction of receptors that are in the open state—is given by the following equation:

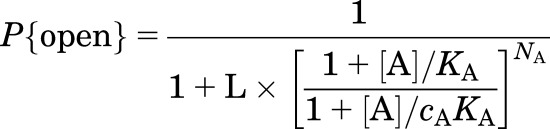(4)

where A is an agonist, K_A is the equilibrium dissociation constant for the agonist when the receptor is in the closed state, and N_A is the number of sites for A. The parameter L is the ratio of the fraction of channels in the closed state to the fraction of channels in the open state in the absence of agonist, and it reflects the difference in the free energies of the closed and open states in the absence of an agonist. A small value for L indicates that the channels activate readily even in the absence of an agonist. The parameter c_A is the ratio of the equilibrium dissociation constants for binding in the open state to that in the closed state, reflecting the selectivity of the agonist between the two states. Agonists, by definition, bind more tightly to the active state of the receptor; hence, the value for c_A is <1. In the absence of an agonist the probability of being open is P{open, min} = 1/(1 + L); the maximal probability of being active in the presence of a saturating concentration of A is 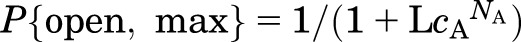. The “stabilization energy” contributed by the binding of an agonist when all sites are occupied is N_ART × ln(c_A), whereas the free energy difference between the fully liganded closed and fully liganded open states is N_ART × ln(Lc_A).

Interactions among Agonists Are Mediated through Change in L.

If a second activator (B) is present that does not bind to the same site as A, eq. 4 becomes

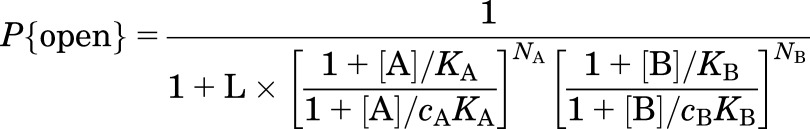(5)

where K_B is the dissociation constant for agonist B binding to its site when the receptor is in the closed state, c_B is the ratio of the dissociation constants for binding of B in the open to that in the closed state, N_B is the number of sites for B, and other terms are as defined earlier. The case in which both compounds (A and B) bind to the same site is considered by Karlin (1967).

Inspection of eq. 5 indicates that in the presence of a constant concentration of agonist B the effects of B on responses to agonist A can be understood simply as a change in the apparent value of L:

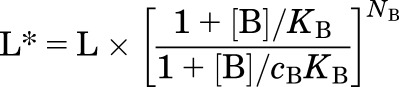(6)

where L* is the modified L reflecting a change due to the presence of agonist B. This equation explains the relationship between activation by one compound and that compound’s ability to potentiate responses to another. This relationship has been investigated and supported for the GABA_A receptor by Forman and collaborators (Rüsch et al., 2004; Ruesch et al., 2012).

The Relationship between the EC₅₀ for an Agonist and L.

The EC₅₀ is the concentration of agonist that produces a response halfway between the baseline current in the absence of the agonist and the maximal response the agonist can generate. In the MWC model, the EC₅₀ for activation of a receptor by an agonist normalized to its affinity to the compound is given by (Karlin, 1967):

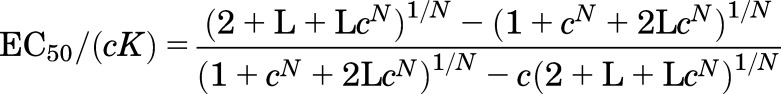(7)

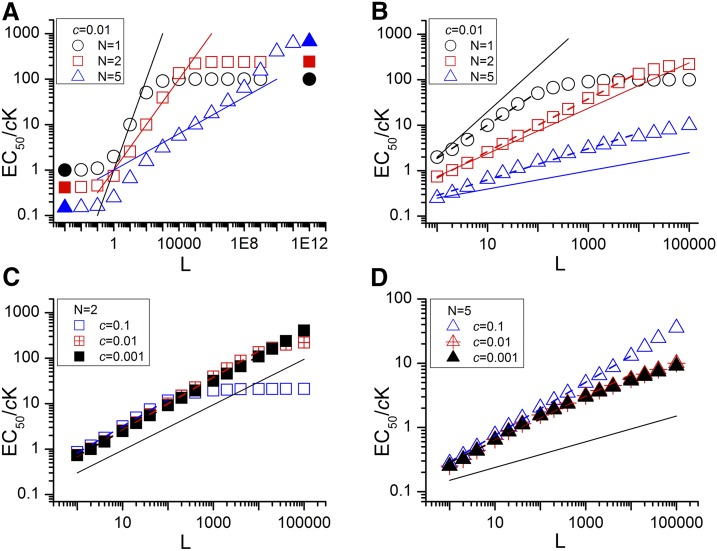
The relationship between EC₅₀ and L for values of N of 1, 2, and 5 (with c = 0.01) is shown in Fig. 2A. The predictions cover a large range of values for L to illustrate that the value for EC₅₀ shows asymptotes at both low and high values of L.

Fig. 2.

The theoretical relationship between normalized EC₅₀ and L. The figure shows the predicted EC₅₀ plotted logarithmically against the value for L. The values for EC₅₀ are normalized to the dissociation constant for the open state. (A) Relationships for N values of 1 (○), 2 (□), and 5 (▵) for c = 0.01 over a wide range of values for L (10⁻² to 10¹²). The filled symbols show the predicted asymptotic values (see Results). The lines show slopes of 1/N. (B) Same as A but over a range of L values previously reported for the GABA_A receptor to illustrate results that might be obtained experimentally. The dashed lines show the linear regression on the logarithmically transformed data; the slopes of the regression lines are 0.75 for N = 1, 0.58 for N = 2 and 0.37 for N = 5. The solid lines show slopes of 1/N. (C and D) Relationships between predicted EC₅₀ and L for N = 2 (C) and N = 5 (D). Three values for c were used—c = 0.1, c = 0.01, and c = 0.001—to cover the range appropriate for the GABA_A receptor (L = 1 to 100,000). The solid lines show lines with slope of 1/N. Table 1 provides slopes for the linear regression on the logarithmically transformed data for a number of combinations for N, L, and c.

Chang and Weiss (1999) were the first to demonstrate experimentally for GABA_A receptors that the relationship shows an asymptote when L < 1. Edelstein and Changeux (1996) provided expressions for the values of these asymptotes. As L approaches 0, EC₅₀ approaches cK(2^1/N − 1), and as L approaches infinity, EC₅₀ approaches K/(2^1/N − 1). Inspection of the relationship in Fig. 2A indicates that the curvature toward the asymptotes becomes marked when L < 1 and L > 1/c^N. When 1/c^N is much larger than 1, the asymptotes are well separated, and the slope of the relationship between log(EC₅₀) and log(L) approaches 1/N, as first pointed out by Karlin (1967). The approximation is good over a particularly wide range for N = 2.

Figure 2B shows plots of the predicted EC₅₀ against L for N values of 1, 2, and 5 to indicate the nature of the relationships that might be experimentally obtained for an intermediate value of c (c = 0.01) and values of L from 1 to 100,000. Figure 2, C and D, shows similar plots for N values of 2 and 5, now calculated with three values for c that cover most of the range of values reported for agonists acting on the GABA_A receptor (c = 0.1, 0.01, and 0.001). In these plots the slopes of the predicted relationships are shown, estimated from the linear regression of log(EC₅₀) on log(L) over the range of values of L where the relationship appeared linear (indicated in the figures). The fitted slope is larger than 1/N when N is greater than 1, and the deviation increases as N increases. The reason for this difference can be seen in Fig. 2A and arises because the predicted values for the EC₅₀ initially lie below the line indicating L^1/N, so the slope for L values not that much larger than 1 is actually greater than 1/N.

The logarithmic regression slopes fitted to the predicted values are shown in Table 1. The slopes were fitted over the linear portion of the relationship (indicated in the table) and demonstrate that the 1/N relationship is most accurate in the case that N = 2, but in general for N > 1 the actual slopes are larger than 1/N.

TABLE 1 .

Slope of the relationship between log(L) and predicted log(EC₅₀)

Results of linear regression of the value for log(EC₅₀) on log(L) (third column), for various values of N (first column) and c (second column). The values were chosen to cover the range of proposed number of sites, and reported values for c for agonists acting on the GABA_A receptor. The predictions were fit over a range of values for L that visually appear largely linear, as indicated in the fifth column. The fourth column gives the value of 1/N.

N	c	Slope	1/N	Range of L
1	0.1	0.42	1.00	1–10
1	0.01	0.75	1.00	1–40
1	0.001	0.86	1.00	1–200
2	0.1	0.59	0.50	1–100
2	0.01	0.58	0.50	1–1000
2	0.001	0.55	0.50	1–1000
3	0.1	0.55	0.33	1–400
3	0.01	0.45	0.33	1–2000
3	0.001	0.44	0.33	1–2000
4	0.1	0.48	0.25	1–2000
4	0.01	0.39	0.25	1–2000
4	0.001	0.39	0.25	1–2000
5	0.1	0.42	0.20	1–1000
5	0.01	0.37	0.20	1–1000
5	0.001	0.37	0.20	1–1000

The values of L for wild-type GABA_A receptors reported in the literature are in the range of 1000–100,000 (Chang and Weiss, 1999; Ziemba and Forman, 2016), and for receptors with gain-of-function mutations L can be less than 1 (Chang and Weiss, 1999). The reported values of c range from about 0.001 for a strong agonist such as GABA (see below) to about 0.5 for a weaker agonist such as diazepam (Chang and Weiss, 1999; Rüsch et al., 2004; Rüsch and Forman, 2005).

Summary.

In summary, there are two major points from this introduction.

1. Interactions between activators in the context of the concerted transition model (Fig. 1) can be understood as resulting from modification of L. An important caveat is that the compounds do not bind to the same site(s) on the receptor.

2. For a given value of L, the EC₅₀ value, and in fact the whole concentration–response relationship, for agonist X can be predicted given values for c_X, K_X, and N_X.

Relating the Model to Experimental Data: Activation of the Wild-Type βαγ+βα Receptor.

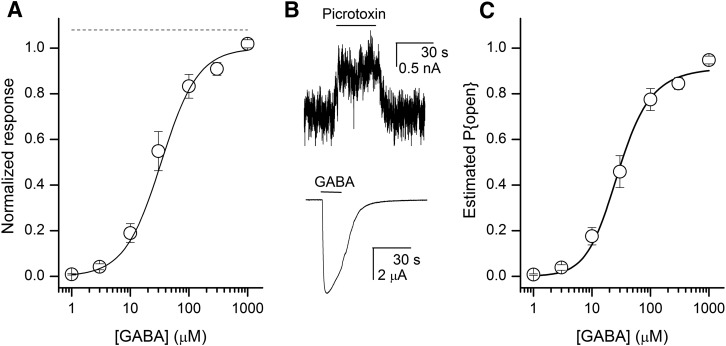
Oocytes expressing wild-type βαγ+βα GABA_A receptors were exposed to 1–1000 μM GABA. The concentration–response curves were fitted to eq. 1. The mean values of the fit were EC_50,GABA = 34 ± 8 µM (n = 5 cells) and n_H,GABA = 1.38 ± 0.07 (Fig. 3A).

Fig. 3.

Properties of the wild-type βαγ+βα concatemeric receptor. (A) Mean current responses elicited by GABA (○) normalized to the maximal fitted response. The line shows predictions of eq. 1 to the data. The mean values of the fit were EC_50,GABA = 34 ± 8 µM and n_H,GABA = 1.38 ± 0.07 (n = 5 cells). (B) Responses to 300 μM picrotoxin and 1000 μM GABA. The current traces are from the same cell. (C) Concentration–response data expressed as the estimated probability of being open plotted against the agonist concentration. The lines show the predictions of the MWC model (eq. 4) fitted to the data with the parameters L_WT = 9000, N_GABA = 2, K_GABA = 72 ± 15 μM, and c_GABA = 0.0033 ± 0.0004.

The peak response in the presence of 3 mM GABA plus 100 µM pentobarbital was 1.08 ± 0.02 times the response to 3 mM GABA alone (n = 7, P = 0.01 that the responses are equal), indicating that P{open, GABA max} = 0.93 ± 0.02. This estimate is in agreement with previous P{open, GABA max} estimates in single-channel and whole-cell studies (Steinbach and Akk, 2001; Lema and Auerbach, 2006; Ruesch et al., 2012; Hernandez et al., 2017). Application of 300 µM picrotoxin resulted in outward current, reflecting block of constitutively active receptors (Fig. 3B). We estimated L for the wild-type βαγ + βα receptor from the relationship (1 − P{open, constitutive})/P{open, constitutive} yielding 8101 ± 1238 (n = 15). This value is close to the geometric middle of the range of estimates for L (1000–100,000) for GABA_A receptors composed of free wild-type subunits (Chang and Weiss, 1999; Ziemba and Forman, 2016). We assumed for the rest of this analysis that the best estimate for the value of L was close to the directly measured value and set L_WT = 9000 for receptors composed of wild-type concatemers in the absence of agonist.

The concentration–response relationship for membrane currents was converted into units of P{open} (Fig. 3C) as described in the Materials and Methods. From fitting the curve to eq. 4, with L_WT set to 9000 and N_GABA to 2, we obtained a K_GABA of 72 µM and c_GABA of 0.0033. The fitted efficacy measure indicates that GABA binds 300-fold (c⁻¹) more tightly to the open than the closed receptor, and that the binding of a GABA molecule contributes −3.37 kcal/mol of free energy to stabilization of the open state.

Changing L by Allosteric Potentiators or Gain-of-Function Mutations Alters the EC₅₀ for GABA in a Predictable Way.

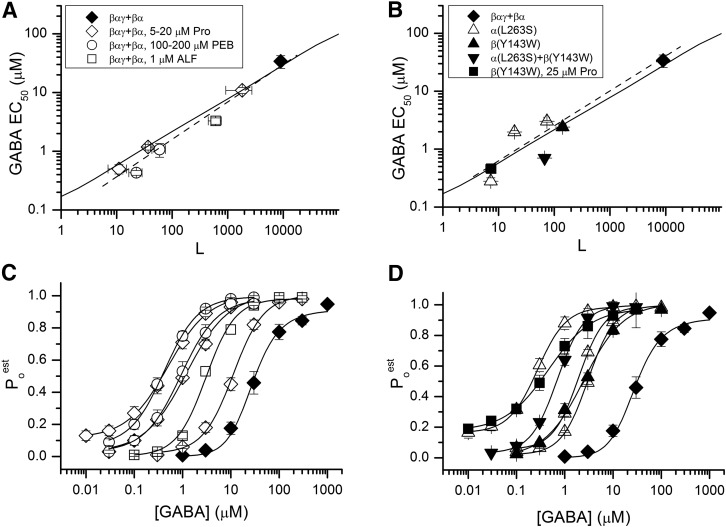
We examined the relationship between the EC₅₀ for GABA and the value for L. We altered L by addition of the allosteric drugs propofol, alfaxalone, or pentobarbital. Figure 4A shows the log-log plot of measured EC₅₀ for GABA against the L value for wild-type βαγ + βα receptors for activity elicited by GABA in the absence or presence of the three allosteric agonists: propofol at concentrations of 5, 10, and 20 µM; pentobarbital at concentrations of 100 and 200 µM; and alfaxalone at 1 µM.

Fig. 4.

Effect of change in L on activation by GABA. The measured EC₅₀ for GABA is plotted logarithmically against the value for L. (A) Data for receptors composed of wild-type concatemers in the absence of any other drug (L_WT; ♦) or in the presence of propofol (◇; concentrations of 20, 10, and 5 µM from lower to higher L), pentobarbital (○; 200 and 100 µM), or alfaxalone (□; 1 µM). The symbols show mean values, and the error bars indicate ± 1 S.E.M. The solid line shows the predicted relationship between the EC₅₀ and L using the values estimated for the wild-type: L_WT = 9000, N_GABA = 2, K_GABA = 72 µM, and c_GABA = 0.0033. The dashed line shows the linear regression of log(EC₅₀) on log(L) (slope = 0.63 ± 0.05). (B) Data for receptors containing the α1(L263S) mutation (▵; from lower L to higher L mutation is in both constructs, in βαγ, or in βα), the β2(Y143W) mutation (▴; mutation is in both constructs), or the combination of β2(Y143W) in βαγ and α1(L263S) in βα (▾). The plot also shows data for the β(Y143W)αγ+βα receptor in the presence of 25 μM propofol (▪). The solid line shows the predicted relationship using the values from fits of data from the wild-type receptor. The dashed line shows the linear regression of log(EC₅₀) on log(L) (slope = 0.60 ± 0.11). The data are summarized in Table 2. (C and D) Corresponding concentration–response relationships. The symbols show the mean ± S.E.M. The symbols are as in graphs A and B. The curves show fits to the Hill equation incorporating a low-concentration offset. The EC₅₀ values are given in Table 2.

The presence of the allosteric agonists shifts the value for L up to 1000-fold from the value for L in the absence of drugs. The corresponding shift in the observed EC₅₀ for GABA is well described by the measured change in L coupled with the parameters estimated for activation by GABA (c_GABA and K_GABA) in the absence of any drugs. That is, no information about the properties of the combination of drugs was used in predicting the relationship. The slope of a linear regression of log(EC₅₀) on log(L) is 0.63 ± 0.05 (mean ± S.E.M.). This is greater than 1/N_GABA (1/2) but not statistically significantly so (P = 0.06 by a two-tailed t test).

We also altered L by mutation of the receptor. Figure 4B shows data for receptors containing the α1(L263S) and/or β2(Y143W) mutation. Both mutations have been reported to enhance constitutive activity in the GABA_A receptor without altering K_GABA (Chang et al., 1996; Chang and Weiss, 1999; Eaton et al., 2016). Introduction of the mutation in either construct shifted the value for L, indicating that both concatemers incorporated in the receptor. The shifts in EC₅₀ with the different L values are close to the predicted values and scatter around the regression for the data for the relationship between EC₅₀ and L seen in Fig. 4A. Furthermore, the shift in GABA EC₅₀ for a mutant receptor (β(Y143W)αγ+βα) in the presence of a background drug (propofol) is close to the predicted value. The slope of a linear regression log (EC₅₀) on log (L) is 0.60 ± 0.11, which did not differ from the slope for wild-type βαγ+βα receptors shown in Fig. 4A. Accordingly, changes in basal activity by mutation or addition of a background agonist can have similar effects on the EC₅₀ for activation by GABA (Table 2).

TABLE 2 .

Experimental observations on GABA EC₅₀ and L

Values for EC_50,GABA and L for the various receptors studied. The first column shows the composition of the receptor, and the second shows the background drug used to modify L. The third shows the EC_50,GABA and the fourth the value of L. The footnotes indicate how L was determined. Values are mean ± S.E.M. for data from five or more oocytes.

Receptor	Background Drug	EC50,GABA (µM)	Value of L
βαγ+βα	None	34 ± 8	9000a
βαγ+βα	5 µM Pro	11 ± 1	1826 ± 904b
βαγ+βα	10 µM Pro	1.2 ± 0.1	37 ± 4c
βαγ+βα	20 μM Pro	0.50 ± 0.09	11 ± 4c
βαγ+βα	1 μM ALF	3.3 ± 0.4	606 ± 161c
βαγ+βα	100 μM PEB	1.1 ± 0.3	59 ± 16c
βαγ+βα	200 μM PEB	0.43 ± 0.04	23 ± 6c
βαγ+βα(L263S)	None	3.0 ± 0.1	74 ± 9a
βα(L263S)γ+βα	None	2.0 ± 0.1	19 ± 2a
βα(L263S)γ+βα(L263S)	None	0.28 ± 0.04	7.3 ± 0.4a
β(Y143W)αγ+β(Y143W)α	None	2.4 ± 0.2	141 ± 20a
β(Y143W)αγ+βα(L263S)	None	0.70 ± 0.06	67 ± 5a
β(Y143W)αγ+βα	25 μM Pro	0.46 ± 0.06	7.4 ± 1.5c
βαγ+β(Y205S)α	none	129 ± 16	9000d
βαγ+β(Y205S)α	5 μM Pro	88 ± 9	539 ± 119c
βαγ+β(Y205S)α	10 μM Pro	24 ± 2	315 ± 58c
βαγ+β(Y205S)α	20 μM Pro	8.2 ± 2.0	42 ± 5c
βαγ+β(Y205S)α	40 μM Pro	3.9 ± 0.5	11 ± 2c
βα(L263S)γ+β(Y205S)α	None	6.1 ± 1.4	35 ± 1a

ALF, alfaxalone; PEB, pentobarbital; Pro, propofol.

^aBased on the effect of picrotoxin on constitutive activity.

^bCalculated from the current response in the presence of the background drug corrected for constitutive activity.

^cCalculated from the current response in the presence of the background drug assuming no constitutive activity.

^dConsidered to equal that of the wild-type receptor.

Changing N_GABA: Effect of the β2(Y205S) Mutation on Activation by GABA.

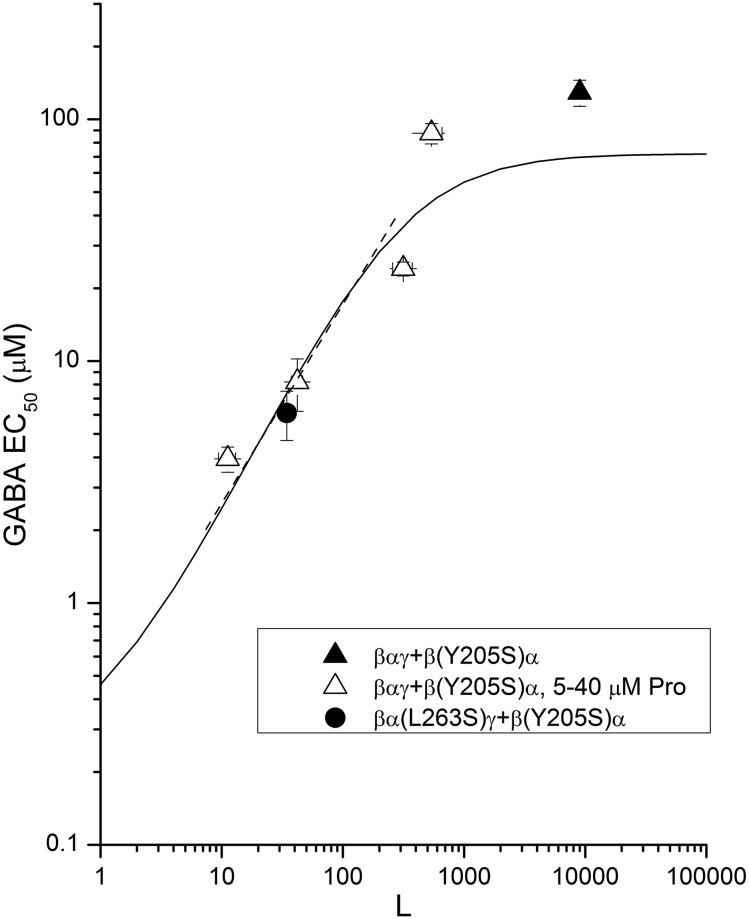
Previous work found that the β2(Y205S) mutation greatly increases EC_50,GABA (Amin and Weiss, 1993; Baumann et al., 2003), effectively removing the GABA-binding site. If placed in a single β2 subunit it should therefore reduce the value of N_GABA from 2 to 1. We expressed receptors composed of the βαγ concatemer and the β(Y205S)α concatemer, and we determined the EC₅₀ values for GABA in the absence and presence of propofol or the α(L263S) mutation.

The results are shown in Fig. 5. The solid line shows the predicted values for the EC₅₀ assuming that values obtained for the wild-type receptor apply (L_WT = 9000, K_GABA = 72 µM, and c_GABA = 0.0033), while N_GABA = 1. The predicted curve, with no free parameters, goes remarkably close to the data.

Fig. 5.

Effect of change in N_GABA on activation by GABA. The figure shows data for receptors composed of a βαγ concatemer and a β(Y205S)α concatemer in the absence of propofol (▴) and in the presence of four different concentrations of propofol (▵; 40, 20, 10, and 5 µM from lower to higher L). The filled circle shows data from a receptor containing two mutations: βα(L263S)γ and β(Y205S)α. The solid line shows the predicted values for the EC₅₀ assuming that L_WT = 9000, K_GABA = 72 µM, and c_GABA = 0.0033 (unchanged from wild-type receptor values), while N_GABA = 1. The dashed line shows the logarithmic regression from the linear region of the predicted line (slope = 0.74 ± 0.1).

The predictions clearly demonstrate that the consequences of a reduced value for N are apparent in the relationship between EC₅₀ and L. Not only is the degree of curvature altered over this range of values for L but the slope for L < 500 is increased when N is decreased. The linear regression for L < 500, shown by the dashed line in Fig. 5, has a slope of 0.74 ± 0.1. The predicted results for the mutated receptor show the asymptotic saturation at high L, supported by the experimental data from the mutant receptors.

Quality of the Description Provided by the Model.

The predictions in the preceding experimental section were made using parameters derived from fitting the experimental concentration–response data for wild-type concatemeric receptors activated by GABA (see Fig. 3). The experimental values for EC₅₀s for GABA were estimated from fitting concentration–response curves. L was estimated from the response to the background drug alone or from inhibition of constitutive activity by picrotoxin. The predictions were then compared with the experimentally determined values for various combinations of drugs or mutations. The agreement is qualitatively acceptable, considering that the predictions covered a range of about 1000-fold in L and 100-fold in EC₅₀. Perhaps the ability to describe the altered relationship between EC₅₀ and L when the number of transmitter binding sites is altered is most striking, as the only parameter derived from data using the mutated subunit was L.

The first step in applying the model was to extract parameter estimates for activation of wild-type receptors by GABA in the absence of other drugs. In fitting the concentration–response curves we restricted the value for N to integer values, and treated N and L as constants with K and c as fitting parameters. All the predictions shown in the experimental section were generated with parameters derived using L_WT = 9000 and N_GABA = 2 for the wild-type receptors.

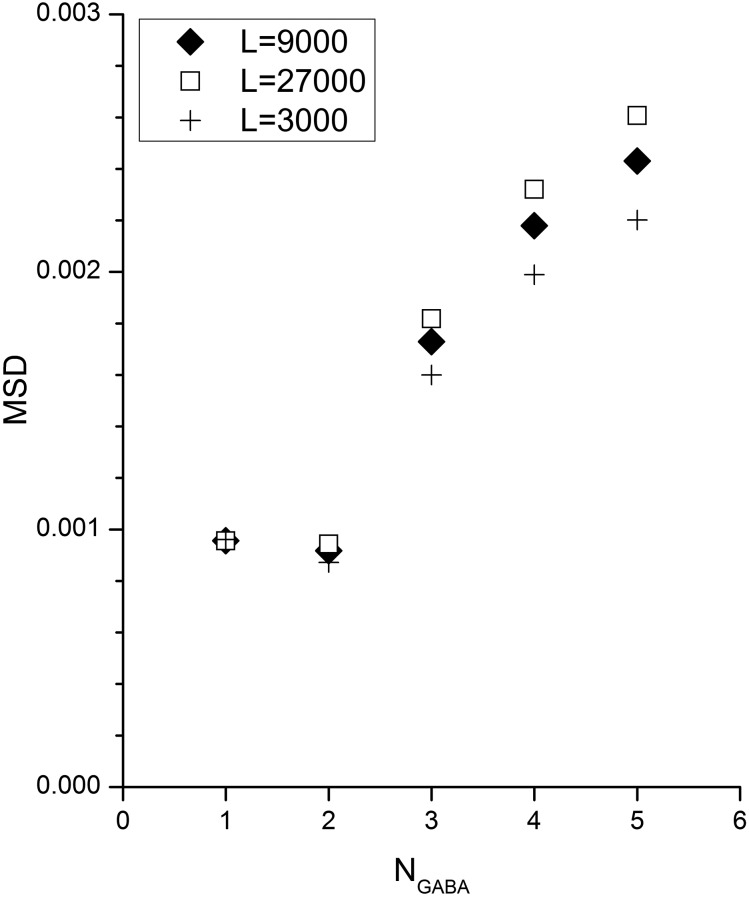
To compare the abilities of different estimates to describe the concentration–response data we also fit with values of L_WT = 27,000 and L_WT = 3000. These values are near the middle of the range of published values for wild-type α1β2γ2L GABA_A receptors formed from free subunits (L = 1000–100,000; Chang and Weiss, 1999; Ziemba and Forman, 2016). N_GABA values of 1 to 5 were used. To examine the quality of the description we computed the mean squared difference (MSD) between the fit and the data. Figure 6 shows results for fits of the concentration–response data for GABA. As can be seen, fitting with different values for L_WT gave similar MSD values. There is a minimum at N_GABA = 2, although an F test on the variance ratios shows no or minor statistical significance.

Fig. 6.

Quality of description of concentration–response data with different assumed values for L_WT and N_GABA. The mean squared differences (MSD) between the predicted and measured concentration–response data are shown for different values of L_WT and N_GABA. The concentration–response data (see Fig. 3B) were fit with various values for N_GABA as indicated on the abscissa and three values for L_WT (9000 ♦, 27,000 □, and 3000 +). An F test on the ratio of MSD values indicated that the difference between N_GABA = 2 and N_GABA = 4 or 5 was marginally statistically significant (P < 0.04 for all L values, uncorrected for multiple comparisons).

It may be surprising that a wide range of values for L_WT can be used to describe the data for activation of wild-type receptors. This is more understandable when the relationship between the concentration-response data and the model is examined: in the data the two asymptotes are P{open, basal} and P{open, max}. The model defines P{open, basal} as 1/(1 + L) and P{open, max} as 1/(1 + Lc^N). When P{open, basal} is very low then both L and c are determined largely by P{open, max}, and for a given P{open, max} pairs of L and c are possible as long as Lc^N = Lʹcʹ^N. For example, fitting the wild-type data with eq. 4 for activation by GABA with N_GABA = 2 and L_WT = 27,000 gave a value for c_GABA of 0.0019 (P{open, max} = 0.91), while L_WT = 9000 gave c_GABA = 0.0033 (0.91) and L_WT = 3000 gave c_GABA = 0.0056 (0.91). These findings are in agreement with previous theoretical studies on the relationships between constitutive activity and MWC parameters (Ehlert, 2014a). Similarly, the value for N can vary. Again, if L is set then pairs of values for c and N are possible provided cʹ^Nʹ = c^N. However, the value for N is additionally constrained by the shape of the concentration-response curve, as indicated by the fact that different values of N affect the MSD to a larger extent (Fig. 6).

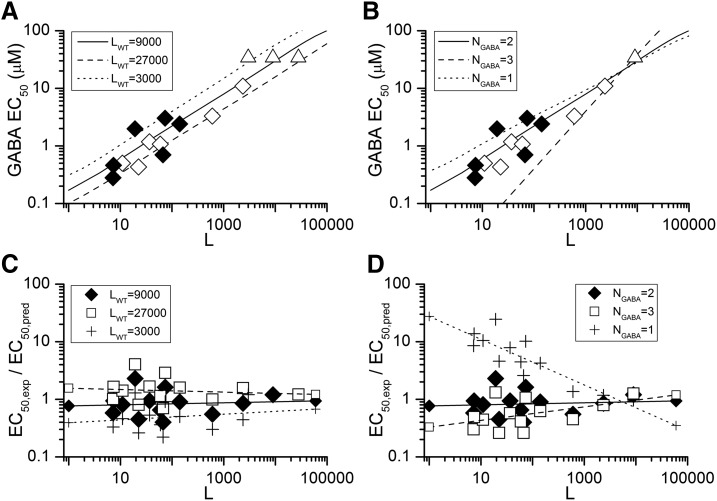
Different values for L_WT and N result in altered relationships between EC₅₀ and L. To assess the ability of the parameters to describe the relationship between EC₅₀ and L we predicted the EC₅₀ values for data for the data in Fig. 4, A and B (wild-type receptors in the absence or presence of background drugs and receptors containing mutations). The wild-type receptor concentration–response data were fitted with eq. 4 using different assumed values for L_WT (3000, 9000, or 27,000) and N_GABA (1, 2, or 3) to obtain estimates for K_GABA and c_GABA. These parameters were used to predict the relationship between EC_50,GABA and L (Fig. 7). The differing values for L_WT shifted the predicted values along the abscissa (Fig. 7A), whereas a change in N_GABA led to a change in slope (Fig. 7B).

Fig. 7.

Predictions of EC₅₀ values made using parameters generated with different values for L and N. (A and B) Data for EC_50,GABA and L replotted from Fig. 4, A and B. (A) Lines show the predicted relationships for three different assumed values of L_WT with N_GABA = 2. (B) Lines show predicted relationships for three assumed values for N_GABA with L_WT = 9000. (▵) Data for wild-type receptors in the absence of other agonists; note that ▵▵▵ are shown in A, corresponding to the assumed values for L_WT. (◇) Values in the presence of a background drug. (♦) Values in the presence of an α1(L263S) mutation. (C and D) Quality of the descriptions assessed by calculating the ratio of the experimental EC_50,GABA to the predicted EC_50,GABA, which is plotted against L. (C) Data when the value of L_WT was changed while N_GABA = 2. (D) Changes in N_GABA with L_WT = 9000.The lines identified by the symbols at the ends of the lines show the linear regression of log(ratio) on log(L). Comparison of (A–C) indicates that an L_WT value of 3000 (N_GABA = 2) provides predictions that consistently lie above the observed values (ratio < 1), for L_WT = 27,000 consistently lie below, and for L_WT = 9000 are relatively close to the observed EC₅₀. Similarly, the predictions for N_GABA = 1 or 3 (B and D) demonstrate increasing large inaccuracies relative to the experimental EC₅₀ values as L departs further from the value for wild-type receptors in the absence of agonists, while the predictions for N_GABA = 2 have a relatively constant relationship to the observed EC₅₀. The results are summarized in Table 3.

We then computed the error from the logarithms of the ratio of the experimental to the predicted EC₅₀ values, to reduce the consequences of the large range in observed EC₅₀ values that would skew the simple squared difference estimate. Figure 7, C–D show the ratio EC_50,exp/EC_50,pred plotted logarithmically against L. The calculations indicate that an L_WT of 9000 and N_GABA of 2 provide predictions that are relatively close to the observed EC₅₀.

The results of a statistical analysis of the data are shown in Table 3. Inspection of the table indicates that for wild-type βαγ + βα the closest description of those tested was obtained with L_WT = 9000 and N_GABA = 2, as also suggested by inspection of Fig. 7.

TABLE 3 .

Quality of description with different values for N and L_WT

The experimental values for EC₅₀ for GABA were compared with values predicted with different assumed values for N_GABA and L_WT using the logarithm of the ratio (EC_50,exp/EC_50,pred) to assess the quality. The first and second columns give the assumed value for L_WT and N_GABA. The third column gives mean ± S.E.M. for the parameter. The fourth column gives the P value that the mean differs significantly from 0 (where a value of 0 indicates identity of EC_50,exp and EC_50,pred; one sample two-tailed t test). The data sets analyzed are shown in Fig. 4, A and B, 13 pairs of values for L and EC_50,GABA.

LWT	NGABA	log(EC50,exp/EC50,pred)	P to 0
3000	2	−0.32 ± 0.07	0.001
9000	2	−0.08 ± 0.06	0.22
27,000	2	0.15 ± 0.06	0.04
9000	1	0.69 ± 0.13	<0.001
9000	2	−0.08 ± 0.06	0.22
9000	3	−0.26 ± 0.07	0.005

Overall these analyses indicate that it can be difficult to accurately estimate the activation parameters from concentration-response curves alone, especially when basal activity is low. However the relationship between EC₅₀ and L can allow us to determine whether some values provide better descriptions than others.

Discussion

The results in this study indicate that the concerted transition model is able to accurately predict the relationship between the EC₅₀ for activation by GABA and basal activity. The agreement is remarkable considering that the parameters for activation by GABA were established by analysis of a single data set: the concentration–response relationship for GABA acting on wild-type βαγ + βα receptors in the absence of any other GABAergic agent. We perturbed the system by altering L_WT by addition of a background drug or introducing a gain-of-function mutation. We altered N_GABA (the number of binding sites for GABA) by mutation. For all cases, the new relationship between EC₅₀ and L was predictable by the model.

It is particularly interesting that predicting the effects of a combination of drugs (e.g., propofol as the background drug in combination with GABA) did not require any data from experiments involving the combination; the effect of the background drug was assessed from modified L measured in the absence of GABA while the activation parameters for GABA were obtained in the absence of the background drug. Removal of one GABA-binding site produced the expected changes in the relationship between EC₅₀ and L for a change in N_GABA from 2 to 1, as would be expected from the ample data supporting the idea that the wild-type receptor has two transmitter binding sites (Amin and Weiss, 1993; Baumann et al., 2003).

The predicted EC_50,GABA values for receptors containing the gain-of-function α1(L263S) or β2(Y143W) mutations were calculated using the value for basal activity (L) from the mutant receptor and the estimate for affinity to the transmitter (K_GABA) in the wild-type receptor. Similarities in the predicted and experimental EC_50,GABA indicated that the effects of the mutations could be accounted for by assuming that the mutations modified L with no effect on K_GABA. There is no a priori reason to expect that a mutation that affects receptor activation by the transmitter acts indirectly, solely through changes in basal activity. These two mutations were selected based on prior reports that had indicated minimal effect on K_GABA (Chang and Weiss, 1999; Eaton et al., 2016). Mutations that additionally modify K_GABA would be expected to exhibit deviations from the predicted, model-based relationship between EC₅₀ and L. Therefore, compliance with the predicted relationship can serve as indicator of the mechanism of action for a mutation.

The GABA_A receptor is a target for many drugs, including sedatives, tranquilizers, and anesthetics. These drugs can both directly activate the receptor and potentiate the responses to GABA. It will be quite useful if our present results can be extended to more complex combinations of drugs, as the use of the MWC model greatly simplifies the task of characterizing the properties of combinations of drugs.

The particular kinetic model we used is a simplified version of a cyclic model, in which thermodynamic cycles are closed. A cyclic model was first proposed to underlie aspects of transmitter-gated channel function in the context of desensitization of nicotinic receptors (Katz and Thesleff, 1957). The particular scheme we used simplified a cyclic model significantly. The basic assumption is that the receptor exists in only two states: active (open channel) and inactive (closed channel), in varying degrees of ligation. That is, there are no intervening states in which the rate constants for one or another transition depend on the degree of ligation of the receptor (e.g., association of drug A in the absence of bound drug B versus in the presence of bound drug B).

This assumption reduces the number of free parameters greatly, as can be seen when the model is compared with a full allosteric model (e.g., the “binary elements” model used by Goldschen-Ohm et al., 2014). The two-state assumption also leads to the idea that the receptor undergoes the gating transition as a unit—all subunits undergo a concerted transition because otherwise a variety of combinations of subunits in various conformational states would ensue. The second assumption is that all sites for a given ligand are identical. The concerted nature of the activation necessitates that the sites change affinity (if they do at all) in a concerted fashion when the receptor as a whole changes state between active and inactive.

These assumptions result in the kinetic scheme shown in Fig. 1. Many alternative possible schemes exist, as laid out initially by Koshland et al. (1966). In terms of full cyclic schemes, MWC analyses have been applied to GABA_A (Chang and Weiss, 1999; Rüsch et al., 2004; Ruesch et al., 2012) and muscle nicotinic (Jackson, 1989; Auerbach, 2012) receptors. Partially cyclic schemes (“flip” and “prime”) have been used for data from glycine (Burzomato et al., 2004; Plested et al., 2007) and nicotinic receptors (Lape et al., 2008; Mukhtasimova et al., 2016). Finally, a “binary element” analysis has been applied to studies of GABA_A receptors, which allows for all possible pairwise interactions between functional elements in a receptor (Goldschen-Ohm et al., 2014).

The peak responses studied here are pseudo steady-state measurements, reflecting both open and brief duration desensitized states while slow desensitization is explicitly excluded from the two-state cyclic model we used. Desensitization of the GABA_A receptor is not fully understood, but it seems likely that there are at least two phases distinguishable by kinetics—a faster and a slower phase (Jones and Westbrook, 1995; Steinbach and Akk, 2001; Bianchi and Macdonald, 2002). In terms of single-channel kinetics, a cluster at high [GABA] has a mean duration of 2 to 3 seconds (Akk et al., 2001), producing slow desensitization that would be observed in oocyte recordings. There are also intracluster closed time components that have been associated with receptor desensitization (Haas and Macdonald, 1999; Steinbach and Akk, 2001; Lema and Auerbach, 2006). In single-channel activity from concatemeric GABA_A receptors these closed states have mean durations ranging from 0.5 to 25 milliseconds (Akk et al., 2009). Our simulations (not shown) indicate that omission of these states in the model (Fig. 1) has a relatively small effect (less than 10%) on the estimated open probability of the peak response and the predicted EC₅₀. We did not analyze responses at the overall steady state, reflecting long-lived desensitization.

The major strength of the MWC model is its simplicity. There is no pairwise specific interaction among agents; all interactions are mediated through the overall energy available to activate the receptor. The fact that the scheme consists of closed cycles means that at equilibrium the state function for a single agonist can be fully described with only four parameters. The energetic contribution of an agonist is defined in a single parameter (c) scaled by the number of sites for the agent (N). Activation is enhanced by the increased affinity of drug for its sites in the open state, reflected in the stabilization energy ΔG_A = N_ART × (ln((1+[A]/K_A)/(1 + [A]/(c_AK_A))), which offsets the free energy difference between the unliganded closed and open states, ΔG_int = RTln(L). Interactions between drugs are predicted to occur because the application of a background drug reduces the free energy difference to be overcome by agonist A [ΔG_int+B = RTln(L) + ΔG_B] rather than as a result of a change in any of the parameters for activation by A.

The three drugs used to potentiate the responses to GABA (propofol, pentobarbital, and alfaxalone) produced similar shifts in the EC₅₀ for GABA for similar shifts in L. These drugs belong to chemically distinct classes of anesthetics and have distinct (although possibly overlapping) binding sites on the receptor (Jayakar et al., 2014). The observation that they produce similar shifts gives circumstantial and model-independent support to the idea that the shifts reflect a nonspecific effect on receptor activation. Our analysis does not address the validity of the MWC model as a detailed description of activation of the GABA_A receptor by a single agonist, but rather explores the mechanism by which interactions between the transmitter and an allosteric agonist might take place. Although the MWC model has been shown to be able to describe the macroscopic activation of GABA receptors and interactions between several anesthetics and GABA (Chang and Weiss, 1999; Rüsch et al., 2004; Ruesch et al., 2012), it is not clear that it is as successful at accounting for responses to combinations of diazepam with GABA (Gielen et al., 2012; Goldschen-Ohm et al., 2014; however, see Rüsch and Forman, 2005; Campo-Soria et al., 2006). In particular, there may be a requirement for an additional activated-but-closed state between inactive and active open (Gielen et al., 2012; Goldschen-Ohm et al., 2014).

We have emphasized the ability of the model to predict the relationship between EC₅₀ and L. However the predictions are not exact; there is some scatter of observed values around the predicted line. The reasons for this disagreement are not known at present. One clear possibility is the presence of variability in the experimental values. Other possibilities are that the MWC model is overly restrictive in its assumptions—for example that there are no specific interactions among drugs or that conformational changes are strictly concerted.

Abbreviations

DMSO

dimethylsulfoxide

GABA_A receptor

γ-aminobutyric acid type A receptor

MSD

mean squared difference

MWC model

Monod, Wyman, and Changeux model

P{open}

probability of being open

Authorship Contributions

Participated in research design: Akk, Steinbach.

Conducted experiments: Shin, Germann.

Performed data analysis: Akk, Shin, Germann, Steinbach.

Wrote or contributed to the writing of the manuscript: Akk, Shin, Germann, Steinbach.