Single-Walled Carbon Nanotubes Probed with Insulator-Based Dielectrophoresis

Abstract

Single-walled carbon nanotubes (SWNTs) offer unique electrical and optical properties. Common synthesis processes yield SWNTs with large length polydispersity (several tens of nanometers up to centimeters) and heterogeneous electrical and optical properties. Applications often require suitable selection and purification. Dielectrophoresis is one manipulation method for separating SWNTs based on dielectric properties and geometry. Here, we present a study of surfactant and single-stranded DNA-wrapped SWNTs suspended in aqueous solutions manipulated by insulator-based dielectrophoresis (iDEP). This method allows us to manipulate SWNTs with the help of arrays of insulating posts in a microfluidic device around which electric field gradients are created by the application of an electric potential to the extremities of the device. Semiconducting SWNTs were imaged during dielectrophoretic manipulation with fluorescence microscopy making use of their fluorescence emission in the near IR. We demonstrate SWNT trapping at low-frequency alternating current (AC) electric fields with applied potentials not exceeding 1000 V. Interestingly, suspended SWNTs showed both positive and negative dielectrophoresis, which we attribute to their ζ potential and the suspension properties. Such behavior agrees with common theoretical models for nanoparticle dielectrophoresis. We further show that the measured ζ potentials and suspension properties are in excellent agreement with a numerical model predicting the trapping locations in the iDEP device. This study is fundamental for the future application of low-frequency AC iDEP for technological applications of SWNTs.

Single-walled carbon nanotubes (SWNTs) possess unique electronic, mechanical, optical, and structural properties which can be exploited for future nanoscale applications.¹⁻⁶ Their use in nanoscale electronics ranges from field-effect Schottky-type transistors,^3,6,7 nanometer-sized semiconducting devices, probes,⁸ and data storage or field emission sensors² to biological transporters and biosensors.⁹ SWNTs have also been exploited as mechanical sensors in living cells thanks to their unique fluorescence properties including superb photostability^10,11 and fluorescence emission in the IR range¹²⁻¹⁴ where autofluorescence in biological samples is minimal.

Typically, SWNTs are produced in processes yielding mixtures with broadly dispersed diameters, lengths (from 10 nm up to 1 cm),¹⁵ and chirality. Chirality is important to determine electrical and optical properties of SWNTs.^16,17 Producing SWNTs with defined lengths or chiralities has not been achieved. One of the most successful fabrication methods is the high-pressure carbon monoxide (HiPco) process, yielding SWNTs in diameters of ∼1 nm, lengths from several tens of nanometers to a few micrometers, and preferred, but not unique, chirality.^18,19 In addition, SWNTs form adducts and bundles through van der Waals forces¹⁴ during fabrication. Applications of SWNTs thus require overcoming the challenges related to postsynthesis separation steps.

Various separation methods of SWNTs have been reported according to their electronic type,^20,21 and these separated nanotubes can be used in future electronic device components.²² In applications requiring SWNTs in aqueous solutions, they must be suspended using a surfactant or wrapping agent, which in turn influences their surface charge and ζ potential. Sorting of suspended SWNTs has been attempted with ion-exchange²³ and size-exclusion chromatography.²⁴ The combination of the two has even allowed the separation of similar sized diameter SWNTs by chirality.²⁵ The method is however not generally applicable to samples with large variation in diameters or chirality. Ultracentrifugation including density gradient methods has been used for sorting, yielding small amounts that can be employed for selected applications.²⁶ In addition, the unique chemical reactivity of ends or side walls of SWNTs has been exploited for sorting as well as to selectively break down nondesired species in SWNT mixtures through etching approaches.²⁷ Sorting of SWNTs can also be carried out in direct current electric fields via electrophoresis employing sieving matrices.^28,29

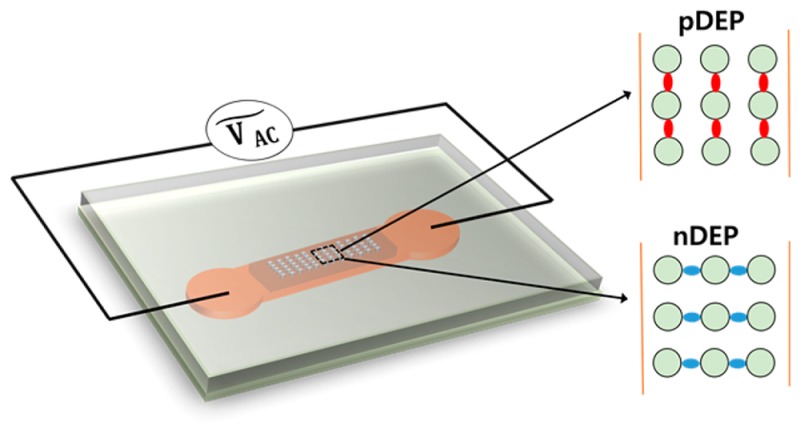
An alternative electrical separation method for SWNTs is dielectrophoresis. Alternating current dielectrophoresis (AC DEP) has gained attention as a potential technique for sorting carbon nanotubes according to their electrical properties.^4,30−32 When a cylindrical nanotube is placed in a nonuniform electric field, it will experience a force due to the induced dipole moment.^4,33 Depending on the polarization properties of the nanoparticles and the surrounding medium, particles can be manipulated or trapped using DEP. Particles experiencing positive DEP (pDEP) drift toward the regions of largest electric field strength, while the underlying dielectrophoretic force is proportional to the carbon nanotube length.³⁴ The dielectrophoretic force strongly depends on the frequency of the electric field and the frequency-dependent electrical properties of the particles, typically described by a frequency-dependent Clausius–Mossotti relation. The DEP behavior of SWNTs can be tuned with the applied frequency. It has been reported that metallic carbon nanotubes always experience pDEP due to their large dielectric constant.⁴ Depending on the electric field frequency and particle surface conductivity, semiconducting SWNTs can show either positive or negative DEP.^17,30,31 Therefore, DEP has been used to separate metallic from semiconducting SWNTs.^4,35 The transport and trapping properties of DEP can also be employed as a means to control large-scale or even single-SWNT deposition for electronic applications.^36,37 Inhomogeneous electric fields for AC DEP can be generated in two different ways: (i) by introducing microelectrodes in a sample chamber or (ii) by constructing topological structures between macroelectrodes.³⁸ Electrode-based DEP (eDEP) is an established method where micrometer-sized electrodes are patterned on a substrate. These electrodes can be quadruple electrodes,³⁹ pairs of electrodes at close distance,⁴⁰ or interdigitated electrodes.³⁴ With eDEP, high frequencies can be reached, and the DEP response of nanoparticles can be investigated in the kHz to MHz regime. The other, newer approach is insulator-based DEP (iDEP) where different dielectric obstacles are introduced in a microfluidic channel producing inhomogeneous electric fields when an electrical potential is applied between the access ports of the microfluidic device.⁴¹ With an iDEP device, DC and low-frequency DEP behavior of particles can be examined.⁴² iDEP devices avoid chemical electrode reactions that can occur in eDEP applications, fabrication steps are facilitated, and the electric field gradient can be generated along the entire depth of microfluidic devices.^43,44

iDEP at low frequencies, <1 kHz, as an alternative approach to manipulate SWNTs has not been used in the past. At low frequencies, the DEP of nanoparticles is mainly governed by their conductivity and that of the surrounding medium^45,46 (see Theory for more detail) and critically depends on the wrapping agent used to suspend the SWNTs.³⁰ We here report on the DEP characteristics of SWNTs using an insulator-based microfluidic system. We have studied the dielectrophoretic behavior of SWNTs wrapped with single-stranded DNA (ssDNA) or with sodium deoxycholate (NaDOC) at frequencies up to 1 kHz. The resultant DEP trapping behavior of semiconducting SWNTs was investigated by infrared fluorescence microscopy in an elastomer microfluidic channel. We correlate the observed dielectrophoretic behavior with differences in the ζ potential, which, in turn, depends on the method used for the suspension of the investigated SWNTs.

Materials and Methods

Chemicals

SWNTs (batch no. 189.2) were obtained from Rice University (TX, USA) through a materials transfer agreement. Sodium hydroxide (NaOH) was purchased from Merck KGaA (Germany), N-(2-hydroxyethyl)piperazine-N′-2-ethanesulfonic acid (HEPES), single-stranded DNA composed of 30 tyrosine bases (dT30), sodium deoxycholate, and Pluronic F-108 were purchased from Sigma-Aldrich (MO, USA). Muscovite Mica (V-5; sheet size, 50 × 75 mm²; thickness, 0.15–0.21 mm) was purchased from Science Service (Germany) and (3-aminopropyl) triethoxysilane (APTES) was obtained from Sigma-Aldrich. Sylgard silicone elastomer kit for poly(dimethylsiloxane) (PDMS) was obtained from Dow Corning Corp. (MI, USA). Glass slides (40 mm × 50 mm) were from Menzel GmbH and purchased through Thermo Scientific (Germany). Deionized (DI) water was produced using an Arium 611 ultrapure water system from Sartorius (Germany).

Microchip Fabrication

The microfluidic chip layout was designed with AutoCAD and then patterned on a silicon wafer by standard photolithography as reported previously. From this master wafer, a PDMS mold was prepared via standard soft lithography procedures.⁴⁷ Briefly, liquid PDMS was mixed with PDMS curing agent in a ratio of 10:1 (w/w). The mixture was poured on the master wafer, degassed using a vacuum desiccator, and heated in an oven for 4 h at 80 °C. The mold was subsequently removed from the master wafer, and 3 mm diameter reservoirs were punched manually by a puncher at the beginning and end of the post array portion of the corresponding microchannel. The PDMS mold was cut into slabs of appropriate size, and these slabs and glass slides were cleaned with isopropanol and distilled water, dried with a stream of nitrogen, and baked on a hot plate at 90 °C until completely dried. Both surfaces were activated with an oxygen plasma (PDC-001; Harrick Plasma cleaner/sterilizer, USA) at high power (18 W) for 30 s. After the plasma treatment, the PDMS slab was pressed against a glass slide to form a closed microchannel system and then placed on a hot plate at 90 °C for 3–5 min. The chamber was then filled with DI water and washed several times with DI water by suction, and then the surface was treated with Pluronic F108 (1% (w/v)) and incubated overnight prior to use as described previously.⁴⁸ With surface treatment, particles can experience strong DEP force and can be immobilized at the dielectric obstacles, even at higher medium conductivity.^45,46

The PDMS channel was 1.5 cm long with an integrated post array section over ∼1 cm as shown in Figure 1c. The posts had a diameter of 10 μm, the row distance was also 10 μm, and the post to post distance in one row was 5 μm.

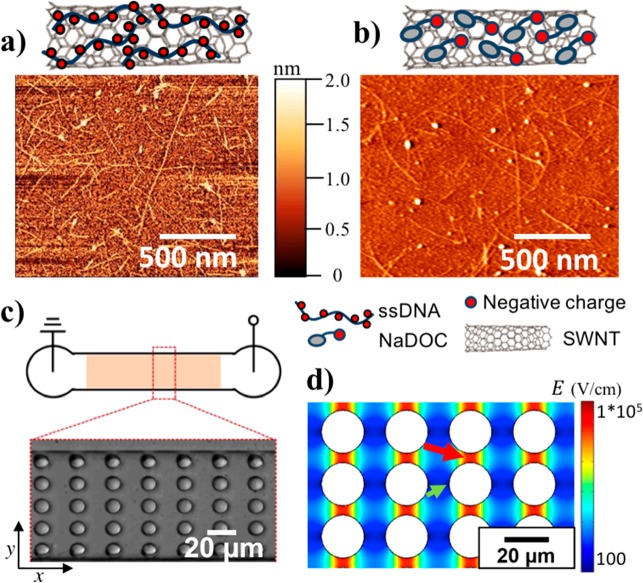
Figure 1.

SWNT characterization and microfluidic device scheme. (a) Schematic drawing of ssDNA-wrapped SWNT and AFM image of ssDNA-suspended single SWNTs. (b) Schematic drawing of NaDOC-wrapped SWNT and AFM image of NaDOC-suspended single SWNTs. (c) Schematic of microfluidic device employed for iDEP and bright field microscopy image of a section of the post array. (d) Electric field distribution as obtained from a COMSOL model in a section of the post array at an applied electric potential of 1000 V across the 1.5 cm long microchannel (green arrow (small), pointing toward the region with the lowest electric field; red arrow (large), pointing toward the region with the highest electric field).

SWNT Sample Preparation

SWNTs were solubilized by wrapping with either surfactant (NaDOC) or single-stranded DNA (dT30). NaDOC (1% (w/v)) was dissolved in 10 mM HEPES buffer at pH 7. A glass scintillation vial was cleaned with ethanol and dried with a stream of nitrogen. Then, ∼2 mg of SWNTs were carefully transferred to the clean vial with a spatula, and 2mL of NaDOC solution were added. The vial was placed in a bucket with ice and sonicated with a 2 mm Microtip sonicator (Sonics & Material Inc., Danbury, CT, USA) at 20 kHz and 20 W. Two types of NaDOC-coated SWNT samples were prepared. Sample A was prepared by 20 min sonication, and sample B was prepared by 60 min sonication. After sonication, the SWNT suspension was transferred to an Eppendorf vial and centrifuged (Sigma 1–14 centrifuge, Germany) at 14000 rpm for 15 min. After centrifugation, the pellet was discarded, and the supernatant was collected to be used in experiments and stored at 4 °C.

For ssDNA wrapping of SWNTs, DI water was added at a ratio of 1:1 (w/w) to dry ssDNA to yield about 0.5 mL of 1 mg/mL concentration. The vial was centrifuged at low spin speed for a few seconds and vortexed for a few seconds repeatedly for approximately 5 min to ensure homogeneous solubilizing of ssDNA. In the next step, ∼1 mg of SWNTs was transferred to a clean glass scintillation vial, and DNA solution was added to the SWNTs. Then the sample was sonicated at 20 kHz and 20 W for 90 min as described above. After sonication, the sample was ultracentrifuged (Optima Ultracentrifuge 28000 rpm, Beckman Coulter, Germany) for 90 min at 4 °C. After centrifugation, the supernatant was collected and stored at 4 °C prior to experiments. Surface charge was measured with a Zetasizer Nano ZS instrument (Malvern, USA). Five trials were made, and the average ζ potential value was determined. An Orion-3 Star conductivity meter from Thermo Scientific was used for measuring the medium conductivity. The conductivity meter was calibrated with a standard NaCl solution (conductivity of 0.1413 S/cm and 692 ppm).

SWNT Imaging

SWNTs were imaged as previously reported.⁹ Briefly, a sample rich in fluorescent (6, 5) carbon nanotubes with an excitation maximum of 567 nm and emission maximum of 975 nm were used in this work. SWNTs were excited by a 561 nm DPSS laser (500 mW cw; Cobolt Jive; Cobolt). A neutral density filter (NDC-50C-4M, Thorlabs) served to adjust the intensity of the beam. The laser beam was directed into the back aperture of a high-NA objective (CFI Plan-Apo IR, 60×, NA = 1.27; Nikon, Japan). Fluorescence light was collected through the same objective and passed through a dichroic beam splitter (630 DCXR; AHF Analysentechnik), further filtered using a 900 nm long-pass filter (F47-900; AHF Analysentechnik) and focused on a short-wave infrared (SWIR) camera with an InGaAs detector (XEVA-SHS-1.7-320 TE-1, Xenics). Images of SWNTs were recorded with 100 ms exposure times. Data analysis was performed with ImageJ software. Five trapping regions were chosen in each case from a representative image, and pixel intensities were extracted, averaged, and normalized with the largest intensity in each case. Origin 8.5 software was used for plotting the normalized data with associated error bars at the different applied potentials.

Atomic Force Microscopy

Atomic force microscopy (AFM) was used to determine lengths and diameters of the SWNTs. The SWNT suspensions were incubated on mica surfaces (Grade V1, Ted Pella, Inc., USA) for 15 min, washed with DI water, and dried. A Nanotec AFM instrument (Nanotec, Spain) was used for imaging SWNTs in tapping mode in air. SWNT length was measured for about 100 nanotubes for each sample.

Computation of Electric Field Distributions

A section of the microfluidic device matching the post array geometry was drawn in COMSOL Multiphysics version 5.2a. Domains for the microchannel material and solvent were assigned and material properties chosen according to predefined parameters in COMSOL for PDMS and water. The electric field in the designed geometry was solved with the Electric Current module choosing a stationary, time-independent solver. The program solves Maxwell’s equations with appropriate boundary conditions, with the posts and side walls considered as electrical insulators. The electrical potential was applied between the inlet boundary and the outlet boundary. In addition, COMSOL was used to compute particle trajectories and investigate the DEP trapping regions of SWNTs in the post array. Details are provided in the Supporting Information.

Theory

Following the literature, we briefly describe the DEP force on a single-walled carbon nanotube. When a cylindrical solid particle is placed in a nonuniform DC electric field, it experiences a dielectric force which can be expressed as^34,46,49

1

where ε_m is the medium permittivity, 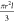is a geometry factor and r and l are the radius and length of the particle, respectively. In the case of a hollow tube, the geometry factor will be replaced by πlδ(2r – δ) with the wall thickness δ. E is the electric field and Re(CM) is the real part of the Clausius–Mossotti factor. The DEP force acting on a SWNT depends on the radius and length as well as the magnitude and sign of the Clausius–Mossotti factor (CM), which describes the electrical polarizability of the material:^30,31,50

2

with

3

where ε_p is the permittivity of the particle; σ_m and σ_p are the conductivity of the medium and particle, respectively; ω is the frequency; and L denotes the dimensionless depolarization factor parallel to the electric field and along the long axis of the nanotube, which is defined as⁴⁶

4

If a suspended particle has a higher polarizability than the medium, the particle is driven toward the region of higher electric field; i.e., particles accumulate where the field has a maximum, which is referred to as positive DEP (pDEP). In contrast, if the polarizability of a suspended particle is lower than that of the medium, it moves toward the region of lower electric field; i.e., particles accumulate where the field has a minimum, which is termed negative DEP (nDEP). In other words, nanotubes with Re(CM) > 0 experience pDEP and nanotubes with Re(CM) < 0 experience nDEP. The real part of eq 2 is

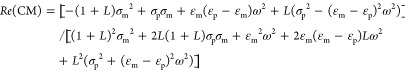5

For ω → 0, Re(CM) becomes

6

It can thus be seen from eq 6 that Re(CM) in the low-frequency range only depends on the medium conductivity, particle conductivity, and depolarization factor relating to the length and diameter of the SWNTs.

The Clausius–Mossotti factor for SWNTs can be estimated based on intrinsic parameters. The relative permittivity for metallic and semiconducting SWNTs was reported as 4000 and 5, respectively.^4,30 For nanoparticles, it has been shown that the effective particle conductivity consists of the intrinsic conductivity and of surface conductivity near the particle. The total particle conductivity can be expressed as⁵¹

7

where σ_int is the intrinsic particle conductivity, λ_s is the surface conductance, and a is the radius of a spherical particle. It was reported that the radius of sodium dodecyl sulfate suspended SWNTs is approximately 2.7 nm because a double layer is formed around the radial direction of the nanotubes.³⁰ This value was used for the particle conductivity calculation in this study. The internal conductivity of semiconducting SWNTs can be taken as approximately zero because of the large band gap.³⁰ The surface conductance λ_s is the sum of the diffuse layer conductance, λ_s,d, and the Stern layer conductance, λ_s,s, where the ratio of diffuse layer conductance and Stern layer conductance has been reported as 0.56.⁵² The diffuse layer conductance can be calculated from the ζ potential of SWNTs and the properties of the electrolyte, using the following equations:^30,53

8

with

9

10

Here, λ_s,d is the diffuse layer conductance, q is the charge of an electron, D is the diffusion constant, k_B is the Boltzmann constant, m is the contribution from electro-osmotic transport, β is the reciprocal Debye length, η is the viscosity of the solution, z is the valence of the ion, and n is the ion concentration. The surface conductivity can be obtained from the ζ potential, which was assessed experimentally in this study (see Table 1). The effective particle conductivity can then be calculated using eqs 8–10, the surface conductivity λ_s (= λ_s,d + λ_s,s) and eq 6. Note that this calculation accounts for an ideally suspended SWNT with no interactions with other particles or aggregation. Results for SWNTs probed in this study are depicted in Figure 5. Parameters used were q = 1.60 × 10^–19 C, n = 2.05 × 10²⁵ m^–3 for NaDOC-wrapped SWNTs (n = 5.5 × 10²³ m^–3 for ssDNA-wrapped SWNTs), z = 1, k_B = 1.38 × 10^–23 J K^–1, T = 297 K, D₊ = 1.334 × 10^–9 m² s^–1, D_– = 1.334 × 10^–9 m² s^–1, η = 0.890 × 10^–3 K g m^–1 s^–1 (for water) as well as the permittivity of water ε = 80 ε₀ with ε₀ = 8.854 × 10^–12 F m^–1.

Table 1. ζ potentials, σ_m, σ_p, Conductivity Ratio, and Clausius–Mossotti Factors for Suspended SWNTs.

sample	sonication time (min)	ζ potential (mV)	σp (S/m)	σm (S/m)	γa	Re(CM)
NaDOC (sample C)	5	–18.6 ± 1.7	0.03	0.15	0.2	–0.8
NaDOC (sample D)	10	–19.4 ± 1.4	0.12	0.15	0.8	–0.2
NaDOC (sample A)	20	–20.2 ± 1.1	0.14	0.15	0.93	–0.07
NaDOC (sample B)	60	–58.6 ± 1.8	2.94	0.15	19.6	18.6
ssDNA	90	–60.7 ± 2.0	0.53	0.04	13.3	12.3

^aγ = conductivity ratio.

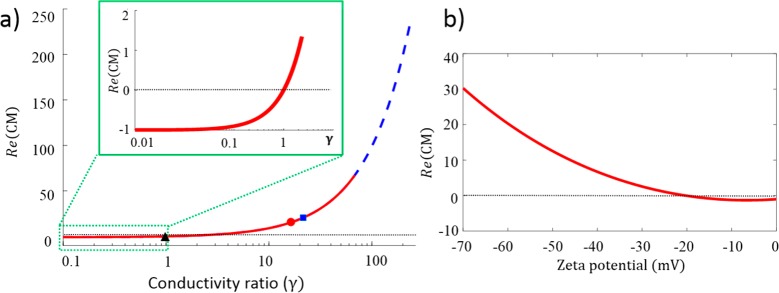
Figure 5.

Calculated Re(CM) in dependence of γ and ζ potential: (a) calculated Re(CM) vs γ in the low-frequency regime, calculated for a frequency of 700 Hz; red lines, for semiconducting NaDOC-wrapped SWNT; blue dashed line, for semiconducting ssDNA-wrapped SWNTs (note that both curves coincide in the low-frequency regime as Re(CM) is only governed by the conductivity ratios); black dashed line, Re(CM) = 0; black triangle, blue square, and red circle, values for sample A, sample B, and ssDNA-wrapped SWNTs, respectively; inset, zoom in for low values of γ < 1, where negative Re(CM) prevails; (b) dependency of Re(CM) on ζ potential for NaDOC-suspended SWNTs. The dashed line indicates Re(CM) = 0. It is apparent that Re(CM) changes sign from positive to negative at low ζ potential (<21 mV).

Results and Discussion

For this study, SWNTs were solubilized by wrapping with the surfactant NaDOC or with dT30 single-stranded DNA, and their iDEP behavior was studied in a microfluidic device. Panels a and b of Figure 1 show AFM images of NaDOC- and DNA-wrapped SWNTs together with schematic drawings of wrapping. AFM imaging revealed a height of 1.52 ± 0.6 nm for NaDOC-coated SWNTs and an average length of 1050 ± 610 nm. For SWNTs wrapped with ssDNA, an average height of 1.33 ± 0.64 nm was found as well as an average length of 1100 ± 550 nm. A PDMS microfluidic chip was used to test the DEP behavior in trapping experiments as shown in Figure 1c. Figure 1d represents the numerically calculated electric field in the circular post array in a representative section of the device. We present iDEP trapping results for two NaDOC-wrapped SWNT samples differing in the sonication time during suspension and one ssDNA-wrapped SWNT sample, as listed in Table 1. All results presented below relate to semiconducting SWNTs observed through their infrared fluorescence upon excitation with a 561 nm laser. Metallic SWNTs do not fluoresce and are not probed with our method.

Prediction of iDEP Trapping Regions for SWNTs

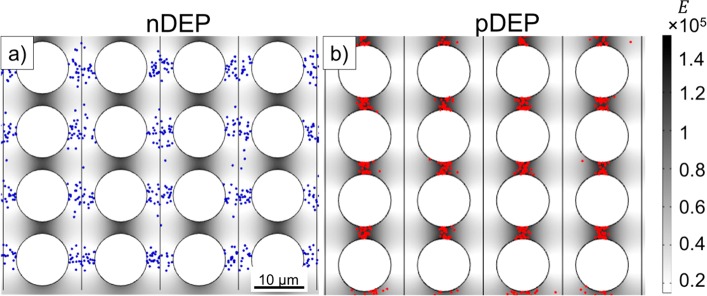
Depending on the sign of Re(CM), nDEP or pDEP particle trapping may occur. Since SWNT DEP trapping behavior at low frequencies has not been reported previously, we developed a numerical model to predict the trapping locations of SWNTs in an iDEP microfluidic device using COMSOL Multiphysics 5.2a. The model accounts for the device geometry, applied potentials scaled to the device section modeled, the resulting electric field as well as electric field gradients, and diffusion properties of the particles and allows one to track the particle positions due to DEP forces in a time-dependent manner. Particles are released at specific positions within the post array section, and their migration can be traced over time. Figure 2 shows the results of simulations for the nDEP and pDEP case. SWNTs released between two post rows and subject to DEP forces consistent with a negative Re(CM) accumulate in the region between two posts of neighboring columns, as shown in Figure 2a. These locations correspond to the lowest electric field regions as indicated by the gray-scale coloring of the fluid-filled space of the device. Figure 2b represents pDEP trapping behavior of SWNTs consistent with a positive Re(CM) . In this case, SWNTs are trapped between two posts of the same column, where the strength of the electric field is the highest. Thus, the pDEP trapping regions are clearly distinct from the nDEP trapping regions. Note that the model parameters were adapted to reflect the case of sample A (nDEP) and sample B (pDEP) for NaDOC-wrapped SWNTs, as experimentally investigated below. Details of the numerical model as well as Movies S1 and S2 showing the migration of SWNTs to the final trapping positions are available as Supporting Information.

Figure 2.

Predicted trapping positions of SWNTs subject to iDEP. (a) SWNT (shown as blue dots) trapping locations predicted by numerical modeling for Re(CM) < 0. The potential applied to this 200 μm long section of the device was adapted to be consistent with 1000 V applied over the entire 1.5 cm long microchannel. The image shows the end position of 1000 SWNTs released from the vertical lines drawn between the columns of posts. SWNTs experienced nDEP and accumulated between two columns of posts where the electric field strength is lowest. (b) SWNT trapping position predicted by numerical modeling for Re(CM) > 0. The applied potential is the same as in panel a. The image shows the end position of 1000 SWNTs (shown as red dots) released from the vertical lines between the columns. SWNTs experienced pDEP and accumulated between consecutive posts in the same row where the electric field strength is highest. The gray-scale color of the fluid-filled part of the device in panels a and b indicates electric field strength.

Experimental Observation of SWNT iDEP

Next, the iDEP trapping behavior of two NaDOC-wrapped SWNT samples was studied. Applied frequencies ranged between 0 and 1000 Hz and potentials between 0 and 1000 V across a channel of 1.5 cm length. Figure 3a shows an image of a microchannel filled with NaDOC-suspended SWNTs without an externally applied potential. SWNTs were evenly distributed around the posts in the channel. Panels b and c of Figure 3 represent the trapping behavior of sample A probed at frequencies of 70 and 700 Hz with an applied potential of 1000 V over the 1.5 cm long microfluidic channel. Figure 3b shows that NaDOC-wrapped SWNTs were trapped at the left and right sides (x-direction) of a post at 70 Hz. These positions correspond to the lowest electric field strength in the post array as apparent from comparison with Figure 1d and the electric field distribution also shown in Figure 2a. The trapping positions correspond to those predicted by numerical modeling assuming nDEP for SWNTs as demonstrated in Figure 2a, indicating excellent agreement between experiment and the numerical model. The observed trapping positions also correspond to those previously observed for polystyrene beads exhibiting nDEP.⁴⁶ At 700 Hz, NaDOC-suspended SWNTs showed the same nDEP trapping behavior (Figure 3c). The trapping behavior was investigated at frequencies up to 1000 Hz (data not shown), with the trapping positions not changing in the post array. This indicates that the DEP behavior is not frequency dependent in the range tested.

Figure 3.

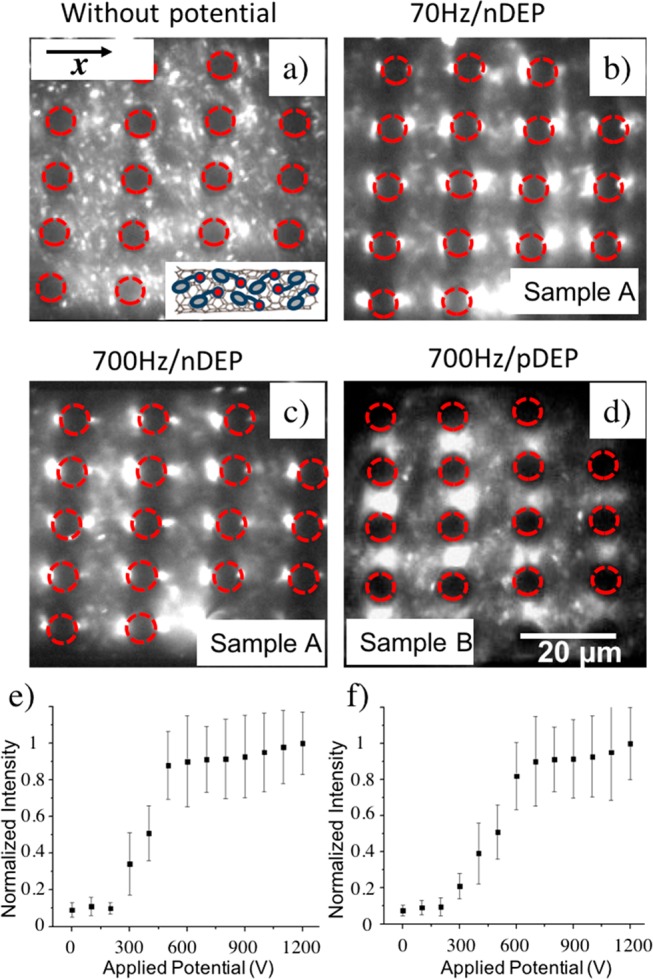
DEP trapping of NaDOC-wrapped SWNTs. IR fluorescence imaging of NaDOC-wrapped SWNTs subject to DEP trapping: (a) without applied potential, no trapping observed; (b) potential of 1000 V applied over the entire microchannel of 1.5 cm length at 70 Hz (external field direction horizontal) for sample A (20 min sonication; SWNTs accumulated in the regions of lowest electric field strength consistent with nDEP); (c) same as panel b but at 700 Hz (SWNTs still accumulated in the regions of lowest electric field strength consistent with nDEP); (d) for sample B, SWNTs (60 min sonication) accumulated in the regions of highest electric field strength, consistent with pDEP (scale bar, 20 μm for panels a–d). Normalized fluorescence intensity indicative of DEP trapping vs applied electric potential: (e) for sample A in the regions where nDEP occurs; (f) similar to panel e but with sample B for pDEP trapping regions.

We also note that some nanotubes were not trapped. We attribute this to the large length distribution (approximately 400–1600 nm) of suspended SWNTs after the sonication process. Smaller SWNTs do not experience large enough DEP forces to be trapped. In addition, a residual flow can be caused by hydrostatic pressure differences or electro-osmotic forces due to a DC voltage offset preventing smaller SWNTs from being trapped.

Next, the DEP behavior of sample B was investigated (Figure 3d) which was prepared with 60 min sonication time. We note that the location of DEP trapping in the post array changed and was now consistent with pDEP; i.e., SWNTs accumulated at the regions with the highest field strength. These trapping regions coincide well with the regions predicted by numerical modeling, indicating excellent agreement between experiment and modeling. However, the change from nDEP for sample A to pDEP for sample B is unexpected and will be further examined below.

In addition, the iDEP trapping behavior was studied for various applied potentials by analyzing the fluorescence intensity in the corresponding trapping regions. The fluorescence intensity is indicative of SWNT concentration due to iDEP trapping. As shown in Figure 3e,f, for both sample A and sample B, above a threshold potential of 300 V accumulation in the pDEP or nDEP trapping regions occurred. In addition, a plateau was reached in both cases upon which no significant increase in the concentration of SWNTs in the trapping regions was observed. This can be explained by the accumulation of all SWNTs experiencing a sufficiently large DEP force.

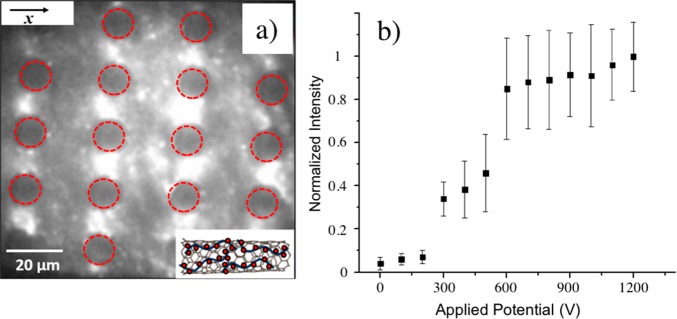
Figure 4a shows the trapping behavior of ssDNA-wrapped SWNTs, which were suspended similarly to sample B by tip sonication for 90 min. At 700 Hz and 1000 V applied over the 1.5 cm long channel, the SWNTs accumulated in the regions of highest electric field strength between posts, consistent with pDEP. We note that, similarly to the NaDOC-wrapped SWNTs, some ssDNA-wrapped SWNTs were not trapped. The pDEP trapping behavior for ssDNA-wrapped SWNTs coincides with sample B of the NaDOC-wrapped SWNTs. The potential origin for the variations in DEP behavior of SWNTs at low frequencies probed in this study will be given in the next section. Figure 4b shows the trapping behavior of ssDNA-wrapped SWNTs at varying applied potentials from 0 to 1200 V. No trapping was observed below 300 V. Above this potential, SWNTs accumulated due to iDEP trapping, whereas a plateau was reached above 600 V. We attribute this plateau to trapping of all available SWNTs for which the DEP trapping force was large enough. Other smaller SWNTs for which the trapping threshold was not reached were not trapped and were still observed in regions of lower electric fields.

Figure 4.

DEP trapping of ssDNA-wrapped SWNTs. (a) IR fluorescence imaging of ssDNA-wrapped SWNTs subject to DEP trapping. At 700 Hz and 1000 V applied over the entire microchannel of 1.5 cm length, ssDNA-wrapped SWNTs accumulated in the regions of highest electric field strength, consistent with pDEP (scale bar, 20 μm; external field direction horizontal, along the x-direction). (b) Normalized fluorescence intensity indicative of DEP trapping vs applied electric potential for ssDNA-wrapped SWNTs in the regions where pDEP occurs. The onset of trapping was observed around 300 V, and above 600 V the fluorescence intensity reaches a plateau.

Origin of Low-Frequency DEP Behavior of Suspended SWNT Species

In the low-frequency regime, the DEP behavior of nanoparticles is governed by their conductivities and that of the medium, determining the magnitude and sign of the Clausius–Mossotti factor, as shown in eq 6. The magnitude of Re(CM) is thus expected to be independent of the applied frequency in the range investigated in this work. Our experimental observations are in agreement, since all SWNT preparations tested showed frequency-independent iDEP trapping behavior in the range probed (0–1000 Hz). Moreover, we observed nDEP or pDEP behavior dependent on how samples were suspended. For NaDOC-suspended SWNTs, the type of DEP behavior was dependent on the sonication time (samples A and B). In the following we discuss possible factors giving rise to this difference in DEP behavior.

According to established models (eqs 1–6), Re(CM) of semiconducting SWNTs is governed by the effective particle conductivity, which is dominantly determined by the double-layer contributions arising from Stern layer and diffuse layer conductance. The latter depends on the ζ potential of the charged nanoparticle suspended in an electrolyte. It is well documented in the literature, that the ζ potential of SWNTs varies for different surfactants and surfactant concentrations.^54,55 We thus independently measured the ζ potential of the SWNTs prepared in the different manners. Table 1 lists the experimentally determined ζ potentials for all samples for which the DEP behavior was studied as well as some cases at even lower sonication time.

Sample B, subjected to a longer sonication time, showed a ζ potential of ζ = −58.6 ± 1.8 mV, which is in reasonable agreement with the literature, considering variations in sonication time and power as well as aqueous solution additives (in our case HEPES buffer).⁵⁵ Sample A with a shorter sonication duration resulted in ζ = −20.2 ± 1.1 mV, about one-third of the value of sample B. Moreover, shorter sonication times of 5 and 10 min resulted in ζ potentials slightly lower than −20.2 mV. We attribute this large difference in ζ potential to a less dense wrapping of the SWNTs with the surfactant in samples A, C, and D. High ζ potentials typically indicate a good stability of dispersed particles due to electrostatic repulsion between suspended particles whereas lower ζ potentials are typically an indication for a higher tendency of aggregation of dispersed particles.⁵⁵ A ζ potential of only −20 mV could therefore signify lower stability of the nanotube suspension and a tendency to aggregate. Our findings are consistent with a report by Mahbubul et al.⁵⁶ who have shown a direct correlation of the ζ potential with sonication time for aluminum oxide nanoparticles suspended in aqueous solutions and the observation by Zaib et al.⁵⁷ that carbon nanotubes increase their electrophoretic mobility and thus ζ potential with longer sonication times.

The measured ζ potentials can now be linked to the observed DEP trapping. For this purpose, we further simplify eq 6 assuming a high aspect ratio, i.e., a vanishing depolarization factor, L. The nanotubes employed in this work had an average length of ∼1000 nm and diameter on the order of 1 nm. Therefore, L ∼ 10^–6, so that eq 6 can be further simplified to

11

where we define the conductivity ratio γ as 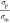. For γ < 1, nDEP is prevalent since Re(CM) < 0, whereas, for γ > 1, Re(CM) is positive resulting in pDEP. Figure 5a shows the dependence of Re(CM) on γ indicating that the sign of the Clausius–Mossotti factor critically depends on the medium used to suspend the SWNTs and the nanotube’s surface conductivity.

Next, we examine the conductivity ratio γ in the different experimental conditions. For a given SWNT suspension, σ_m is defined by the solution employed during the suspension process and can be assessed experimentally through conductivity measurement. The particle conductivity is governed by the surface conductivity, which in turn is defined via the diffuse layer and Stern layer conductance as described in Theory. Based on the experimentally determined ζ potentials, λ_s,d (eq 8) can be calculated, yielding σ_p according to eq 7. Table 1 lists the calculated conductivity ratios for the SWNT samples. The calculated particle conductivity was 0.14 S/m for NaDOC-wrapped SWNTs for sample A, 2.94 S/m for sample B, and 0.53 S/m for DNA-wrapped SWNTs. The medium conductivity was also determined experimentally and found to be 0.15 S/m for both NaDOC-wrapped samples and 0.04 S/m for ssDNA-wrapped SWNTs, respectively.

Figure 5a shows the dependence of Re(CM) on the conductivity ratio γ, with the symbols corresponding to SWNT samples studied experimentally. For NaDOC-wrapped sample B, Re(CM) is positive with a value of 18.6 corresponding to γ = 19.6. For DNA-wrapped SWNTs, γ = 13.25 with a corresponding Re(CM) = 12.3. This calculation matches the experimentally observed trapping behavior of NaDOC-coated SWNTs (sample B) and ssDNA-wrapped SWNTs where pDEP was observed. The numerical study underlines this experimental observation since the trapping regions match in both model and experiment.

We further examined the relationship between ζ potential and Re(CM) for the NaDOC-wrapped SWNTs. When ζ drops, the Clausius–Mossotti factor decreases and eventually becomes negative, leading to nDEP (Figure 5b). This occurs below a value of −21 mV. Note that the measured ζ potential of sample A is within the region where the Re(CM) drops below zero (corresponding to ζ < −21 mV) and that of sample B in the range where a positive Re(CM) is expected according to Figure 5b. We thus conclude that the SWNT dielectrophoretic behavior is dependent on the ζ potential, which in turn is determined by the suspension quality, i.e., sonication duration. This conclusion is in agreement with reports by Kang et al., who observed a relation between the dielectrophoretic behavior of surfactant-suspended SWNTs with the type of surfactant and concomitant changes in the ζ potential.⁵⁰ Similar observations were also recently made with biological cells. Tang et al. reported that the dielectrophoretic behavior of yeast cells changes through the surface interaction with surfactants such as sodium dodecyl sulfate.⁵⁸ Our observations for the SWNT samples subject to short sonication times (20 min and below) also agree with the commonly accepted zipping mechanism responsible for SWNT suspension with surfactants.^59,60 Sonication is needed to unzip bundle ends of SWNTs followed by adsorption of the charged surfactant and eventually leads to full unzipping and release of individual SWNTs. At small sonication times, this process is not fully finalized leading to a large distribution of species, including a variety of large bundles, individual long SWNTs as well as smaller individual SWNTs. Based on this mechanism we can also explain why sample A, exhibiting a small negative ζ potential leading to a very small negative Re(CM), can be trapped at potentials similar to those of sample B. Since bundles and long SWNTs are predominant in sample A, trapping occurs above 300 V similar to shorter well dispersed SWNTs exhibiting a larger ζ potential since the DEP forces are increased due to an overall larger geometry. In summary, the observed pDEP trapping of NaDOC-suspended (sample B) and ssDNA-wrapped SWNTs is in agreement with the observed ζ potentials, models relating the ζ potential of nanoparticles to the Clausius–Mossotti factor and suspension behavior of individual SWNTs. The nDEP behavior observed in experiments for NaDOC-suspended SWNTs prepared with shorter sonication time coincides with a smaller ζ potential of not ideally suspended SWNTs and correspondingly negative Re(CM).

Conclusions

We have studied the DEP properties of semiconducting SWNTs in the low-frequency regime (<1 kHz) with insulator-based dielectrophoresis, a frequency range not previously investigated with SWNTs. The study was carried out in PDMS microfluidic devices where the semiconducting SWNTs could be visualized with near-infrared microscopy. As predicted by established models, the observed DEP trapping behavior was frequency independent. We could show, however, that the sign of the Clausius–Mossotti factor can switch, depending on the ζ potential and the corresponding suspension properties of the nanotubes. Well suspended NaDOC- and ssDNA-wrapped SWNTs exhibited pDEP, which is in accordance with the measured ζ potential and related positive Re(CM). In contrast, less densely NaDOC-wrapped SWNTs exhibited lower ζ potential and demonstrated nDEP. The experimental observations were in excellent agreement with numerical modeling. Our work shows that carbon nanotubes can be effectively manipulated and even trapped with iDEP in low-frequency AC electric fields and suggests that poorly suspended constituents may be effectively removed in DEP sorters exploiting the variations in pDEP and nDEP. Moreover, the DEP response can be tuned by the surfactant properties and suspension quality, which may in turn be exploited for optimization of purification and separation of carbon nanotubes based on DEP or alignment and positioning of SWNTs.⁵² In addition, the near IR microscopy imaging of DEP of semiconducting SWNT allows the observation of DEP trapping and migration directly in a microfluidic device without the need for post-DEP analysis involving Raman spectroscopy or nanoscale imaging techniques following tedious recovery procedures.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.analchem.7b03105.

• Details on the numerical model describing the time-dependent particle tracing analysis used to investigate the trapping positions in the cases of nDEP and pDEP (PDF)

• Movie S1 showing the result of the time-dependent particle tracing analysis for nDEP (AVI)

• Movie S2 showing the result of the time-dependent particle tracing analysis for pDEP (AVI)

The authors declare no competing financial interest.