Aggressive prostate cancer cell nuclei have reduced stiffness

Abstract

It has been hypothesized that highly metastatic cancer cells have softer nuclei and hence would travel faster through confining environments. Our goal was to prove this untested hypothesis for prostate cells. Our nuclear creep experiments using a microfluidic channel with a narrow constriction show that stiffness of aggressive immortalized prostate cancer nuclei is significantly lower than that of immortalized normal cell nuclei and hence can be a convenient malignancy marker. Nuclear stiffness is found to be the highest for cells expressing high levels of lamin A/C but lowest for cells expressing low lamin A/C levels. Decreased chromatin condensation found in softer nuclei suggests that the former can also be a marker for aggressive cancers.

I. INTRODUCTION

Cells migrate across barriers in numerous physiological and pathological processes, including wound healing, immune response to inflammation, and cancer metastasis.^1–3 During metastasis, cancer cells leave the primary tumor by both pushing and pulling their way through surrounding tissues⁴ and by entering and exiting blood vessels on their way to colonize distant sites.^4,5 Since extracellular matrix pores and microvessel diameters can be significantly smaller than the typical epithelial cancer cell (∼3–7 μm vs. 20–30 μm),^6,7 cancer cells deform significantly while metastasizing.

Increased deformability of cancer in comparison with normal cells has been postulated as a universal cancer marker.^8,9 Studies have found that some highly malignant cancer cells have a less stiff cytoplasm with an elastic modulus about 2–4 times lower than that of the less aggressive or normal cells.^10–12 Cytoskeletal actin structural changes associated with cancer may underlie these observed mechanical differences.^4,8,13 However, some highly malignant cancer cells show a higher elastic modulus (for prostate cancer^14,15 and chondrosarcoma¹⁶), thus negating the deformability of the cytoplasm as a universal marker.

The nucleus, the largest cell organelle, is the limiting factor in metastasis via migration through narrow pores^17–19 since it is about 5–10 times stiffer than the surrounding cytoplasm.^2,20 Despite the importance of nuclear deformability in cancer invasion and its potential to replace cytoplasmic deformability as a marker of cancer invasiveness, the correlation of nucleus deformability with metastatic potential has not been investigated for many types of cancers. The connection between an increased nuclear deformability and cancer invasiveness has been studied only for two breast cancer cell lines (highly metastatic MDA-MB-231 and lowly metastatic MCF-7)¹⁷ and two melanoma cell lines (metastatic murine Lu1205²¹ and non-metastatic human WM35)²² in vitro under controlled conditions. However, quantitative nuclear rheology has also not been used to compare cancer cells with different metastatic potentials.

Nuclear deformability can be affected by several factors, including nuclear envelope protein expression levels and the chromatin structure.^5,23–26 The nuclear lamina, composed of A-type and B-type lamins, forms overlapping networks in the nuclear envelope and has different effects on the nuclear shape and mechanical properties.^3,27,28 Cells with low levels of A-type have irregularly shaped nuclei, while those with high levels of A-type have rounded nuclei.^2,5,29,30 Nuclei of cells with low levels of B-type have blebs, and those with high B-type levels have invaginations.² Micropipette aspiration experiments show that B-type lamins contribute primarily to the elasticity of the nucleus while A-type contributes to the viscosity of the viscoelastic nucleus.²⁸ These studies also demonstrated that the time dependence of nuclear elongation depends on the lamins-A/B ratio: cells with a low ratio deform more rapidly than those with a high ratio.^22,28,31,32 Further studies have shown that the ability of cells to migrate through narrow pores also depends on the lamins-A/B ratio.³³ Lamin expression alteration is currently considered as one of the steps involved in malignant transformation.^30,34,35 Changes in lamin expression alter the nuclear shape—a hallmark of cancer.^2,36 Therefore, cancer nucleus deformability may depend on lamin expression levels.

The structure of chromatin, and its compactness, can also influence the stiffness of the nucleus.^{23–25,37,38} Cells treated with divalent cations, which condense chromatin, were shown to have significantly stiffer nuclei than untreated cells.²³ Similarly, cells treated with chromatin decondensing drugs have softer²⁵ and more deformable nuclei.²⁴ Stem cells have high transcription activity and decondensed chromatin; these cells also have softer more deformable nuclei.^23,24 As a result, chromatin condensation can also affect cancer nucleus rheology, as highly metastatic cancer cells may have high levels of transcriptional activity.²⁵

Nuclear creep experiments using micropipette aspiration have provided insights into the effects of nuclear envelope proteins on nuclear rheology during cell development²³ and in diseases such as Hutchinson-Gilford progeria syndrome—a lamin A mutation disease.³⁹ Micropipette nuclear creep experiments have been performed both on isolated nuclei and on nuclei within cells treated with F-actin depolymerizing drugs to minimize the contribution of the cytoskeleton to nuclear extension into the micropipette. In these experiments, the length of the fluorescently labeled nucleus L(t) inside the pipette was tracked in time, typically for 2–4 decades (from fractions of a second to minutes).^23,40 The nuclear extension length L(t) was then converted to rheological creep J(t) by dividing it by the stress applied at the beginning of the experiment, t = 0,⁴¹ which for micropipette aspiration is $J(t)=(2\pi \varphi L(t))/(3R_P\Delta P)$, where R_P is the pipette radius, ΔP is the pressure drop acting across the cell (or isolated nucleus), and ϕ is a constant which depends on the thickness of the micropipette's wall.^23,40,42 This expression was derived as the initial stress for the aspiration of an infinite elastic half-space into a micropipette.⁴²

With the appropriate creep expression, its behavior against time reveals the appropriate model to use to extract rheological parameters. For example, the model that consists of a spring and dashpot in series (the Maxwell model) has $J(t)=\frac{1}{E}+\frac{t}{\eta }$, where E is the elastic modulus and η is the viscosity. Here, J(t) is linear in time. Another example that consists of a spring and dashpot in parallel (the Voigt model) has $J(t)=\frac{1}{E}(1-e^{-Et/\eta })$. This creep function is approximately a power law in time at early times, leading to a plateau at later times. Finally, an often-used creep function for nuclei is derived from the power-law model.^23,39,40 In this model, $J(t)=\frac{A}{\alpha \Gamma (\alpha )}{(\frac{t}{t_0})}^{\alpha }$, where the exponent α is the fluidity, and its value ranges from 0 for an elastic solid to 1 for a viscous fluid.⁴¹ All viscoelastic objects have 0 ≤ α ≤ 1, where a low value indicates a more solid-like substance and a high value indicates a more fluid-like substance.^23,40,41 The constant t₀ = 1 s is chosen such that the exponential term is dimensionless, which gives the pre-factor A's units of Pa⁻¹ and is typically interpreted as an inverse stiffness.^23,38,40 Cell and nucleus stiffnesses and fluidities can be altered by protein expression linked to the cell differentiation state²³ and drug treatments.^23,43

One drawback of using micropipette aspiration is the small number of nuclei analyzed—typically 5–10 per experiment^23,28,40—due to the complexity of the measurement. Since cancer is a heterogeneous disease,⁴⁴ larger sample sizes are required. Here, we used a microfluidic device with a constricted channel, instead of micropipettes, to perform nuclear creep experiments and achieved a throughput 10 times or more than previous micropipette studies. Several prior microfluidic approaches have been used to measure cell deformability. Di Carlo and colleagues have developed high throughput hydrodynamic cell stretching devices where cells (stem cells, fibroblasts, granulocytes, cells from patients suffering from inflammation and cancer) are mechanically phenotyped based on their elongation in flow.^45,46 Lange et al. claim to have developed a high throughput method to measure cell power law rheology parameters from cell entry time, fluid pressure, and maximum cell elongation in flow through a narrow channel.³⁸ This method, however, does not yield the known fluidity of well characterized objects. See supplementary material for a detailed discussion.

Nuclear deformability has also been measured using microfluidic devices. Rowat et al. determined that the multi-lobed neutrophil nuclear shape had no significant effect on the passage time of cells flowing through a channel narrower than the nucleus, whereas lamin A expression levels had a strong effect.³¹ Other works established that nuclear deformability and lamin A expression levels affect the ability of fibroblasts to migrate through channels smaller than the nucleus.^19,47 The dynamics of nuclear rupture and repair in migrating breast cancer, breast epithelial, fibrosarcoma, and fibroblast cells have also been studied on these platforms.⁴⁸ None of these previous microfluidic nuclear deformability studies have used quantitative nuclear rheology metrics to compare cancer cells with different metastatic potentials.

We compared the nuclear stiffness and fluidity of highly, moderately, and non-metastatic immortalized prostate cancer cell nuclei as well as normal prostate epithelial cell line nuclei. It was found that fluidity cannot be used to distinguish cancers with different metastatic potentials, while the stiffness can be used in most cases. We also found that the stiffness of highly metastatic prostate cancer nuclei is significantly lower than that of moderately metastatic and normal prostate cell nuclei. The nuclear stiffness measurements were compared with nucleus entry time (where the entry time is the time for the nucleus to enter a narrow channel upon first encounter) which is a conceptually simple qualitative deformability metric.^49,50 Based on our findings, the nuclear stiffness is a more sensitive metric of prostate cell metastatic potential than the entry time. We quantified Lamin A/C and B levels using Western blots and found that the stiffest and least stiff nuclei have high and low lamin A/C levels, respectively. Highly as well as lowly metastatic cells both have low lamin A/C levels. Decondensing chromatin in cell nuclei with a drug treatment showed that the nuclear stiffness also depends on chromatin condensation, as we found that chromatin decondensed nuclei from moderately metastatic and normal cells were less stiff. This may suggest that highly metastatic cells have less condensed nuclear chromatin than moderately metastatic and normal cells, and hence, chromatin condensation may be an effective cancer marker. We confirmed this using high spatial resolution fluorescence microscopy via the measurement of fluorescently stained DNA in nuclei. A technique that senses the chromatin structure, as well as lamin A/C levels, may be useful for early cancer diagnostics.

II. METHODS

A. Cell culture, preparation, and treatments

All cells were cultured at 37 °C in a 5% CO₂ environment. Prostate cancer cells (PC3, CL2, DU145, and LNCaP) were cultured in RPMI 1640 media with L-glutamine (Gibco 10-040-CV, Thermo Fisher Scientific, Massachussets) supplemented with 5% fetal bovine serum (FBS) (Gibco 10437-028). LNCaP cells had an additional supplement of 1% penicillin-streptomycin antibiotics (Gibco 15140-122). RWPE-1 prostate epithelial cells were cultured in keratinocyte media (Gibco 10724-011) supplemented with recombinant human Epidermal Growth Factor (rhEGF) and Bovine Pituitary Extract (BPE) (Gibco 37000-015). Two hours and twenty minutes before experiments were performed, Hoechst 33342 fluorescent nuclear stain (Life Technologies R37605, Thermo Fisher Scientific) was applied to the cells following manufacturer's instructions. Two hours before experiments, the media containing the stain was removed and replaced with media containing 10 μM latrunculin A (latA) (Sigma-Aldrich L5163)²³ for 2 h to depolymerize cytoskeletal F-actin. To decondense nuclear chromatin,^24,38 cells were additionally treated with 250 nM 5-AZA-2'-deoxycytidine (AZA) (Sigma-Aldrich A3656) for 2 h.²⁴ Chromatin decondensation in live cells with AZA was confirmed by staining DNA with Hoechst 33342 and imaging with a Nikon Eclipse microscope at 30× magnification in the DAPI (4',6-diamidino-2-phenylindole) fluorescence mode. Cell cycle synchronization experiments (p > 0.1, two-sample Kolmogorov-Smirnov test) showed no significant effect on nuclear mechanical properties (data not shown).

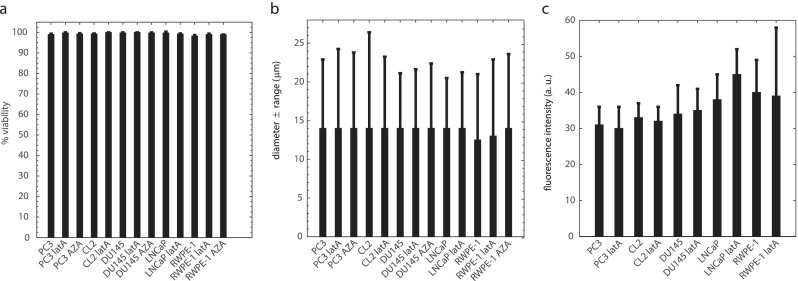
Possible changes in cell viability and morphology (i.e., diameter) on suspended cells due to drug treatments were evaluated using Trypan Blue exclusion stain (Corning 25900CI) and an automated cell counter (Bio-Rad TC20) following manufacturer's instructions. No significant changes in viability were observed [see Fig. 1(a)], as assessed by stain exclusion, which rules out latA and AZA induced necrosis.^51,52 No changes in the cell diameter were observed [see Fig. 1(b)]—ruling out drug-induced apoptosis.^51,52 To test if latA altered prostate cell chromatin condensation, we imaged control and latA cells treated with Hoechst 33342 fluorescent nuclear stain according to manufacturer's instructions at 30× magnification in the DAPI fluorescent mode with a Nikon Eclipse microscope at 37 °C. Figure 1(c) shows that latA treatment does not affect average fluorescent nuclear brightness and therefore does not alter chromatin condensation.^53,54

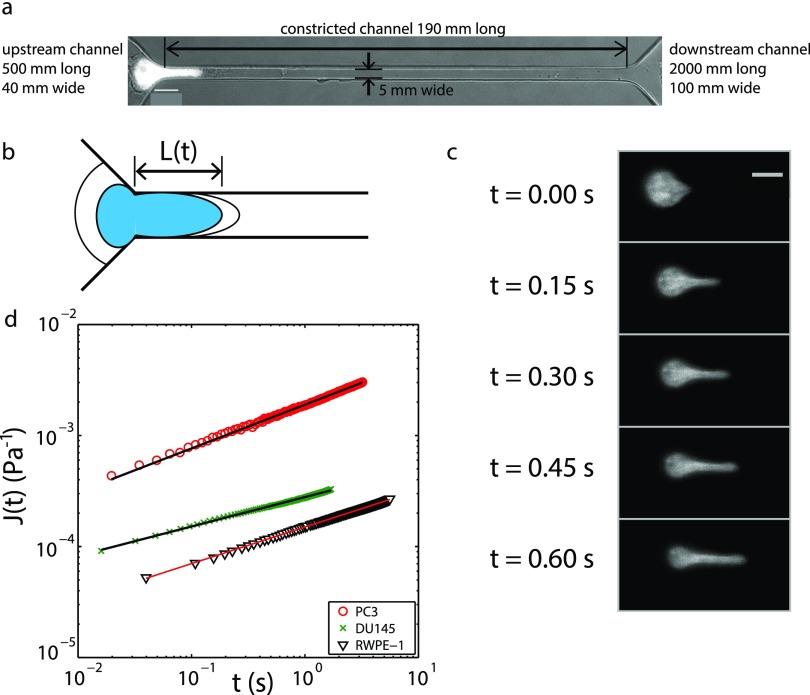
FIG. 1.

Experimental overview. (a) The microfluidic device used in these experiments has a height of 7 μm. Here, a PC3 prostate cancer cell nucleus, labeled with Hoechst 33 342 fluorescent stain, is shown entering the constricted channel. Scale bar: 10 μm. (b) The length L(t) of the portion of the nucleus inside the constricted channel is measured in time. By dividing L(t) by the initial nuclear stress, the creep compliance function J(t) is obtained; see text for details. (c) A labeled PC3 nucleus is advancing into the constricted channel over time. Scale bar: 10 μm. (d) The creep compliance function J(t) for PC3 and DU145 prostate cancer cell line nuclei and a RWPE-1 prostate epithelial cell nucleus. J(t) follows a power law for approximately 2 decades in time, where each cell shown has a different exponent α and intercept A (PC3, α = 0.39, A = 2.2 × 10⁻³Pa⁻¹; DU145, α = 0.26, A = 2.5 × 10⁻⁴Pa⁻¹; RWPE-1, α = 0.33, A = 1.3 × 10⁻⁴Pa⁻¹).

To suspend cells for experiments, all cells were rinsed with 10 ml of Dulbecco's phosphate buffer saline (DPBS) (Gibco 21-031-CV). PC3, CL2, and DU145 prostate cancer cells were incubated with 5 ml of trypsin (Gibco 25302-062) for 2 min at 37 °C and 5% CO₂, and the trypsin was neutralized with 500 μl of FBS. LNCaP cancer cells were treated with 1 ml of trypsin and 3 ml of DPBS for 1 min at room temperature, and the trypsin solution was neutralized with 500 μl of FBS. RWPE-1 prostate epithelial cells were treated with 2.5 ml of trypsin and 2.5 ml of DPBS for 8 min at 37 °C and 5% CO₂, and the trypsin was neutralized with a 0.1% FBS in DPBS solution. All cells were centrifuged for 5 min at 1000 rpm and resuspended in a 0.01% Pluronic F-127 (BASF) and growth medium solution at a concentration of 3 × 10⁶ cells per ml. 1 ml of cell solution was used for experiments. The nuclear rheology data were obtained for PC3 from 4 independent experiments, CL2 from 3 independent experiments, DU145 from 4 independent experiments, LNCaP from 3 independent experiments, and RWPE-1 from 3 independent experiments. The two-sample Kolmogorov-Smirnov test was used for statistical comparisons between conditions (e.g., control vs. drug treated or highly metastatic vs. normal cells); this test, appropriate for non-normally distributed data, is equivalent to the Student's T-test for normally distributed data.

To image nuclei with high spatial resolution, cells were fixed, permeabilized, washed, and blocked as previously described.⁵⁵ Cells were plated on 12 mm round coverslips until confluent. The media was then removed, and cells were washed with phosphate buffer saline (PBS) and fixed with 4% paraformaldehyde (Sigma-Aldrich 158127) in PBS for 15 min. PBS contained 5 l water, 40 g NaCl (Fisher 7647-14-5), 1 g KH₂PO₄ (Sigma-Aldrich P5655), 5.75 g Na₂HPO₄ (Sigma-Aldrich S9763), and 1 g KCl, (Sigma-Aldrich P3911). Then, cells were washed twice for 2 min each with fresh PBS and quenched with 50 mM ammonium chloride (Sigma-Aldrich 213330) in PBS for 5 min. Cells were washed again with PBS for 5 min and permeabilized with 0.1% Triton X100 (Sigma-Aldrich 93443) in PBS for 10 min. They were then washed for 2 min, blocked with 1% bovine serum albumin (BSA) (Sigma Aldrich A2153) in PBS for 15 min, and washed 6 times with fresh PBS. The slides were mounted in Prolong gold antifade reagent with DAPI (Life Technologies P36935). Samples were visualized using a Nikon Eclipse microscope with 90× magnification, and fluorescence intensity was measured using ImageJ software. For display purposes, 16-bit raw images were inverted by altering the greyscale intensity g(x, y) as $g^{\prime }(x,y)=65535-g(x,y)$ and converted to 8-bit images. Inverted images were linearly contrast enhanced, as needed, to make differences between the cell lines more apparent. This was done as $g^{\prime }(x,y)=\mathit{\text{floor}}(\frac{255}{G{L}_{max}-G{L}_{min}}[g(x,y)-G{L}_{min}])$, where GL_max = 245 and GL_min = 160, where the floor operator rounds numbers down to the nearest integer value.

B. Microfluidic device design and fabrication

The device consists of two parallel channels (40 μm wide, 500 μm long) each tapering to a constricted channel (channel length L = 190 μm, width W = 5 μm, and height H = 7 μm) as shown in Fig. 1(a). The constricted channels join a single wider channel (100 μm wide, 2 mm long). The inlet of one of the two parallel channels was plugged during experiments, until a channel became clogged by debris or cell clusters, and then, the other channel was used. Nuclear elongation into the constricted channel was measured at the channel entrance. The time for the nucleus to enter into the channel, called the entry time, was measured simultaneously.

FIG. 2.

Cell viability and morphology: (a) cell viability ± SE does not change appreciably with 2 h drug treatments to depolymerize F-actin (latrunculin A—latA, 10 μM) and to decondense chromatin (5-AZA-2′-deoxycytidine—AZA, 250 nM), each sample >5 × 10⁵ cells. (b) Mode cell diameter ± range also does not change with drug treatment. (c) Average fluorescent nuclear intensity (±SD) of cells treated with Hoechst nuclear stain. PC3 control n = 305; PC3 latA n = 327; CL2 control n = 386; CL2 lat A n = 278; DU145 control n = 168; DU145 latA n = 238; LNCaP control n = 198; LNCaP latA n = 308; RWPE-1 control n = 301; RWPE-1 latA n = 351. Cells were taken from 3 independent samples (from each of CL2, LNCaP, and RWPE-1) or 4 independent samples (from each of PC3 and DU145).

Microfluidic devices were made using standard soft lithography techniques.⁵⁶ A mold was fabricated by spin-coating SU8–5 negative photoresist (MicroChem Corp.) on a 76.2 mm diameter silicon wafer. The height of the channels corresponds to the thickness of the spin coated layer. Polydimethylsiloxane (PDMS) (Sylgard 184 silicone elastomer kit, Dow Corning) was poured into the mold, degassed, and baked at 80 °C for 2 h. The PDMS was cut and peeled from the mold, and then, inlet and outlet holes were punched using Harris Uni-core punches with a 0.75 mm outer diameter (GE Healthcare Bio-Sciences). The devices were bonded to glass coverslips by exposing the device and glass surfaces to air plasma (Plasma Cleaner PDC-32G, Harrick Plasma), putting the device and glass into contact, and baking at 80 °C for 20 min.

C. Microfluidic device operation

For experiments, cells were split, centrifuged, and resuspended in cell culture medium containing 0.01% Pluronic F-127 to prevent cell adhesion to channel surfaces.³¹ Cell suspensions were placed in MFCS-EZ (microfluidic flow control system, model EZ) microfluidic flow controller (Fluigent) reservoirs. Reservoirs were attached to the flow controller, and the suspensions were pushed with a constant driving pressure of 7500 Pa. The hydrostatic pressure due to the height of the media in the reservoir was added to the driving pressure. The reservoirs were connected to the devices using ETFE tubing (MicroSolv Technology Corporation) inserted into tygon tubing (Cole Parmer Instrument Company) and stainless steel blunt pins (Instech Laboratories Inc.). Images were recorded at 40× magnification (0.16 μm/pixel) in the DAPI fluorescence mode using a Nikon Eclipse motorized microscope with incubator. Imaging used a Zyla 4.2 sCMOS (Andor) at 60-120 fps [see Fig. 1(c)]. All experiments were conducted at 37 °C.

D. Power law rheology measurements

To determine the power law rheology parameters—stiffness 1/A and fluidity α—the extension length of the nucleus into the constricted microfluidic was measured from fluorescence images. The entry of the channel, defined as the region where the channel entrance was no longer tapered, was determined by drawing straight lines along the constricted channel sidewalls and along the tapered channel. The nucleus length L(t) [see Fig. 1(b)] was the distance of the edge of the nucleus from the channel entrance. The nucleus creep $J(t)=(2\pi \varphi L(t))/(3R_P\Delta P)$^23,40 was calculated for the duration of the nuclear entry into the channel and plotted against time. The constant ϕ depends on the thickness of the micropipette walls and the micropipette inner diameter and has the value 1.4 (using Force Model proposed by Theret et al.⁴²) for these experiments. Here, R_P = (W × H)/(W + H) is the hydraulic radius of the constricted channel with a value of 2.7 μm, and ΔP = 7550–7730 Pa is the pressure drop across the cell while it is entering the constricted channel. Both radius and pressure drop values are consistent with previous micropipette aspiration experiments.²³ The inverse nuclear stiffness A and fluidity α were obtained from power law fits to nucleus creep against time $J(t)=\frac{A}{\alpha \Gamma (\alpha )}{(\frac{t}{t_0})}^{\alpha }$ [see Fig. 1(d)].⁴¹ Here, Γ is the Gamma function, and setting the constant t₀ = 1 s, consistent with prior works,^23,40 gives the pre-factor A in units of Pa⁻¹. Image and data analysis were performed using Matlab.

E. Entry time and nucleus size measurements

The entry time τ_e was measured from the images using ImageJ software, where τ_e is defined as the time for a nucleus to enter the constricted channel once it has first encountered the entrance.^49,50 The uncertainty in τ_e was taken to be the time to obtain two images. The nuclear area was determined in Matlab by thresholding a fluorescent image of the nucleus prior to its entry in the channel using the Otsu method.⁵⁷ From the thresholded image, the number of pixels above the threshold gave the nuclear area. The equivalent circular radius R_N was calculated from the nuclear area.

F. Nuclear fractionation and western blots

Prostate cells were trypsinized (see above), washed twice with cold PBS, and resuspended in 3 ml of homogenizer buffer—1.3 M sucrose (Sigma-Aldrich S7903i), 1 mM MgCl₂ (Sigma-Aldrich M4880), and 10 mM potassium phosphate buffer pH 6.8 (Sigma-Aldrich P5379) supplemented with a protease inhibitor cocktail (Thermo-Fisher Scientific 88265) at a concentration of one tablet per 50 ml. Cells were homogenized in a Teflon/glass dounce homogenizer 20 times and centrifuged for 15 min at 4 °C and 1000 g (Eppendorf 5804R). The resulting crude nuclear fraction pellet was resuspended in suspension buffer containing 0.25 M sucrose, 4.0 mM MgCl₂, 20 mM Tris-HCl pH 7.4 (Tris - Fisher Chemical T395–500, HCl - Fisher Chemical SA49), and protease inhibitor cocktail (Thermo-Fisher Scientific 88265)—one tablet per 50 ml. All samples were stored at –80 °C. Prior to the Western blots, the protein concentration was determined with a spectrophotometer/fluorometer (DeNovix DS-11 FX+).

Proteins from crude nuclear fractions—30 μg diluted 1:1 in Laemmli sample buffer (Bio-Rad 161-0737) containing 2-mercaptoethanol (Bio-Rad161-0710, 50 μl in 950 μl Laemmli buffer)—were separated by SDS-PAGE in 4%–20% gradient acrylamide gels (Bio-Rad 456-8093) and transferred to nitro-cellulose membranes (Bio-Rad 170-4158) using the Trans-Blot system (Bio-Rad). The membranes were incubated for 1 h in a 3% milk, Phosphate Buffer Saline (PBS), Tween solution on a plate shaker (blocked). The blocking solution was made from 3 g of milk powder (Nestle), dissolved in 100 ml of PBS.

At the time of the experiment, Tween was added to PBS (Bio-Rad, 170-6531, 1:1000 dilution). Membranes were washed 3 times in the PBS-Tween solution for 5 min. Then, membranes were incubated with primary antibodies against lamin A/C [Developmental Studies Hybridoma Bank MANLAC1(4A7), 1:300 dilution] and lamin B1 (Santa Cruz Biotechnology sc-30264, 1:500 dilution), and β-actin was used as loading control (Sigma-Aldrich A3854, 1:25000 dilution) for 2 h at 37 °C. Finally, the membranes were incubated with horseradish peroxidase-conjugated secondary antibodies—anti-mouse IgG for lamin A/C (Jackson ImmunoResearch 115035068) and anti-goat IgG for lamin B1 (Jackson ImmunoResearch 805035180). The dilution used for secondary antibodies was 1:1000. The blots were revealed using ECL (Clarity western luminol/enhancer reagent) solution (Bio-Rad 170-5060) and were visualized using the Image Analyzer system (Bio-Rad ChemiDoc MP). Expression levels were quantified using ImageJ software and normalized by β-actin loading control levels.

G. Immunocytochemistry experiments

Cells were plated on coverslips until sub-confluent, fixed with 4% paraformaldehyde, quenched with PBS with 50 mM NH₄Cl (213330, Sigma-Aldrich) for 10 min, permeabilized with 0.1% PBS with Triton X-100 (X100, Sigma Aldrich) for 10 min, blocked with 1% PBS-BSA (A2153, Sigma-Aldrich) for 15 min, and incubated (1 h) with primary antibodies for lamin A/C [MANLAC1 (4A7), DSHB] and lamin B1 (sc-6217, Santa Cruz Biotechnology). After staining, coverslips were washed 7 times with PBS and incubated (1 h) with lamin A/C and B1 secondary antibodies conjugated to Alexa fluor-594 (R37121, anti-mouse for lamin A/C; R37117, anti-goat for lamin B1–Thermo Fisher Scientific). Then, coverslips were washed again 7 times in PBS with Triton X-100 and mounted on glass slides using Prolong Gold antifade reagent (P36935, Molecular probes by Life Technologies). Images were obtained at 90× using a Texas Red excitation filter and Nikon Eclipse microscope. Images were inverted and linearly contrast enhanced as described above.

III. RESULTS AND DISCUSSION

A. Aggressive prostate cancer cells have low nuclear stiffness

The hypothesis that more metastatic cancer cells have more deformable nuclei facilitating their metastatic spread^2,19,58,59 was tested by performing creep measurements using a microfluidic device with a narrow constricted channel as shown in Fig. 1. The cell lines used were highly metastatic PC3⁶⁰ and CL2,^15,61 moderately metastatic DU145,⁶² and non-metastatic LNCaP^15,63,64 prostate cancer. RWPE-1 normal human prostate epithelial cells were used as control. The length of fluorescent nuclei was measured in time as cells entered the channel. The nuclear length normalized by the initial stress acting on the cell—also referred to as the creep compliance function J(t)—consistently forms a power law in time [see Fig. 1(d) and Materials and Methods for representative examples].^23,40 By performing fits of the form $J(t)=(A/\alpha \Gamma (\alpha )){(t/t_0)}^{\alpha }$ to the nuclear creep compliance, we obtained the nuclear stiffness 1/A and power law exponent, or fluidity, α.

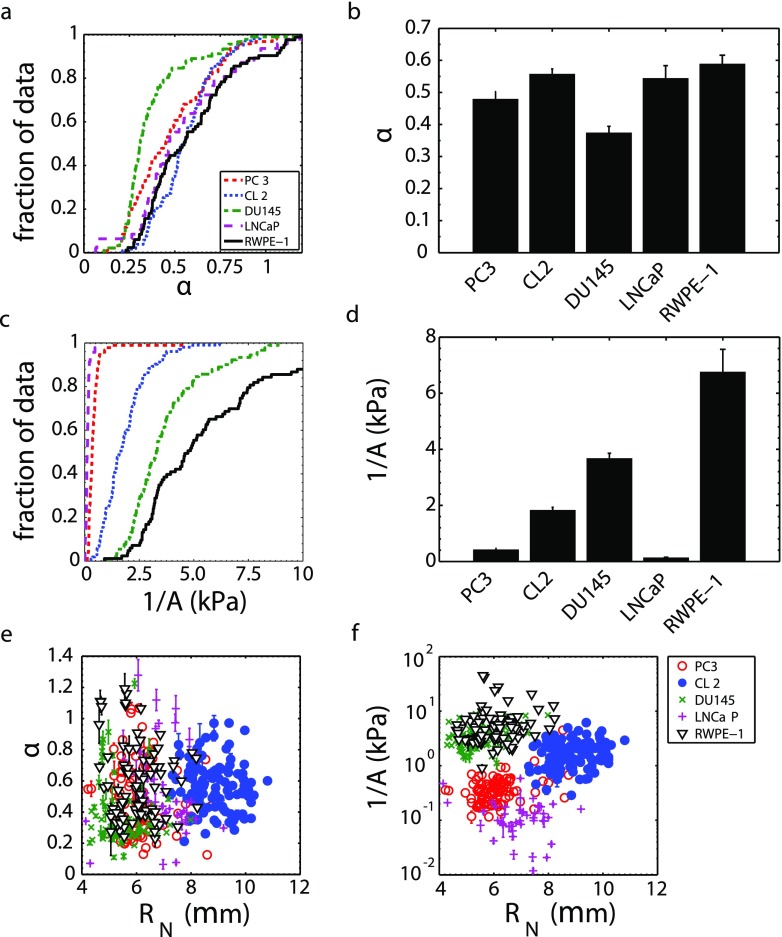
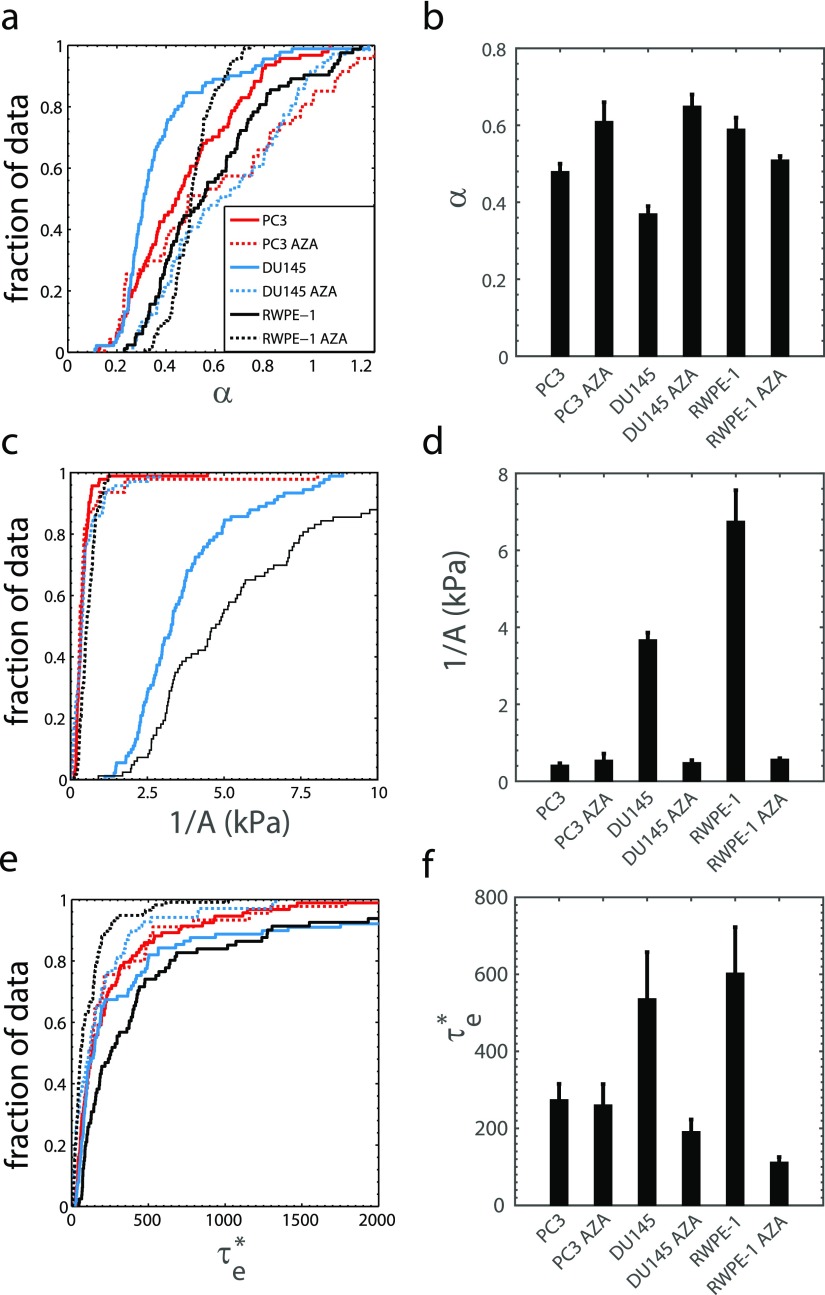
We found that the fluidity α of highly metastatic (PC3, CL2) cell nuclei is not different from that of non-metastatic and normal (LNCaP, RWPE-1) cell nuclei [Figs. 3(a) and 3(b)]; therefore, nuclear fluidity does not appear to be a good marker for metastatic prostate cancer. Conversely, the nuclear stiffness 1/A of highly metastatic (PC3, CL2) cell lines is significantly smaller than the moderately metastatic (DU145) and normal (RWPE-1) cell nuclear stiffness [Figs. 3(c) and 3(d)], which indicates that a reduced nuclear stiffness can be a marker for aggressive prostate cancer. Statistical comparisons are shown in Table I. The PC3 cell line was derived from bone metastasis, where cells leave the primary tumor and travel through extracellular matrices, intravasate the blood circulation system, enter the sinusoids of the bone-marrow cavity, migrate through the marrow, and travel to the inner bone surface to form a secondary tumor. A low nuclear stiffness likely confers an advantage on PC3 cell expansion into the outer bone surface, where the tissue stiffness is large (18–22 GPa) and the pore sizes are small (10–50 μm).^65,66

FIG. 3.

Highly metastatic prostate cancer cells (PC3, n = 94; CL2, n = 103) have similar nucleus fluidity to moderately metastatic prostate cancer cells (DU145, n = 91), non-metastatic cells (LNCaP, n = 47), and normal prostate epithelial cells (RWPE-1, n = 83). (a) Fluidity α cumulative distribution function (CDF) and (b) mean α (±SE). Highly metastatic prostate cancer cells have a lower nucleus stiffness than moderately metastatic and normal cells. (c) Stiffness 1/A CDF with the abscissa truncated to emphasize differences and (d) mean 1/A (±SE). (e) Nucleus fluidity and (f) stiffness do not depend on the nucleus radius R_N.

TABLE I.

Statistical power for comparison of nuclear stiffness 1/A distributions of different prostate cancer and normal cell lines. All comparisons were done using the two-distribution Kolmogorov-Smirnov test.

Cell line	Cell line	p-value
PC3	CL2	≪1 × 10−6
PC3	LNCaP	≪ 1 × 10−6
CL2	DU145	≪1 × 10−6
DU145	RWPE-1	7 × 10−5

DU145, a moderately metastatic cell line, was obtained from brain metastasis. Much like PC3, these cells intravasated into blood vessels; however, they had to reach the arterial circulation and pass through the heart and aorta to reach the systemic circulation. From there, the tumor cells became arrested in the brain capillary bed and crossed into brain parenchyma to form a secondary tumor, where the blood brain barrier is easily overcome by cancer cells.⁶⁷ It is possible that an increased nuclear stiffness contributed to DU145 brain metastasis as these cells had to survive high shear stresses in the heart and aorta that are three orders of magnitude higher than in capillaries,⁶⁸ and an increased nuclear stiffness may have contributed to their resistance to breakup in flow.

We found that non-metastatic LNCaP nuclei have the lowest stiffness of all cell lines examined. LNCaP cells were originally obtained from a supraclavicular lymph node metastasis; however, they are now non-metastatic when transplanted into mice.^63,64 For most lymph node metastases, tumor cells arrive at the node via lymphatic capillaries, possibly carried by fluid flow from the primary tumor.^69,70 Lymphatic capillaries may be less challenging to invade than typical blood capillaries, as they have a larger diameter and a single thin endothelial cell layer lacking tight junctions on a discontinuous layer of the basement membrane. Additionally, the smaller vessels lack smooth muscle cells or pericytes and have frequent fenestrations.⁷⁰ A lymphatic capillary offers primary tumor cells unrestricted access to a nearby lymph node, where they can reside and grow. The tumor cells were transported to the supraclavicular lymph node through lymphatic vessels at speeds ranging from 0.01 to 0.5 cm/s.⁷¹ These speeds are similar to the speed of blood flow in capillaries; however, due to the larger size of lymphatic vessels [200 μm vs. 5–10 μm (Ref. 68)], the tumor cells experience considerably less shear stress than they would in the bloodstream—possibly evading breakup—as LNCaP cells can fragment easily under shear stress.⁷² These features of the lymphatic system may explain why fragile LNCaP cells with soft nuclei metastasized to lymph node and do not metastasize in blood flow. LNCaP has androgen receptors, unlike the other prostate cancer cell lines used here. The CL2 cell line is derived from LNCaP but is androgen receptor insensitive.⁶³

Finally, we note that the nuclear fluidity [Fig. 3(e)] and stiffness [Fig. 3(f)] do not depend on nuclear size—as expected—demonstrating that these parameters are not influenced by additional nuclear properties, as may be expected for other metrics of mechanical properties such as entry time and transit velocity.^31,38,49

B. Prostate cancer nucleus entry times are correlated with nuclear stiffness, not fluidity

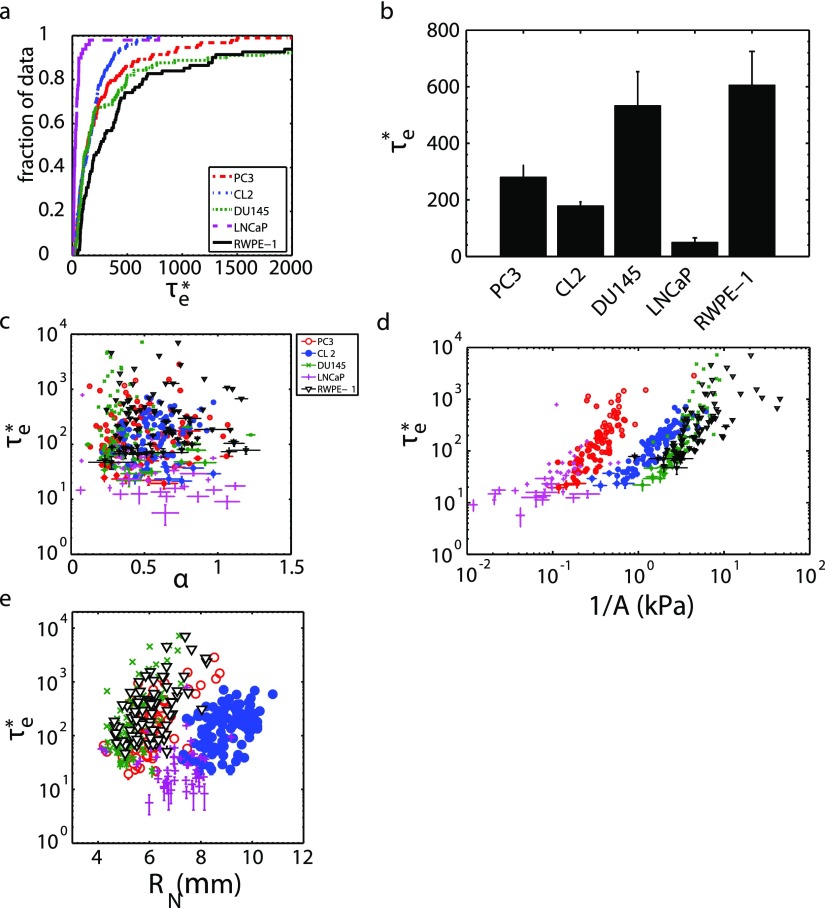
We also measured nucleus entry times to determine if reduced entry times can be a marker for increased prostate cancer aggressiveness, as cellular and nuclear entry times have been previously used as deformability metrics.^31,49 We nondimensionalized the nucleus entry times τ_e as ${\tau }_e^{*}={\tau }_e{V}_m/L_{CH}$ in order to take into account the slightly different driving pressures used, due to the slightly different heights of fluid in the MFCS-EZ driving pressure source (see Sec. II C). Here, V_m is the average fluid velocity in the constricted channel and L_CH is the channel length. We found that highly metastatic PC3 and CL2 have shorter ${\tau }_e^{*}$ than moderately metastatic DU145 and normal RWPE-1 cells [Figs. 4(a) and 4(b)]. We also found that non-metastatic LNCaP cells have the shortest ${\tau }_e^{*}$. Refer to Table II for statistical comparisons. Note that the statistical comparisons between these cell lines' stiffnesses have lower p-values, indicating a more reliable comparison.

FIG. 4.

Prostate cancer cell nondimensional nucleus entry time ${\tau }_e^{*}$ can reflect cell line invasiveness. (a) Entry time cumulative distribution function; the abscissa truncated to emphasize different distributions. (b) Average (±SE) entry times for each cell line. PC3 (n = 93), CL2 (n = 102), DU145 (n = 89), LNCaP (n = 49), RWPE-1 (n = 81). (c) ${\tau }_e^{*}$ does not depend on nucleus fluidity α, (d) but does depend on nucleus stiffness 1/A. (e) ${\tau }_e^{*}$ also depends on nucleus radius R_N.

TABLE II.

Statistical power for comparison of nuclear nondimensional entry time ${\tau }_e^{*}$ distributions of different prostate cancer and normal cell lines. All comparisons were done using the two-distribution Kolmogorov-Smirnov test.

Cell line	Cell line	p-value
PC3	CL2	4 × 10−1
CL2	LNCaP	≪1 × 10−6
PC3	DU145	6 × 10−1
DU145	RWPE-1	3 × 10−2

We first established that ${\tau }_e^{*}$ and stiffness both tend to be smaller for highly metastatic cells, and we then examined if nuclear entry times were correlated with fluidity [Fig. 4(c)] and stiffness [Fig. 4(d)] as has been suggested for whole cells in a study by Lange et al.³⁸ (see supplementary material); this, if true, implies that viscoelastic cell's mechanical properties can be fully characterized by a single metric. We observe that the entry times are not correlated with nuclear fluidity α but are correlated with nuclear stiffness 1/A. This implies that, for a prostate cell nucleus, its entry time does not fully characterize its mechanical properties. Finally, we confirmed that ${\tau }_e^{*}$ depends on the nucleus size [Fig. 4(e)], as expected from previous studies on whole cells.⁴⁹ With the limited range of radius values, a power law dependence is neither clear nor dismissible.

C. Nuclear stiffness sometimes correlates with lamin A/C or lamin B expression levels

It has been hypothesized that lamin expression levels affect nuclear rheology^5,23,28 and demonstrated that lamin A/C contributes to nuclear viscosity and lamin B1 contributes to nuclear elasticity.²⁸ If this was the case, we would expect cells that express high levels of lamin A/C to have high fluidity α values and cells that express low lamin A/C values to have lower fluidity values since they would behave more like an elastic solid. These previous experiments, however, consisted of nuclear strain relaxation experiments performed under a constant stress and may be of limited relevance.²⁸ Other studies show that control cell nuclei are softer than nuclei from cells engineered to over-express lamin A/C^31,73 and Δ50 lamin A (a lamin A mutant).²² Lamin A/C knockdown cell nuclei are known to deform more under an applied strain than wild-type cell nuclei.^5,23,74 Note that one study found that lamin B1 over-expression decreases nuclear deformability,⁷⁵ while another found that lamin B1 under-expression had no effect on nuclear deformation;⁵ this contradiction is surprising but remains unresolved.

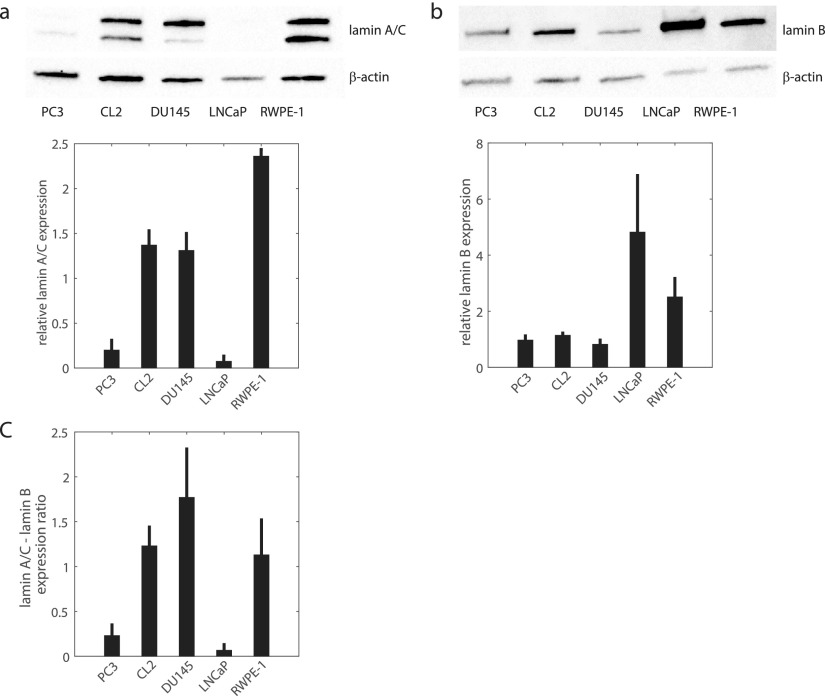
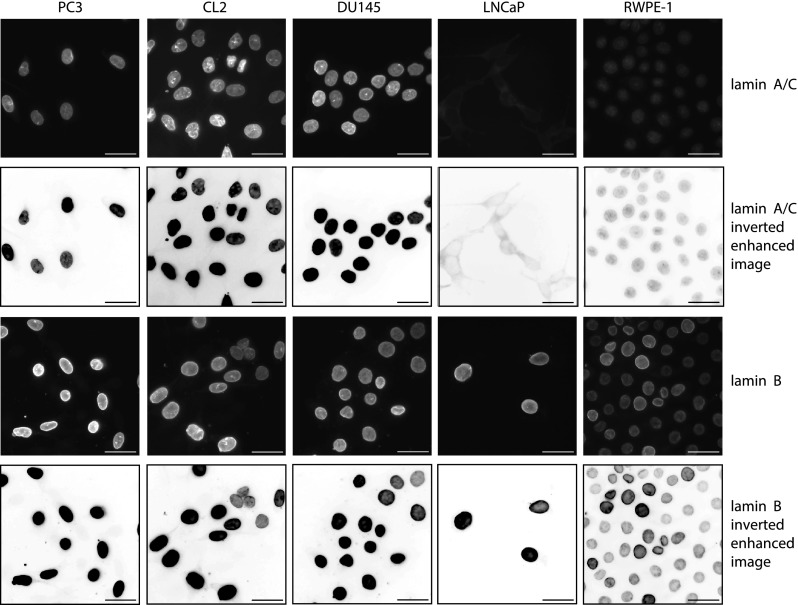
Lamin expression alteration is currently considered as one of the steps involved in the malignant transformation process.^30,34,35 Changes in lamin expression alter the nuclear shape—a hallmark of cancer.^2,36 Increases or decreases in A- and B-type lamin expression have been reported for several types of cancers;^{30,34,76–82} however, alterations in lamin expression have not yet been proven to be a cancer marker since no consistent patterns of over- or under- expression have been observed.^35,83 For example, A-type lamins were found to be down-regulated in some cancers (lung,⁸⁰ gastrointestinal tract,⁸⁴ and basal cell carcinoma⁸⁵) but up-regulated in others (basal cell carcinoma,⁸⁶ lung,⁸⁰ and ovarian cancer⁸⁷). The use of B-type lamin expression as a cancer marker has not been adopted since it can be over-expressed (hepatocellular carcinoma⁸⁸) or under-expressed (lung⁸⁰ and gastrointestinal tract cancers⁸⁴). Due to the presumed importance of lamin A and B expression levels in nuclear deformability, these levels and their ratio may be correlated with the invasiveness of prostate cancer cells. Western Blots for lamin A/C and lamin B1 in nuclear fractions, quantification of expression levels from the blots, and lamin A/C-lamin B1 ratio are shown in Fig. 5. Prostate cancer is considered to be a lamin A/C over-expressing disease, where highly metastatic cancer cells express high lamin A/C levels and lowly metastatic cells express lower levels.⁸⁹ We observed that normal RWPE-1 cells express the highest lamin A/C levels, while highly metastatic PC3 and non-metastatic LNCaP cells exhibit approximately 10 times lower levels [Fig. 5(a)], which is consistent with RWPE-1 having the stiffest nuclei and PC3 and LNCaP having the softest nuclei. Highly metastatic CL2 and moderately metastatic DU145 express similar lamin A/C levels, while the DU145 nuclei are approximately 2 times stiffer than CL2. We note that the aforementioned trend in the literature for prostate cancer lamin A/C expression, inexplicably, is not manifested in our immortalized cell lines. We also observed that lowly metastatic LNCaP and normal RWPE-1 cells have high lamin B1 expression levels [Fig. 5(b)], while the moderately and highly metastatic cells express low levels—indicating that nuclear stiffness is not directly correlated with lamin B1 expression for these immortalized prostate cancer cells. We confirmed the presence or lack of lamins in the blots using immunofluorescent staining in Fig. 6, in the case of protein insolubility affecting the Western Blots. The low levels of lamin A/C expressed by LNCaP in the blots [Fig. 5(a)] are supported by immunofluorescent staining.

FIG. 5.

Lamin A/C and B1 expression in cell nuclear fractions. (a) Western blot (upper panel) and band density (lower panel) quantifying nuclear envelope protein lamin A/C expression and β-actin loading control. Lamin band densities are normalized by β-actin loading control band densities. (b) Western blot (upper panel) and band density (lower panel) of lamin B1 and β-actin expression. (c) The ratio of lamin A/C and lamin B1 expression, obtained from the density graphs in (a) and (b). Four independent samples were used for all blot quantifications.

FIG. 6.

Immunofluorescent staining for lamin A/C (top row), inverted linearly enhanced images of lamin A/C (for better visualization, second row), immunofluorescent staining for lamin B1 (third row), and inverted linearly enhanced images of lamin B1 (fourth row) in highly metastatic PC3 and CL2, moderately metastatic DU145, lowly metastatic LNCaP, and normal RWPE-1 prostate cells. Scale bars are 33 μm.

DU145 has one of the highest lamins-A/B ratios in our study [Fig. 5(c)]; however, it has the lowest fluidity α [Fig. 3(b)]. DU145 also has nuclei with intermediate stiffness [Fig. 3(d)]. Furthermore, the normal prostate RWPE-1 and highly metastatic CL2 cell lines have similar lamin A/C-lamin B1 ratios [Fig. 5(c)]. We find that RWPE-1 nuclei have the highest fluidity and the highest stiffness of all the cell lines studied [Figs. 3(b) and 3(d)], and the mean stiffness of RWPE-1 is nearly three times higher than for CL2. Due to these observations, we conclude that lamin A/C expression levels affected nuclear stiffness for cells which express high (RWPE-1) or low (LNCaP, PC3) levels. The nuclear stiffness of the remaining cells—highly metastatic CL2 and moderately metastatic DU145—does not follow this trend.

D. Decreasing chromatin condensation decreases nuclear stiffness

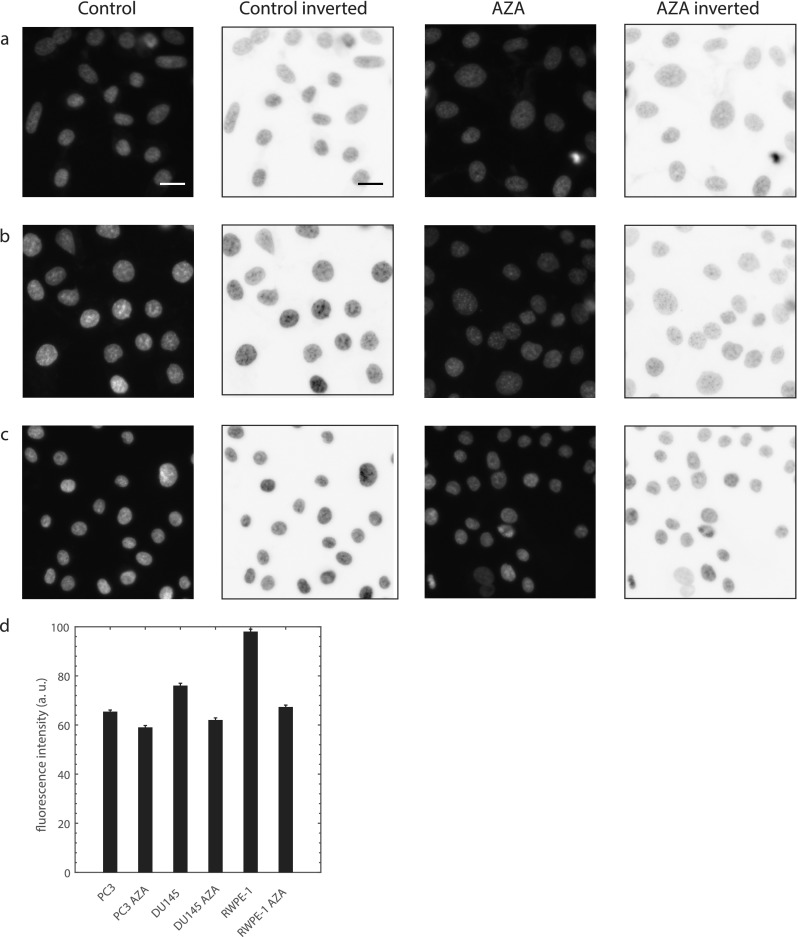
It has been previously demonstrated that the chromatin structure, in addition to lamin expression levels, can affect nuclear deformability and rheology. These conclusions were drawn from micropipette power law rheological measurements of isolated nuclei and nuclei in intact cells which were treated with divalent salts to condense chromatin.^23,40 These studies found that the nuclear fluidity α decreased and stiffness 1/A increased significantly. Other studies demonstrated that decondensing chromatin with drug treatments increased nuclear strain by ∼30% (Ref. 24) and reduced the nuclear stiffness by ∼50%.²⁵ To assess the role of chromatin in prostate cancer and normal prostate cell nuclear deformability and rheology with our experimental conditions, we treated highly metastatic PC3, moderately metastatic DU145, and normal RWPE-1 cells with chromatin decondensing drug 5-AZA-2'-deoxycytidine (AZA).^24,38 Chromatin decondensation by AZA is confirmed in Fig. 7 by imaging DNA in cell nuclei using Hoechst 33342 (fluorescent stain).

FIG. 7.

Confirmation of chromatin decondensation by drug 5-AZA-2'-deoxycytidine (AZA). Fluorescence and inverted fluorescence images of nuclei stained with Hoechst 33 342 for control and treated cells: (a) PC3, (b) DU145, and (c) RWPE-1. Scale bar is 20 μm. (d) AZA reduces the average nuclear fluorescence intensity, and therefore, chromatin is less condensed. PC3 n = 331, PC3 AZA n = 217, p < 1 × 10⁻⁵. DU145 n = 296, DU145 AZA n = 291, p ≪ 1 × 10⁻⁶. RWPE-1 n = 303, RWPE-1 AZA n = 362, p ≪ 1 × 10⁻⁶. The two-sample Kolmogorov-Smirnov test was used for statistical comparisons. Data obtained from 3 independent samples and average intensities were taken from raw fluorescence images.

We observe that AZA treated cancer cells had higher fluidity; however, this drug did not increase the fluidity of normal cell nuclei that have the highest fluidity [Figs. 8(a) and 8(b)]. We also find that chromatin decondensation significantly reduces the stiffness of the moderately metastatic and normal cell nuclei but not the highly metastatic PC3 with the softest nuclei of those treated with AZA [Figs. 8(c) and 8(d)]. All cell lines showed reduced nondimensional entry times with chromatin decondensation [Figs. 8(e) and 8(f)]. See Table III for statistical comparisons. These findings indicate that chromatin condensation influences nuclear stiffness, with the strongest effects (on 1/A and ${\tau }_e^{*}$) on less metastatic cells. This is possible if highly metastatic cancer cells have less condensed chromatin than moderately metastatic or normal cells and if the chromatin decondensing drug has less effect on cells with less condensed chromatin.

FIG. 8.

Effects of chromatin decondensing drug 5-AZA-2'-deoxycytidine (AZA) on nuclear mechanics. (a) Fluidity cumulative distribution function (CDF) for AZA treated (n = 47) and control (n = 94) PC3 cells, AZA treated (n = 69) and control (n = 89) DU145 cells, and AZA treated (n = 117) and control (n = 83) RWPE-1 cells. (b) The mean fluidity (±SE) of AZA treated cells in comparison with control. (c) Stiffness CDFs for AZA treated and control cells with the abscissa truncated to emphasize different conditions. (d) The mean stiffness (±SE) of AZA treated cells in comparison with control cells. (e) Nondimensional entry time CDF for AZA treated and control cells. The abscissa has been truncated to emphasize differences between the curves. (f) The mean (±SE) entry times of treated and control cells. Samples were obtained from 3 or more independent experiments.

TABLE III.

Statistical power for comparison of nuclear fluidity α, stiffness 1/A, and nondimensional entry time ${\tau }_e^{*}$ distributions of different cell lines treated with chromatin decondensing drug AZA. All comparisons were done using the two-sample Kolmogorov-Smirnov test.

Cell line	Cell line	Metric	p-value
PC3	PC3 AZA	α	9 × 10−3
PC3	PC3 AZA	1/A	0.3
PC3	PC3 AZA	${\tau }_e^{*}$	0.6
DU145	DU145 AZA	α	≪1 × 10−6
DU145	DU145 AZA	1/A	≪1 × 10−6
DU145	DU145 AZA	${\tau }_e^{*}$	0.02
RWPE-1	RWPE-1 AZA	α	9 × 10−5
RWPE-1	RWPE-1 AZA	1/A	≪1 × 10−6
RWPE-1	RWPE-1 AZA	${\tau }_e^{*}$	≪1 × 10−6

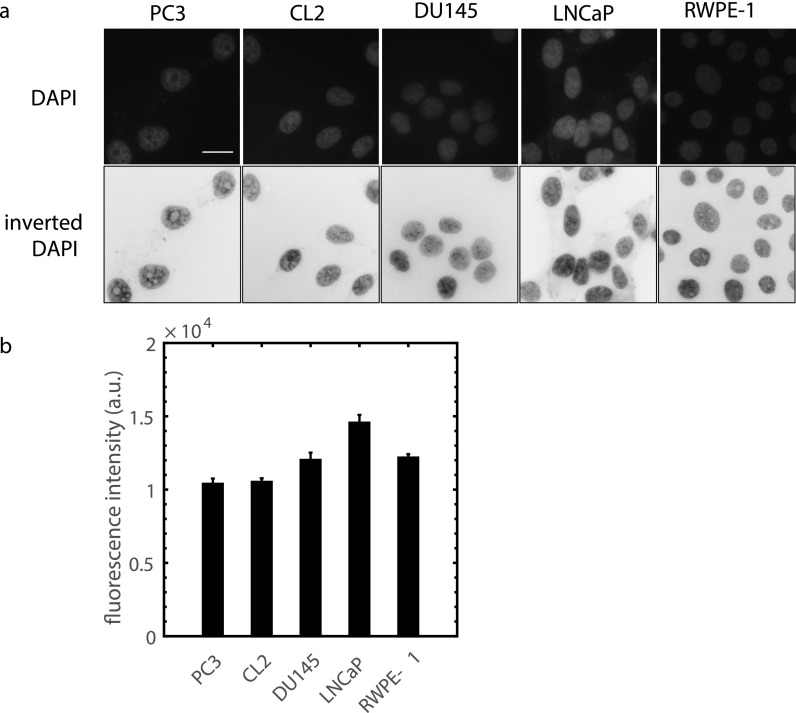
To determine if highly metastatic prostate cancer cells have less condensed chromatin than lowly metastatic and normal cells, we stained DNA in fixed cell nuclei using DAPI (fluorescent stain) imaged with a high spatial resolution (90× magnification). More intense fluorescence and bright spots indicate that chromatin is condensed with a high concentration; thus, less intense fluorescence and fewer bright spots indicate lower condensation.^53,54 Figure 9(a) shows that highly metastatic PC3 and CL2 have less bright nuclei than moderately metastatic DU145, non-metastatic LNCaP, and normal RWPE-1 cells. Fluorescence intensity levels were quantified by averaging over regions in the nucleus images and avoiding nucleoli [Fig. 9(b)]. Highly metastatic prostate cancer cells can have less condensed chromatin, as implied by our nuclear stiffness and DNA stain measurements. This is reasonable, as highly metastatic cells can have high levels of transcriptional activity and chromatin is decondensed during phases of high transcription activity.²⁴

FIG. 9.

(a) Imaging DNA in prostate cell nuclei with DAPI to quantify chromatin condensation. The upper row is raw fluorescence images and the second row shows inverted images to enhance visualization. PC3 and CL2 are highly metastatic, DU145 is moderately metastatic, LNCaP is non-metastatic, and RWPE-1 is a normal cell. Scale bar is 20 μm. (b) Average nuclear fluorescence intensity, taken from the raw images, for different prostate cell lines (n = 40, p < 0.05 for all comparisons except PC3-CL2 and RWPE-1-DU145, two-sample Kolmogorov-Smirnov test from 3 independent samples).

IV. CONCLUSIONS

We have performed quantitative nuclear rheology experiments on highly, moderately, and lowly metastatic prostate cancer and normal prostate epithelial immortalized cell lines using a microfluidic device with a narrow constricted channel. The experiments were performed with significantly larger sample sizes than previous micropipette aspiration experiments.^22,23,40 Our results show that the nuclei of normal cells are stiffer than moderately metastatic cell nuclei and that the moderately metastatic cell nuclei are stiffer than highly metastatic cell nuclei. The softer nuclei may assist cancer cells to metastasize more efficiently.^2,19,58,59 Western blot analysis showed that nuclear stiffness is not reflective of lamin A/C nuclear envelope protein expression levels for cells with intermediate levels. Decondensing nuclear chromatin with a drug treatment significantly reduced moderately metastatic and normal cell nuclear stiffness, suggesting that nuclear stiffness is sensitive to chromatin condensation. This implies that highly metastatic prostate cancer cells have less condensed chromatin than moderately metastatic and normal prostate cells and that the highly metastatic cells are likely in a high state of transcriptional activity in comparison with moderately metastatic and normal cells, suggesting that chromatin condensation may be an effective cancer marker. Having a technique that is sensitive to the chromatin structure and lamin A/C expression may be useful for early cancer detection.

V. SUPPLEMENTARY MATERIAL

See supplementary material for a demonstration that the entry time, maximum elongation, and fluid pressure for objects flowing into a narrow channel, as proposed by Lange et al.,³⁸ fail to yield the correct power law fluidity.