POVME 3.0: Software for Mapping Binding Pocket Flexibility

Abstract

We present a substantial update to the open-source POVME binding pocket analysis software. New capabilities of POVME 3.0 include a flexible chemical coloring scheme for feature identification, post-analysis tools for comparing large ensembles of pockets (e.g., from molecular dynamics simulations), and the introduction of scripts and methods that facilitate binding pocket comparison and analysis. We envision the use of this software for visualization of binding pocket dynamics, selection of representative structures for ensemble docking, and incorporation of molecular dynamics results into ligand design efforts.

Graphical Abstract

Introduction

Shape complementarity between a ligand and a binding pocket is a central concept in rational drug design. For this reason, many early structure-guided drug design efforts focused on developing tools to determine which molecules fit into a given binding cavity.¹ While these techniques gained widespread appeal, scientists have since realized that protein-ligand binding is not so much a question of rigid fit as it is question of complementarity between the energetic landscapes of the protein, ligand, and solvent.

Improvements in structure-guided virtual screening have attempted to close the gap between rigid docking methods and flexible thermodynamic reality. One of the more difficult steps in this effort is the handling of molecular flexibility.² While algorithms have been developed to efficiently sample a small molecule ligand’s conformational landscape,^{3,4,5,6,7,8,9,10} proteins are considerably more complex and proper handling of their flexibility is a more challenging question. ^11,2,12,13

The “ensemble docking” method is used to bridge the gap between the available rigid docking techniques and existing models of protein flexibility. ^14,15,16 This technique allows researchers to integrate the results of another powerful tool in biophysics research - molecular dynamics (MD) simulations - into drug design work. MD simulations can provide hundreds of thousands of snapshots of a protein’s conformation through the course of thermal motion. While it is currently computationally intractable to perform docking on these hundreds of thousands of structures, is it possible to do so for tens of structures. In the ensemble docking method, a large set of protein structures is filtered to a smaller representative set, which is selected to preserve the full range of observed conformational diversity.¹⁷ Performing docking on each member of this smaller representative set is therefore feasible, and should ideally yield the same information as docking to every single snapshot of the protein from the simulation.

The process by which a representative set is selected remains an open question.^16,18,19 Inherent in the process of representative selection is the concept of finding meaningful differences between the binding sites in different structures, and ensuring that all of these differences are represented in the reduced set of structures. If done correctly, this categorization of differences should also be useful in itself. Viewing a human-interpretable summary of the major areas and types of variation in a binding pocket would make researchers more efficient and effective in answering a range of scientific questions. For example, a visual summary of binding pocket differences around a promising ligand can inform drug designers about new directions of scaffold functionalization. Further, establishing the characteristics of a target binding pocket that distinguish it from other, similar pockets can enable ligand design with high specificity and fewer off-target effects. As computational methods become more powerful, finding correlations between the binding site shape and distant functional regions of a target protein can enable the design of allosteric ligands.

Previous research has been done on the topic of pocket-studying algorithms.^19,20 In discussing the context of this work, it is important to draw a distinction between “pocket analysis” and “pocket detection”. POVME is a pocket analysis tool. Pocket analysis is the process of characterizing the shape and flexibility of a cavity in detail. Pocket detection is the process of finding druggable cavities on a protein structure where small molecule ligands might bind. Though these processes seem similar, each is best suited to different mathematical representations. For example, a pocket detection algorithm might rely largely on comparison of a user’s query pocket to a set of known druggable pockets. Such a comparison algorithm would favor easily-rotatable (or even rotation-invariant) representations of binding pockets to accurately perform comparisons independent of reference frame. However, pocket analysis algorithms must preserve fine detail and be able to analyze thousands of frames quickly. The generalizations required to create a rotation-invariant representation of a pocket lead to a significant loss of detail and may incur a high computational cost. Therefore, while compatibility between the tools should be a consideration for creating scientific workflows, one single tool is unlikely to be best for both pocket detection and analysis. Readers interested in pocket representation styles are directed to a separate publication.²¹

The conformational flexibility of a binding pocket can be investigated by studying the differences between many related structures, from sources such as molecular dynamics snapshots, crystallography under different conditions, and homologous protein structures. Previous work has been done to investigate the different approaches that can be used to generate meaningful protein conformations for pocket analysis.²² However, there is not a single standard for the definition of a region of space as a “binding pocket”. Furthermore, it is possible that given the range of reasons for studying a binding pocket and the geometric diversity of cavities where drugs bind, a single standard may not even be appropriate. For example, rules which work for deep pockets may not work well for shallow pockets,²³ and parameters aimed at predicting small molecule druggability may be unsuitable for finding peptide binding sites.

Different pocket analysis programs represent binding pockets in different ways - the two most popular representation types are voxel/grid-based and alpha sphere-based. Although both are suitable for visualizing pocket shape, POVME employs a voxel/grid-based pocket representation, as we have found this to better enable pocket comparison. An in-depth discussion of the advantages of grid-based shape methods is available in the publication of another pocket-analysis tool, TRAPP.²⁴

A major disagreement in the field of pocket definition arises from the variety of methods that different programs use to define the boundary of a pocket. While most programs are consistent in how they represent the buried portions of cavities (stopping pocket definition at protein atoms and excluding channels too narrow to host a ligand), existing methods diverge in the logic used to define a boundary at the surface-exposed end of a pocket. This is a long-studied issue in pocket definition, and is sometimes referred to as a “can of worms” problem.²⁵ Some algorithms terminate the pocket when new points are no longer adjacent to a ligand or pocket-lining residue atom.²⁴ Others draw numerous vectors out from each possible pocket voxel in different directions and may require a certain fraction of these vectors to intersect a protein atom within a cutoff distance.^26,27,28 Another option, employed in POVME²⁹ and other programs ^30,31 is to “gift wrap” the protein with a convex mesh and exclude all voxels outside the mesh from being defined as part of the pocket.

These differences make it difficult to establish a meaningful definition of “volume” and hinder the rigorous comparison of pocket shapes. The example workflows bundled with POVME 3.0 show best practices for different situations, including the disabling of the convex hull algorithm when performing analysis for quantitative comparison.

Various tools have been developed for the analysis of binding pockets, including fpocket^32,29,33, TRAPP^24,22, PocketAnalyzer(PCA)³⁴, trj_cavity²⁷, Epock³⁵, and Volsite.²⁶ As the use of integrative modeling and data science continues to grow in biomedical research, it is necessary to develop a tool for analysis of binding pocket shapes that is both suitable for immediate visualization, and also able to interface with more complex data analysis tools. We build off of previous developments in this field to create a package that combines precision in pocket analysis with the ability to integrate results into larger data workflows.

In this paper, we present POcket Volume MEasurer (POVME)³⁶ 3.0 as a tool for analysis of flexible protein cavities. Version 3.0 contains many additional capabilities, including: post-processing tools to perform clustering and principal component analysis; a chemical coloring scheme for defining pocket features; python classes for custom analyses of pocket shape output; pre-built workflows for a variety of tasks; and easy installation using the pypi package index.

Methods

All of the functionality available in POVME2.0 has been maintained, and readers interested in a detailed description are directed to that paper.²⁹ The new features in POVME3.0 are detailed in this section.

Ligand-based pocket definition

POVME relies on a user-defined inclusion region to define the boundary of the pocket of interest, similar to the Maximum Encompassing Region in Epock.³⁵ Based on feedback for POVME 2.0, we learned that users frequently found the existing region-definition methods to be unwieldy. For this reason, we added three new features for pocket definition, including defining the pocket based on the 1) residue name of a ligand present in the trajectory, 2) a saved POVME shape file (a 3xN numpy array of grid points), and 3) 3D cylinders (in addition to the previously implemented boxes and spheres). The ligand-based pocket definition is likely to be the most popular option, especially for defining appropriate inclusion regions to analyze tight pockets. When given the DefinePocketByLigand keyword and a ligand residue name, POVME will pre-process the trajectory, map each ligand atom in each frame to its nearest grid point, and define those grid points as the seed region for all frames. It will then grow this seed region 3 Angstroms out in each direction, and define that superset of points as the inclusion region.

Convex hull options

The ConvexHullExclusion keyword can be set to 4 options: “each”, “none”, “first”, or “max”. The first two options were available in an earlier version of POVME. “none” will forego the convex hull exclusion process altogether, as was standard behavior for the original POVME. “each” will calculate a convex hull for each frame of a trajectory, as was standard behavior for POVME 2.0. It is worth noting that the “each” setting is not advised if the final goal of POVME analysis will include quantitative analysis such as clustering or PCA, as the outer boundary of the pocket may shift each frame, and the magnitude of this shift can dwarf motions inside of the pocket. The other two options are new additions and apply the same convex hull to each frame. “first” applies the convex hull from the first frame in the trajectory, and “max” applies a convex hull drawn around all frames in the trajectory superimposed on each other.

Coloring

A chemical coloring scheme has been implemented to characterize portions of the pocket that can host favorable interactions with small molecule ligands. The coloring scheme is based on the BINANA binding site description algorithm,³⁷ but has not been validated for a quantitative purpose as it is applied in POVME and so is primarily suited for visualization. Currently, this coloring scheme depicts hydrogen bond donors, hydrogen bond acceptors, aromatic stacking, hydrophobicity, and hydrophilicity. The colors are output as separate POVME maps with variable intensity assigned to each grid point. POVME provides time-averaged color maps after analysis of an entire trajectory.

Because the colors are defined by continuous functions but are only defined at discrete points, the total contribution of each feature (for example, a single O-H donor group, or a single aromatic ring) may vary depending on how the intensity of the 3D function falls on the fixed cartesian grid. For this reason, the total contribution of each feature to the grid is normalized, so that the summed value of the feature’s contributions to the color grid is equal to 1. Further, in order to ensure that buried points are not assigned color magnitudes, only points that are defined as part of the pocket in a frame (or are within a skin distance of the surface) will receive these color values.

The magnitude of the hydrogen bond donor color is defined as a gaussian in spherical coordinates, with a center beyond the hydrogen atom as measured along O-H or N-H axis. The magnitude of the hydrogen bond acceptor color is defined as a gaussian in Cartesian coordinates, emanating from the center of all O atoms. The aromatic color is defined in a cylinder above and below aromatic rings, with uniform magnitude along the radius (dropping to 0 at an outer radial cutoff) and with magnitude defined by a gaussian along the height of the cylinder. The magnitude of the hydrophobic color is defined as a gaussian around all C atoms, and the hydrophilic is a gaussian around each N, O, and S.

The pocket coloring scheme is extensible to python programmers, and the POVME package contains the “featureMap” class which enables coloring based on a number of shapes at user-defined atom motifs.

Adjacency and surface

Two boundary-defining colors are also defined as “adjacency” and “surface”. Adjacency represents a thick layer of binding pocket volume near the surface of the protein, and may be of interest in measuring buriedness of voxels. Surface represents a thin layer of volume on top of the protein surface lining the binding pocket, and is used in surface area calculation.

File conventions

POVME3.0 requires a pre-aligned trajectory in PDB format. POVME 3.0 outputs 3 file types: pdb, dx, and npy. The first two are chosen for ease of visualization. Boolean grid data, for example individual pocket volumes and regions where color maps exceed a threshold magnitude, are output in Protein Data Bank “pdb” format. Non-boolean grid data are output in Data Explorer “dx” format, which is compatible with a variety of visualization programs including VMD and PyMol. Examples of such data include the average pocket shape of many frames, or color maps in full detail. Every single-frame .pdb and .dx file output from POVME 3.0 also has a .npy equivalent. The NumPy file format was selected for its efficiency, interconvertibility with other file types, and compatibility with major data analysis packages. Efforts to involve POVME in more elaborate integrative modeling efforts should work directly with these npy files.

Clustering

POVME 3.0 offers scripts to perform pocket shape-based clustering and examples to exhibit their use. Pocket shape clustering is handled in two steps. First, a pairwise binding pocket similarity matrix is generated for all binding pocket structures in the ensemble. Second, this similarity matrix is clustered and useful depictions of the clusters and their differences are created.

The similarity matrix is calculated using the Tanimoto overlap score of each pair of pockets. As the grid points in POVME are defined in the same Cartesian reference frame for each pocket, the Tanimoto score is calculated by counting how many pocket points each pair of pockets has in common, divided by the number of points in either. Therefore, the Tanimoto score of a pair of frames can be at maximum 1 (the two pockets are identical) or at minimum 0 (the two pockets share no volume in common). Alternatively, the similarity matrix can be calculated using the Tversky similarity metric, in which the overlap term is the same but the denominator is the volume of one frame instead of the union of both.

In the clustering step, users may select to use SciPy’s hierarchical or k-means libraries.^38,39 By default, hierarchical clustering is performed, based on SciPy’s average linkage implementation. The desired number of clusters can be input manually, otherwise cluster.py will compute the Kelley penalty⁴⁰ to determine a reasonable number. For each cluster, cluster.py extracts the representative structure (the pdb structure corresponding to the cluster member with the maximum summed overlap score with all of the others) and generates two dx files depicting 1) the cluster’s average pocket shape and 2) the difference between this cluster’s average and the entire ensemble’s average. VMD scripts are produced to load these volume maps and overlay them on the representative structure for each cluster. Figures are also created to show cluster membership as a function of frame number and to create a “kinetic network” diagram of the clusters, linked by the number of transitions the ensemble took between them.

PCA

Principal component analysis (PCA) is a common tool in data science that has recently been applied to pocket shape analysis.^28,24 PCA of pocket shapes can serve a variety of purposes. First, it can act as a way to define meaningful subpockets. As subpockets can come in a variety of shapes and sizes, it is difficult to select a single method or heuristic to define them. However, it is possible to find mutually correlated groups of voxels that join or leave the pocket together. These mutually correlated groups are often physically contiguous and represent entire subpockets available for ligands. Second, it is possible to find multiple subpockets present in the same eigenvector, with coefficients that indicate positive or negative correlation with one another. Information such as negatively correlated subpockets may be valuable in ligand design, as it would indicate two areas of the binding pocket that are unfavorable for a ligand to occupy simultaneously. Third, PCA allows researchers to define meaningful axes by which structures can be compared quantitatively, which may be useful in selecting structures and rationalizing differences between families of structures.

PCA in POVME is performed by constructing a matrix of pocket points M, in which rows correspond to the different structures in the ensemble, and columns correspond to individual grid points. For each position i, j in the matrix, M(i, j)=1 if grid point j (for example (10,-7,5)) is defined as part of the pocket in structure i of the ensemble. Otherwise M(i, j)=0. Mean normalization, but not feature scaling, is performed on the columns of this matrix. After eigenvalue decomposition of this matrix, each eigenvector is mapped back to a density map defined at each point on the grid and saved as a dx file. These dx files can be visualized by a number of programs, and the workflow outputs a VMD⁴¹ script to load them all simultaneously and prepare a default visualization. This default visualization loads each eigenvector as a different object and displays regions in green and red to denote positive and negative coefficients respectively.

Common workflows

The POVME 3.0 download contains example workflows that users can adapt to their own data, including combined multiple-trajectory analysis, clustering, and principal component analysis.

Pypi distribution

POVME is now available on the Python Package Index (https://pypi.python.org/pypi/povme). This improvement streamlines the installation and updating process. The POVME source code is also now version controlled on GitHub (https://github.com/POVME/POVME), which makes it easier to download, modify, and manage bug reports and feature requests.

HSP90 MD simulations

Twenty 250-ns molecular dynamics simulations were run beginning from different HSP90 crystal structures in the Protein Data Bank (PDB).⁴² These PDB codes were selected on the basis of ligand diversity, structure resolution, and pocket characteristics. The final 20 PDB codes selected are 1BYQ,⁴³ 1UYF,⁴⁴ 1UYI,⁴⁴ 1UYL,⁴⁴ 2VCI,⁴⁵ 2WI7,⁴⁶ 2XHR,⁴⁷ 2YEJ,⁴⁸ 3B26,⁴⁹ 3D0B,⁵⁰ 3HEK,⁵¹ 3K98,⁵² 3K99,⁵² 3RKZ,⁵³ 3RLR,⁵⁴ 4CWN,⁵⁵ 4FCR,⁵⁶ 4LWE,⁵⁷ 4R3M,⁵⁸ 4W7T.⁵⁹ Active site ligands were parameterized using GAFF,⁶⁰ with charges derived using Gaussian⁶¹ and the RED server.^62,63,64 All crystal waters and ligand counterions were preserved. Sodium ions were added to balance the system charge. Schrodinger protein preparation was used to model missing loops, replace unresolved sidechains, and assign protons at pH 7. The full commandline instruction passed to Schrodinger’s prepwizard is provided in the SI. The twenty systems were prepared for simulation using LEaP from the AMBERTOOLS package.³ The FF99SB force field was used for simulation.^65,3 The tleap solvatebox command was used to add a TIP4P water box with 10A padding.

The AMBER MD input scripts are provided in the Supporting Information.

Results and Discussion

Coloring scheme

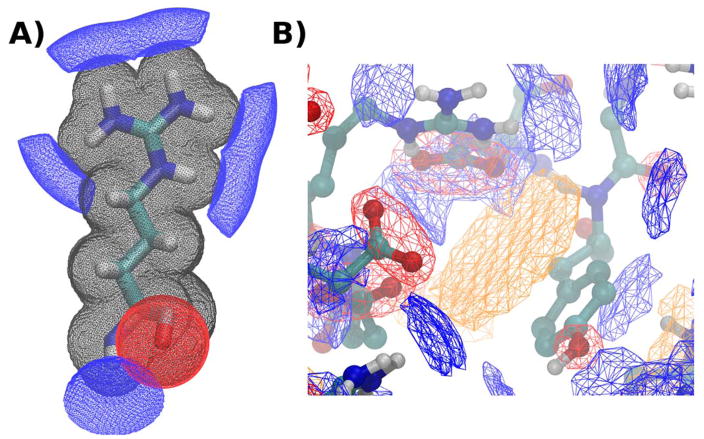
The coloring process is performed by default when POVME 3.0 is run. Figure 1 shows two examples of the coloring process. As no appropriate weighting scheme has been determined, the clustering and PCA workflows do not consider the color data (only the pocket shape). However, due to their qualitative utility, the color files are provided as pdb, dx, and npy files for visualization and custom user analysis.

Figure 1.

POVME coloring scheme. Black mesh shows occupancy, blue shows hydrogen bond donor regions, red shows hydrogen bond acceptor, and orange shows pi-stacking. A) The POVME coloring scheme applied at 0.1 Angstrom grid resolution to a single arginine residue from a protein structure. B) The POVME coloring scheme applied to a binding pocket at 0.75 Angstrom resolution, with occupancy not shown.

Validation of pocket similarity metric

We anticipate that researchers will use POVME to guide ligand design based on pocket geometry. Therefore, one of our major scientific objectives is to ensure that the similarity score that POVME reports when comparing binding pockets is related to the similarity of the ligands which fit in those pockets. In other words, if POVME analysis indicates that two pockets are similar, they should bind similar ligands. Conversely, if POVME determines that two pockets are dissimilar, they should bind dissimilar ligands. Establishing such a correlation would provide evidence that POVME’s selection of “diverse” pockets from an ensemble of protein structures will enable discovery of diverse ligands.

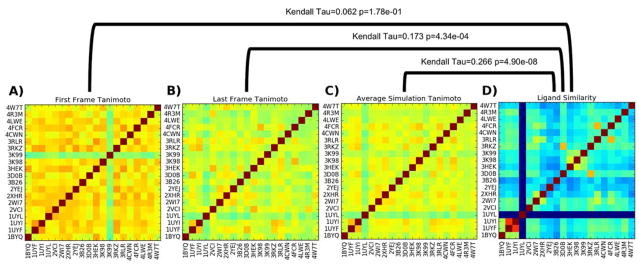
As a simple study of POVME’s pocket similarity metric (Tanimoto scoring), we attempt to use it to distinguish between the same protein crystallized and simulated with 20 different ligands. Each simulation was run for 250 ns, and frames were extracted every 1 ns. To determine the similarities between pockets, POVME was run on each trajectory, and the results were used to make three 20×20 similarity matrices. These matrices show the POVME similarity of the pockets from the first frame of each simulation (Figure 2A), the POVME similarity of the pockets from the last frame of each simulation (Figure 2B), and the average POVME similarity of all 250 frames taken from each simulation (Figure 2C). In order to compare pocket similarity to ligand similarity, it is necessary to compute a ligand similarity matrix. RDKit FingerprintMol objects were generated for each ligand, and the default RDKit similarity metric (Tanimoto) was used to compute a 20×20 ligand similarity matrix (Figure 2d).

Figure 2.

Tanimoto similarity matrices of A) initial simulation pocket shapes (following equilibration), B) final simulation pocket shapes (after 250 ns MD), C) average similarity of all pocket shapes throughout simulation, and D) RDKit chemical fingerprint Tanimoto score. Kendall Tau analyses of the matrices are shown above the brackets.

To compare the information contained in each similarity matrix, the Kendall rank correlation coefficient⁶⁶ is employed, which indicates the similarity between two sets of ranked objects. In this case, the ranked objects are pairs of nonidentical HSP90-ligand systems, each denoted by a pair of PDB codes, and they are ranked by their Tanimoto scores. For example, in the ligand similarity matrix (Figure 2D), the bright red (1UYI,1UYF) hotspot has the highest nonidentical similarity value (See figure S1 for ligand structures). The (1UYI,1UYF) pair therefore has rank 1. The rest of the PDB code pairs are ranked in order of decreasing ligand similarity to create the ordered ligand similarity list. The 1UYL simulation does not have a ligand, therefore it has a similarity score of 0 to all other ligands.

This process is repeated on each pocket similarity matrix to generate the three ordered pocket similarity lists. The Kendall rank correlation coefficient indicates how similar each pair of orderings is, with a maximum possible value of 1 (indicating identical ordering) and a minimum value of -1 (indicating completely opposite ordering). A Kendall Tau of 0 indicates random ordering. Comparing the average simulation Tanimoto similarity matrix (Figure 2C) to the ligand similarity matrix (Figure 2B) yields a Kendall Tau value of 0.266, with a p of 4.90 × 10⁻⁸, indicating moderate agreement with high confidence. Comparisons of only the first and last frame indicate weaker agreement between the rankings; analysis of the last frames of each simulation yields a Kendall Tau of only 0.173, and analysis of the first frames yields a Kendall Tau of 0.062.

The correlation between pocket shape similarity and ligand similarity suggests that using POVME to pick diverse pocket shapes will enable discovery of diverse ligands. To efficiently pick diverse structures, clustering analysis is performed on the complete 5000 × 5000 Tanimoto similarity matrix.

Clustering analysis

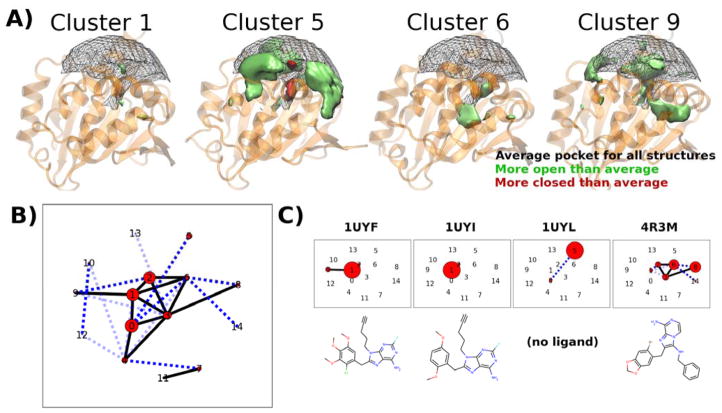
The clustering workflow was run on frames taken from the HSP90 trajectories at 1 ns intervals, for a total of 5,000 structures (250 snapshots per simulation x 20 simulations). The workflow is capable of choosing a number of clusters automatically using the Kelley penalty method.⁴⁰ However, this number is somewhat arbitrary, and in a project-driven analysis the number of clusters would be better determined by the computational resources available for ensemble docking. As an example, this study sets it to return 15 clusters for ease of visualization, to show how 20 simulations can be reduced. The 15 clusters are numbered 0 to 14, in order of decreasing size. These clusters represent frequently visited pocket shapes (Figure 3A). Each frame that is analyzed is assigned to a single cluster. Scientists using POVME to select diverse structures for ensemble docking will be primarily interested in the frames identified as cluster representatives by this step.

Figure 3.

POVME clustering of 20 HSP90-ligand complexes using cluster.py

A) 3D depictions of selected clusters. The representative protein structure for each cluster is shown as a transparent orange cartoon. The average shape for all analyzed frames is shown as a black mesh, with solid shapes (green and red) showing how each cluster is more open or closed than this average. B) “Kinetic network” depiction of the combined dynamics of the 20 HSP90 trajectories. Black numbers indicate cluster index (0–14). Red circles indicate the number of frames assigned to each cluster. Edges indicate the number of transitions observed between clusters in the MD trajectories (light blue dashes = 1 or 2, dark blue dashes = 3 to 5, solid black line = greater than 5). Clusters are arranged in 2D according to a force-based layout, in which each pair of clusters is pulled together by a force proportional to the number of observed transitions. C) Kinetic network depiction of individual trajectories. These network diagrams have the same 2D cluster locations, but only show cluster populations and transitions from individual trajectories. The corresponding ligand is shown below each diagram. 1UYL is the only apo structure, and is the only simulation that visits cluster 5.

As ligand kinetics are increasingly recognized to play an important role in drug efficacy (exemplified by recent interest in slow-k_off ligands)⁶⁷, understanding the kinetics of ligand-binding pockets also becomes a valuable topic of study. POVME clustering offers a way to discretize pocket conformations, and scientists can study pocket kinetics by observing how the systems transition between clusters. While the clustering process analyzes the trajectories together (as one large concatenated trajectory), the results of clustering can be mapped back over the different systems, and the time evolution of the simulations through the clusters can be studied (Figure 3B and C).

In the HSP90 data, we observe that the low-numbered (and therefore larger) clusters contain frames from multiple simulations, while clusters numbered 10 and above are all populated by a few outlier frames from individual simulations (complete data in Figure S2). Further, it is observed that the simulations of HSP90 bound to highly similar ligands, 1UYI and 1UYF, are the two largest occupants of cluster 1, but that only 1UYF makes excursions to cluster 9, which exhibits the opening of a side channel. An apo crystal structure uploaded as part of the same publication, 1UYL, starts in the most populated cluster, 0, but quickly transitions to cluster 5, which features a collapsed binding region and is populated exclusively by the apo simulation. The ligand from the 4R3M crystal structure, while sharing limited structural similarity with the 1UYF and 1UYI ligands, populates in small parts clusters 1 and 2, but is found the majority of the time in conformations bordering cluster 6. This cluster represents a higher-volume binding pocket with a unique deep subpocket open (Figure 3A). While this paper does not go in-depth on the SAR linking ligand chemotype to pocket conformation, it demonstrates that POVME enables the analysis of ligand-induced changes in protein dynamics.

Principal Component Analysis

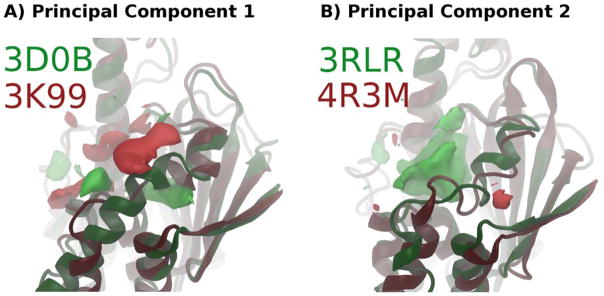
Principal Component Analysis was performed on the 20 HSP90 trajectories. Figure S3 shows that the pocket dynamics are complex with regard to subpockets - the first 10 principal components describe only about 30% of the pocket dynamics. However, reviewing the most significant principal components can be informative, as they explain major areas of pocket variation and how they relate to ligand structure. PC1 shows a change in pocket shape corresponding to the interruption of a binding site-adjacent helix (Figure 4A). This change opens a subpocket below the helix. PC2 corresponds to a complete loss of the same helix, and the inward bulging of secondary structure on the far side of the pocket (Figure 4B).

Figure 4.

POVME principal component analysis of 20 HSP90-ligand simulations. PCs were derived from analysis of 250 ns of MD of each system. Bright green and red regions are spatial depictions of each principal component in pocket space - A structure with a high PC value would have the green areas included in the pocket and the red areas closed off. Protein structures are snapshots from simulations corresponding to the high and low values in each PC. A) PC1, showing the final frame of the highest (3D0B, green) and lowest (3K99, red) valued systems. B) PC2, showing the final frame of the highest (3RLR, green) and lowest (4R3M, red) valued systems.

Conclusions

We present POVME 3.0, a substantial update to the POVME package that performs pocket selection for ensemble docking and provides outputs suitable for quantitative analysis. A number of new features have been added, including a chemical coloring scheme for binding pockets, the option to define pocket regions based on the position of a ligand molecule, and detailed manual pocket definition options. Further, post-processing workflows have been provided to perform the principal component and clustering analysis shown in this paper. Finally, POVME 3.0 has been redesigned for distribution on PyPI, simplifying its installation and use.

Great strides in molecular modeling are currently being made, thanks largely to the continued development of open-source software and the standardization of data formats. POVME 3.0 aims to make the field of drug design more open to machine learning techniques by providing a tool that connects MD simulations, pocket shapes, and ligand binding. The workflows for pocket clustering and PCA are initial examples of how POVME 3.0 can interface with statistical learning methods. Pocket shape data will become more valuable when it is combined with other forms of information to, for example, study allostery and correlate pocket shape to ligand structure.