Abstract
A better understanding of ultrasound transmission through human skull is fundamental to develop optimal imaging and therapeutic applications. In this study, we present global attenuation values and functions that correlate apparent density calculated from computed tomography (CT) scans to shear speed of sound. For this purpose, we used a model for sound propagation based on the viscoelastic wave equation (VWE) assuming isotropic conditions. The model was validated using a series of measurements with plates of different plastic materials and angles of incidence of 0°, 15° and 50°. The optimal functions for transcranial ultrasound propagation were established using the VWE, scan measurements of transcranial propagation with an angle of incidence of 40° and a genetic optimization algorithm. Ten (10) locations over three (3) skulls were used for ultrasound frequencies of 270 kHz and 836 kHz. Results with plastic materials demonstrated that the viscoelastic modeling predicted both longitudinal and shear propagation with an average (± s.d.) error of 9(±7)% of the wavelength in the predicted delay and an error of 6.7(±5)% in the estimation of transmitted power. Using the new optimal functions of speed of sound and global attenuation for the human skull, the proposed model predicted the transcranial ultrasound transmission for a frequency of 270 kHz with an expected error in the predicted delay of 5(±2.7)% of the wavelength. The sound propagation model predicted accurately sound propagation regardless either shear or longitudinal sound transmission dominated. For 836 kHz, the model predicted accurately in average with an error in the predicted delay of 17(±16)% of the wavelength. Results indicated the high importance of the specificity of the information at a voxel level to better understand ultrasound transmission through the skull. These results and new model will be very valuable tools for the future development of transcranial applications of ultrasound therapy and imaging.
Keywords: Ultrasound, skull, shear properties, attenuation, speed of sound, therapy, imaging
1. Introduction
A better understanding and prediction of ultrasound transmission through human skull remains a critical aspect for better design of imaging and minimally invasive therapeutic applications with ultrasound. For simplicity reasons, many efforts have modeled transcranial ultrasound by considering the skull bone as a fluid medium where purely longitudinal sound propagation properties can be specified (Connor et al. 2002, Aubry et al. 2003, Marquet et al. 2009, Pichardo et al. 2011, Almquist et al. 2016, Marsac et al. 2017). To improve accuracy of predictions, most models correlate the speed of sound in the skull bone to its density, which can be approximated at a voxel level from calibrated computed tomography (CT) scans (Clement & Hynynen 2002, Connor et al. 2002, Aubry et al. 2003, Marsac et al. 2017). From these studies, we know that the average the longitudinal speed of sound in the skull ranges from 2200 to 2600 m·s−1 while longitudinal attenuation is roughly in the range of 10 Np·(m·100 kHz)−1. Previous numerical studies have successfully predicted sound propagation where longitudinal transmission is expected to dominate. This is especially valid when, by example, the ultrasound wave front crosses the skull in normal incidence conditions. This is the scenario utilized to refocus therapeutic ultrasound for targets located in the thalamic region, as it has been done for focused ultrasound-based thalamotomy for the treatment of essential tremor (Elias et al. 2016). However, the approximation of the skull bone as a purely compressible medium has important limitations as it disregards the contributions of shear-mode conversion where a part of the ultrasound energy reaching the skull is converted in a transverse wave. The shear wave, which is often much slower than longitudinal waves but also much more attenuated (White et al. 2006), is converted back into a longitudinal wave when it reaches the skull cavity. Because the average speed of sound of shear waves in the skull is close to the speed of sound in water or soft tissue (Clement et al. 2004, White et al. 2006), accounting for this shear-mode conversion is of interest for applications targeting the cortex and subcortex brain tissue (Pichardo & Hynynen 2007). Recent studies have proposed transcranial sound transmission models that consider shear-wave propagation (Pichardo & Hynynen 2007, Pulkkinen et al. 2014) but the lack of precise correlation between the density and the shear speed of sound often limits the applicability of the models.
In this study, and inspired from a previous work from our team where we characterized the sound transmission in longitudinal transmission conditions (Pichardo et al. 2011), we established the relationship between apparent density calculated from CT scans and shear speed of sound. The viscoelastic wave equation (VWE) was adapted for the specific case of the transcranial ultrasound. The VWE is well suited to model sound propagation in solids as the bulk and shear properties are intrinsically considered. Special considerations were taken to model water-solid interfaces and the highly heterogenous distribution of bone density in the skull (Fry & Barger 1978, Clement & Hynynen 2002, Connor et al. 2002, Aubry et al. 2003, Pichardo et al. 2011). The VWE has been proposed previously for the study of sound transmission for cortical bone (Bossy et al. 2004). For transcranial propagation, the VWE has been used to distinguish absorption and scattering effects in longitudinal sound transmission (Pinton et al. 2012). To the best of our knowledge, there has not been work on applying the VWE to characterize shear wave propagation through the skull.
This study is divided in three main sections. The first section presents the VWE adapted for the specific case of transcranial ultrasound. The second section presents a validation of the VWE with measurements done on plastic plates with different thicknesses at angles of incidence of 0°, 15° and 50°. The third section used the VWE to characterize human skull shear speed of sound and attenuation of using samples of human calvaria at ultrasound frequencies of 270 and 836 kHz. Results indicated the high importance of accounting for the subject-to-subject density distribution on the resulting ultrasound propagation at different frequencies. These results will be highly valuable for a better design of ultrasound imaging and therapeutic applications.
2. Sound propagation model
2.1. Viscoelastic wave equation
Propagation of longitudinal and shear waves in heterogeneous skull bone was approximated considering the bone as a viscoelastic isotropic medium using the viscoelastic wave equation (VWE) system in Cartesian conditions:
| (1) |
where υi and σij are the displacement vectors and stress tensors, respectively, in each of i, j-directions: x, y or z. λ and μ are the Lamé parameters of the material.
2.2. Staggered-grid Finite Difference Time Difference (FDTD) solution
The VWE was solved using a 4th-order in space and 2nd-order in time (Levander 1988, Robertsson et al. 1994, Bohlen 2002) finite-difference time-difference (FDTD) implementation using a staggered grid arrangement of the displacement and tensor nodes in the evaluation domain (Virieux 1986). In this arrangement, displacement vectors and stress tensors are placed in half-spaced locations.
2.3. Attenuation effects
Attenuation was included in the simulations using a quality factor Q that indicates the number of wavelengths a wave propagates until losing amplitude by e−π (Blanch et al. 1995). Q was calculated for narrowband conditions and introduced in the viscoelastic equation system as stress relaxation times τl and τs for each of the longitudinal and shear waves, respectively (Bohlen 2002). Calculation of tensor stresses σij, where i = j (e.g., σxx, σyy, σzz), are modified to
| (2) |
where rij is the memory variable required to track dissipation effects and is calculated by
| (3) |
For i ≠ j (e‥g, σxy, σxz, σyz), the tensor stress equation becomes
| (4) |
with
| (5) |
τσ is a relaxation time common to τl and τs and is equal to ω−1, where ω is the central frequency in radians. Each of τl and τs were calculated by applying the so called Standard Linear Solid (SLS) modelling of the losses (Blanch et al. 1995). In our case, τk (where k = l, s) was calculated by minimizing the least square error EQk given by
| (6) |
where is the number of wavelengths λk = ckf−1 required to attenuate the amplitude by e−π with a given attenuation coefficient αk (Np·m−1). Q(τk, ω) is the SLS approximation for relaxation time τk and is given by
| (7) |
τk was established by solving (6) numerically over a narrow-band range of frequencies (±20% the central frequency). As noted in Bohlen (2002), the use of the SLS method requires to calculate the effective Lamé coefficients defining the material in function of the relaxation times τk using
| (8) |
where cl,0 and cs,0 are, respectively, the original longitudinal and shear speeds of sound and τl and τs their corresponding relaxation parameters.
2.4. Water-solid interfaces and heterogeneity of solid
The following averaging operators of the density ρ and shear modulus μ were used to model fluid-solid interfaces and allow heterogeneity of solid properties (Moczo et al. 2002):
| (9) |
where i, j and k are the indexes of the material grid in the x, y and z directions, respectively. When using averaging operators of the density ρ and shear modulus μ, the staggered grid method has been demonstrated to be very effective to model wave propagation in heterogenous media, including fluid-solid interfaces (Graves 1996, van Vossen et al. 2002, Moczo et al. 2002).
2.5. Numerical implementation
The FDTD algorithm, including stress relaxation times to model attenuation effects, was implemented as detailed in the Appendix A1 of Bohlen (2002). There exists an equivalent open source implementation of this method (http://www.simsonic.fr/, accessed July 27, 2016), but in this study a new implementation was made to use general-purpose graphics processing units (GPGPUs) because of the computing performance required. The numerical implementation allowed for the definition of voxel-level properties for ρ, cl, cs, αl and αs. A perfect matching layer (PML) condition was implemented as detailed in Collino & Tsogka (2001)†. Software modules were implemented using the CUDA specification for GPGPUs (Nvidia, Santa Clara, CA). Spatial step h was set to (one eighth of the smallest wavelength) and time step Δt to (a fraction based on the fastest speed of sound), both steps satisfying stability conditions (Bohlen 2002). Simulations were executed using a dual-Xeon E2640 (Intel, Santa Clara, CA) workstation with 32 GB RAM and a Titan X GPGPU (Nvidia, Santa Clara, CA) with 12 GB RAM.
3. Experimental validation
The staggered FDTD viscoelastic model was validated with experimental measurements of sound transmission through different types and thicknesses of plastic material with properties representative of transcranial ultrasound.
3.1. Material and Methods
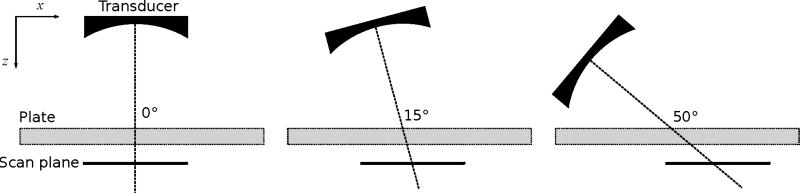
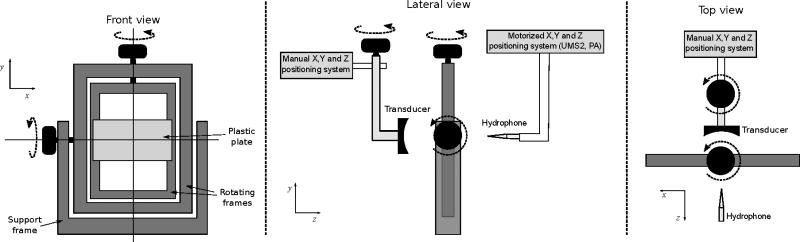
Figure 1 shows the experimental setup where a focused transducer (FUS Instruments, Toronto, Ontario, Canada), with both focal length and diameter of 5 cm was positioned such that the geometric focus was at the water-plate interface. A customized rotational arm was used to rotate the transducer at 0° to 15° and 50° around the geometrical focus. As shown in Figure 2, this arm was mounted in a manual 3D positioning stage. The plastic plate was mounted in a customized frame that allowed to adjust the orientation of the plate. For calibration of the distance and initial normal incidence conditions, the echo signal obtained with a pulse-receiver (DPR300, JSR Ultrasonics, Pittsford, NY USA) connected to the transducer was collected with an oscilloscope (WaveRunner 62Xi-A, LeCroy, Chestnut Ridge, NY, USA). The 3D positioning stage was used to adjust the distance between the transducer and the plate to 5 cm. Initial normal incidence conditions were obtained using the rotational stages by ensuring the pulse-echo signal had the same time-of-flight (less than 1% of deviation) over a region of ±2 cm in x and y directions.
Figure 1.
Experimental setup with plates of plastic material. The transducer geometrical focal point (focal length of 5 cm) was placed right at the interface with the plastic plate. A customized arm (not shown) allowed aligning the acoustic axis to achieve 0°, 15° and 50° with respect to the surface of the plastic plate. For each location, a scan plan was performed 2 cm below the plastic plate.
Figure 2.
Setup for the transducer positioning and customized frame used to hold the plastic plate for measurements. The setup uses a 3D positioning and rotational stages that allow aligning the plastic plate and adjusting the transducer orientation.
3.1.1. Plastic materials
Plates 25 cm × 6 cm and made of acrylic, polyethylene or polycarbonate were used for the testing. All those materials exhibit longitudinal speed of sound faster than water (Selfridge 1985). To demonstrate the accuracy of the proposed VWE model, the exact speed of sound of each of the tested samples was calculated using a time-of-flight technique in transmission mode. Attenuation effects were established using analytic formulas for sound transmission through solid material (Folds & Loggins 1977). Plates with industrial thickness labels of in and in were used. The real thickness of each plate was measured with a caliper. Table 1 shows the density (ρ) (Selfridge 1985) and measured thickness (d) for each plate.
Table 1.
Material properties of plastic plates used for the experimental validation
| Material |
ρ (kg·m−3) |
id |
d (mm) |
|---|---|---|---|
| Acrylic | 1190 | 1/8 | 2.88 |
| 1/4 | 5.71 | ||
|
| |||
| Polycarbonate | 1200 | 1/8 | 3.12 |
| 1/4 | 5.65 | ||
|
| |||
| Polyethylene (high density) | 950 | 1/8 | 3.16 |
| 1/4 | 6.28 | ||
3.1.2. Scanning conditions
Predicted acoustic fields were compared with measurements captured with a 0.2 mm-diameter needle hydrophone (Precision Acoustics, Dorset, UK) at angles of incidence of 0°, 15° and 50°. Experiments at 0° validated the model for purely longitudinal transmission. Experiments at 50° validated the model for purely shear transmission. Experiments at 15° validated the model for sound propagation where longitudinal transmission is expected to dominate. In total, eighteen (18) combinations of material-thickness-angle were tested.
The HIFU transducer was driven with 30 pulses at 1 MHz, an amplitude of 10 Vpp and a repetition rate of 1 kHz using a function generator (WS 8101, Tabor Electronics, Israel). As shown in Fig 2, the hydrophone was mounted in a computer-controlled 3D robotic arm (UMS2, Precision Acoustics, Dorset, UK). The hydrophone signal was pre-conditioned and amplified (HA2, Precision acoustics, Dorset, UK). Digitization of hydrophone signal was done with an oscilloscope (WaveRunner 62Xi-A, LeCroy, Chestnut Ridge, NY). A computer (XPS, Dell, Texas, USA) controlled the robotic arm and collected data from the oscilloscope using Matlab (R2011a, Mathworks, Bethesda, MD, USA).
For each combination of plastic plate and angle of incidence, 2D-(x, y) scan measurements were performed both in water-only and in the presence of the plastic plate. Each 2D scan consisted of a plan of 27.3 mm × 27.3 mm, with a spatial step of 0.7 mm (half wavelength). The location of this scanning was placed 2 cm below the plastic material (Fig. 1). A 2D-x, z scan with the plastic in place was also performed with 27.3 mm on the x direction and 13 mm on the z direction and a spatial step of 0.7 mm. This (x, z) scan was used to corroborate that the simulation model could predict accurately the refraction effects following the propagation direction.
A map of the experimental delay δ̂(x, y) was constructed using a direct correlator estimator (Nandi 1995)† between the signals with water only and in the presence of the plastic plate. A positive value of δ̂ indicated that longitudinal (faster than water) propagation dominated and was expected for 0° and 15°. A negative value of δ̂ indicated that shear wave propagation dominated and was expected for 50°. A map of the experimental pressure p̂(x, y) was constructed with the root-mean-squared pressure over time of the value measured by the hydrophone.
3.1.3. Estimation of speed of sound and attenuation using layered transmission theory
For an accurate validation of the viscoelastic modeling, and because there is a lack of reported values for shear speed of sound and attenuation for acrylic material, the values of longitudinal speed of sound (cl), shear speed of sound (cs), longitudinal attenuation (αl) and shear attenuation (αs) were established for each of the plates by comparing the data collected in presence and absence of the plastic plates. Analytic solutions for wave transmission through layered media (Folds & Loggins 1977, Brekhovskikh & Godin 1990, Pichardo et al. 2011) were used to calculate the speeds of sound and attenuation values (see appendix).
3.1.4. Simulation with the VWE system
Simulations with the VWE system were carried out by mimicking the same experimental conditions. The source function introduced in the simulation was established with measurements of the acoustic field on a perpendicular plane of 2.7 cm by 2.7 cm (0.7-mm step) situated 1 cm in front of the transducer and rotated to match experimental conditions. A series of virtual sensors were added to reproduce the experimental scanning conditions. The simulated delay δ(x, y) and pressure amplitude p(x, y) were calculated with the same methods as their experimental δ̂(x, y) and p̂(x, y) counterparts. The quality of the prediction for the prediction of p was established by comparing the transmitted powers P̂ and P (see appendix equation A.6) and the normalized mean square error Ξ given by
| (10) |
where N is the total number of observations in a scan plane. Comparison of P̂ and P is useful to establish a global precision of the model, while Ξ is useful to measure the similitude of the spatial distribution of the pressure between simulations and experiments.
3.2. Results
3.2.1. Acoustic properties of samples
Table 2 shows that measured acoustic properties for each of material tested were in good agreement with values available in the literature.
Table 2.
Measured and literature acoustic properties of plastic materials.
| Measured | ||||
|---|---|---|---|---|
| Material |
cl (m·s-1) |
cs (m·s−1) |
αl (Np·m−1) |
αs (Np·m−1) |
| Acrylic | 2848 | 1026 | 34.5 | 163 |
| Polycarbonate | 2200 | 1192 | 44 | 338 |
| Polyethylene (high density) | 2557 | 1011 | 23.12 | 256 |
| Reported in literature | ||||
|
| ||||
| Acrylic | 2750† | n/a | 14.7† | n/a |
| Polycarbonate | 2270†, 2160‡ | 950‡ | 57.3†, 34.5‡ | 575.75‡ |
| Polyethylene (high density) | 2430†, 2378‡ | 940‡ | 11‡ | 230‡ |
and
denote, respectively, values reported in (Selfridge 1985) and (Wu 1996).
Values from (Wu 1996) were extrapolated from Figures 4 and 6 in that study. Attenuation coefficients from (Selfridge 1985) were extrapolated here assuming a relationship αfβ, with f being the frequency in MHz and β = 1. “n/a” indicates not available reported values.
3.2.2. Prediction of pressure distribution and delay map with viscoelastic modeling
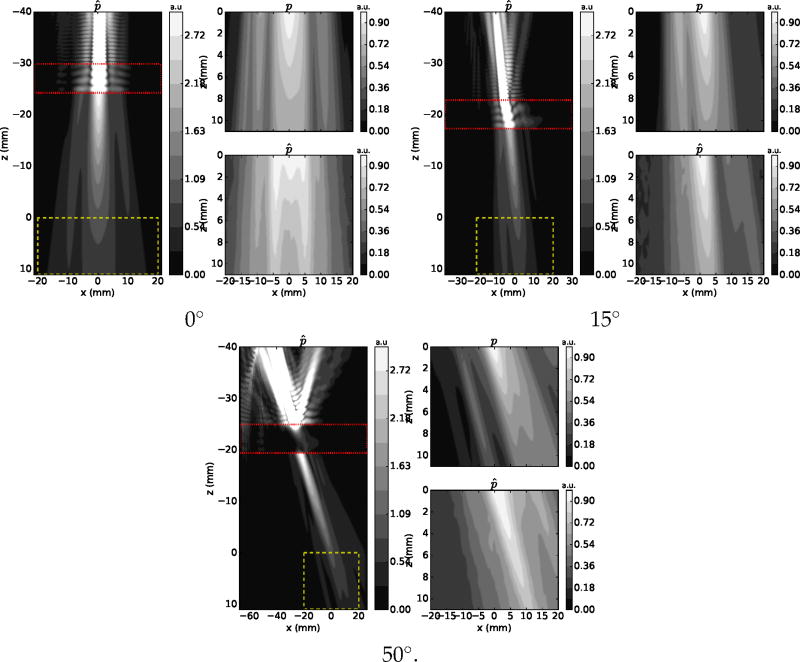
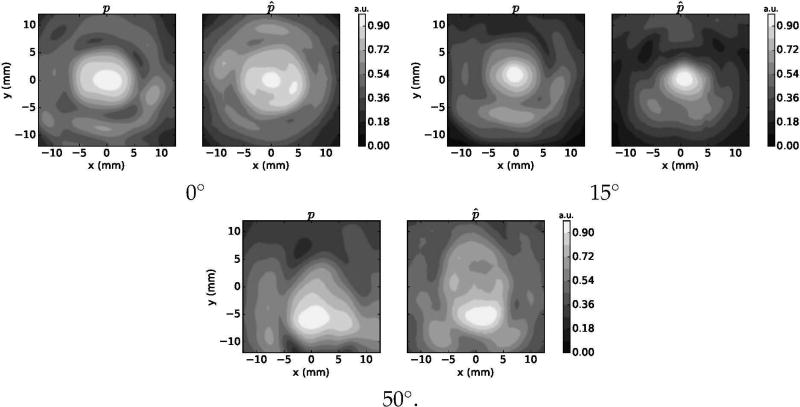
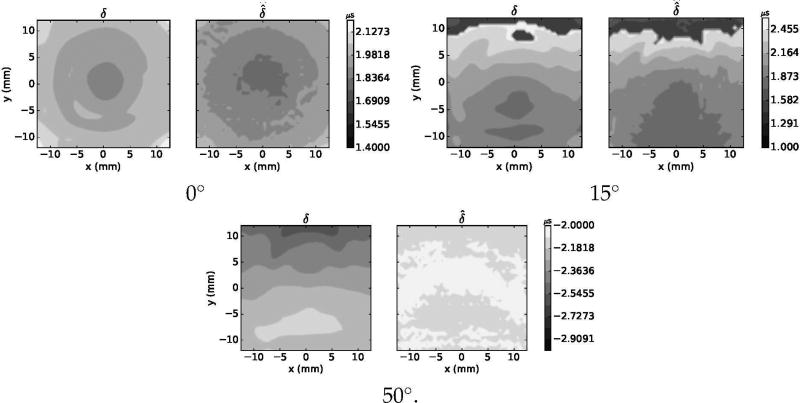
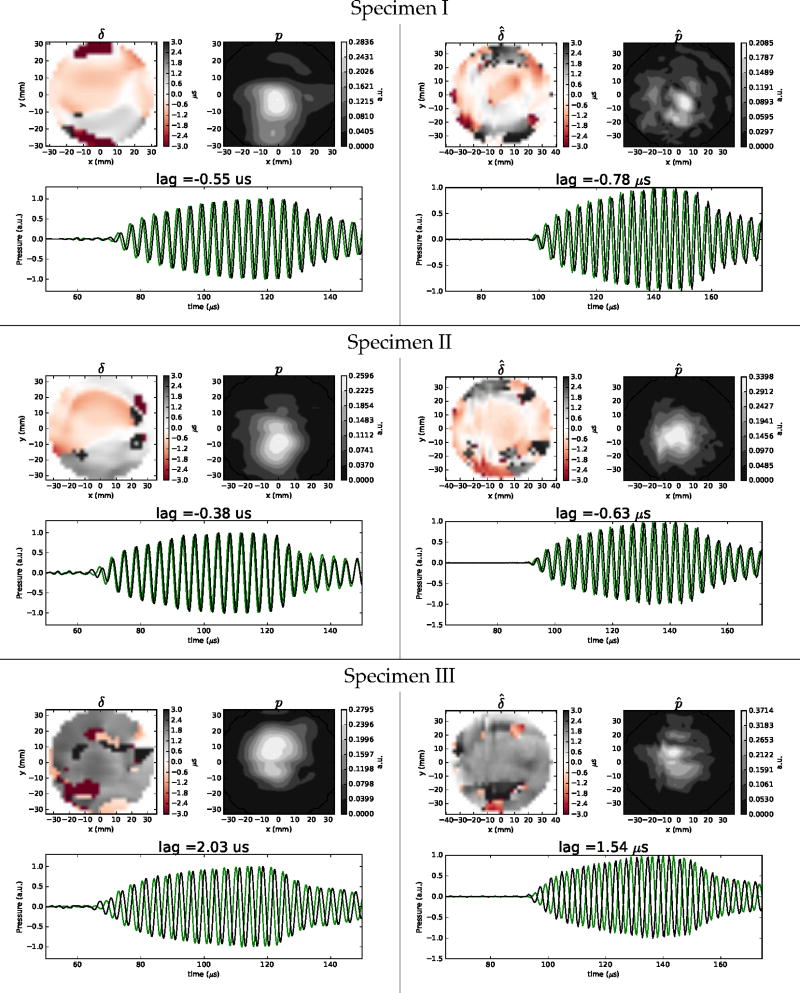
Results indicated that the viscoelastic model predicted accurately the pressure and delay distributions for all tested combination of material, thickness and angle of incidence. Figures 3 and 4 show, respectively, the experimental and simulated normalized pressure distribution on the central XZ, XY planes for the test with the 5.71-mm acrylic plate. Figure 5 shows the experimental and simulated XY delay maps. Refraction effects, where either longitudinal or shear propagation dominated, are clearly observable on the XZ planes.
Figure 3.
Pressure distribution maps on the XZ plane for simulations (p) and experiments (p̂) for acrylic material plates with a thickness of 5.71 mm. Maps are shown for each of the tested angle of incidence conditions. In each subplot, the image on the left shows a large view of the pressure map, including the plastic region (delineated by “⋯”). The zone enclosed by “--” indicates the region used to compare p and p̂. Pressure was normalized to the maximal pressure on the XY plane at Z = 0 mm.
Figure 4.
Pressure distribution maps on the XY plane for simulations (p) and experiments (p̂) for acrylic material plates with a thickness of 5.71 mm. Maps are shown for each of the tested angle of incidence conditions.
Figure 5.
Simulated (δ) and experimental (δ̂) delay distribution maps on the XZ plane for acrylic material plates with a thickness of 5.71 mm. Maps are shown for each of the tested angle of incidence conditions.
Table 3 shows the average of the experimental δ̂ and simulated δ delay, the respective transmitted powers P̂ and P, and the normalized error Ξ. The VWE model predicted accurately the delay either when longitudinal or shear propagation dominated. Longitudinal propagation (with positive delay) was clearly observed in all experiments and simulations with angles of incidence of 0° and 15°, while shear propagation dominated (negative delay) in all experiments and simulations with angle of incidence of 50°. All cases combined, the average (±s.d.) of the absolute difference |δ − δ̂| was 0.09(± 0.07) µs, which represents a precision of 9(±7)% of a period signal at 1 MHz. For the transmitted energy, the average of the absolute difference was 6.7(±4.8)%, while the normalized spatial error Ξ was 0.11(±0.03). These results indicated that our implementation of VWE is capable to reproduce the transmitted acoustic fields where either of each transmissions mode, longitudinal or shear, dominates.
Table 3.
Experimental and simulated spatial average of the delay (δ̂ and δ), transmitted energy (P̂ and P) and normalized spatial error (Ξ) for each material and combination of angle of incidence (ϕ) and thickness (d). The spatial averages of δ̂ and δ were calculated on the XY region showing normalized pressure greater than 0.5 in water-only conditions. P̂, P and Ξ were calculated over the whole XY plane of the measurements. |Δ| indicates the absolute of the difference.
| Material |
ϕ (°) |
d (mm) |
δ̂ (µs) |
δ (µs) |
|Δ| (µs) |
P̂ % |
P % |
|Δ| % |
Ξ |
|---|---|---|---|---|---|---|---|---|---|
| Acrylic | 0 | 2.88 | 1.0 | 1.0 | 0.0 | 76 | 63 | 13 | 0.13 |
| 5.71 | 1.85 | 1.94 | 0.09 | 57 | 42 | 15 | 0.11 | ||
|
| |||||||||
| 15 | 2.88 | 0.99 | 1.08 | 0.09 | 45 | 51 | 6 | 0.1 | |
| 5.71 | 1.9 | 1.98 | 0.08 | 42 | 36 | 6 | 0.14 | ||
|
| |||||||||
| 50 | 2.88 | −1.26 | −1.27 | 0.01 | 18 | 22 | 4 | 0.14 | |
| 5.71 | −2.09 | −2.29 | 0.20 | 14 | 9 | 5 | 0.15 | ||
|
| |||||||||
| Polyethylene | 0 | 3.16 | 0.87 | 0.92 | 0.05 | 87 | 68 | 19 | 0.09 |
| 6.28 | 1.72 | 1.88 | 0.16 | 67 | 61 | 6 | 0.12 | ||
|
| |||||||||
| 15 | 3.16 | 0.8 | 1 | 0.20 | 70 | 64 | 6 | 0.03 | |
| 6.28 | 2.15 | 1.94 | 0.21 | 56 | 53 | 3 | 0.11 | ||
|
| |||||||||
| 50 | 3.16 | −1.37 | −1.42 | 0.05 | 7.2 | 9 | 1.8 | 0.13 | |
| 6.28 | −2.6 | −2.68 | 0.08 | 3.3 | 2.5 | 0.8 | 0.1 | ||
|
| |||||||||
| Polycarbonate | 0 | 3.26 | 0.64 | 0.7 | 0.06 | 66 | 70 | 4 | 0.10 |
| 5.65 | 1.33 | 1.31 | 0.02 | 59 | 48 | 11 | 0.10 | ||
|
| |||||||||
| 15 | 3.12 | 0.68 | 0.75 | 0.07 | 60 | 50 | 10 | 0.11 | |
| 5.65 | 1.41 | 1.38 | 0.03 | 40 | 38 | 2 | 0.11 | ||
|
| |||||||||
| 50 | 3.12 | −0.76 | −0.79 | 0.03 | 4 | 10 | 6 | 0.11 | |
| 5.65 | −1.1 | −1.29 | 0.19 | 1.6 | 3.5 | 1.9 | 0.16 | ||
|
| |||||||||
| Mean (±s.d.) | 0.09(±0.07) | 6.7(±4.8) | 0.11(±0.03) | ||||||
4. Characterization of shear speed of sound and attenuation of human skull
Samples of human calvaria were mounted in a stereoscopic positioning system to control the angle of incidence of a focused acoustic beam and measurements were performed at different locations for two frequencies. The focus of the acoustic beam was placed at the water-skull interface to ensure a tight narrow beam crossing the skull barrier and consequently ensuring control of the incidence angle of the sound transmission. By using such configuration, the numerical model could be evaluated in conditions where shear propagation was expected to be present.
4.1. Material and Methods
4.1.1. Acquisition of acoustic insertion losses and delay
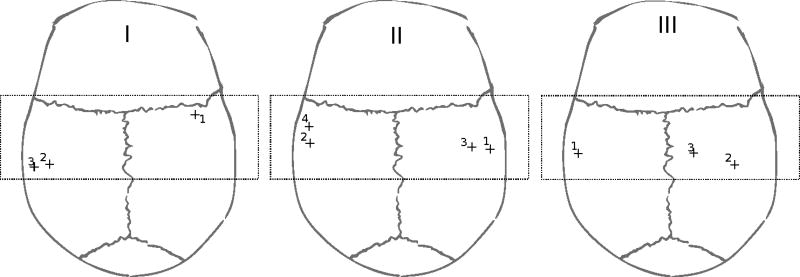
Ten (10) locations for measurements were selected on three specimens of preserved human calvaria. Specimens were obtained with an ethics approved protocol for human samples (School of Anatomy, University of Toronto) and were fixed in 5% formalin and never desiccated. Apparent density ρ was calculated from computed tomography (CT) scans (LightSpeed VCT, GE Healthcare, Chalfont St Giles, UK) (Connor et al. 2002) with the skulls immersed in degassed water and using a bone kernel. Both voxel resolution and slice thickness were set to 0.625 mm. Hounsfield units data of the water regions in each CT dataset were used to calibrate the water density and calculate the apparent density of the skull. Measurements of the acoustic field were performed with a 0.2-mm needle hydrophone (SN 1378, Precision Acoustics, Dorchester, Dorset, UK) to characterize both delay effects and transmitted power. Figure 7 shows the experimental setup used for measurements. Details for the skull preparation and selection of the location are detailed somewhere else (sections 2.2 and 2.3 in Pichardo et al. (2011), with the difference of an angle of incidence of 40°.
Figure 7.
Position of measurements on each skull. The dotted rectangle indicates the attainable region with the experimental set-up.
An in-house built gold-plated lead zirconate titanate (PZT) air-backed transducer with a diameter of 5 cm, a focal length of 10 cm and a central frequency of 254 kHz was electrically matched to work at 270 kHz or 836 kHz. The transducer was driven with a 15-cycles burst signal at 1-kHz repetition produced by a function generator (Wavetek 395, Fluke, Everett, WA, USA) and amplified to obtain an equivalent continuous 6W electrical power using a wide-band linear amplifier (275LC-CE, Kalmus, Bothell, WA, USA).
At each frequency tested, 2.5 cm × 2.5 cm scans perpendicular to the acoustic axis were performed at half-wavelength resolution in the presence and absence of the skull. The hydrophone was mounted on a computer-controlled 3D positioning system (Velmex, Bloomfield, NY). An oscilloscope (TDS3012B, Tektronix, Beaverton, OR, USA) recorded the hydrophone signal that was previously adapted (DC1/253, Precision Acoustics, Dorchester, Dorset, UK) and filtered using a passive 5 MHz low-pass filter (BLP-5+, Mini-circuits, Brooklyn, NY, USA). The hydrophone was positioned between 2 and 3 cm from the skull surface. The skull was positioned to ensure the focal point was placed right at the water-skull interface. Measurements were repeated after removing the skull. This procedure was then repeated for each location on the skull specimens for each frequency.
As done for the experiments with the plastic plates, maps of δ̂ and pressure p̂ were reconstructed. Also, the experimental relative transmitted acoustic power (P̂) was calculated (A.6).
4.1.2. Simulation with VWE and optimization for functions of shear speed of sound and attenuation
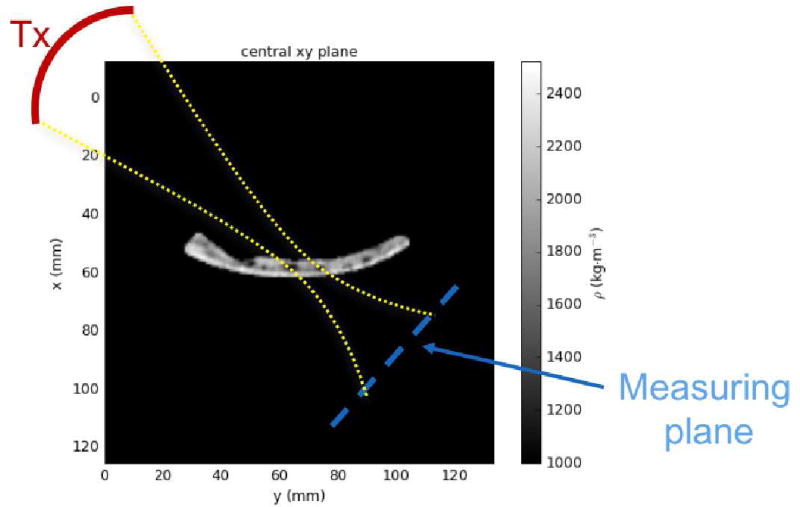
As for the plastic materials, the numerical setup reconstructed experimental conditions. Figure 6 shows a representation of the numerical setup. A 2D-scan of the incoming field towards the skull was measured with the hydrophone situated 2 cm in front of the transducer and was used as source in the VWE implementation. Virtual sensors were placed to recreate the same locations used for experimental measurements. Maps of simulated pressure p, delay δ and relative transmitted power P were calculated using the same methods used for experiments.
Figure 6.
Numerical set-up. Skull bone was oriented by aligning the region crossing the acoustic beam of the transducer (Tx) to the xz-plan. The measuring plan was reconstituted to match experimental conditions.
Following a similar approach as in Pichardo et al. (2011), a genetic optimization algorithm was used to establish the functions of cs(ρ) and αs(ρ) indirectly from measurements of delay and pressure. The measured acoustic fields in the presence and in the absence of skull samples were used for this optimization. The non-dominated sorting genetic algorithm (Deb et al. 2000) of the Pygmo library (http://esa.github.io/pygmo/index.html, accessed Oct 1, 2016) was used to minimize the sum of squared errors in the spatial distribution of the delay and pressure given by
| (11) |
and
| (12) |
respectively, for all i = 1‥N skull locations. Based on the results from our previous study (Pichardo et al. 2011), which showed a quasi-linear relationship between speed of sound and density, and others (Clement & Hynynen 2002, Aubry et al. 2003, Marsac et al. 2017) cs(ρ) was modeled as a linear function. Because of memory limitations in the graphics processor, the attenuation function was modeled as homogeneous (αs(ρ) = αs,0) in the skull ranging from 20 to 500 Np·m−1. The impact on the memory comes mostly from eq. (8) that requires a few hundred of GB of memory to keep the stability conditions if both cs(ρ) and αs(ρ) remain variable during the genetic optimization. Keeping attenuation constant while allowing arbitrary functions cs(ρ) for the skull bone produced a satisfactory compromise with an execution under the limit of 12 GB and with 32-bit float precision. Longitudinal speed of sound (cl) and average attenuation (αl = αl,0) was calculated from previous data (Pichardo et al. 2011). For 270 kHz, αl was set to 33 Np·m−1, while for 836 kHz it was set to 231 Np·m−1.
4.2. Results
4.2.1. Experimental delay and transmitted power
Figure 7 shows a scheme of all locations measured on the skull samples. Table 4 shows the average (± s.d.) of the angle of incidence ϕ, density ρ, delay δ̂ and transmitted acoustic power P̂ observed for each location and tested frequency. It is worth noting that specimen III showed positive delay for frequency of 270 kHz, indicating longitudinal propagation may still be dominating the sound transmission. However, when sonicating with a frequency of 836 kHz a negative delay, or closer to 0 µs, was observed for all samples. Also of importance, the average density of the specimen III was in overall 20% lower when compared to specimens I and II. The observations on the delay were also confirmed later during the simulations.
Table 4.
Experimental measurements on angle of incidence (ρ), density (ρ), delay (δ̂) and transmitted power (P̂) for each skull specimen, location (Loc.) and frequency. Data for location 1 in specimen I and a frequency of 836 kHz was discarded because poor conditioning of the captured signal.
| Specimen | Loc. | ϕ(°) | ρ (kg·m−3) | δ̂ (µ/s) | P̂ (%) | ||
|---|---|---|---|---|---|---|---|
| 270 kHz | 836 kHz | 270 kHz | 836 kHz | ||||
| I | 1 | 40.4(±7.2) | 2003(±320) | −0.38(±0.38) | − | 9.7 | − |
| 2 | 40.8(±6.2) | 1914(±321) | −0.34(±0.6) | 0.35(±0.46) | 1.9 | 0.26 | |
| 3 | 44.3(±13.9) | 1944(±330) | −0.1(±0.35) | 0.33(±0.17) | 2.8 | 0.92 | |
|
| |||||||
| II | 1 | 41.3(±8.6) | 1908(±266) | −0.57(±0.2) | −0.28(±0.16) | 10.7 | 0.97 |
| 2 | 39.7(±6.7) | 1914(±268) | −0.50(±0.146 | 0.03(±0.16) | 10.8 | 0.37 | |
| 3 | 40.6(±5.2) | 1927(±269) | −0.32(±0.29) | −0.02 (±0.6) | 9.4 | 0.55 | |
| 4 | 40.7(±8.2) | 1910(±270) | −0.4(±0.11) | −0.03(±0.07) | 10.9 | 0.8 | |
|
| |||||||
| III | 1 | 40.8(±8.9) | 1612(±235) | 0.76(±0.46) | −0.21 (±1.18) | 4.5 | 0.09 |
| 2 | 40.0(±5.5) | 1642(±212) | 1.61(±0.22) | −0.1 (±0.34) | 3.7 | 0.03 | |
| 3 | 40.2(±9.4) | 1669(±224) | 1.66(±0.16) | −0.01 (±0.78) | 8.7 | 0.16 | |
4.3. Optimal functions of cs and αs
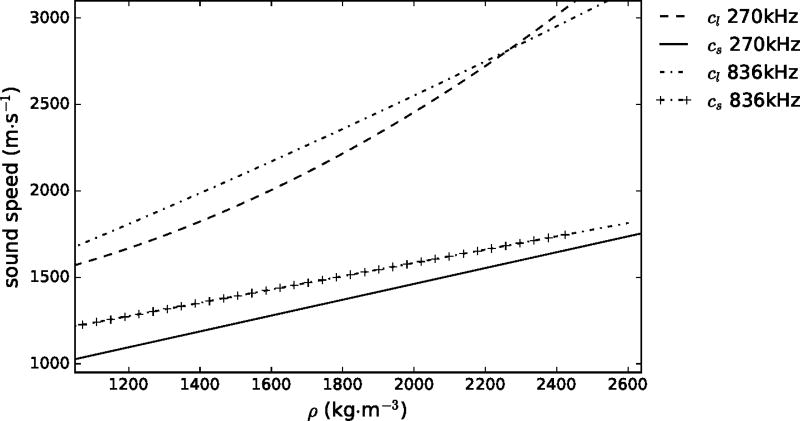
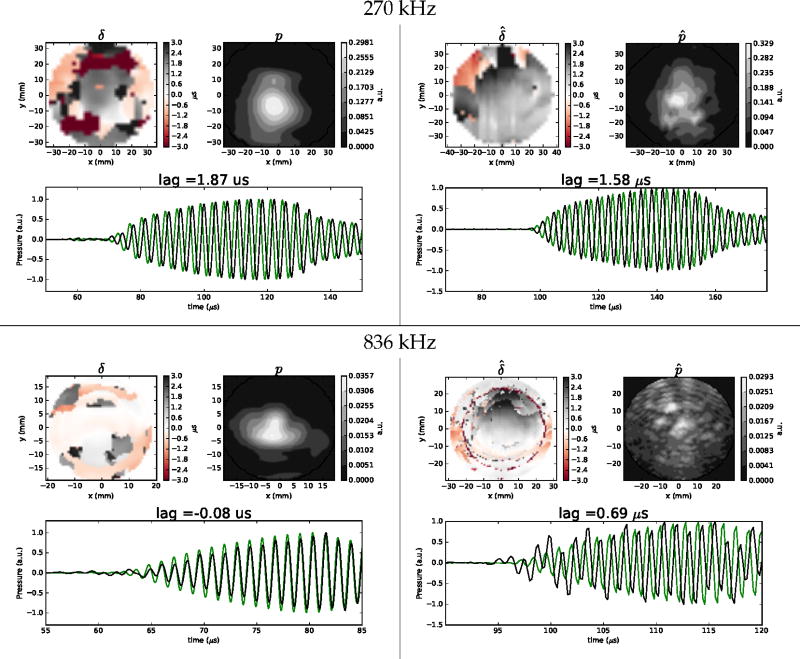
Figure 8 shows the optimal functions of shear speed of sound for 270 kHz and 836 kHz, along with the previously defined functions for longitudinal speed of sound (Pichardo et al. 2011). The optimal function cs(ρ) for 270 kHz was cs(ρ) = 0.458ρ + 545.52, while for 836 kHz was cs(ρ) = 0.386ρ + 815.51. The observed shear speeds of sound at different frequencies followed a similar trend as their longitudinal counterparts where shear speed at 836 kHz was higher than for 270 kHz. The optimal value of attenuation αs that predicted the transmitted energy among all locations for frequencies of 270 kHz and 836 kHz was, respectively, 57 Np·m−1 and 373 Np·m−1. Figures 9 and 10 show examples of delay and pressure maps for each of the skulls and each of the tested frequencies. For a frequency of 270 kHz (Fig 9), the VWE and the optimal functions of cl, cs, αl and αs predicted both qualitatively and quantitatively the delay and pressure distributions. For specimens I and II, which showed a negative delay, experiments and simulations showed transmitted fields slightly refracted towards the −y direction. For specimen III, which showed a positive delay, the measured and predicted pressured distribution was slightly refracted towards the +y direction.
Figure 8.
Optimal longitudinal (cl) and shear (cs) speed of sounds in function of density (ρ) for frequencies of 270 kHz and 836 kHz. cl was calculated functions established in Pichardo et al. (2011). cs was obtained after executing the minimization algorithm.
Figure 9.
Examples of simulated (left) and experimental (right) maps of delay and pressure for a frequency of 270 kHz for each skull. Plots of pressure vs. time at central location are also shown where measurements in water and in the presence skull are shown, respectively, in green and black.
Figure 10.
Examples of experimental (right) and simulated (left) maps of delay and pressure for a frequency of 836 kHz for each skull. The locations are the same shown for Fig 9. Plots of pressure vs. time at central location are also shown where measurements in water and in the presence skull are shown, respectively, in green and black.
For a frequency of 836 kHz (Fig 10), the pressure distribution was mainly quantitatively accurate for the total transmitted energy, but an important degradation of the precision of the spatial distribution was observed. A similar situation was observed for the delay distribution. It is worth noting that when compared with experiments with a frequency of 270 kHz, measurements at 836 kHz showed the presence of reverberations as the signal clearly showed trends of deformation. A potential reason of these reverberations may originate from the fact that the porous consistency of the trabecular section may increase its influence as a function of the frequency Compared to experimental pressure distributions at 270 kHz, which showed highly concentrated acoustic fields, the coherence of the experimental transmitted fields at 836 kHz was severely affected.
Table 5 shows the comparison of the experimental δ̂ and simulated δ average delay and the respective transmitted (P̂ and P) and spatial error in pressure (Ξ). For 270 kHz, the VWE model predicted accurately the expected delay with an overall absolute error of 0.19(±0.1) µs, which represents an expected error of 5(±2.7)% in terms of wavelength. For 836 kHz, the overall absolute error in the delay was 0.21(±0.2) µs, which represents an expected error of 17(±16)% in terms of wavelength.
Table 5.
Experimental and simulated spatial average of the delay (δ̂ and δ) and transmitted energy (P̂ and P) for the different skull locations. The spatial averages of δ̂ and δ were calculated on the XY region showing normalized pressure greater than 0.5 in water-only conditions. The transmitted powers P̂ and P were calculated over the whole XY plane of the measurements. |Δ| indicates the absolute of the difference.
| 270 kHz | ||||||||
|---|---|---|---|---|---|---|---|---|
| Specimen | Loc. |
δ̂ (µs) |
δ (µs) |
|Δ| (µs) |
P̂ % |
P % |
|Δ| % |
Ξ |
| I | 1 | −0.38 | −0.14 | 0.23 | 9.7 | 8.6 | 1.02 | 0.23 |
| 2 | −0.34 | −0.48 | 0.13 | 2.9 | 6.5 | 4.56 | 0.37 | |
| 3 | −0.1 | −0.09 | 0.01 | 2.8 | 1.9 | 0.9 | 0.38 | |
|
| ||||||||
| II | 1 | −0.57 | −0.31 | 0.25 | 10.7 | 6.0 | 4.7 | 0.32 |
| 2 | −0.50 | −0.34 | 0.16 | 10.8 | 6.12 | 4.7 | 0.58 | |
| 3 | −0.32 | −0.34 | 0.02 | 9.4 | 7.7 | 1.7 | 0.20 | |
| 4 | −0.4 | −0.2 | 0.20 | 10.9 | 9.0 | 1.8 | 0.26 | |
|
| ||||||||
| III | 1 | 0.76 | 1.06 | 0.29 | 4.5 | 6.6 | 2.08 | 0.21 |
| 2 | 1.61 | 1.97 | 0.35 | 3.7 | 16.7 | 13 | 0.17 | |
| 3 | 1.66 | 1.93 | 0.27 | 8.7 | 8.7 | 0.0 | 0.15 | |
|
| ||||||||
| Mean (±s.d.) | 0.19(±0.10) | 3.46(±3.56) | 0.29(±0.12) | |||||
| 836 kHz | ||||||||
|---|---|---|---|---|---|---|---|---|
| Specimen | Loc. |
δ̂ (µs) |
δ (µs) |
|Δ| (µs) |
P̂ % |
P % |
|Δ| % |
Ξ |
| I | 1 | – | – | – | – | – | – | |
| 2 | 0.35 | 0.17 | 0.18 | 0.26 | 0.19 | 0.08 | 0.36 | |
| 3 | 0.33 | 0.39 | 0.06 | 0.92 | 0.06 | 0.87 | 0.40 | |
|
| ||||||||
| II | 1 | −0.28 | 0.37 | 0.65 | 0.97 | 0.35 | 0.62 | 0.37 |
| 2 | 0.03 | 0.37 | 0.33 | 0.37 | 0.13 | 0.24 | 0.57 | |
| 3 | −0.02 | 0.05 | 0.07 | 0.55 | 0.11 | 0.44 | 0.34 | |
| 4 | −0.03 | 0.39 | 0.43 | 0.8 | 0.22 | 0.59 | 0.28 | |
|
| ||||||||
| III | 1 | −0.21 | −0.27 | 0.06 | 0.09 | 0.23 | 0.13 | 0.36 |
| 2 | −0.1 | −0.06 | 0.04 | 0.03 | 0.14 | 0.1 | 0.30 | |
| 3 | −0.01 | 0.09 | 0.1 | 0.16 | 0.15 | 0.02 | 0.34 | |
|
| ||||||||
| Mean (±s.d.) | 0.21(±0.20) | 0.34(±0.28) | 0.37(±0.08) | |||||
4.3.1. Performance of numerical implementation
For simulations at 270 kHz, a typical simulated 3D volume of 15 cm × 14 cm × 8.8 cm (including PML boundaries) required a domain of 170×163×100 grid points (2.77 × 106 points in total) using h = 0.89mm. Using a sonication length of 150 µs with Δt = 0.0256 µs required 5864 time iterations for a total computing time of 34 s, which translated to a performance of 478 × 106 VWE finite-difference operations per second. For a simulation at 836 KHz, a 3D volume of of 10 cm × 9.8 cm × 4.7 cm required a domain of 354×342×166 grid points (20.1 × 106 points in total) using h = 0.287mm. Using a sonication length of 100 µs with Δt = 0.02 µs required 5000 time iterations for a total computing time of 217s, which translated to a performance of 463×106 VWE finite-difference operations per second.
5. Discussion
In this study, we adapted the viscoelastic equation system to predict sound transmission through the human skull. Results shown here demonstrated, for the first time to the best of our knowledge, that a single numerical model is capable to predict both longitudinal and shear propagation for the human skull, especially for low frequency transmission. The predictions using the optimal values of longitudinal and shear speeds of sound will help to predict much more accurately transcranial sound transmission.
The effect of formalin fixation in the acoustic properties skull may represent a source of incertitude. For this specific study with human samples, skipping the formalin fixation was unfortunately not an option as specimens were obtained from fresh cadavers and the fixation was a protocol requirement for preservation of the original tissue material. However, prior studies have shown that formalin fixation does not have a major impact on the skull properties either in human (Fry & Barger 1978) or animal skull bone (White et al. 2007).
An important limitation of the current implementation was the choice of using a global attenuation coefficient for the skull bone. Previous studies have clearly showed the importance of correlating the attenuation coefficient to the density (Connor et al. 2002, Pichardo et al. 2011). As mentioned in the methods, the limitation in this study obeyed mainly because in the WVE the attenuation effect was included as a quality factor that introduces dispersion effects that need to be compensated (Bohlen 2002). The compensation in (8) made that the spatial step needs to be adjusted to ensure stability conditions. Because the WVE requires 30 3D-matrices to preserve σij, υi and rij at times t and t − Δt (15 matrices per each t and t − Δt), the number of simulations to execute in the tens of thousands and the limited GPU memory, choosing a global attenuation coefficient was mostly a necessity. However, the results in this study indicated that the choice of a global attenuation was precise enough to predict the overall transmitted power (Table 5). We anticipate that the use of more advanced computing setups (such as multiple GPU-based systems) with more GPU memory will mitigate this limitation in future studies.
5.1. Influence of the frequency
As shown in Figs 9 and 10, experimental measurements of the pressure distribution showed remarkable differences in terms of the coherence in the transmitted acoustic field depending on the frequency. The acoustic fields at 270 kHz showed well concentrated acoustic fields, slightly shifted and in good agreement given the refraction effects caused by the skull bone. This result indicates clearly that low-frequency ultrasound is preferred to ensure coherent transmitted acoustic fields using shear propagation. This result is highly relevant for low-frequency applications such as neuromodulation (King et al. 2013), where frequencies in the range of 270 kHz requires a very small pressure intensity to produce an effect. Also, the results in this study indicate that the proposed implementation of VWE is a prediction tool precise enough for frequencies close to 270 kHz, which will allow using this model in studies for refocusing ultrasound using both shear and longitudinal sound transmission, especially when targeting the cortex and sub-cortex brain tissue.
For experiments with a frequency of 836 kHz, the degree of coherence was severely reduced. The deformation of the captured signal (Fig 10) suggests that the dephasing caused by the porosity of the trabecular bone was important enough to disrupt the coherence of the transmitted acoustic field. The observed deformation of the signal (Fig 10) is very characteristic of transmission measurements through anisotropic bone materials with large angles of incidence (Hughes et al. 1999). This deformation was not observed for any experiments with a frequency of 270 kHz. However, estimation of the experimental delay δ̂ (Table 4) showed values close to 0 µs, which suggested clearly an overall slower speed of sound compared to longitudinal propagation. Using the optimal functions for longitudinal and shear speed of sound, Table 6 shows the average speeds of sound and their corresponding wavelengths for the cortical, trabecular and whole skull bone. The values of shear wavelengths for 836 kHz in the trabecular layer are smaller than the average thickness of trabecular layer bone in the human skull of 2.7 mm (McElhaney et al. 1970), while the wavelength for 270 kHz is roughly twice this thickness. These observations can explain the significant loss of coherence observed for 836 kHz as the porous material will have much more effect (Hughes et al. 1999). For this frequency, and as indicated by the higher value of Ξ for 836 kHz compared to 270 kHz, the VWE with isotropic conditions was unable to predict with enough precision the spatial distribution of the pressure. Future improvements for the current implementation can explore including anisotropic conditions, such as suggested in many studies concerning sound transmission through cancellous bone using the Biot model for porous materials (Haire & Langton 1999), but such effort will require very different approach. Precision of the model improves for a frequency of 270 kHz, especially in terms of prediction of the spatial distribution of the pressure. Because the larger wavelength in such conditions, results indicate that modeling the skull bone as an isotropic medium is adequate for low-frequency conditions.
Table 6.
Average of the shear (cs) and longitudinal (cl) speeds of sound, and their respective wavelengths (λs and λl), of the cortical, trabecular and whole bone for each specimen using the optimal functions and the density distribution of each specimen. Values were calculated over a cross section area of 1 cm2 centered at the skull location where focused beam was concentrated.
| 270 kHz | 836 kHz | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Specimen |
cs (m·s−1) |
λs (mm) |
cl (m·s−1) |
λl (mm) |
cs (m·s−1) |
λs (mm) |
cl (m·s−1) |
λl (mm) |
|
| Cortical | I | 1577 | 5.8 | 2796 | 10.3 | 1758 | 2.1 | 3008 | 3.6 |
| II | 1498 | 5.55 | 2562 | 9.5 | 1674 | 2.0 | 2786 | 3.3 | |
| III | 1313 | 4.8 | 2095 | 7.76 | 1545 | 1.84 | 2456 | 2.93 | |
|
| |||||||||
| Trabecular | I | 1227 | 4.55 | 1919 | 7.1 | 1574 | 1.86 | 2538 | 3.03 |
| II | 1365 | 5.05 | 2220 | 8.2 | 1252 | 1.5 | 1756 | 2.1 | |
| III | 1200 | 4.44 | 1850 | 6.85 | 1327 | 1.58 | 1928 | 2.3 | |
|
| |||||||||
| Whole skull | I | 1440 | 5.33 | 2434 | 9 | 1574 | 1.88 | 2538 | 3.03 |
| II | 1423 | 5.27 | 2375 | 8.8 | 1557 | 1.86 | 2491 | 2.98 | |
| III | 1297 | 4.8 | 2064 | 7.64 | 1449 | 1.73 | 2224 | 2.6 | |
5.2. Influence of the density distribution specific to each specimen
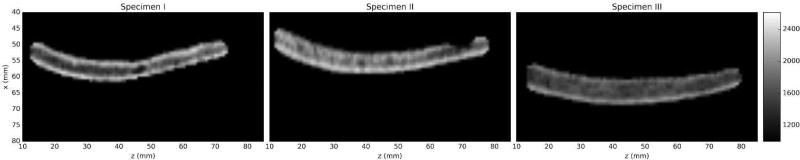
As shown in Tables 4, 5 and Fig 9, it is worth noting that specimen III did not show dominating shear wave transmission when using a frequency of 270 kHz. As shown in Fig 11 and indicated in Table 4, closer inspection of ρ indicated that specimen III showed an average value (± s.d.) of 1640(±210) kg·m3, which is 20% less when compared to the specimens I and II that showed, respectively, values of 1910(±320) kg·m3 and 1910(±270) kg·m3. Figure 11 also shows a less differentiated cortical bone for specimen III. When coupling the distribution of ρ for specimen III with the cl(ρ) for 270 kHz in Fig 8 (Pichardo et al. 2011), results in Table 6 indicated that the longitudinal speed of sound in the cortical bone was 2090 m·s−1. The cortical bone plays an very important role as this is the material in contact with the water interface. Using a simplified homogeneous model and the Snell’s law, this average speed of sound indicates that the critical angle for specimen III was 45°, which was higher than the tested angle of incidence of 40°. This observation means that it is completely expected that longitudinal propagation should dominate in the tested conditions for specimen III. Specimens I and II showed a critical angle of 32° and 35°, respectively.
Figure 11.
Central view of density map for each of specimens. Units are in kg·m−3
These results have very important implications as they reinforce greatly that considering the acoustic properties at voxel level is fundamental to ensure a correct prediction of transcranial sound transmission. These results also confirm that the optimal functions for the speeds of sound as a function of the frequency and density information established in the present study and in our previous work (Pichardo et al. 2011) are important tools to better understand transcranial sound transmission. This is observed in the results of specimen III at 836 kHz which showed a negative delay, instead of positive delay observed at 270 kHz. As shown in Table 6, the average value of longitudinal speed using the optimized function was 2456 m·s−1, which translated in a critical angle of 37°. Under these conditions, it was expected that specimen III could show shear propagation at 836 kHz as it was shown in the experimental and model results.
5.2.1. Applicability for other skull specimens
One challenge when performing studies based on the specificity of sample information is the limited number of specimens. There is a risk that the optimal functions can be applicable mainly for the specimens used during the optimization. A supplemental series of acquisitions in three locations were performed with a specimen that was not part of the optimization study. Figure 12 shows an example of the experimental and predicted maps of delay and pressure for 270 kHz and 836 kHz for this specimen. Table 7 shows the experimental and simulated average of delay, transmitted power and spatial error in pressure. Results indicated that the optimal functions were able to predict the transcranial propagation for the new specimen with the similar level of error in spatial distribution (Ξ) as in the first specimens (I, II, and III), but a small degradation in the overall precision was observed. As more samples are added to a library of specimens, the optimization process described above can be re-executed to find the functions that minimizes the error between simulation and observations across all specimens.
Figure 12.
Examples of simulated (left) and experimental (right) maps of delay and pressure for a frequency of 270 kHz (top) and 836 kHz for specimen IV. Plots of pressure vs. time at central location are also shown measurements in water and in the presence skull are shown, respectively, in green and black.
Table 7.
Experimental and simulated spatial average of the delay (δ̂ and δ) and transmitted energy (P̂ and P) for specimen IV. The spatial averages of δ̂ and δ were calculated on the XY region showing normalized pressure greater than 0.5 in water-only conditions. The transmitted powers P̂ and P were calculated over the whole XY plane of the measurements. |Δ| indicates the absolute of the difference.
| 270 kHz | ||||||||
|---|---|---|---|---|---|---|---|---|
| Specimen | Loc. |
δ̂ (µs) |
δ (µs) |
|Δ| (µs) |
P̂ % |
P % |
|Δ| % |
Ξ |
| IV | 1 | −1.29 | −0.36 | 0.93 | 22 | 3.7 | 18 | 0.32 |
| 2 | 1.88 | 0.82 | 1.06 | 12 | 3.6 | 8.6 | 0.32 | |
| 3 | 1.53 | 1.85 | 0.32 | 7.3 | 7.4 | 0.15 | 0.18 | |
|
| ||||||||
| Mean (±s.d.) | 0.77(±0.32) | 9.1(±7.5) | 0.27(±0.07) | |||||
| 836 kHz | ||||||||
|---|---|---|---|---|---|---|---|---|
| Specimen | Loc. |
δ̂ (µs) |
δ (µs) |
|Δ| (µs) |
P̂ % |
P % |
|Δ| % |
Ξ |
| IV | 1 | 0.69 | 0.23 | 0.46 | 4.4 | 0.8 | 3.6 | 0.29 |
| 2 | 0.69 | 0.22 | 0.47 | 4.2 | 0.4 | 3.8 | 0.44 | |
| 3 | 0.94 | −0.04 | 1.00 | 0.07 | 0.01 | 0.02 | 0.48 | |
|
| ||||||||
| Mean (±s.d.) | 0.65(±0.27) | 2.5(±2) | 0.4(±0.08) | |||||
5.2.2. Advantages of VWE for transcranial ultrasound modeling
It is worth mentioning that a previous study (Pinton et al. 2012) used also the VWE to study the transmission of ultrasound through skull bone. In that study, authors used the VWE to differentiate the absorption from scattering in the attenuation of ultrasound in longitudinal sound transmission conditions at 1 MHz. The main differences with the present study include the incident angle conditions (around 0°† vs. 40° here), the resolution of CT data (7.46 µm vs. 625 µm here) and the approach to include attenuation effects (single mechanism for both longitudinal and shear attenuation vs. separate mechanisms here). Also, the objectives of each study were very different. Regardless of these differences, there are very important aspects in each study that highlights the value of the VWE for transcranial ultrasound modeling. In Pinton et al. (2012), thanks to the much higher CT-resolution, the scattering of ultrasound crossing the trabecular bone could be better modeled and differentiated from the pure ultrasound absorption. In the present study, the larger voxel size does not allow the separation of scattering and absorption effects, so the results for attenuation in the present study must be taken only in the context of global attenuation. However, the larger voxel size is compatible to CT-scanning conditions in clinic, which allows transposing results for potential studies in humans. At global level, the results of the global attenuation in longitudinal conditions are comparable to our previous study: 16.6 dB/cm for 1 MHz in Pinton et al. (2012) and 20 dB/cm for 836 kHz in (Pichardo et al. 2011), which is critical for a correct modeling of ultrasound reaching the brain tissue.
6. Conclusions
In this study, we presented a model for transcranial ultrasound propagation that can predict both shear and longitudinal dominant transmission. This model is based on the viscoelastic wave equation assuming isotropic conditions and includes in its formulation attenuation affects and handling of liquid-solid interfaces. The validity of the model to predict longitudinal and shear dominant ultrasound transmission was firstly validated with measurements performed with plastic materials plates showing acoustic properties comparable to human skull and tests with angles of incidence of 0°, 15° and 50°. Transcranial ultrasound measurements with an angle of incidence of 40° were performed in ten locations over three skull samples and for frequencies of 270 kHz and 836 kHz. The optimal functions of shear speed of sound and global attenuation as a function of skull density based on computed tomography scans and frequency were established using a genetic optimization. Experimental results indicated that sound transmission with 270 kHz ensured a much more coherent transmitted acoustic field. Degradation of coherence with 836 kHz was linked to the shorter wavelength, which was smaller than the average size of the trabecular layer in the skull bone. The proposed model predicted accurately the ultrasound transmission at a frequency of 270 kHz with an expected error of 5(±2.7)% in terms of the wavelength in water. For 836 kHz, the model predicted accurately only at global level with an error of 17(±16)%. The proposed model, optimal functions for the speed of sound and the experimental measurements offered new important insights regarding the high relevance of accounting for the specific properties of each specimen on transcranial ultrasound transmission. These results and new model will be very valuable tools for the future development of transcranial applications for ultrasound therapy and imaging.
Acknowledgments
Authors acknowledge support of the Ministry of Research of Ontario, Canada (Ontario Research Fund), the Natural Sciences and Engineering Research Council of Canada (NSERC, Discovery Program), grant (No. R01-EB003268) from the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (K.H.), the Canada Research Chair program (K.H.), and Consejo Nacional de Ciencia y Tecnología (Conacyt, México, Scholarship Program) for the support to conduct this research.
Appendix
Estimation of acoustic properties of plastic material using layered transmission theory
cl and cs were calculated by averaging the speeds of sound calculated for each combination of θ and d with
| (A.1) |
where c0 is the speed of sound in water (1482 m/s), dn is the thickness of the plate, the subscript k denotes the type of experiment (l or s) and ‖SA is the spatial average of the delay. cl was calculated with θm ∈ [0°, 15°] and dn for each of two measured thickness. In total, four combinations of measurements were used to calculate cl. Analogously, cs was calculate with θm ∈ [50°] and dn using data of the two tested thicknesses.
Attenuation coefficients of the plastic materials were calculated by minimizing the absolute value of the error E(θ) given by
| (A.2) |
between the theoretical (P) and experimental (P̂) transmitted acoustic power ratio in the presence of the solid layer with the angle of incidence θ. P(θ) was calculated with the product of TT*, where T is the complex ultrasound transmission coefficient, including attenuation effects, and T* its conjugate of a layer of solid material surrounded by water (Folds & Loggins 1977). T was calculated with
| (A.3) |
where coefficients Mij were calculated for the case of a single layer of solid material with an angle of incidence θ as detailed in (Folds & Loggins 1977). In (Folds & Loggins 1977), k2 and k2 are the complex wavenumbers for longitudinal and shear propagation in the solid, respectively, and were calculated with
| (A.4) |
and
| (A.5) |
where ω is the ultrasound frequency in radians, αl and αs are, respectively, the longitudinal and shear attenuation coefficients (Np·m−1).
The normalized experimental transmitted power P̂(θ) was calculated with
| (A.6) |
where and are the root-mean-squared pressure over time of the value measured with the hydrophone of the pressure in the presence of solid and in water-only conditions, respectively. dx and dy are the spatial step of scan, which both are 0.7 mm. The function optimize.least_squares of Scipy library (Jones et al. 2001) was used to apply a least-square optimization algorithm to fit the attenuation coefficients that minimized E including all measurements for the same material plastic.
Footnotes
Subsection “The Virieux finite-difference scheme“.
Section III-a "Direct Correlator (DC) Estimator"
The incident angle was not reported but it can be inferred from illustrations of the setup that experiments were done in conditions close to normal incidence.
Contributor Information
Samuel Pichardo, Thunder Bay Regional Research Institute, Thunder Bay, ON, Canada; Electrical Engineering, Physics, Biotechnology, Lakehead University, Thunder Bay, ON, Canada.
Carlos Moreno, Universidad Nacional Autonoma de México, Mèxico City, México.
Andrew Drainville, Biotechnology, Lakehead University, Thunder Bay, ON, Canada.
Vivian Sin, Sunnybrook Research Institute, Toronto, ON, Canada.
Laura Curiel, Electrical Engineering, Physics, Biotechnology, Lakehead University, Thunder Bay, ON, Canada; Thunder Bay Regional Research Institute, Thunder Bay, ON, Canada.
Kullervo Hynynen, Sunnybrook Research Institute, Toronto, ON, Canada.
References
- Almquist S, Parker DL, Christensen DA. Journal of Therapeutic Ultrasound. 2016;4(1):30. doi: 10.1186/s40349-016-0074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aubry JF, Tanter M, Pernot M, Thomas JL, Fink M. The Journal of the Acoustical Society of America. 2003;113(1):84–93. doi: 10.1121/1.1529663. [DOI] [PubMed] [Google Scholar]
- Blanch JO, Robertsson JO, Symes WW. Geophysics. 1995;60(1):176–184. [Google Scholar]
- Bohlen T. Computers & Geosciences. 2002;28(8):887–899. [Google Scholar]
- Bossy E, Talmant M, Laugier P. The Journal of the Acoustical Society of America. 2004;115(5):2314–2324. doi: 10.1121/1.1689960. [DOI] [PubMed] [Google Scholar]
- Brekhovskikh LM, Godin OA. Springer-Verlag New York chapter 4. Plane-wave reflection from boundaries of solids. 1990:87–112. [Google Scholar]
- Clement G, Hynynen K. Ultrasound in medicine & biology. 2002;28(5):617–624. doi: 10.1016/s0301-5629(02)00503-3. [DOI] [PubMed] [Google Scholar]
- Clement G, White P, Hynynen K. The Journal of the Acoustical Society of America. 2004;115(3):1356–1364. doi: 10.1121/1.1645610. [DOI] [PubMed] [Google Scholar]
- Collino F, Tsogka C. Geophysics. 2001;66(1):294–307. [Google Scholar]
- Connor CW, Clement GT, Hynynen K. Phys. Med. Biol. 2002;47:3925–3944. doi: 10.1088/0031-9155/47/22/302. [DOI] [PubMed] [Google Scholar]
- Deb K, Agrawal S, Pratap A, Meyarivan T. International Conference on Parallel Problem Solving From Nature. Springer; 2000. pp. 849–858. [Google Scholar]
- Elias WJ, Lipsman N, Ondo WG, Ghanouni P, Kim YG, Lee W, Schwartz M, Hynynen K, Lozano AM, Shah BB, et al. New England Journal of Medicine. 2016;375(8):730–739. doi: 10.1056/NEJMoa1600159. [DOI] [PubMed] [Google Scholar]
- Folds D, Loggins C. The Journal of the Acoustical Society of America. 1977;62(5):1102–1109. [Google Scholar]
- Fry F, Barger J. The Journal of the Acoustical Society of America. 1978;63(5):1576–1590. doi: 10.1121/1.381852. [DOI] [PubMed] [Google Scholar]
- Graves RW. Bulletin of the Seismological Society of America. 1996;86(4):1091–1106. [Google Scholar]
- Haire T, Langton C. Bone. 1999;24(4):291–295. doi: 10.1016/s8756-3282(99)00011-3. [DOI] [PubMed] [Google Scholar]
- Hughes ER, Leighton TG, Petley GW, White PR. Ultrasound in medicine & biology. 1999;25(5):811–821. doi: 10.1016/s0301-5629(99)00034-4. [DOI] [PubMed] [Google Scholar]
- Jones E, Oliphant T, Peterson P, et al. SciPy: Open source scientific tools for Python. 2001 URL: http://www.scipy.org/
- King RL, Brown JR, Newsome WT, Pauly KB. Ultrasound in medicine & biology. 2013;39(2):312–331. doi: 10.1016/j.ultrasmedbio.2012.09.009. [DOI] [PubMed] [Google Scholar]
- Levander AR. Geophysics. 1988;53(11):1425–1436. [Google Scholar]
- Marquet F, Pernot M, Aubry J, Montaldo G, Marsac L, Tanter M, Fink M. Physics in medicine and biology. 2009;54(9):2597–2613. doi: 10.1088/0031-9155/54/9/001. [DOI] [PubMed] [Google Scholar]
- Marsac L, Chauvet D, La Greca R, Boch AL, Chaumoitre K, Tanter M, Aubry JF. International Journal of Hyperthermia. 2017:1–11. doi: 10.1080/02656736.2017.1295322. [DOI] [PubMed] [Google Scholar]
- McElhaney JH, Fogle JL, Melvin JW, Haynes RR, Roberts VL, Alem NM. Journal of biomechanics. 1970;3(5):495–496. doi: 10.1016/0021-9290(70)90059-x. [DOI] [PubMed] [Google Scholar]
- Moczo P, Kristek J, Vavryčuk V, Archuleta RJ, Halada L. Bulletin of the Seismological Society of America. 2002;92(8):3042–3066. [Google Scholar]
- Nandi AK. IEEE Transactions on ultrasonics, ferroelectrics, and frequency control. 1995;42(6):993–1001. doi: 10.1109/tuffc.2015.620605. [DOI] [PubMed] [Google Scholar]
- Pichardo S, Hynynen K. Physics in medicine and biology. 2007;52(24):7313–7332. doi: 10.1088/0031-9155/52/24/008. [DOI] [PubMed] [Google Scholar]
- Pichardo S, Sin VW, Hynynen K. Physics in medicine and biology. 2011;56(1):219–250. doi: 10.1088/0031-9155/56/1/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinton G, Aubry JF, Bossy E, Muller M, Pernot M, Tanter M. Medical physics. 2012;39(1):299–307. doi: 10.1118/1.3668316. [DOI] [PubMed] [Google Scholar]
- Pulkkinen A, Werner B, Martin E, Hynynen K. Physics in medicine and biology. 2014;59(7):1679–1700. doi: 10.1088/0031-9155/59/7/1679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertsson JO, Blanch JO, Symes WW. Geophysics. 1994;59(9):1444–1456. [Google Scholar]
- Selfridge AR. IEEE transactions on sonics and ultrasonics. 1985;32(3):381–394. [Google Scholar]
- van Vossen R, Robertsson JO, Chapman CH. Geophysics. 2002;67(2):618–624. [Google Scholar]
- Virieux J. Geophysics. 1986;51(4):889–901. [Google Scholar]
- White P, Clement G, Hynynen K. Ultrasound in medicine & biology. 2006;32(7):1085–1096. doi: 10.1016/j.ultrasmedbio.2006.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White PJ, Palchaudhuri S, Hynynen K, Clement GT. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2007;54(8):1708–1710. doi: 10.1109/tuffc.2007.443. [DOI] [PubMed] [Google Scholar]
- Wu J. The Journal of the Acoustical Society of America. 1996;99(5):2871–2875. [Google Scholar]