Abstract
Cryo-electron tomography (cryo-ET) has rapidly emerged as a powerful tool to investigate the internal, three-dimensional spatial organization of the cell. In parallel, the GPU-based technology to perform spatially resolved stochastic simulations of whole cells has arisen, allowing the simulation of complex biochemical networks over cell cycle timescales using data taken from -omics, single molecule experiments, and in vitro kinetics. By using real cell geometry derived from cryo-ET data, we have the opportunity to imbue these highly detailed structural data—frozen in time—with realistic biochemical dynamics and investigate how cell structure affects the behavior of the embedded chemical reaction network. Here we present two examples to illustrate the challenges and techniques involved in integrating structural data into stochastic simulations. First, a tomographic reconstruction of Saccharomyces cerevisiae is used to construct the geometry of an entire cell through which a simple stochastic model of an inducible genetic switch is studied. Second, a tomogram of the nuclear periphery in a HeLa cell is converted directly to the simulation geometry through which we study the effects of cellular substructure on the stochastic dynamics of gene repression. These simple chemical models allow us to illustrate how to build whole-cell simulations using cryo-ET derived geometry and the challenges involved in such a process.
TOC image
Introduction
Over the last three decades, computational biologists have developed the ability to model the structure and function of biological systems at the molecular—and more recently—cellular levels. Key approaches in this pursuit are bioinformatics, molecular visualization, molecular simulation, and most recently, stochastic cell simulations. Computing complements experimentation, transforming static atomic force microscopy maps, structures derived from X-ray crystallography, super-resolution microscopy data, cryo-electron microscopy (cryo-EM) maps, and cryo-electron tomography (cryo-ET) 3-D reconstructions into dynamic systems through simulations which integrate single molecule fluorescence data, -omics, and kinetic data. Increasingly often, computing correctly predicts missing structural information and interactions at both the molecular and cellular levels. The work by Klaus Schulten and his co-workers to create a model of a photosynthetic chromatophore and analyze its overall energy conversion efficiency is perhaps one of the best examples of the power of molecular modeling.1–5 This undertaking involved the modeling of vesicles measuring hundreds of nanometers, and required many methodological and algorithmic improvements to molecular dynamics flexible fitting (MDFF), the molecular dynamics simulation program NAMD, and the visualization and analysis program VMD.
During its early phase, computational biology was considered a valuable, but limited tool, the limits being mainly due to restrictions in size and timescales. Computational cell biology has now matured such that its descriptions of subcellular systems and whole-cell processes compare favorably with observations for both bacterial and eukaryotic organisms. A revolution in structural biology has taken place with the combination of cryo-EM and cryo-ET with cryo-focused-ion-beam (cryo-FIB) milling, allowing for the collection of three-dimensional, high resolution snapshots of complex molecular landscapes in individual cells.6–8 To keep pace with this revolution, the development of simulation software that extends to the timescales of a cell cycle (measured in minutes) and the length scales of entire cells (measured in microns) will be required. While current efforts to build an atomic scale model of a minimal cell measuring 0.4 μm in diameter9 are expected to be fruitful within the next five to ten years, the dynamical timescales will continue to be a bottleneck.
Whole-cell simulations performed with the Lattice Microbes (LM)10,11 stochastic simulation package provide a bridge to describe dynamical processes over several cell cycles and generate snapshots of complex cellular states that result in clear, testable predictions for further experiments. LM is a GPU-based simulation code that was designed from the ground up to be highly computationally efficient10 in order to reach the length and time scales necessary to study biological systems across entire cells. Reaction processes within the cell are modeled within the framework of reaction–diffusion master equations (RDME), whose specification requires kinetic parameters obtained from many disparate sources including super-resolution imaging, fluorescence, and biochemical experiments as well as other computational techniques such as molecular dynamics and Brownian dynamics. To date, LM has been used to study the lac genetic switch,8 ribosome biogenesis,12,13 and the effect of DNA replication on gene expression networks.13,14 The probabilistic description of ribosome biogenesis in a replicating cell, requiring 251 species and over 1000 reactions, was one of the largest systems modeled with LM. Using a NVIDIA TITAN X graphics card, a full 90-minute cell cycle of an Escherichia coli cell could be simulated in approximately 24 hours.13
The importance of environmental fluctuations and the discrete nature of chemical reactions on the fate of individual cells are now well known. While the stochastic dynamics of the genetic switches in bacteria have been well studied, the determination of how transcription factors find specific DNA binding sites in eukaryotes is a challenging problem. These studies are complicated by the increased size of the system, the sequestration of the DNA in a spatial compartment separate from the cytoplasm, and the variation in chromatin states.15,16 Using 3-D chromatin density inferred from structured illumination imaging of a DAPI-stained mammalian nucleus15 and soft X-ray tomography,16 Isaacson et al. performed lattice-based simulations of the diffusive search of a hypothetical transcription factor to its DNA binding site. These simulations model the search as the 3-D diffusion of a single particle with an assumed diffusivity of 10 μm2 s−1 through an external potential, U(r) = Cρ(r), where ρ(r) is the density of chromatin, and C is a free parameter of their model. They revealed that the search times are exponentially distributed and that there exists a proportionality constant C > 0 where the search time is minimized, implying that the chromatin structure helps to direct the transcription factor to its binding site.
The implication is that there can be features of the spatial environment which affect the reaction–diffusion dynamics in unexpected ways. Attempts to construct generic, ideal geometry in whole-cell simulations can overlook these details. For instance, it would be difficult to construct an idealized endoplasmic reticulum due to its convoluted structure. Getting the details wrong means that the search times of mRNA to find ER-bound ribosomes and export times of their products, such as membrane-bound proteins, would be inaccurate. Thus, it is prudent to construct the simulation volume using experimental data when available.
Here, we present two examples illustrating the integration of cryo-ET data into whole-cell simulations. First, using a tomographic reconstruction of a ~1 μm3 volume of an individual Saccharomyces cerevisiae cell, we extrapolate the remaining geometry to build the simulation environment. Second, we translated the pre-segmented EM density acquired about the nuclear periphery of a HeLa cell6 directly to the simulation lattice, leading to non-idealized cellular geometries. In both cases, we investigate how the geometry affects the behavior of idealized genetic switch models. We are able to break down the induction of these genetic switches into several steps: (i) diffusion of an inducer molecule from its transporter in the plasma membrane through the cytoplasm and into the nucleus through a nuclear pore complex (NPC) and its binding to a specific gene triggering transcription; (ii) diffusion of the mRNA through the nucleus into the cytoplasm where it is translated by one of the ribosomes surrounding the nucleus; and (iii) transport of the resulting permease into the cell membrane. Since there was insufficient information available in the tomogram to reconstruct a realistic ER, only transport of the permease through cytoplasm is considered. In the case of the HeLa cell, since our simulation volume is restricted to the nuclear periphery, we study the local dynamics of a repressor protein and its mRNA in the nucleus and cytoplasm (ii). The simple form of these reaction networks allows us to demonstrate the challenges and possible simplifications that can be made in modeling chemical reactions in eukaryotic cells. The results should be viewed as a basis for introducing further complexity into the dynamics as more structural details become available from the analysis of the cryo-electron tomography data.
Methods
Cryo-electron tomography
Haploid Saccharomyces cerevisiae cells (W303a) were cultured in YPD (20 g/L peptone, 10 g/L yeast extract, 20 g/L glucose) at 30 °C to a density of 107 cells/ml. 7 μl of this culture were deposited onto glow-discharged holey carbon grids (QUANTIFOIL R 2/1 200 mesh, copper; Electron Microscopy Sciences), blotted and rapidly vitrified in a liquid ethane and propane mixture (50:50) using a custom-built plunger (Max Planck Institute of Biochemistry, Germany). The lamellas (250 to 300 nm thickness) containing several sliced yeast cells were prepared using cryo-FIB milling as previously described.6 Cryo-electron tomography was obtained using a Titan Krios transmission electron microscope (FEI) equipped with a Quantum energy filter (Gatan) and a K2 Summit direct detection device (Gatan). Imaging was performed at 300 kV under low-dose conditions with 5.31 Å sampling. Tilt series (±62°) for tomography were collected around a single axis with a 2° sampling increment using SerialEM software17 (~100 e/Å2 cumulative dose). Tomographic reconstructions were calculated using the IMOD tomography package.18
Subtomograms containing ribosomes are picked using EMAN219 and subsequently averaged, classified, and placed in their location in the original tomogram using Dynamo.20 In order to segment individual organelles, the tomogram data was filtered using nonlinear anisotropic diffusion using the IMOD tomography package.18 The membranes (cell wall, plasma membrane, nuclear envelope, mitochondrial and ER membranes) were automatically segmented using TomoSegMemTV.21 Segmentation of tomography volumes for the representation of various organelles and nuclear density were performed with Amira software (FEI Visualization Sciences Group).
The HeLa tomography data were previously reported.6
Simulations
Spatially resolved stochastic chemical reaction trajectories were simulated using Lattice Microbes v2.3.0.10,22,23 Lattice Microbes (LM) efficiently samples particle number trajectories from the solution to the underlying RDME describing the chemical system embedded in a lattice-based representation of the system geometry. The RDME is
| (1) |
where P (x, t) is the probability distribution to find a configuration x at time t, and the configuration vector x contains the number of species present of each type at each subvolume. The first term in Equation 1 describes the flow of probability between different copy number states at each lattice site. The reaction propensities ar(xν) give the transition probabilities due to reaction r firing at site ν. The r row of the stoichiometry matrix S is the change in species counts when reaction r occurs. The second term describes the flow of probability due to diffusion between neighboring lattice sites, indexed by ξ. The diffusive propensity for a particle of species α to leave subvolume ν is computed from the diffusion constant and lattice spacing λ as . The notation represents a single molecule of species α in volume ν, i.e. . All simulations were performed on a local cluster consisting of three Cirrascale GB5600 Multi-GPU nodes, two equipped with eight NVIDIA GeForce GTX TITAN X GPUs, and one equipped with four NVIDIA Tesla K80 GPUs. The multi-GPU capabilities of LM were used to share the simulation workload for the S. cerevisiae simulation over eight GPUs, and for the HeLa simulation over four GPUs.
Simulation design, visualization, and analysis of simulation results were performed using Python 3.5.3 in the Jupyter environment24 with the SciPy Stack.25 EM data was injected into the Python workflow by converting density files from the MRC format to NumPy26 native data files using EMAN2,19 which currently does not support Python 3.
Visual Molecular Dynamics (VMD)27 was used for interactive visualization of experimental tomography volumes and LM simulation trajectories, enabling several different data modalities to be inspected and superimposed for comparison. The VMD MRC plugin was extended to support several IMOD-specific variants of the MRC file format, allowing it to read the experimental tomogram volumes produced as described above. The volume visualization and ray tracing capabilities of VMD were enhanced to permit visualization of volumes containing more than 2 billion voxels. The large size and geometric complexity of the graphical representations for the experimental tomograms and the LM simulation trajectories presented a significant performance challenge for interactive display in VMD using conventional OpenGL rasterization. The GPU-accelerated interactive ray tracing capabilities of VMD were used to overcome the performance challenge posed by complex scenes.4 For the complex structures studied herein, ray tracing acceleration algorithms avoid consideration of occluded geometry, and the use of progressive refinement ray tracing permits very high interactivity, even for visualizations using rendering techniques such as ambient occlusion lighting or depth-of-field focal blur that require large numbers of stochastic lighting samples to be computed.28
Results and Discussion
Inferring the architecture of a yeast cell from cryo-ET
Using cryo-FIB with cryo-ET, we have acquired the 3-D structure of a 2.04×1.91×0.242 μm3 volume of an individual S. cerevisiae cell with a sampling rate (pixel size) of 0.53 nm (Figure 1). The structure clearly shows a portion of the nuclear envelope with 12 nuclear pores, 750 ribosomes in the cytoplasm, a section of the plasma membrane, and portions of the ER and a mitochondrion. Using the data available to us through this tomogram, we have constructed the internal geometry of an entire cell, filling in any missing data using measurements published in the literature as well as numerical optimization.
Figure 1.
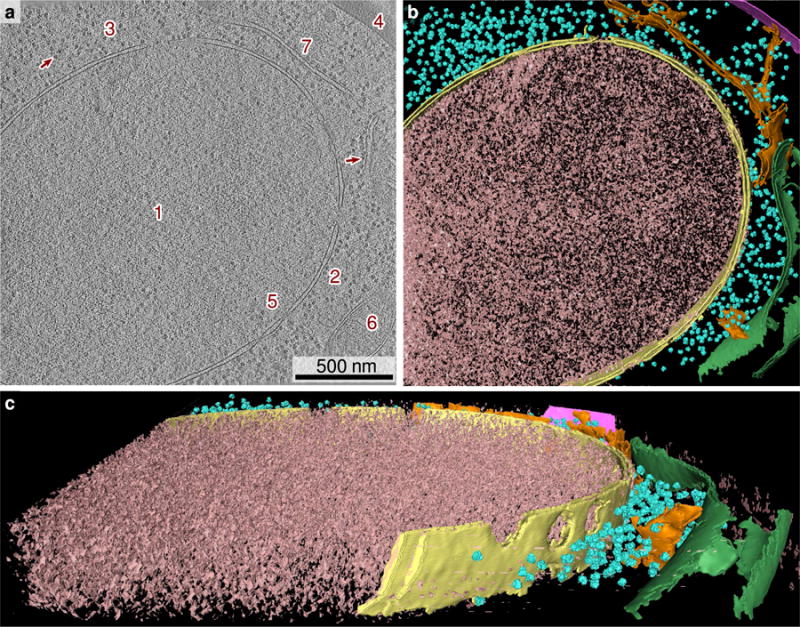
(a) Tomographic slice of a S. cerevisiae cell (16 nm thickness). The nucleus (1), separated by the nuclear envelope (2) from the cytoplasm (3), occupies the majority of the tomogram. Ribosomes are visible in the cytoplasm (3) as dark spots (arrow). A portion of the cell wall (4) appears in the upper right corner. Nuclear pores (5) are present in the nuclear envelope. A mitochondrion (6) is present on the right edge of the tomogram, as well as a portion of the ER (7). (b, c) Annotated view of the tomographic data (240 nm thickness). Nuclear envelope, yellow; ribosome, cyan; cell wall, magenta; mitochondrion, green; ER, orange.
The simulation geometry consists of ten distinct spatial regions: extracellular, cell wall, plasma membrane, cytoplasm, vacuole, mitochondria, ribosomes, nuclear pores, nuclear envelope, and nucleoplasm (Figure 2). Each region can have its own set of species-specific diffusion constants and set of reactions allowing for spatially heterogeneous reaction–diffusion behavior. The starting point to reconstruct a realistic yeast cell from the tomography data is the 3-D binary mask resulting from the segmentation of the nuclear envelope and plasma membrane surfaces (Figure 1a), which we resample to the dimensions of the simulation lattice. A 3–D representation of this mask is shown in Figure 1b–c. The original tomogram data was resampled from a sampling rate of 0.53 nm to a simulation lattice spacing of 28.7 nm—a 54-fold reduction.
Figure 2.
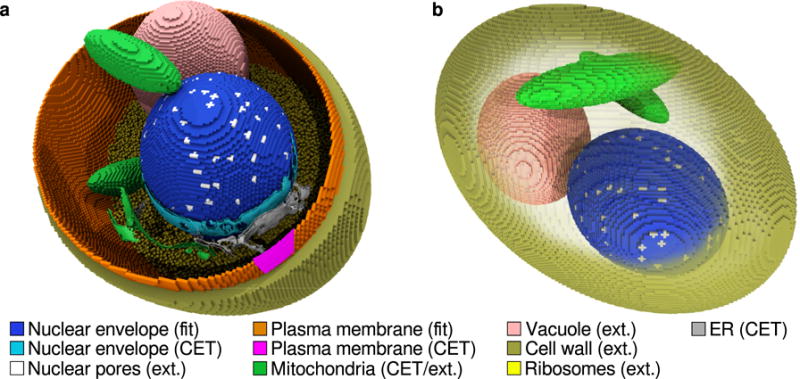
(a) Construction of the simulation geometry of a S. cerevisiae cell derived from cryo-ET data and other literature sources. Regions marked “CET” are the segmentation surfaces from the tomogram, regions marked “fit” are derived from fitting ellipsoids to the cryo-ET segmentation data, and the regions marked “ext” are simulation compartments which were not derived from tomography. The nuclear envelope from the tomogram volume (cyan) is used to fit an ellipsoid (blue). A small segment of plasma membrane identified in the tomogram (magenta) is used to fit an ellipsoid (orange) along with constraints on its centroid and volume. Ribosomes (yellow) are distributed uniformly throughout the cytoplasm and act as molecular crowders to cytoplasmic protein and inducer. The mitochondria (green) and ER (gray) surfaces are included from the tomogram for context, however are not incorporated into the simulation. (b) Another view of the model yeast cell showing the placement of mitochondria (green), the vacuole (pink), the 129 nm thick cell wall (gold), and nuclear pores (silver).
To extrapolate the geometry of the nucleus and cell volume outside of the tomographic volume, we fit ellipsoids to the mask coordinates using local optimization. To ensure that the result is both biologically reasonable and faithfully reflects the data, we augment the squared error with terms penalizing deviations from an expected volume and aspect ratio.29,30 These penalizing terms are small compared to the squared error, ensuring that only perturbations to the parameters which do not affect the fit to the mask coordinates significantly are allowed.
To construct the nucleus, we started with initial ellipsoid parameters computed from the mask coordinates: the center from the mean of the mask coordinates and the ellipsoid axes from the maximum distance between two mask coordinates. Assuming that the volume of the cell in the tomogram is ~40 μm3 29 and that the volume percentage of the nucleus is 7%,30 we use an expected volume of 2.8 μm3 and an aspect ratio of 1.0 in our fitness function. This results in a nucleus of volume 3.17 μm3 and aspect ratio 1.2. For the cell volume, we used an expected volume of 33.6 μm3, which is assuming that the cell wall occupies 15.9% of the cell volume,30 and an expected aspect ratio of 1.5. Since only a small portion of the plasma membrane is present in the tomogram, we used the center of the nucleus as the initial position and the radius of a sphere of volume 33.6 μm3 as the initial ellipsoid axes. The resulting ellipsoid spanned a volume of 33.9 μm3 and had an aspect ratio of 1.50. Figure 2a compares the cryo-ET-derived masks to the extrapolated geometry.
A natural way to work with the RDME site-type lattice is in terms of set operations. We define the set of lattice sites to be
| (2) |
Then an ellipsoid embedded in the lattice is the set,
| (3) |
where A = diag(1/a, 1/b, 1/c), a matrix with the inverse of the ellipsoidal semi-axes on the diagonal, is an Euler rotation matrix, and n0 is the centroid of the ellipse. By representing the site type lattice in this way, we can easily describe the construction of more complicated structures in the language of set operations and binary morphology.
These ellipsoids are used to form the nucleoplasm and cytoplasm, as well as the nuclear envelope, plasma membrane, and cell wall. The membrane regions are constructed as,
| (4) |
where Ellipsoid⊕Smem denotes the dilation of Ellipsoid with a structuring element Smem. The resulting mask, Membrane is a shell one subvolume thick surrounding Membrane. The structuring element, Smem, is a cube with edge length 3 with all elements set to 1, which matches all 26 neighbors. This choice ensures that all subvolumes within Membrane have at least one neighbor along the principal axes. This is critical for membrane-bound particles since diffusion in Lattice Microbes is modeled as transitions between the 6 nearest neighbor subvolumes. Otherwise, there would be regions of the membrane compartment which would be topologically separated to diffusing particles. The resulting membranes are 28.7 nm thick which is reasonable for the nuclear envelope (typically ~30 nm thick in S. cerevisiae31). However, this is considerably larger than the thickness of the plasma membrane (9.2 nm32). Lattice-based simulations such as this limit the smallest features to the lattice spacing, however we must choose a coarser lattice resolution in order to accelerate the simulation. Fortunately, the plasma membrane thickness does not affect the outcome of the simulation since the chemical species which pass through the membrane are represented by separate external and internal species types, allowing for particles to be on different sides of the membrane within a single lattice site. The cell wall is formed from an ellipsoid with the same shape, orientation, and location as the cell volume ellipsoid. The axes are scaled such that the resulting ellipsoid has the expected volume of the cell (40 μm3). From this ellipsoid region, we subtract the union of the cell volume and plasma membrane regions to arrive at the cell wall. The resulting shell is 129 nm thick, which compares well with measurements performed with single-molecule AFM.33
By observing the number of pores in the nuclear envelope (12) and its surface area (0.91 μm2) from the tomogram, we computed the expected number of pores on the full nucleus to be 139. This quantity is consistent with the value of 119 ± 39 pores per nucleus reported in the literature34 for haploid yeast cells grown in similar conditions. Since the pores visible in the tomogram do not include the full nuclear pore complex, we used a pore diameter of 40 nm,35 instead of measuring the diameter from the segmentation. The pores are initially represented as the union of 139 cylinders i.e.,
| (5) |
where r is the nuclear pore radius, ℓ is one half the nuclear radius, and the transformation parameters Ri and n0,i are chosen as follows. Each cylinder is placed at the center of the nucleus, rotated to a random polar and azimuthal angle, and translated to place the centroid of the cylinder in the nuclear envelope. The random position is checked against all previous placements to ensure that the new pore does not merge with the remaining pores. The nuclear pore lattice is then the intersection, Membranenuc∩ PoreCylinders, and the the nuclear envelope is the difference, Membranenuc\ PoreCylinders.
Using volume percentages measured from cryo-FIB-milled scanning electron microscopy data of entire budding yeast cells,30 we add ellipsoids representing the mitochondria and vacuole. The ER, which can occupy 2.2% of the cell volume,30 is not included. The presence of the ER would affect diffusion throughout the cell due to its folded morphology, however there is not enough information from the tomogram to infer the geometry outside of the imaged volume. Finally, 180,000 ribosome sites36 are placed uniformly throughout the cytoplasm. The resulting geometry requires a lattice size of 192 × 192 × 192, which represents a cube of edge length 5.5 μm.
To explore the effects of the cell geometry on a behavior of a biochemical network, we simulated a model of a simple inducible genetic switch (introduced in Table 1) in the extrapolated yeast lattice. A concentration of 4 μM of inducer is placed in the extracellular space, where it may enter the cell via passive diffusion across the plasma membrane. Inducer molecules diffuse through the cytoplasm into the nucleus through a nuclear pore, where it may interact with a gene species located in a single subvolume of the nucleus, activating the transcription of mRNA coding for a transporter protein. The mRNA diffuses out of the nucleus through the nuclear pores into the cytoplasm. Since dwell times of exported molecules in the pore are reported to be on the order of milliseconds,37 we approximated the mRNA export process as simple diffusion out of the nucleus. The actual process is certainly more complicated than this,37,38 however it is an appropriate approximation for the level of detail in this model. After leaving the nucleus, the mRNA binds to a ribosome in the cytoplasm to begin translation The translated protein, being a membrane-bound transporter, normally would be translated by ribosomes associated with the ER and exported to the plasma membrane through the Golgi apparatus. However without a large volume of tomographic structures of these organelles, it is difficult to incorporate their geometry in our model realistically. Furthermore, the development of a plausible RDME-based protein targeting model is beyond the scope of this work. Instead, we allow the transporter protein to diffuse through the cytoplasm and into the plasma membrane. Once installed in the membrane, the protein transports more inducer into the cell through active transport.
Table 1.
Reactions and rate parameters used in the S. cerevisiae gene expression model.
| Description | Reaction | Stochastic rate [s−1] | Defined regions | |
|---|---|---|---|---|
| Inducer/TF binding |
|
1.599 | Nucleoplasm | |
| Transcription |
|
6.202 × 10−3 | Nucleoplasm | |
| SSU/mRNA association |
|
7.043 × 103 | Ribosome | |
| Translation elongation |
|
1.393 | Ribosome | |
| mRNA degradation |
|
7.889 × 10−4 | Nucleoplasm, Ribosome, NPC, Cytoplasm | |
| mRNA degradation |
|
7.889 × 10−4 | Ribosome | |
| Transcription (other) |
|
5.895 × 10−5 | Nucleoplasm | |
| SSU/mRNA association (other) |
|
7.043 × 103 | Ribosome | |
| Translation elongation (other) |
|
1.101 | Ribosome | |
| mRNA degradation (other) |
|
5.776 × 10−4 | Nucleoplasm, Ribosome, NPC, Cytoplasm | |
| mRNA degradation (other) |
|
5.776 × 10−4 | Ribosome | |
| Passive diffusional transport |
|
2.33 × 10−3 | Membrane | |
| Passive diffusional transport |
|
2.33 × 10−3 | Membrane | |
| Transporter/inducer association |
|
2.134 | Membrane | |
| Active inducer transport |
|
12.000 | Membrane | |
| Transporter/inducer dissociation |
|
0.120 | Membrane | |
| Transporter degradation |
|
2.567 × 10−4 | Cytoplasm, Membrane | |
| Transporter degradation |
|
2.567 × 10−4 | Cytoplasm, Membrane |
The transcription and translation rates were estimated from steady-state mRNA and protein abundance, protein lifetime,36 and mRNA lifetime39 using the gene expression model
| (6a) |
| (6b) |
| (6c) |
| (6d) |
where the mean number of mRNA, m, is given by the ratio of transcription to mRNA decay rates,
| (7) |
and the mean number of protein, P, is given by the ratio of the total translation rate to the protein decay rate,
| (8) |
To represent this hypothetical transporter, we chose values describing the high-affinity glucose transporter HXT6. These parameters result in a steady state mRNA abundance of 7.86 and protein abundance of 42,600 per cell. In the interest of computational efficiency, the passive and active transport parameters as well as the rate of gene activation were adapted from a previous model of the lac genetic switch in E. coli.8 Since competitive binding to ribosomes between different mRNA species can have a significant effect on the copy number statistics,13 we added a second series of transcription, translation, and mRNA degradation reactions. The rates were chosen to yield 12,200 mRNA36 and 5 × 107 protein40 at steady state. Through we do not track these “background” proteins in our simulation, their translation rate impacts the simulation through their effect on the average ribosome occupancy.
We ensured the proper localization of molecules to their respective compartments by choosing the transition rates between the ten different regions explicitly. In Lattice Microbes, the diffusion rate between two subvolumes is specified by the type of chemical species, the type of the site the particle currently occupies, and the type of the site that the particle may diffuse to. This allows for the specification of one-way transitions between compartments by setting the reverse diffusion rate to zero. We will use this technique extensively in both models presented in this work. The gene species is fixed in place in the nucleus by setting its diffusion constant to zero. mRNA can diffuse freely in the nucleoplasm, cytoplasm, nuclear pores, and ribosome regions with a diffusion rate of 0.5 μm2 s−1. To prevent mRNA from reentering the nucleus, we define the site-dependent diffusion rate for mRNA from cytoplasm to nuclear pores to be zero. Transporter proteins diffuse through the cytoplasm in three dimensions (1 μm2 s−1) and in the plasma membrane in two dimensions. (0.01 μm2 s−1). To allow for the proper progression of transporter diffusion from the ribosome, through the cytoplasm, to the membrane, we set all transitions into the nuclear pore and ribosome regions to zero. Since transporters are created at ribosome site types, they are allowed to diffuse in these regions. However their reentry is forbidden, in order to allow for the ribosome sites to act as crowding agents in the cytoplasm. Finally, the transporters can diffuse from the cytoplasm to the membrane, however the reverse rate is set to zero to prevent their detachment.
The inducer is represented by two separate species types: internal and external. External inducer can diffuse freely through the extracellular, cell wall, and plasma membrane regions with a diffusion constant of 2 μm2 s−1. This rate is significantly lower than what would be expected for a small molecule (100–1000 μm2 s−1), however in this model it is necessary to slow the diffusion of inducer since the maximum acceptable time step in an RDME simulation scales with 1/D. It has been shown previously that this approximation has a limited effect on the outcome of the simulation,8 so long as the correct ordering of diffusion constants, DmRNA < Dprot. < Dind., is maintained. However, validity of the approximation notwithstanding, it is not necessary to treat a species found in such a high concentration (2 μM) using a stochastic representation. The solution to this problem is to use multiple coupled simulation methods each for different concentration and diffusivity regimes, e.g. a deterministic, well-mixed representation using ODEs for small molecules in large concentrations or a deterministic, spatially resolved representation using PDEs for slowly diffusing molecules in high concentrations. Work on Lattice Microbes is underway to enable this ability. The external inducer species is transformed to internal through passive diffusion, represented as the first order reactions
| (9) |
which occurs only in the plasma membrane site type, and active transport, represented by the Michaelis-Menten scheme
| (10) |
The internal species is free to diffuse through the plasma membrane, cytoplasm, and nucleoplasm regions. By dividing the inducer into internal and external species, we are able to model transport into the cell simply by using the plasma membrane compartment as a staging area.
Using the multi-GPU capabilities of Lattice Microbes,10 we complete a 60-minute simulation in 28 hours using eight NVIDIA TITAN X GPUs, taking 67-μs time steps. A summary of the simulation parameters and diffusion rates is provided in Table 2. Representative particle abundance time series are presented in Figure 3a–c. The concentration of inducer in the nucleus rises slowly, leading to the gene switching on at 4.2 minutes. The first transporter protein reaches the membrane 9.3 minutes after the gene is activated (Figure 3d). At about 21.7 minutes, the nuclear inducer concentration dynamics becomes dominated by active transport with the appearance of 1900 transporter proteins in the membrane. Due to the finite size of the simulation volume and closed boundary conditions, the extracellular inducer is depleted to 1% of its original concentration after 46.7 minutes of simulated time.
Table 2.
Model parameters and diffusion rates used in the S. cerevisiae and HeLa models.
| Parameter | Model | |
|---|---|---|
| S. cerevisiae | HeLa | |
| Time step [μs] | 67.0 | 10.7 |
| Lattice dimensions | 192 × 192 × 192 | 224 × 128 × 224 |
| Lattice spacing [nm] | 28.7 | 8.0 |
| Inducer diffusion rate [μm2 s−1] | 2.045 | – |
| mRNA diffusion rate [μm2 s−1] | 0.5 | 0.5 |
| Protein diffusion rate [μm2 s−1] | 1.0 | 1.0 |
| Protein diffusion rate (membrane) [μm2 s−1] | 0.01 | – |
| Maximum diffusion rate [μm2 s−1] | 2.045 | 1.0 |
Figure 3.
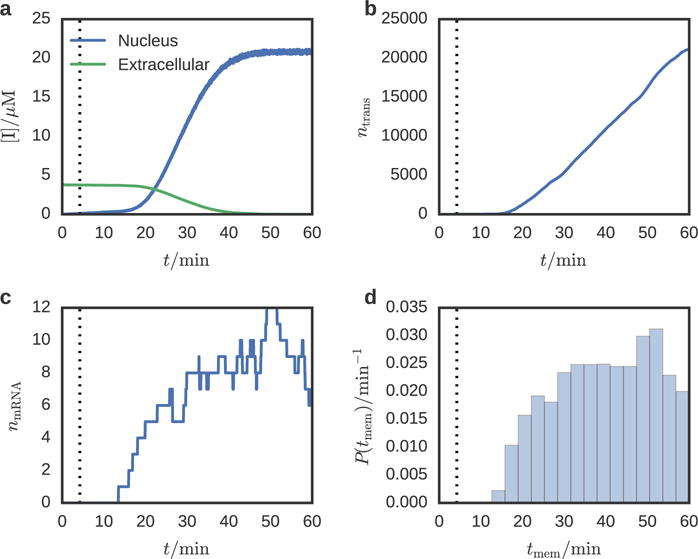
Species abundance time series for (a) inducer, (b) transporter protein, and (c) transporter mRNA for a single replicate. The vertical dotted line denotes the time at which the gene is activated. The extracellular inducer concentration decreases slowly due to passive transport into the cell until 21.7 minutes, after which transporter proteins begin to appear in the membrane and active transport of inducer begins. The distribution of transporter arrival times at the membrane (d) shows that the first membrane transporters appear at 10 minutes (5 minutes after gene induction).
Exploring the nuclear periphery in a HeLa cell
Starting from an EM map of the periphery of a HeLa cell nucleus obtained through cryo-ET/cryo-FIB,6 we constructed a discrete environment to explore a simple gene expression system. The density has been pre-segmented into six regions corresponding to actin filaments, microtubules, ER, large and small ribosomal subunits, and the nuclear pore complexes (Figure 4). Instead of using measurements derived from the EM density, the problem one is now posed with is how to directly map a 3D density represented on a grid sampled at 0.35 nm to a coarse-grained lattice which is faithful to the dimensions of the original tomogram. Solving this problem entails choosing a suitable threshold to discriminate cellular substructures from the background density, and determining an optimal lattice spacing for the RDME simulations.
Figure 4.
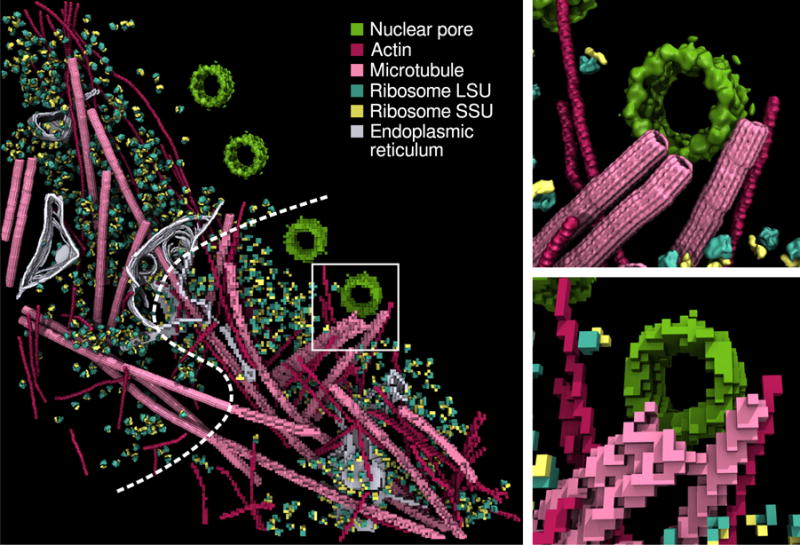
Adaptation of a segmented cryo-electron tomogram of the nuclear periphery of a HeLa cell6 to RDME simulations using an 8-nm lattice spacing. The upper panel shows both the processed tomography data (upper left) and the discretized RDME lattice (lower right). The inset shows detail of the vicinity of a nuclear pore for both the original data (top), and the RDME lattice (bottom).
To minimize the computational time necessary to perform the simulations, the lattice spacing must be large as possible while accurately reproducing the cellular substructure. In order to resolve the actin filaments we have chosen a lattice spacing of 8 nm, larger than their actual diameter (~6 nm), to ensure that the voxelized actin filaments remain contiguous while not excessively overestimating their impact on the excluded volume. To begin constructing the system geometry, the EM map was resampled to the dimensions of the RDME lattice using trilinear interpolation. A unique threshold is determined for each of the six segmented maps, which is used to compute a binary lattice such that lattice elements for which their density is below the threshold are interpreted as background. These thresholds were chosen such that the dimensions of the identified cellular substructures are correctly recovered. Figure 4 shows a comparison between the segmented tomogram and the derived site type lattice.
Our simulation domain consists of four active regions, cytoplasm, nuclear pore, nucleoplasm, and ribosomal small subunit. The nuclear pore region allows the transport of particles between the cytoplasm and nucleus to be monitored, and the small subunit region contains the reaction sites for translation. The obstructions include the NPC, actin, microtubules, large subunit, and ER, as well as the nuclear envelope. Due to the orientation of the sample, the nuclear envelope was not resolved in the tomogram. To include this region, we will approximate its position and shape from the context of the tomogram.
To begin the construction of the RDME geometry, first two auxiliary binary lattices are constructed to aid in the construction of the simulation volume: the convex hull of all of the cryo-ET derived site type lattices,
| (11) |
and the neighborhood around the nuclear pores, NpcDomain, which is constructed by thresholding a Gaussian-filtered version of the NPC density. The nuclear envelope is constructed starting with a spherical shell,
| (12) |
where rn and rne are the radius of the nucleus and thickness of the nuclear envelope respectively, and xn is the position of the center of the nucleus, necessarily outside of the lattice space. The nuclear envelope region is then,
| (13) |
where • denotes the morphological closing operation and Snpc is a structuring element sufficient to fill the interior of the pores without joining adjacent NPCs. This allows us to construct the obstruction lattice as the union,
| (14) |
The nucleoplasm is constructed starting with the sphere,
| (15) |
then cropping to fit the simulation volume and subtracting the NPCs,
| (16) |
The interior of the nuclear pores is simply,
| (17) |
Finally, the cytoplasm is the convex hull excluding all other regions,
| (18) |
The resulting simulation volume (Figure 5) is 1.554 × 0.296 × 1.496 μm3 (194 × 37 × 187 lattice sites).
Figure 5.
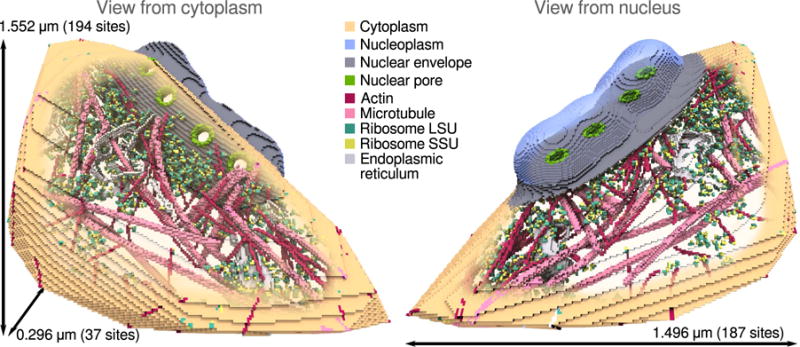
RDME simulation volume for the HeLa nucleus periphery. The nucleoplasm and cytoplasm are shown in light blue and tan respectively. The cytoplasm is created from the convex hull of the cryo-ET derived site type lattices, where as the nucleoplasm is created from the neighborhood surrounding the nuclear pore complexes. The total accessible simulation volume is 0.329 μm3. The nucleoplasm and cytoplasm are connected by channels through the nuclear pore complexes.
To explore this lattice geometry, we will use a simple model of gene expression (Table 3). mRNA diffuses from gene sites in the nucleoplasm, through the nuclear pores, to find ribosome species positioned in the small subunit site type. The mRNA and ribosome species react to form a translating ribosome, which then decays yielding the original mRNA and ribosome species as well as a transcription factor. Finally, the protein is able to diffuse back through the nuclear pores and repress its originating gene. The same diffusion constants were used for mRNA (0.5 μm2 s−1) and protein (1.0 μm2 s−1) in the HeLa model as in yeast, and the same deterministic rate constants were used as well. The numerical difference between the values in Table 1 and Table 3 arises from a factor of (λyeast/λHeLa)3 converting between lattice site volumes. We would not expect either the reaction rates or the diffusion constants to be identical between the two organisms, however going to slower, more realistic values will require tens of hours of simulated time to observe the same repression behavior. Since only the broad effects of the cell geometry on the reaction model are of interest, this is an acceptable approximation. We use a similar scheme as the S. cerevisiae model to keep particles in their proper compartments. The gene has a diffusion rate of zero in order to fix it in place inside the nucleus. The protein and mRNA species are forbidden from entering the obstruction regions. mRNA is prevented from reentering the nucleus by setting its transition from the cytoplasm into the nuclear pore to zero, however protein is not restricted from the nucleus. A summary of the simulation parameters and diffusion rates is provided in Table 2 in comparison to the S. cerevisiae model.
Table 3.
Simple model of a self repressing gene used in the HeLa model.
| Description | Reaction | Stochastic rate [s−1] | Defined regions | |
|---|---|---|---|---|
| Repressor/gene association |
|
73.622 | Nucleoplasm | |
| Translation initiation |
|
3.243 × 105 | SSU | |
| Translation termination |
|
1.393 | SSU |
As shown in Figure 6a the dynamics begins with the formation of mRNA from a gene located in the nucleoplasm. Within 0.85 seconds, it escapes through the nuclear pore into the cytoplasm and diffuses to one of the ribosome sites where it is translated into a repressor protein. The repressor protein appears on average 0.60 seconds after formation of the translating complex. Finally the newly translated protein diffuses back through the nuclear pore and represses the originating gene, taking an average time of 75.6 seconds measured from the birth of the mRNA. Since the mean translation time is 0.498 seconds and the gene/repressor and ribosome/mRNA binding rates are fast, the first passage time (FPT) distribution of gene repression events is dominated by the return of protein into the nucleus—a consequence of the geometry of the simulation domain. There are many ribosome sites near the nuclear pores, allowing a newly exported mRNA to immediately begin translation, however a newly translated protein has no preferred direction to diffuse, so it will typically diffuse far from the pore before returning.
Figure 6.
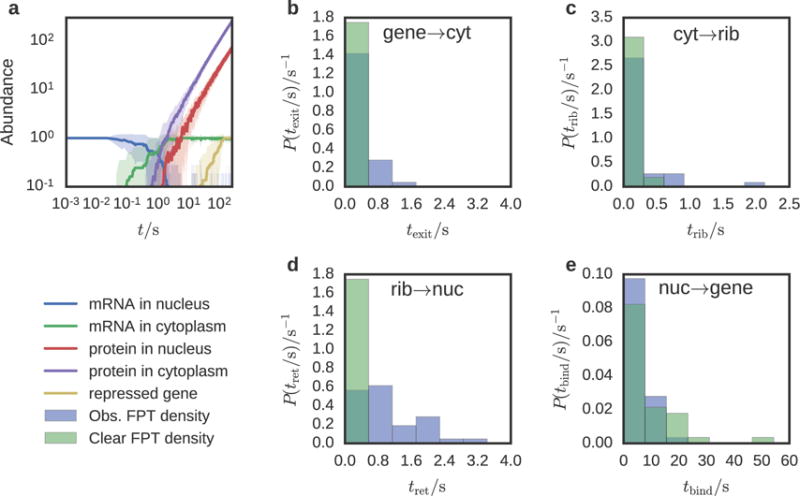
Abundance and escape dynamics for a simple genetic switch simulated in the intracellular environment of a HeLa cell. (a) Mean particle abundance (solid line) and standard deviation (shaded area) were computed over 37 simulation replicates. The time for a mRNA to diffuse out of the nucleus and find a ribosome is two orders of magnitude larger than the time for a newly translated protein to return and bind to its originating gene. The mRNA abundance in the cytoplasm is the sum of free mRNA and mRNA bound to ribosomes. (b–e) First passage time distributions of diffusion between compartments and reaction sites for the complete HeLa cell geometry (blue) and with all obstructions removed (green). These simulations were performed with instantaneous reaction rates in order to measure the time for diffusion alone over 222 simulation replicates. mRNA diffuses from the gene site into the cytoplasm (b), from the cytoplasm to the ribosome (c), the protein diffuses back into the nucleus (d), and the protein binds to the gene (e).
To study how obstructions such as the nuclear membrane and microtubules affect the time for a particle to diffuse between compartments and reaction sites, a second set of simulations were performed where all reactions were instantaneous, using both the previously defined geometry (Figure 5) and a version where the obstacles were removed. By requiring that the ribosome make a single protein, only a single particle is present at any time in the simulation. This allows the FPTs to be measured without ambiguity (Figure 6b–e).
We find that the transition times between gene to nuclear pore, nuclear pore to ribosome, and ribosome to nuclear pore are greater in the presence of obstacles. The transition from the gene site to the nuclear pore is 9.7 times greater, simply due to the fact that the particle must find one of the four nuclear pores to exit. The transition from nuclear pore to ribosome is only 2.2 times greater with obstacles. Here, the structures impeding the search are the large subunits, microtubules, actin filaments, and ER. With little opportunity to become trapped away from the ribosomes, it is not surprising that the difference in transition time is not as profound. The transition from the ribosome to a pore is 20.5 times greater with obstacles, which arises for the same reason as the gene to pore transition. However the mean time between encounters with the nuclear envelope or nuclear pores must be smaller for a particle in the nucleus versus a particle in the cytoplasm due to the fact that the volume of the cytoplasm is 3.5 times that of the nucleus. Interestingly, the time for the repressor to find the gene site after entering the nucleus is 1.18 times faster when obstacles are present. This is because the repressor is less likely to escape the nucleoplasm with the nuclear envelope intact.
Conclusions
Acquiring the capacity to simulate stochastic biochemistry in whole cells at a spatially resolved level over cell-cycle-long timescales, is a crucial step in the development of the field of computational biology. Through the availability of massively parallel computational hardware, such as GPUs, and the development of methods to measure the 3-D structure of cells in their native environment at high resolution, such as cryo-ET, it is now possible to build integrative computational models of whole cells. We have presented two vignettes of the integration of structural data into RDME models of gene expression. Though limited in realism, they provide an illustration of the techniques necessary for this sort of data integration and hint at the challenges faced in undertaking such a task.
Using the 3-D structure of a fraction of a yeast cell, we have shown a way to infer the remaining cell geometry from the tomogram supplemented with data from the literature, and simulated a multi-compartment model of an inducible genetic switch in this environment. From a previously published cryo-ET structure of the HeLa nuclear periphery, we have shown how to use the EM map data directly to construct a spatial model and simulate a gene repression model, which was used to study the effect of the cellular substructure on the molecular search times. Models built using these techniques, compiling experimental data from many disparate sources into a single cohesive whole, will form a computational framework capable of making testable predictions of the effects of perturbations to both the underlying biochemical network and the architecture of the cell.
Acknowledgments
The authors thank Robert Buschauer for assisting with the analysis of the yeast tomogram. This work is supported by the National Science Foundation (NSF) grant MCB-1244570 (TME, ZLS), the National Institutes of Health grants 9 P41 GM104601-23 (JS, ZLS) and GM112659 (ZLS), the National Institutes of Health New Innovator Award 1DP2GM123494-01 (RW, EV), the U.S. Department of Energy, Office of Science, Biological and Environmental Research as part of the Adaptive Biosystems Imaging Scientific Focus Area (TME), the CUDA Center of Excellence at the University of Illinois (JS), postdoctoral fellowships from the European Molecular Biology Organization and Human Frontier Science Program (JM), the Weizmann Institute Women in Science Program (JM), and the Center for Integrated Protein Science Munich (WB). This work was made possible, in part, by resources from the National Center for Supercomputing Applications (TME).
References
- 1.Chandler DE, Strümpfer J, Sener M, Scheuring S, Schulten K. Light Harvesting by Lamellar Chromatophores in Rhodospirillum photometricum. Biophys J. 2014;106:2503–2510. doi: 10.1016/j.bpj.2014.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cartron ML, Olsen JD, Sener M, Jackson PJ, Brindley AA, Qian P, Dickman MJ, Leggett GJ, Schulten K, Hunter CN. Integration of Energy and Electron Transfer Processes in the Photosynthetic Membrane of Rhodobacter Sphaeroides. Biochim Biophys Acta – Bioener. 2014;1837:1769–1780. doi: 10.1016/j.bbabio.2014.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Sener M, Stone JE, Barragan A, Singharoy A, Teo I, Vandivort KL, Isralewitz B, Liu B, Goh BC, Phill JC. Visualization of Energy Conversion Processes in a Light Harvesting Organelle at Atomic Detail. Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis. 2014 [Google Scholar]
- 4.Stone JE, Sener M, Vandivort KL, Barragan A, Singharoy A, Teo I, Ribeiro JV, Isralewitz B, Liu B, Goh BC, et al. Atomic Detail Visualization of Photosynthetic Membranes With GPU-accelerated Ray Tracing. Parall Comp. 2016;55:17–27. doi: 10.1016/j.parco.2015.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sener M, Strumpfer J, Singharoy A, Hunter CN, Schulten K. Overall Energy Conversion Efficiency of a Photosynthetic Vesicle. eLife. 2016;5 doi: 10.7554/eLife.09541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mahamid J, Pfeffer S, Schaffer M, Villa E, Danev R, Cuellar LK, Forster F, Hyman AA, Plitzko JM, Baumeister W. Visualizing the Molecular Sociology at the HeLa Cell Nuclear Periphery. Science. 2016;351:969–972. doi: 10.1126/science.aad8857. [DOI] [PubMed] [Google Scholar]
- 7.Beck F, Unverdorben P, Bohn S, Schweitzer A, Pfeifer G, Sakata E, Nickell S, Plitzko JM, Villa E, Baumeister W, et al. Near-atomic Resolution Structural Model of the Yeast 26S Proteasome. Proc Natl Acad Sci USA. 2012;109:14870–14875. doi: 10.1073/pnas.1213333109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Roberts E, Magis A, Ortiz JO, Baumeister W, Luthey-Schulten Z. Noise Contributions in an Inducible Genetic Switch: A Whole-cell Simulation Study. PLoS Comput Biol. 2011;7:e1002010. doi: 10.1371/journal.pcbi.1002010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hutchison CA, Chuang RY, Noskov VN, Assad-Garcia N, Deerinck TJ, Ellisman MH, Gill J, Kannan K, Karas BJ, Ma L, et al. Design and Synthesis of a Minimal Bacterial Genome. Science. 2016;351 doi: 10.1126/science.aad6253. [DOI] [PubMed] [Google Scholar]
- 10.Hallock MJ, Stone JE, Roberts E, Fry C, Luthey-Schulten Z. Simulations of Reaction Diffusion Processes over Biologically-relevant Size and Time Scales Using Multi-GPU Workstations. Parallel Comput. 2014;40:86–99. doi: 10.1016/j.parco.2014.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Peterson JR, Hallock MJ, Cole JA, Luthey-Schulten ZA. A Problem Solving Environment for Stochastic Biological Simulations. PyHPC 2013. 2013 [Google Scholar]
- 12.Earnest TM, Lai J, Chen K, Hallock MJ, Williamson JR, Luthey-Schulten Z. Toward a Whole-Cell Model of Ribosome Biogenesis: Kinetic Modeling of SSU Assembly. Biophys J. 2015;109:1117–1135. doi: 10.1016/j.bpj.2015.07.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Earnest TM, Cole JA, Peterson JR, Hallock MJ, Kuhlman TE, Luthey-Schulten Z. Ribosome Biogenesis in Replicating Cells: Integration of Experiment and Theory. Biopolymers. 2016;105:735–751. doi: 10.1002/bip.22892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Peterson JR, Cole JA, Fei J, Ha T, Luthey-Schulten ZA. Effects of DNA Replication on mRNA Noise. Proc Natl Acad Sci USA. 2015;112:15886–15891. doi: 10.1073/pnas.1516246112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Isaacson SA, McQueen DM, Peskin CS. The Influence of Volume Exclusion by Chromatin on the Time Required to Find Specific DNA Binding Sites by Diffusion. Proc Natl Acad Sci USA. 2011;108:3815–3820. doi: 10.1073/pnas.1018821108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Isaacson SA, Larabell CA, Gros MAL, McQueen DM, Peskin CS. The Influence of Spatial Variation in Chromatin Density Determined by X-Ray Tomograms on the Time to Find DNA Binding Sites. Bull Math Biol. 2013;75:2093–2117. doi: 10.1007/s11538-013-9883-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mastronarde DN. Automated Electron Microscope Tomography Using Robust Prediction of Specimen Movements. J Struct Biol. 2005;152:36–51. doi: 10.1016/j.jsb.2005.07.007. [DOI] [PubMed] [Google Scholar]
- 18.Kremer JR, Mastronarde DN, McIntosh J. Computer Visualization of Three-Dimensional Image Data Using IMOD. J Struct Biol. 1996;116:71–76. doi: 10.1006/jsbi.1996.0013. [DOI] [PubMed] [Google Scholar]
- 19.Galaz-Montoya JG, Flanagan J, Schmid MF, Ludtke SJ. Single Particle Tomography in EMAN2. J Struct Biol. 2015;190:279–290. doi: 10.1016/j.jsb.2015.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Castaño-Díez D, Kudryashev M, Arheit M, Stahlberg H. Dynamo: A Flexible, User-friendly Development Tool for Subtomogram Averaging of Cryo-EM Data in High-performance Computing Environments. J Struct Biol. 2012;178:139–151. doi: 10.1016/j.jsb.2011.12.017. [DOI] [PubMed] [Google Scholar]
- 21.Martinez-Sanchez A, Garcia I, Asano S, Lucic V, Fernandez J-J. Robust Membrane Detection Based on Tensor Voting for Electron Tomography. J Struct Biol. 2014;186:49–61. doi: 10.1016/j.jsb.2014.02.015. [DOI] [PubMed] [Google Scholar]
- 22.Roberts E, Stone JE, Luthey-Schulten Z. Lattice Microbes: High-performace Stochastic Simulation Method for the Reaction-diffusion Master Equation. J Comp Chem. 2013;3:245–255. doi: 10.1002/jcc.23130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hallock MJ, Luthey-Schulten Z. Improving Reaction Kernel Performance in Lattice Microbes: Particle-Wise Propensities and Run-Time Generated Code. IPDPS Workshops. 2016:428–434. [Google Scholar]
- 24.Pérez F, Granger BE. IPython: a System for Interactive Scientific Computing. Comput Sci Eng. 2007;9:21–29. [Google Scholar]
- 25.Jones E, Oliphant T, Peterson P. SciPy: Open Source Scientific Tools for Python. 2017 http://www.scipy.org/, (accessed January 19, 2017)
- 26.van der Walt S, Colbert SC, Varoquaux G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput Sci Eng. 2011;13:22–30. [Google Scholar]
- 27.Humphrey W, Dalke A, Schulten K. VMD: Visual Molecular Dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 28.Stone JE, Sherman WR, Schulten K. Immersive Molecular Visualization with Omnidirectional Stereoscopic Ray Tracing and Remote Rendering. International Parallel and Distributed Processing Symposium Workshop (IPDPSW) 2016:1048–1057. doi: 10.1109/IPDPSW.2016.121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tyson CB, Lord PG, Wheals AE. Dependency of Size of Saccharomyces cerevisiae Cells on Growth Rate. J Bacteriol. 1979;138:92–98. doi: 10.1128/jb.138.1.92-98.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Wei D, Jacobs S, Modla S, Zhang S, Young CL, Cirino R, Caplan J, Czymmek K. High-resolution Three-dimensional Reconstruction of a Whole Yeast Cell using Focused-ion Beam Scanning Electron Microscopy. BioTechniques. 2012;53:41–48. doi: 10.2144/000113850. [DOI] [PubMed] [Google Scholar]
- 31.Yang Q, Rout MP, Akey CW. Three-Dimensional Architecture of the Isolated Yeast Nuclear Pore Complex: Functional and Evolutionary Implications. Mol Cell. 1998;1:223–234. doi: 10.1016/s1097-2765(00)80023-4. [DOI] [PubMed] [Google Scholar]
- 32.Schneiter R, Brügger B, Sandhoff R, Zellnig G, Leber A, Lampl M, Athenstaedt K, Hrastnik C, Eder S, Daum G, et al. Electrospray Ionization Tandem Mass Spectrometry (Esi-Ms/Ms) Analysis of the Lipid Molecular Species Composition of Yeast Subcellular Membranes Reveals Acyl Chain-Based Sorting/Remodeling of Distinct Molecular Species En Route to the Plasma Membrane. J Cell Biol. 1999;146:741–754. doi: 10.1083/jcb.146.4.741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Dupres V, Dufrêne YF, Heinisch JJ. Measuring Cell Wall Thickness in Living Yeast Cells Using Single Molecular Rulers. ACS Nano. 2010;4:5498–5504. doi: 10.1021/nn101598v. [DOI] [PubMed] [Google Scholar]
- 34.Maul G. Quantitative Determination of Nuclear Pore Complexes in Cycling Cells with Differing DNA Content. J Cell Biol. 1977;73:748–760. doi: 10.1083/jcb.73.3.748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aitchison JD, Rout MP. The Yeast Nuclear Pore Complex and Transport Through It. Genetics. 2012;190:855–883. doi: 10.1534/genetics.111.127803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.von der Haar T. A Quantitative Estimation of the Global Translational Activity in Logarithmically Growing Yeast Cells. BMC Syst Biol. 2008;2:87. doi: 10.1186/1752-0509-2-87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Grünwald D, Singer RH, Rout M. Nuclear export dynamics of RNA–protein complexes. Nature. 2011;475:333–341. doi: 10.1038/nature10318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wickramasinghe VO, Laskey RA. Control of Mammalian Gene Expression by Selective mRNA Export. Nat Rev Mol Cell Biol. 2015;16:431–442. doi: 10.1038/nrm4010. [DOI] [PubMed] [Google Scholar]
- 39.Geisberg JV, Moqtaderi Z, Fan X, Ozsolak F, Struhl K. Global Analysis of mRNA Isoform Half-Lives Reveals Stabilizing and Destabilizing Elements in Yeast. Cell. 2014;156:812–824. doi: 10.1016/j.cell.2013.12.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Futcher B, Latter GI, Monardo P, McLaughlin CS, Garrels JI. A Sampling of the Yeast Proteome. Mol Cell Biol. 1999;19:7357–7368. doi: 10.1128/mcb.19.11.7357. [DOI] [PMC free article] [PubMed] [Google Scholar]


