Estimating Initial Viral Levels during Simian Immunodeficiency Virus/Human Immunodeficiency Virus Reactivation from Latency

ABSTRACT

Human immunodeficiency virus (HIV) viremia rebounds rapidly after treatment interruption, and a variety of strategies are being explored to reduce or control viral reactivation posttreatment. This viral rebound arises from reactivation of individual latently infected cells, which spread during ongoing rounds of productive infection. The level of virus produced by the initial individual reactivating cells is not known, although it may have major implications for the ability of different immune interventions to control viral rebound. Here we use data from both HIV and simian immunodeficiency virus (SIV) treatment interruption studies to estimate the initial viral load postinterruption and thereby the initial individual reactivation event. Using a barcoded virus (SIVmac239M) to track reactivation from individual latent cells, we use the observed viral growth rates and frequency of reactivation to model the dynamics of reactivation to estimate that a single reactivated latent cell can produce an average viral load equivalent to ∼0.1 to 0.5 viral RNA (vRNA) copies/ml. Modeling of treatment interruption in HIV suggests an initial viral load equivalent of ∼0.6 to 1 vRNA copies/ml. These low viral loads immediately following latent cell reactivation provide a window of opportunity for viral control by host immunity, before further replication allows viral spread. This work shows the initial levels of viral production that must be controlled in order to successfully suppress HIV reactivation following treatment interruption.

IMPORTANCE Current treatment for HIV is able to suppress viral replication and prevent disease progression. However, treatment cannot eradicate infection, because the virus lies silent within latently infected cells. If treatment is stopped, the virus usually rebounds above the level of detection within a few weeks. There are a number of approaches being tested aimed at either eradicating latently infected cells or controlling the virus if it returns. Studying both the small pool of latently infected cells and the early events during viral reactivation is difficult, because these involve very small levels of virus that are difficult to measure directly. Here, we combine experimental data and mathematical modeling to understand the very early events during viral reactivation from latency in both HIV infection of humans and SIV infection of monkeys. We find that the initial levels of virus are low, which may help in designing therapies to control early viral reactivation.

INTRODUCTION

Despite the effectiveness of current combination antiretroviral therapy (cART) in controlling human immunodeficiency virus (HIV) replication, treatment must be continued for life because in the vast majority of individuals, treatment interruption results in rapid viral recrudescence, reseeding of the viral reservoir, and disease progression. A number of studies have demonstrated that the rebounding viral population after treatment interruption is less diverse than that observed either pretreatment or in the proviral reservoir during therapy (1–5). The distribution of viral quasispecies appears similar to that of the “founder virus(es)” observed during primary HIV infection (6), consistent with the concept of a small number of “reactivation founder” viruses arising from individual latent cells. However, where the initial reactivation event occurs, how frequently it occurs, and how this virus subsequently spreads are difficult to determine because this event likely occurs stochastically, producing extremely low levels of virus, and in diverse tissue sites where latently infected cells reside within the body.

We have recently developed two novel methods for studying HIV reactivation from latency. The first utilizes the time to recrudescence of virus after treatment interruption across a cohort of patients to estimate an average frequency for the cohort. The second method estimates the frequency of reactivation, using the relative sizes of different reactivation founder clonotypes observed during viral recrudescence, and the growth rate of virus (7, 8). Here we use a modeling approach on data from a cohort of patients undergoing treatment interruption to estimate the equivalent level of virus in plasma produced during a single HIV reactivation event. Furthermore, we utilize data from a recently developed macaque model of reactivation from latency involving infection with a barcoded simian immunodeficiency virus, SIVmac239 (SIVmac239M), and analytical treatment interruption to determine reactivation rates (7). The use of a barcoded virus allows for the identification of individual reactivation events. The reactivation rates and initiation of new rounds of infection ranged between once every 0.75 h and once every 3 days, depending on the timing and duration of suppressive cART (7). The frequency of latent cell reactivation within an individual animal allowed for extrapolation back to the initial viral load levels at the time of reactivation from latency. Using a modeling approach that considers the initial timing and growth rate of virus, we estimate the plasma virus equivalent level of virus produced by a single reactivating cell in HIV and SIV infection. Together, this provides important insights into the early dynamics of virus reactivation following treatment interruption.

RESULTS

Estimating the initial viral level during HIV reactivation after treatment interruption.

Analysis of HIV and SIV sequence diversity during viral rebound following interruption of combination antiretroviral therapy (cART) suggests that individual latently infected cells reactivate randomly and independently, leading to the observation of a limited number of distinct viral genomes initiating recrudescence (1, 7). This is thought to result from viral production by individual latent cells, followed by the spread and exponential expansion of this virus at the site of reaction and then its spread to other sites. At the time of detection, virus from several reactivation founders may be detected in plasma or within tissues. A major question is, how much virus is produced by a single reactivating cell? That is, how much virus is available for successful transfer of virus to new targets allowing for outgrowth of each reactivating lineage? One way to estimate this would be to simply extrapolate back from the growth curve of virus, to find what viral level it predicted at the moment of interruption (Fig. 1A). However, there are two significant caveats with this approach: first, there is an unknown delay between treatment interruption and when drug levels decrease sufficiently to allow viral replication (“drug washout time” [w]), and second, because reactivation is assumed to occur randomly, the first reactivation event would not necessarily occur immediately once the drug had been removed (i.e., a stochastic delay to the first event). If, for example, reactivation occurred on average once a day, then in 50% of patients the first reactivation would occur sometime on the first day after sufficient drug washout. However, in another 25%, reactivation would occur between the first and second days, and for another 25%, reactivation would occur sometime after the second day. Thus, if extrapolation back from the viral growth curve is used to estimate the initial viral growth at the time of reactivation, it remains unclear whether this reactivation occurred on day 1, 2, or 3. Uncertainty in estimates from any individual subject leads to different estimates of initial viral load depending on which day reactivation occurred.

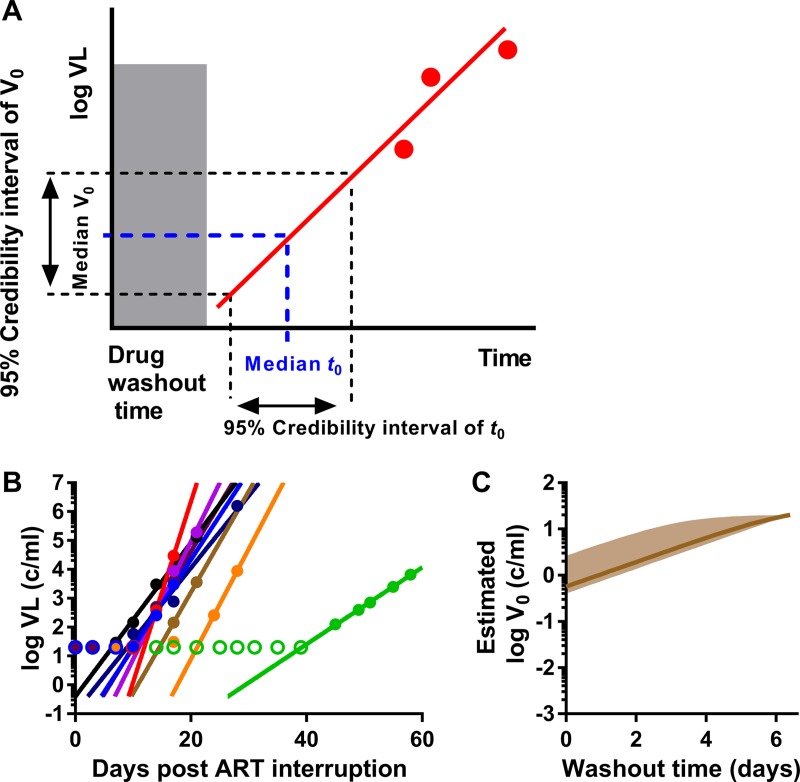
FIG 1.

Estimation of initial viral load during HIV reactivation. (A) Schematic of estimation of median expected initial viral load (V₀) and 95% confidence interval of plasma virus level during reactivation. For a given drug washout time and knowing the frequency of reactivation, we estimate the median and confidence intervals of the initial reactivation time. Then, based on extrapolation of the viral growth, we can estimate the corresponding median initial viral load and its confidence interval. Red solid circles are the measured viral loads after reactivation, and the red line is the fitted viral growth trajectory. (B) Best-fit trajectories of viral growth for 9 patients undergoing treatment interruption. Empty circles represent the detection threshold. (C) Estimated initial viral load dependent on drug washout time. Solid line, expected median of initial viral load; shaded area, 95% credibility band.

Previous work on HIV reactivation after treatment interruption suggests that the average frequency of reactivation is approximately once a week (8, 9). Thus, after interruption and drug washout, there is a large potential stochastic delay and therefore considerable uncertainty about when the first reactivation event might occur in a given patient. However, if a cohort of patients are examined together, then the probability of reactivation occurring in at least one patient in a short interval after treatment interruption becomes much higher. To estimate the initial viral load in humans, data from an analytical treatment interruption (ATI) study testing the impact of the latency-reversing agent panobinostat was utilized (10). This study was chosen because patients were sampled regularly (twice weekly) after ATI, and thus we can more accurately estimate both the initial time of viral reactivation and the viral growth rate. The average frequency of reactivation was estimated by fitting a survival curve of time to detection of reactivation (as described previously [8]), resulting in an average time between reactivation events of 7.6 days (i.e., the frequency of reactivation, λ, is 0.132 per day). Taking into account the total number of assessable patients across the cohort (n = 9), we have an median delay between any reactivation event occurring in any patient of 14 h (i.e., n × λ = 1.19 reactivations per day across the cohort). Thus, we can extrapolate the growth curves of all patients to estimate the viral load at the predicted time of the first reactivation (Fig. 1A and B) (see Materials and Methods).

The relationship between the assumed drug washout time and the estimated values of initial viral load is shown in Fig. 1C. By way of example, if drug washout was completed by time zero (the first-time therapy is omitted), then the best estimate for the initial viral load would be 0.57 copies/ml (95% confidence interval [CI] = 0.4 to 2.63). If the drug washout time was 24 h after the first missed dose, then the expected median initial viral level would be equivalent to around 1.0 copies/ml (95% CI = 0.74 to 4.75). If washout time was 2 days, then the initial viral level would be equivalent to around 1.9 copies/ml plasma (95% CI = 1.36 to 8.2). Therefore, the initial estimated viral load changes with the estimate of the therapeutic half-life.

One caveat to this study is that the patients came from a study of the latency-reversing agent panobinostat, and all subjects were previously treated with panobinostat. However, given that panobinostat had minimal effects on the HIV reservoir and was administered 36 to 46 weeks before the treatment interruption, it is unlikely that this would affect the initial viral load of rebounding virus.

Estimating the initial level of virus in SIV infection.

We have recently developed a macaque model of infection with a barcoded virus (SIVmac239M), in which animals are infected with a swarm of 10,000 different SIV clonotypes and treated soon after infection for various amounts of time (7). SIV rebound from the tagged-viral reservoir occurs soon after treatment interruption, and individual clonotypes can be identified within the rebounding pool through deep sequencing of plasma virus. We have recently used this approach to estimate the frequency of reactivation after treatment interruption. As part of this study, one cohort of 6 animals was infected and treated at day 4 for 300 to 480 days. These animals had slightly higher reactivation rates than those observed for HIV, with rates ranging from approximately once every 1.4 days to once every 3 days. Thus, we considered the cohort of animals as a group and considered the time to the first reactivation event across the cohort. That is, taking into account the reactivation rates of individual animals across the whole cohort, the median time to the first reactivation event in the cohort becomes short (5.1 h), and the probability of at least one virus (in any animal) not reactivating after a certain time becomes very low. Using this approach, we estimate that if the drug washout time is zero, then the best estimate for the initial viral load (V₀) is 0.06 vRNA copies/ml (95% CI, 0.049 to 0.16). If the delay in drug washout is estimated at 1 day, then the estimate of median V₀ is 0.17 copies/ml (95% CI, 0.14 to 0.46) (Fig. 2B and C).

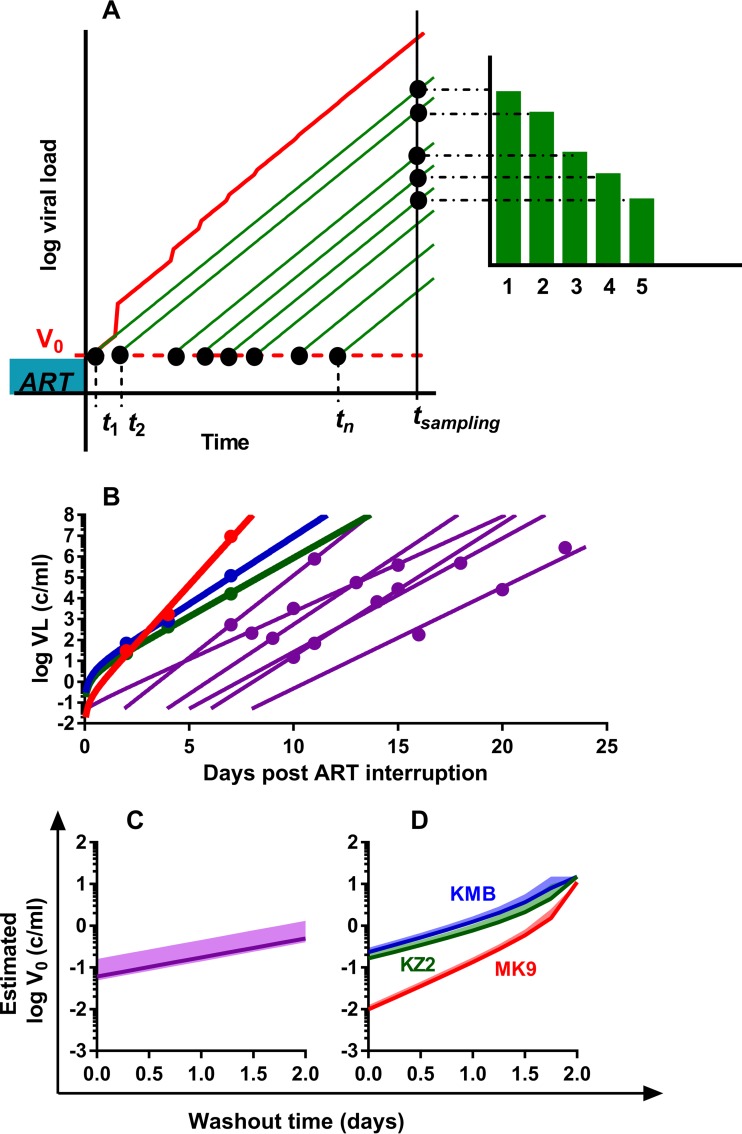
FIG 2.

Estimation of the initial viral load in SIVmac239M-infected macaques. (A) Correcting the trajectory of total viral load in animals with frequent reactivation. In monkeys with frequent reactivation, the total viral load (red) increases faster than the growth of virus from individual reactivation events (green). Time points t₁,.,t_n are the times of reactivation of individual latently infected cells; green curves are the viral loads of each reactivation founder; the red curve is the total viral load. Green bars are the counts of sequences that correspond to the viral load of i-th rebounder. (B) Best-fit trajectories of viral growth for 9 monkeys. Best-fit trajectories of viral growth for a cohort of three animals with a high reactivation rate, analyzed individually (results for MK9, KMB, and KZ2 are shown by red, blue, and green curves, respectively), and for a cohort of animals treated on day 4 (purple lines, n = 6). (C) Estimated initial viral load of a cohort of 6 animals treated day 4 postinfection, assuming different drug washout times. Solid line, expected median of initial viral load; shaded area, 95% credibility band. (D) Estimated initial viral load for the three individual animals assuming different washout times. Solid line, expected median of initial viral load for each animal (colored as described for panel B); shaded area, 95% credibility band.

Our previous study also included a cohort of three animals (MK9, KMB, and KZ2) that were treated on day 6 postinfection for 80 days. Upon interruption of treatment, these animals showed very high rates of viral reactivation of between 16 and 32 events per day, which likely resulted from the short course of treatment in these animals. Importantly, the high level of latent cell reactivation in these animals treated on day 6 significantly increases our confidence that the first reactivation event occurred very soon after drug washout (i.e., that the stochastic delay in an individual animal was extremely short, so individual animals can be studied rather than the group as a whole). However, this high rate of reactivation also creates a separate issue to consider in these animals. When total viral load during rebound is measured, it represents the sum of all the reactivation events that have occurred up to that time (the cumulative viral load). In the case of frequent reactivation, this means that extrapolation from the total viral load may be misleading, as it overestimates the contribution of a single reactivation event (Fig. 2A).

In order to estimate the initial viral level from a single reactivating latent cell, we developed a mathematical model to take into account multiple reactivation events in one individual (see Materials and Methods), as well as a distribution of the estimated time of viral reactivation. For each animal, we estimated the median and 95% confidence intervals of the initial viral load assuming different drug washout times (Fig. 2D). If the washout time of drug is short (i.e., w = 0, meaning that virus is able to grow immediately after the first missed treatment), then the estimated initial plasma viral load produced by a single reactivation event was 0.01 vRNA copies/ml (95% CI = 0.009 to 0.013), 0.23 vRNA copies/ml (95% CI = 0.22 to 0.3), or 0.16 vRNA copies/ml (95% CI = 0.16 to 0.21) for animal MK9, KMB, or KZ2, respectively. Alternatively, if the washout time was 1 day, then the estimated initial plasma viral load produced by a single reactivation event was 0.134 (95% CI = 0.127 to 0.173), 1.24 (95% CI = 1.17 to 1.67), or 0.77 (95% CI = 0.71 to 1.07) vRNA copies/ml, respectively. The very low estimates of initial viral load for animal MK9 appear to arise largely from the very high estimated replication rate of virus in this animal (2.55/day, versus 1.5 and 1.3/day for KMB and KZ2, respectively) (Fig. 2B), meaning that extrapolation backwards from the time of detection leads to much lower values. It is unclear whether this estimated difference in SIV replication rate arose from host, viral, or measurement factors.

Analysis of the reactivating clonotypes in animal KZ2 also shows an unusual feature: one clonotype that is at a much higher proportion than the other rebounding clones. This dominant clonotype was 94-fold higher than the next clonotype, but the average ratio of all the subsequent clonotypes was 1.13. We reasoned that the largest clonotype may have contributed to a measurable “blip” of 40 vRNA copies/ml observed on day 0 post-ATI. In this case, it is interesting to consider the expected ratios if both the “blip clonotype” and the next-largest clonotype were growing at the same time. The blip clonotype was 94 times larger than the next largest clonotype when virus was sequenced at day 7. Thus, if both clonotypes were growing at the same rate, this suggests that the second-largest clonotype would have needed to be at 0.43 vRNA copies/ml (40 copies divided by 94) at time zero. If the second-largest clonotype represents a new “rebound” clonotype growing soon after ATI, then it would have been at 0.43 vRNA copies/ml, similar to the estimates based on extrapolation of viral growth.

DISCUSSION

A number of strategies are currently being investigated aimed at providing remission or cure from HIV by either decreasing the number of latently infected cells or prolonging the time to viral rebound after stopping ART (11–13). At the same time, efforts are also being made to enhance HIV-specific immune responses to facilitate control of HIV replication after reactivation from latency. Understanding the dynamics of reactivation and viral production from latently infected cells is important to guiding these strategies aimed at preventing or controlling viral recrudescence after treatment cessation. For example, the amount of virus produced by a reactivating latent cell may affect the ease with which it may be neutralized by antibodies. However, this is extremely difficult to measure directly, due to both the low levels of virus and the random timing of reactivation events. Here we have combined mathematical modeling with experimental data from HIV and SIV infections to better understand the dynamics of these early events.

Using our models of viral reactivation, we extrapolated from the observed viral growth trajectories to estimate the initial level of plasma virus produced by a single reactivation event. We used three different approaches to estimate the initial viral load across two cohorts of animals (total, n = 9). This estimate is strongly dependent on the drug washout time (when the virus was first able to replicate), and thus we calculated the initial viral load for different washout times. For SIVmac239M, a single reactivation event is estimated to result in 0.01 to 0.23 vRNA copies/ml if drug washout is very short (w = 0, i.e., virus replicates immediately after the first missed dose). If drug washout takes longer (w = 1, i.e., viral replication occurs 24 h after the first missed dose), then the initial viral level was around 0.13 and 1.25 vRNA copies/ml. For HIV, we also estimate the initial level of virus produced, based on data from a cohort of 9 individuals. The initial level of virus produced by a single reactivating cell in HIV is 0.57 vRNA copies/ml (95% CI = 0.4 to 2.63) for immediate viral growth and 1.0 vRNA copies/ml (95% CI = 0.74 to 4.75) when washout time is 1 day (Fig. 3). This estimate of initial viral level is based upon our estimated average frequency of reactivation in HIV of approximately once a week. However, if the reactivation rate in HIV were greater, e.g., at one reactivation per day, this would change the estimated initial viral load only slightly. For example, for washout time of 0, the estimated level would change from 0.57 vRNA copies/ml (for a frequency of once a week) to 0.41 vRNA copies/ml (95% CI = 0.36 to 0.51) for a frequency of once a day.

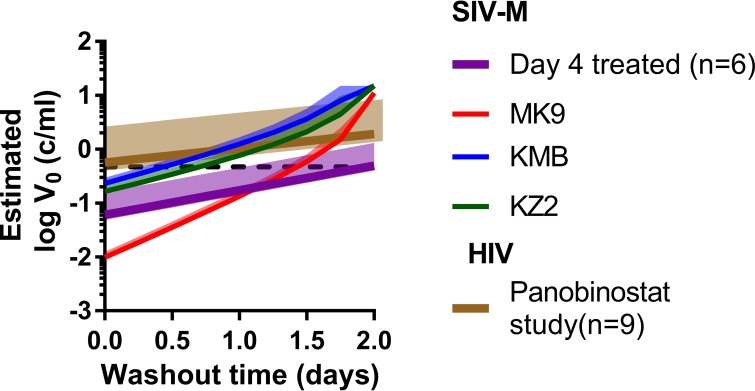
FIG 3.

Summary of the estimated initial viral load during HIV/SIV reactivation from latency. Median expected initial viral loads for a cohort of patients undergoing ART interruption (n = 9, brown line), for a cohort of monkeys treated on day 4 postinfection (n = 6, purple line), and for three individual monkeys treated on day 6 postinfection (red, blue, and green lines) and the estimated value using the viral blip in animal KZ2 (dashed line). For each, the solid line is the expected median of initial viral load, and the shaded area is the 95% credibility band.

These estimates of “plasma viral load equivalent” do not imply that this level of virus was necessarily present or detectable in plasma at that time of latent cell reactivation. It may be that the reactivating latent cell resided in an anatomical site with little or no migration to blood or that there was a delay in this initial migration of virus to blood. In addition, in estimating the initial viral load equivalent in plasma, we assumed that viral growth is exponential from the initial reactivation event in a given latently infected cell through to our later observation, when viral levels were detectable. If early viral growth was faster or slower than the rate that we later observed, then the initial viral load may have been lower or higher, respectively. This might occur if early viral reactivation and growth were to occur in a “permissive site” (leading to faster early growth) or if viral reactivation stimulates immune activation, leading to faster viral replication over time. In the absence of knowledge of early replication rates, we assume constant viral growth rates.

The estimated initial plasma viral load equivalent also does not have a direct prediction of the number of viral copies produced by the reactivated latent cell. We previously estimated that a single virion diluted in the plasma volume of a rhesus macaque would equate to around 2.6 × 10⁻³ copies per ml (7). On this basis, 0.4 copies/ml equates to ∼160 copies of virus produced by the reactivating cell and diluted evenly in the plasma. This can be further translated into a rate of production of virus by reactivating cells. Thus, for example, to produce a steady level of 160 copies of virus and knowing the clearance rate of virus is around 23 day⁻¹ (14), a reactivated cell would need to produce around 3,680 virions per day. The half-life of productively infected cells has been estimated to be around 1 day (15), so if recently reactivated cells had a similar half-life, this implies a “burst size” (total viral production over the cell's life span) of around 3,680 virions. Using a similar calculation for HIV, assuming 3 liters of plasma and a viral level of 1 copy/ml, this implies an HIV burst size of 69,000 virions. Previous estimates of HIV and SIV burst size using a variety of methods have ranged between 10² (16) and 5 × 10⁴ copies (17) (reviewed in reference 18). Thus, given the diversity of methods and estimates, our estimates of viral production rate by recently reactivated latent cells are compatible with previous estimates of viral production from productively infected cells, suggesting that viral production may be similar in recently infected and recently reactivated cells.

A number of modeling studies have investigated the dynamics of viral recrudescence after treatment interruption (19–22). The stochastic nature of individual cell reactivation is difficult to model, and thus many studies have attempted to estimate an average “viral (or infected cell) production rate.” This effectively assumes a constant stream of virus/infected cells, which acts to seed infection, and ignores any potential delays until reactivation or stochastic effects of individual cell behavior. For example, Luo and colleagues found a “reservoir contribution rate” that ranged over 3 orders of magnitude (from 2 × 10⁻⁶ to 1 × 10⁻³ infected cells μl⁻¹ day⁻¹) (21). Modeling by Conway and Perelson also used this “constant production” framework and concluded that the level of (constant) viral production may determine the likelihood of postinterruption immune control (22). However, if viral recrudescence is seeded by reactivation of individual latent cells, patients may vary in both the initial viral load (of an individual reactivation event) and the frequency of these events. However, the viral production by a single reactivated cell sets a “floor” on the minimal level of virus that can reseed infection. More recently, stochastic modeling has been used by Hill et al. to estimate the initial viral load of individual reactivation events (23). That work estimated the initial viral levels to be between 0.03 and 10 vRNA copies/ml for different cohorts, dependent on a number of other parameter assumptions. An important difference between that study and our work is the assumption of high frequencies of HIV reactivation from latency, versus our fitting of the reactivation rate from the data (9, 23).

In our study, the only viral reactivation events observed were those that successfully grew to a level at which we were able to detect plasma virus. Thus, there may also be numerous “failed” reactivation events, where either viral production in latently infected cells produces defective virus or replication competent virus fails to infect sufficient cells to sustain progressive infection. Studies of integrated HIV DNA suggest that over 90% of integrated virus may be defective (24), and it is also possible that replication-competent virus is produced in tissues where it fails to find sufficient target cells to infect. If unsuccessful reactivation events result in similar levels of plasma virus, frequent and overlapping failed reactivation events may help explain the low levels of residual virus observed even under successful ART (25, 26), as well as the occurrence of viral “blips” under therapy (27).

Immune control of HIV after treatment interruption is one strategy for long-term ART remission. Understanding and controlling the earliest events in viral reactivation may prove crucial to such strategies. However, these remain unmeasurable by standard assays. The combination of experimental data and modeling provides insights into events occurring below the level of current detection, and the results suggest that the initial level of virus in plasma produced by a cell reactivating from latency is equivalent to around 0.1 to 1 vRNA copies/ml. Neutralization of these low levels of initial virus is one potential mechanism to prevent viral rebound. Future work to identify the cellular and anatomic sources of rebounding virus may further inform the optimal strategies for preventing HIV rebound after treatment interruption.

MATERIALS AND METHODS

Estimating the effective viral load from a single reactivation event.

Our modeling assumes that viral recrudescence occurs as a result of reactivation of an individual latently infected cell, which produces a level of virus, V₀, which grows exponentially at rate g until detection. The level of virus that can be detected at time t is given by V(t),

$$V\left(t\right)=V_0{e}^{g\left(t-t_0\right)}$$ (1)

where t₀ is the time of reactivation.

The initial level of virus, V₀, can be estimated by extrapolating from the observed viral growth trajectory (after detection) back to an estimated time of initiation of viral growth, t₀. This requires us to estimate both the timing of the initial reactivation event, t₀, and the subsequent viral growth rate, g.

Estimating the time of initial reactivation.

The time of the initial successful reactivation event depends on two factors: first, the initial drug levels and drug half-life (which affect the time until drug levels have decreased sufficiently to allow viral replication, which we term “drug washout time,” denoted as w), and second, the subsequent (stochastic) delay until the first reactivation event occurs. The first factor, drug washout, is difficult to characterize, as it may depend on drug concentrations in cells and tissues. Therefore, we do not attempt to estimate this for different drugs and instead estimate the initial viral load based on different assumptions of the duration of the washout time.

We let F(t,t_d,w) denote the probability that the first reactivation has occurred by time t, where t_d denotes the time at which virus is first detected. The function F(t,t_d,w) can be derived using the frequency, f, of latent cell reactivation. Since virus could have reactivated only between times t = w and t = t_d, the time until the next reactivation event is exponentially distributed on the truncated interval (w, t_d), and the probability that the first reactivation occurs by time t is simply the cumulative distribution of this truncated exponential distribution up until the time of detection. Thus, we have

$$F\left(t,t_d,w\right)=\{\begin{array}{ll}\frac{1-e^{-f\left(t-w\right)}}{1-e^{-f\left(t_d-w\right)}}& w<t<t_d\\ 0& \text{otherwise}\end{array}$$ (2)

For a given washout time w, we expect that the median time to reactivation will be given by the drug washout time plus the time at which there is a 50% probability of reactivation having occurred. This occurs at the time when F(t,t_d,w) = 0.5 (its midpoint value). Thus, the median time to reactivation is given by

$$\text{Median}\hspace{0.17em}\left(t_0\right)=w+F({t,t}_d,w{)}^{-1}\left(0.5\right)$$ (3)

Similarly, the upper and lower 95% confidence bounds can also be calculated using F(t,t_d,w)⁻¹(0.975) and F(t,t_d,w)⁻¹(0.025), respectively.

Estimating the time to reactivation in HIV.

HIV reactivation from latency in humans is thought to occur on average once every 5 to 8 days (8). At this low frequency, we can effectively ignore the contribution of all but the initial reactivation event to total viral load, and we can extrapolate the trajectory of growth of virus for each patient. However, because of the low frequency of reactivation in HIV, the stochastic delay is potentially significant. If we have a population of individuals, the stochastic delay to the first event (in the population) is reduced by the number of individuals. Thus, in a population of n individuals with average reactivation rate f, the cumulative distribution function of time to the first reactivation, F_n(t,t_d,w), is

$$F_n\left(t,t_d,w\right)=\{\begin{array}{ll}\frac{1-e^{-nf\left(t-w\right)}}{1-e^{-nf\left(t_d-w\right)}}& w<t<t_d\\ 0& \text{otherwise}\end{array}$$ (4)

We can again find the median and 95% confidence intervals of the time of the first reactivation event in the population for a given washout time.

Estimating the initial viral load.

Having determined the median and confidence intervals for t₀, we can use these to estimate the median and confidence intervals for the initial viral load, V₀.

Estimation of the initial viral load in subjects with low reactivation rate. (i) Initial viral load at a fixed time of initial reactivation.

In HIV-infected patients who have a low reactivation rate, we can estimate the value of the initial viral load, V₀, at a given value of t₀ (time of initial reactivation) by extrapolating back the observed viral load trajectories of all individuals in the cohort to find the viral load for each patient at time t = t₀. We then take the highest estimated viral load to be the value of V₀ (the highest estimated viral load being assumed to be the earliest reactivator) (Fig. 1A).

(ii) Median and confidence intervals on initial viral load.

To determine the median and 95% confidence intervals of V₀, we perform this calculation at both the median and 95% confidence limits of t₀.

Estimation of the initial viral load in subjects with high reactivation rates.

Extrapolation of the viral growth curve is accurate only when there is a low underlying frequency of reactivation (as we observed in HIV). When the reactivation rate is high, as observed in SIV infection, it is not as simple to estimate the viral growth rate simply from the viral loads measured after detection. That is, the viral growth rate that we measure is for the total viral load (of all reactivation events) and is therefore the sum of the viruses produced by all successful reactivation events up until the time of detection and not the viral load of a single reactivation event. Depending on the initial viral level and the frequency of reactivation, the total viral load may grow significantly faster than the true growth rate of individual reactivation events (Fig. 2A). This is particularly important early on, as the additional virus contributed by each successive reactivation event makes the total viral load rise very quickly, meaning that we cannot simply extrapolate back in time using the observed viral growth trajectory. Therefore, we developed a model that we can use to estimate the initial viral load and the viral growth rate associated with an initial time of viral reactivation, t₀, based on the total viral load and the viral load of the i-th rebounding clonotype (identified by high-throughput sequencing of the barcoded virus [7]), V_i, assuming that rebounding clonotypes are sorted according to their relative counts in descending order. The derivation of the model is shown elsewhere (7, 9).

$$\ln V\left(t\right)=\ln V_0+\ln (e^{g\left(t-t_0\right)}-e^{-\frac{1}{n-1}{\displaystyle \sum _{i=1}^{n-1}\ln (V_i/V_{i+1})}})-\ln (1-e^{-\frac{1}{n-1}{\displaystyle \sum _{i=1}^{n-1}\ln (V_i/V_{i+1})}})$$ (5)

To determine the median value of V₀, we use the model in equation 5 to estimate the value of V₀ at the median value of t₀ previously estimated using equation 3. To derive an estimate for the upper and lower 95% confidence limits for V₀, we substitute the upper and lower confidence limits for t₀ into equation 5 and solve the equation.

Ethics statement.

This work involves the analysis of previously published data from original human and animal studies published elsewhere (7, 10). Details of the ethical approval for the original studies may be found in the original publications.