Simulations of a Vibrissa Slipping along a Straight Edge and an Analysis of Frictional Effects during Whisking

Abstract

During tactile exploration, rats sweep their whiskers against objects in a motion called whisking. Here we investigate how a whisker slips along an object’s edge and how friction affects the resulting tactile signals. First, a frictionless model is developed to simulate whisker slip along a straight edge and compared with a previous model that incorporates friction but cannot simulate slip. Results of both models are compared to behavioral data obtained as a rat whisked against a smooth, stainless steel peg. As expected, the frictionless model predicts larger magnitudes of vertical slip than observed experimentally. The frictionless model also predicts forces and moments at the whisker base that are smaller and have a different direction than those predicted by the model with friction. Estimates for the friction coefficient yielded values near 0.48 (whisker/stainless steel). The present work provides the first assessments of the effects of friction on the mechanical signals received by the follicle during active whisking. It also demonstrates a proof-of-principle approach for reducing whisker tracking requirements during experiments and demonstrates the feasibility of simulating a full array of vibrissae whisking against a peg.

1 INTRODUCTION

RATS use their vibrissae (whiskers) as highly sensitive tactile sensors [1–3]. There are no sensors along the whisker’s length; instead, all mechanical information is transmitted to mechanoreceptors embedded in a follicle at the whisker base. During many exploratory behaviors, rats sweep their whiskers back and forth in a motion known as “whisking” [3, 4] to determine object location, size, orientation, and texture. As yet, however, researchers have little quantitative understanding of the mechanical signals that will be generated at the whisker base as the rat explores different objects.

Recent work has shown that as a rat whisks against a peg, a whisker will slip vertically along the length of the peg, sometimes by as much as 6.1 mm on a single whisk [5]. The vertical slip will affect the shape of the whisker and the tactile signals (forces and moments) that the rat obtains at the whisker base.

In the present work we expand an existing model of whisker bending [5] to include a frictionless mode that simulates the whisker’s slip against a peg (or any straight edge). Results from these frictionless simulations are compared with those obtained with friction to explore the effects of friction on whisking behavior. This comparison allows us to ask how friction affects the forces and moments that the rat will experience at the whisker base. We also use results from simulations with and without friction to predict how much friction changes the contact point location on the peg. Finally, we explore how much of the whisker’s vertical slip can be explained by the kinematic profile with which the rat drives it whiskers.

We conclude by demonstrating the potential utility of the slip model to reduce some requirements for whisker tracking during experiments and to simulate deflections of multiple vibrissae during active whisking behavior.

2 METHODS

2.1 Developing a Model to Compute Whisker Slip

Previous work [5] developed a three-dimensional (3D) model for quasistatic whisker deflections based on principles of linear elastic beam bending. To create this model, first the 3D shape of an undeflected whisker is found, and then the whisker shape is divided into a series of 100 straight, rigid links all of the same length. These links are connected by torsional springs that allow rotation in all directions. The stiffnesses of the springs are determined by Young’s modulus of the whisker. The shear modulus is determined by Poisson’s ratio, and the area moment of inertia is determined by the whisker’s radius at each point.

In all simulations of the present work, Young’s modulus was set to 3.3 GPa [6], and Poisson’s ratio was set to 0.38 [7]. The length of the whisker was obtained from video data gathered during behavioral experiments (see Section 2.3). The base and tip radii for the simulated whisker were based on typical values from the literature. The base radius was chosen to be 100 µm, similar to a C2 whisker [8]. The ratio of the base radius to tip radius [9, 10] was set to 15, resulting in a tip radius of 6.67µm.

The whisker-centered coordinate system is defined as in [5]. The origin is placed at the whisker base, and the positive x-axis points in the direction in which the whisker emerges from the follicle. The x-y plane is defined as the best-fit plane to the proximal 70% of the whisker arc length [11]. The whisker curves concave forward in the positive y-direction. The z-axis is defined according to the right-hand rule. The coordinate system moves with the whisker.

In the model of [5] a force applied out along the whisker creates a moment at the adjacent joint that can be broken down into the components [M_x, M_y, and M_z]. Then linear elastic beam equations determine the angle of bending in all three dimensions about that joint. First the link rotates about its own axis by the amount

$$d\phi =\frac{M_{x}ds}{GJ}$$ (1)

where dφis the amount of rotation about the rigid link’s own axis, M_x is the moment component about the link’s axis, ds is the length of the link, J is the torsional constant for a circular bean defined by J = π⁴/2, and G is the shear modulus. The shear modulus is found using

$$G=\frac{E}{2(1+\nu )}$$ (2)

where E is Young’s modulus of the whisker, and ν is Poisson’s ratio.

The link then rotates according to the bending moment, defined as $M_B=\sqrt{M_y^2+M_z^2}$. It rotates in the direction in which the bending moment acts M_B = tan⁻¹ M_z/M_y and with a magnitude described by the equation:

$$d\theta =\frac{M_{B}ds}{EI}$$ (3)

where ds is the length of the link, d θ is the angle through which the link rotates, E is Young’s Modulus, and I is the area moment of inertia defined by I = πR⁴/4.

The whisker link is simulated to rotate, and the process is iterated down the arc length of the whisker to the base until the entire whisker is deflected. The first node of the whisker, as it inserted into the follicle, was modeled with an elastic boundary condition. This boundary condition forces the displacement y(x) to equal zero at the base but does not constrain the initial slope (dy/dx) of the whisker. Because the whisker is stiffest at the base, the elastic boundary condition gives almost exactly the same result as a rigid boundary condition.

The force remains perpendicular to the whisker at the point of contact (i.e., a frictionless assumption is made along the length of the whisker), but because the model uses the real-world contact point, friction exists in the vertical direction along the peg, acting perpendicular to the whisker. A Nelder-Mead algorithm optimizes over the magnitude and orientation of the applied force and the arc length along the whisker at which it was applied. The cost function is the Euclidean distance from the simulated point of whisker-peg contact to the user-specified contact point location. The model is declared solved when this distance becomes zero, and the two points coincide.

The present work extends this previous model [5] to simulate the whisker’s slip along an edge. Specifically, since the desired contact point along the length of the edge is unknown, the cost function had to be altered. The altered cost function used in the present work requires two quantities to become zero. The first quantity is the Euclidean distance from the point of contact on the whisker to the edge. This requirement forces the whisker to make contact with the edge. The second quantity is the dot product between the edge’s 3D orientation and the direction in which the force was applied on the whisker. This requirement enforces a completely frictionless assumption by constraining the force to be normal to the edge as well as to the whisker. The altered cost function is the only difference between the two models.

In summary, previous work makes explicit use of the 3D location of the tracked contact point. Friction is modeled to exist in the vertical direction along the peg but not along the length of the whisker. We term simulations run in this mode “contact-point” simulations. The present work extends this model to develop “edge-mode” simulations, which assume zero friction and do not require 3D tracking of the contact point.

2.2. Simulations of Rat Whisking Kinematics

In some portions of Results (Figs. 1 and 4), we needed to simulate whisking kinematics. For these figures, we used a morphologically-correct model of the rat head and whisker array [12] and the simulation tool PuppetMaster [13]. These methods have been described in detail previously [13] and all code is available for public download on The Digital Rat website [14]. Briefly, the model combines data from two studies [11, 12] to establish each whisker’s length, intrinsic curvature, and 3D resting angles relative to the rostrocaudal midline. The model then uses kinematic equations obtained from awake whisking rats [11] to simulate a protraction. These equations assume a linear relationship between the whisker’s dorsoventral elevation angle (φ) and the protraction angle (θ) as well as a linear relationship between the roll (ζ) of the whisker about its own axis and the protraction angle (θ). The slopes of these linear relationships vary with whisker row [11], so that each row has a unique kinematic equation of motion.

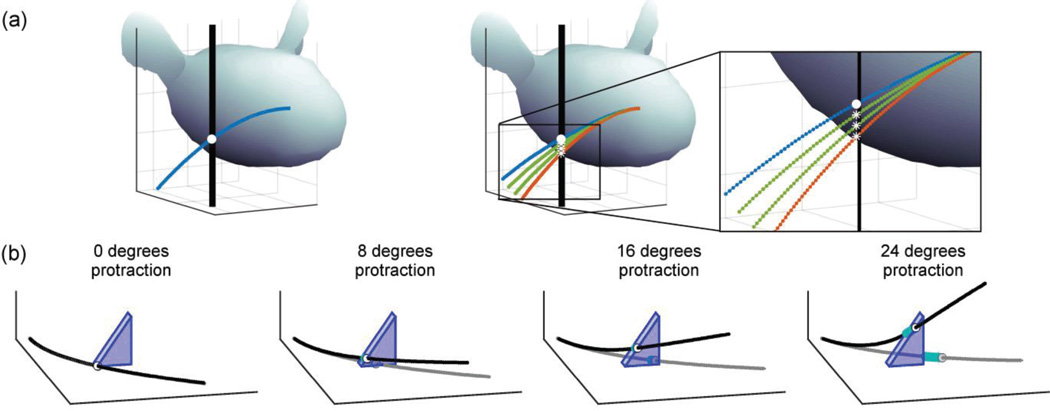
Fig. 1.

Simulations of whisker slip as a rat whisks against a peg or an edge. (a) Illustration of the slip problem. The trajectory of the whisker prior to making contact with the peg is assumed to follow the kinematics defined in [11]. In the left panal, the whisker is shown in blue and the initial contact point location of the whisker on the peg is indicated as a white dot. As the rat protracts further against the peg (right panal) the contact point could be at a wide range of locations along the length of the peg. Three plausible contact point locations are shown as white asterisks. The orange whisker represents the case with no friction. (b) Frames from Supplementary Video 1 show results of a simulation that used “edge mode” to model whisker slip along the edge of a triangular prism. The gray traces represent where the whisker would be had it not contacted the triangular prism, and the black trace illustrates the shape of the deflected whisker.

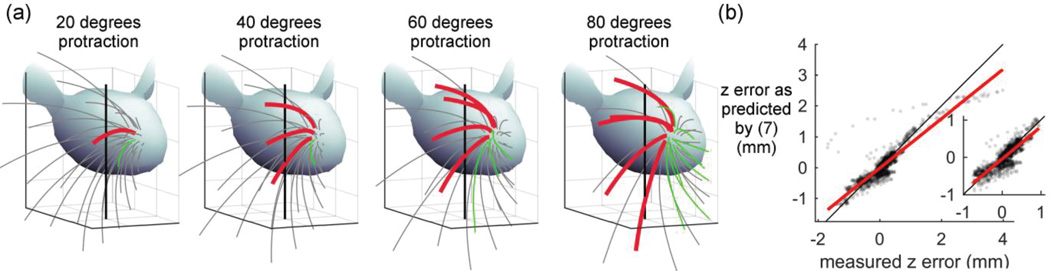
Fig. 4. Edge mode (frictionless) simulations can be used to predict how multiple whiskers will slip against a peg and to place error bounds on the resulting contact point location.

(a) Four frames from Supplementary Video 3, which simulates a rat whisking against a vertical peg. Thick red whiskers are those currently in contact with the peg, and green whiskers are those that came in contact with the peg and subsequently pushed past it. Light gray whiskers never contact the peg. (b) The measured distance in contact point location between edge and contact point mode (z_error) is well predicted by equation (7). This equation thus allows error bounds to be placed on the contact point location calculated during simulations using edge mode. The dots are semi-transparent to show the data density. The inset excludes outliers as defined in the text. Measured z_error ranges between −0.76 and 0.96 mm, and predicted z_error ranges between −1.0 and 1.1 mm. In both Fig. 4b and the inset the identity line is plotted in black and the best fit line is plotted in red (see text for equations).

2.3 Behavioral Experiments

All procedures involving animals were approved in advance by Northwestern’s Animal Care and Use Committee. A female Long-Evans rat between the age of 3–6 months was body restrained and allowed to whisk against a peg. Two Photron 1024 PCI monochrome cameras (1,000 fps, 1/3000 s shutter speed, 60 mm Nikon AF Micro-Nikkor lenses) captured front and top views of the whisking rat. A 2×2 mm² checkerboard grid was used to match pixel length (58 µm) between the two cameras at their distances from the rat (~60 cm). On the left side of the rat’s face, the whiskers were trimmed to lengths < 2mm to leave only the Gamma whisker. The whisker in the top view was tracked using the open-source software Whisk [15], and the whisker in the front view was manually tracked. Both 2D views of the tracked whisker were splined such that nodes were spaced 1 pixel apart, so that nodes were matched between the cameras. The tracked nodes in the two views could then be combined into a 3D whisker [16]. The location of the contact point between whisker and peg was also tracked manually in both views.

To obtain the three orientation angles of the whisker, we directly measured protraction angle (θ) as well as the elevation angle (φ). However, the ζ angle measured during contact is distorted from the ζ angle measured during non-contact. We therefore took advantage of the tight linear relationship between θ and ζ that occurs during whisking [11]. We used θ and ζ measurements from the frames in which the whisker did not make contact with the peg (1,645 frames), found the slope of the best linear fit between θ and ζ and extrapolated ζ angles during contact.

The tracked whisker base point, contact point, and the whisker’s orientation angles were then filtered at 85 Hz, chosen to preserve quasistatic mechanical signals while eliminating tracking jitter. Altering the filtering frequency changes the exact numerical results a little, but does not affect overall results. In contact-point simulations the 3D location of the tracked contact point was used as an input parameter. In edge mode simulations only the (x, y) location of the peg was used, and the z-coordinate of the contact point was not provided to the model.

Both types of simulation (contact-point mode and edge mode) require an accurate estimate of the undeflected shape of the whisker. This shape was determined separately for each contact period using the shape of the whisker at the very end of contact when the whisker is least deflected and least blurred.

In one figure of Results (Fig. 2b) we determine the mean error of the deflected whisker shape as predicted by the simulation model against the experimentally-tracked deflected whisker shape. For each node of the simulated whisker, error was calculated as the absolute value of the shortest Euclidean distance to the experimentally-tracked whisker shape. The mean error was determined by averaging the errors from the whisker base to the point of contact with the peg.

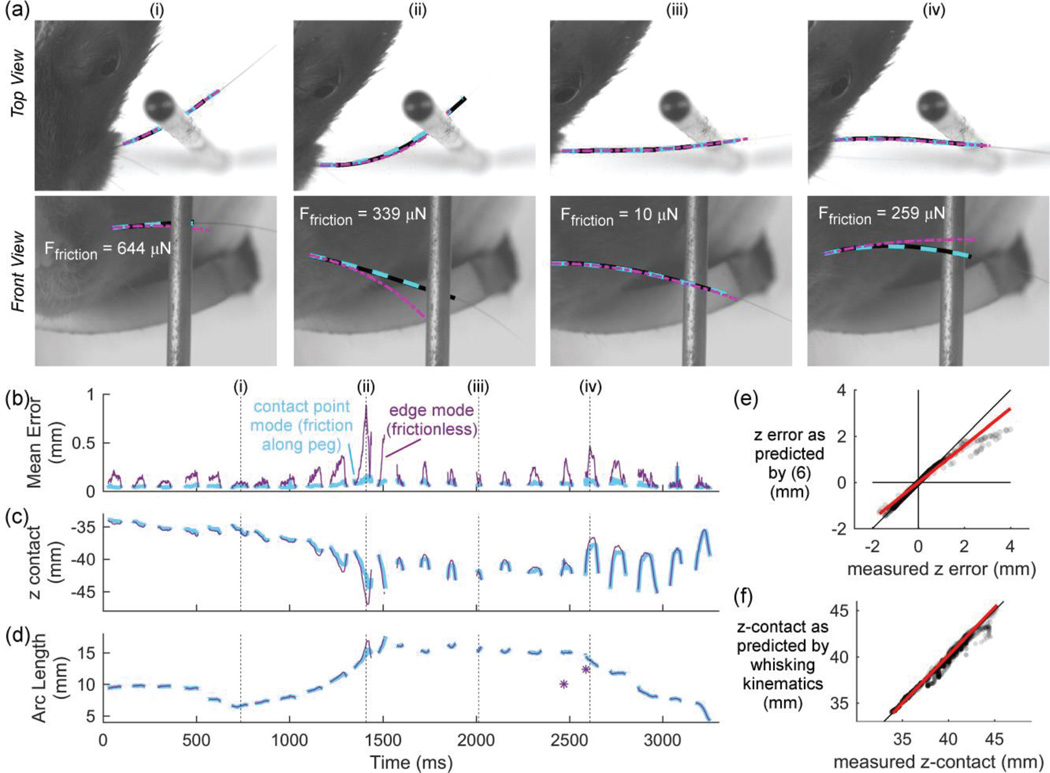
Fig. 2.

Friction affects the shape of the deflected whisker as the rat whisks against a peg. The four vertical dashed lines in (b), (c), and (d) mark the times shown in (a). (a) Top and front views of four video frames from a 3,300 msec trial of contact whisking behavior. The lines show the experimentally-tracked whisker (black), whisker shape predicted using contact-point mode (dashed cyan), and whisker predicted using edge mode (purple dashed-dot). Simulations using contact point mode accurately match the experimentally-tracked whisker in both camera views. The accuracy of this match is seen as a striped black-cyan line because the two traces overlie each other nearly exactly. In contrast, when the simulation is run using edge mode, the predicted whisker shape does not always accurately match the experimentally-tracked whisker. The match is particularly poor in frames (ii) and (iv). (b) The mean error between the experimentally-tracked whisker and the two modes of simulation. (c) The vertical location of contact simulated using contact-point mode and edge mode. Traces are color coded as in (b). (d) The arc length of contact (s_applied) with the peg predicted by the two modes of simulation. Traces are color coded as in (b). (e) Equation (6) offers a good prediction for z_error, the difference in contact point location when computed by edge mode and contact point mode. The dots are semi-transparent to show the data density. The best fit line is plotted in red, and the identity line is plotted in black. (f) In this figure, values on the x-axis show the vertical position of contact of the whisker on the peg as measured by the 3D video. Values on the y-axis represent the predicted vertical point of intersection between the peg and the whisker as computed only with whisking kinematics, with no information about the actual contact point. The dots are semi-transparent to show the data density. The best fit line is plotted in red, and the identity line is plotted in black.

Fig. 2f of Results analyzes how non-contact whisking kinematics affect the geometry of contact. The idea behind this analysis is that even during non-contact whisking the whisker will change its 3D orientation relative to a peg fixed in the laboratory frame. Specifically, elevation and roll of the whisker ensure that there is significant vertical motion associated with non-contact whisking kinematics [5, 11, 13, 17–20]. Thus, once the whisker does actually make contact with a peg, its natural kinematics will tend to drive the contact point location vertically on the peg. This analysis leads to the hypothesis that the amount of vertical slip during contact with the peg can be predicted by projecting the kinematic whisker position from non-contact whisking onto a plane that is oriented parallel to the peg and approximately parallel to length of the whisker.

To test this hypothesis (the analysis of Fig 2f), we placed the 3D non-deflected whisker shape in its non-contact position and orientation and then projected that whisker into the front-on camera view. The 2D projected shape of the whisker yields an imaginary intersection point that the whisker would have made with the peg had its trajectory remained undisrupted by the peg. In Fig. 2f, the vertical component of this (imaginary) intersection point is plotted on the x-axis and the actual vertical contact point location is plotted on the y-axis.

2.4 Force Analysis

The simulations output forces and moments in whisker-centered coordinates as described in Section 2.1. The transverse force and bending moment are defined as $F_T=\sqrt{F_y^2+F_z^2}$ and $M_B=\sqrt{M_y^2+M_z^2}$. The directions of the transverse force and bending moment are defined as F_D = tan⁻¹(F_z/F_y) and M_D = tan⁻¹(M_z/M_y). In the plots of Fig. 3 the first two and last two frames of each contact period were omitted because of the high tracking error associated with contact and detach dynamics.

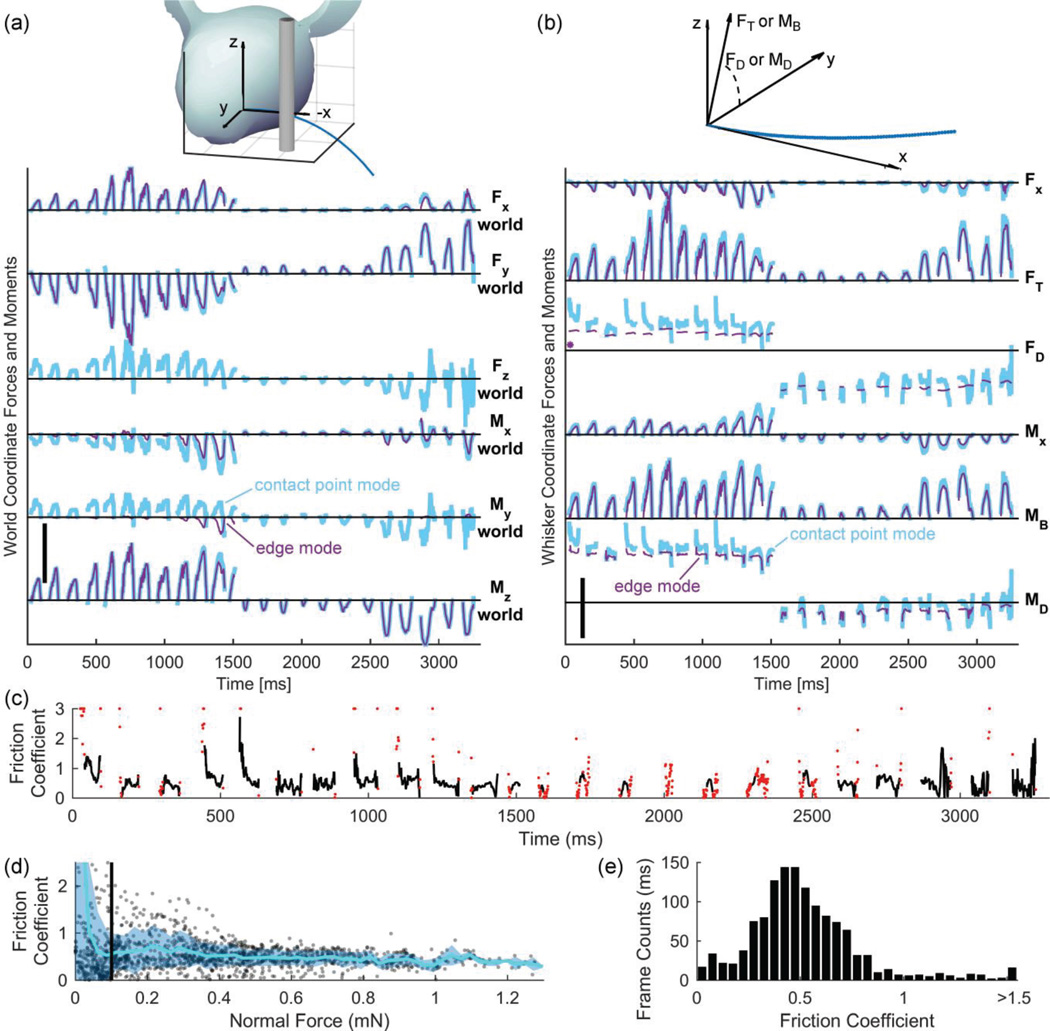
Fig. 3.

The effects of friction on forces and moments at the whisker base. (a) Top: Schematic showing x-, y-, and z- directions in world coordinates. bottom: Forces and moments in world coordinates. Scale bar: F_x-world, F_y-world, and F_z-world: 1 mN; M_x-world: 5 µNm; M_y-world and M_z-world: 10 µNm. (b) Top: Schematic showing x-, y-, and z- directions in whisker-centered coordinates, as well as the definitions for F_T, M_B, F_D, and M_D. Bottom: Forces and moments in whisker-centered coordinates correspond to the mechanical signals directly transmitted to the follicle. One point in the F_D subplot was an outlier and is marked by an asterisk. Scale bar: F_x and F_T: 1 mN; F_D and M_D: 180°; M_x: 2.5 µNm; M_B: 10 µNm. (c) A plot of the value of the friction coefficient (μ) over time. Outlier values are plotted as red dots. Outliers larger than 3 (some as large as 70) are plotted at 3 for clarity. (d) A plot of normal force versus μ. The mean of μ across normal forces is plotted as a blue line, and the shaded region denotes the standard deviation above and below the mean. Normal forces below 0.1 mN, marked by the black vertical line, result in highly variable μ values. Therefore, any μ values resulting from normal forces below this are treated as outliers. (e) Histogram of all calculated values for the friction coefficient (μ), excluding outliers.

Because the whisker’s location had already been tracked in laboratory coordinates defined by the orthogonal cameras, we could transform between whisker and world coordinates in each frame.

Frictional force is defined as F_{z_world} in world coordinates, and the normal force is calculated as $F_{N\_\mathit{\text{world}}}=\sqrt{F_{x\_\mathit{\text{world}}}^2+F_{y\_\mathit{\text{world}}}^2}$. The friction coefficient (μ) was found by dividing the frictional force in every frame by the normal force in that frame, or μ = F_{z_world}/F_N. Because the whisker was always moving up and down the peg, it was not possible to distinguish between static and kinetic friction coefficients: the whisker’s motion is likely to involve stick-slip, which necessarily involves both static and kinetic friction.

3 RESULTS

We begin by describing the simulations that calculate whisker slip, and compare the difference in the geometry of the deflected whisker in the presence and absence of friction. This comparison is then used to examine how friction is likely to affect the tactile experience of the rat and to estimate the friction coefficient. Results conclude by demonstrating the potential utility of whisker slip simulations to model deflections of all whiskers in the array during active whisking behavior.

3.1 Simulations of Slip Along an Edge

As a rodent whisks against a peg, the whisker will slip along its own length, and it will also slip along the length of the peg [5, 21–28]. Recent experiments that have used high-speed video to track the whisker in 3D have shown that the slip along the length of the peg can be quite large – well over 5 mm – even when the peg is placed perpendicular to the primary plane of rotation of the whisker, which should in principle minimize slip magnitude [5]. This same work [5] developed a model for 3D quasistatic whisker deflection during peg contact; however, the model required the contact point location to be input at every time step. The model of [5] could not predict the contact point location after the whisker had slipped along the peg.

The first goal of the present work, then, was to develop a frictionless model that could predict the contact point location of the whisker on the peg during an arbitrary kinematic trajectory. With the assumption of zero friction, there is a single possible contact location for a given kinematic trajectory and peg geometry. The frictionless case represents an upper bound on the amount of slip that the whisker will experience for a given protraction, except for extreme cases of stick-slip.

An example is illustrated in Fig. 1a, which shows whisker-peg contact after a simulated 15° protraction against the peg. The left panel depicts the initial contact location (white dot) that a whisker might make as a rat whisks against the peg. The right panel illustrates the contact point location assuming zero friction (orange whisker), as well as three other possible contact point geometries that assume non-zero friction. With friction, the contact location will always be between the frictionless contact point location and the whisker’s previous path on the peg, except in extreme cases of stick-slip (not shown). One of the possibilities (blue whisker, solid white dot) is that the contact point remains fixed, so that the deflected whisker passes through the same white dot marking the point of initial contact. This situation would occur if the force the whisker exerts parallel to the peg could not overcome friction along the peg, for example, if the whisker got stuck on a small imperfection or protuberance on the peg. Although the whisker might get “stuck” in this manner under real-life conditions, it is unlikely to occur in laboratory experiments with smooth edges.

The other two possibilities show the whisker (green) in contact with the peg at two different locations along its length, both marked with white asterisks, and both plausible locations for the contact point in the presence of uncertain friction. Each of these contact geometries would cause the whisker to assume a slightly different shape and hence generate different mechanical signals at the whisker base. Current 3D models for quasistatic whisker deflection [5] are insufficient to simulate this slip because they require as input the location of the contact point at every time step.

Summarizing, Fig. 1a highlights the need to develop a frictionless model that can predict the exact contact point location after the whisker has slipped along an arbitrary edge. To solve for the frictionless case, we altered the cost function in the optimization of [5] to account for the effects of the whisker slipping along the edge (see Methods). The model could then be run in two complementary modes:

• In contact-point mode, already used in a prior study [5], the inputs to the model are the shape of the undeflected whisker, its position and orientation at every time step, and the 3D position of the whisker-object contact point at every time step. This mode inherently contains the effects of friction along the object, because the movement of the real-world contact point along the edge is provided as an input to the model.

• In edge mode, the inputs to the model are the shape of the undeflected whisker, the position and orientation of the edge, and the position and orientation of the whisker at every time step. The output of the model is the deflected whisker shape, which includes the contact point location, as well as the forces and moments at the whisker base. This mode assumes zero friction.

Fig. 1b shows four frames from Supplementary Video 1, which depicts the changing geometry of the whisker as it is simulated using edge-mode to deflect against a triangular prism. In each subplot, the gray trace represents the shape of the undeflected whisker, while the black trace illustrates the shape of the deflected whisker. As the whisker pushes against the edge the contact point location, indicated by the white dot, is observed to slip along the edge. The point of contact also slips along the whisker’s length, and the history of these locations is shown in blue.

3.2 Friction Affects the Deflected Geometry of the Whisker

Because contact-point mode inherently incorporates friction along the peg, while edge mode operates with the assumption of zero friction, the two modes can be used to quantify the effects of friction in naturalistic whisking conditions. Specifically, we used the model in the two modes to analyze behavioral data obtained with high speed video (1,000 fps) as a rat whisked freely against a peg (see Methods). These simulations allowed us to compare the difference in the geometry of the deflected whisker in the presence and absence of friction.

Fig. 2a shows four frames from Supplementary Video 2. The frames show rat whisking behavior in top (bird’s eye) and front-on views. Each frame shows the experimentally-tracked whisker as a black solid line. The whisker shape predicted using contact-point mode is shown with a dashed cyan line, while the whisker shape predicted using edge mode is represented by a thin purple dashed-dot line. The top row of the figure shows that in the bird’s eye camera view, both modes of simulation yield results that accurately match the tracked whisker: all three lines overlie each other almost exactly. In the front-on view, however, shown in the second row of the figure, the two modes of simulating whisker deflection yield very different solutions. The whisker simulated using contact-point mode accurately captures the shape of the tracked whisker, while the whisker simulated using edge mode is an accurate match in some frames but not in others.

This result is generalized over all frames of contact in Fig. 2b, which plots the errors between the experimentally-tracked whisker and the output of the two modes of the simulation. Error is calculated as the mean distance between the experimentally-tracked whisker and simulation output, measured along the arc length of the whisker from base point to contact point. The error obtained in edge mode, represented by the thin purple line, varies considerably with respect to that obtained from the contact-point mode simulations shown in cyan.

Edge mode error is consistently greater than contact point mode error as a result of two compounded effects. First, unsurprisingly, edge mode always predicts a greater magnitude of vertical slip than occurs in reality. In contrast, simulations in contact-point mode exploit the real-world contact point and thus include the friction that prevents the whisker from slipping up and down the peg. Edge mode therefore predicts a different vertical location for the contact point, as shown in Fig. 2c. For this trial, the contact point location predicted by the edge mode differed from the tracked contact point on average by 0.40 mm but at one point became as large as 4.0 mm.

The second, smaller source of error is that the two modes of simulation predict slightly different locations for the arc length of whisker-object contact (s_applied). Fig. 2d plots s_applied for both simulation modes and illustrates that the predictions differ most during the large deflections immediately before and as the whisker pushes past the peg. In these cases, s_applied is predicted to be significantly larger when the simulation is run in edge mode, consistent with the frictionless assumption.

Summarizing so far, the edge mode simulations (frictionless) clearly predict a different whisker-peg contact point than is observed during real behavior (with friction). To better understand the origin of this difference, we asked whether it could be predicted by the component of the frictional force that acts parallel to the peg and normal to the whisker.

Specifically, we asked whether we could predict the contact-point error in the edge-mode simulations by using the frictional force as input to the standard equation for the linear deflection of a tapered cantilever beam (Equation (4) from reference [29]). When a point force F is applied at location s_applied to a tapered cantilever beam, the vertical deflection y at the contact point s_applied is given by:

$$y(s_{\mathit{\text{applied}}})=\frac{4F}{3E\pi R_{\mathit{\text{base}}}^4}\left(\frac{L{s}_{\mathit{\text{applied}}}^3}{(L-s_{\mathit{\text{applied}}})}\right)$$ (4)

In (4), the variable L is the length of the whisker assuming a truncated cone with linear taper:

$$L=\frac{R_{\mathit{\text{base}}}}{R_{\mathit{\text{base}}}-R_{\mathit{\text{tip}}}}{S}_{\mathit{\text{whisker}}}$$ (5)

where R_base is the radius at the whisker base, R_tip is the radius at the whisker tip, and s_whisker is the arc length of the entire whisker.

To use (4) with the frictional force, we ran the simulation in contact point mode to obtain values for s_applied and F_friction (see section 3.3). The displacement y(s_applied) was taken to be the difference in contact point locations between edge-mode and the experimentally-observed contact point, denoted as z_error. Equation (4) then becomes:

$$Z_{\mathit{\text{error}}}=\frac{4L}{3E\pi R_{\mathit{\text{base}}}^4}\frac{F_{\mathit{\text{friction}}}{s}_{\mathit{\text{applied}}}^3}{L-s_{\mathit{\text{applied}}}}$$ (6)

Fig. 2e plots the relation between z_error predicted from (6) and z_error measured experimentally. The best fit line is shown in red (y = 0.80x + 0.00, r² = 0.95) and the identity line in black (r² = 0.89). Note that the quality of the fit decreases significantly for large bending angles (z error > 2 mm) because equations (4) and (6) assume small angle deflections. Thus, for small angles, (6) is a reasonable method to predict the error that will be generated when assuming a model of frictionless slip.

Notably, the use of (6) does not save the experimenter any effort at all. In order to obtain s_applied and F_friction on the right-hand-side of (6), the simulations had to be run in contact point mode, which requires the contact point to be tracked in all frames. The point of the analysis of (4) – (6) and Fig. 2e is not to reduce tracking effort, but simply to show that there is a predictable relationship between the models with and without friction. Later, in Fig. 4, we will show that the frictionless simulations can be combined with an estimate of the friction coefficient to reduce some tracking requirements.

The frames in Fig. 2a (indicated by vertical lines in Fig. 2b) were specifically chosen to illustrate the relative effects of the parameters used in Fig 2e, namely, friction and s_applied. At the frame marked (i), although the frictional force is large, the contact point is near the base of the whisker, so the shape of the whisker predicted using edge mode is quite similar to the shape of the experimentally-tracked whisker. At frame (ii), both s_applied and the frictional force are large, so the edge-mode simulation predicts the whisker’s shape poorly. Although the arc length of contact at frame (iii) is very large, the frictional force is low, so the shape of the whisker predicted by edge mode closely matches that of the tracked whisker. In the last frame (iv), s_applied is large while the frictional force is intermediate, so the difference between predicted and experimental whisker shape is moderate.

Finally, we performed an analysis intended to predict the magnitude of vertical slip under conditions of low friction. The motivation here is to help experimentalists determine if a 3D model of whisker bending is needed instead of a 2D model. This question was left open by [5], and here we show it can be answered before tracking the entire whisker shape in each frame and before computing any whisker bending.

As described in Methods, we computed the orientation that the whisker would have had if it had not made contact with the peg. For each frame of the non-contact whisking simulation we computed the vertical point of intersection between the peg and the whisker as projected into the front-on camera view. This point of intersection – computed without any whisker bending – predicted with surprising accuracy the actual vertical position of the whisker against the peg. These results are plotted in Fig. 2f on top of the identity line (black). The best fit line, plotted in red, has a slope of 1.03, an intercept of 0.00, and r²= 0.98. The r² value between the fit and the identity line is also 0.98.

Note that the prediction accuracy of this method relies on the chosen plane of projection. The front-on plane worked well in this case because that plane is parallel to the peg and generally parallel to the length of the whisker.

Together, Figs 2c, 2e and 2f demonstrate that in the case that the rat whisks against a smooth, stainless steel peg, the vertical motion of the whisker while in contact can primarily be predicted by 3D whisking kinematics. If the peg were near frictionless (e.g., covered in Teflon), this method of prediction would be even more accurate. As it is, friction is the main factor that causes the whisker to deviate from the vertical location predicted by non-contact kinematics, although this effect is generally less than 1 – 2 mm over the full 10 mm range of Fig. 2f. The consequences of these frictional effects for the tactile signals that the rat will experience are explored in the next section.

3.3 The Mechanical Signals Experienced by the Rat and an Estimate of the Friction Coefficient

Comparing the predictions of contact-point mode and edge mode can also be used to estimate how friction will affect the mechanical signals (i.e., forces and moments at the whisker base) that the rat will experience during whisking behavior. For this analysis, the same behavioral trial is used as in Fig. 2.

First, to gain intuition for how the forces differ when the model does and does not contain friction, we compared the output forces of both modes in world coordinates. The schematic at the top of Fig. 3a shows the directions of the forces represented in world coordinates, and the bottom part of Fig. 3a shows all six force and moment components that the whisker experiences in world coordinates.

Fig. 3a shows that – by definition, given that the peg is oriented vertically – only the simulation with friction (contact-point mode) yields force in the z-direction (F_z). The value of F_z defines the frictional force used in equation (6) to generate Fig. 2e. The z-direction force for the edge mode simulation is exactly zero because it assumes zero friction.

In contrast, the forces F_x and F_y in world coordinates are quite similar between the two simulation modes, as is the moment M_z. The reason they are similar is that the contact point in the two modes has the same x-y location, so the x-and y- directional forces are nearly the same. Because M_z results from a cross product involving F_x and F_y, it is also similar between the two modes of simulation. The magnitudes of these three variables differ slightly between edge mode and contact-point mode only because the whisker tended to slip to a different arc length in the two modes.

Finally, the components of moment M_x and M_y are completely different when computed in the two modes of simulation. In fact, edge mode and contact-point mode often compute M_y to have opposite signs. The sign difference is difficult to see when the magnitude of M_y is low but is particularly visible between 1,100 and 1,500 msec in Figure 3a. This result again illustrates the large effect that friction has on the forces and moments between the peg and whisker.

Fig. 3a shows forces and moments in world coordinates, but the rat’s tactile sensation is based on the mechanical signals measured in the whisker-centered coordinate system (Fig 3b). It is important to use whisker-centered coordinates to describe what a rat will sense because this coordinate system takes into account the orientation of the follicle, including the whisker’s rotation about its own axis as the rat protracts and retracts [11].

In the lower part of Fig. 3b, F_x represents the axial force pushing straight back into the whisker follicle, and M_x represents the twisting moment about the whisker’s own axis. F_T is the transverse force at the whisker base ( $F_T=\sqrt{F_y^2+F_z^2}$), and M_B is the bending moment at the whisker base ( $M_B=\sqrt{M_y^2+M_z^2}$).F_D and M_D are the directions about the follicle in which the transverse force and bending moment act.

Fig. 3b shows that the two modes of simulation yield similar trends for F_x, M_x, F_T, and M_B but that the signals computed using edge mode are all slightly smaller in magnitude. The magnitude reduction occurs because frictional forces have vanished, generating a smaller overall force. It thus becomes clear that friction will tend to alter all forces and moments experienced by the follicle, not just the force in the direction of friction. Comparing Fig. 3a with Fig. 3b reveals some important effects of the frictional force. In world coordinates, friction only affects the force in the direction of the peg. Once converted to whisker-centered coordinates – the signals that the rat will actually obtain via the follicle – the frictional force can be seen to have an influence on all components of force and moment.

Friction plays an even larger role in determining the direction of the transverse force and the direction of the bending moment. Two clear effects can be seen in the F_D and M_D traces in Fig. 3b. First, for each whisk, the direction in which the forces and moments act is more variable in the presence of friction. In edge mode, without friction, the average range of F_D over a whisk is 3.7°, and the average range of M_D over a whisk is 23°. By contrast, the average ranges for F_D and M_D in contact point mode (with friction) are 77°, much higher.

The second effect is an offset in M_D and F_D. The simulation in contact-point mode predicts a direction for the transverse force that is, on average, 23° higher than that predicted using edge-mode. Contact-point mode also predicts a direction for the bending moment that is an average of 16° higher than that predicted using edge-mode. Because the data in this study represent only ~3 sec of whisking, these offsets are probably unique to this whisking configuration, but other configurations are likely to produce similarly significant offsets. Friction will therefore have a large effect on the responses of neurons at multiple levels of the trigeminal system, given that these neurons are well known to be strongly directionally tuned [30–34].

Finally, we used the frictional forces in world coordinates to estimate the friction coefficient (μ) between the whisker and the stainless steel peg. The value of μ was calculated by dividing the frictional force by the normal force at every frame, as shown in Fig. 3c. The value of μ varied greatly over the course of a contact event but generally remained between 0.0025 and 2. The red dots in Fig. 3c represent “outlier” values, which were defined as values of μ derived from a normal force less than 0.1 mN.

The motivation for this definition of an “outlier” is as follows. When we examined the data in Fig. 3c, we found that the first and last few frames of each contact event often had values of μ as high as 70. In Fig. 3c, these extremely high values for μ are the red dots plotted at exactly μ = 3. We further found that the reason these values were so high was that the normal forces were very small (and hence difficult to measure) near the beginning and end of contact.

To remove these artificially high values, we plotted the friction coefficient μas a function of normal force (Fig. 3d). The cyan line shows the mean friction coefficient, and the shaded light blue area represents the standard deviation above and below the mean. As is evident in Fig 3d, as the normal force increases, the friction coefficient drops in variability, yielding more reliable μ measurements. Any friction coefficient derived from a normal force less than 0.1 mN was treated as an outlier.

As is shown by the red dots in Fig. 3c, this outlier removal process eliminated not only very high values of μ, but also seemingly “reasonable” values of μ computed from very small force signals (e.g., between 1,500 and 2,500 ms). Thus this procedure ensured that the estimate of μ was obtained only from the most reliable (least variable) contact measurements available in this particular data set.

The values of μ, excluding outliers, are displayed in a histogram in Fig. 3e; they have a median value of 0.48. These values are higher than previous estimates of μ for human hair in contact with polyurethane film, which range between 0.1 and 0.2. (Polyurethane film was chosen because it is often used as a model for human skin) [35].

3.4 The Utility of Edge Mode in Simulations of Whisking

Fig. 4 shows four still frames from Supplementary Video 3, which simulates a rat whisking against an infinitesimal peg. Several whiskers in succession make contact with the peg, bend against it, and eventually slip past it. Forces and moments can be computed at each whisker base, and these signals could be compared with those generated by simulations in which the rat pitches its head to different angles. These kinds of simulations would provide a first estimate of how the mechanics of touch will change across the entire array as the rat changes its head angle with respect to an object.

Of course, the caveat to this type of simulation is that it is frictionless. It predicts the upper bound for vertical slip of a rat whisker under real world conditions. As shown in Fig. 3, the primary differences are that the forces will all be slightly smaller than real-world forces, and the transverse force and bending moment will act in different directions.

The accuracy of the edge mode prediction for the entire array of whiskers could be further improved by noting that contacts with low frictional force will also have low normal force. This allows us to generate an error estimate analogous to Fig. 2e, but based entirely on edge mode simulations, obviating the need to track the 3D contact point.

In analogy to (6), we can write an equation that predicts z_error, the difference in contact point location (along the peg) between edge mode and contact point mode:

$$z_{\mathit{\text{error}}}=\mathrm{s}\mathrm{g}\mathrm{n}(z_{\mathit{\text{edge}}\_\mathit{\text{mode}}}-z_{\mathit{\text{onset}}})\frac{4L}{3E\pi R_{\mathit{\text{base}}}^4}\frac{\mu F_N{s}_{\mathit{\text{applied}}}^3}{L-s_{\mathit{\text{applied}}}}$$ (7)

where F_N is the normal force, and both F_N and s_applied are obtained from edge mode simulations.

In (7) the function (z_{edge_mode} – z_onset) is the sign function, providing the directionality of the error. The variable z_onset is the height of the contact point along the peg at the initial onset of contact, and z_{edge_mode} is the height of the contact point along the peg as calculated by edge mode. Although this method of determining directionality worked well in the present study, we caution that it may not be as reliable in cases where the whisker does not break contact with the peg between whisks.

To quantify how well (7) predicts z_error, Fig. 4b plots z_error predicted by (7) as a function of the measured z_error. Note that – unlike (6) and Fig. 2e – the prediction of (7) uses data only from edge mode.

Fig. 4b shows that the error predicted by (7) matches the measured error reasonably well. The best fit line has a slope of 0.80, an intercept of −0.02, and an r² value of 0.81. A fit to the identity line has an r² value of 0.76. The inset focuses on data that eliminates outliers, defined as z_error values outside the first and third quartiles by more than 1.5 times their interquartile range. For data excluding outliers, the best fit line (red) has a slope of 0.86, an intercept of −0.05, and an r² value of 0.75. A fit to the identity line has an r² value of 0.70.

Intuitively, the figure shows that contacts with low normal force (and therefore low frictional force) and small arc length of contact result in smaller errors, which means that these forces and moments will be more accurate.

Summarizing, edge mode simulations can be used to computethe locations of contact and the forces and moments during frictionless contact. Equation (7) can then estimate the error to the predicted contact point location when friction is included. The simulations can then be rerun in contact point mode to re-estimate the mechanical signals.

4 DISCUSSION

This paper has presented a model of whisker bending and slip that can predict the location of contact between a whisker and an edge assuming frictionless conditions. Previous 3D models have required the point of contact between the whisker and the edge to be known [5], but the present model solves for the contact point location along the edge as well as the deflected whisker shape and the forces and moments generated at the whisker base.

The importance of this work is threefold. First, it provides the first estimates of the effects of friction on the mechanical signals received by the follicle during active whisking (Fig. 2). Second, it demonstrates a proof-of-principle approach for reducing whisker tracking requirements during experiments. Third, the work demonstrates the feasibility of simulating a full array of vibrissae whisking against a peg. We first describe study limitations, and then discuss each of these results of the work in turn.

4.1 Caveats and study limitations

The behavioral data of the present work contain multiple sources of error. Because it is not possible to measure experimentally the forces and moments at the whisker base, it is important to consider how the model’s parameters could affect the predicted forces and moments.

Two parameters – Young’s modulus and the radius of the whisker base – will simply scale the forces and moments shown in Fig. 3. If either of these two parameters were to change, all mechanical signals would scale proportionately, so relative magnitudes would remain unaltered.

In contrast, two other parameters – Poisson’s ratio and whisker taper – will affect the shape of the deflected whisker, and therefore the forces and moments will differ by more than a scaling factor. Simulation results could potentially be improved by optimizing over these two parameters. However, given that the shape of the experimentally-tracked whisker is very similar to the shape generated by the contact-point mode simulations, estimates for these parameters appear to be reasonable.

The peg used in the experimental setup also introduced experimental error. Some debris was clearly visible on the peg, which could have a large effect on frictional forces. Additionally, the peg was not directly aligned with the top-down camera view, even though it was simulated to be perfectly vertical. Thus there was a slight misalignment between the actual peg and the peg as modeled in edge mode. Despite these known errors, whisking kinematics still dominated the motion of the whisker along the peg, as shown in Fig. 2f.

This study also used non-telecentric lenses to record behavioral data. However, mechanical signals were calculated only when the whisker was in contact with the peg. This constraint meant that changes in depth could only be on the order of about 1–2 cm over the full scale of ~60 cm.

In addition to these sources of experimental error, the present work analyzed only 3.3 seconds of data. A reasonable question is to what extent the results will generalize over different whisking conditions.

The results of equation (6) and Fig. 2e are based on fundamental beam bending equations, so these results are likely to hold as long as the peg is approximately perpendicular to the whisker and the bending due to friction remains in the linear elastic regime.

The results of equation (7) and Fig. 4b are subject to similar linear beam-bending constraints. In addition, the accuracy to which z_error can be predicted will depend on the extent of stick-slip and friction along the whisker length (as distinct from friction up and down the peg).

Frictional effects will also affect how well the contact point can be predicted based on whisking kinematics (Fig. 2f). The predictive power will deteriorate as friction increases.

Last, the value of the constant offset in F_D and M_D as a result of friction (Fig. 3b) depends strongly on the exact whisker orientation to the peg, especially the ζ angle. Other orientations are likely to generate relatively constant offsets as well, but with different values than the present study.

4.2 Insights into frictional effects during whisking

Analyzing naturalistic whisking behavior using edge mode and contact point mode sheds light on how friction affects the deflected whisker shape (Fig. 2) and the forces and moments generated at the whisker base (Fig. 3). In the frictionless case, the whisker slips more on the peg. Therefore, although the frictionless whisker always matches well with the tracked whisker in the top-down camera view, it can sometimes be significantly different in the front-on view (Fig 2a). The error is larger for distal contacts and for larger frictional forces (Fig 2e).

The overall shape of the mechanical signals at the whisker base is similar with and without friction, but the signals simulated without friction are somewhat smaller. More importantly, the directions in which the transverse force and bending moment act can be strongly affected by the presence of friction. Simulations that include friction reveal highly-variable directions for bending moment and transverse force, while these directions are much more constant in the absence of friction. These changes will be more pronounced when the rat whisks against objects with greater coefficients of friction or with rougher textures because forces parallel to the edge or peg will increase.

The simulations of the present work also provide key insights into how to predict the magnitude of vertical slip during real behavior. Specifically, Fig. 2f illustrates that the magnitude of vertical slip on the peg during a whisk can be predicted with remarkable accuracy based entirely on whisking kinematics (no bending). The projected vertical intersection between the peg and the shape that the whisker would have had, had it not made contact with the peg, provides an excellent estimate of the actual vertical position of the whisker along the peg.

Finally, the ratio of the frictional force parallel to the peg and the normal force perpendicular to the peg yields an estimate for the coefficient of friction between the whisker and smooth stainless steel. The histogram of μ values in Fig. 3c has a median value of 0.48, higher than previous friction estimates (0.1 or 0.2) for human hair against polyurethane [35].

Obviously the method of the present study provides only an indirect estimate ofμ; a direct measurement would employ a high-resolution tribology setup. Nevertheless, at high normal forces, the value of μ is fairly constant (Fig. 3d), suggesting that it was estimated accurately.

Several factors could explain why the friction coefficient for whiskers is higher than that reported for hair. First, the present study does not include the effects of friction along the whisker’s length; this omission would increase the apparent friction coefficient. Second, although both hairs and whiskers have scales, the sizes of their scales and the ridges between them could be different [35, 36]. Third, the present study used a stainless steel peg instead of polyurethane. The peg had some nicks and debris, and the whisker’s motion likely included small stick-slip events, which would increase the apparent friction coefficient.

4.3 Reducing whisker tracking requirements during experiments

It is clear that in order to obtain the most realistic estimate of the tactile signals that the rat experiences during behavior, experimentalists should always track the complete 3D whisker shape as well as the 3D contact point, and they should use a model that includes friction. Fitting the full shape of the deflected whisker in each frame will give the best estimate of F and M. If the experimentalist is willing to make some approximations, however, several reductions in tracking requirements are possible.

The first possible reduction in tracking is to track only the orientation of the whisker instead of its full 3D shape. The experimenter can use contact point mode by acquiring a single estimate of the 3D undeflected shape of the vibrissa and then obtaining for all frames:

• The 3D position of the vibrissa base and the 3D orientation of the vibrissa. The angle ζ is extrapolated from θ as described in Methods.

• The 3D whisker-peg contact point.

The forces and moments calculated using this approach will implicitly include the effects of friction along the peg.

A second possible reduction in tracking can be achieved by using edge mode instead of contact point mode. In this case, instead of tracking the 3D whisker-peg contact point in all frames, the experimenter only needs to obtain one estimate of the 3D position and orientation of the peg.

The whisker shape can then be used as an input to edge mode simulations to obtain estimates of F and M at the whisker base, as well as the arc length of contact (s_applied), the normal force (F_N), and the location of the contact point.

The estimates for F and M will often be poor because they assume frictionless contact. They can be improved, however, by inserting the values for s_applied and F_N, along with an estimate of the friction coefficient, into (7). Equation (7) then yields an estimate of the error in the calculated contact point location. Figs. 2e and 4b show that as long as the bending in the front-on view remains within the linear regime, the estimate of z_error will be quite accurate (less than 0.5 mm off), so that an accurate contact point can be computed.

After correcting for the contact point error, the model can be rerun in contact point mode to improve the estimate of forces and moments at the whisker base.

Independent of the other two reductions in tracking, a third reduction may also be possible. In the present study, the roll (ζ) orientation of the whisker was tracked along with the protraction angle (θ) in all non-contact frames (1,645 frames). Tracking the roll is challenging and time consuming. As an alternative, the experimenter could potentially use a single measurement of the roll orientation in conjunction with equations from [11] to estimate the roll orientation of the whisker in each frame.

Although not demonstrated in Results, we anticipate that this approach will yield a reasonable approximation for the magnitudes of the forces and moments for two reasons. First, when we plotted the relation between θ and ζ we obtained results similar to those of given in [11]. Second, even if there is a small error in curvature orientation, it will be dominated by forces due to bending. In contrast, the directions of the bending and transverse forces (F_D and M_D) will be very susceptible to any error in ζ.

Note that we do not recommend using this approach for the elevation angle φ, even though [11] gives equations for this angle in addition to ζ The elevation angle will have a much larger effect on the forces and moments at the base, and errors will be much larger.

We note that any of the proposed tracking reductions could be used as part of a compromise “sparse tracking” solution. The experimentalist could track contact point location and the full 3D whisker orientation as a “sanity check” in only a subset of frames. This approach would greatly reduce tracking load but would also ensure that the model was regularly validated against experimental data.

Finally, Fig. 2f suggests that non-contact whisking kinematics can predict the amount of vertical slip on the peg in low friction conditions. If vertical slip is small, a 2D model may be sufficient; a 3D model may not be needed.

4.4 The utility of the frictionless model in simulations of whisking

One of the largest problems in the field of vibrissal research is that it is not yet possible to track the 3D shapes of all whiskers in the array as the rat whisks against a peg. It would be yet more challenging to quantify these shapes as the rat pitches its head to different angles relative to the peg. Because the shapes cannot be tracked, it is not possible to compute the mechanical signals entering the follicle at the whisker base.

Given that these behavioral experiments are as yet infeasible, edge mode simulations could be used to model the full whisker array protracting against an edge (Fig 4a). These simulations could provide an initial estimate for the forces and moments generated across the entire vibrissal array across multiple head pitches.

The input to these simulations would be the position and orientation of the edge, the 3D shapes of all undeflected whiskers [12], and their positions and orientations over time [11, 12]. The edge mode simulation will then return the deflected whisker shapes, contact point locations, and the forces and moments at the whisker base for the frictionless case. If desired, (7) could be used to place error bounds on the contact point locations, and the simulation could be rerun using contact point mode for a more realistic output.

Finally, an important area of future work will be extending the edge-mode model to include friction. A large challenge will be incorporating information about whisker contact history and velocity.

Biographies

Lucie A. Huet received the B.S. degree in mechanical engineering from the University of California at Berkeley in 2009. She received the M.S. degree in 2013 and is currently working towards the PhD, both in mechanical engineering from Northwestern University. Her research interests include biomechanics, simulation, and their application to bioinspired robotics.

Mitra J. Z. Hartmann received the B.S. degree in applied and engineering physics from Cornell University in Ithaca, NY, and the Ph.D. degree in integrative neuroscience from the California Institute of Technology in Pasadena CA. From 2000–2003, she was a Postdoctoral Scholar at the Jet Propulsion Laboratory, Pasadena, CA, where she worked in the Bio-Inspired Technology and Systems Group. She is currently an Associate Professor in the Departments of Biomedical Engineering and Mechanical Engineering, Northwestern University and a member of the Northwestern University Institute for Neuroscience (NUIN). Dr. Hartmann’s research interests involve understanding the mechanics and neuroscience of active sensing behaviors.