Estimating the effect of treatment on binary outcomes using full matching on the propensity score

Abstract

Many non-experimental studies use propensity-score methods to estimate causal effects by balancing treatment and control groups on a set of observed baseline covariates. Full matching on the propensity score has emerged as a particularly effective and flexible method for utilizing all available data, and creating well-balanced treatment and comparison groups. However, full matching has been used infrequently with binary outcomes, and relatively little work has investigated the performance of full matching when estimating effects on binary outcomes. This paper describes methods that can be used for estimating the effect of treatment on binary outcomes when using full matching. It then used Monte Carlo simulations to evaluate the performance of these methods based on full matching (with and without a caliper), and compared their performance with that of nearest neighbour matching (with and without a caliper) and inverse probability of treatment weighting. The simulations varied the prevalence of the treatment and the strength of association between the covariates and treatment assignment. Results indicated that all of the approaches work well when the strength of confounding is relatively weak. With stronger confounding, the relative performance of the methods varies, with nearest neighbour matching with a caliper showing consistently good performance across a wide range of settings. We illustrate the approaches using a study estimating the effect of inpatient smoking cessation counselling on survival following hospitalization for a heart attack.

1 Introduction

There is an increasing interest in estimating the causal effects of treatments using observational (non-randomized) data. Methods based on the propensity score, which is defined as the probability of receiving the active treatment conditional on observed baseline covariates, are increasingly being used to estimate the effects of treatments, interventions and exposures when using observational data.¹ There are four broad ways in which the propensity score can be used to estimate the effect of treatment in observational studies: matching, inverse probability of treatment weighting (IPTW), stratification and covariate adjustment.^1–3 An advantage to the first three approaches is that they are design-based approaches that allow the investigator to separate the design of an observational study from the analysis of the study.⁴ Thus, one can create a matched sample, a weighted sample, or a stratification of the sample while blinded to the outcomes. Of the different propensity-score methods, many applied investigators favour the use of propensity-score matching, due to the simplicity of the approach and the transparency with which the methods and results can be communicated. The most common implementation of propensity score matching is pair-matching, in which pairs of treated and control subjects are formed who share a similar value of the propensity score.⁵ Methods for forming matched pairs include nearest neighbour matching, with or without a caliper.⁶ Alternative matching methods include many-to-one matching and variable ratio matching.^7,8 A rarely-used alternative matching method is full matching.^9,10 For a review of different matching methods, the reader is referred elsewhere.¹¹

Full matching constructs strata consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject. While full matching is described as a matching method, it falls at the intersection of matching, stratification and weighting: it involves the formation of strata consisting of treated and control subjects; the analysis then incorporates weights that are derived from the stratification. There are at least two attractive features of full matching compared to other matching approaches. First, it includes all subjects in the analytic sample. This is in contrast to conventional matching methods in which some subjects are excluded from the final matched sample. Because of this, it avoids bias due to incomplete matching, which can occur when some treated subjects are excluded from the matched sample.¹² Second, it permits estimation of either the average treatment effect (ATE) or the average treatment effect in the treated (ATT), whereas conventional pair-matching only allows for estimation of the ATT.

Despite having attractive conceptual properties, full matching is infrequently used in the applied literature. Furthermore, it appears to have been used rarely with binary or dichotomous outcomes, despite the frequency with which these outcomes occur in the medical and epidemiological literature.¹³ Accordingly, the objective of the current paper is two-fold. First, to describe different methods that can be used for estimating the effect of treatment on binary outcomes when using full matching. Second, to evaluate the relative performance of these methods using Monte Carlo simulations. The paper is structured as follows: in section 2, we briefly describe propensity scores, full matching and statistical methods for estimating the effect of treatment on binary outcomes when using full matching. In section 3, we describe a series of Monte Carlo simulations to compare the relative performance of full matching with that of other propensity-score methods for estimating the effect of treatment on binary outcomes when the estimand of interest is the ATT. Section 4 reports the results of these simulations. In section 5, we examine the utility of the bootstrap for estimating the standard error of estimated treatment effects when using full matching. In section 6, we provide a case study in which we illustrate the use of full matching for estimating the effect of smoking cessation counselling on mortality in patients who were current smokers and who were discharged from hospital following admission for a heart attack. Finally, in section 7, we summarize our findings and place them in the context of the existing literature.

2 Statistical methods

2.1 The propensity score

In an observational study of the effect of treatment on outcomes, the propensity score is the probability of receiving the treatment of interest conditional on measured baseline covariates: $e=\text{Pr}(Z=1|X)$, where X denotes the vector of measured baseline covariates and Z denotes treatment status (Z = 1 for treated and Z = 0 for control).¹ The propensity score is often estimated using a logistic regression model, with the propensity scores being the predicted probabilities generated by that model. As noted above, there are four ways in which the propensity score is typically used for estimating the effects of treatments or interventions: matching, stratification, weighting and covariate adjustment.^1–3

A conditional treatment effect denotes the average subject-specific treatment effect, while the marginal treatment effect denotes the average effect of the treatment at the population level.¹⁴ A measure of treatment effect is said to be collapsible if the conditional and marginal effects coincide. As noted by Gail et al., marginal and conditional effects coincide for linear treatment effects (such as differences in means or risk differences), but do not coincide for commonly-used epidemiological measures of effect such as the odds ratio or hazard ratio.¹⁵ Propensity scores are intended to estimate marginal treatment effects.¹⁶

2.2 Full matching

Conventional pair-matching on the propensity score forms pairs of treated and control subjects who have a similar value of the propensity score. Optimal pair-matching forms pairs of treated and control subjects such that the average within-pair difference in the propensity score is minimized. Stratification on the propensity score forms strata of treated and control subjects. The strata are often defined using specified quantiles of the propensity score (e.g. the quintiles of the propensity score).¹⁷ Full matching can be thought of as a synthesis of these two methods. Full matching forms strata consisting of either one treated subject and at least one control subject or one control subject and at least one treated subject.⁹ An optimal full match is a full match that minimizes the mean within matched-set differences in the propensity score between treated and control subjects. For the remainder of the paper, we will use the term full matching to refer to optimal full matching. A refinement of optimal full matching is optimal full matching with a caliper restriction, in which treated and control subjects can only be included in the same matched set if their propensity scores differ by less than a pre-specified distance.¹⁸

Weights can be derived from the stratification imposed by the full matching. One set of weights permits estimation of the ATE, while a second set of weights permits estimation of the ATT. Weights that permit estimation of the ATT are constructed as follows: treated subjects are assigned a weight of one, while each control subject has a weight proportional to the number of treated subjects in its matched set divided by the number of controls in the matched set.^19,20 The control group weights are scaled such that the sum of the control weights across all the matched sets is equal to the number of uniquely matched control subjects. As the current paper focuses on estimation of the ATT, we refer the reader elsewhere for a description of ATE weights for use with full matching.²¹

2.3 Estimating the effect of treatment on binary outcomes using propensity-score methods

When outcomes are binary, four different measures of effect can be estimated: the risk difference or absolute risk reduction, the relative risk, the odds ratio and the number needed to treat (NNT). If p₁ and p₀ denote the probability of the outcome in treated and control subjects, respectively, then the first three quantities are defined as $p_1-p_0$, $\frac{p_1}{p_0}$, and $\frac{p_1/(1-p_1)}{p_0/(1-p_0)}$, respectively. The NNT is simply the reciprocal of the risk difference. Clinical commentators have suggested the risk difference, the relative risk and the NNT provide more information for clinical decision making, while the odds ratio provides limited information.^22–26 In this sub-section, the primary focus is on how full matching on the propensity score can be used to estimate these different metrics (for the remainder of the study we do not discuss the NNT, since it is simply the reciprocal of the risk difference). We complement this information by describing how alternative propensity-score methods can be used to estimate these quantities.

2.3.1 Full matching

We describe two different approaches that can be used with full matching on the propensity score to estimate the effect of treatment on binary outcomes. The first approach involves computing the marginal probabilities of the occurrence of the outcome. Using the weights induced by full matching, one can estimate the probability of the occurrence of the outcome in treated subjects and in control subjects, separately. These denote the marginal probabilities of the occurrence of outcome, reflecting the probability of the outcome in the treated population (if using the ATT weights) if all these subjects were treated and if all these subjects received the control condition. Formally, define $P_1=\text{E}[Y(1)=1]=\frac{1}{N_1}\sum _{i=1}^{N_1}{w}_i{Y}_i$ and $P_0=\text{E}[Y(0)=1]=\frac{1}{N_0}\sum _{i=1}^{N_0}{w}_i{Y}_i$, where N₁ and N₀ denote the number of treated and control subjects, respectively, and w_i denotes the weight induced by full matching. The estimators of the risk difference, the relative risk and the odds ratio are $P_1-P_0$, $P_1/P_0$ and $\frac{P_1/(1-P_1)}{P_0/(1-P_0)}$, respectively. We refer to this approach as full matching with marginal computations. Note that this approach does not control or adjust for baseline covariates in an outcome model, although such an approach is possible. Subsequent adjustment for the propensity score, as a summary covariate, as in the recently-described method of double-propensity score adjustment, is also possible.²⁷

The second approach involves regressing the binary outcome on a treatment status indicator using a logistic regression model. The model incorporates the weights induced by full matching. A robust, sandwich-type variance estimator can be used to account for the clustering of subjects within strata. We refer to this approach as a model-based approach. It produces an estimate of the odds ratio.

2.3.2 Pair-matching

Pair-matching on the propensity score can be used to estimate risk differences and relative risks,^28,29 however, it has been shown previously to result in biased estimation of both conditional and marginal odds ratios.^30,31 When using pair-matching on the propensity score, marginal computations similar to those described above can be used to estimate the risk difference and the relative risk (except that the calculations omit the weight and are conducted in the matched sample). Variance estimates that account for the matched nature of the sample have superior performance compared to naïve variance estimates that ignore the matched nature of the sample.^32,33 In the simulations below we consider two versions of pair-matching: a basic approach using nearest neighbour matching (NNM), and one that imposes a caliper and only allows matches if the within-pair difference in propensity scores is below a specified threshold (referred to as NNM-caliper).

2.3.3 Inverse probability of treatment weighting

The standard IPT weights that permit estimation of the ATE are defined as $w=\frac{Z}{e}+\frac{1-Z}{1-e}$, where e denotes the propensity score. Alternate weights that permit estimation of the ATT are defined as $w=Z+\frac{e(1-Z)}{1-e}$. When using IPTW, the effect of treatment on binary outcomes can be estimated in two different ways. As with full matching, a model-based approach can be used in which the binary outcome is regressed on an indicator variable denoting treatment status. The model incorporates the ITP weights and a robust variance estimator can be used.³⁴ Alternatively, marginal computations can be conducted to estimate the marginal probabilities of the occurrence of the outcome, using an approach that is a modification of that described by Lunceford and Davidian.³⁵ Define $P_1=\text{E}[Y(1)=1]=\frac{1}{N_1}\sum _{i=1}^{N_1}{w}_i{Y}_i$ and $P_0=\text{E}[Y(0)=1]=\frac{1}{N_0}\sum _{i=1}^{N_0}{w}_i{Y}_i$, where N₁ and N₀ denote the number of treated and control subjects, respectively. The difference and ratio of these probabilities can be used to estimate the risk difference and the relative risk, respectively. The odds ratio can be similarly estimated. These estimators are identical to the full matching estimators, except that the weights induced by full matching are replaced by the IPTW weights.

3 The design of Monte Carlo simulations for examining the relative performance of different propensity-score methods for estimating the effects of treatment on binary outcomes

We conducted a series of Monte Carlo simulations to examine the performance of full matching on the propensity score for estimating the effect of treatment on binary outcomes when the target estimand is the ATT. We compare its performance to that of IPTW and pair-matching on the propensity score. We considered a range of scenarios in terms of the extent of confounding and the prevalence of treatment. The methods’ performances were assessed using the following two criteria: (i) bias in estimating the true treatment effect; and (ii) the mean squared error (MSE) of the estimated treatment effect.

3.1 Data-generating process

For each subject, we simulated 10 baseline covariates (X₁, … , X₁₀) from independent standard normal distributions. For each subject, we randomly generated a treatment status using the following logistic model:

$$\text{logit}(\text{Pr}(Z=1))={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3+{\beta }_4{X}_4+{\beta }_5{X}_5+{\beta }_6{X}_6+{\beta }_7{X}_7+{\beta }_8{X}_8+{\beta }_9{X}_9+{\beta }_{10}{X}_{10}$$

A second logistic model was used to generate binary outcomes for each subject:

$$\text{logit}(\text{Pr}(Y=1))={\alpha }_0+{\alpha }_{\text{treat}}{Z}_i+{\alpha }_1{X}_{1,i}+{\alpha }_2{X}_{2,i}+{\alpha }_3{X}_{3,i}+{\alpha }_4{X}_{4,i}+{\alpha }_5{X}_{5,i}+{\alpha }_6{X}_{6,i}+{\alpha }_7{X}_{7,i}+{\alpha }_8{X}_{8,i}+{\alpha }_9{X}_{9,i}+{\alpha }_{10}{X}_{10,i}$$

We simulated two potential outcomes for each subject: Y(1) and Y(0), the outcomes under treatment and control, respectively. The observed outcome, Y, was the potential outcome corresponding to the actual treatment received (Y = ZY(1) + (1 − Z)Y(0)). We simulated data such that the true conditional odds ratio for the effect of treatment on the odds of the outcome was 0.8 (i.e. α_treat = log(0.8)). By simulating both potential outcomes, we are able to determine what the true marginal treatment effect was on the risk difference scale, the relative risk scale and the odds ratio scale.

The regression coefficients in the treatment-selection model, β₁ through β₁₀ were set equal to log(k × 1.05), log(k × 1.10), log(k × 1.20), log(k × 1.25), log(k × 1.50), log(k × 1.75), log(k × 2.00), log(k × 1.50), log(k × 1.25) and log(k × 1.10), respectively. The intercept, β₀, in the treatment-selection model was selected so that the prevalence of treatment was equal to the desired value. In the outcomes model, the regression coefficients, α₁ through α₁₀ were set equal to 2, 1.75, 1.50, 1.25, 1.10, 1.05, 1.50, 1.75, 2 and 1.25, respectively. The intercept, α₀, in the outcomes model was selected so that the marginal probability of the outcome if all subjects were untreated was 0.20.

We used a full factorial design in which two factors were allowed to vary. The first factor was the magnitude of the effect of covariates on treatment-selection. To do so, we allowed the scalar k (defined above in the coefficients for the treatment-selection model) to range from one to five in increments of one. Second, we allowed the prevalence of treatment to take on the following values: 0.05, 0.10, 0.20, 0.30, 0.40 and 0.50. We thus examined 30 (5 × 6) different scenarios. For each of the 30 scenarios, we simulated 1000 datasets, each consisting of 1000 subjects.

3.2 Statistical analyses in simulated datasets

As our target estimand was the ATT, we used both simulated potential outcomes to determine the true value of the treatment effect. To do so, in each simulated dataset we computed ${\overline{Y}}_{Z=1}(1)=\frac{1}{N_{Z=1}}\sum _{Z_i=1}{Y}_i(1)$ and ${\overline{Y}}_{Z=1}(0)=\frac{1}{N_{Z=1}}\sum _{Z_i=1}{Y}_i(0)$, where $N_{Z=1}$ denotes the number of subjects who received the treatment, and the summation is over all subjects who received the treatment. These quantities denote the mean potential outcome under treatment and control, respectively, in those subjects who ultimately received the treatment. The marginal risk difference, the marginal relative risk and the marginal odds ratio were computed as ${\overline{Y}}_{Z=1}(1)-{\overline{Y}}_{Z=1}(0)$, $\frac{{\overline{Y}}_{Z=1}(1)}{{\overline{Y}}_{Z=1}(0)}$ and $\frac{{\overline{Y}}_{Z=1}(1)/(1-{\overline{Y}}_{Z=1}(1))}{{\overline{Y}}_{Z=1}(0)/(1-{\overline{Y}}_{Z=1}(0))}$, respectively. The mean of each of these three quantities was then determined across the 1000 simulated datasets. These means will serve as the true target marginal estimands. Since the averages of the potential outcomes are over all treated subjects, our target estimand is the ATT.

In each simulated dataset, we estimated the propensity score using a logistic regression model to regress treatment assignment on the 10 variables X₁ through X₁₀ (thus, the propensity score model was correctly specified). In each simulated dataset, two full matched samples were constructed. First, an optimal full matching was created using the estimated propensity score (referred to as Full). This method resulted in the inclusion of all subjects in the matched sample. Second, full matching with a caliper restriction was used. Subjects were matched on the logit of the propensity score with the restriction that matched treated and control subjects could not have a difference in the logit of the propensity score of more than 0.2 of the standard deviation of the logit of the propensity score (referred to as full with caliper). Individuals who were not included in a matched set due to this restriction were dropped from the analysis. Methods identical to those described in section 2 were used to estimate the effect of treatment on the binary outcome using full matching, pair-matching and IPTW. When using pair-matching, we used two different methods to form matched pairs: NNM on the propensity score and nearest neighbour caliper matching on the logit of the propensity score using calipers of width equal to 0.2 of the standard deviation of the logit of the propensity score (referred to as NNM and NNM-caliper, respectively).^6,36

Let θ denote the true effect of treatment on a given metric (risk difference, relative risk, or odds ratio), and let θ_i denote the estimated treatment effect on the given metric, in the ith simulated sample ($i=1,\dots ,1000$). Then, the mean estimated treatment effect was estimated as $\frac{1}{1000}\sum _{i=1}^{1000}{\theta }_i$, the MSE was estimated as $\frac{1}{1000}\sum _{i=1}^{1000}({\theta }_i-\theta )2$ and the mean relative bias was estimated as $\frac{1}{1000}\sum _{i=1}^{1000}100\times \frac{{\theta }_i-\theta }{\theta }$.

Methods for estimating confidence intervals (CIs) when using full matching with marginal computations have not been developed. Since the focus of this paper was on the use of full matching to estimate the effect of treatment on binary outcomes, and the other estimation methods were of interest only as a comparator to full matching, we did not consider variance estimation and CI coverage for any of the methods. However, section 5 below describes the use of bootstrap methods for estimating the variance of treatment effects when using full matching.

Although the focus of the current study was on the estimation of marginal estimands, at least one applied paper used conditional logistic regression in conjunction with full matching to estimate a conditional odds ratio.³⁷ Thus, as a secondary analysis, we examined the performance of this approach. We used conditional logistic regression to regress the occurrence of the binary outcome on an indicator variable denoting treatment status. The model stratified on the matched sets induced by full matching. The estimated conditional odds ratio was compared to the true conditional odds ratio used in the data-generating process (0.8). We evaluated the performance of conditional logistic regression in conjunction with full matching by determining the mean estimated log-odds ratio and the percentage of estimated CIs that contained the true value. We did not examine the MSE, as we were not comparing the performance of full matching with other methods for estimating the true conditional odds ratio.

Apart from NNM and NNM-caliper matching, which were implemented using custom-written programs in the C programming language for computational speed in the simulations, all other analyses were conducted in the R statistical programming language (version 3.1.2). Full matching was implemented using the matchit function from the MatchIt package (version 2.4-21).^19,20 Full matching with a caliper restriction was implemented using the fullmatch function in the optmatch package (version 0.9-3).

4 Monte Carlo simulations: Results

4.1 Balance of baseline covariates

Standardized differences comparing the mean of each of the 10 baseline covariates between treated and control subjects in the original (unweighted and unmatched) sample are described in Figure 1. There is one panel for each of the six prevalences of treatment. On each panel we have superimposed horizontal lines denoting standardized differences of ±0.1, as some authors have suggested that standardized differences that exceed these thresholds may be indicative of meaningful imbalance.³⁸ This figure is intended to inform the reader about the initial imbalance in the 10 baseline covariates between the treated and control groups in the original sample. In each of the 30 scenarios there was substantial imbalance in the 10 baseline covariates between the treated and control groups. After imposing the stratification induced by full matching, the minimum and maximum standardized differences for the 10 baseline covariates across the 30 scenarios were −0.005 and 0.135, respectively. After imposing the stratification induced by full matching with a caliper restriction, the minimum and maximum standardized differences for the 10 baseline covariates across the 30 scenarios were −0.011 and 0.026, respectively. After incorporating the IPT weights, the minimum and maximum standardized differences for the 10 baseline covariates across the 30 scenarios were −0.002 and 0.169, respectively. In the matched samples constructed using NNM, the minimum and maximum standardized differences for the 10 baseline covariates across the 30 scenarios were −0.009 and 0.627, respectively. In the matched samples created using NNM-caliper matching, the minimum and maximum standardized differences for the 10 baseline covariates across the 30 scenarios were −0.011 and 0.023, respectively. Thus, the greatest balance in measured baseline covariates was induced by full matching with a caliper restriction and NNM-caliper matching.

Figure 1.

Mean standardized differences for the 10 baseline variables in original sample.

4.2 Relative bias in estimating marginal risk differences, relative risks and odds ratios

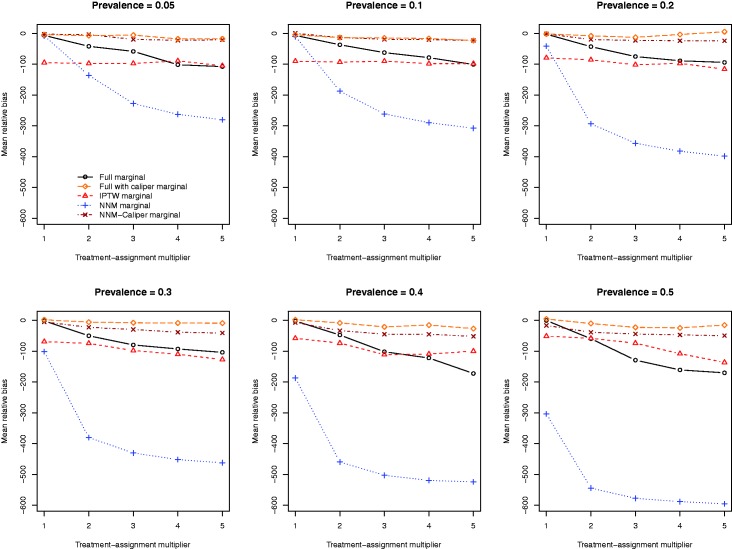
The mean relative biases for the five different methods of estimating the marginal risk difference are reported in Figure 2. There is one panel for each of the six different prevalences of treatment. The two caliper-based approaches (full matching with a caliper restriction and NNM-caliper) tended to result in estimates with the lowest relative bias across the 30 different scenarios. When the prevalence of treatment was high, full matching with a caliper restriction tended to result in estimates with marginally less bias compared to NNM-caliper. The two full matching approaches tended to have superior performance compared to that of IPTW across the range of scenarios.

Figure 2.

Relative bias in estimating the risk difference.

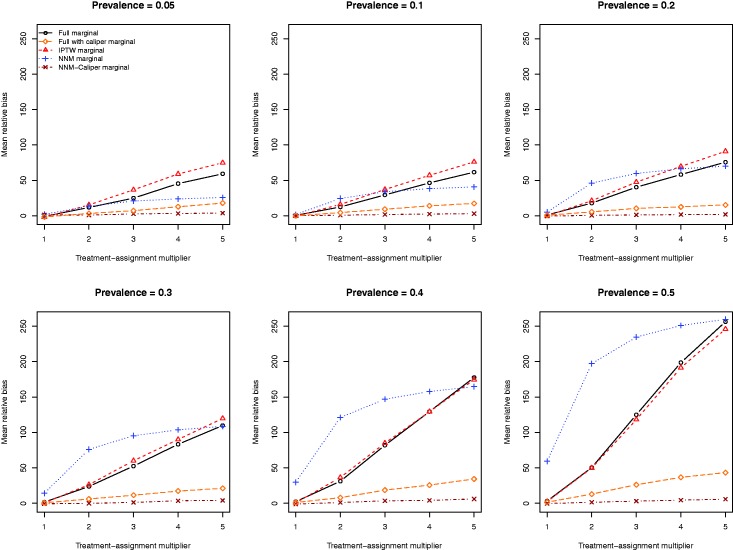
The mean relative biases for the five different methods of estimating the marginal relative risk are reported in Figure 3. Full matching and IPTW resulted in estimates with very similar relative bias. NNM-caliper matching resulted in estimates of the relative risk with the lowest relative bias. Full matching with a caliper restriction tended to result in estimates with substantially less bias than full matching or IPTW. Once the prevalence of treatment was at least 20%, then NNM tended to result in estimates with the greatest relative bias.

Figure 3.

Relative bias in estimating the relative risk.

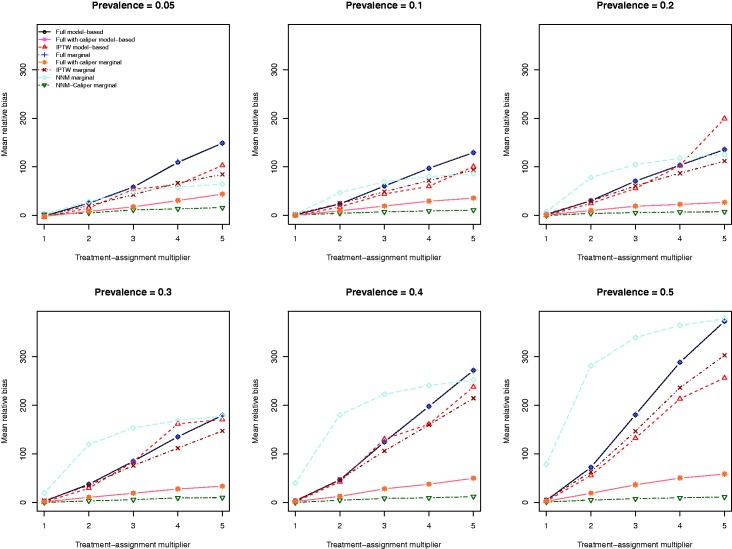
The mean relative biases for the eight different methods of estimating the marginal odds ratio are reported in Figure 4. For each of the eight estimation methods, the relative bias increased as the strength of the treatment-selection process increased. The relative bias was lowest for the estimate obtained using NNM-caliper matching. NNM tended to result in estimates with the greatest relative bias, except when the prevalence of treatment was very low. The two IPTW-based estimation methods tended to result in estimates with lower bias compared to the estimates obtained using the two methods based on full matching. However, full matching with a caliper restriction tended to result in estimates with lower bias than those obtained using full matching or IPTW.

Figure 4.

Relative bias in estimating the odds ratio.

4.3 MSE of estimated marginal odds ratios, relative risk and risk differences

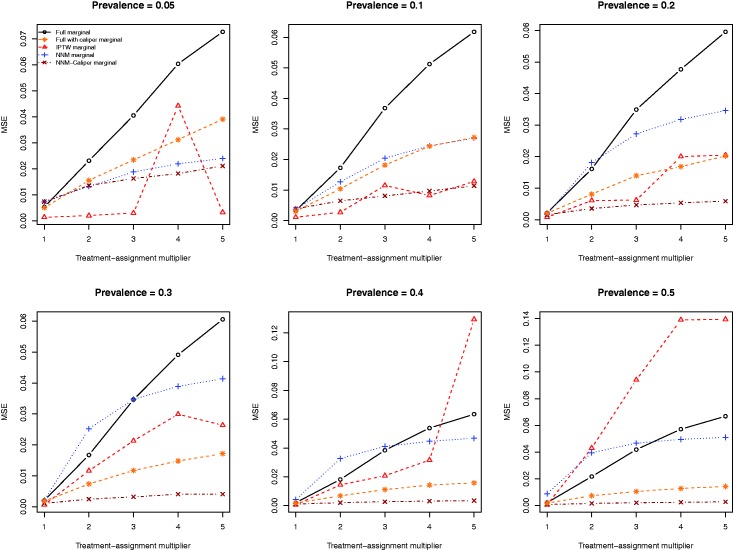
The MSE of the estimates of the marginal risk difference obtained using the five different estimation methods are described in Figure 5. The relative performance of the five different estimation methods displayed some inconsistency as to which method resulted in estimates with the lowest MSE. When the prevalence of treatment was 20% or lower, the full matching tended to result in estimates with higher MSE than did the other methods. However, when the prevalence of treatment was 50%, the IPTW tended to result in estimates of the risk difference with higher MSE than the competing methods.

Figure 5.

Mean squared error (MSE) of estimated risk difference.

The MSE of the estimates of the marginal relative risk obtained using five different estimation methods are described in Figure 6. Full matching tended to result in estimates with the highest MSE, whereas NNM-caliper matching tended to produce estimates with the lowest MSE. As the prevalence of treatment increased, differences in MSE between NNM and NNM-caliper matching diverged. Furthermore, as the prevalence of treatment increased, differences between full matching with a caliper restriction and NNM-caliper decreased. Estimates obtained using IPTW tended to have lower MSE than those obtained using full matching, but tended to have higher MSE than those obtained using pair-matching.

Figure 6.

Mean squared error (MSE) of estimated relative risk.

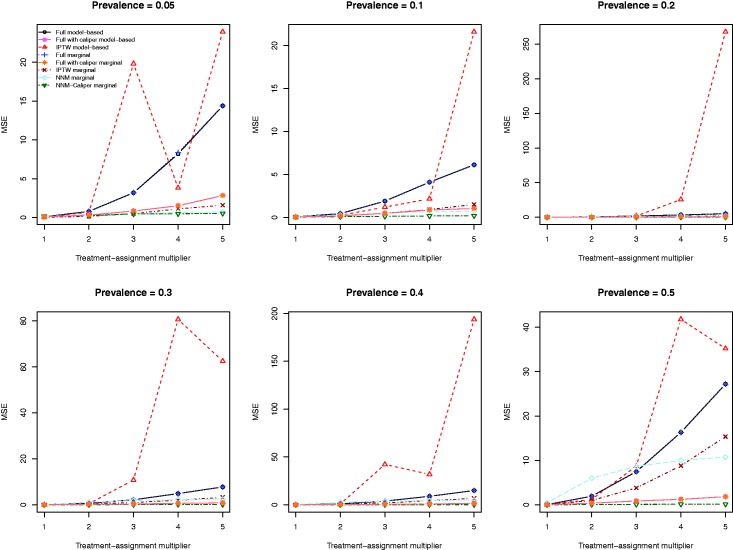
The MSE of the estimates of the marginal odds ratio obtained using the eight different estimation methods are described in Figure 7. The two estimation methods based on full matching resulted in estimates with very similar MSE. The use of logistic regression with IPTW-ATT weights tended to result in estimates with the highest MSE across the 30 different scenarios. NNM-caliper matching tended to result in estimates with the lowest MSE. The IPTW-marginal method tended to result in estimates with lower MSE than did the two methods based on full matching.

Figure 7.

Mean squared error (MSE) of estimated odds ratio.

4.4 Estimation of conditional odds ratios using full matching and conditional logistic regression

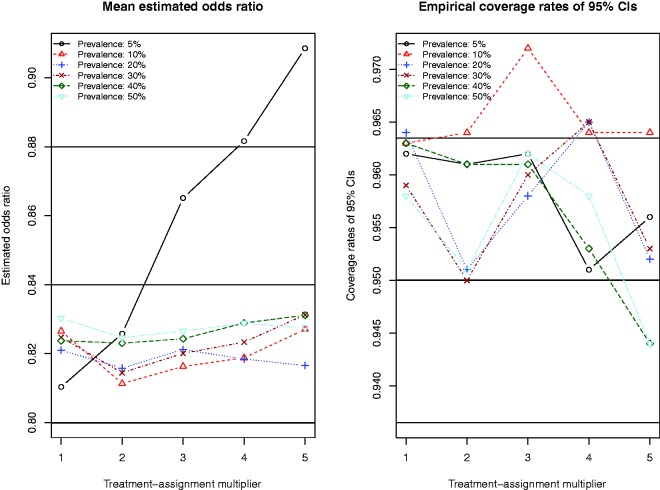
The performance of conditional logistic regression in conjunction with full matching for estimating the underlying conditional odds ratio is reported in Figure 8. The exponential of the mean of the estimated log-odds ratio across the 1000 iterations for each scenario are reported in the left panel, while empirical coverage rates of estimated 95% CIs are reported in the right panel. On the left panel, we have superimposed three horizontal lines: one at 0.80 (denoting the true conditional odds ratio used in the data-generating process), and two at 0.84 and 0.88, denoting relative biases of 5% and 10%, respectively. When the prevalence of treatment was 5%, bias increased as the magnitude of the treatment-selection model increased. However, in all other scenarios, the bias tended to be low (<5%).

Figure 8.

Full matching and conditional logistic regression.

Due to our use of 1000 iterations per scenario, an empirical coverage rate that was less than 0.9365 or greater than 0.9635 would be statistically significantly different from 0.95 based on a standard normal-theory test. In general, empirical coverage rates of the estimated CIs were not statistically significantly different from the advertised coverage rates.

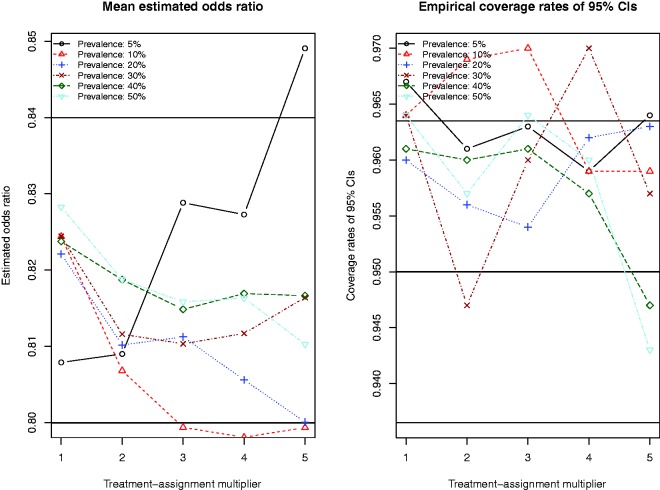
Comparable results (with minor reductions in bias) were observed when full matching with a caliper restriction was employed (Figure 9).

Figure 9.

Full matching with calipers and conditional logistic regression.

5 The use of the bootstrap for variance estimation with full matching

The primary objective of the paper was to examine two methods for using full matching on the propensity score to estimate the effects of treatment on binary outcomes. The first approach, which we described as model-based, used logistic regression to regress the outcome on a binary variable denoting treatment status. The model incorporated the weights induced by the full matching and used a robust variance estimator. The second approach involved computing the marginal probabilities of the occurrence of outcome in the sample weighted by the weights induced by the full matching. A limitation of the second approach is that methods for estimating the sampling variance of the estimated treatment effect have not been developed. In this section, we conducted a limited set of Monte Carlo simulations to examine the performance of bootstrap methods to estimate both CIs and the sampling variability of the estimated treatment effect when using marginal computations using the weights induced by full matching.

5.1 Methods

Due to the time-intensive nature of using Monte Carlo simulations to examine the performance of resampling-based methods, such as the bootstrap, we restricted our attention to a subset of the simulations described above. In particular, we restricted our examination to those scenarios in which the treatment-assignment multiplier (k) was equal to one. We thus examined six scenarios defined by the prevalence of treatment: 5%, 10%, 20%, 30%, 40% and 50%. In each of the 1000 simulated dataset for each of the six scenarios, we estimated the treatment effect (on the risk difference scale, the log-relative risk scale, and the log-odds ratio scale) using full matching with marginal computations. Let ${\hat{\theta }}_i$ denote the estimated treatment effect in the ith simulated dataset ($i=1,\dots ,1000$). The standard deviation of the empirical sampling distribution of the estimated treatment effects was estimated as the variance of the ${\hat{\theta }}_i$ across the 1000 simulated datasets. In each of the 1000 simulated datasets, we drew B = 200 bootstrap samples. In each bootstrap sample we re-estimated the propensity score model and constructed a full matching. Using the weights induced by the full matching, we estimated the treatment effect using marginal computations. Let ${\hat{\theta }}_{i,j}^b$ denote the estimated treatment effect in the jth bootstrap sample drawn from the ith simulated dataset. Within each simulated dataset, the bootstrap estimate of the standard error of the estimated treatment effect was the standard deviation of the distribution of the estimated ${\hat{\theta }}_{i,j}^b$ (j = 1, … , 200). Thus, for each of the 1000 simulated datasets, we had a bootstrap estimate of the standard error of the estimated treatment effect. We determined the mean bootstrap estimate of the standard error of the estimated treatment effect across the 1000 simulated datasets. This quantity was compared to the standard deviation of the empirical sampling distribution of the estimated treatment effect that was computed earlier. We also computed bootstrap CIs in each of the 1000 simulated datasets as ${\hat{\theta }}_i\pm 1.96\times \text{SD}({\hat{\theta }}_{\text{i},\text{j}}^{\text{b}})$. We determined the proportion of bootstrap CIs that contained the true value of the treatment effect. We did not examine the use of bootstrapping in conjunction with model-based estimates obtained using the weights induced by full matching, as the robust, sandwich-type variance estimator can be used with this estimation method. In contrast, variance estimates have not been previously described for use with the marginal computation method.

5.2 Results

The results of the simulations are reported in Table 1. Each cell in the top half of the table contains the average bootstrap estimate of the standard error of the sampling distribution of the measure of effect divided by the standard deviation of the empirical sampling distribution of the measure of effect. Across all six scenarios and for the three measures of treatment effect, on average, the bootstrap estimate of the standard error of the estimated treatment effect overestimated the standard deviation of the estimated treatment effect. However, as the prevalence of treatment increased, the degree of over-estimation decreased. When the prevalence of treatment was 50%, the bootstrap estimate of standard error over-estimated the standard deviation of the empirical sampling distribution by 3% for the risk difference and 5% for the log-relative risk and the log-odds ratio. In general, the bootstrap estimate was marginally more accurate for the risk difference than for the log-relative risk or the log-odds ratio.

Table 1.

Performance of the bootstrap with full matching: variance estimation and confidence interval coverage.

Measure of effect	Prevalence of treatment
	5%	10%	20%	30%	40%	50%
Ratio of the mean bootstrap estimate of standard error to empirical estimate of standard error
Risk difference	1.12	1.11	1.11	1.07	1.06	1.03
Relative risk	1.14	1.11	1.13	1.09	1.08	1.05
Odds ratio	1.14	1.11	1.12	1.08	1.07	1.05
Empirical coverage rates of estimated bootstrap confidence intervals
Risk difference	0.978	0.966	0.970	0.965	0.958	0.951
Relative risk	0.988	0.965	0.967	0.971	0.964	0.957
Odds ratio	0.988	0.965	0.967	0.971	0.962	0.956

Each cell in the bottom half of the table contains an estimate of the empirical coverage rate of the bootstrap CIs. Due to our use of 1000 simulated datasets, an empirical coverage rate that is less than 0.9365 or greater than 0.9635 is statistically significantly different from the nominal rate of 0.95, based on a standard normal-theory test. When the prevalence of treatment was 40% or 50%, then five of the six bootstrap CIs had empirical coverage rates that were not statistically significantly different from the advertised rates. When the prevalence of treatment was less than 40%, the bootstrap CIs had empirical coverage rates that were slightly higher than the advertised rates.

6 Case study

The case study used data from a previously-published tutorial article on propensity-score methods (in which full matching was not considered).³⁹ The sample consisted of patients hospitalized with acute myocardial infarction (AMI or heart attack), who survived to hospital discharge and who had documented evidence of being current smokers. For the purposes of the current case study, the treatment or exposure of interest was whether the patient received in-patient smoking cessation counselling. Smokers whose counselling status could not be determined from the medical record were excluded from the current study. These data were collected as part of the Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, an initiative intended to improve the quality of care for patients with cardiovascular disease in Ontario.⁴⁰

For the current study, the dichotomous outcome was survival to three years. The study sample for the case study consisted of 2342 subjects, of whom 1588 (67.8%) received in-patient smoking cessation counselling and 754 (32.2%) did not. For further information on the study sample and for a detailed comparison of treated and control subjects, the reader is referred to the previously-published tutorial article. In the current case study, the target estimand was the ATT.

The propensity score model for receipt of smoking cessation counselling was estimated using 33 baseline covariates: demographic characteristics (age and sex), presenting signs and symptoms (acute pulmonary oedema), vital signs on admission (systolic blood pressure, diastolic blood pressure, heart rate, respiratory rate), classic cardiac risk factors (diabetes, hyperlipidaemia, hypertension, family history of coronary artery disease), comorbid conditions and vascular history (cancer, dementia, previous myocardial infarction, asthma, depression, peptic ulcer disease, peripheral vascular disease, previous coronary revascularization, chronic congestive heart failure), laboratory tests (glucose, white blood count, haemoglobin, sodium, potassium, creatinine), and prescriptions for cardiovascular medications at hospital discharge (statin, beta-blocker, angiotensin converter enzyme (ACE) inhibitor/angiotensin receptor blockers (ARBs), plavix and acetylsalicylic acid (ASA)). The propensity score model incorporated restricted cubic smoothing splines to model the relationship between the 11 continuous covariates (age, vital signs on admission, and laboratory tests) and the log-odds of treatment. Interactions between select covariates were included in the propensity score model, as described in the previous tutorial article. Full matching on the estimated propensity score was used to create a stratification of the study sample. Standardized differences of the mean were computed for each of the 33 covariates in the sample that incorporated the weights induced by the full matching. The standardized differences ranged from −0.109 to 0.063. Thus, incorporating the full matching weights resulted in a sample in which differences between treated and control subjects were negligible on these 33 baseline covariates. When using full matching with a caliper restriction, the standardized differences ranged from −0.089 to 0.062. Thus, comparable balance was achieved using the two full matching approaches.

Logistic regression was used to regress the occurrence of death within three years of discharge on an indicator variable denoting receipt of smoking cessation counselling. The model incorporated the weights induced by the full matching and a robust variance estimator was used. The estimated marginal odds ratio was 0.818 (95% CI: (0.551, 1.214)). The effect of smoking cessation counselling on the odds of three-year death was not statistically significant (p = 0.3188). When using full matching with a caliper restriction, the estimated marginal odds ratio was 0.778 (p = 0.1730) (95% CI: (0.543, 1.116)).

Marginal computations that incorporated the weights induced by full matching were used to estimate the risk difference, relative risk and odds ratios. Two hundred bootstrap samples were used to estimate the standard error of the estimated treatment effects. The estimated treatment effects were −0.019 (−0.053, 0.015), 0.835 (0.615, 1.134) and 0.818 (0.580, 1.154) for the risk difference, relative risk and odds ratio, respectively. When using full matching with a caliper restriction, the estimated effects were −0.023 (−0.062, 0.014), 0.799 (0.568, 1.126) and 0.778 (0.530, 1.144) for the risk difference, relative risk and odds ratio, respectively.

Our conclusions were consistent across the four different estimates and the two different implementations of full matching: smoking cessation counselling did not have a statistical significant impact on the risk of death within three years of hospital discharge in those patients who ultimately received such counselling.

The case study provides a good illustration of the advantages of full matching for estimating causal treatment effects. In the sample, the majority of subjects (67.8%) received the treatment, smoking cessation counselling. This is a setting in which conventional pair-matching would not perform well for estimating the ATT. Pair-matching typically requires a reservoir or pool of potential control subjects that is larger than the number of treated subjects. In contrast to this limitation of pair-matching, full matching does not place any constraints on the relative sizes of the treated and control samples. Due to fact that the reservoir of potential controls was smaller than the number of treated subjects, pair-matching was not considered in the current case study.

For comparative purposes, we used IPTW with the ATT weights to estimate the effect of smoking cessation counselling. When using a model-based approach, the estimated odds ratio was 0.855 (95% CI: 0.685–1.067). Thus, the effect of smoking cessation counselling on three-year death was not statistically significant (p = 0.1663). When the probability of the occurrence of the outcome was directly computed in treated and control subjects in the sample weighted by the IPT-ATT weights, the estimated risk difference, relative risk and odds ratios were −0.014 (−0.383, 0.354), 0.869 (0.119, 6.359) and 0.855 (0.004, 201.954), respectively (95% CIs were estimated using 200 bootstrap samples to estimate the standard error of the estimated treatment effect). The estimated CIs were substantially wider than those for the full matching estimates. This may indicate that the IPT weights are subject to greater instability in this setting.

7 Discussion

Propensity-score matching is frequently used in the medical and epidemiological literature for estimating the effects of treatments, exposures and interventions when using observational data. While pair-matching appears to be the most common implementation of propensity-score matching,⁵ other matching algorithms, including variable-ratio matching and optimal full matching, have been proposed.^7–9,41 Of these, the latter appears to be used infrequently in applications of propensity-score methods, despite having attractive conceptual properties. Furthermore, when used, its use is primarily in settings with continuous outcomes. Methods have recently been described to use full matching to estimate the effect of treatment on survival or time-to-event outcomes.⁴² In biomedical research, binary or dichotomous outcomes occur frequently.¹³ The objective of the current study was to describe and evaluate different methods in which full matching on the propensity score can be used to estimate the effects of treatment on binary outcomes.

When the target estimand was the risk difference, full matching resulted in less bias than IPTW methods in the majority of scenarios examined. Full matching with a caliper restriction tended to result in estimates with the lowest bias. Furthermore, NNM-caliper matching resulted in estimates with comparable bias to those from full matching with a caliper restriction. When estimating relative risks, full matching and IPTW tended to result in estimates with similar bias. Again, full matching with a caliper restriction tended to out-perform these two methods. However, NNM-caliper matching resulted in estimates with the lowest bias. We found that full matching tended to result in estimates of the true odds ratio with greater bias than conventional IPTW methods. However, full matching with a caliper restriction had superior performance to IPTW. For all three target estimands, biases tended to be minimal when the treatment-selection process was weaker, and increased as the magnitude of the effect of the covariates on treatment-selection increased. Furthermore, NNM-caliper matching tended to result in estimates with the lowest MSE, suggesting that the decrease in bias was not accompanied by an overly-large increase in variability. The superior performance of full matching with a caliper restriction compared to conventional full matching was previously observed in a study comparing the performance of full matching for estimating the effect of treatment on survival outcomes when the target estimand was the ATE.⁴³

We described how marginal computations incorporating the weights induced by full matching permit estimation of the risk difference, the relative risk and the odds ratio. While this approach is analytically simple, a disadvantage to this approach is that methods for estimating the standard error of the estimated treatment effect have not been described. We examined the utility of bootstrap methods in this context. We found that bootstrap methods of estimating the standard error tended to modestly over-estimate the standard deviation of the empirical sampling distribution; however, the degree of over-estimation decreased as the prevalence of treatment increased. Bootstrap CIs had the correct coverage rates when the prevalence of treatment was moderate, while the coverage rates were slightly higher than advertised when the prevalence of treatment was low. Bootstrap methods appear to be infrequently used in combination with propensity score matching. Abadie and Imbens found that the standard bootstrap estimator was not valid for use with nearest-neighbour matching estimators with replacement and a fixed number of neighbors.⁴⁴ One of the causes of the bias in the bootstrap estimator appeared to be that whenever a treated unit and the control unit to which the treated unit was originally matched both appear in the bootstrap sample, the treated unit is matched to the same control unit. In a more recent paper, it was demonstrated that bootstrap methods tended to perform well when using matching without replacement.⁴⁵ Based on our findings, we suggest that the bootstrap be used in conjunction with full matching, although this merits further study. Due to the computationally intensive nature of Monte Carlo simulations of bootstrap methods, we were not able to consider a range of different bootstrap methods. In particular, we did not consider non-parametric percentile-based CI estimates. It has been recommended that one use a minimum of 1000 bootstrap samples when estimating percentile-based CIs.⁴⁶ This would have substantially increased the computation time required for our limited set of simulations.

The focus of the current study was describing and evaluating methods for using full matching to estimate the effect of treatment on binary outcomes. For comparative purposes, we compared its performance to that of other design-based approaches, including IPTW and pair-matching on the propensity score (with and without caliper restrictions). We did not consider other proposed methods for estimating the effect of treatment on binary outcomes. Imbens suggested that parametric regression models, using either a set of covariates or the propensity score, could be used to develop models to impute the missing potential outcomes. Once these had been imputed, causal outcomes could be estimated directly.⁴⁷ Austin proposed a similar approach, in which tree-based ensemble methods were used for estimating the missing potential outcomes and then estimating the causal treatment effects directly.⁴⁸ Finally, Gutman and Rubin explored the use of two independent splines and multiple imputation for estimating the effects of binary treatments on dichotomous outcomes.⁴⁹ While comparing the performance of these diverse methods merits examination in subsequent research, it is beyond the scope of the current study. The focus of the current study was on describing and evaluating the performance of methods based on full matching for estimating the effect of treatment on binary outcomes. The performance of these methods was then compared with that of several commonly-used propensity-score methods. We refer the interested reader to a paper by Gutman and Rubin comparing the performance of a variety of estimators for estimating treatment effects when outcomes are continuous.⁵⁰

In summary, we found that both IPTW and full matching tended to result in unbiased estimation of odds ratios, relative risks and risk differences when the ATT was the target estimand and the treatment-selection process was weak to moderate. Full matching with a caliper restriction resulted in improved estimation compared to the use of conventional full matching. When the treatment-selection process was strong, both full matching methods and IPTW resulted in biased estimation of the true estimand, even when the propensity score model was correctly specified. Bias was substantially attenuated when full matching with a caliper was employed. When the treatment-selection process was strong and the target estimand was the risk difference then full matching with a caliper restriction resulted in estimates with the lowest bias. However, in the same settings when the target estimand was either the relative risk or the odds ratio then NNM-caliper resulted in estimates with the lowest bias.

Authors’ note

The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. The datasets used for the reported analyses were linked using unique, encoded identifiers and analyzed at the Institute for Clinical Evaluative Sciences (ICES).

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC); this study was supported in part by an operating grant from the Canadian Institutes of Health Research (CIHR) (Funding number: MOP 86508). Dr Stuart’s time was supported by the National Institute of Mental Health, R01MH099010. The EFFECT study was funded by a Canadian Institutes of Health Research (CIHR) Team Grant in Cardiovascular Outcomes Research. Dr Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation.