Quantitative assessment of Cerenkov luminescence for radioguided brain tumor resection surgery

Abstract

Cerenkov luminescence imaging (CLI) is a developing imaging modality that detects radiolabeled molecules via visible light emitted during the radioactive decay process. We used a Monte Carlo based computer simulation to quantitatively investigate CLI compared to direct detection of the ionizing radiation itself as an intraoperative imaging tool for assessment of brain tumor margins. Our brain tumor model consisted of a 1 mm spherical tumor remnant embedded up to 5 mm in depth below the surface of normal brain tissue. Tumor to background contrast ranging from 2:1 to 10:1 were considered. We quantified all decay signals (e^+/−, gamma photon, Cerenkov photons) reaching the brain volume surface. CLI proved to be the most sensitive method for detecting the tumor volume in both imaging and non-imaging strategies as assessed by contrast-to-noise ratio and by receiver operating characteristic output of a channelized Hotelling observer.

1. Introduction

1.1. Cerenkov luminescence imaging

Cerenkov radiation, hereafter referred to as Cerenkov luminescence, is visible light emitted by charged particles that exceed the phase velocity of light in a dielectric, such as tissue (Jelley 1958). In the medical setting, charged particles can be produced by decay of radiolabeled molecules or as secondary products from high energy therapy beams (Axelsson et al 2011). Cerenkov luminescence has a continuous emission spectra with intensity proportional to λ⁻² . For a typical beta-emitting medical radionuclide, 1~100 optical photons are produced for every nuclear decay (Gill et al 2015).

Cerenkov luminescence imaging (CLI) is a relatively new modality (Robertson et al 2009) that involves using a sensitive camera to image Cerenkov luminescence produced by radionuclide decay. CLI has found applications in both preclinical and clinical biomedical settings (Tanha et al 2015). CLI allows straightforward and low-cost optical imaging of radiolabeled molecules. In some cases, these radionuclides (e.g. ⁹⁰Y, an almost pure β⁻ emitter) would otherwise be difficult to image (Nickles et al 2004). CLI harnesses the power and flexibility of small, specific, radiolabeled molecules, many of which are approved for clinical use, and simultaneously liberates the user from the confines of dedicated tomographic nuclear imaging instrumentation.

One of the touted advantages of CLI is the ability to image radiolabeled molecules in settings where a nuclear scan would not be possible. An obvious use is to locate tumor margins during the course of oncologic surgery, and given the abundance of tumor-specific radionuclides (Gulyas and Halldin 2012), this is an appealing application. Radioguided surgery via e^+/− or gamma detection has been actively explored (Hoffman et al 1999, Menard 2011, Bogalhas et al 2008, Povoski et al 2009). Additionally, several groups have also demonstrated instrumentation or feasibility of this concept using Cerenkov luminescence (Holland et al 2011, Liu et al 2012, Thorek et al 2014). A recent review article on this topic has excellently covered some of the most relevant work on this topic (Grootendorst et al 2016). However, none have quantitatively investigated the relative merits of all signals (gamma, x-ray, e^+/−, Cerenkov optical photons) emitted by medical radionuclides in the context of an intraoperative detection task.

1.2 Scope and objective of this report

In this paper, we use computer simulation to perform quantitative investigation of the potential of intraoperative Cerenkov luminescence for guided brain tumor resection. Brain tumor resection is a task where preserving tissue is of the utmost importance and where real-time tumor margin contrast could be of benefit. We assume use of ¹⁸F, a ubiquitous and clinically deployed PET radionuclide, which may be readily conjugated to many targeting molecules (Gulyas and Halldin 2012). We consider the fundamental signals (positron, gamma rays, Cerenkov photons generated by the positron) generated in the tumor, background volume and signals reaching the tissue surface. Our analysis addresses the fundamental physics of detectability of the tumor from these signals and is unencumbered by assumptions of detector efficiency or technology. To evaluate the utility of any signal during a surgical endeavor, we consider two detection tasks: non-imaging and imaging. The non-imaging case is analogous to an intraoperative probe, a wand-like device tipped with a detector that allows the surgeon to identify hotspots of radiopharmaceutical accumulation. The imaging case is analogous to a camera and provides a spatially-resolved map of radionuclide distribution in the field of view.

1.3. Brain tumor resection surgery

Clinical outcomes of resection surgery of glioblastoma are highly dependent on the quality and extent of the tumor resection. It is generally desirable to achieve a total gross resection, defined as no detectable tumor mass on post-operative imaging (Ammirati et al 1987). The literature, collectively, is unambiguous that a more complete tumor resection improves both quality and duration of life (Schulz et al 2012, Sanai and Berger 2008, Wirtz et al 2000, Barbosa et al 2014).

1.4. Intraoperative guidance

Numerous techniques have been developed to provide intraoperative guidance based on imaging or physiological signals. We will briefly describe a few imaging-based strategies for which strong evidence of efficacy, measured by extent of resection and/or progression-free survival, is available. These include: neuronavigation, intraoperative imaging, and fluorescence guidance (Barbosa et al 2014).

Neuronavigation uses an operating room based camera system to track position of surgical instruments and register them to the patient’s pre-operative volumetric imaging scan (typically MRI or CT) (Mezger et al 2013). Neuronavigation makes contrast rich volumetric imaging datasets surgically relevant and is beneficial for improving completeness of tumor resection (Wirtz et al 2000) when deemed advantageous by the surgeon (Willems et al 2006). Accuracy of neuronavigation is diminished as surgery progresses due to brain shift, which is caused by tissue excision, cerebral spinal fluid drainage and edema.

When neuronavigation is paired with intraoperative imaging (via MRI or CT) it may be possible to maintain accuracy, even in the case of brain shift (Barbosa et al 2014). Intraoperative MRI provides the best soft tissue contrast, but is costly and adds the most complex workflow. Intraoperative MRI is supported by moderate to strong evidence based on a comprehensive review (Kubben et al 2011) and a high quality, controlled study which demonstrated a substantial increased extent of resection and patient survival (Senft et al 2011).

Intraoperative fluorescence guidance is accomplished with a surgical microscope fitted with an excitation light source, filter set, and a camera to detect faint or non-visible fluorophores (Nguyen and Tsien 2013). It has the benefit of being low cost, real time, non-ionizing, and minimally disruptive to surgical workflow, and can provide enhanced molecular-based contrast from endogenous or exogenous molecules (Rosenthal et al 2015). One promising contrast agent is aminolevulinic acid (5-ALA, a heme precursor that is converted to protoporphyrin-IX), which preferentially accumulates in highly metabolic cells. A phase-III, multicenter, controlled trial of 270 patients found that patients receiving 5-ALA had more complete tumor resections and progression-free survival twice that of the control group (42% vs 21% at 6 months) (Stummer et al 2006).

The task for the surgeon is demanding: resect completely but minimize damage to surrounding healthy brain tissue. Excessive resection can result in significant morbidity and poor quality of life. There remains an immense need to provide the surgeon with better contrast, in real time, during the procedure. This need is being addressed by development of new imaging technology and more specific contrast agents (Menard 2011). However, none have proven sufficient, as evidenced by survival rates that do not typically exceed one year after initial diagnosis. Even the best outcomes to date result in life increase measured in months rather than years.

2. Materials and methods

2.1. Simulation methods and geometry

All simulations were performed using GAMOS version 5.0.0, a GEANT4-based software package for Monte Carlo simulation of particle and nuclear physics (Agostinelli et al 2003, Arce et al 2008). GAMOS was compiled with the Dartmouth Tissue Optics plugin (Glaser et al 2013). Multiple statistically independent, parallel instances of simulations were run on different processor cores, using GNU Parallel (Tange 2011). Measured optical properties of real brain tissues were used (Yaroslavsky et al 2002). ¹⁸F beta energy spectrum was obtained from the LBNL Isotopes Project: http://ie.lbl.gov/toi.html (Firestone and Ekström 1999). The wavelength range from 400 nm to 800 nm was considered. Both tumor and brain tissue density and atomic properties used are from the ICRP four component soft tissue model (density = 1 g/cm³; composition: %weight/weight H=10, C=11, N=3, O=76) (Berger et al 2005).

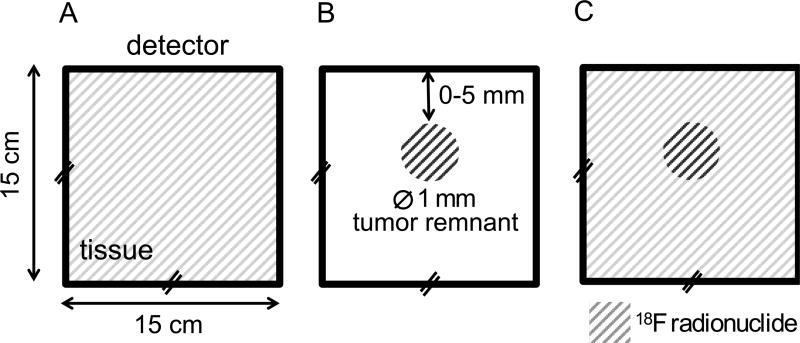
The simulation geometry was intended to recapitulate a brain tumor resection after the obvious tumor has been debulked and a small portion of the tumor tissue may remain. It addresses the scenario where the surgeon is tasked with determining if the margins are clear or if tumor remains in the surgical cavity. The geometry consists of a 15 × 15 × 15 cm³ brain volume containing a 1 mm spherical tumor remnant. Each volume contains radionuclide in different concentrations and activity is first simulated separately (i.e. only activity in background or only activity in tumor remnant as illustrated in figure 1(a)–(b)). The spherical tumor remnant is positioned at increasing depths (0 – 5 mm distance of nearest approach). For each desired configuration of tumor depth and activity ratio, the background and tumor remnant data are scaled appropriately and combined as in figure 1c.

Figure 1.

Geometry for Monte Carlo simulations (not to scale). Background activity distributions (A) and tumor remnant activity distributions (B) were independently simulated. Background (A) and tumor remnant simulations (B) can be scaled and summed to effectively create a tumor remnant in warm background condition (C) with desired tumor remnant:background contrast levels (10:1, 5:1, 3:1, and 2:1 are investigated in this study).

A simulated 15 cm × 15 cm ideal detector placed at the brain volume surface records the position and energy of incident radiation (gamma/x-ray, e^+/−, Cerenkov optical). Radiations generated in the tumor remnant and background volume are recorded separately. One medically-relevant radionuclide, ¹⁸F, was simulated. Tumor-to-background contrast ratios, based on brain tumor specific PET tracers (Menard 2011), ranging from 2:1 (low contrast) to 10:1 (high contrast) were considered.

For the geometry consisting of only a warm background (figure 1a), N = 10⁷ events were simulated (10 statistically independent simulations of 10⁶ decays). For the geometry containing only the tumor remnant (figure 1b), N = 10⁷ events (10 simulations × 10⁶ decays) were simulated per condition (defined as given tumor depth, radionuclide, and tissue optical property). Data are first presented as quanta of emitted radiation (photons or particles) per decay, in order to gain a sense of the strength of each signal, and then scaled to relevant, clinically-achievable activity levels.

2.2. Optical properties of brain tissue

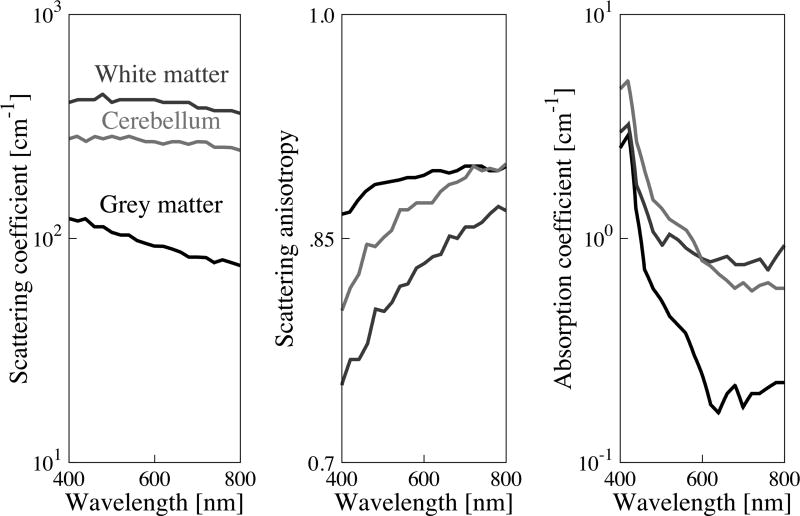
Brain tissue optical property spectra (cerebellum, grey brain matter, white brain matter) were obtained from Yaroslavsky et al 2002. Simulations were also run using optical properties for the pons and thalamus but results are not shown as they did not greatly different from those of grey matter. Additionally, tumors within these regions are rare (Ostrom et al 2013) and difficult to access owing to their deep location. Figure 2 shows the optical properties used in the simulations. A constant refractive index of n = 1.4 was assumed for all wavelengths due to lack of available spectral data for human brain. The refractive index of tissue is dominated by properties of water and can be approximated according to: n = 1.514 −(1.514 – 1.33)W, where W is the fraction of water content (Jacques 2013). W can range from 0.49–0.8 in healthy and diseased brain tissue, corresponding to refractive indices ranging from n = 1.3951 to 1.4470, a variation of ~3.6% (Biswas and Luu 2009). Given that the refractive index of water varies <1.2% over the 400 – 800 nm wavelength range (Daimon and Masumura 2007), we reasoned that uncertainty in n due to water content is large compared to wavelength dependence and therefore elected to use a constant value.

Figure 2.

Optical properties of brain tissues used in simulation are based on measured values from literature (Yaroslavsky et al 2002). Grey shades are consistent across plots.

2.3. Data analysis

Data were processed using custom software developed in MATLAB. Radiation quanta reaching the detector were grouped based on type (gamma/x-ray, e^+/−, Cerenkov optical) and whether they were a primary or secondary radiation. For the purpose of this study, which exclusively used ¹⁸F, we defined a primary radiation as a positron, positron-generated Cerenkov photon, or gamma annihilation photon. All other radiations were defined as secondary. Statistical uncertainty was determined by computing the standard deviation of radiation quanta from statistically independent simulations, seeded with different random numbers.

2.4. Calculation of contrast-to-noise ratio to quantify detectability

Detectability of a hot tumor remnant in a warm background is quantified with the contrast to noise ratio (CNR) metric, according to equation 1. For a surgical scenario we assume a 10 second integration time, 50 Bq/mm³ background activity concentration, and a typical range (2:1 to 10:1) of tumor:background ratios (Menard 2011).

CNR is computed as the ratio of signal originating in the tumor remnant and expected uncertainty in counts from background:

$$\mathit{\text{CNR}}=\frac{S_{\mathit{\text{tumor}}}}{{\sigma }_{\mathit{\text{background}}}}$$ (1)

For Poisson statistics, uncertainty is the square root of total background counts from a single measurement:

$${\sigma }_{\mathit{\text{background}}}=\sqrt{S_{\mathit{\text{background}}}}$$ (2)

Monte Carlo simulations provide a probability distribution of radiation reaching the detector from a given decay event. Some further computation, detailed in equation 3–equation 11, is required to scale these data into meaningful quantities of signal reaching a detector for a given observation time, radiotracer uptake and contrast ratio.

The signal reaching the detector from either background or tumor are the product of an efficiency term (E), activity (A) and total observation time (T).

$$S_{\mathit{\text{background}}}[\mathit{\text{counts}}]=E_{\mathit{\text{background}}}[\frac{\mathit{\text{counts detected}}}{\#\mathit{\text{decay events}}}]\times A_{\mathit{\text{background}}}[\mathit{\text{Bq}}]\times T[s]$$ (3)

$$S_{\mathit{\text{tumor}}}[\mathit{\text{counts}}]=E_{\mathit{\text{tumor}}}[\frac{\mathit{\text{counts detected}}}{\#\mathit{\text{decay events}}}]\times A_{\mathit{\text{tumor}}}[\mathit{\text{Bq}}]\times T[s]$$ (4)

Efficiency terms E_background and E_tumor are determined from the Monte Carlo simulation and are the maximum theoretical efficiencies for detecting various signals (gamma, e^+/−, Cerenkov photons) from tumor or background, given transport losses through the tissue volume and geometric efficiency. E_background is provided in table 1 and E_tumor is provided in figure 3.

$$E_{\mathit{\text{background}}}=\frac{\mathit{\text{counts detected}}}{\#\mathit{\text{decay events}}}{E}_{\mathit{\text{tumor}}}=\frac{\mathit{\text{counts detected}}}{\#\mathit{\text{decay events}}}$$ (5)

Table 1.

Radiation events generated in the background and detected (× 10 ⁻⁵) in a 1 cm² detector.

Generated [events / decay]
	γ and x-ray	e+/−	Cerenkov photons (400 – 800 nm)
Primary	1.95	0.98	2.72
Secondary	0.01	1.74	0.55
Total	1.96	2.72	3.27

Detected [events × 10−5 / decay]
γ and x-ray	e+/−	Cerenkov photons (400 – 800 nm)
		Grey Matter	White Matter	Cerebellum
187	0.42	24.9	9.26	9.62
0.18	0.38	4.89	1.85	1.81
187.2	0.80	29.8	11.1	11.4

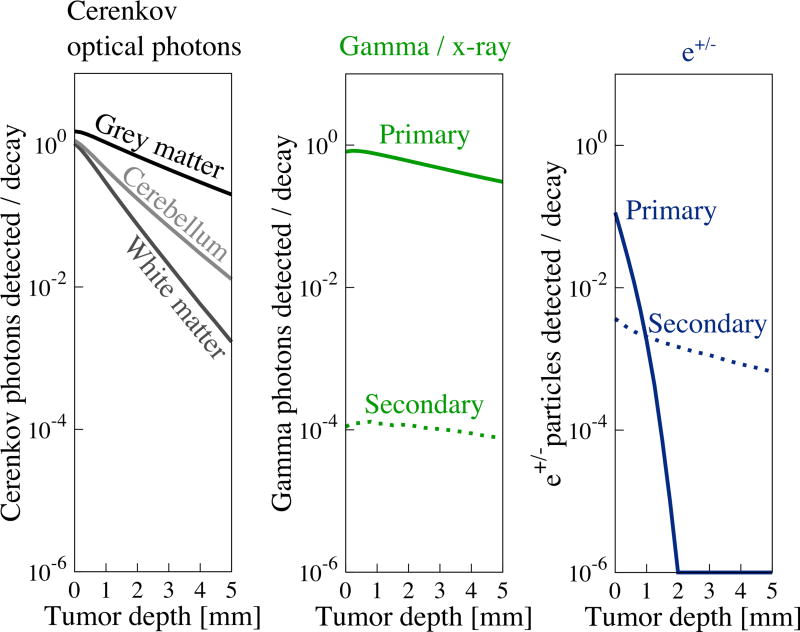
Figure 3.

Strength of signals reaching the detector from activity in the tumor remnant are depth dependent. The strength of all signals decreases with depth due to attenuation and reduction in solid angle. Gamma photons are least attenuated with depth, while e⁺ particles are most attenuated. Detection of Cerenkov optical photons depends on tissue optical properties. Grey matter, which has the lowest µ_a and µ_s’, is least depth sensitive, while white matter, which has higher µ_a and µ_s’ is more sensitive to depth.

Next, the total number of decays occurring in the volumes $(V_{\mathit{\text{tumor}}}=\frac{1}{6}\pi {\text{ mm}}^3,V_{\mathit{\text{background}}}={(150\mathit{\text{ mm}})}^3)$ given a background activity concentration of $C_{\mathit{\text{background}}}=50\frac{\text{Bq}}{{\text{mm}}^3}$, and tumor:background uptake ratio $U=\frac{C_{\mathit{\text{tumor}}}}{C_{\mathit{\text{background}}}}$ = 2 to 10 are computed:

$$A_{\mathit{\text{tumor}}}[\mathit{\text{Bq}}]=V_{\mathit{\text{tumor}}}[{\mathit{\text{mm}}}^3]\times (U-1)\times C_{\mathit{\text{background}}}[\frac{\mathit{\text{Bq}}}{{\mathit{\text{mm}}}^3}]$$ (6)

$$A_{\mathit{\text{background}}}[\mathit{\text{Bq}}]=V_{\mathit{\text{background}}}[{\mathit{\text{mm}}}^3]\times C_{\mathit{\text{background}}}[\frac{\mathit{\text{Bq}}}{{\mathit{\text{mm}}}^3}]$$ (7)

However, because the task is to determine if any hot tumor remnant exists in a warm background, we would actually determine S_tumor and σ by making two measurements: S_{tumor+background} and S_backgroundand computing their difference.

$$\mathit{\text{CNR}}=\frac{S_{\mathit{\text{tumor}}+\mathit{\text{background}}}-S_{\mathit{\text{background}}}}{\sigma }$$ (8)

Because we had to make two measurements to estimate S_tumor, each measurement contributes additional uncertainty that is accounted for as follows:

$${\sigma }_{\mathit{\text{tumor}}+\mathit{\text{background}}}=\sqrt{S_{\mathit{\text{tumor}}}+S_{\mathit{\text{background}}}}$$ (9)

Consequently the total uncertainty is:

$$\sigma =\sqrt{{{\sigma }_{\mathit{\text{background}}}}^2+{{\sigma }_{\mathit{\text{tumor}}+\mathit{\text{background}}}}^2}$$ (10)

The final equation to compute CNR reduces to:

$$\text{CNR}=\frac{{\mathrm{S}}_{\text{tumor}}}{\sqrt{2\ast {\mathrm{S}}_{\text{background}}+{\mathrm{S}}_{\text{tumor}}}}$$ (11)

2.5. Quantitative assessment of surgical task using imaging

In order to quantitatively assess detection limits in the imaging case, we used an ideal numerical observer (Barrett et al 1993, Eckstein et al 2000, Myers 2000). Functions from the Image Quality Toolbox (Kupinski 2001) were used to implement the numerical observer. An approach using Laguerre-Gauss channels, similar to Park et al 2007, was followed. Multiple statistically independent, noisy realizations of background and tumor were created. Realizations were created efficiently as follows: 1) 2D histograms with pixels corresponding to 1 mm² (150 × 150 pixels) of signals impinging on the detector were created from Monte Carlo simulation, 2) the histograms were fit to a 2D Gaussian function, 3) expected counts reaching the detector were computed by multiplying an efficiency term for each signal by the number of decays, 4) the Gaussian functions of background and tumor were sampled according to an expected number of detector counts and random Poisson noise was added to each realization, and finally, 5) pairs of noisy realizations with signal present and absent were fed into a channelized Hotelling observer to generate receiver-operating characteristics. Five Laguerre-Gauss templates with width parameter of 4 pixels were used as channels.

3. Results

Overview: The source and fate of every ¹⁸F decay product generated in the simulation volume was recorded and tabulated. Radiation generated in the “warm” background only condition (figure 1(a)) and the fraction of that radiation reaching the detector are recorded in table 1. Radiations generated in the “hot” tumor only condition (figure 1(b)), are shown in table 2. Signals reaching the detector that were generated in the “hot” tumor only condition are plotted in figures 3 and 4 and show a strong depth dependence. Finally, in order to understand possible spectral information content, energy spectra of all signals (in all materials and over the depth range studied) are plotted in figure 5.

Table 2.

Radiations generated from activity localized to tumor volume. Radiations scored in table 2 have statistical variability of < ±0.1% (primary) or <±5% (secondary). Range of values is due to the different depths simulated for tumors.

	Generated from decays occurring in tumor volume [events / decay]
	γ and x-ray	e+/−	Cerenkov photons
Primary	1.73 to 1.99	0.98	2.54 to 2.73
Secondary	0.008 to 0.011	1.22 to 1.65	0.38 to 0.52
Total	1.74 to 2.00	2.20 to 2.63	2.92 to 3.25

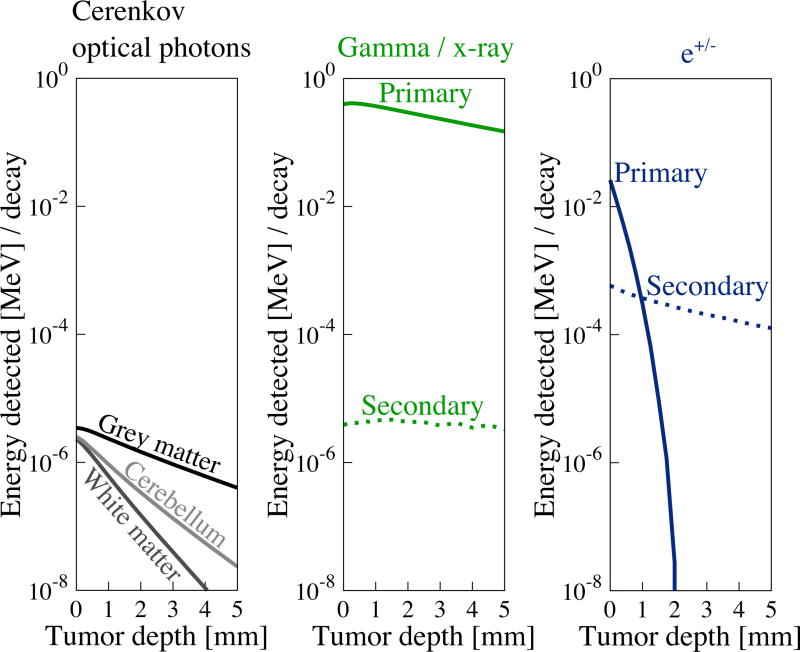
Figure 4.

Energy of signals reaching the detector from activity in the tumor remnant are depth dependent. This figure demonstrates the potential for each radiation signal to generate charge carriers in a detector. Gamma photons, the most energetic, least attenuated signal, provide the greatest energy to be detected at all depths. Electrons and positrons provide a relatively energetic signal, but are rapidly attenuated with increasing depth. Optical photons provide the least energy but are less depth sensitive than the e^+/− signal.

Figure 5.

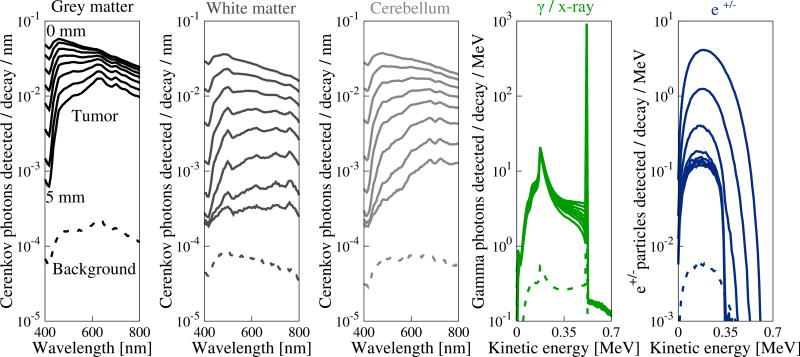
Radiation events detected from signals reaching the tissue surface are plotted as a function of wavelength (Cerenkov optical) or energy and are in units of events detected / decay / MeV or events detected / decay / nm. Sets of curves are variations of the energy spectra over the 0 – 5 mm depth range. Dashed curves on each plot are decays events originating in the background whereas solid curves are from decay events occurring in the tumor.

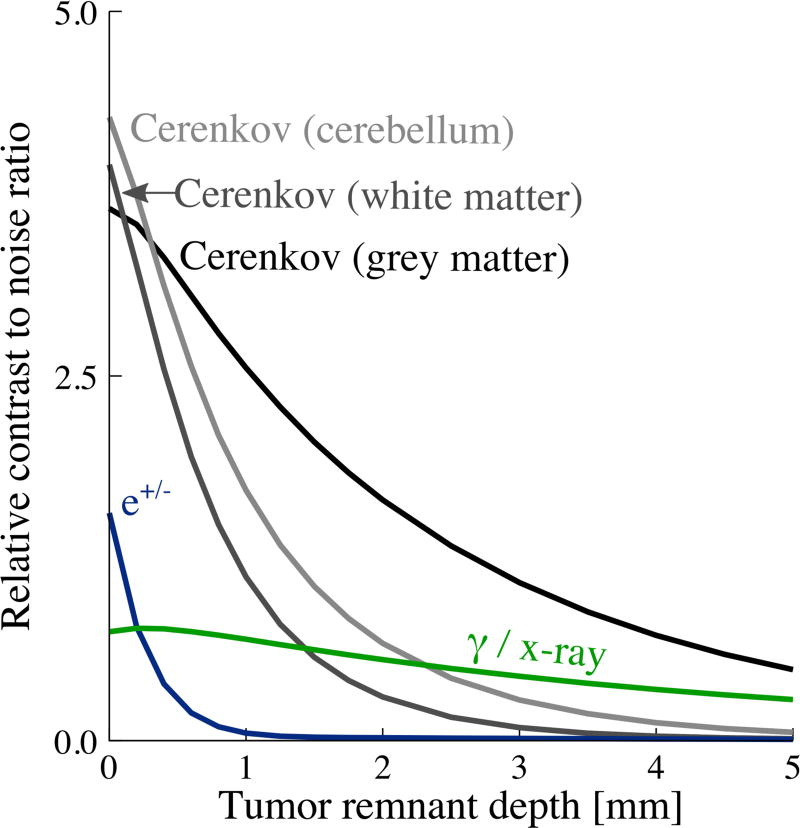
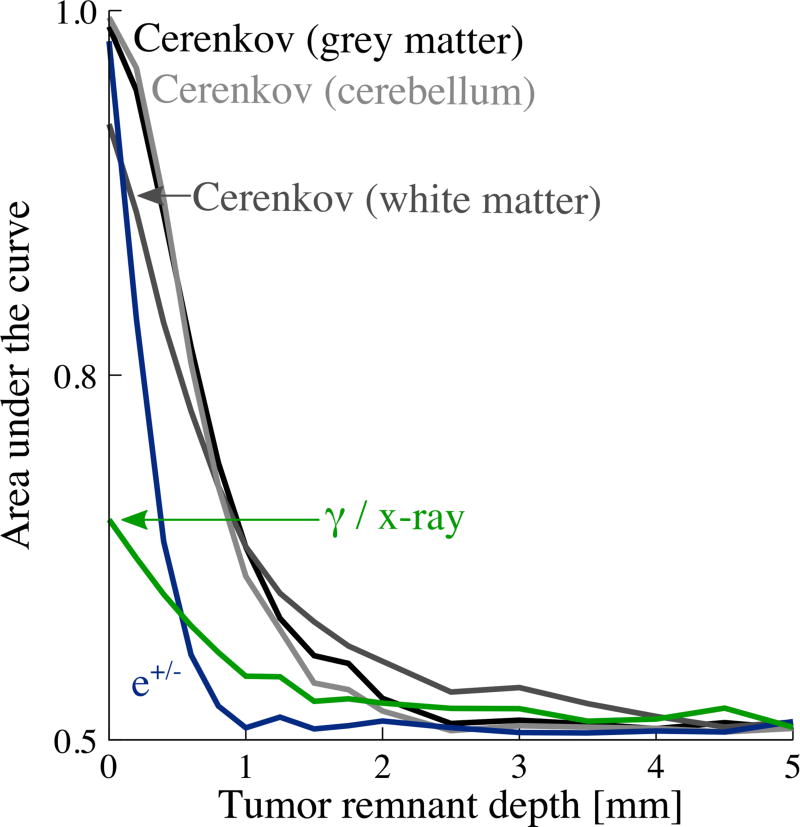
To quantify the diagnostic power of these signals, two figures of merit were computed. CNR, plotted in figure 6, addresses a scenario where a 1 cm × 1 cm non-imaging detector (similar to a surgical gamma probe) was used. We also evaluated a scenario in which the 15 cm × 15 cm field of view was captured with an imaging detector. In this case, images were analyzed using a numerical observer that produces a receiver-operating characteristic (ROC). The ROC demonstrates the performance of a binary classifier as a discrimination threshold is varied (Barrett et al 1993). The ROC was integrated and is presented as area-under-the-curve (AUC). AUC is plotted as a function of tumor depth for each signal in figure 8.

Figure 6.

Relative CNR for a 1 cm × 1 cm non-imaging detector, 10 s integration time, 10:1 tumor : background contrast ratio and 50 Bq/mm³ background activity; 1 mm diameter spherical tumor in 15 cm tissue volume cube.

Figure 8.

Area-under-the-curve (AUC) vs depth for Tumor detection with an imaging detector assessed with channelized Hoteling observer. For a 1 cm × 1 cm non-imaging detector, 60 s integration time, 10:1 tumor:background contrast ratio and 50 Bq/mm³ background activity; 1 mm diameter spherical tumor in 15 cm tissue volume cube.

3.1. Signals created in background volume and reaching detector

In a realistic surgical setting, radiotracer will localize to normal surrounding tissue in a diffuse and nonspecific manner. This background activity carries no information helpful in detecting the tumor yet produces an indistinguishable signal at the detector surface. Signals from the background interfere with detection of the “hot” tumor remnant by contributing noise in the form of additional measurement uncertainty.

Table 1 separately shows radiation generated in the warm background volume (figure 1(a)) and quantity detected by a 1 cm × 1 cm detector centered on the volume. All values in table 1 have statistical variability of < ±0.5%, calculated by the standard deviation of 10 statistically independent simulations. As expected, ~2 annihilation photons, ~1 beta particle and 2.7 Cerenkov photons (Gill et al 2015) are created per ¹⁸F decay (branching ratio to positron emission is 0.967) (Eckerman and Endo 1989). The observed gamma signal of 187 × 10–⁵ photons/decay agrees well with a rough approximation accounting for fractional surface area of the cube alone (as a surrogate or solid angle): $1.96\frac{\gamma \text{ emitted}}{\mathit{\text{decay}}}\times \frac{1\mathit{\text{ detector}}}{6\mathit{\text{ sides}}}\times \frac{1c{m}^2\mathit{\text{ window}}}{{(15\mathit{\text{cm}})}^2\mathit{\text{detector}}}=144\times {10}^{-5}\frac{\mathit{\text{detected}}}{\mathit{\text{decay}}}$. Abundant electrons and Cerenkov photons are also produced from secondary interactions.

3.2. Radiation signals created from radionuclide localized to the tumor volume and reaching detector

Activity localized to the tumor creates signal both within and external to the tumor volume, all of which potentially contribute information to detect the tumor. Due to the proximity of the tumor volume to the surface of the tissue volume, radiation signals generated from activity in the tumor remnant will exhibit a depth dependence. The number of radiations generated increased slightly with tumor depth, owing to greater envelopment of the tumor and, consequently, increased secondary interactions in the surrounding medium. Table 2 quantifies the fundamental radiation signals generated due to decays in the tumor remnant volume, over the depth range of the tumor.

Signals generated in the tumor have a moderate depth dependence, while those reaching the detector are highly depth-dependent, as revealed by figure 3. Gamma annihilation photons are essentially un-attenuated with depth and data are well approximated by considering solid angle alone (not shown). e^+/− particles are strongly attenuated and none were detected when the tumor depth exceeded 2 mm. Cerenkov optical photons were moderately attenuated with depth, depending on the optical properties of the medium. Secondary Cerenkov optical photons are not shown as they appeared with a frequency of < 10⁻⁶ photons / decay. White brain matter, which has the highest scattering and a high absorption coefficient, attenuates the optical signal most rapidly. Finally, the depth profile of secondary particles, regardless of source, is essentially flat due to these particles originating diffusely from the background volume and therefore having little depth dependence.

Cerenkov photons are the most abundant signal reaching the tissue surface when the radionuclide is located at depths < 2 mm. At depths exceeding 3 mm, gamma photons are most abundant due to Cerenkov photon attenuation.

Although, under shot noise-limited circumstances, quanta of detected radiations originating from the tumor will fundamentally determine its detectability, this is unlikely to be the case with real detectors and during a real detection task. In order to account for the fact that not all quanta will produce the same number of charge carriers, data from figure 3 are plotted in figure 4 as energy available for detection from each signal type as a function of tumor remnant depth.

Gamma annihilation photons provide the greatest energy for detection at the surface. Beta particles provide ~10¹ less energy than gamma photons when located near the surface. Cerenkov photons provide ~10⁵ less energy at the surface compared to gamma photons.

A comparison of figure 3 and figure 4 shows that the most abundant signal reaching the surface, by quanta, are gamma and Cerenkov optical photons (at shallow depths). However, gamma annihilation photons deliver, by orders of magnitude, the most energy to the surface to be detected, followed by e^+/− (at shallow depths), followed by Cerenkov optical photons.

3.3. Energy spectra for signals originating in tumor and background

Detected energy spectra are shaped by absorption that occurs as the signal propagates through the phantom. Figure 5 reveals energy spectra for signals reaching a 15 cm × 15 cm field-of-view at the brain volume surface from the tumor (from a subset of various depths). The corresponding energy spectra of background events is plotted as a dashed line.

Detected Cerenkov optical photon spectra exhibit features that can be related to their optical property spectra. The grey matter detection spectra (figure 5), for example, strongly resemble an inverted plot of its absorption spectrum (figure 2). The gamma spectra demonstrate expected features including peaks at 0.511 MeV, the energy of annihilation photons, and at 0.17 MeV Compton edge, corresponding to a 180-degree Compton-scattered gamma photon. Counts appearing at > 0.511 MeV correspond to positrons that annihilated in flight, which occurs with ~0.5% probability for ¹⁸F positrons in water (Azuelos and Kitching 1976). Beta energy spectra at shallow depths strongly resemble the ¹⁸F beta emission spectra, which is peaked at ~250 keV.

All signals are attenuated with depth, though gamma photons and e^+/− particles exhibit less obvious changes in spectral shape. Cerenkov optical spectra, in all tissues, shift dramatically to longer wavelengths with increased tumor depth. This effect is caused by absorption that increases strongly at shorter wavelengths (figure 2) and λ⁻² weighting of the Cerenkov emission spectrum. Overall, e^+/− particles and Cerenkov photons are most depth sensitive.

3.4. Detectability of tumor in warm background

CNR is an image quality metric that reflects the difference between a desired signal and its surrounding and is scaled by the uncertainty in that observation. Activity ratios and resulting quantities of activity in the tumor remnant and background volume are listed in table 3.

Table 3.

Activity concentration ratios simulated and resulting computed activities in a given tissue volume.

Activity ratio, $U[\frac{{\mathit{\text{CA}}}_{\mathit{\text{tumor}}}}{{\mathit{\text{CA}}}_{\mathit{\text{background}}}}]$	Activity in 1 mm3 tumor, Atumor [Bq]	Activity in 15 cm × 15 cm × 15 cm background, Abackground [MBq]	Activity tumor / Activity background [×10−6]
2:1	26	169	0.15
3:1	52	169	0.31
5:1	105	169	0.62
10:1	236	169	1.40

We computed CNR for a range of contrast ratios (3:1 to 10:1) and found that it scaled with integration time, contrast ratio, or background activity. The relative relationships of different radiation signals did not change significantly and therefore only one representative data set is shown in figure 6.

Figure 6 demonstrates that CNR decreases with increasing tumor remnant depth for all signals. This metric is dominated by background noise, owing to A_background ≫ A_tumor. Cerenkov photons in grey matter, the least absorbing tissue, provide the highest CNR at all but the shallowest depths. White matter and cerebellar tissue, which are more absorbing, have slightly better CNR at the shallowest depths owing to higher scattering which favors collection of photons not directly emitted toward the detector. Beta particles provide moderate CNR at very shallow depths < 0.5 mm. Gamma photons provide relatively low, yet consistent CNR, that is insensitive to depth and favorable compared to Cerenkov photons at depths > ~1.5 mm.

Figure 7 shows sample noisy realizations of background and tumor alone conditions for cerebellar tissue with a 10:1 tumor:background ratio and 50 Bq/mm³ background activity concentration. Background image colormaps range linearly from approximate maximum to one-third maximum value. The gamma background image has obvious vignetting because it is dominated by solid angle effects. Photon and e^+/−background images have less of this effect because the signal is coming from shallower depths. Tumor images demonstrate the spread of the respective radiation signals at the detector surface. Background and tumor images are combined to be evaluated by the numerical observer.

Figure 7.

Example realizations of respective decay signals in counts per second (CPS) per mm² for background alone and tumor alone at 0 and 1 mm depths. Images are 50 × 50 pixels and represent the 15 × 15 cm detector. Tumor:background ratio is 10:1. Background activity concentration is 50 Bq/mm³.

Figure 8 shows the area-under-the-curve (AUC) for the scenario where an imaging detector captures the 15 cm × 15 cm field-of-view under the following conditions: 60 s integration time, 10:1 contrast ratio, and 50 Bq/mm³ background activity. AUC of 1 indicates perfect specificity and sensitivity (100% true positives) while 0.5 indicates discriminating power no better than guessing. The results provided do not necessarily reflect the absolute ability of a human observer to detect a tumor. This would require calibration with a set of human observers and additional noise terms to be added into our calculation. However, it is useful for making relative quantitative comparisons of one source of imaged signal to another.

Cerenkov optical photons provide the most discrimination power for depths from 0 to ~2 mm, and thereafter converge with that of gamma photons. For depths <0.5 mm, the e^+/− signal also performs well. As depth increases, AUC for e^+/− falls most rapidly, followed by Cerenkov photons then gamma photons.

4. Discussion

The purpose of this study was to quantitatively evaluate the relative merits of different decay signals emitted from ¹⁸F during a brain tumor remnant detection task. We considered both imaging and nonimaging detection strategies. To evaluate the detectability of a tumor, we computed two quantitative metrics: CNR and AUC from a numerical observer.

4.1. Source of decay signals and role of “secondary” radiations

Each ¹⁸F decay to ¹⁸O produces ~1 positron which generates ~2.7 Cerenkov optical photons as it propagates through tissue, eventually combining with a free electron and annihilating to produce 2 gamma annihilation photons. Each of these three signals, if originating from the tumor remnant, provides a “primary” signal that is relatively well localized to the targeted tissue. Additionally, the positron and gamma photons will produce a shower of “secondary” x-rays and electrons, via ionization interactions in the surrounding medium. Though also potentially providing useful signal for tumor detection, “secondary” interactions, occurring at a distance, will tend to degrade localizability of the tumor.

The data obtained from the simulation allows us to distinguish “primary” from “secondary” interactions and, though moderate numbers of secondary radiations (10⁻² γ / x-ray, 1 e^+/−, and 0.5 Cerenkov optical /decay) are generated in the background (table 2), contribution to signal on the detector (figure 3) is minimal (10⁻⁴, 10⁻³, < 10⁻⁶ /decay, respectively).

4.2. Relative merits of each decay signal

Gamma annihilation photons

The highly penetrating nature of energetic photons is both beneficial and detrimental to a task aimed at discriminating a small, 1 mm tumor remnant from a large bed of normal surrounding tissue. Annihilation photons are the most penetrating radiation and the greatest fraction thereof reach the surface to be detected. Gamma photon background signal is also efficiently detected and uncertainty introduced by this signal dominates the task performance metrics. Gamma annihilation photons and their secondary products carry some depth-dependent spectral information content, as demonstrated by the decrease in 0.511 MeV photopeak and increase in multiple Compton scatter region between gamma signals originating from tumors at different depths (figure 5).

Annihilation photons are the most energetic radiation events available for detection (figure 4) and have the potential to produce the greatest number of charge carriers. This property is favorable for overcoming the noise floor in real radiation detectors, where spontaneous production of charge carriers will fundamentally limit the smallest signal detectable. The penetrating nature of energetic photons requires thick, dense detectors with high stopping power in order to fully convert these energetic photons to electronically measurable charge carriers.

Positrons

Positrons from ¹⁸F are energetic (634 keV endpoint), quickly shed energy and have a short range in tissue. These properties reduce both the tumor and background signal and fundamentally limit the maximum depth from which any ¹⁸F positron decay signal can be detected. The tradeoff between attenuating the tumor signal and reducing the background signal creates favorable conditions for sensitive detection of radionuclide decay at shallow depths (< 0.5 mm). Positrons exhibit minimal changes in spectral shape with increased depth (figure 5).

Unlike gamma photon detectors, even relatively thin detectors can efficiently capture the entire positron energy due to rapid energy loss in matter. High energy content is favorable for producing abundant charge carriers in real detectors and improving SNR.

The relative improved performance of e^+/− in the AUC vs the CNR metric is likely due to the limited spatial spread of positrons reaching the detector (see figure 8), which is advantageous in the imaging case.

Cerenkov optical photons

Cerenkov optical photons are moderately attenuated (depending on optical properties) and also have a moderate background signal. Because they are produced along the track of the positron (and high energy secondary charged particles) and are strongly scattered in biological tissues, they tend to be more spatially diffuse than other radiation signals studies. Cerenkov optical photons produce large shifts in detected spectra shape, depending on tumor depth and tissue type (figure 5).

Cerenkov optical photons are readily absorbed and converted to charge carriers in a photodetector. However, they carry the least energy content of any radiation signal studied, making the most challenging case for gaining SNR with real detectors.

Both CNR and AUC show that the Cerenkov signal is most sensitive for the tumor remnant detection task at depths < 2 mm, and is significantly better than the signal from e^+/− particles at depths greater than 0.5 mm. Grey matter and cerebellar tissue are most favorable for detecting the tumor and white matter is least, owing to high scattering and absorbing properties.

4.3 Limitations

Our study has several limitations including use of an ideal detector, uncertainty in optical properties, simulation geometry and evaluation of only a single radionuclide.

Quantum efficiency and detector: To forego the need to select a specific detector and geometry, and make assumptions of noise characteristics, we elected to use an ideal detector. The ideal detector has perfect efficiency, perfect energy and spatial resolution, and is noiseless. This is not without drawback as it unfairly gives equal weight to all signals reaching the detector, regardless of energy content. However, by providing fundamental signals reaching the surface, the reader could make further assumptions about detection efficiency and noise to consider a more realistic detector, if desired. Optical properties: Because the Cerenkov signal is highly dependent on optical properties of the medium, our results will only be as reliable as the accuracy of the optical properties. These optical properties are difficult to measure and can vary spatially and in time, even within the same tissue type. There is also variation in the reported measurements of these quantities (Yaroslavsky et al 2002, Gebhart et al 2006). However, the range of properties considered here should cover the possible values found in a medical or surgical situation. Geometry: The brain tumor simulation geometry is roughly the volume of a real brain but the square shape is not accurate. Furthermore, the background volume is homogeneous, having no variations in optical properties, density or atomic composition. Radionuclide uptake also is assumed uniform in both the tumor and background volumes. Radionuclide: The present study has been limited to use of only one radionuclide, ¹⁸F. Other brain tumor specific PET tracers based on radionuclides such as ¹¹C also exist and were not evaluated. ¹⁸F is a relatively weak source of Cerenkov luminescence and ¹¹C, while it has a short half-life, produces ~5 times more visible light per decay (Gill et al 2015). However the vast majority of approved PET radiotracers are based on ¹⁸F, hence it was the focus of this study.

4.4 Summary and future directions

All signals, to some extent, encode source depth information in their spectral signal and there is likely potential for improved depth sensitivity by using spectral information of one or more signals. Future work will evaluate the possibility of gaining depth information using one or more radiation signals as well as designing and testing a surgical Cerenkov detector.

Our data suggest that Cerenkov luminescence from radiolabeled tumor-specific molecules could be a potential source of contrast for surgical resection. We demonstrated that at depths < 2 mm, Cerenkov luminescence from ¹⁸F provides a more sensitive means for tumor detection, compared to e^+/− particles or gamma photons.

Bringing CLI into the surgical theatre will have its own unique set of challenges. Sensitive optical detectors necessary for CLI are overwhelmed in ambient light conditions that range from 10⁻¹ to 10⁻³ W/cm² and are much greater than the Cerenkov signal (10⁻⁸ to 10⁻¹² W/cm²) (Glaser et al 2012). Both active and passive means could potentially ameliorate this problem, which has also been encountered and addressed in intraoperative fluorescence imaging (DSouza et al 2016).

Passive means include physical barriers such as: endoscopy, where the body acts as the primary light shield; a dedicated light-shielded operating room that can be completely blackened; or physical draping of the patient and surgical field with light shielding fabric; optical notch filters combined with spectrally well-defined room lighting.

Active means rely on modulation of the excitation source and gating the detector. These have been demonstrated for fluorescence imaging (Sexton et al 2013, Zhu et al 2014) and CLI of radiotherapy beams (Glaser et al 2012) in ambient light conditions. However, they cannot be applied to imaging Cerenkov luminescence, which is emitted unpredictably. We propose a slightly different approach: modulating the room lighting and gating detector acquisition to the ambient light off phase. This could allow Cerenkov sensing in an apparently lighted room. All other sources of light (surgical monitoring equipment, leakage of outside room light, fluorescent/phosphorescent objects) would need to be tightly controlled.

It is likely that a combination of both active and passive means will be necessary to attenuate ambient lighting conditions by a factor of 10⁶ to 10¹² necessary to achieve reasonable signal-to-background ratios.